3.1. Dataset Acquisition
Physionet, also known as “Research Resources for Complex Physiologic Signals”, is a repository of extensive clinical and physiological data samples. The dataset, published under the Physionet CINC challenge 2016, contains PCG recordings ranging from 5 to 100 s, recorded under clinical or non-clinical conditions [
43]. The dataset is a collection of eight independent heart sound recording datasets referenced in previous research and collected through various clinical and non-clinical settings. For simplicity, all the individual datasets are labeled ‘a’ through ‘i’ [
11].
The PCG data sample recordings available in the challenge were collected from 1072 patients, along with information on their heart conditions. More than one recording sample is available from a single patient, as these were recorded from different chest locations as mentioned above; therefore, the overall available recordings are 4430. Additionally, the data sample is labeled with one of two values: abnormal or normal. Therefore, this qualifies the dataset for training the supervised machine learning classification model.
Figure 4 and
Figure 5 display wave plots of normal and abnormal patient PCG samples from the dataset. Moreover, these figures display the harmonic–percussive source separation (HPSS), where harmonic and percussive sources will be further processed to extract the features from the presented PCG files for input into the ANN. The primary requirement of the challenge was to segment each sample and then develop a model to automatically classify the PCG recording as normal or abnormal. Additionally, the effectiveness of the submitted solutions was evaluated based on the sensitivity, specificity, and accuracy of the model.
Moreover, the dataset has been divided into training and test datasets, which are mutually exclusive based on the patient records. The training dataset contains the recordings from 764 patients, with 3153 recordings. The test dataset contains the mutually exclusive records from datasets ‘b’ through ‘e’ and a complete dataset from the ‘g’ and ‘i’ datasets, consisting of 308 patients with 1277 recordings.
Table 3 highlights the training and test dataset record statistics [
29]:
Based on the research analysis from the results reported in [
29], datasets ‘b’ and ‘c’ contain the highest number of unsure recordings in both the training and test datasets. Here, the “unsure” recording label refers to audio with poor signal quality, but the dataset still contains a label for it, i.e., abnormal or normal. Also, training sets ‘a’, ‘c’, and ‘d’ contain the most abnormal cases, while training sets ‘b’, ‘d’, ‘e’, and ‘f’ contain the most normal cases. As reported in [
11], the recordings labeled as abnormal may include the following pathologies: innocent or benign murmurs, aortic disease, coronary artery disease, mitral valve prolapse, and miscellaneous pathological conditions. Moreover, under pathologic recordings, the following conditions are mentioned: cardiomyopathies, congenital heart defects, arrhythmia, or valvular diseases. However, these are not specifically mentioned for each patient record.
Our study specifically excluded datasets ‘b’ and ‘c’ due to a high prevalence of recordings marked as “unsure,” which indicates poor signal quality. According to the challenge data documentation, recordings labeled as ‘unsure’ are typically characterized by significant noise and artifacts, which can compromise the reliability of machine learning models when used for classification tasks. This work chose to exclude these subsets to ensure that the training data provided a cleaner and more consistent signal, which is crucial for the robustness of our classification model. Therefore, to accommodate the optimal proportion of the abnormal and normal cases for the neural network training and to avoid overfitting, this research will use the composition of the original datasets, as mentioned in
Table 4. However, the categorizations of unsure signals are highlighted in
Table 5 for analysis purposes to compose a balanced dataset, while for training the model, the audio signals identified as “unsure” are included in the training, along with their designated label of abnormal or normal. Similarly, the test dataset also included the unsure records for testing the model after training.
This selection of datasets for the training of the model arguably yields a few advantages:
- (a)
Through considering a training dataset with less than 10.00% of unsure recordings (i.e., dropping training datasets ‘b’ and ‘c’), training a machine learning model with higher accuracy will become much easier. Also, this research did not segment the dataset recordings, but instead directly worked on the short-term features. This reduction in unsure recordings by 3.73% facilitates more effective training of the machine learning model. This led to removing 137 patient records (521 recordings) from the training dataset and 59 patient records (219 recordings) from the test dataset.
- (b)
With the exclusion of training datasets ‘b’ and ‘c’, the training and test datasets’ overall composition changed toward a more balanced set. As a result, in the training dataset, the abnormal recordings increased from 18.10% to 39.71%, and normal recordings decreased from 73.00% to 60.29%. It should be noted that 8.80% of the unsure recordings were merged into abnormal or normal classes as per the labels mentioned in the original dataset. Similarly, in the test dataset, the abnormal recordings increased from 12.00% to 36.00%, while normal recordings decreased from 77.10% to 64.00%. As in the training dataset, 10.90% of the unsure recordings of the test dataset were merged into abnormal or normal classes as per the labels mentioned in the original dataset.
- (c)
With the dataset now more balanced between normal and abnormal recordings, this should discourage the neural network from overfitting the model concerning normal heart recordings and lead it toward an effective solution. Although these conditions will not prevent the model from overfitting, they will help reduce the likelihood of model overfitting.
Moreover, based on the new dataset composition, this work considered the following dataset-wise pathologies [
11].
3.2. Feature Extraction and Selection
Based on the literature survey, the proposed work skipped the segmentation phase, based on the arguments of its high complexity and computation. Additionally, the research conducted by [
44,
45,
46,
47] presented valid arguments for skipping the segmentation step. The selected heart sound recording datasets from the Physionet CINC Challenge [
11] were used, as discussed previously. Since the dataset was not preprocessed for noise, it was extremely important to process each recording for noise removal.
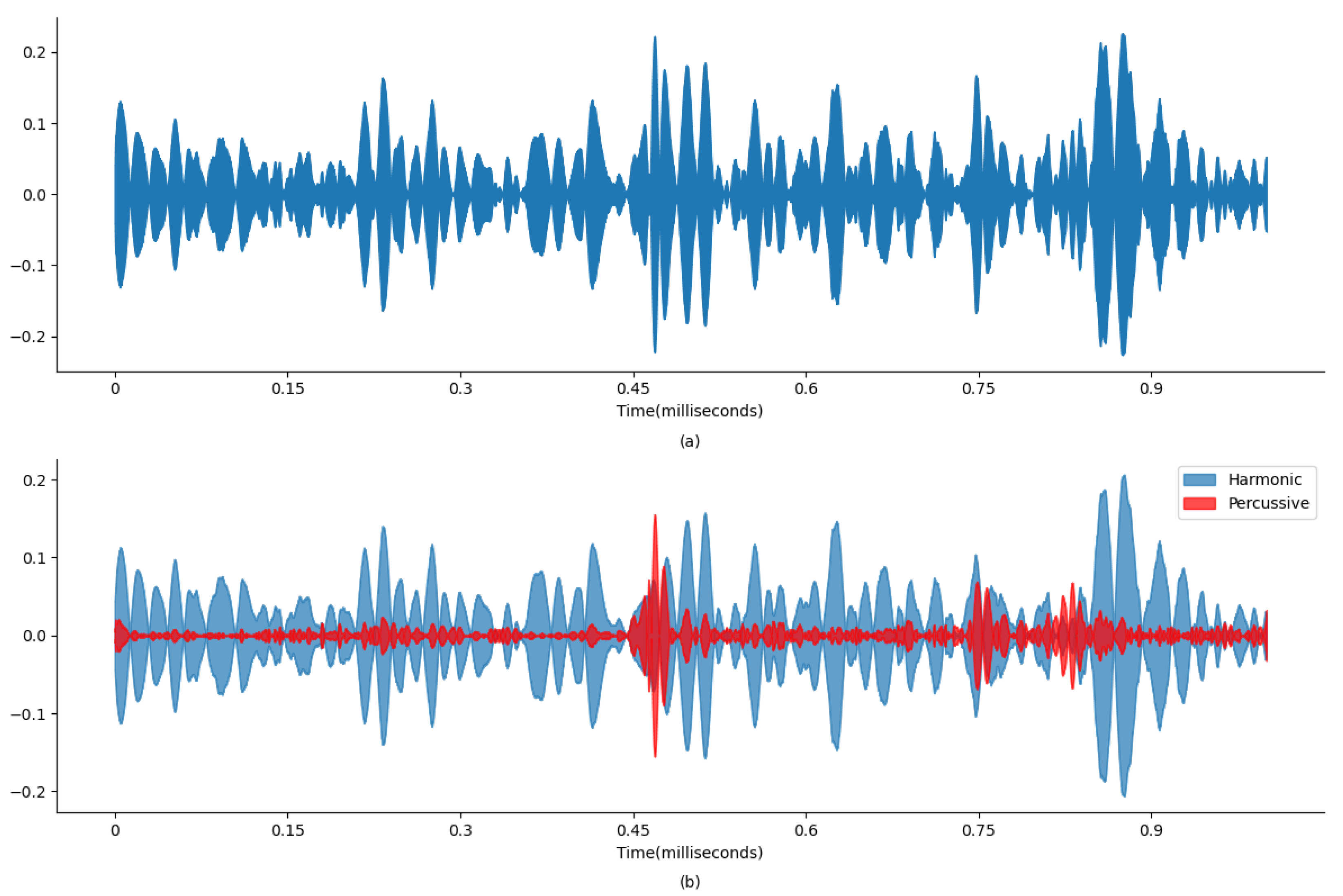
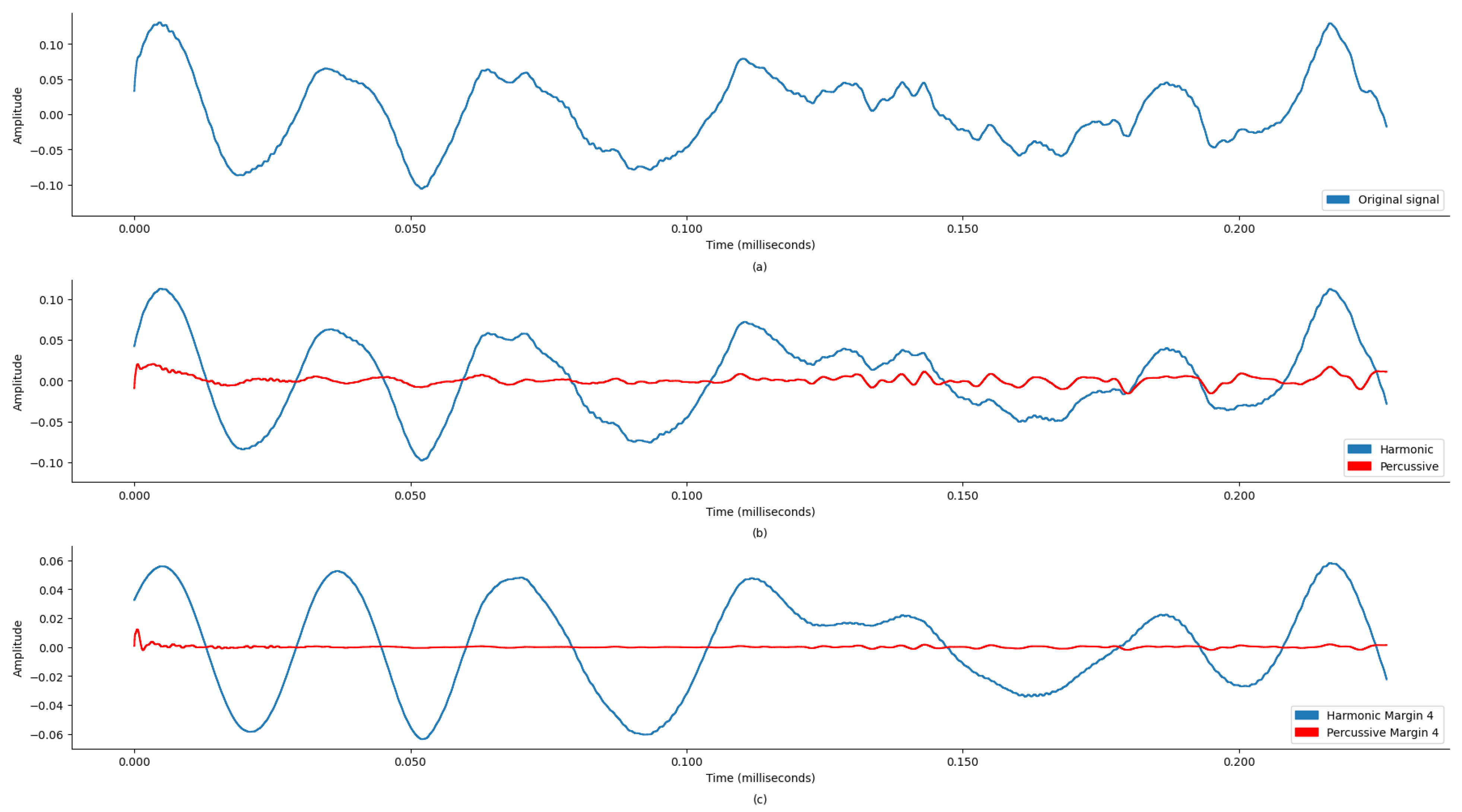
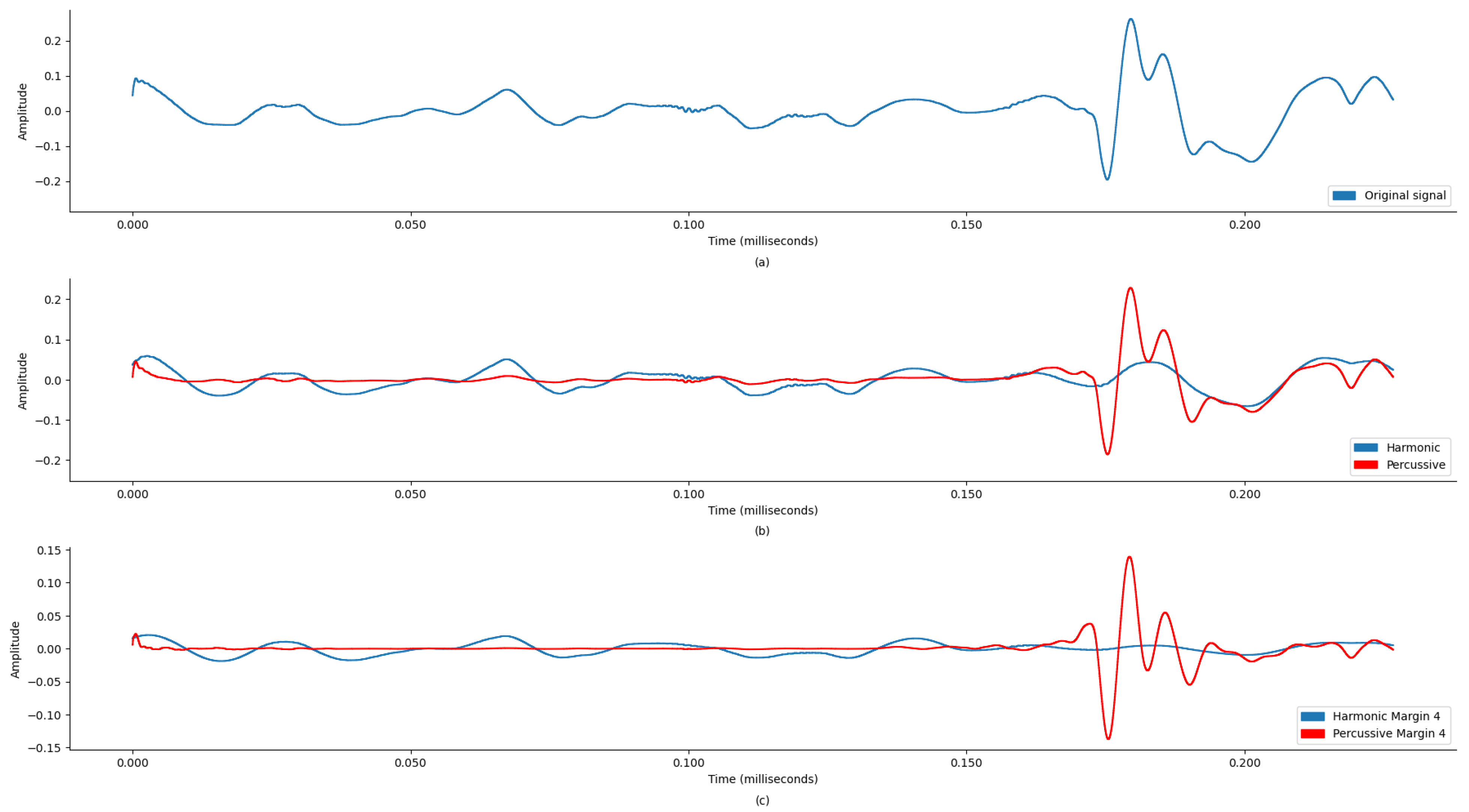
Figure 4a and
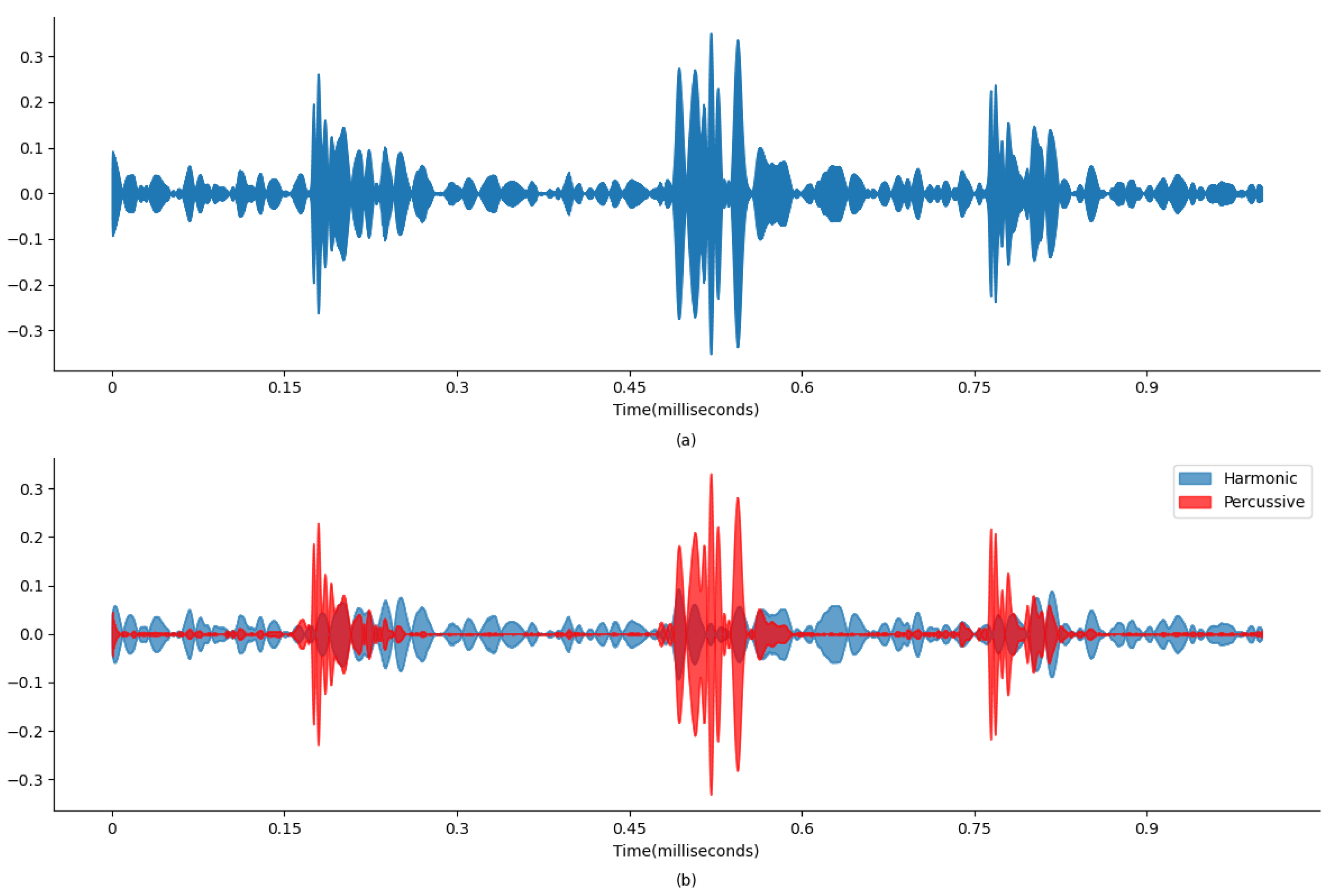
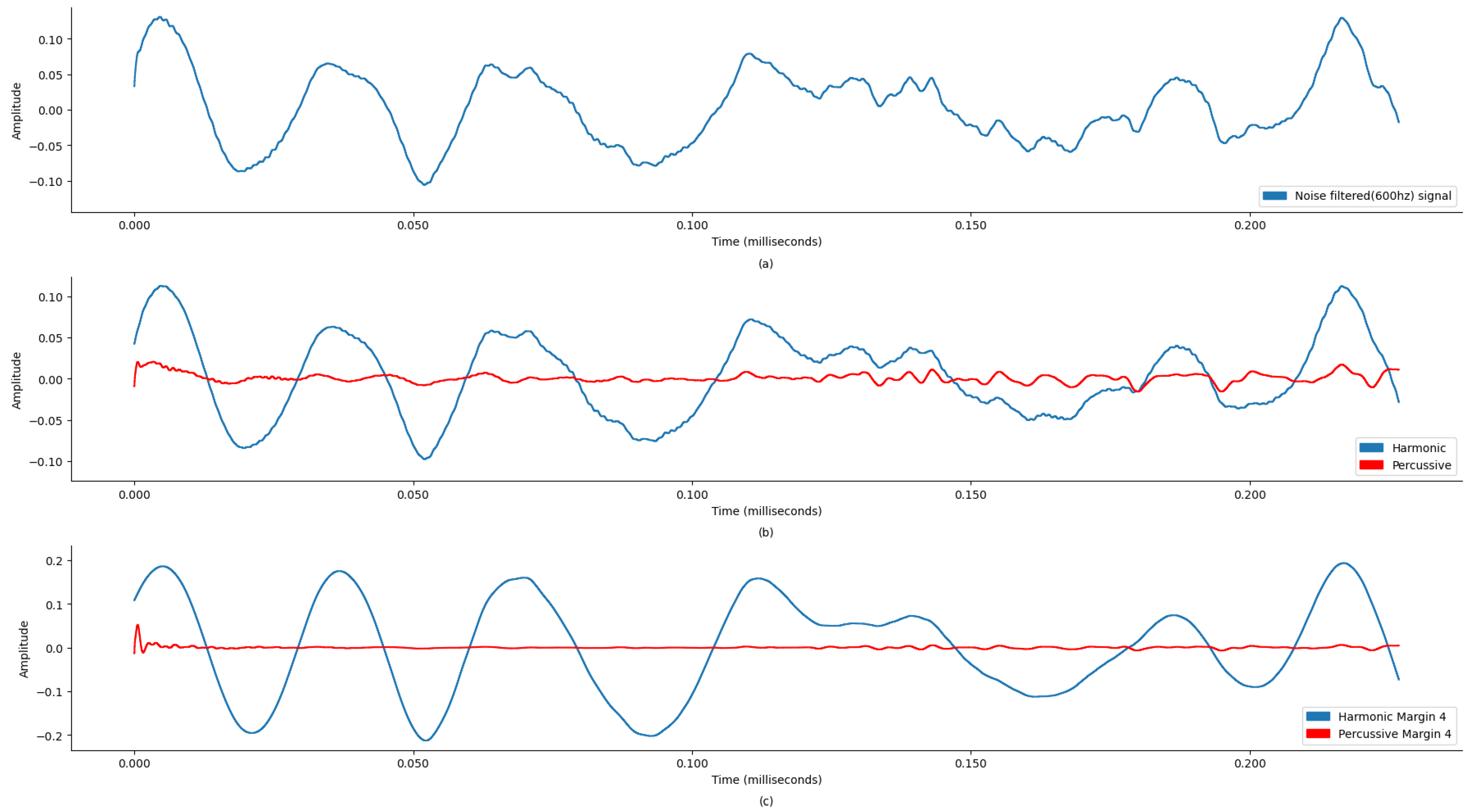
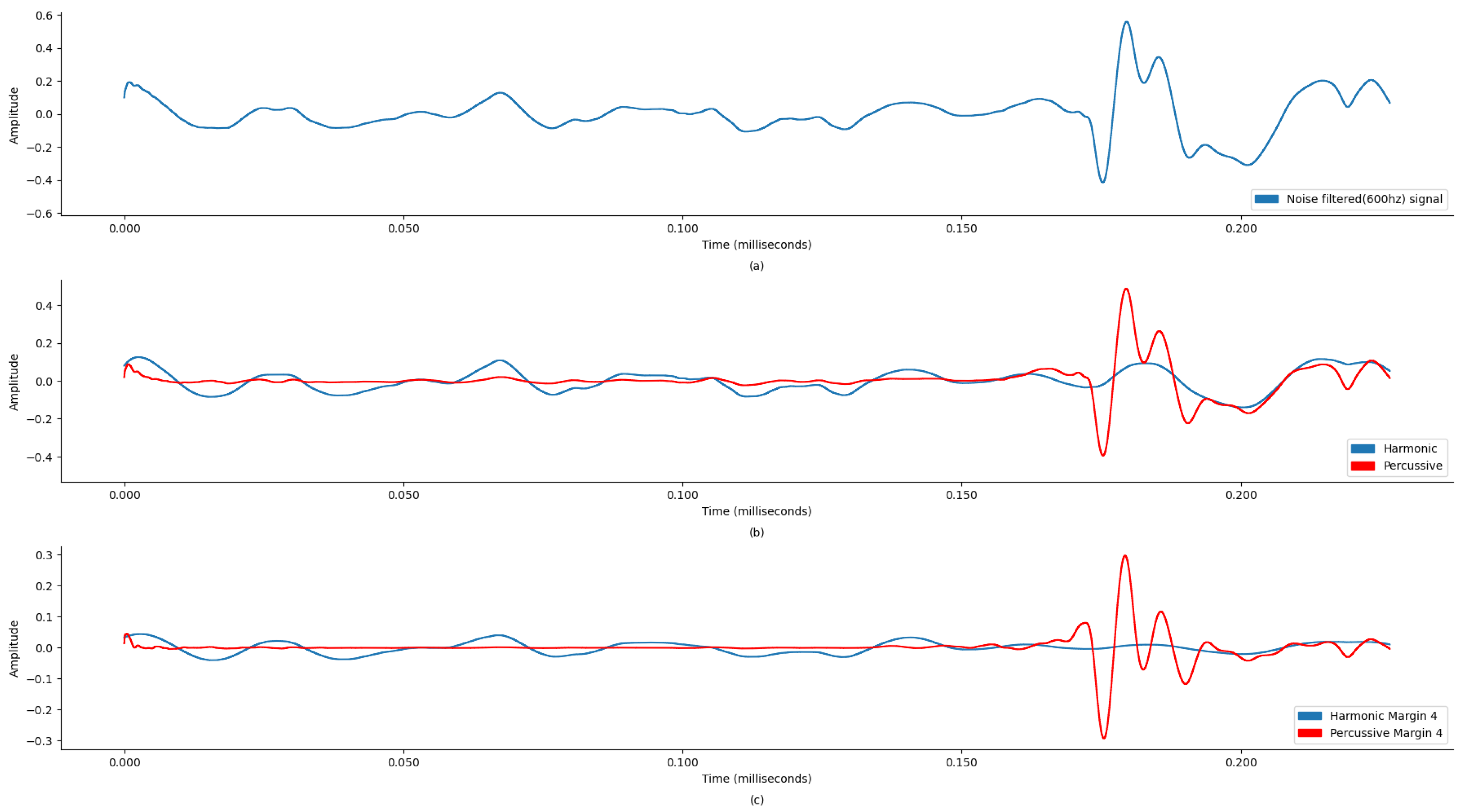
Figure 5a display the original state of the audio signal provided in the dataset. And,
Figure 4b and
Figure 5b display the harmonic and percussive component separation of the original audio signal, which was further processed for noise removal. Based on the findings in
Table 1, the sound signal was clipped at 600 Hz.
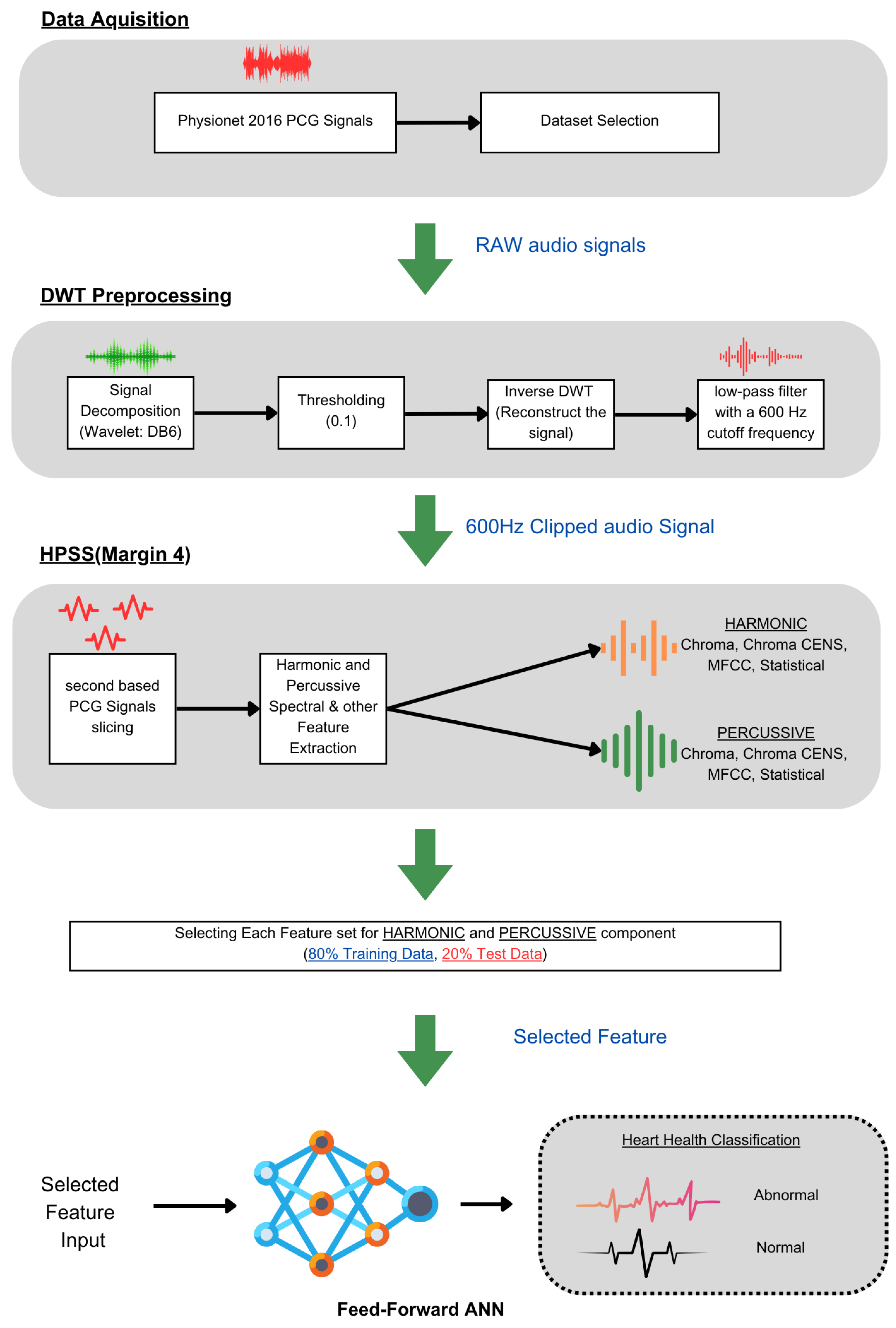
This preprocessing step is crucial as it ensures that the subsequent audio analysis operates on cleaner, noise-reduced signals, thereby improving the reliability and accuracy of this machine learning model in detecting and classifying audio features. To enhance the quality and accuracy of the audio analysis, the preprocessing for noise reduction on the audio files was performed using thinkDSP, which is a library for systematically filtering out high-frequency noise components and other audio processing functions. This preprocessing is based on a Discrete Wavelet Transform (DWT) using the Daubechies 6 (DB6) wavelet and a threshold value of 0.1. Additionally, a low-pass filter with a 600 Hz cutoff frequency was applied for further signal refinement.
The DWT is particularly effective for analyzing non-stationary signals like PCGs because it provides a time–frequency representation, enabling localized analysis to isolate noise from the desired signal features. The DB6 wavelet, known for its compact support and orthogonality properties, was chosen for its ability to efficiently capture both smooth and transient features of the PCG signal, providing a balance between time and frequency localization. A soft thresholding technique with a threshold value of 0.1 was employed to reduce noise components while preserving the signal’s important features. The methodology involved decomposing the PCG signal using the DWT with DB6, applying the threshold to specific coefficients, reconstructing the signal using the inverse DWT, and finally applying a low-pass filter with a 600 Hz cutoff frequency to eliminate any residual high-frequency noise (
Figure 3 (DWT preprocessing)).
This process reduced noise, improved the signal-to-noise ratio (SNR), and preserved essential diagnostic features. The results show that the denoised signals were diagnostically useful. This filtered signal was further processed to separate harmonic and percussive components with margin 4, enhancing the SNR and accuracy of subsequent analyses and diagnoses.
For better classification between abnormal and normal PCGs, extracting features that contain the essence of the unsegmented audio is very important. Therefore, for this work, the PCG audio files (
Table 6) were processed to extract features using Librosa music and audio analysis API [
48]. The feature extraction required three steps, starting with preprocessing each file for basic noise removal using the DWT, and then the denoised signal was decomposed further for HPSS with margin 4. The HPSS margin value selection was carried out through an iterative process based on preliminary experiments and performance observations. The margin value of 4 was found to provide a balanced separation between harmonic and percussive components.
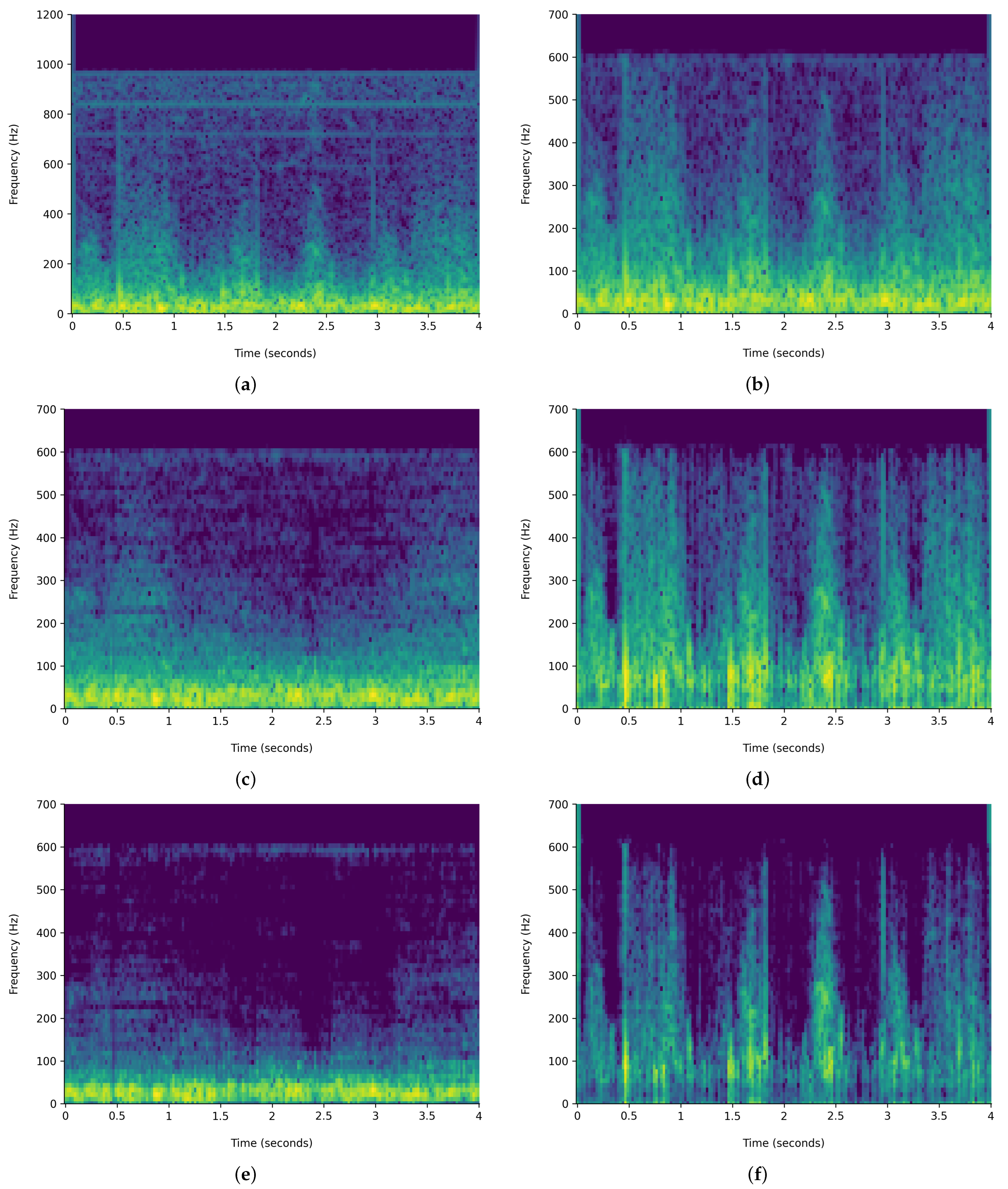
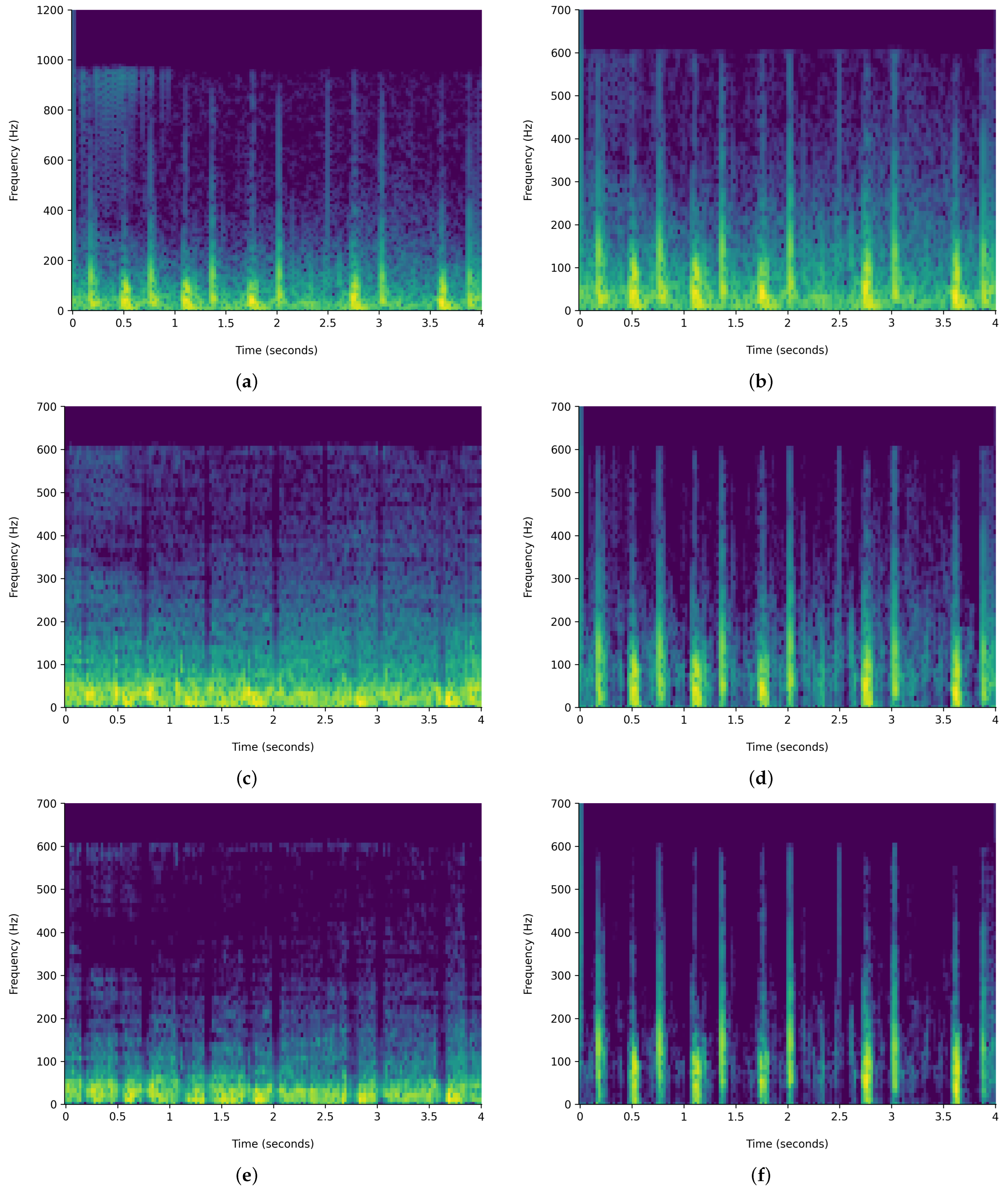
Figure 6 and
Figure 7 demonstrate the comparison of time-frequency signal representation for abnormal VS normal patients. Additionally,
Figure 8 and
Figure 9 demonstrate the waveplot comparison of abnormal patient HPSS original VS noise reduced PCG signal. Whereas
Figure 10 and
Figure 11 demonstrate the waveplot comparison of normal patients. Following this, both harmonics and percussive signals were separately processed to extract the Chroma STFT (pitch), Chroma CENS (tempo), MFCC, Chroma CQT (frequency domain), root mean square energy (signal magnitude), spectral centroid (weighted mean on the spectrum), spectral bandwidth (variance in spectral centroid), spectral roll-off, zero crossing rate (change in signal), and applicable statistical features.
3.2.1. Harmonic–Percussive Source Separation
As mentioned in the Introduction, the PCG consists of a beat rhythm with intensity variation. Therefore, extracting separate features (chroma, MFCC, etc.) based on HPSS will provide a better encoding of unsegmented audio data, potentially increasing the effectiveness of the neural network training.
The HPSS technique is particularly useful in audio signal processing, where it can enhance the analysis of audio elements by isolating the tonal and rhythmic aspects of the audio. The HPSS process involves the following steps: First, the audio signal is transformed into the time–frequency domain using a STFT. Then, the spectrogram is subjected to median filtering along the time axis to emphasize percussive components and the frequency axis to emphasize harmonic components. Finally, binary masks are created based on the filtered spectrograms to separate the harmonic and percussive components, which are then reconstructed into the time domain using an inverse STFT, displayed in
Figure 6 and
Figure 7. For this analysis, the margin value of 4 is used to separate harmonic and percussive components. This process is carried out using the Librosa library. The margin parameter in HPSS is used to control the sensitivity of the separation process. The margin parameter simply defines a threshold that controls how aggressively the filtering should separate the components.
A larger margin value makes the separation more tolerant, while a smaller margin value makes it more stringent. This choice of margin value in this analysis was guided by the need to achieve a more balanced separation between the harmonic and percussive elements of the PCG signals. Therefore, it was selected through an iterative process based on preliminary experiments and performance observations. PCGs typically contain both periodic heart sounds (S1, S2) and transient noise components (e.g., murmurs, clicks, etc.). Using a higher margin value ensures that subtle percussive elements, which could be indicative of pathological conditions, were adequately captured without overshadowing the harmonic components that represent the primary heart sounds.
HPSS will be effective because the harmonics will provide the pitch in audio, whereas percussive components will provide beats with localization in time. It provides an improved estimation of tempo and chroma features. Therefore, this hypothesis is based on the assumption that the features extracted from harmonic components, which detect the abnormalities in pitch, offering a better approach to detecting abnormal heart conditions in an individual patient.
3.2.2. Chroma STFT
The Chroma STFT is a powerful tool for audio signal analysis, especially in music and speech processing. At its core, the Chroma STFT was designed to capture the harmonic content of an audio signal by focusing on the relative intensity of twelve distinct pitch classes, often corresponding to the twelve traditional Western music pitches.
The primary motivation behind the Chroma STFT is rooted in the observation that many musical pieces exhibit harmonic shifts over time, but often within the same set of pitch classes. By mapping these pitch classes to a fixed set of twelve bins, regardless of the number of octaves, the Chroma STFT provides a compact representation of the audio signal’s harmonic content.
Mathematically, the Chroma STFT
C of an audio signal
can be represented as
where
n is the time index.
k corresponds to one of the twelve pitch classes.
is a window function, which is typically chosen based on the application (e.g., Hamming or Hann window).
is the angular frequency corresponding to the k-th pitch class.
The resulting Chroma STFT matrix provides a time-pitch representation, where each column corresponds to a specific time frame, and each row represents one of the twelve pitch classes. The intensity or magnitude in each cell of the matrix indicates the strength or prominence of a particular pitch class at a specific time.
By extracting the Chroma STFT feature, researchers and practitioners can profile an audio signal based on the intensity of each extracted pitch. This profiling is invaluable in various applications, including music genre classification, chord recognition, and even in some speech processing tasks where pitch and tonality play a crucial role.
3.2.3. Chroma CENS
The Chroma CENS (Chroma Energy Normalized Statistic) is an enhancement over the traditional chroma feature, aiming to provide a more robust representation of harmonic content in audio signals. The primary distinction of the Chroma CENS is its focus on short-time statistics over energy distributions within chroma bands rather than just the energy itself.
Mathematically, the Chroma CENS for a given chroma vector
C can be represented as
where
C is the chroma vector, typically obtained from the Chroma STFT or a similar method.
is the mean energy of the chroma vector over a short time window.
is the standard deviation of the energy of the chroma vector over the same window.
Through normalizing the chroma vector in this manner, the Chroma CENS effectively reduces the influence of dynamics (loudness variations) and timbral characteristics, focusing primarily on the harmonic content. This normalization process ensures that the resulting feature is less sensitive to variations in dynamics, recording conditions, or specific instrument timbres, making it particularly robust for tasks like music similarity and retrieval.
The low temporal resolution of the Chroma CENS is intentional. By averaging out the chroma values over longer time frames, it captures the essence of the harmonic progression while being less affected by short-term fluctuations or transients. This makes the Chroma CENS efficient for extracting stable harmonic features from the audio, providing a summarized yet informative representation of the audio’s tonal content.
3.2.4. Chroma CQT
The Chroma CQT (Chroma Constant-Q Transform) is designed to extract chroma features from an audio signal using a logarithmically spaced frequency axis. The Constant-Q Transform is unique in that it provides a constant ratio between the center frequencies of adjacent filters, making it particularly suited for musical/non-stationary signals, where pitches are often geometrically spaced.
The formula for the Constant-Q Transform is given by
where
is the audio signal.
is the center frequency of the k-th filter, determined by the geometric spacing.
is the window function for the k-th filter, which is typically designed to have a constant Q value, where Q is the ratio of the center frequency to the bandwidth.
The Chroma CQT then maps the resulting spectrum from the CQT onto 12 chroma bands corresponding to the 12 pitch classes. This is achieved by summing the energies in the CQT bins that correspond to the same pitch class, regardless of the octave.
The logarithmically spaced frequency axis of the CQT ensures that each octave is represented with an equal number of filters, aligning well with the perception of pitch in human hearing. This makes the Chroma CQT an effective tool for capturing the harmonic and melodic content, providing a meaningful and computationally efficient representation.
3.2.5. MFCC
The application of Mel-frequency cepstral coefficients (MFCCs) is prevalent in speech and audio processing. The auditory features are obtained from the spectral information of an audio signal and are specifically engineered to replicate the human ear’s non-linear auditory perception of sounds. The process of computing MFCCs involves several steps:
Fourier Transform: The audio signal is first transformed into the frequency domain using a Fourier transform:
where
is the time-domain audio signal, and
is its frequency representation.
Mel Filterbank Processing: The magnitude spectrum obtained from the Fourier transform is then passed through a series of overlapping filters, typically triangular and spaced uniformly on the Mel scale. The Mel scale is a perceptual scale that approximates the human ear’s response to different frequencies. The output of this stage is the energy in each Mel filter:
where
is the
m-th Mel filter, and
F is the total number of frequency bins.
Logarithmic Compression: The energies from the Mel filterbanks are log-transformed to mimic the logarithmic perception of amplitude and loudness in human hearing:
Discrete Cosine Transform (DCT): Finally, the MFCCs are obtained by taking the Discrete Cosine Transform of the log energies. This step decorrelates the filterbank coefficients and yields a compressed representation of the filterbank energies:
for
, where
M is the number of Mel filters, and
K is the desired number of MFCCs.
For the research in context, a filter bank with 40 Mel filters was utilized, implying that in the above equations.
MFCCs are widely preferred in various audio and speech-processing applications because of their capability to capture the phonetically significant attributes of an audio signal while also exhibiting resilience against specific signal changes.
3.2.6. Root Mean Square Energy
The root means square energy (RMSE) feature uses a spectrogram to extract the information on signal energy over time. To extract the RMSE, this research work used a frame length of 2048 and a hop length of 512, where frame length is the size of samples from the audio signal used for energy calculation and hop length for performing an intermediate STFT. The RSME is defined as
3.2.7. Spectral Centroid
This is a simple measure based on the spectral position and shape. The centroid provides the center of the gravity/mass of the signal spectrum and is calculated based on frames. A general observation is that the greater the value presented, the more prominent the sounds.
where
represents the weighted frequency value, or magnitude, of bin number
n, and
represents the center frequency of that bin.
3.2.8. Spectral Bandwidth
This is the difference between the upper and lower frequencies in a continuous band of frequencies. This feature identifies the frequency range for PCGs. Librosa computes the p-order spectral bandwidth, and it is defined by
where
is the spectral magnitude at frequency bin
k,
is the frequency at bin
k, and
is the spectral centroid. When
p = 2, this is like a weighted standard deviation.
3.2.9. Spectral Roll-Off
This is a spectral shape descriptor used to discriminate between different audio spectra. This audio feature defines the frequency below which the max percentage of the magnitude distribution of the spectrum is concentrated. This work used the Librosa library and used 85.00% as the roll percentage.
The spectral roll-off frequency is usually normalized by dividing it by , so that it takes values between 0 and 1. This type of normalization implies that a value of 1 corresponds to the maximum frequency of the signal, i.e., to half the sampling frequency.
3.2.10. Zero Crossing Rate
This is the rate of change in the sign of the signal during the frame, or it can be said to be the frequency of change in sign in a signal divided by the length of the frame. It is defined as
where the sgn function is defined as
3.2.11. Statistical Features
Mean
This is the signal’s average amplitude over a considered time interval. This feature is considered because the mean value of abnormal PCGs vs. normal PCGs is higher. It is defined by
where
represents ith amplitude instance in the signal, and N is the total number of instances.
Mode
The mode is a fundamental measure of central tendency that identifies the value or values that occur most frequently within a dataset. Unlike the mean and median, which provide a numerical average or a central value, respectively, the mode offers insights into the most common or repetitive patterns in the data.
There are a few key characteristics of the mode:
It directly reflects the highest peak of the data distribution, indicating where data samples are most densely concentrated.
A dataset can have one mode (unimodal), more than one mode (bimodal or multimodal), or no mode at all.
The mode is particularly robust against outliers or extreme values. Since it is based solely on the frequency of occurrence, it remains unaffected by the magnitude of data points, making it a reliable measure in datasets with potential anomalies.
In the context of signal analysis, the mode becomes especially pertinent. Given that signals often contain repetitive patterns or recurring values, identifying the mode can provide insights into the inherent characteristics or the “essence” of the signal. For instance, in medical signal analysis, the mode can help differentiate between normal and abnormal signals by highlighting the most common patterns present. If a particular value or pattern frequently appears in a normal signal but is absent or less frequent in an abnormal one, the mode can be a distinguishing feature.
By incorporating the mode as a feature in the analysis, this work aimed to harness its resilience against extreme values and its ability to capture the core patterns of the signal. This ensures a more accurate and reliable differentiation between different classes or categories of signals, enhancing the overall efficacy of the analysis.
Standard Deviation
This is an important statistical feature that helps determine how much the sample under process deviates from its mean value. A higher standard deviation indicates that the data are spread over a wider range, whereas a lower deviation means the data points are closer to the mean. This helps differentiate between normal and abnormal PCGs.
Here, N represents the total number of observations; represents the mean of the given data; and is the value of each amplitude point considered.
Skewness
The primary purpose of using skewness is to determine whether the sample under process is normally distributed or not. A normally distributed sample will have zero skewness, whereas if it is left- or right-distributed, then the sample is asymmetrical and points out to be an abnormal PCG.
Quantile25
The 25th percentile, often referred to as the first quartile or Quantile25, is a statistical measure that provides insights into the distribution of data in a dataset. It represents the value below which 25.00% of the observations can be found. In other words, it is the value at which one-quarter of the data lie below it, serving as a marker that separates the lowest 25.00% of the data from the rest.
To compute the Quantile25 for a given dataset, we have the following steps:
First, the data points are sorted in non-decreasing order.
Then, the position
p is calculated using the formula
where
n is the total number of data points in the dataset.
If p is an integer, then the data point at position p is the 25th percentile.
If p is not an integer, then the 25th percentile is typically computed by linear interpolation between the data points at positions (the largest integer less than or equal to p) and (the smallest integer greater than or equal to p).
Thus, Quantile25 serves as a threshold, distinguishing the lower quarter of data points from the upper three-quarters in terms of magnitude.
Quantile75
The 75th percentile, often referred to as the third quartile or Quantile75, is a statistical measure that delineates the distribution of data in a dataset. It represents the value below which 75% of the observations fall. In essence, it is the value at which three-quarters of the data lie below it, serving as a boundary that separates the lowest 75% of the data from the highest 25%.
To compute the Quantile75 for a given dataset, we have the following steps:
Initially, the data points are sorted in non-decreasing order.
Subsequently, the position
p is determined using the formula
where
n denotes the total number of data points in the dataset.
If p is an integer, then the data point at position p is the 75th percentile.
If p is not an integer, then the 75th percentile is typically derived by linear interpolation between the data points at positions (the largest integer less than or equal to p) and (the smallest integer greater than or equal to p).
Thus, Quantile75 acts as a demarcation, distinguishing the lower three-quarters of data points from the uppermost quarter in terms of magnitude.
IQR
The Interquartile Range, commonly abbreviated as IQR, is a robust measure of statistical dispersion or spread in a dataset. It specifically describes the range within which the central 50% of values lie when the data are ordered from the lowest to the highest value. By focusing on the middle 50%, the IQR effectively eliminates the influence of extreme values or outliers, making it a particularly valuable metric in datasets that may contain such anomalies.
Mathematically, the IQR is the difference between the third quartile (Quantile75) and the first quartile (Quantile25). It can be represented by the formula
Given that Quantile75 represents the value below which 75% of the data fall, and Quantile25 represents the value below which 25% of the data fall, their difference (IQR) encapsulates the range of the middle 50% of the data. This range is particularly significant in statistical analyses as it provides insights into the variability and spread of the central portion of the dataset, excluding potential outliers.
In many statistical applications, the IQR is used in conjunction with other metrics, such as the median, to provide a comprehensive understanding of the data distribution. Moreover, the IQR is frequently employed to identify outliers. Observations that fall below or above are typically considered outliers, as they lie outside the range expected for the central bulk of the data.
Kurtosis
This significant statistical feature provides information about the signal distribution within the data sample. This feature helps in detecting the high-amplitude peaks in the PCG signal, which is beyond a threshold point and indicates an abnormal heart condition. This is formulated as
In the research referenced in the literature, features are extracted on a per-second basis. They are only extracted from a part of the audio file, i.e., 3 to 8 s only. However, when training a simple sequential artificial neural network, it was observed that the number of records was not adequate. Therefore, for this work, features were extracted on a per-second basis for the full duration of each PCG file. This results in an increase of 3.5 times in the total record of the extracted feature set dataset, further aiding the effective training of a neural network and improving the classification of abnormal cases. Precisely, the data were extracted with dimensions of 164 feature columns and 65,940 rows in comparison to 19,034 rows based on 7 s of audio.
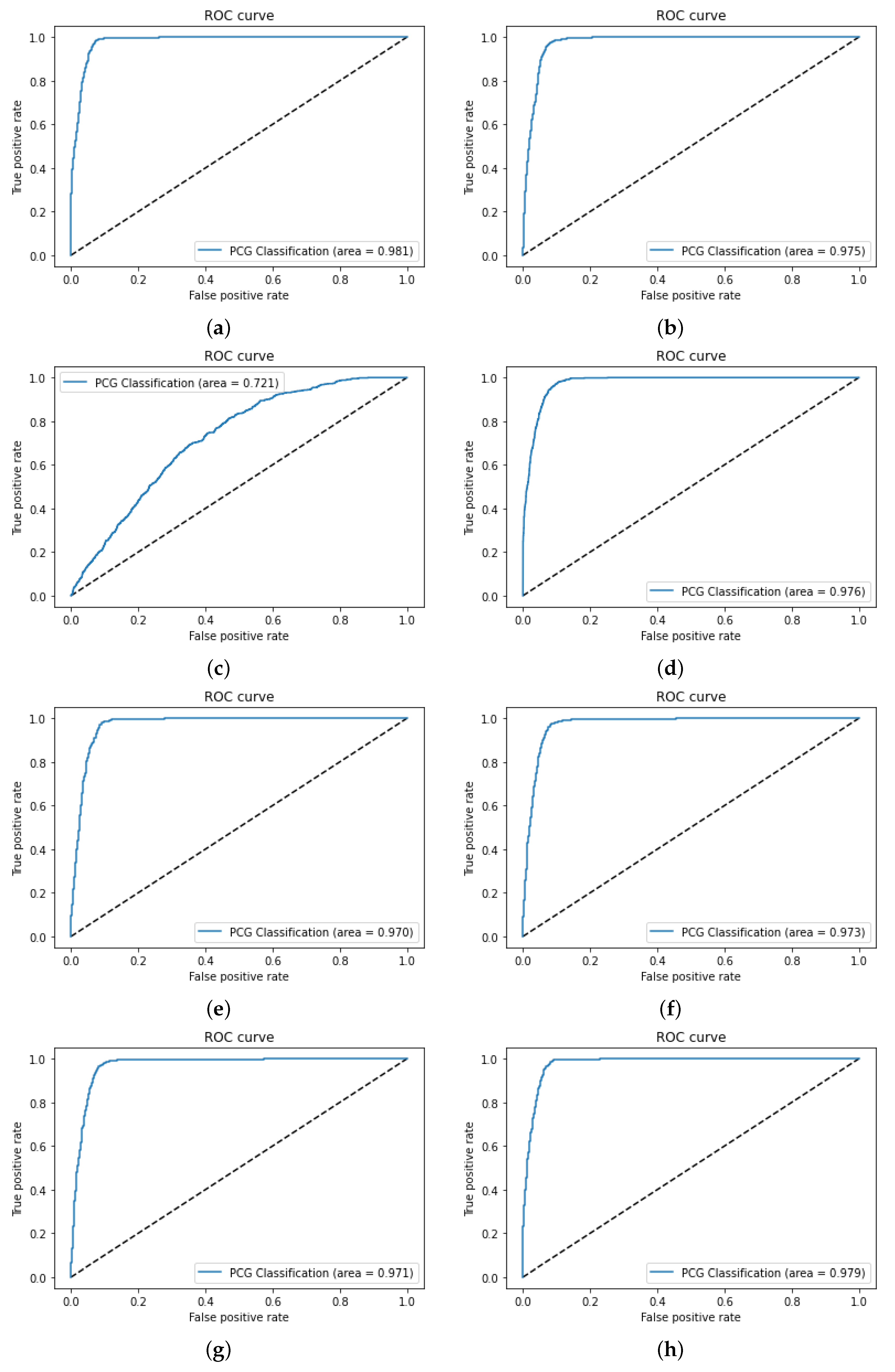
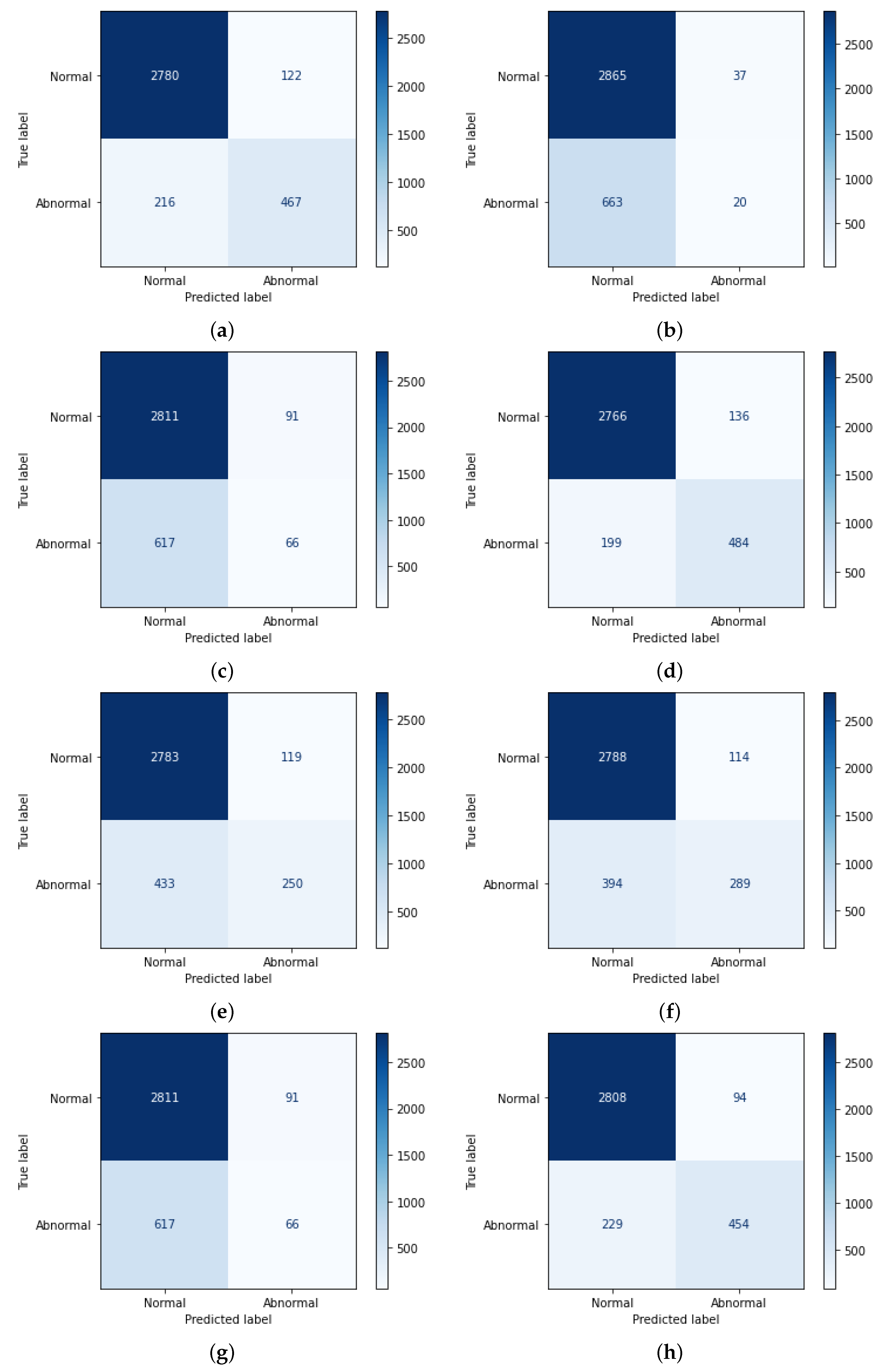
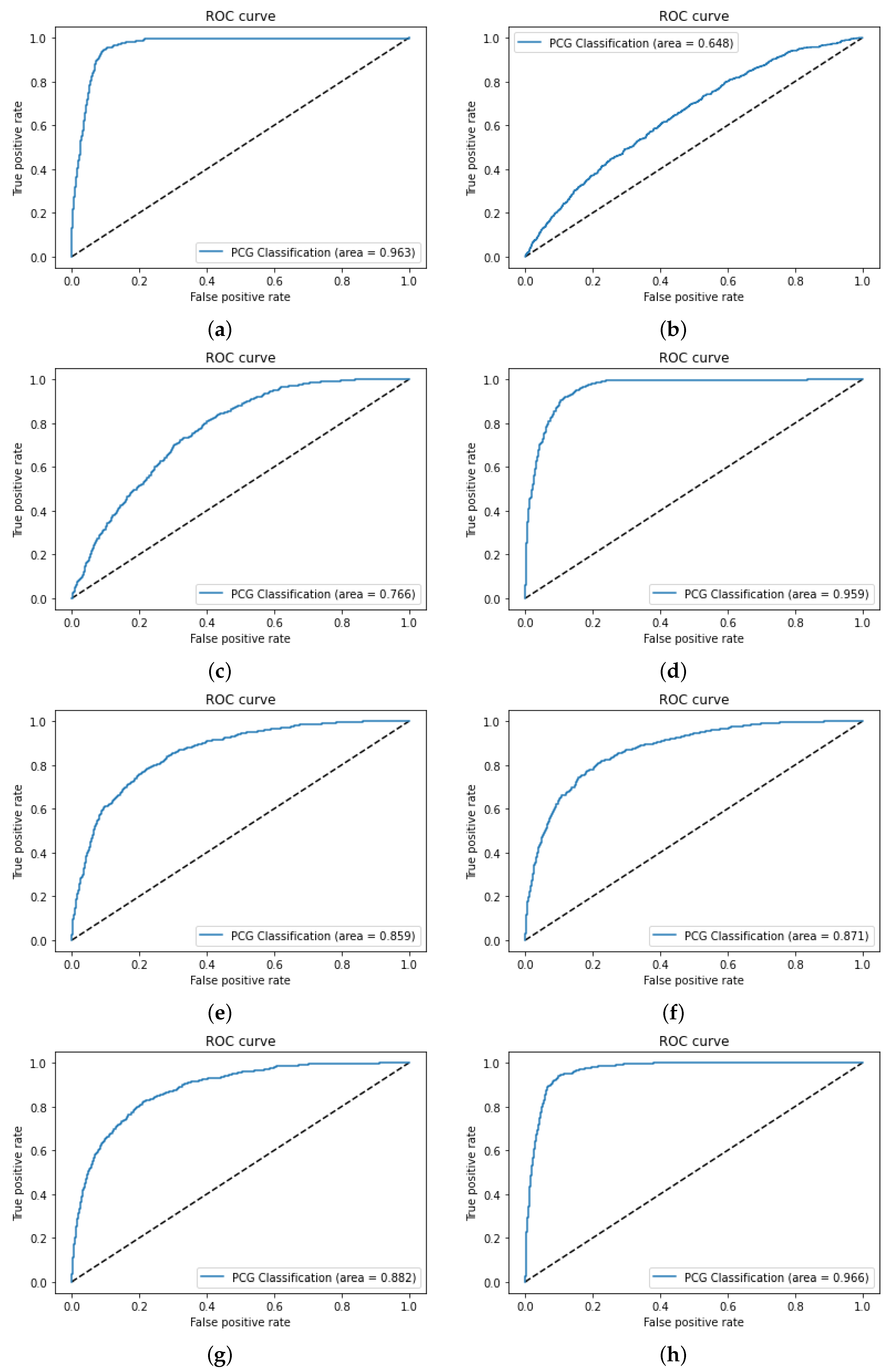
The next step is feature selection, which is performed based on a careful analysis of the reviewed literature. In this study, the ROC-AUC method [
49], along with the count of features, was employed for feature selection to prioritize those features that exhibit strong discriminatory power between normal and abnormal PCG signals. Various feature set combinations were manually evaluated and selected (
Table 7) by observing their individual contributions to classification accuracy, using ROC-AUC scores to select the top-performing features. This step involved evaluating feature sets in a systematic manner to ensure a balanced representation of harmonic and percussive characteristics.
The choice of ROC-AUC over other feature selection techniques such as PCA, Ranker and Info Gain [
42], and the Wilcoxon method [
49] was driven by its ability to directly evaluate the classification performance of individual features across varying thresholds. Unlike PCA, which focuses on dimensionality reduction through linear combinations of features, ROC-AUC provides a more interpretable and the direct assessment of each feature’s relevance to the binary classification task. Additionally, while Ranker and Info Gain assesses feature importance based on information gain, and the Wilcoxon method evaluates features based on statistical significance, ROC-AUC offers a more holistic approach by considering both true positive and false positive rates. This method ensures that selected features contribute to model accuracy and overall balance between sensitivity and specificity, which is critical for reliable medical diagnostics.
3.3. Feed-Forward Artificial Neural Network
An ANN is a simplified mathematical model consisting of artificial neuron functions that imitate the behavior of human brain neurons. This work utilized the power and simplicity of feed-forward neural networks implemented using the TensorFlow Keras library. Multiple hyperparameter tunings were performed, as mentioned in
Table 8, and these are discussed further.
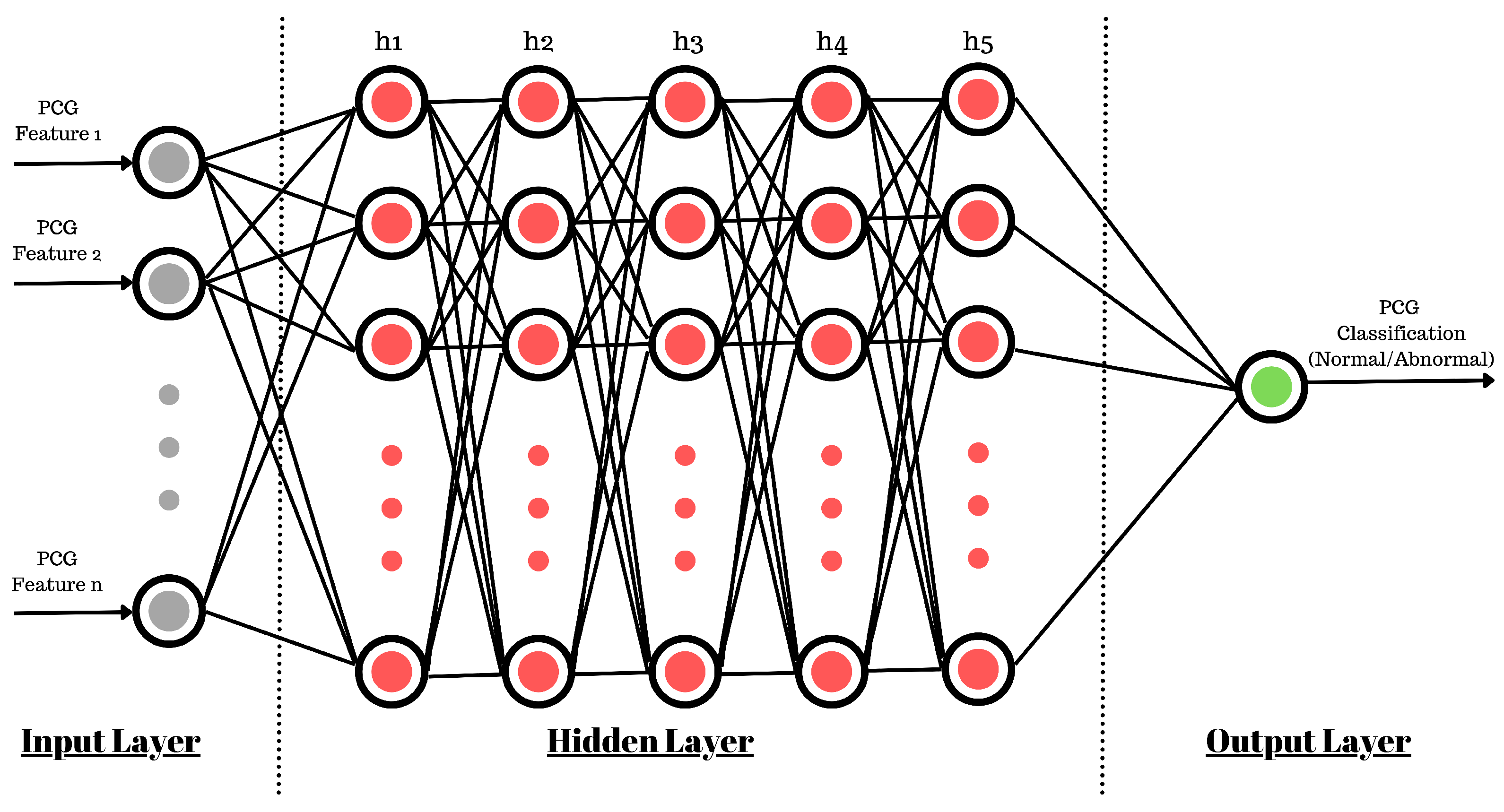
The use of a sequential model (
Figure 12) allows us to create five hidden layers of neurons with a density of 512 neurons at each inner layer. For the smooth training of the ANN model, the learning rate was kept at 1
(0.00001). This controls the rate at which the model adapts to the problem at hand. The learning rate is one of the most important parameters used to control the rate of change in neuron connection weights. If it is too large, it will quickly converge to a suboptimal solution, or if it is too small, then it can cause the process to stall. Therefore, identifying a trade-off value is important and may require multiple runs of model training. Also, based on the feature selection discussed in the previous section, the input shape for the ANN varies for each experiment.
Before the start of the ANN training, the neuron connection weights must be initialized. This work utilized a random uniform initializer for model weights in the range of −0.05 to +0.05. Accordingly, the weights were uniformly distributed, ensuring that each weight had an equal chance of being assigned any value between the minimum and maximum. This helped prevent overfitting and enabled the network to converge more quickly to an optimal solution. Ultimately, this impacted the outcome of the optimization procedure of the ANN and its ability to generalize based on the problem.
Now, because initializers were used, the ANN may have become sensitive to initial random weights, which may lead to slow model convergence. To counter this, a batch normalization layer was used, which normalizes the inputs to a layer for each batch of inputs. It helps reduce the internal covariate shift, thereby speeding up the learning process and reducing the chances of overfitting. Batch normalization also helps reduce the vanishing/exploding gradients problem and improves generalization ability. This leads to stable model training due to regularization, fewer generalization errors, and reduced training epochs, resulting in accelerated learning.
For each neuron in the hidden layers, the ReLU activation function was used to introduce non-linearity into the network. ReLU is computationally efficient, prevents the neural network from becoming saturated, and helps to train the model faster. It is utilized to overcome the vanishing gradient problem as well as for faster computations.
Since this work performed the classification of PCGs as normal or abnormal, the final layer contains only one neuron with a sigmoid activation function. For overall model learning adaptation, the Adamax optimizer was utilized; it extends the functionality of the Gradient Descent Optimization algorithm, inherently accelerating the optimization process. Adamax is a variant of the popular Adam optimization algorithm and is often preferred for training deep neural networks. It combines the advantages of the AdaGrad and RMSprop algorithms, both of which maintain per-parameter learning rates and update parameters based on adaptive learning rate methods. Unlike those algorithms, however, Adamax uses the infinity norm rather than the Euclidean norm to calculate parameter updates. This allows it to better handle sparse gradients, making it more suitable for training deep neural networks with a large number of parameters and layers. Additionally, Adamax uses a combination of momentum and decay rates to improve convergence while maintaining stability. This makes it well suited for heart sound classification. Finally, the computing loss during the model training process was calibrated through binary cross entropy.
These data were not yet ready to be fed directly to the neural network, so the dataset was further processed to remove the outlier records. This study used the Interquartile Range (IQR) method to detect and remove outliers from the dataset. For each feature, the first quartile (Q1) and third quartile (Q3) were calculated, with the IQR defined as Q3 − Q1. Data points outside the range of Q1 − 1.5 × IQR to Q3 + 1.5 × IQR were considered outliers and removed. This method, which is robust to non-normal data distributions, helped ensure that only statistically relevant data remained for model training, thereby improving classification accuracy. These exercises help prevent models from being over/underfit. After outlier removal, the dataset was reduced from 65,940 to 37,243 rows, which is still a decent volume of data that can be used to train a neural network. Going forward, these data were split into test and training sets with a ratio of 10:90 for the training of the neural network. This was carried out separately based on the classification category (normal/abnormal). This activity helped maintain the effectiveness of the model training and the model’s testing on unseen data.