An Analysis of Vertical Infiltration Responses in Unsaturated Soil Columns from Permafrost Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Properties of the Materials
2.2. Chemical and Mineral Analysis
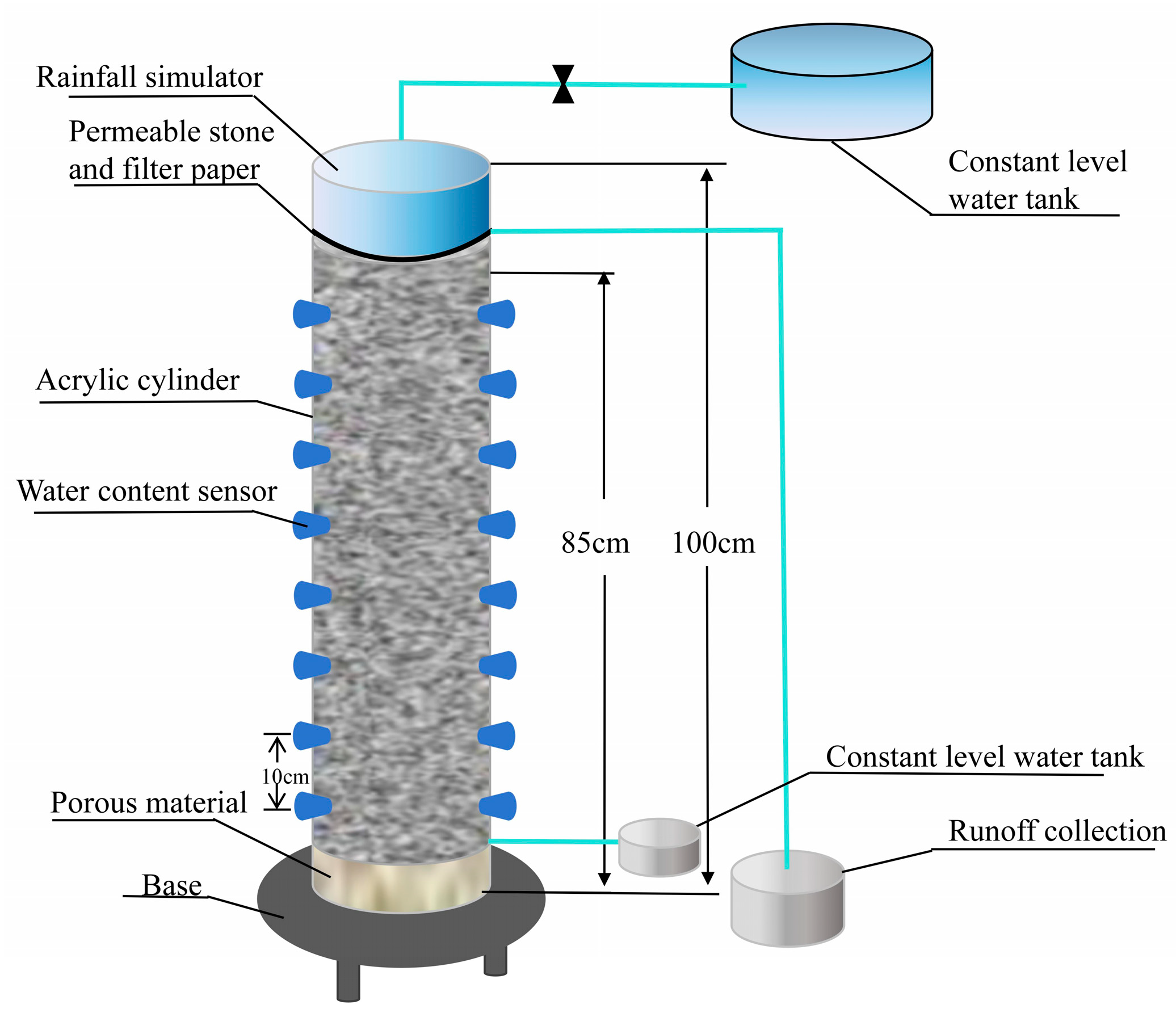
2.3. Test Procedure
2.3.1. Saturated and Unsaturated Infiltration Procedures
2.3.2. Filter Paper Test
3. Results and Discussion
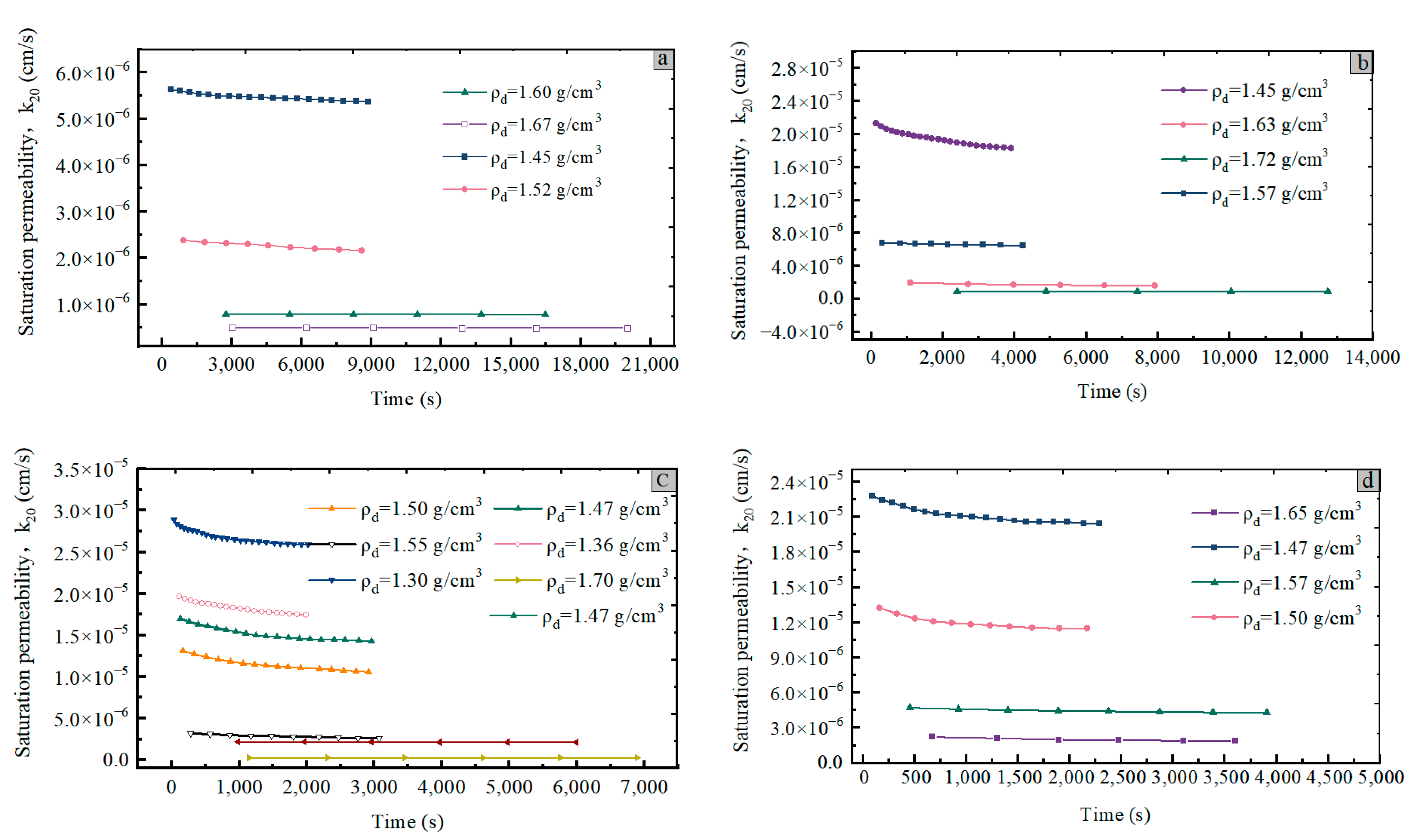
3.1. Deterioration of Loess Due to Saturated Infiltration
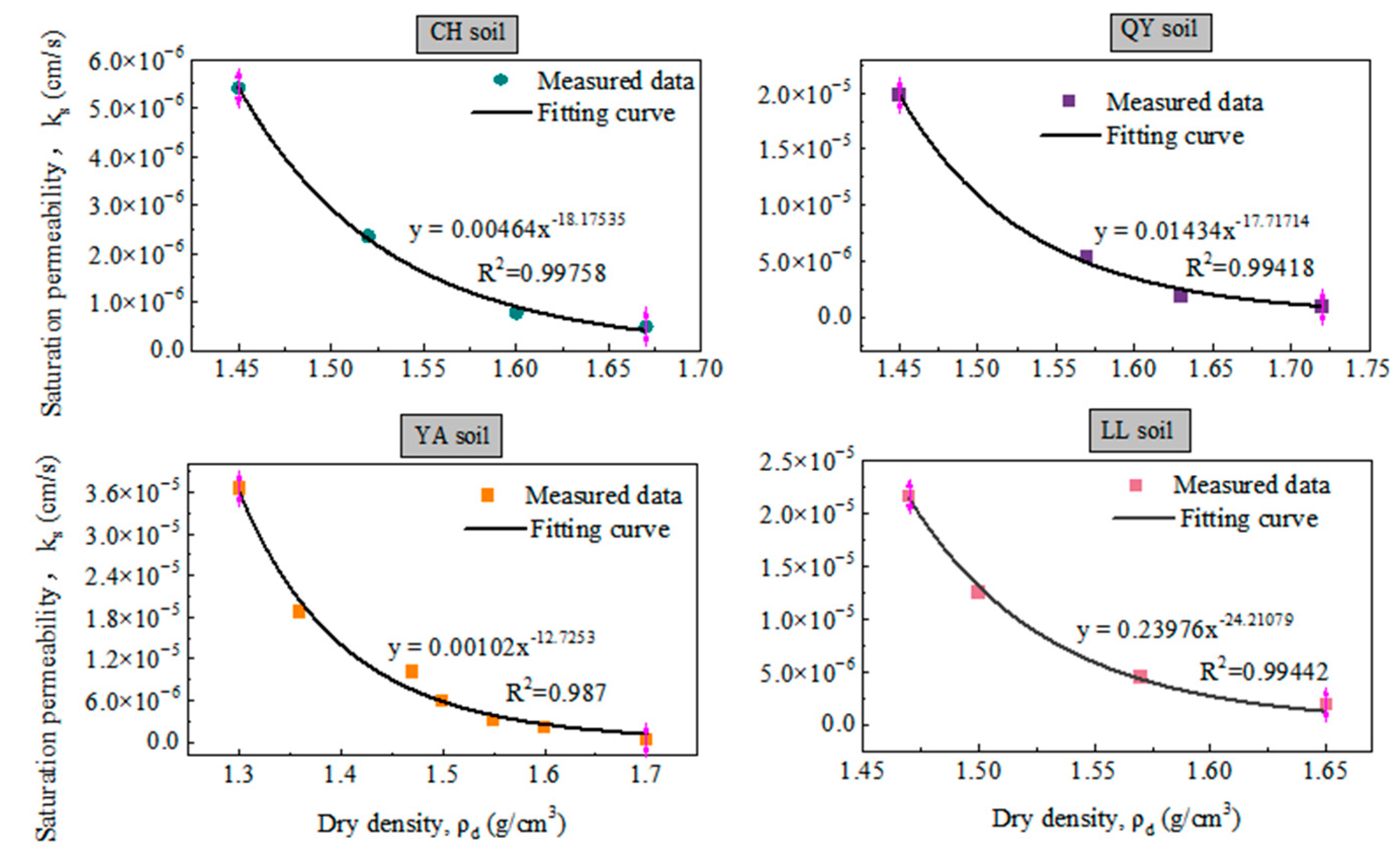
3.2. Influence of Dry Density on Saturated Permeability
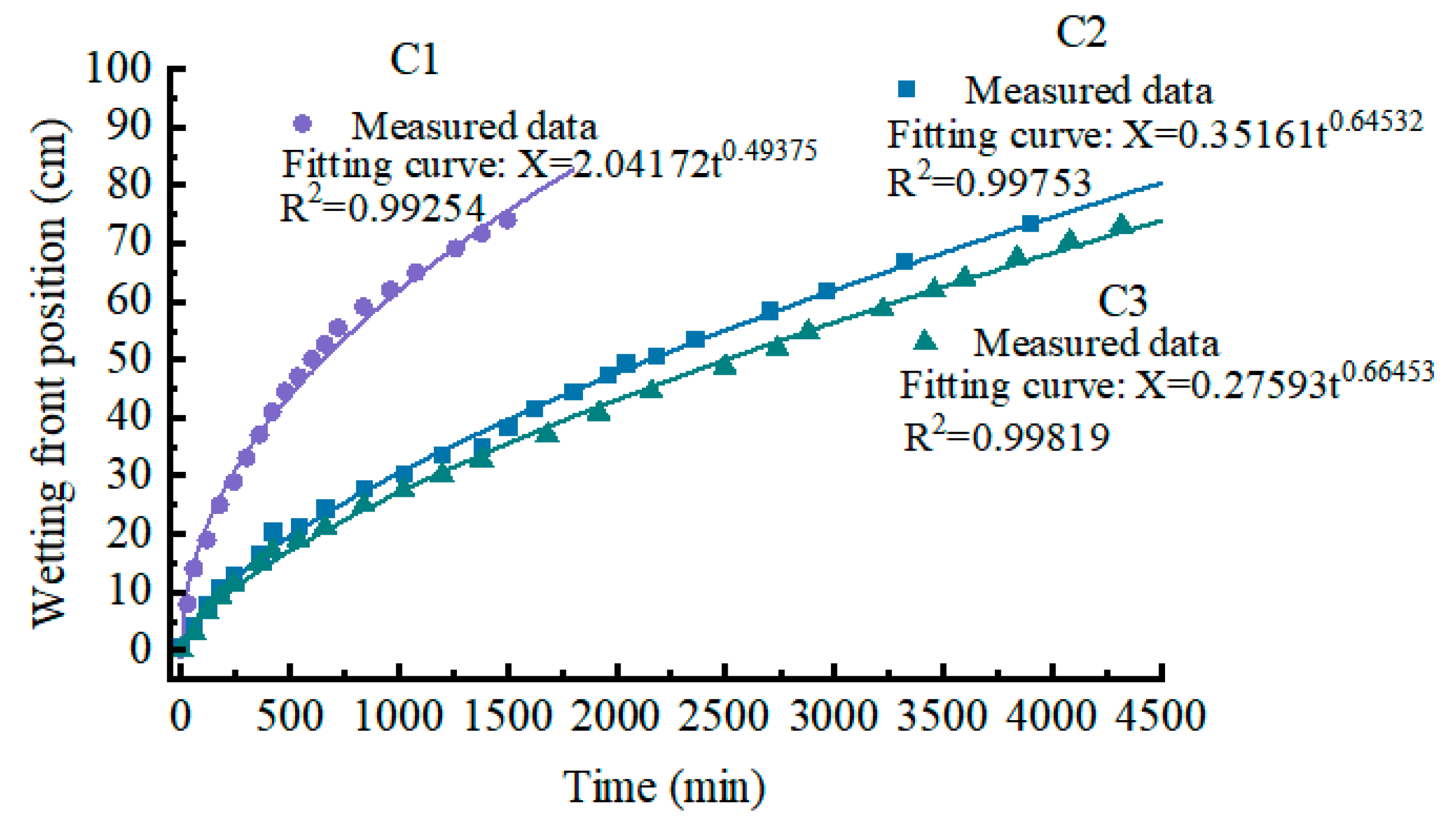
3.3. Wetting Front Under Unsaturated Infiltration
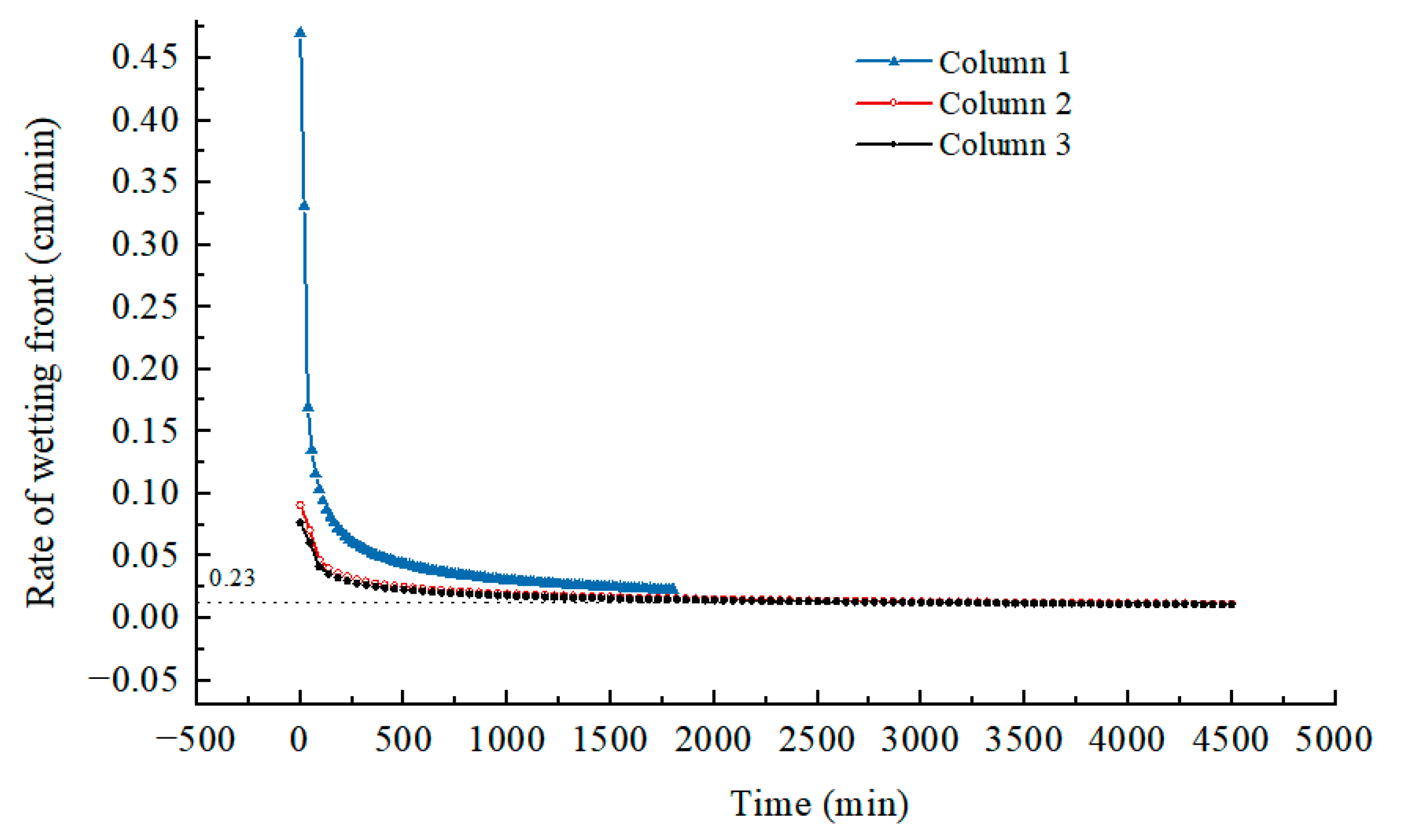
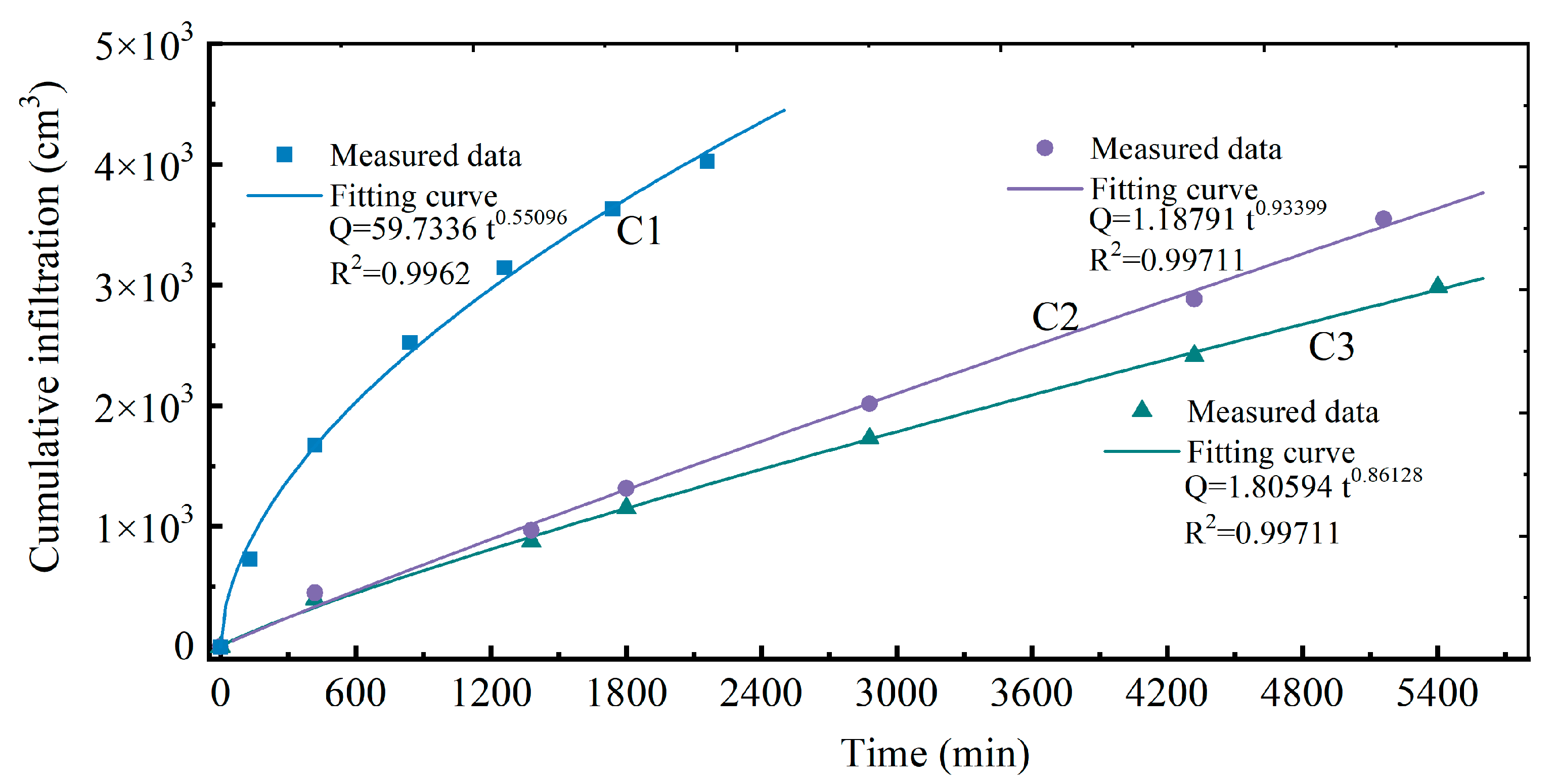
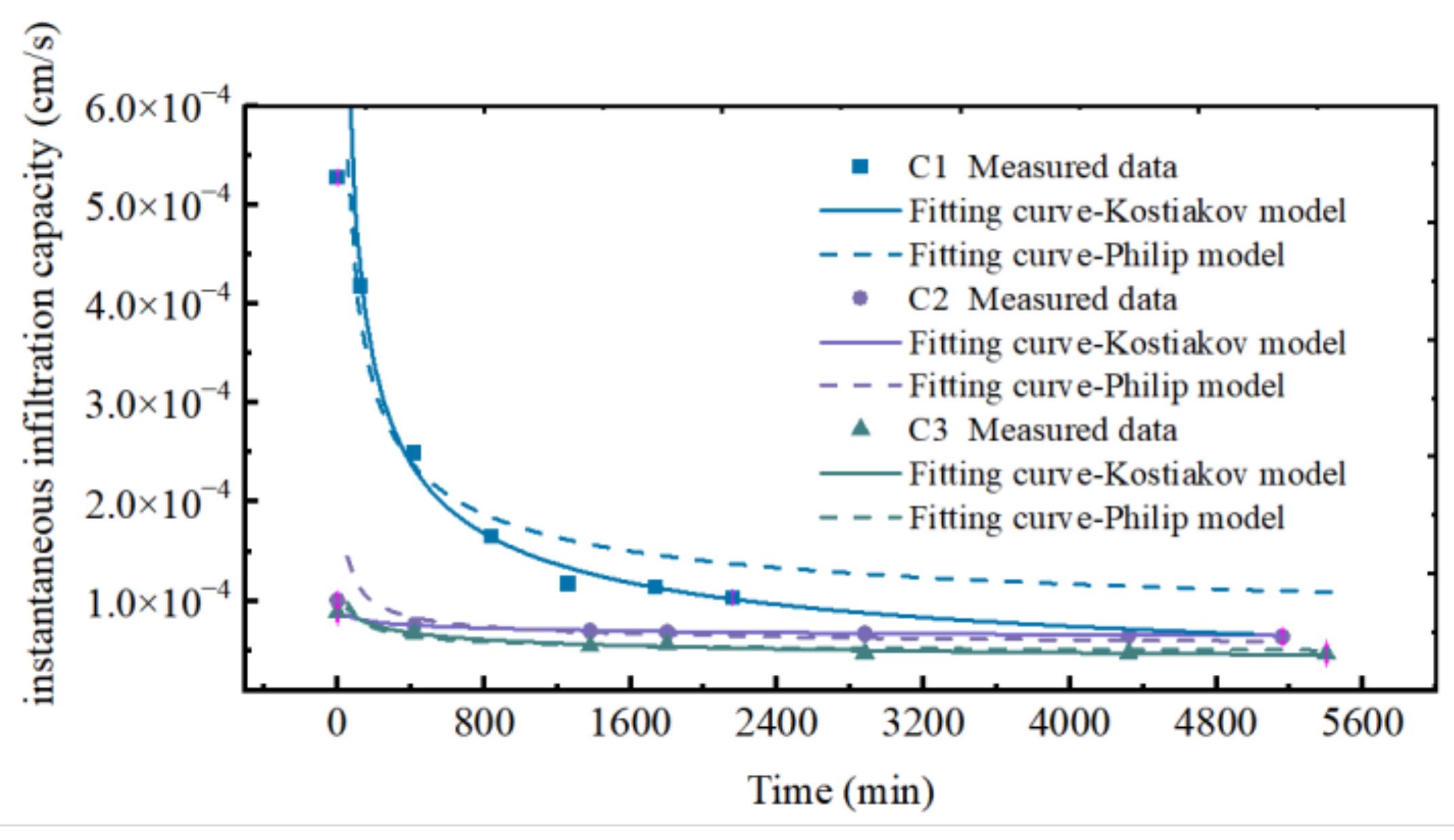
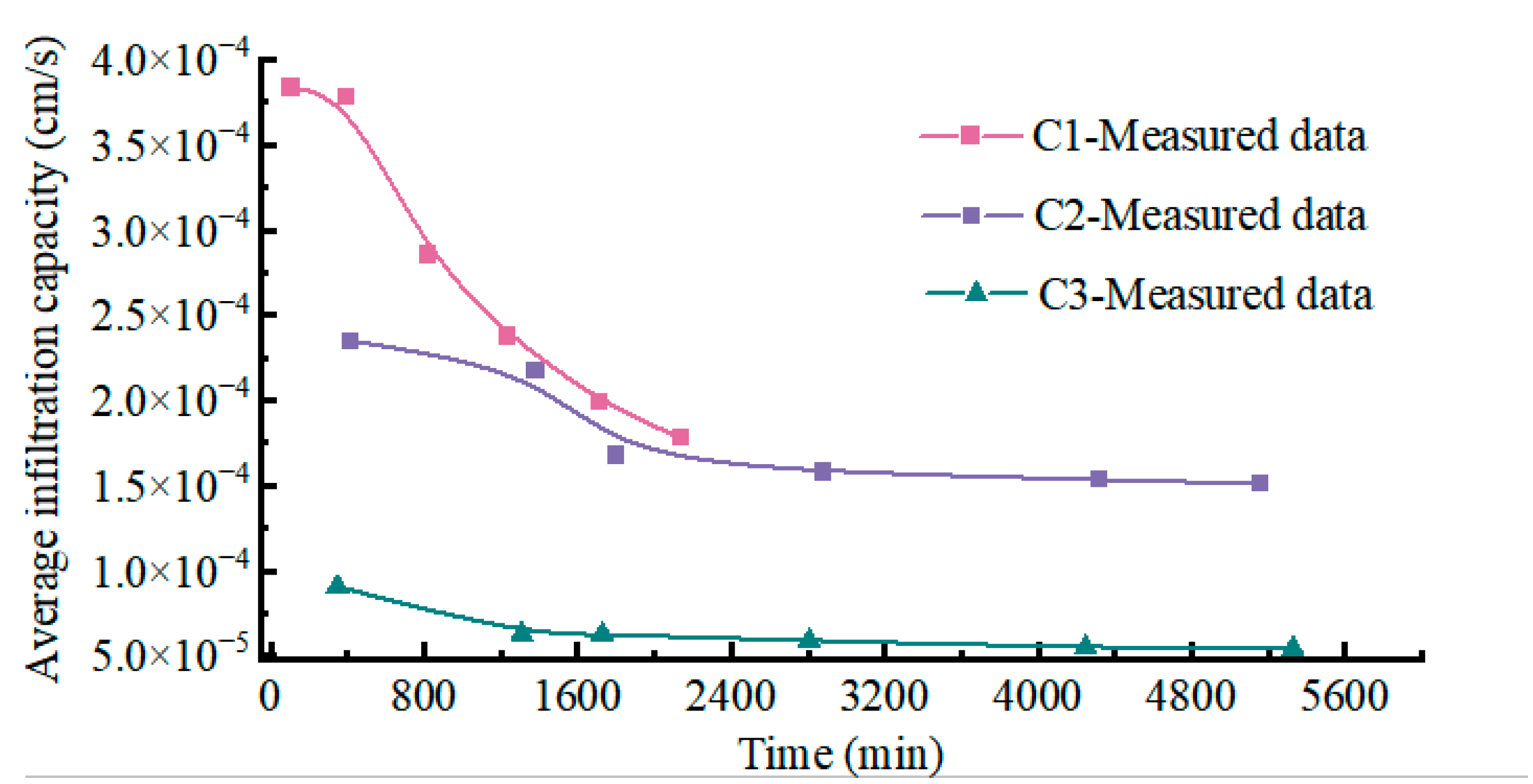
3.4. Infiltration and Infiltration Rate
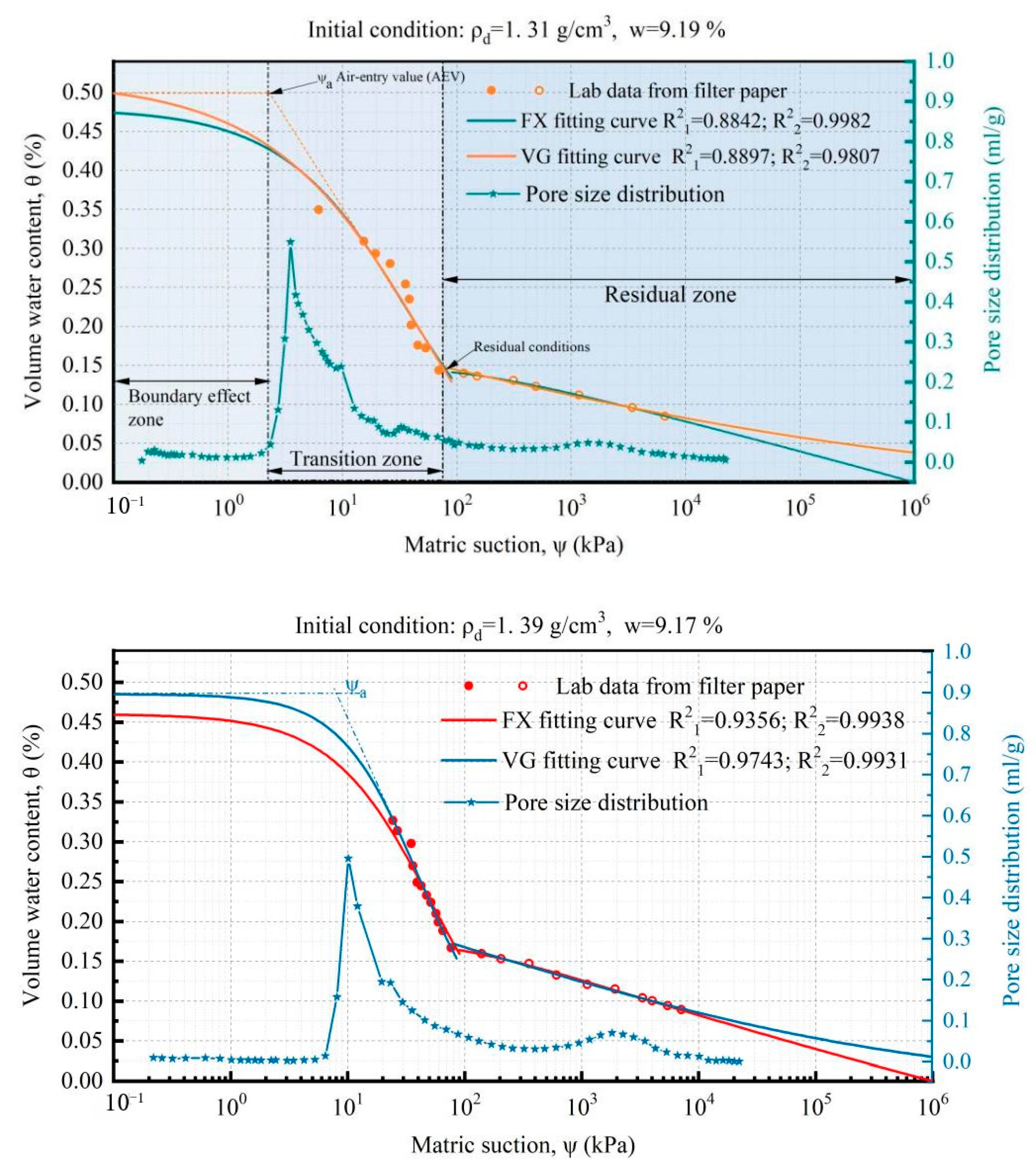
3.5. SWCC and Pore Size Distribution (PSD) Curves
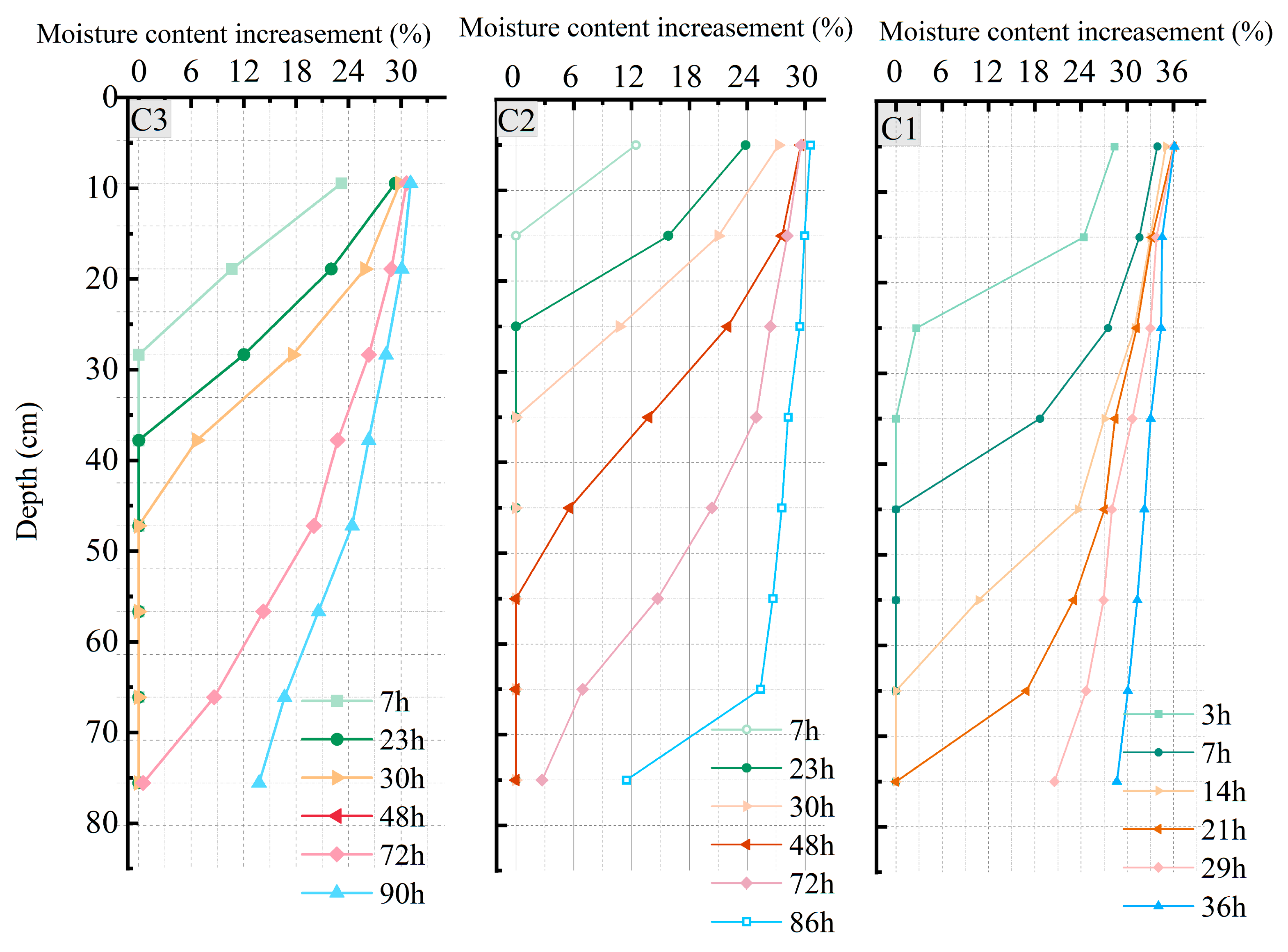
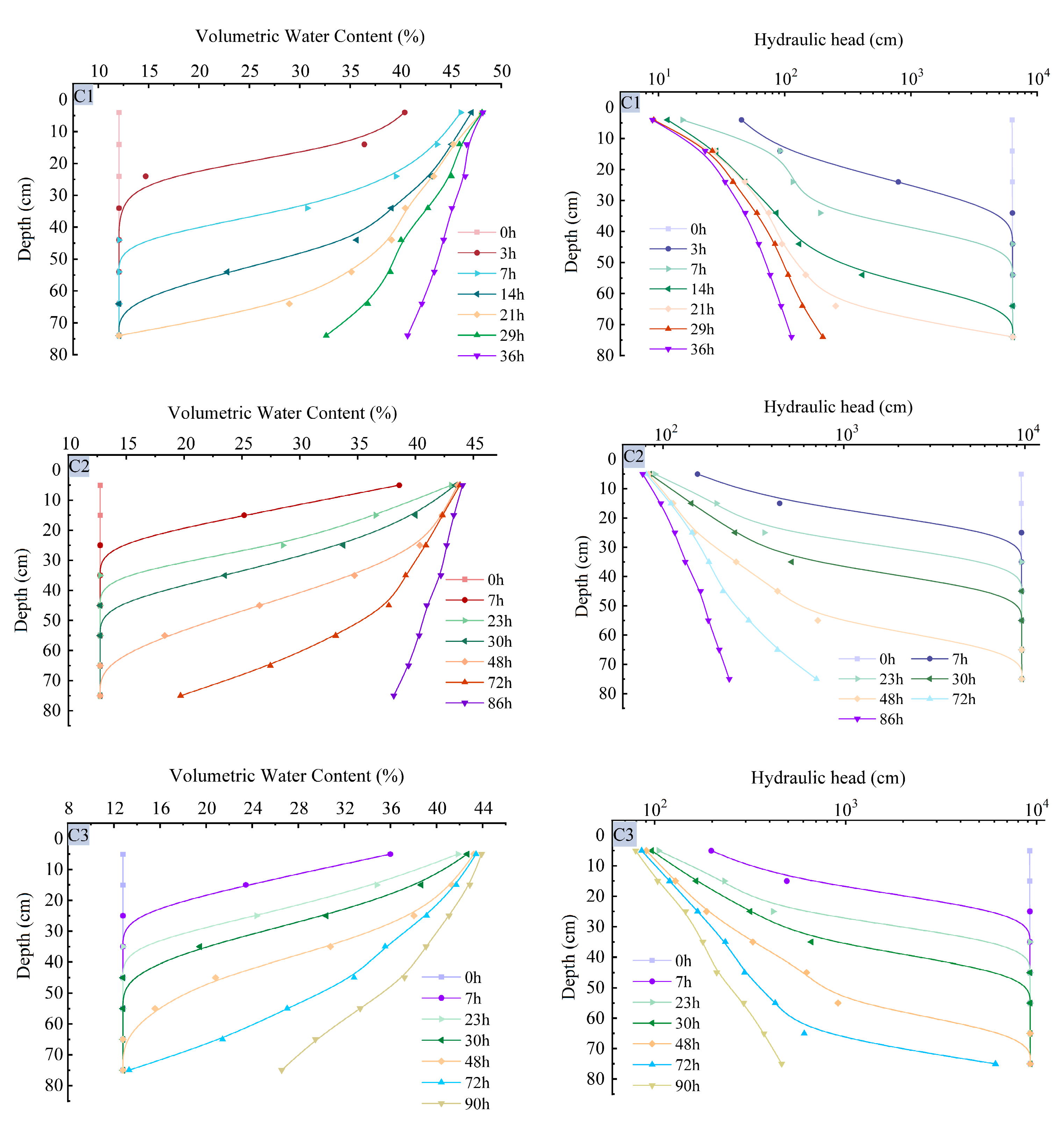
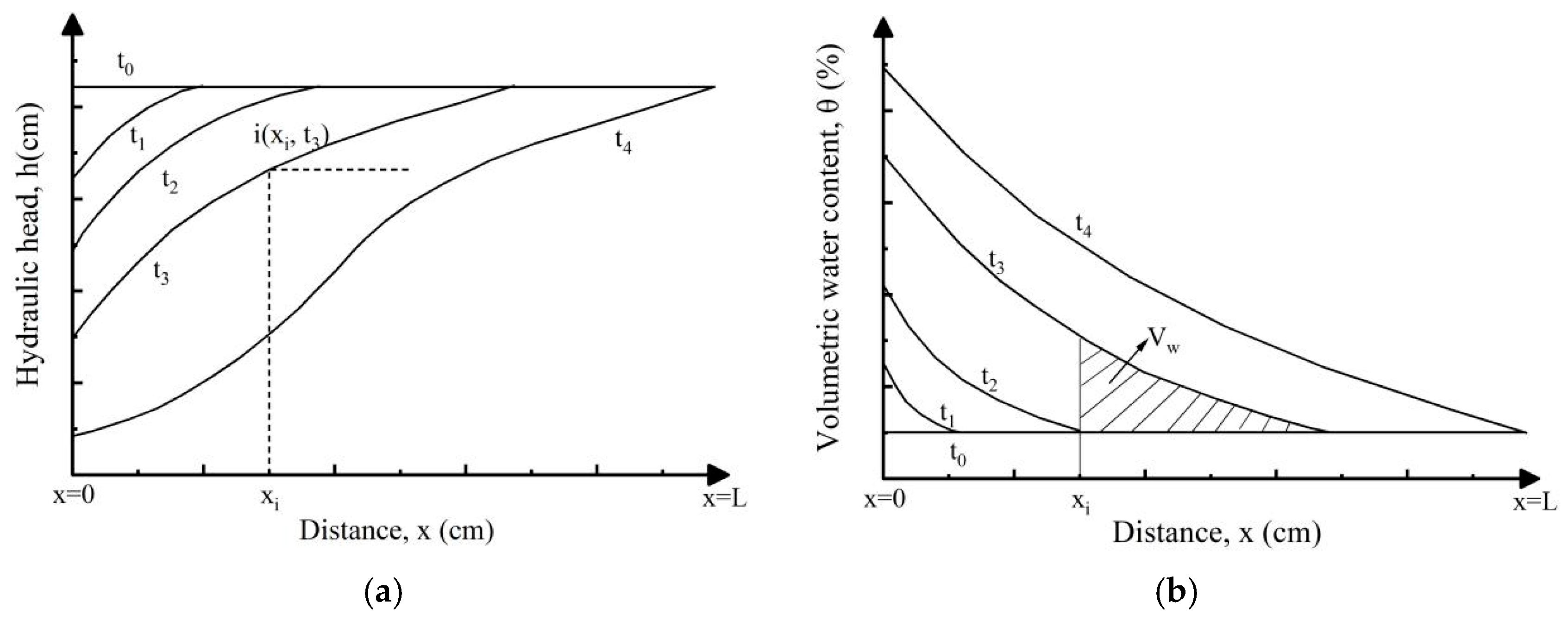
3.6. Soil Column Moisture Profile
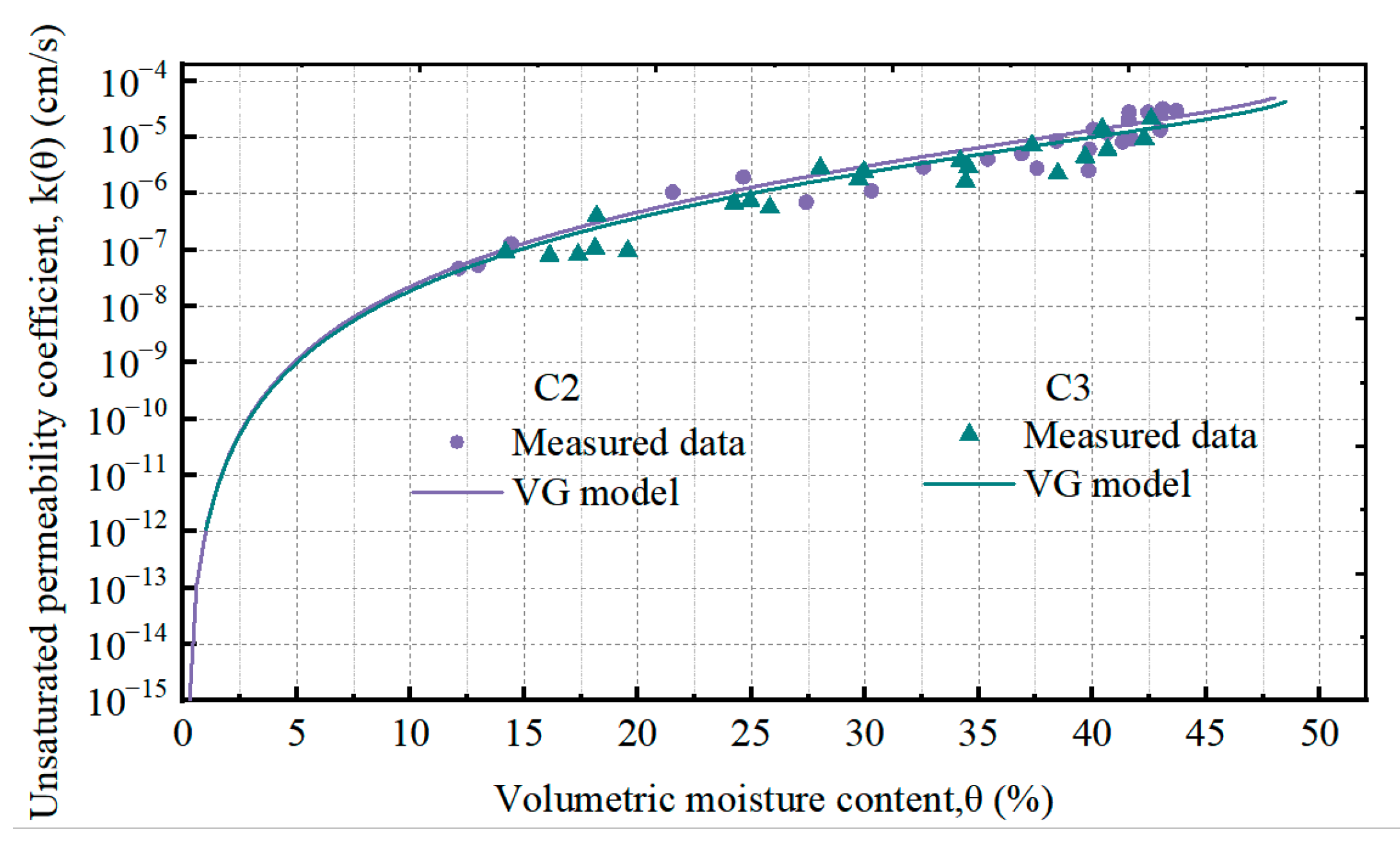
3.7. HCF
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.Y.; Chen, H.W.; Wu, W.C. Numerical modeling of interactions of rainfall and earthquakes on slope stability analysis. Environ. Earth Sci. 2021, 80, 524. [Google Scholar] [CrossRef]
- Chen, L.; Voss, C.I.; Fortier, D.; McKenzie, J.M. Surface energy balance of sub-Arctic roads with varying snow regimes and properties in permafrost regions. Permafr. Periglac. Process. 2021, 32, 681–701. [Google Scholar] [CrossRef]
- Vonk, J.E.; Tank, S.E.; Bowden, W.B.; Laurion, I.; Vincent, W.F.; Alekseychik, P.; Amyot, M.; Billet, M.F.; Canario, J.; Cory, R.M.; et al. Reviews and syntheses: Effects of permafrost thaw on Arctic aquatic ecosystems. Biogeosciences 2015, 12, 7129–7167. [Google Scholar] [CrossRef]
- Lin, H.Z.; Yu, Y.Z.; Li, G.X.; Peng, J.B. Influence of rainfall characteristics on soil slope failure. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock. Mech. Eng. 2009, 28, 198–204. (In Chinese) [Google Scholar]
- Bujang, J.S.; Zakaria, M.H.; Arshad, A.B. Distribution and significance of seagrass ecosystems in Malaysia. Aquat. Ecosyst. Health Manag. 2006, 9, 203–214. [Google Scholar] [CrossRef]
- Gofar, N.; Lee, L.M.; Kassim, A. Instrumented soil column model for rainfall infiltration study. In Proceedings of the International Conference of Geotechnical & Highway Engineering, Kuala Lumpur, Malaysia, 26–27 May 2008. [Google Scholar]
- Shaw-Shong, L. Slope failures in tropical residual soil. In Tropical Residual Soils Engineering; Huat, B.B.K., Sew, G.S., Ali, F.H.J., Eds.; Balkema: Leiden, The Netherlands, 2004; pp. 71–102. [Google Scholar]
- Srivastava, R.; Yeh, J.T.-C. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Leconte, R.; Brissette, F.P. Soil moisture profile model for two-layered soil based on sharp wetting front approach. J. Hydrol. Eng. 2001, 6, 141–149. [Google Scholar] [CrossRef]
- Huat, B.B.K.; Ali, F.H.; Low, T.H. Water infiltration characteristics of unsaturated soil slope and its effect on suction and stability. Geotech. Geol. Eng. 2006, 24, 1293–1306. [Google Scholar] [CrossRef]
- Guo, X.L.; Huang, K.; Li, J.; Kuang, Y.; Chen, Y.; Jiang, C.; Luo, M.; Zhou, H. Rainfall–runoff process simulation in the karst spring basins using a sac–tank model. J. Hydrol. Eng. 2023, 9, 28. [Google Scholar] [CrossRef]
- Zhao, S.Y.; Zheng, Y.R.; Shi, W.M.; Wang, J.L. Analysis on safety factor of slope by strength reduction FEM. Chin. J. Geotech. Eng. 2002, 24, 343–346. [Google Scholar]
- Zheng, Y.R. Development and application of numerical limit analysis for geological mater. Chin. J. Rock. Mech. Eng. 2012, 31, 1297–1316. [Google Scholar]
- Xu, B.N.; Pei, X.; Li, J.-J.; Yang, H.; Wang, X. Exploring the stability of unsaturated soil slope under rainfall infiltration conditions: A study based on multivariate interrelated random fields using R-vine copula. Catena 2024, 234, 107587. [Google Scholar] [CrossRef]
- Fred, T.; Vahedifard, F. Analytical solution for coupled hydro-mechanical modeling of infiltration in unsaturated soils. J. Hydrol. 2022, 612, 128198. [Google Scholar]
- Yang, H.; Rahardjo, H.; Leong, E.C. Behavior of Unsaturated Layered Soil Columns during Infiltration. J. Hydrol. Eng. 2006, 11, 329–337. [Google Scholar] [CrossRef]
- Ibrahim, A.; Mukhlisin, M.; Jaafar, O. Effect of rainfall infiltration into unsaturated soil using soil column. AIP Conf. Proc. 2018, 1930, 020022. [Google Scholar]
- Zhang, L.; Jiang, X.; Sun, R.; Gu, H.; Fu, Y.; Qiu, Y. Stability analysis of unsaturated soil slopes with cracks under rainfall infiltration conditions. Comput. Geotech. 2024, 165, 105907. [Google Scholar] [CrossRef]
- Mohd, A.M.I.; Nur, H.H.; Ng Soon, M.; Mohd, H.Z.A.; Saiful Azhar Ahmad, T.; Aziman, M. Analysis of infiltration-suction response in unsaturated residual soil slope in Gelugor, Penang. J. Phys. Conf. Ser. 2018, 995, 012052. [Google Scholar]
- Serrano, S.E. Stochastic differential equation models of erratic infiltration. Water Resour. Res. 1990, 264, 703–711. [Google Scholar] [CrossRef]
- Kargas, G.; Kerkides, P. A Contribution to the Study of the Phenomenon of Horizontal Infiltration. Water Resour. Manag. 2011, 25, 1131–1141. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Morgenstern, N.R. Stress state variables for unsaturated soils. J. Geotech. Eng. Div. 1977, 103, 447–466. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil mechanics principles for highway engineering in Arid regions. In Soil Mechanics Considerations: Arid and Semiarid Areas; Transportation Research Record: Washington, DC, USA, 1987; Volume 1137, pp. 1–11. [Google Scholar]
- Meyer, M.P.; Knight, S.J. Trafficability of Soils: Soil Classification; University of Illinois: Urbana, IL, USA, 1961. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kim, H.; Ganju, E.; Tang, D.; Prezzi, M.; Salgado, R. Matric suction measurements of compacted subgrade soils. Road Mater. Pavement Des. 2015, 16, 358–378. [Google Scholar] [CrossRef]
- Likos, W.J.; Lu, N. Filter paper column for measuring transient suction profiles in expansive clay. Transp. Res. Rec. J. Transp. Res. Board 2023, 1821, 83–89. [Google Scholar] [CrossRef]
- Li, L.C.; Li, X.A.; Wang, L.; Hong, B.; Shi, J.; Sun, J. The effects of soil shrinkage during centrifuge tests on SWCC and soil microstructure measurements. Bull. Eng. Geol. Environ. 2020, 79, 3879–3895. [Google Scholar] [CrossRef]
- Li, L.C.; Li, X.A.; Lei, H.N.; Hong, B.; Wang, L.; Zheng, H. On the characterization of the shrinkage behavior and soil-water retention curves of four soils using centrifugation and their relation to the soil structure. Arab. J. Geosci. 2020, 13, 1259. [Google Scholar] [CrossRef]
- Xie, X.; Li, P.; Hou, X.; Li, T.; Zhang, G. Microstructure of Compacted Loess and Its Influence on the Soil-Water Characteristic Curve. Adv. Mater. Sci. Eng. 2020, 1, 3402607. [Google Scholar] [CrossRef]
- Hou, X.K.; Qi, S.W.; Li, T.; Guo, S.; Wang, Y.; Li, Y.; Zhang, L. Microstructure and soil-water retention behavior of compacted and intact silt loess. Eng. Geol. 2020, 277, 105814. [Google Scholar] [CrossRef]
- Birle, E.; Heyer, D.; Vogt, N. Influence of the initial water content and dry density on the soil–water retention curve and the shrinkage behavior of a compacted clay. Acta Geotech. 2008, 3, 191–200. [Google Scholar] [CrossRef]
- Bulut, R.; Lytton, R.; Wray, W. Soil suction measurements by filter paper. In Proceedings of the Geo-Institute Shallow Foundation and Soil Properties Committee Sessions at the ASCE 2001 Civil Engineering Conference, Houston, TX, USA, 10–13 October 2001; pp. 243–261. [Google Scholar]
- Li, H.; Li, T.L.; Jiang, R.J.; Fan, J.W. Measurement of unsaturated permeability curve based on filter paper method. Rock Soil Mech. 2020, 41, 1–10. [Google Scholar]
- Chandler, R.; Gutierrez, C. The filter-paper method for suction measurement. Geotechnique 1986, 36, 265–268. [Google Scholar] [CrossRef]
- Crilly, M.; Chandler, R. A Method for Determining the State of Desiccation in Clay Soils; Building Research Establishment: Garston, UK, 1993. [Google Scholar]
- An, P.; Zhang, A.J.; Liu, H.T.; Wang, T. Degradation mechanism of long-term seepage and permeability analysis of remolded saturated loess. Rock Mech. 2013, 34, 147–153. [Google Scholar]
- Green, W.H.; Ampt, G.A. Studies on soil physics I. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Kostiakov, A.N. On the dynamics of the coefficient of water-percolation in soils and on the necessity of studying it from a dynamic point of view for purposes of amelioration. Trans. 6th Comm. Int. Soc. Soil Sci. Russ. 1932, A, 17–21. [Google Scholar]
- Horton, R.E. An Approach Toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of Infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar]
- Wang, X.J. The Water Potential Description, Theoretical Models Study of Rainfall Infiltration and Application. Ph.D. Thesis, Tsinghua University, Beijing, China, 2010; pp. 90–91. [Google Scholar]
- Romero, E.; Gens, A.; Lloret, A. Water permeability, water retention and microstructure of unsaturated compacted Boom clay. Eng. Geol. 1999, 54, 117–127. [Google Scholar] [CrossRef]
- Simms, P.H.; Yanful, E.K. Measurement and estimation of pore shrinkage and pore distribution in a clayey till during soil-water characteristic curve tests. Can. Geotech. J. 2001, 38, 741–754. [Google Scholar] [CrossRef]
- Aung, K.K.; Rahardjo, H.; Leong, E.C.; Toll, D.G. Relationship between porosimetry measurement and soil-Water characteristic curve for an unsaturated residual soil. Geotech. Geol. Eng. 2001, 19, 401–416. [Google Scholar] [CrossRef]
- Zhang, L.M.; Li, X. Micro Porosity Structure of Coarse Granular Soils. J. Geotech. Geoenvironmental Eng. 2010, 136, 1425–1436. [Google Scholar] [CrossRef]
- Mascarenha, M.; Cordão-Neto, M.P.; Romero, E. Influence of the Microstructure on the Hydro-Mechanical Behaviour of a Natural Silty Clay; Taylor & Francis: Abingdon, UK, 2011. [Google Scholar]
- Washburn, W.E. Note on a Method of Determining the Distribution of Pore Sizes in a Porous Material. Proc. Natl. Acad. Sci. USA 1921, 7, 115–116. [Google Scholar] [CrossRef]
- Cai, G.; Zhou, A.; Liu, Y.; Xu, R.; Zhao, C. Soil water retention behavior and microstructure evolution of lateritic soil in the suction range of 0-286.7 MPa. Acta Geotech. 2020, 15, 3327–3341. [Google Scholar] [CrossRef]
- Burton, G.; Pineda, J.A.; Sheng, D.C.; Airey, D.W. Microstructural changes of an undisturbed, reconstituted and compacted high plasticity clay subjected to wetting and drying. Eng. Geol. 2015, 193, 363–373. [Google Scholar] [CrossRef]
- Liu, X.; Buzzi, O.; Yuan, S.Y.; Mendes, J.; Fityus, S. Multi-scale characterization of the retention and shrinkage behaviour of four Australian clayey soils. Can. Geotech. J. 2015, 53, 854–870. [Google Scholar] [CrossRef]
- Sun, D.A.; Gao, Y.; Zhou, A.N.; Sheng, D.C. Soil–water retention curves and microstructures of undisturbed and compacted Guilin lateritic clay. Bull. Eng. Geol. Environ. 2016, 75, 781–791. [Google Scholar] [CrossRef]
- Gardner, W.R. Some Steady-State Solutions of the Unsaturated Moisture Flow Equation with Application to Evaporation from a Water Table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 1023–1025. [Google Scholar] [CrossRef]
- Burdine, N.T. Relative Permeability Calculations From Pore Size Distribution Data. Petr. Trans. Am Inst. Min. Metall. Eng. 1953, 98, 71–78. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]




| Soil Particle Composition/Parameter | Classification Criteria | Percent (%) | |||
|---|---|---|---|---|---|
| USDA | CH | QY | YA | LL | |
| Grit | d ≥ 2 mm | 0.00 | 0.00 | 0.00 | 0.00 |
| Sand | 2 > d ≥ 0.05 mm | 5.62 | 9.79 | 28.97 | 30.30 |
| Silt | 0.05 > d ≥ 0.002 mm | 77.08 | 70.20 | 65.59 | 62.90 |
| Clay | d < 0.002 mm | 17.30 | 10.01 | 5.44 | 6.80 |
| Soil particle composition | USCS classification | CH | QY | YA | LL |
| Grit | d ≥ 4.75 mm | 0.00 | 0.00 | 0.00 | 0.00 |
| Sand | 4.75 > d ≥ 0.075 mm | 0.29 | 3.30 | 8.69 | 9.77 |
| Silt | 0.075 > d ≥ 0.005 mm | 73.92 | 80.87 | 82.52 | 80.06 |
| Clay | d < 0.005 mm | 25.79 | 15.83 | 8.79 | 10.17 |
| Cu—Unevenness coefficient | 42.95 | 14.27 | 6.28 | 8.48 | |
| Cc—Coefficient of curvature | 6.15 | 16.95 | 1.56 | 1.66 | |
| Optimal moisture content (%) | 17.34 | 16.91 | 15.68 | 15.80 | |
| Maximum dry density (g/cm3) | 1.71 | 1.73 | 1.76 | 1.77 | |
| Liquid limit (%) | 35.12 | 32.23 | 31.33 | 27.60 | |
| Plastic limit (%) | 19.96 | 18.29 | 18.33 | 17.05 | |
| Plastic index | 15.16 | 13.94 | 13.00 | 10.55 | |
| Oxide Mass Wt (%) | SiO2 | A12O3 | CaO | Fe2O3 | MgO | K2O | Na2O | TiO2 | P2O5 | MnO | |
| XRF results | CH | 56.85 | 15.15 | 13.51 | 5.44 | 3.51 | 2.88 | 1.26 | 0.76 | 0.20 | 0.11 |
| QY | 59.72 | 14.50 | 11.77 | 4.68 | 3.51 | 2.70 | 1.79 | 0.71 | 0.21 | 0.10 | |
| YA | 59.47 | 14.72 | 11.82 | 5.07 | 3.21 | 2.79 | 1.59 | 0.72 | 0.20 | 0.10 | |
| LL | 58.41 | 14.90 | 13.32 | 5.65 | 3.19 | 2.81 | 1.65 | 0.71 | 0.22 | 0.11 | |
| Element Content (%) | Si | Ca | A1 | Fe | K | Mg | Na | Ti | Px | Sum | |
| Normalized mass percent (%) | CH | 51.95 | 13.53 | 15.57 | 7.14 | 4.67 | 4.01 | 2.08 | 0.84 | 0.21 | 100% |
| QY | 51.33 | 15.42 | 14.13 | 6.92 | 4.50 | 3.69 | 3.08 | 0.77 | 0.17 | 100% | |
| YA | 51.93 | 15.79 | 14.55 | 6.63 | 3.62 | 2.20 | 4.32 | 0.80 | 0.15 | 100% | |
| LL | 50.52 | 15.15 | 15.34 | 6.95 | 3.42 | 3.66 | 3.95 | 0.80 | 0.22 | 100% | |
| Samples | Density (g/cm3) | ||||||
|---|---|---|---|---|---|---|---|
| CH soil | 1.45 | 1.52 | 1.60 | 1.67 | |||
| QY soil | 1.45 | 1.57 | 1.63 | 1.72 | |||
| YA soil | 1.31 | 1.39 | 1.47 | 1.50 | 1.55 | 1.60 | 1.70 |
| LL soil | 1.45 | 1.50 | 1.57 | 1.65 | |||
| Column Number | Dry Density | Initial Moisture Content | Runoff | Hydraulic Head Difference | Water Supply Rate | Rainfall Intensity |
|---|---|---|---|---|---|---|
| C1 | 1.31 g/cm3 | 9.19% | None | 8 | 22 mm/min | Heavy rain |
| C2 | 1.39 g/cm3 | 9.17% | None | 8 | 22 mm/min | Heavy rain |
| C3 | 1.39 g/cm3 | 9.17% | Yes | 8 | 22 mm/min | Heavy rain |
| Soil Column No. | Kostiakov Model | R2 | Philip Model | R2 | |
|---|---|---|---|---|---|
| Instantaneous infiltration rate | C1 | I(t) = 0.00495t−0.50578 | 0.9545 | I(t) = 6 × 10−4 + 0.0036t−0.5 | 0.8721 |
| C2 | I(t) = 1.08 × 10−4t−0.0596 | 0.9576 | I(t) = 5 × 10−4 + 0.00068t−0.5 | 0.9623 | |
| C3 | I(t) = 1.70 × 10−4t−0.1532 | 0.9831 | I(t) = 4.5 × 10−4 + 0.00040t−0.5 | 0.9473 | |
| Parameters Model | Gardner | VG | |||||
|---|---|---|---|---|---|---|---|
| n | a | R2 | n | a | R2 | ||
| k(ψ) | C1 | 1.38377 | 0.54747 | 0.7536 | 1.64234 | 0.09035 | 0.8463 |
| C2 | 3.18836 | 0.13933 | 0.81379 | 2.58966 | 0.06578 | 0.8167 | |
| C3 | 2.63563 | 0.1457 | 0.7698 | 1.50646 | 0.02109 | 0.7378 | |
| k(θ) | C1 | 2.32000 | 0.8791 | ||||
| C2 | 2.11924 | 0.7871 | |||||
| C3 | 2.16766 | 0.7714 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, X.; Li, Y.; Li, C.; Li, Y.; Wang, L.; He, Y.; Yao, C. An Analysis of Vertical Infiltration Responses in Unsaturated Soil Columns from Permafrost Regions. Appl. Sci. 2024, 14, 10195. https://doi.org/10.3390/app142210195
Li L, Li X, Li Y, Li C, Li Y, Wang L, He Y, Yao C. An Analysis of Vertical Infiltration Responses in Unsaturated Soil Columns from Permafrost Regions. Applied Sciences. 2024; 14(22):10195. https://doi.org/10.3390/app142210195
Chicago/Turabian StyleLi, Lincui, Xi’an Li, Yonghong Li, Cheng Li, Yong Li, Li Wang, Yiping He, and Chaowei Yao. 2024. "An Analysis of Vertical Infiltration Responses in Unsaturated Soil Columns from Permafrost Regions" Applied Sciences 14, no. 22: 10195. https://doi.org/10.3390/app142210195
APA StyleLi, L., Li, X., Li, Y., Li, C., Li, Y., Wang, L., He, Y., & Yao, C. (2024). An Analysis of Vertical Infiltration Responses in Unsaturated Soil Columns from Permafrost Regions. Applied Sciences, 14(22), 10195. https://doi.org/10.3390/app142210195






