Experimental Investigations of Seismic Performance of Girder–Integral Abutment–Reinforced-Concrete Pile–Soil Systems
Abstract
:1. Introduction
2. Methodology
3. Experimental Tests
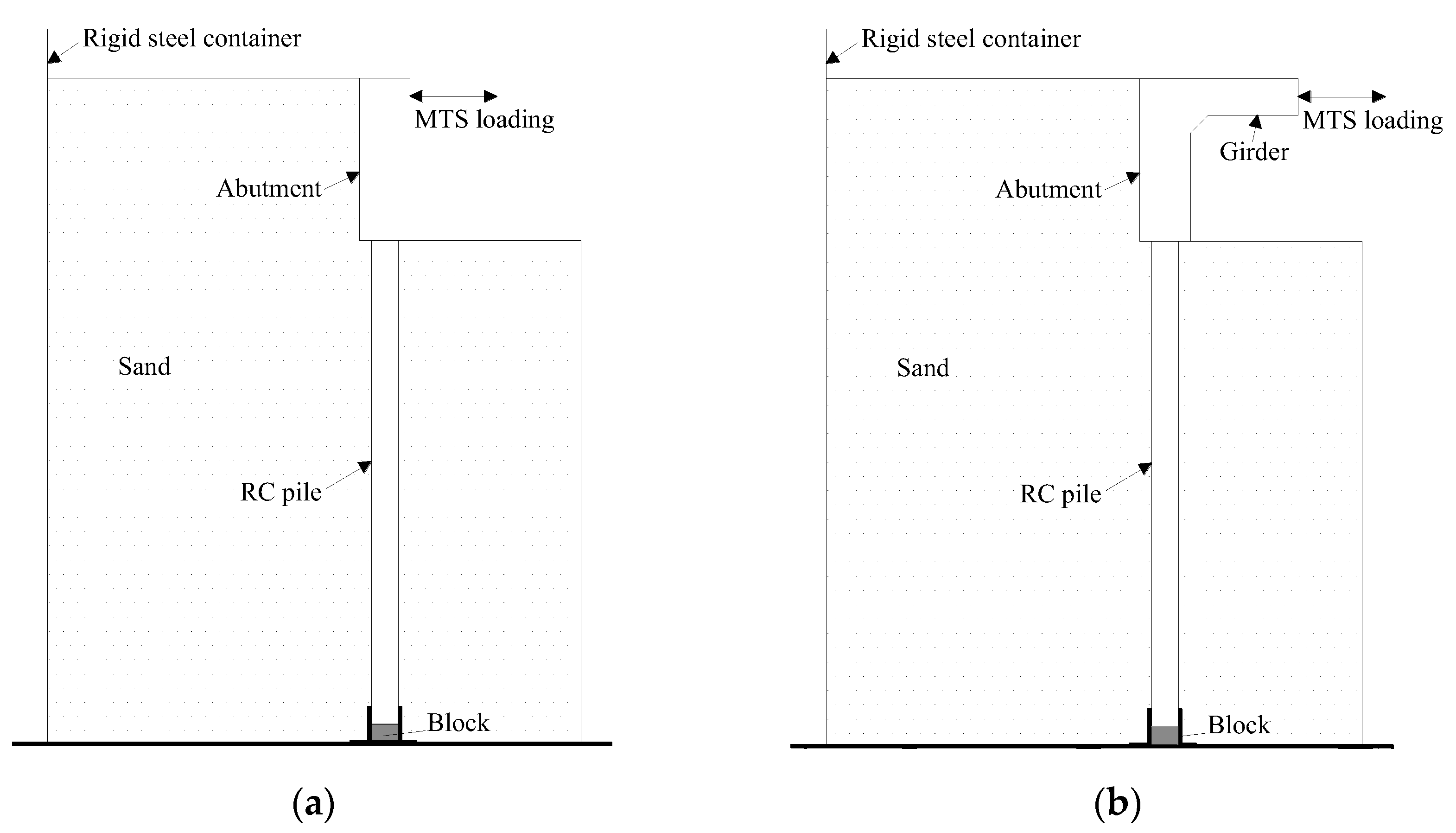
3.1. Case Study
3.2. Specimen Design
3.2.1. Girder Specimen Design
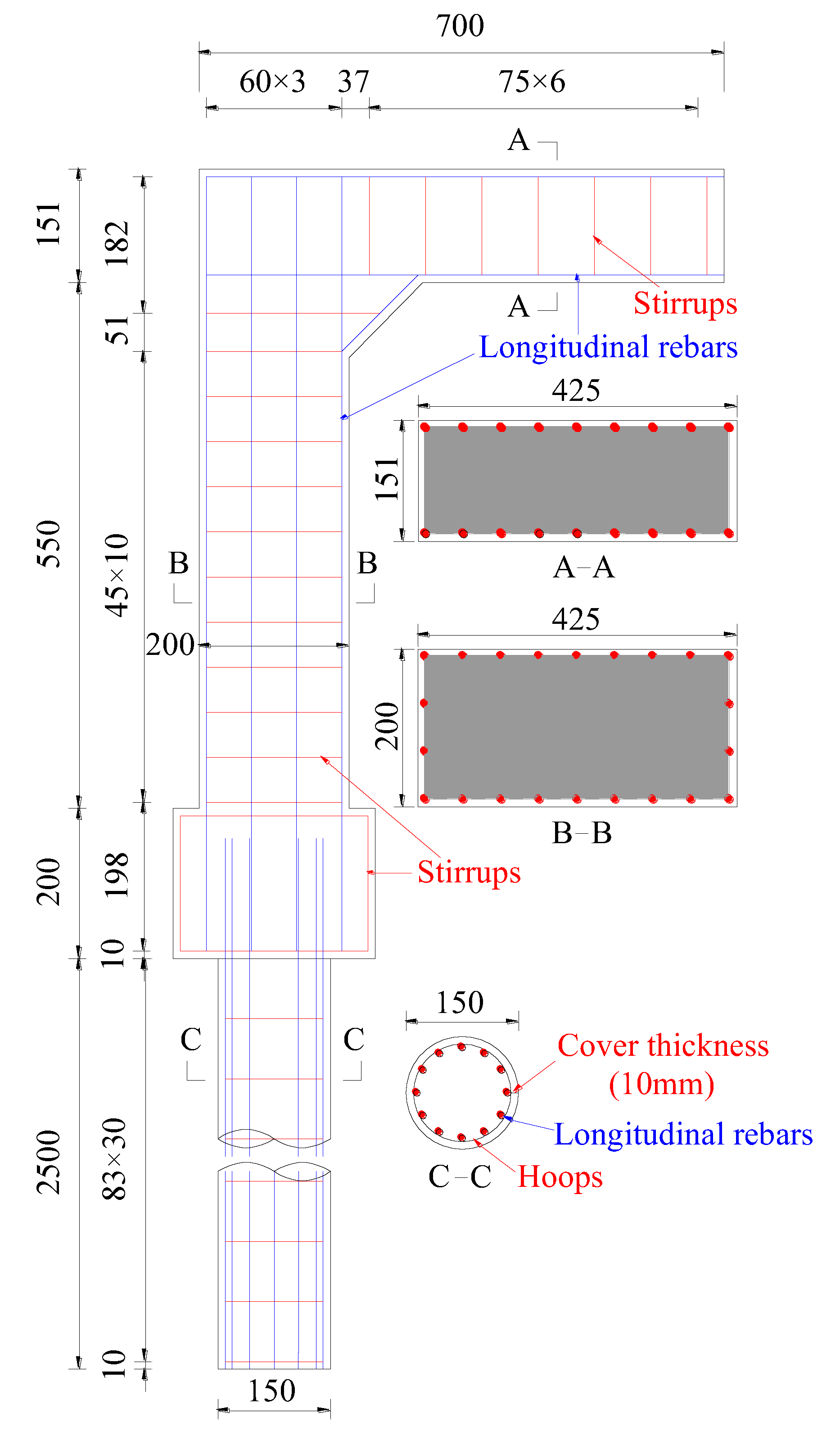
3.2.2. Integral Abutment and Pile Specimen Design
3.3. Specimen Fabrication
- The rebar cages for the girder–integral abutment–pile cap connection and pile were fabricated, as shown in Figure 4a,b;
- The rebar cages for the girder–integral abutment–pile cap connection were placed in the timber formwork, and two high-strength threaded rods with a 30 mm diameter were embedded to connect the girder to the MTS hydraulic actuator, as shown in Figure 4c;
- The pile was cast using C30 concrete and cured at normal atmospheric temperature for 28 days, as shown in Figure 4d;
- The rebars that extended from the top surface of the pile were welded to the rebar cages of the pile cap to form the girder–integral abutment–pile cap connection, as shown in Figure 4e;
- The girder–integral abutment–pile cap connection was cast using C50 concrete and cured at normal atmospheric temperature for 28 days. The girder–integral abutment–pile specimen can be obtained, as shown in Figure 4f.
3.4. Soil Container and Filling Materials
3.5. Test Setup
3.5.1. Loading Devices
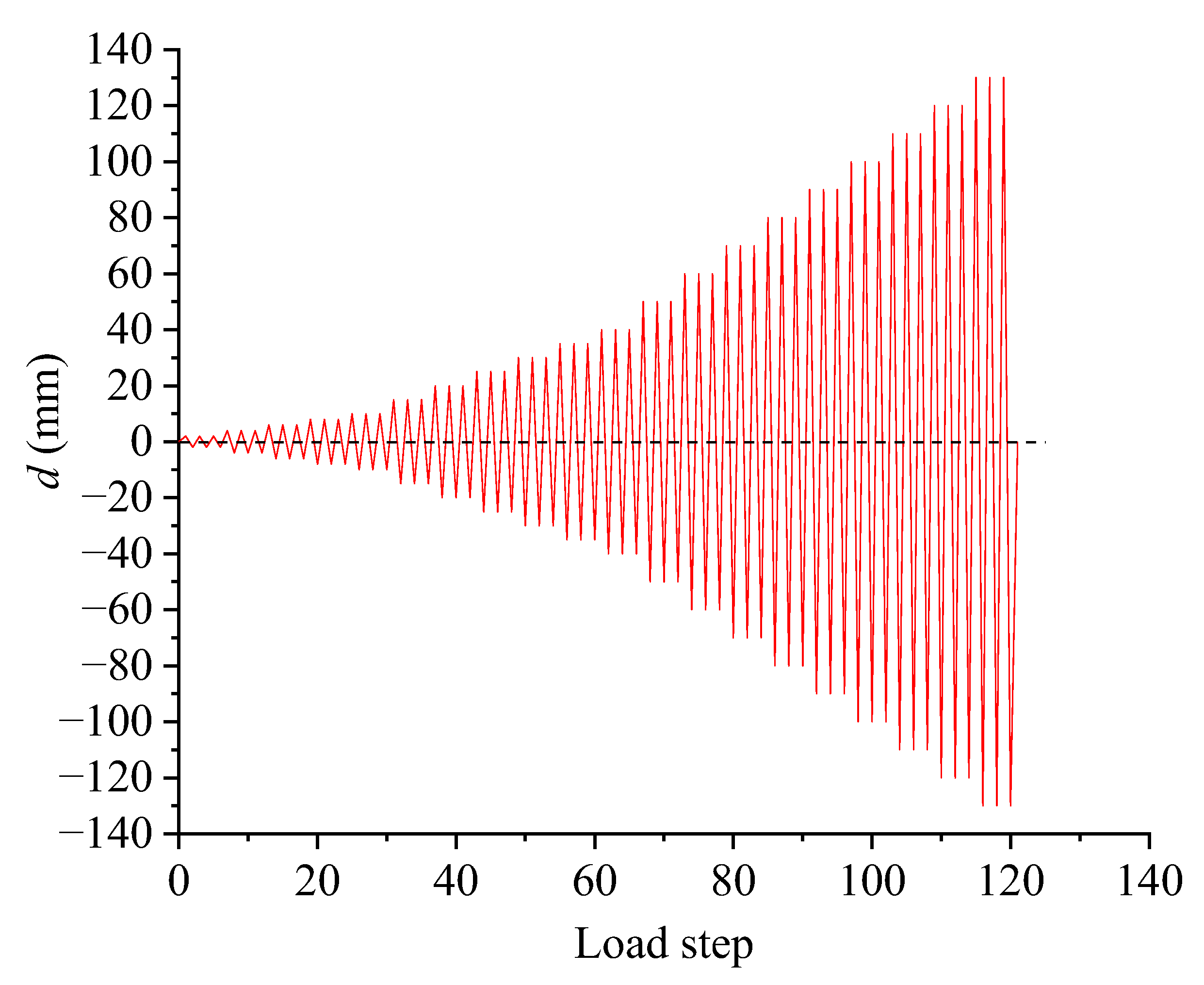
3.5.2. Loading Protocol
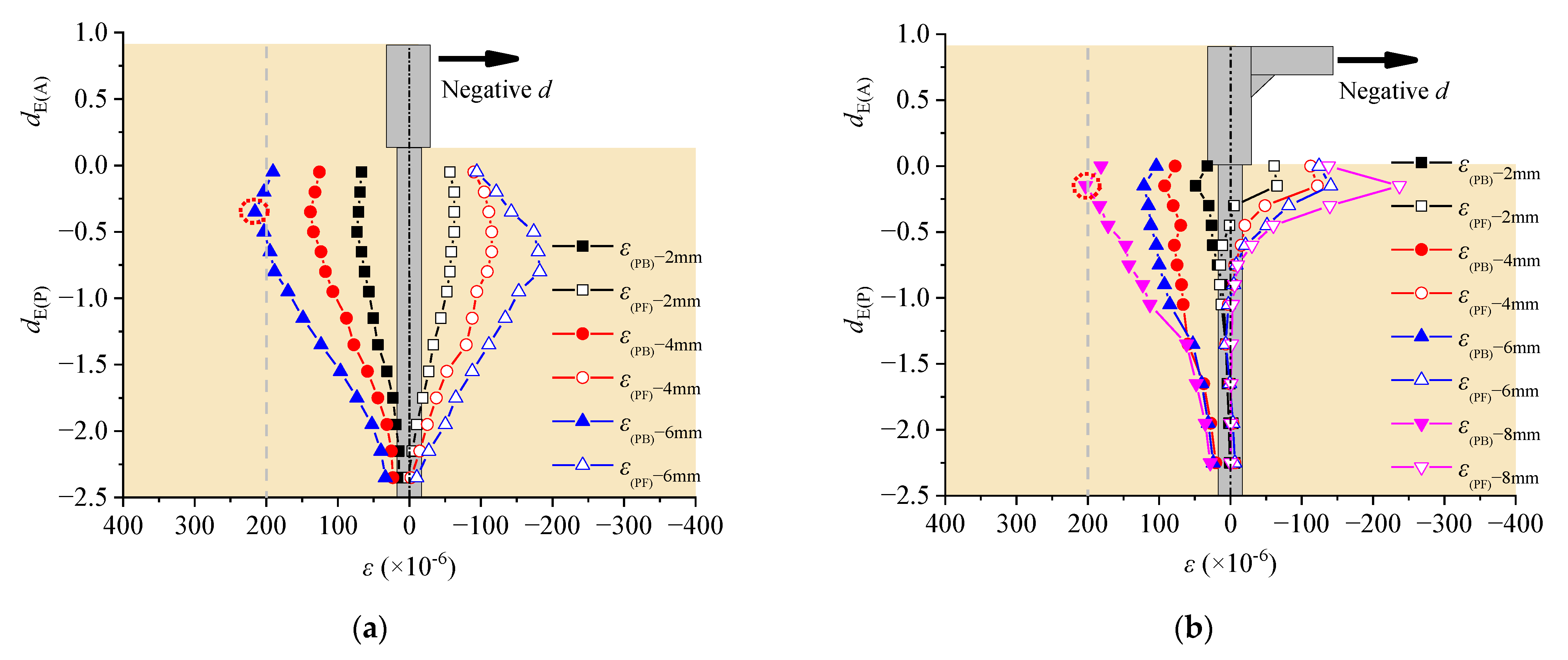
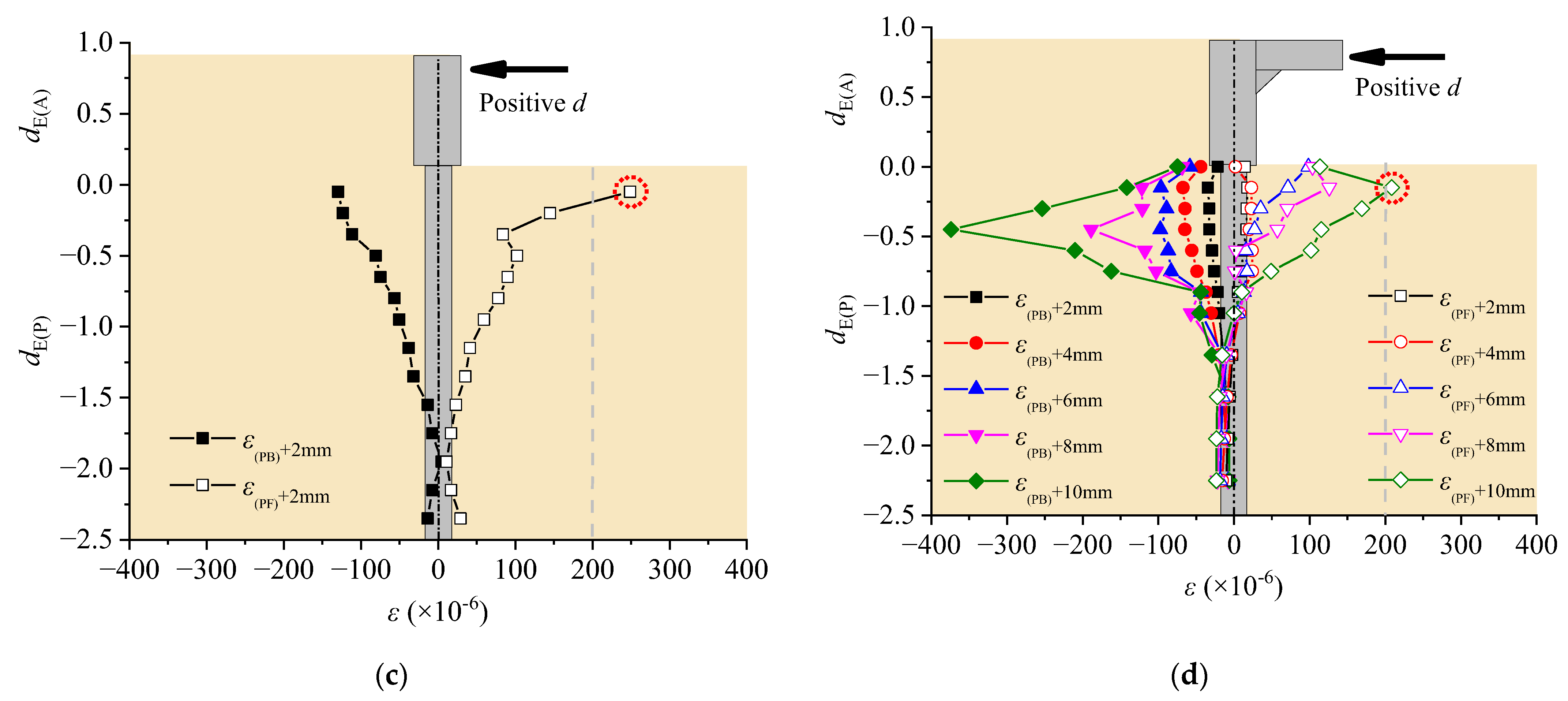
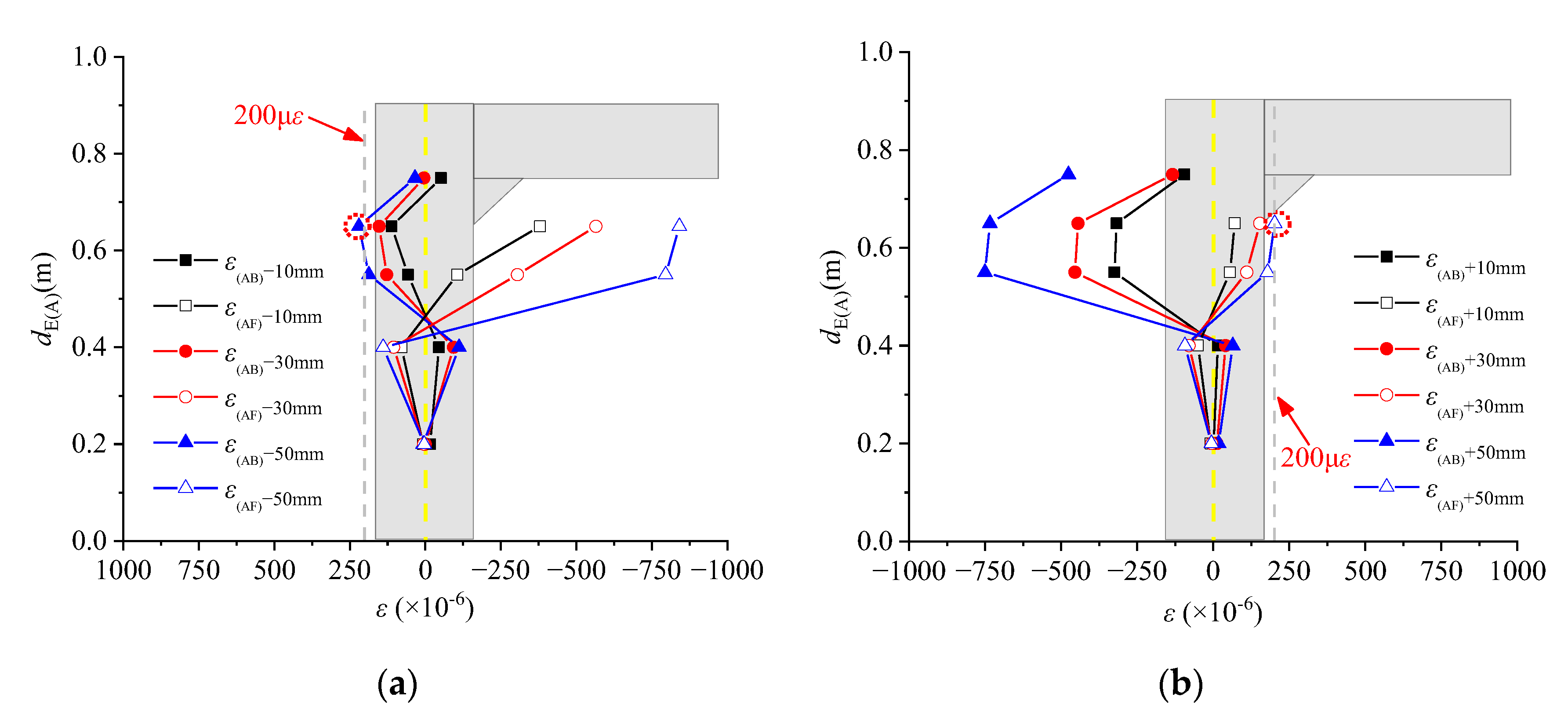
3.6. Instrument Setup
4. Experimental Results
4.1. Failure Mode
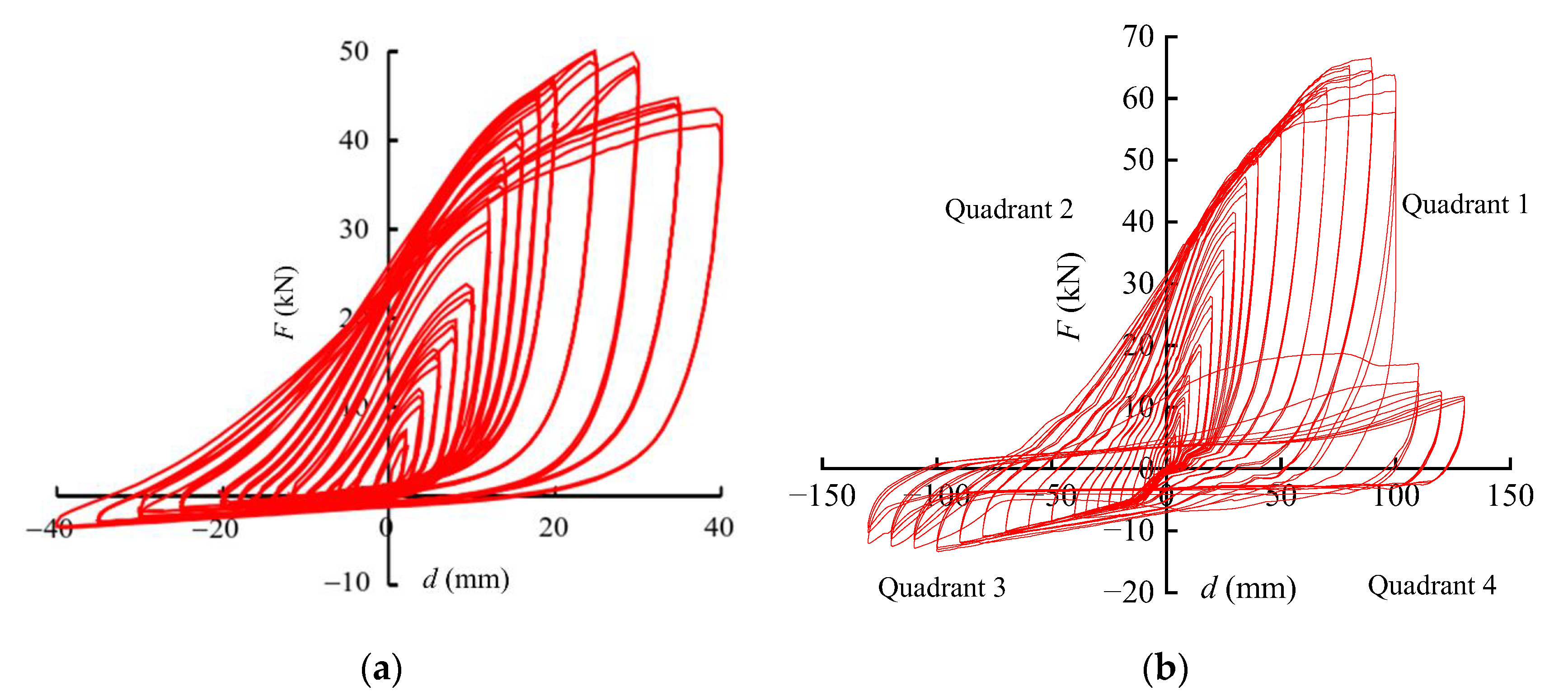
4.2. Hysteresis Curve
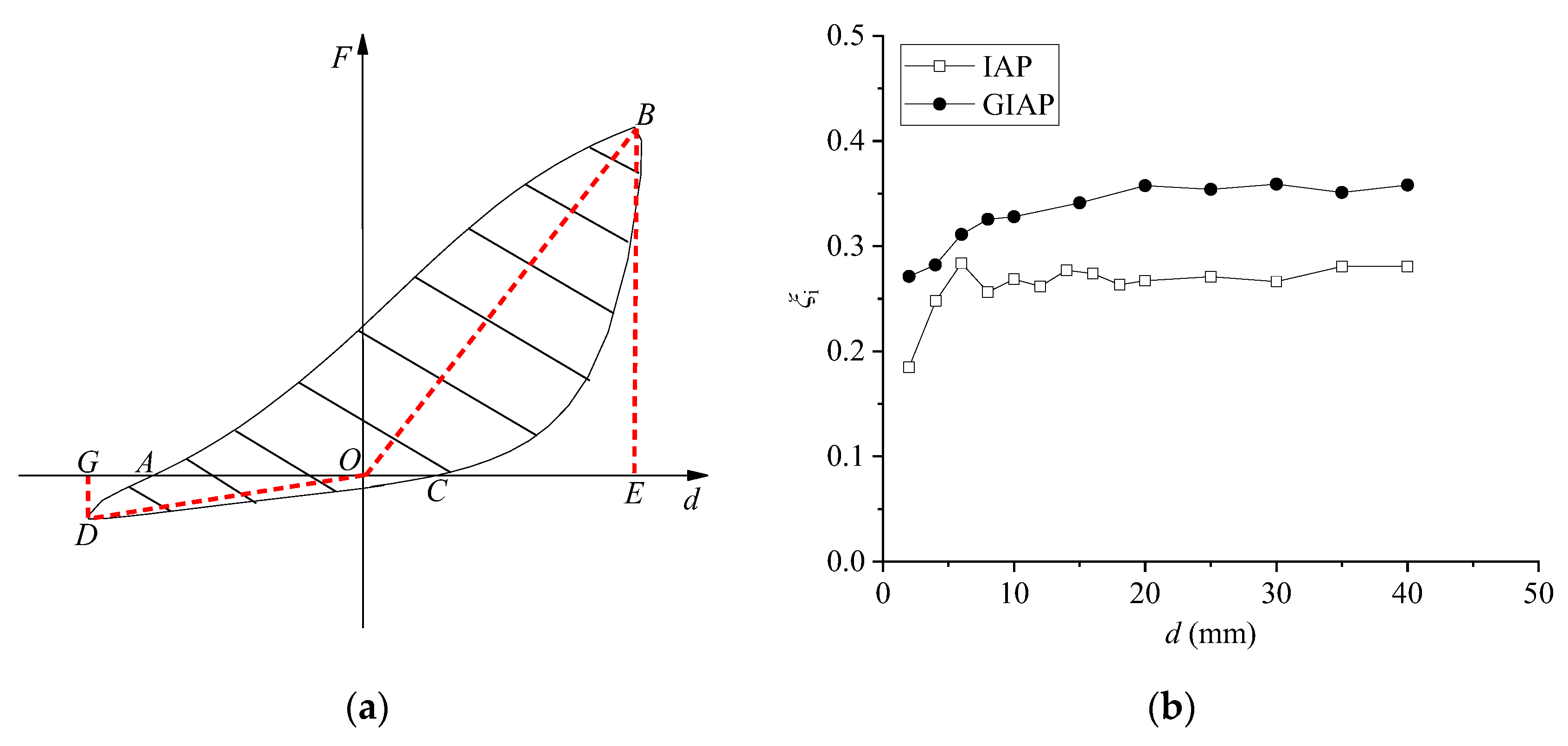
4.3. Equivalent Viscous Damping Ratio
4.4. Skeleton Curve
4.5. Displacement Ductility
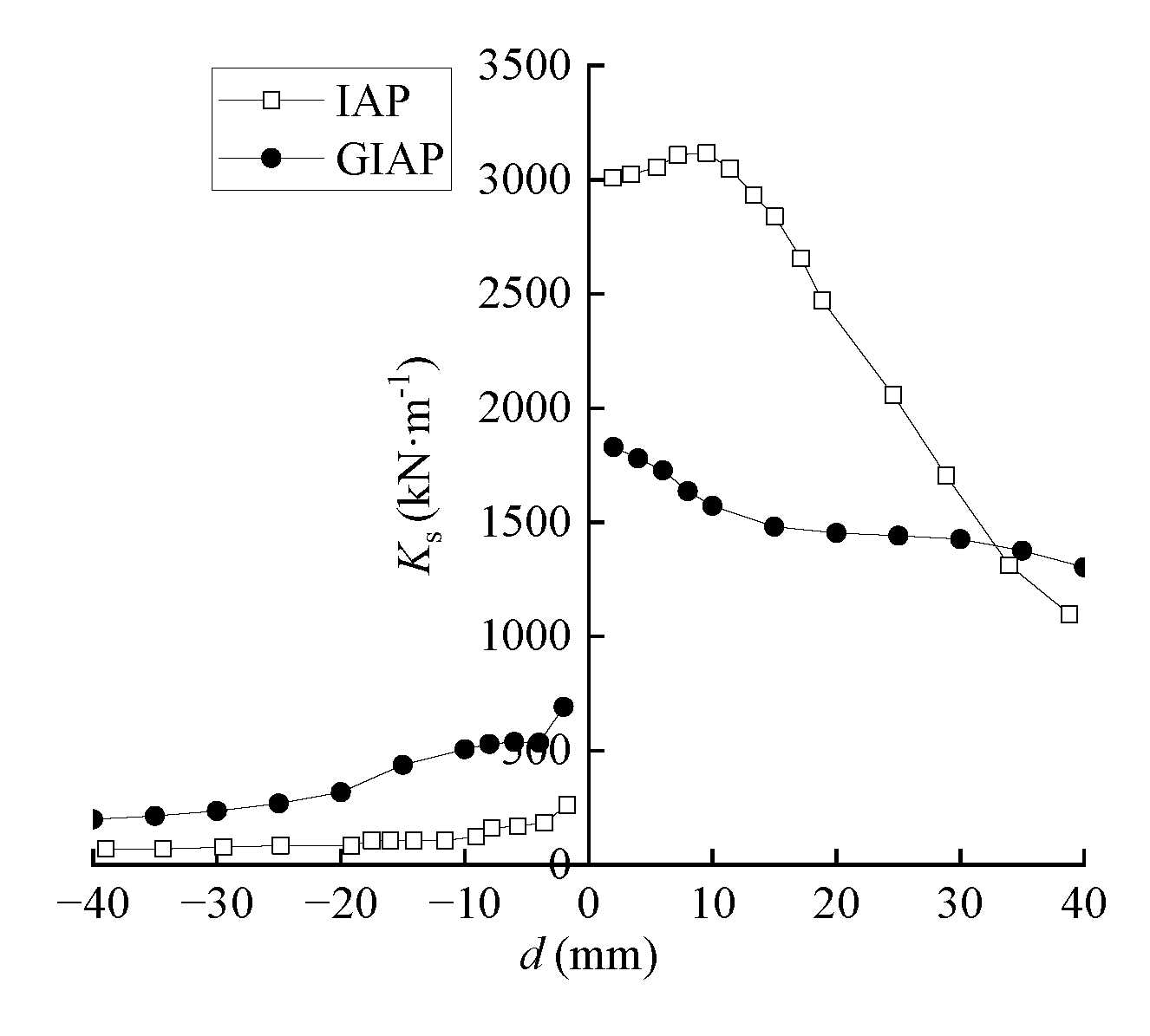
4.6. Stiffness Degradation
5. Conclusions
- The failure modes of the girder–integral abutment–pile system with or without the girder were different. For the integral abutment–pile system, only the piles were severely damaged, and no damage could be found to the abutments. For the girder–integral abutment–pile system, the piles were damaged at the beginning and then the abutments were also damaged under a large horizontal displacement. Compared to the system without the girder, the horizontal displacement corresponding to the first crack on the pile of the girder–integral abutment–pile system was larger, and the damage to the pile was less severe, which is beneficial to the piles. The damage to the abutments in the girder–integral abutment–pile system should attract attention;
- Compared to the system without a girder, reductions of 39.2%, 22.6%, and 12.6% in the initial stiffness under positive horizontal displacement, residual force accumulation, and residual deformation were observed in the girder–integral abutment–pile system, respectively. Increments of 112.6%, 67.2%, 30.8%, 20.4%, and 7.8% in the initial stiffness under negative horizontal displacement, displacement ductility ratio, average equivalent viscous damping ratio, yield load, and ultimate load were observed in the girder–integral abutment–pile system, respectively;
- Compared to the system without the girder, a smaller elastoplastic stage range and a larger elastic stage range of the skeleton curve, as well as less reduction in the stiffness, were observed in the girder–integral abutment–pile system;
- To accurately reflect the seismic performance of a girder–integral abutment–RC pile–soil system, it is suggested to consider the girder. When the girder was considered, the resistance of the girder–integral abutment–RC pile–soil system against earthquakes increased because of the increased energy dissipation capacity and displacement ductility, as well as the decreased stiffness degradation. Moreover, the failure mode of the specimen changed from severe damage to the pile top under a small displacement to damage to both the abutment and pile top under a large displacement. From a practical point of view, the repair of abutments is easier than that of piles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, F.Y.; Lin, Y.W.; Chen, J.F.; Yang, F.F. Interaction of integral abutment-H-shaped steel pile-soil under reciprocating low-cycle pseudo-static test. China J. Highw. Transp. 2019, 32, 100–114. (In Chinese) [Google Scholar]
- Aloisio, A.; Pelliciari, M.; Xue, J.Q.; Fragiacomo, M.; Briseghella, B. Effect of pre-hole filled with high-damping material on the inelastic response spectrum of integral abutment bridges. J. Earthq. Eng. 2023, 27, 3319–3340. [Google Scholar] [CrossRef]
- Dicleli, M.; Erhan, S. Effect of soil and substructure properties on live-load distribution in integral abutment bridges. J. Bridge Eng. 2008, 13, 527–539. [Google Scholar] [CrossRef]
- Khodair, Y.A.; Hassiotis, S. Analysis of soil–pile interaction in integral abutment. Comput. Geotech. 2005, 32, 201–209. [Google Scholar] [CrossRef]
- Arockiasamy, M.; Butrieng, N.; Sivakumar, M. State-of-the-art of integral abutment bridges: Design and practice. J. Bridge Eng. 2004, 9, 497–506. [Google Scholar] [CrossRef]
- Kim, W.; Laman, J.A.; Zareian, F.; Min, G.; Lee, D. Influence of construction joint and bridge geometry on integral abutment bridges. Appl. Sci. 2021, 11, 5031. [Google Scholar] [CrossRef]
- Sigdel, L.D.; Al-Qarawi, A.; Leo, C.J.; Liyanapathiranaet, S.; Hu, P. Geotechnical design practices and soil–structure interaction effects of an integral bridge system: A review. Appl. Sci. 2021, 11, 7131. [Google Scholar] [CrossRef]
- Ní Choine, M.; O’Connor, A.J.; Padgett, J.E. Comparison between the seismic performance of integral and jointed concrete bridges. J. Earthq. Eng. 2015, 19, 172–191. [Google Scholar] [CrossRef]
- Kozak, D.L.; LaFave, J.M.; Fahnestock, L.A. Seismic modeling of integral abutment bridges in illinois. Eng. Struct. 2018, 165, 170–183. [Google Scholar] [CrossRef]
- Mahjoubi, S.; Maleki, S. Finite element modelling and seismic behaviour of integral abutment bridges considering soil–structure interaction. Eur. J. Environ. Civ. Eng. 2020, 24, 767–786. [Google Scholar] [CrossRef]
- Salman, N.N.; Issa, M.A. Calibration and parametric investigation of integral abutment bridges. Eng. Struct. 2021, 227, 111381. [Google Scholar] [CrossRef]
- Faraji, S.; Ting, J.M.; Crovo, D.S.; Ernst, H. Nonlinear analysis of integral bridges: Finite-element model. J. Geotech. Geoenviron. Eng. 2001, 127, 454–461. [Google Scholar] [CrossRef]
- Perić, D.; Miletić, M.; Shah, B.R.; Esmaeily, A.; Wang, H.Y. Thermally induced soil structure interaction in the existing integral bridge. Eng. Struct. 2016, 106, 484–494. [Google Scholar] [CrossRef]
- Naji, M.; Firoozi, A.A.; Firoozi, A.A. A review: Study of integral abutment bridge with consideration of soil-structure interaction. Lat. Am. J. Solids Struct. 2020, 17, e252. [Google Scholar] [CrossRef]
- Briseghella, B.; Huang, F.Y.; Fiorentino, G. Seismic behaviour of novel integral abutment bridges. NED Univ. J. Res. 2019, 1, 1–20. [Google Scholar] [CrossRef]
- Liang, C.; Liu, Y.; Yang, F. Flexural strengths of steel girder-concrete abutment connections incorporating the effect of perfobond connectors. Eng. Struct. 2020, 214, 110611. [Google Scholar] [CrossRef]
- Xue, J.Q.; Aloisio, A.; Lin, Y.B.; Fragiacomo, M.; Briseghella, B. Optimum design of piles with pre-hole filled with high-damping material: Experimental tests and analytical modeling. Soil Dyn. Earthq. Eng. 2021, 151, 106995. [Google Scholar] [CrossRef]
- Goel, R.K. Earthquake characteristics of bridges with integral abutments. J. Struct. Eng. 1997, 123, 1435–1443. [Google Scholar] [CrossRef]
- Peng, D.W.; Hong, J.X.; Guo, A.M.; Fang, D.M. Dynamic field-test of integral abutment bridge. China J. Highw. Transp. 2004, 17, 59–63. (In Chinese) [Google Scholar]
- Peng, D.W.; Hong, J.X.; Guo, A.M.; Fang, D.M. Dynamic analysis and field-test of jointless bridge. Earthq. Eng. Eng. Dyn. 2005, 25, 72–76. (In Chinese) [Google Scholar]
- Zhao, Q.H.; Qi, Z.Y.; An, Z.Y.; Chen, B.C. Parametric analysis on seismic behavior of integral abutment steel bridge considering SSI. J. Traffic Transp. Eng. 2018, 18, 35–46. (In Chinese) [Google Scholar]
- Erhan, S.; Dicleli, M. Comparative assessment of the seismic performance of integral and conventional bridges with respect to the differences at the abutments. Bull. Earthq. Eng. 2015, 13, 653–677. [Google Scholar] [CrossRef]
- Kozak, D.L.; Fahnestock, L.A.; Lafave, J.M. Effect of soil conditions on the seismic response of three-span integral abutment bridges. In Proceedings of the Structures Congress, Fort Worth, TX, USA, 19–21 April 2018; pp. 100–110. [Google Scholar]
- Huang, C.G. Seismic response analysis of integral abutment skew beam bridges under earthquake excitation. J. Water Resour. Archit. Eng. 2020, 18, 182–188. (In Chinese) [Google Scholar]
- An, Z.Y. Seismic Performance Studies of Integral Abutment Steel Bridges Considering Soil-Structure Interaction. Master’s Thesis, Tianjin University, Tianjin, China, 2016. (In Chinese). [Google Scholar]
- Hong, J.X.; Peng, D.W. Effect of the abutment stiffness on integral abutment bridges. J. Highw. Transp. Res. Dev. 2006, 23, 77–81. (In Chinese) [Google Scholar]
- Vasheghani-Farahani, R.; Zhao, Q.H.; Burdette, E.G. Seismic analysis of integral abutment bridge in Tennessee, including soil–structure interaction. Transp. Res. Rec. 2010, 2201, 70–79. [Google Scholar] [CrossRef]
- Shi, L.F.; Xu, M. Analysis of seismic response of integral bridge abutments. Rock Soil Mech. 2014, 35, 3289–3297. (In Chinese) [Google Scholar]
- Dhar, S.; Dasgupta, K. Seismic soil structure interaction for integral abutment bridges: A review. Transp. Infrastruct. Geotech. 2019, 6, 249–267. [Google Scholar] [CrossRef]
- Frosch, R.J.; Kreger, M.E.; Talbott, A.M. Earthquake Resistance of Integral Abutment Bridges; Technical Report; Purdue University: West Lafayette, IN, USA, 2009. [Google Scholar]
- Wilson, J.C.; Tan, B.S. Bridge abutments: Formulation of simple model for earthquake response analysis. J. Eng. Mech. 1990, 116, 1828–1837. [Google Scholar] [CrossRef]
- Easazadeh Far, N.; Barghian, M. Safety identifying of integral abutment bridges under seismic and thermal loads. Sci. World J. 2014, 2014, 757608. [Google Scholar] [CrossRef]
- Elmy, M.H.; Nakamura, S. Static and seismic behaviours of innovative hybrid steel reinforced concrete bridge. J. Constr. Steel Res. 2017, 138, 701–713. [Google Scholar] [CrossRef]
- Huang, F.Y.; Wu, S.W.; Luo, X.Y.; Chen, B.C.; Lin, Y.W. Pseudo-static low cycle test on the mechanical behavior of PHC pipe piles with consideration of soil-pile interaction. Eng. Struct. 2018, 171, 992–1006. [Google Scholar] [CrossRef]
- Huang, F.Y.; Shan, Y.L.; Javanmardi, A.; Luo, X.Y.; Chen, B.C. Seismic performance of various piles considering soil–pile interaction under lateral cycle loads for integral abutment jointless bridges (IAJBs). Appl. Sci. 2020, 10, 3406. [Google Scholar] [CrossRef]
- Huang, F.Y.; He, L.F.; Shan, Y.L.; Hu, C.X.; Zhou, Z.M. Experiment on interaction of soil-abutment-RC pile in integral abutment jointless bridges (IAJBs). Rock Soil Mech. 2021, 42, 1803–1814. (In Chinese) [Google Scholar]
- Fu, R.H.; Briseghella, B.; Xue, J.Q.; Aloisio, A.; Lin, Y.B.; Nuti, C. Experimental and finite element analyses of laterally loaded RC piles with pre-hole filled by various filling materials in IABs. Eng. Struct. 2022, 272, 114991. [Google Scholar] [CrossRef]
- Durante, M.G.; Di Sarno, L.; Mylonakis, G.; Taylor, C.A.; Simonelli, A.L. Soil–pile–structure interaction: Experimental outcomes from shaking table tests. Earthq. Eng. Struct. Dyn. 2016, 45, 1041–1061. [Google Scholar] [CrossRef]
- XTRACT Analysis User’s Manual, v3.0.5; XTRACT Inc.: Charlotte, NC, USA, 2006.
- Zhao, M.H.; Chen, C.F. Soil Mechanics and Foundation Engineering; Wuhan University of Technology Press: Wuhan, China, 2014; pp. 96–97. (In Chinese) [Google Scholar]
- Qian, H.M. Experimental Investigation on Seismic Performance of PHC Pile in Integral Abutment Bridge. Master’s Thesis, Fuzhou University, Fuzhou, China, 2016. (In Chinese). [Google Scholar]
- Lou, M.L.; Wang, W.J.; Zhu, T.; Ma, H.C. Soil lateral boundary effect in shaking table model test of soil-structure system. Earthq. Eng. Eng. Vib. 2000, 20, 30–36. (In Chinese) [Google Scholar]
- Lawver, A.; French, C.; Shield, C.K. Field performance of integral abutment bridge. Transp. Res. Rec. 2000, 1740, 108–117. [Google Scholar] [CrossRef]
- William, G.W.; Shoukry, S.N.; Riad, M.Y. Study of thermal stresses in skewed integral abutment steel girder bridges. Struct. Eng. Int. 2012, 22, 308–317. [Google Scholar] [CrossRef]
- Dicleli, M.; Erhan, S. Effect of soil–bridge interaction on the magnitude of internal forces in integral abutment bridge components due to live load effects. Eng. Struct. 2010, 32, 129–145. [Google Scholar] [CrossRef]
- Gama, D.; Almeida, J.F. Concrete integral abutment bridges with reinforced concrete piles. Struct. Concr. 2014, 15, 292–304. [Google Scholar] [CrossRef]
- Noorzaei, J.; Abdulrazeg, A.A.; Jaafar, M.S.; Kohnehpooshi, O. Non-linear analysis of an integral bridge. J. Civ. Eng. Manag. 2010, 16, 387–394. [Google Scholar] [CrossRef]
- Pan, W.T. Research on Reduced Scale Effect on Pre-Hole Pile-Soil Interaction of Integral Abutment Bridge. Master’s Thesis, Fuzhou University, Fuzhou, China, 2020. (In Chinese). [Google Scholar]
- Huang, F.Y.; Li, L.; He, L.F.; Hu, C.X. Mechanical behavior of abutment-RC pile-soil structure in integral abutment bridges. Harbin Inst. Technol. 2023, 55, 128–138. (In Chinese) [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015. (In Chinese)
- Ye, X.G.; Wang, H.B.; Sun, L.M.; Zuo, X.M.; Wang, R.G. Experimental research on seismic energy dissipation performance of reinforced concrete bridge pier. J. Hefei Univ. Technol. (Nat. Sci.) 2005, 28, 1171–1177. (In Chinese) [Google Scholar]
- Wang, K.H. Seismic Research of Bridge; China Railway Publishing House: Beijing, China, 2014; pp. 544–554. (In Chinese) [Google Scholar]





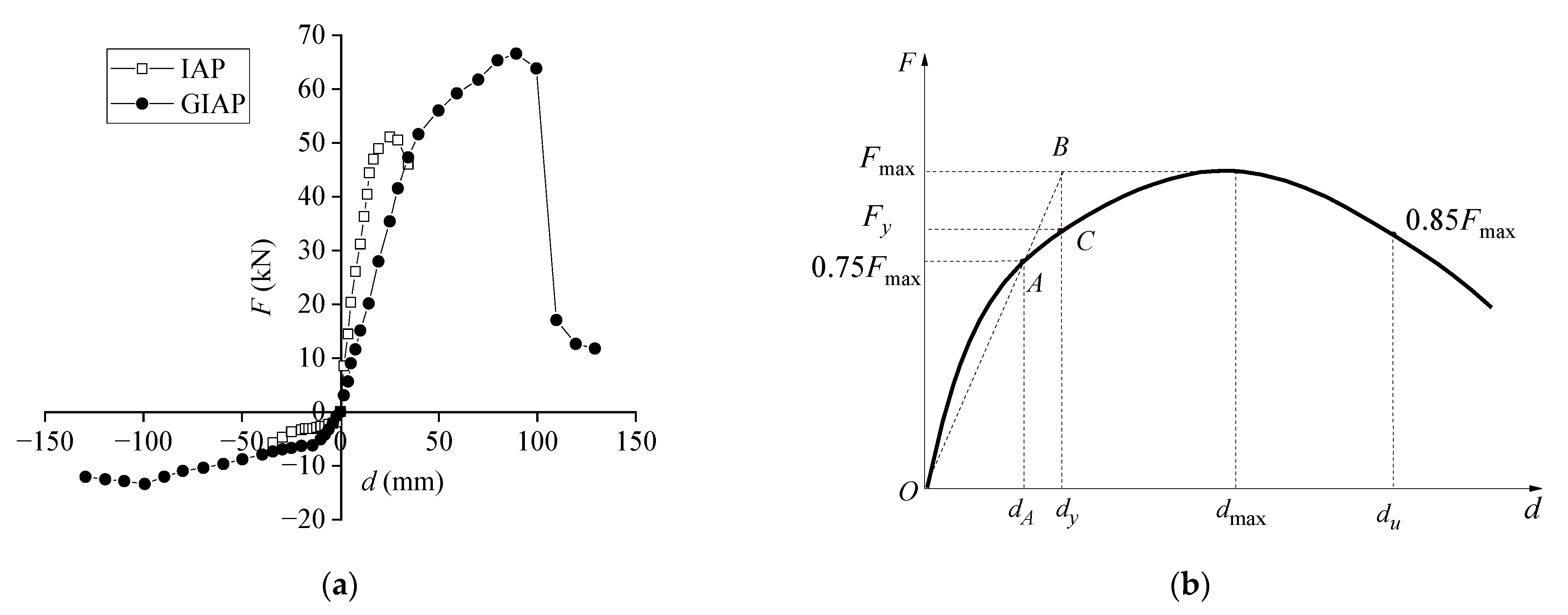
| Components | Dimension | Values (m) |
|---|---|---|
| Girder (prestressed concrete, single-box girder with three cells) | Width | 17 |
| Height | 1.6 | |
| Abutments (rectangular wall) | Height | 5.5 |
| Thickness | 1.0 | |
| Width | 17 | |
| Piles beneath each abutment (4 piles with a circular cross-section) | Length | 25 |
| Diameter | 1.5 | |
| Piers (rectangular twin-column piers) | Height | 6.06 |
| Thickness | 1.2 | |
| Width | 1.8 | |
| Piles beneath each pier (2 piles with a circular cross-section ) | Length | 32 |
| Diameter | 1.8 |
| Specimen | Fy (kN) | Fu (kN) | Elastic Range (0~dA) (mm) | Elastoplastic Range (dA~dy) (mm) | du (mm) |
|---|---|---|---|---|---|
| IAP [36] | 46.6 | 52.5 | 0~12 | 12~19.4 | 24.8 |
| GIAP | 56.1 | 56.6 | 0~37.7 | 37.7~50.5 | 108.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Briseghella, B.; Xue, J.; Nuti, C.; Huang, F. Experimental Investigations of Seismic Performance of Girder–Integral Abutment–Reinforced-Concrete Pile–Soil Systems. Appl. Sci. 2024, 14, 10166. https://doi.org/10.3390/app142210166
Guo W, Briseghella B, Xue J, Nuti C, Huang F. Experimental Investigations of Seismic Performance of Girder–Integral Abutment–Reinforced-Concrete Pile–Soil Systems. Applied Sciences. 2024; 14(22):10166. https://doi.org/10.3390/app142210166
Chicago/Turabian StyleGuo, Weiqiang, Bruno Briseghella, Junqing Xue, Camillo Nuti, and Fuyun Huang. 2024. "Experimental Investigations of Seismic Performance of Girder–Integral Abutment–Reinforced-Concrete Pile–Soil Systems" Applied Sciences 14, no. 22: 10166. https://doi.org/10.3390/app142210166
APA StyleGuo, W., Briseghella, B., Xue, J., Nuti, C., & Huang, F. (2024). Experimental Investigations of Seismic Performance of Girder–Integral Abutment–Reinforced-Concrete Pile–Soil Systems. Applied Sciences, 14(22), 10166. https://doi.org/10.3390/app142210166









