Analysis of Changes in the Stress–Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone with Casing and Perforation Channels
Abstract
1. Introduction
2. Methodology
- −
- Equations of motion (moments):
- −
- Geometric equations:
- −
- Physics relations (in this case, Hooke’s law of linear elasticity):
- ANTYPE, STATIC: this command was used for static analysis, which is used in calculating stresses in a linearly elastic medium and pressure for a poroelastic medium.
- NROPT, full: This command configures the Newton–Raphson method for a static or full transient analysis. The “full” parameter means using the full Newton–Raphson method with nonsymmetric element matrices, if such an option is available.
- A linear elastic model was used to describe the behavior of a steel production column, since it adequately describes the properties of durable steel in the range of design stresses.
- The plastic properties of the reservoir rock have not been studied in the laboratory, so it was decided to consider it as a poroelastic medium. It is worth noting that during the operation of the well, the near-well zone and the rock areas around the perforation channels are subjected to multiple cycles of loading and unloading. The experience of experimental studies has shown that, after the third cycle, such deformations of the rock are not observed, which confirms the choice of a poroelastic model for this study.
- Cement stone has been accepted as impenetrable, which is to some extent an assumption. However, experiments show that the permeability of cement stone can manifest itself during gas filtration due to its greater mobility compared to liquid. Nevertheless, when modeling an environment saturated with water and oil, cement stone can be considered practically impenetrable.
- 4.
- The calculations did not take into account phase permeability; that is, it was assumed that only oil is filtered, and residual water saturation does not affect the phase permeability of oil.
- Vertical movements were fixed at the lower boundary;
- Movements along the normal to the surface were fixed at the left and right lateral boundaries;
- wo boundary conditions were set at the outer lateral surface:
- −
- Fluid pressure based on the differential pressure drawdown and the pressure on the supply circuit:
- −
- Horizontal stress based on the values of vertical stress and Poisson’s ratio;
- 4.
- Vertical movements were set at the upper boundary for the casing and cement stone (imitation of a cased well); vertical stresses were applied to the rock, based on the reservoir depth and the average volume weight of the overlying rock stratum;
- 5.
- Fluid pressure was set inside the well and in the perforation channels, taking into account the pressure drawdown value.
3. Results and Discussion
- −
- For the casing,
- −
- For the cement stone,
4. Discussion
- In order to exclude stress concentration at the boundaries of adjacent media, the present model includes the contact elements between the casing–cement stone and cement stone–rock. As a result, it is possible to distribute stresses both in the rock and in the structural elements of the well more accurately. The reservoir rock was modeled as a poroelastic media with permeability varying due to the effective stresses.
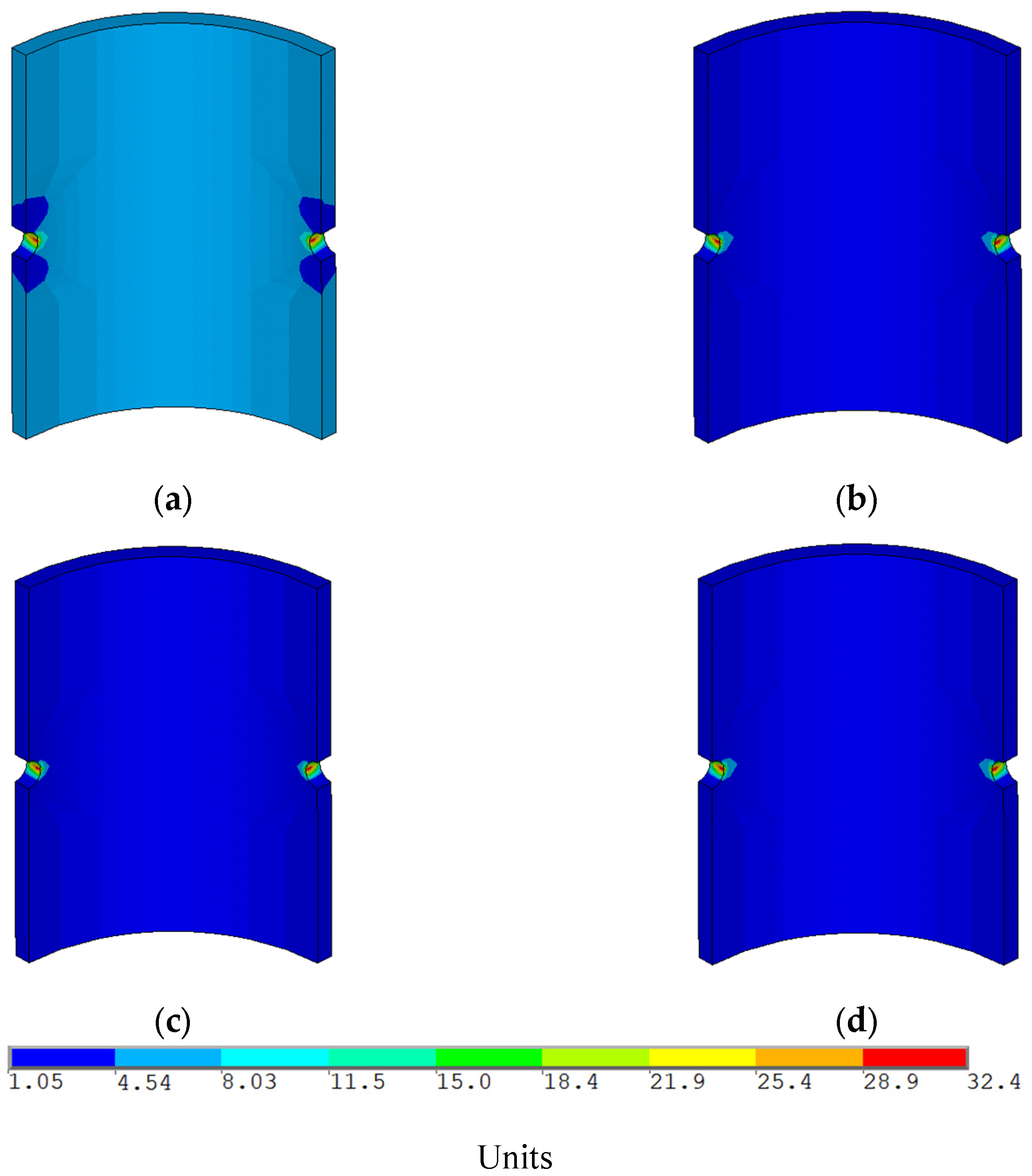
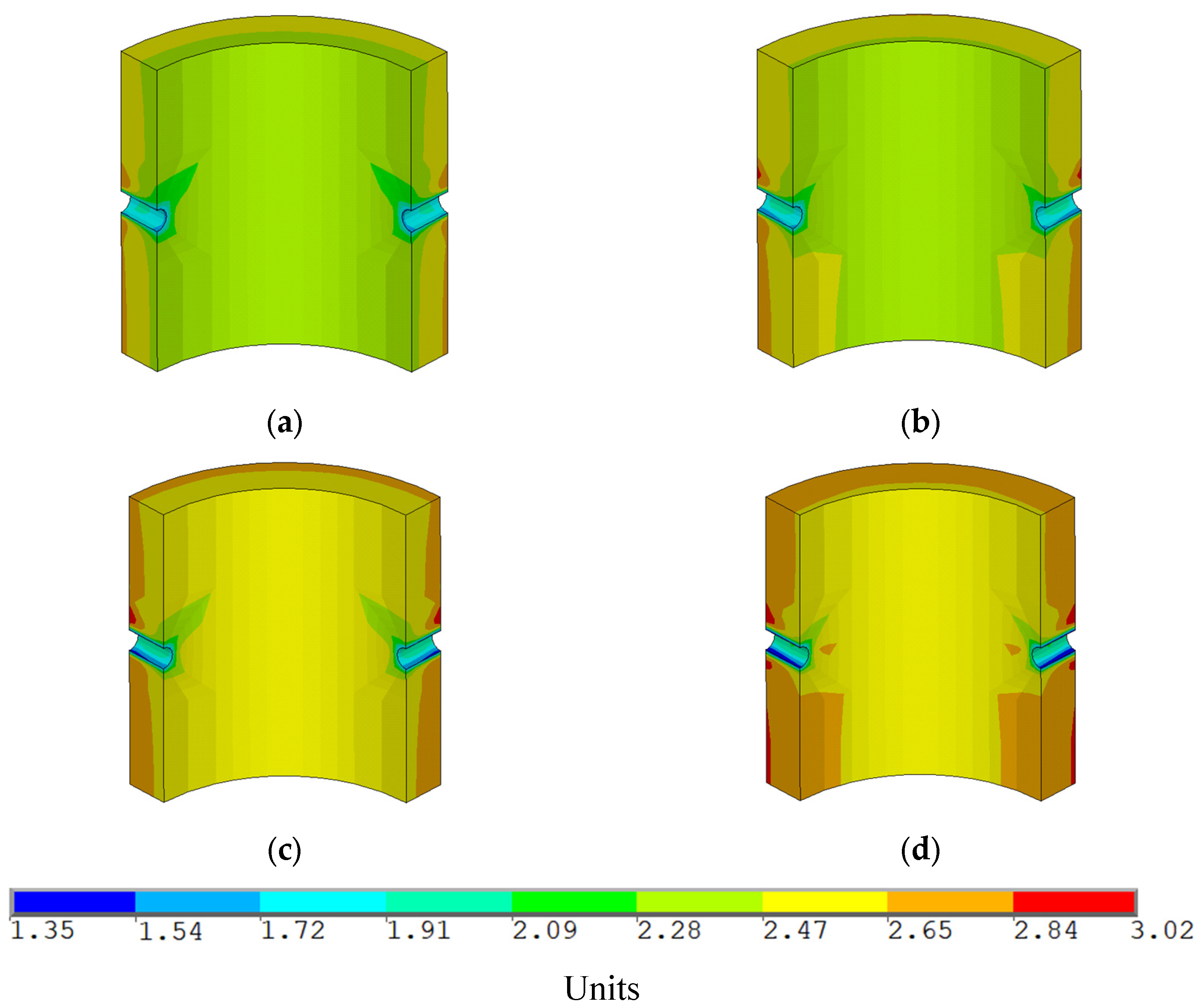
- Analysis of the stress distribution in the casing based on the safety factor shows that, in the main part of the casing, the value of this parameter represents 3–4 units, which indicates its high stability. The exception is small parts near the perforation channels, where this value is close to one unit.
- The safety factor for the main part of the cement stone reaches 2–3 units, which also indicates its sufficient strength. The safety factor of the cement stone reaches the minimum value under the maximum pressure drawdown. The parts with its minimum value are located near the perforations.
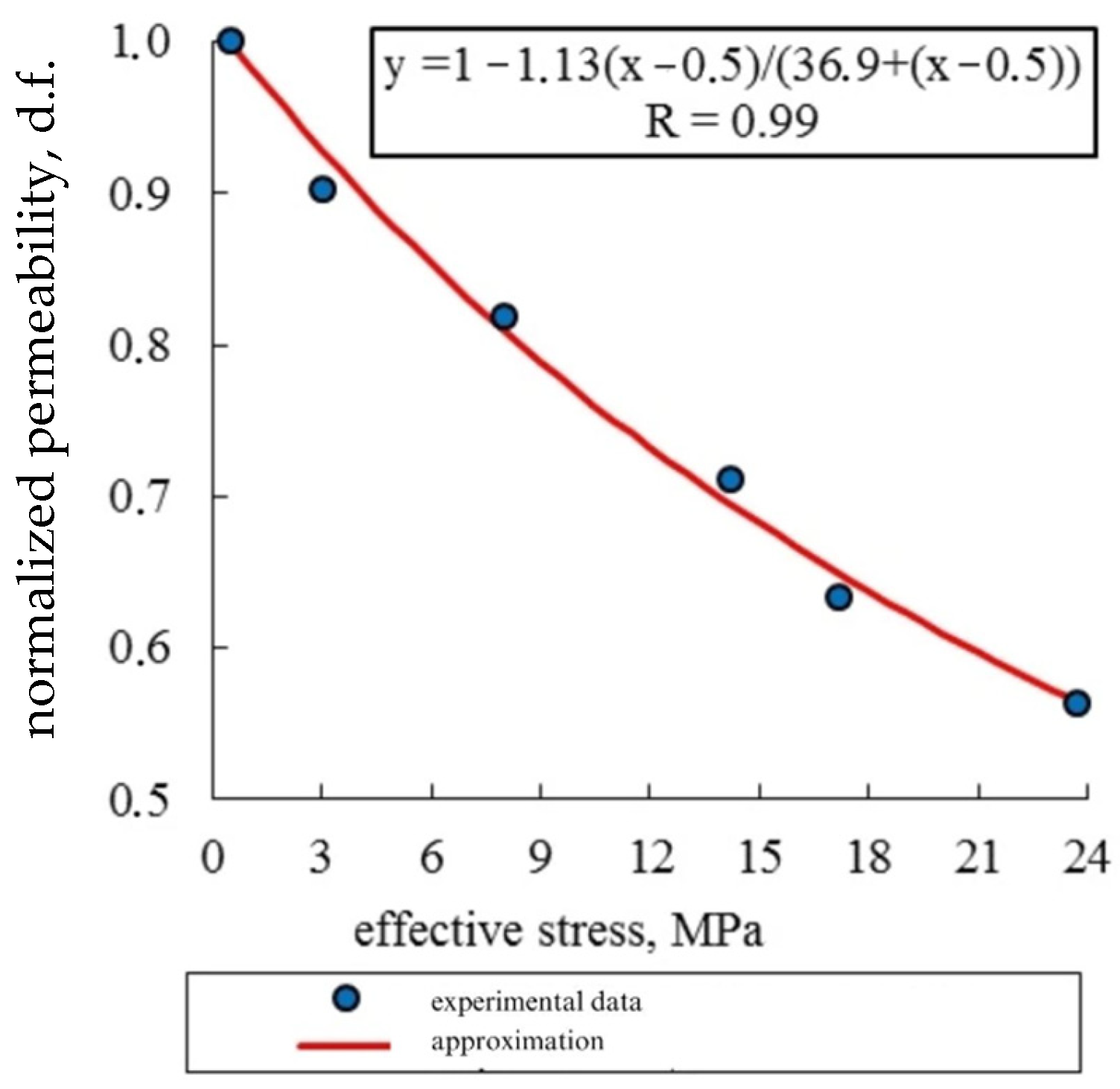
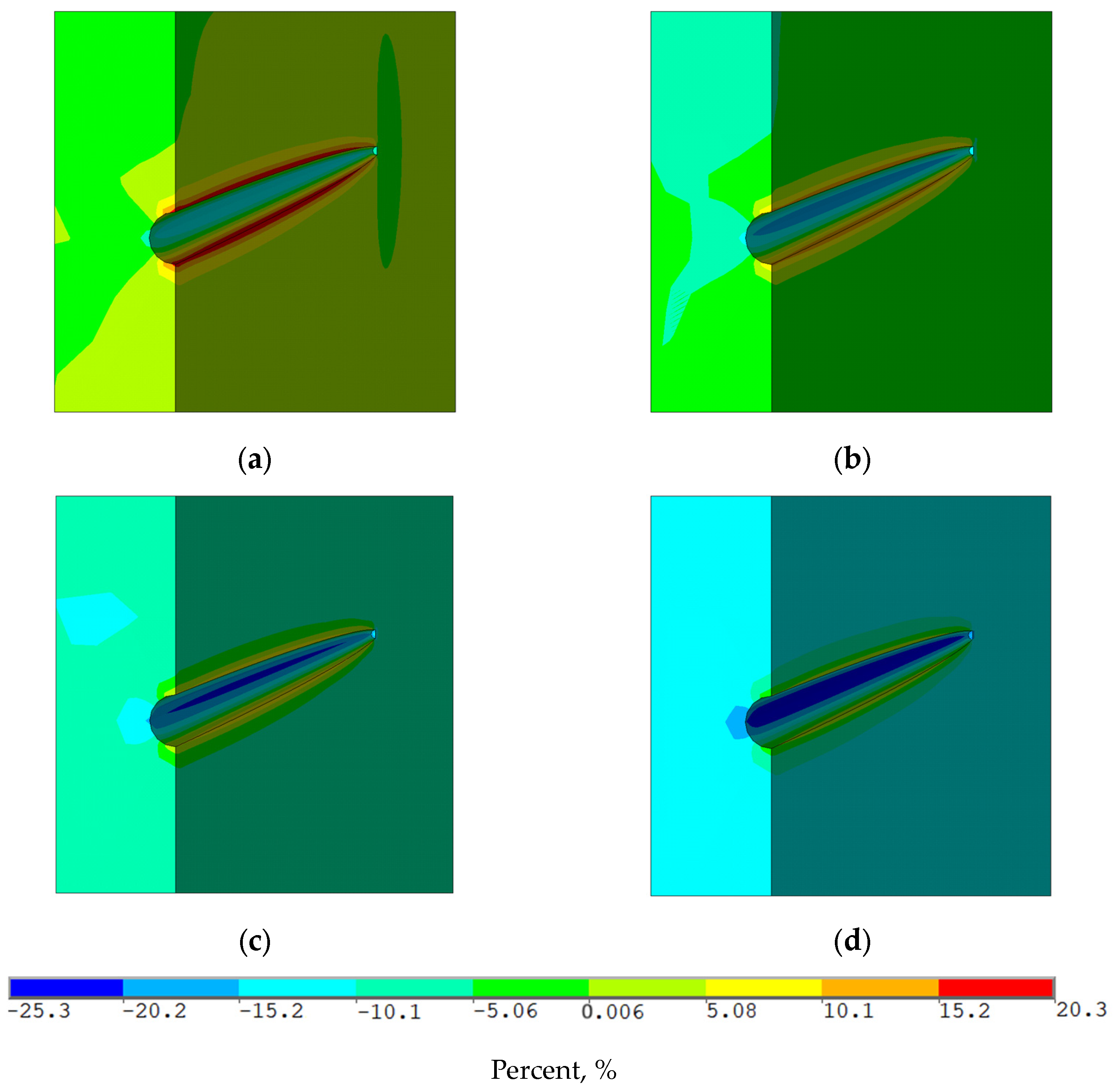
- The permeability dependence on effective stresses, previously determined on core samples, proves that areas of increased (in the lateral parts) and decreased (in the upper and lower parts) stresses arise on the perforation channels’ surface. As a result, these areas have both an increase (up to 20%) and a decrease (up to 25%) in permeability from the initial values caused by variable effective stresses.
- With an increase in pressure drawdown, the areas with increasing permeability diminish, while the areas with decreasing permeability grow, which is caused by an increase in effective stresses.
- Analysis of the destruction areas of reservoir rocks, based on the Mohr–Coulomb criterion and the impact of effective stress, shows that areas of destruction due to both compressive and tensile stresses appear near the perforations. With an increase in pressure drawdown, tensile stress areas decrease and then disappear completely, while compressive stress areas increase, which is also explained by an increase in effective stresses.
- Due to a decrease in permeability and an increase in pressure drawdown to 12 MPa, the well productivity index can decrease by up to 15%, which indicates the need to optimize well production in order to prevent intensive reservoir compaction due to a decrease in bottom hole and reservoir pressures.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zoback, M.D. Reservoir Geomechanics; Cambridge University Press: Cambridge, UK, 2007; 505p. [Google Scholar]
- Fjear, E.; Holt, R.M.; Horsrud, P.; Raaen, A.M.; Risnes, R. Petroleum Related Rock Mechanics; Elsevier: Amsterdam, The Netherlands, 2008; 492p. [Google Scholar]
- Kashnikov, Y.U.A.; Ashihmin, S.G. Mechanics of Rocks in the Development of Hydrocarbon Deposits; OOO «Nedra Biznes-Centr»: Moscow, Russia, 2007; 476p. [Google Scholar]
- Ma, T.; Liu, J.; Fu, J.; Qiu, Y.; Fan, X.; Martyushev, D.A. Fully Coupled Thermo-hydro-mechanical Model for Wellbore Stability Analysis in Deep Gas-Bearing Unsaturated Formations Based on Thermodynamics. Rock Mech. Rock Eng. 2024. [Google Scholar] [CrossRef]
- Lukin, S.V.; Esipov, S.V.; Zhukov, V.V.; Ovcharenko, Y.u.V.; Khomutov AYu Shevchuk, T.N.; Suslyakov, I.V. Borehole stability prediction to avoid drilling failures. Neft. Hozyajstvo 2016, 6, 70–73. [Google Scholar]
- Vashkevich, A.A.; Zhukov, V.V.; Ovcharenko, Y.u.V.; Bochkov, A.S.; Lukin, S.V. Development of integrated geomechanical modeling in “Gazprom neft” PJSC. Neft. Hozyajstvo 2016, 12, 16–19. [Google Scholar]
- Popov, S.N.; Chernyshov, S.E. Development of a geomechanical model and determination of the drilling fluid “density window” in the interval of famennian productive deposits (on the example of a site of one of the Timano-Pechora oil and gas province oilfield). Geol. Geophys. Dev. Oil Gas Fields 2023, 11, 32–39. [Google Scholar]
- Wang, L.; Shen, X.; Wu, B.; Shen, T.; Shi, J. Integrated analysis of the 3D geostress and 1D geomechanics of an exploration well in a new gas field. Energies 2023, 16, 806. [Google Scholar] [CrossRef]
- Kashnikov, Y.A.; Ashikhmin, S.G.; Shustov, D.V.; Yakimov, S.Y.; Kukhtinskii, A.E. Increasing efficiency of hydrocarbon fields development based on complex geomechanical research. Neft. Hozyajstvo 2019, 3, 66–69. (In Russian) [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Sun, Z.; An, S.; Zhang, W.; Liu, P.; Yao, J.; Ma, J. Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef]
- Galkin, V.I.; Martyushev, D.A.; Ponomareva, I.N.; Chernykh, I.A. Developing features of the near-bottomhole zones in productive formations at fields with high gas saturation of formation oil. J. Min. Inst. 2021, 249, 386–392. [Google Scholar] [CrossRef]
- Li, W.; Chen, L.; Wang, X.; Fan, Q.; Xu, G.; Xiao, W.; Li, X.; Ye, Z. Acid fracturing technology and effect evaluation of carbonate horizontal well in Fuman oilfield. J. Phys. Conf. Ser. 2024, 2679, 012010. [Google Scholar] [CrossRef]
- Liu, F.; Fan, Y.; Li, L.; Li, J.; Chen, Y.; Lv, Z.; He, T. Case study of successfully staged acid fracturing on the ultra-deep horizontal well for the Qixia fm HTHP tight carbonate gas reservoir in China. Front. Energy Res. 2022, 10, 917740. [Google Scholar] [CrossRef]
- Safari, R.; Smith, C.; Fragachan, F. Improved Recovery of Carbonate Reservoir by Optimizing Acidizing Strategy: Coupled Wellbore, Reservoir, and Geomechanical Analysis. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13 November 2017. [Google Scholar] [CrossRef]
- Al-Awad, M.N.J.; Al-Ahaidib, T.Y. Estimating the amount of free sand in the yielded zone around horizontal oil wells. In Proceedings of the SPE Technical Symposium of Saudi Arabia Section, Dhahran, Saudi Arabia, 14 May 2005. [Google Scholar] [CrossRef]
- Araujo-Guerrero, E.F.; Alzate-Espinosa, G.A.; Arbelaez-Londono, A.; Pena Clavijo, S.; Cardona Ramirez, A. Analytical prediction model of sand production integrating geomechanics for open hole and cased—perforated wells. In Proceedings of the SPE Heavy and Extra Heavy Oil Conference, Latin America, Medellín, Colombia, 24 September 2014. [Google Scholar] [CrossRef]
- Ermolayev, A.I.; Efimov, S.I.; Pyatibratov, P.V.; Minikhanov, E.D.; Dubinya, N.V.; Leonova, A.M. Estimation of the maximum downhole pressure, excluding the destruction of the bottom-hole zone of the formation, based on geomechanical core studies. SOCAR Proc. 2023, 1, 61–69. (In Russian) [Google Scholar] [CrossRef]
- Chernyshov, S.E.; Popov, S.N.; Savich, A.D.; Derendyaev, V.V. Analysis of wells cement sheath stability during shaped charge perforating based on geomechanical modeling. Georesursy = Georesources 2023, 25, 245–253. [Google Scholar] [CrossRef]
- Fallahzadeh, S.H.; Shasizadeh, S.R. Modeling the Perforation Stress Profile for Analyzing Hydraulic Fracture Initiation in a Cased Hole. In Proceedings of the Nigeria Annual International Conference and Exhibition, Tinapa, Calabar, Nigeria, 31 July 2010. [Google Scholar] [CrossRef]
- Strelchenko, V.V.; Melnichyk, D.A.; Abrosimov, A.A. Modelling the stress-strain state change of near-wellbore area and its reservoir properties during drilling. Vestn. Assoc. Burovyh Podryadchikov 2014, 1, 35–37. [Google Scholar]
- Popov, S.N.; Chernyshov, S.E.; Krivoshchekov, S.N. Comparative analysis of the analytical and numerical methods for calculating the stress-strain state of the near-wellbore zone based on the elastic model taking into account the main structural elements of the well. Bull. Tomsk. Polytech. Univ. Geo Assets Eng. 2023, 334, 94–102. (In Russian) [Google Scholar] [CrossRef]
- Zhang, J.; Moridis, G.; Blasingame, T.A. Message passing interface (MPI) parallelization of iteratively coupled fluid flow and geomechanics codes for the simulation of system behavior in hydrate-bearing geological media. Part 1: Methodology and validation. SPE Reserv. Eval. Eng. 2022, 25, 600–620. [Google Scholar] [CrossRef]
- Kharlamov, S.N.; Janghorbani, M.; Chernov, A.G. Transportation of cuttings by drilling mud in horizontal wells. Part 2. Numerical results of drilling at optimal rheological properties of mud. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2023, 334, 7–24. [Google Scholar] [CrossRef]

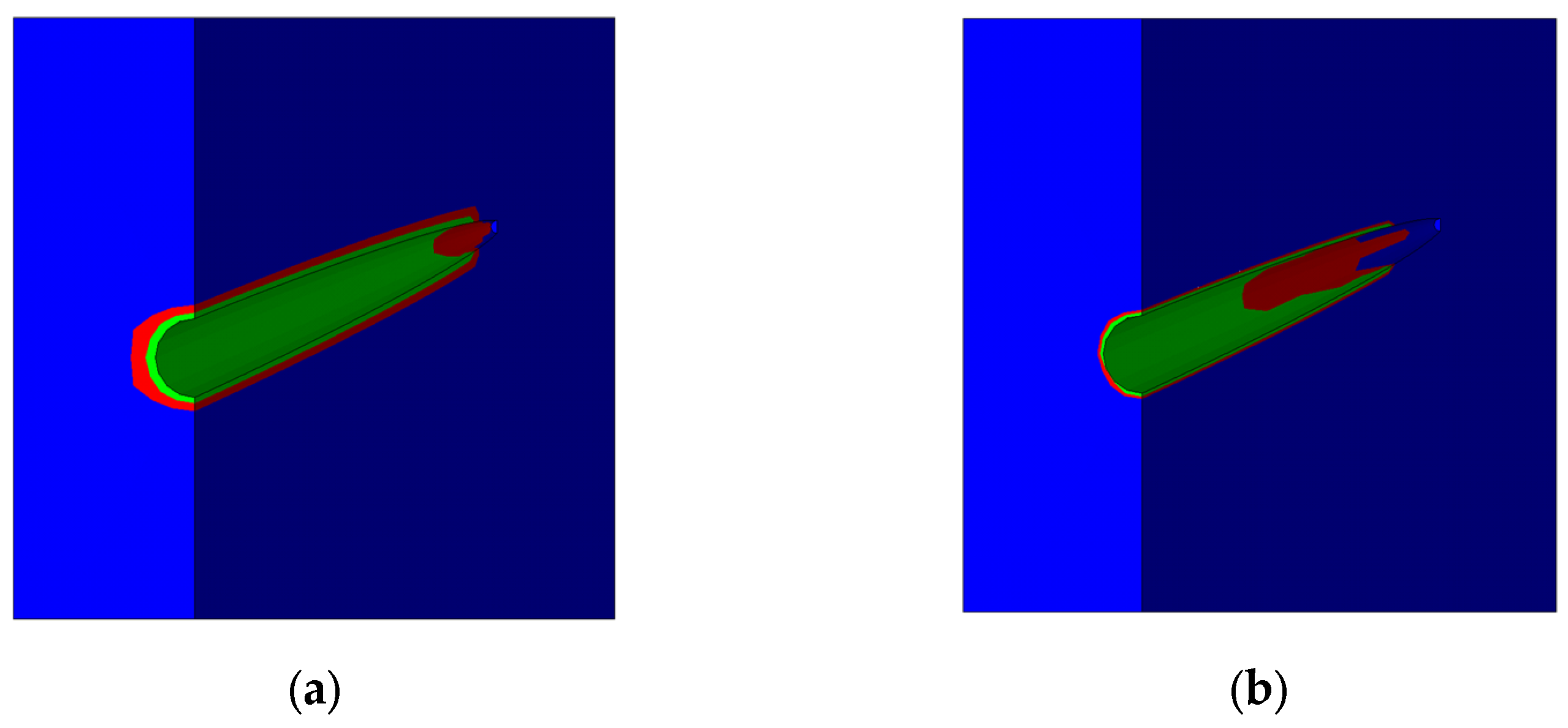
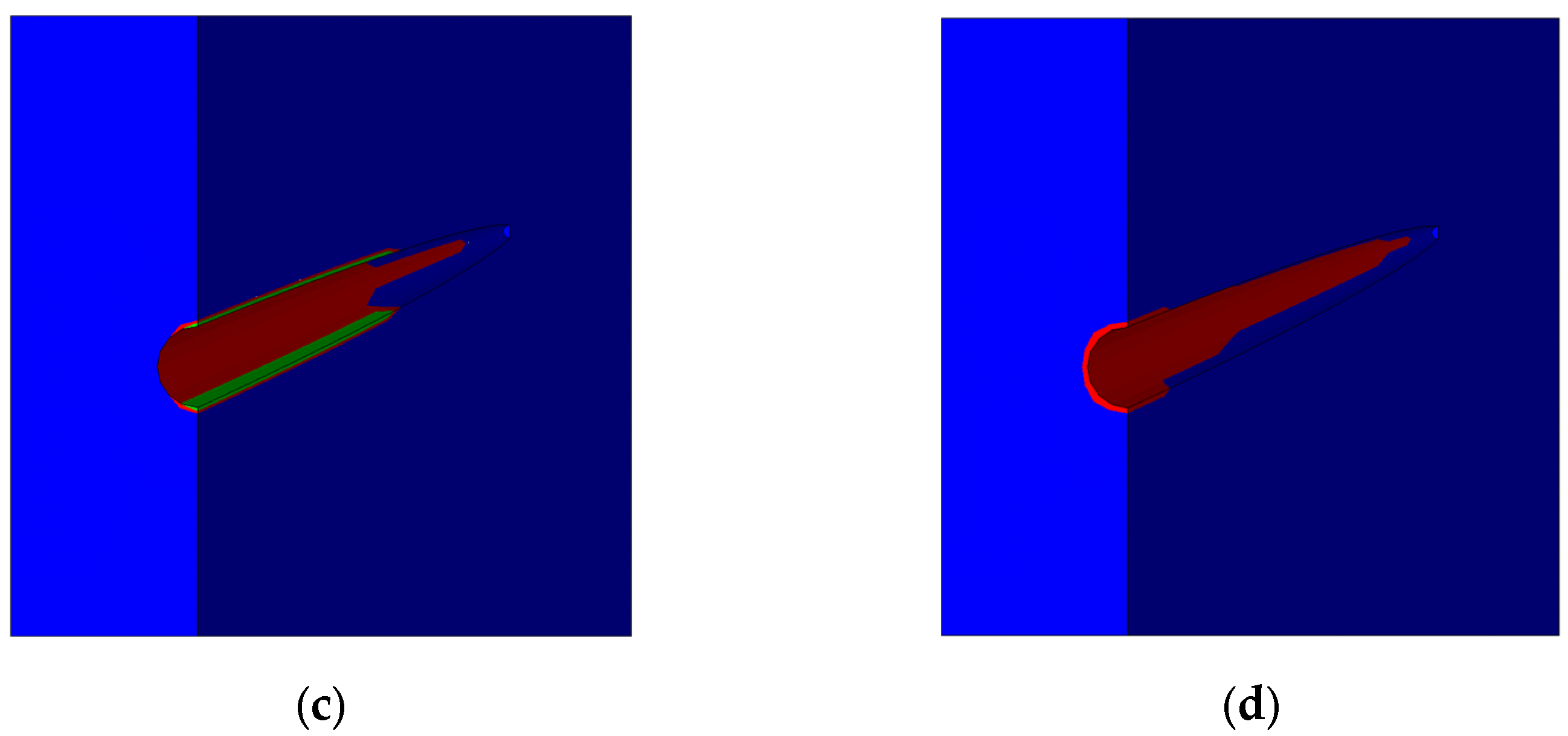

| № | Characteristic | Value |
|---|---|---|
| 1 | Outer diameter of the casing, mm | 168.3 |
| 2 | Casing thickness, mm | 7.3 |
| 3 | Drilling size, mm | 215.9 |
| 4 | Radius of the model, m | 5 |
| 5 | Young’s modulus of the casing, GPa | 200 |
| 6 | Poisson’s ratio of the casing, d.f. | 0.2 |
| 7 | Yield strength of casing steel, MPa | 372 |
| № | Characteristic | Value |
|---|---|---|
| 1 | Young’s modulus, GPa | 11.3 |
| 2 | Poisson’s ratio, d.f. | 0.179 |
| 3 | Compressive strength, MPa | 31.5 |
| 4 | Angle of internal friction, ° | 29.6 |
| № | Characteristic | Value |
|---|---|---|
| 1 | Young’s modulus, GPa | 9.4 |
| 2 | Poisson’s ratio, d.f. | 0.32 |
| 3 | Biot coefficient, d.f. | 0.75 |
| 4 | The average depth of the reservoir, m | 1489 |
| 5 | Initial reservoir pressure, MPa | 14.5 |
| 6 | Differential pressure drawdown, MPa | 0–12 |
| 7 | Compressive strength, MPa | 36.3 |
| 8 | Angle of internal friction, ° | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chernyshov, S.; Popov, S.; Wang, X.; Derendyaev, V.; Yang, Y.; Liu, H. Analysis of Changes in the Stress–Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone with Casing and Perforation Channels. Appl. Sci. 2024, 14, 9993. https://doi.org/10.3390/app14219993
Chernyshov S, Popov S, Wang X, Derendyaev V, Yang Y, Liu H. Analysis of Changes in the Stress–Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone with Casing and Perforation Channels. Applied Sciences. 2024; 14(21):9993. https://doi.org/10.3390/app14219993
Chicago/Turabian StyleChernyshov, Sergey, Sergey Popov, Xiaopu Wang, Vadim Derendyaev, Yongfei Yang, and Huajie Liu. 2024. "Analysis of Changes in the Stress–Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone with Casing and Perforation Channels" Applied Sciences 14, no. 21: 9993. https://doi.org/10.3390/app14219993
APA StyleChernyshov, S., Popov, S., Wang, X., Derendyaev, V., Yang, Y., & Liu, H. (2024). Analysis of Changes in the Stress–Strain State and Permeability of a Terrigenous Reservoir Based on a Numerical Model of the Near-Well Zone with Casing and Perforation Channels. Applied Sciences, 14(21), 9993. https://doi.org/10.3390/app14219993








