1. Introduction
Airplanes are subjected to complex mechanical loads during flight, influenced by factors such as flight speed, altitude, ambient temperature, and atmospheric pressure. Consequently, stress analysis of aircraft structures is a crucial step in ensuring the overall structural health of the aircraft. The traditional approach to stress analysis involves using finite element method (FEM) software (patran 2018) to simulate the aircraft structure under various operating conditions to obtain the stress field response for corresponding flight scenarios, followed by an evaluation of the aircraft’s structural strength [
1,
2,
3]. While FEM-based methods are effective in capturing changes in the aircraft’s stress field, they are computationally intensive and time-consuming, especially for different aircraft structural models and systems that vary in complexity [
4]. The process can become highly resource-demanding. Real-time structural life management requires continuous access to and monitoring of structural stress data, making traditional methods costly and time-prohibitive. Therefore, there is a pressing need to establish a method capable of rapidly predicting the aircraft’s stress conditions to provide effective data support for aircraft structural health monitoring and service life analysis.
With the rapid advancement of artificial intelligence, big data, and information technology, data-driven approaches to structural strength assessment, supported by powerful computational capabilities and vast datasets, have proven highly effective in monitoring the health of structures [
5]. For instance, structural health monitoring techniques are employed to continuously track the condition of aircraft structures [
6]. This method involves real-time monitoring through advanced sensor networks, which collect structural health data in real time. Signal processing techniques are then used to analyze these signals, enabling the detection of structural conditions, identification of damage or performance degradation, and assessment of the remaining lifespan of the aircraft structure [
7].
Broer et al. conducted an analysis of the current state of the art in structural health inspection for aerospace vehicles, identifying two critical aspects of aircraft compliance with the maturity of materials in the structural field. They proposed a multi-sensor data fusion concept and demonstrated a conceptual design study of a fusion-based structural health monitoring (SHM) system. The results indicate that the multi-sensor data fusion concept can significantly benefit condition-based maintenance (CBM) applications in the aircraft industry, particularly in advancing the field of composite aircraft structures [
8].
Weijiang et al. developed a nonlinear unsteady aerodynamic model and proposed a theoretical method based on static aeroelasticity, utilizing flight data mining and a fuzzy logic modeling technique. This method assists in the certification of competency holders in aircraft maintenance facilities by enabling them to monitor static aeroelastic behavioral changes and address flight safety warning issues in aging transport aircraft. Additionally, it serves as a valuable tool in structural maintenance programs, enhancing aviation safety as well as operational efficiency [
9].
Digital twin technology creates a virtual model of a physical entity by integrating finite element analysis, sensor technology, and visualization techniques. This virtual model enables the simulation, analysis, and prediction of structural behavior, as well as the online and offline monitoring of the structure’s operation. As a result, it facilitates real-time monitoring and management of the aircraft’s structural health, significantly enhancing maintenance and operational decision-making [
10].
Lai et al. [
11] constructed the measurement-computation combined digital twin (MCC-DT) framework by integrating measurement and computational data. The construction process consists of four key steps. First, an artificial-intelligence-driven load recognition method is employed to identify the loads applied to physical entities, using both measurement and computational data, with two recognition methods proposed: one based on a single-fidelity agent model and the other on deep learning. Second, a multi-fidelity surrogate model (MFS) is applied to enhance the accuracy of the MCC-DT, with two implementation approaches presented, along with an analysis of their respective advantages and disadvantages. Third, an algorithm is developed to estimate cumulative damage to the physical entity in near real time, allowing for damage assessment. Finally, the data generated from the first three steps is integrated into a 3D scene using a web-based graphics library, providing an intuitive visualization of the MCC-DT. An airplane model is used to validate the applicability and effectiveness of this framework [
11].
Data prediction methods based on learning algorithms analyze both the linear and nonlinear relationships among input data features, enabling the discovery of underlying correlations between individual features and the prediction of aircraft structural strength [
12,
13]. Common learning algorithms include clustering, random forests, and neural networks. The primary objective is to understand the data structure and fit it into models that are interpretable and useful for researchers [
14,
15]. These algorithms are trained on input data sources, employing statistical analysis techniques to generate output values within a specified range. Structural models are then developed from sample data, automating the decision-making process.
Zhen et al. investigated a method for predicting the stress field of a two-dimensional linear elastic cantilever structure using volume data and neural networks. The study employed two distinct prediction architectures: a single-channel input network and a multi-channel input network. By comparing the predictive performance of these models, it was observed that the multi-channel input network exhibited a significantly lower prediction error compared to the single-channel input network. This study indicates that deep learning models could serve as an effective alternative to traditional prediction methods [
16].
To provide effective data input for engine turbine disk life management and subsequent engineering applications, Xu et al. developed a turbine disk stress prediction model for aero-engines, leveraging dimensionality reduction and random forest techniques grounded in statistical learning and machine learning methods. The model uses measurable parameters as initial features and performs dimensionality reduction through correlation analysis, principal component analysis, and cluster analysis to extract key control factors. A prediction model is then constructed using the random forest algorithm. The results demonstrate that this approach achieves higher prediction accuracy compared to a random forest model without dimensionality reduction, highlighting its effectiveness in turbine disk stress prediction and its significant technical value for aero-engine life management [
17].
Ultrasonic nanocrystalline surface modification (UNSM) is a surface treatment technique that uses ultrasonic vibrational energy to enhance the mechanical properties of materials. The dynamic nature of UNSM induces deformation in the surface and sub-surface layers at very high strain rates, making direct observation of residual stresses and refinement layers challenging. Sembiring et al. proposed an alternative approach using artificial neural networks (ANNs) to predict residual stresses and hardness in various nickel-based alloys treated with UNSM. After training and validating the ANN with experimental data, the model demonstrated strong predictive capability. The study concludes that an ANN can serve as a more accurate alternative in the absence of a mathematical model, providing a useful tool for optimizing UNSM processing parameters [
18].
In the design, analysis, and optimization of aerodynamics, flow fields are typically simulated using computational fluid dynamics (CFD). However, CFD simulations are often computationally expensive, memory-intensive, and time-consuming, which limits the exploration of the design space and possibilities for interactive design. Guo et al. employed a convolutional neural network (CNN) to construct an approximate model capable of predicting non-uniform steady laminar flows in 2D or 3D domains in real time, while exploring various geometric representations and network architectures. The results demonstrate that the CNN is two orders of magnitude faster than a GPU-accelerated CFD solver and four orders of magnitude faster than a CPU-based CFD solver in predicting the velocity field, all while maintaining a low error rate. This approach offers a valuable reference for real-time design iterations in the early stages of design development [
19].
Wang et al. sought to enhance the full-envelope acceleration performance of a gas turbine engine (GTE) by integrating an input selection strategy (CIS) with a multilayer perceptron (MLP). The CIS strategy is employed to identify the most relevant inputs, which, combined with a weighted integral loss function, results in the design of a highly accurate and robust full-envelope acceleration schedule (FEAS). The MLP further improves the accuracy of the FEAS. Compared to other classical machine learning models, the MLP network demonstrates superior effectiveness in enhancing FEAS accuracy [
20].
Wang et al. developed an MLP model for accurately predicting the stress and temperature of a compressor disk using artificial neural network techniques. Engine measurable parameters were used as input for the MLP model, and the back-propagation (BP) neural network algorithm was applied for training. The study also examined the impact of various optimization algorithms on the model’s prediction performance. The results indicate that the model’s predictions are highly consistent with traditional finite element calculations, with relative deviations under 1%, coefficients of determination exceeding 0.95, and root-mean-square errors (JRMSE) within 5. Additionally, the computational time was reduced from hours to minutes or seconds, significantly enhancing the efficiency of the engineering applications. This approach is essential for the life analysis of engine compressor disks and provides a critical foundation for future engineering practices [
21].
Existing studies have demonstrated that artificial-neural-network-based modeling methods are increasingly being adopted by scholars in various fields of research. However, there is relatively limited literature in the area of structural stress prediction, where convolutional neural networks (CNNs) are commonly used for prediction modeling. Although CNNs perform well in field prediction tasks, they impose strict requirements on the input and output data structures, which limits the model’s flexibility, particularly when handling unstructured data or multidimensional feature combinations. This increases the complexity of training and the time required. While traditional machine learning methods offer good performance and speed in regression tasks, they face challenges in dealing with complex nonlinear relationships and high-dimensional data, often necessitating intricate feature analysis and processing, which not only increases the workload but can also result in information loss. In the context of aircraft structural health management, real-time, reliable data sources and rapid prediction capabilities are essential.
The MLP possesses strong fitting capabilities and excels at complex nonlinear mapping [
22,
23]. Compared to other machine learning algorithms, MLP is more adept at capturing intricate nonlinear relationships between input and output when processing high-dimensional data. Additionally, the flexible architecture and numerous adjustable parameters of MLP allow for effective optimization across different application scenarios, making it suitable for adapting to the complex environmental factors and flight conditions encountered by aircraft during operation. However, MLP is highly dependent on data quality and quantity; the presence of noise or incomplete data can reduce prediction accuracy, and insufficient data can lead to overfitting. The ideal application scenario for MLP involves predicting aircraft structural stresses with reliable, high-quality, and sufficient data to ensure model accuracy and reliability. With advancements in big data and health monitoring technologies, the large datasets required for MLP training are increasingly available, supporting its broader application.
To enable rapid prediction of stresses in aircraft structures, this paper establishes a stress prediction model using an MLP neural network, capable of quickly forecasting the stress field. By performing finite element meshing of the wing ribs, the angle of attack, incoming flow velocity, and node coordinates are used as input tensors to the model, allowing it to learn the stress distribution of the wing ribs. The successful application of this model also opens the door for its potential use in predicting stresses in other structural components of the aircraft, such as rotor blades, tail blades, and other wing structures, thereby enhancing the structural safety and reliability of the aircraft.
In this study, a finite element model is developed based on the wing design requirements of an air-to-air aircraft. Through the analysis of aerodynamic elasticity results, the equivalent stress distribution patterns of the wing ribs are summarized. A static aerodynamic elasticity calculation is employed to generate a wing rib stress dataset, comprising 173,700 data samples across 300 flight conditions. The MLP neural network is then utilized to construct a prediction model for the wing rib stress field, as well as a model for predicting the peak stress of the wing ribs. The dataset is used for training and prediction. The primary workflow of this paper is illustrated in
Figure 1, and the key steps are as follows:
Perform finite element modeling and static aerodynamic elasticity calculations of the wing based on the design requirements, followed by an analysis of the stress distribution.
Establish the wing stress field dataset from the numerical simulation results and divide the dataset into training, validation, and test sets according to standard dataset partitioning practices.
Identify the input variables for the model and build the MLP model, setting the hyperparameters based on the structure of the input variables. Different hyperparameters are tested to observe the model loss and performance indicators, and the model with the best overall performance is selected to predict the wing’s stress.
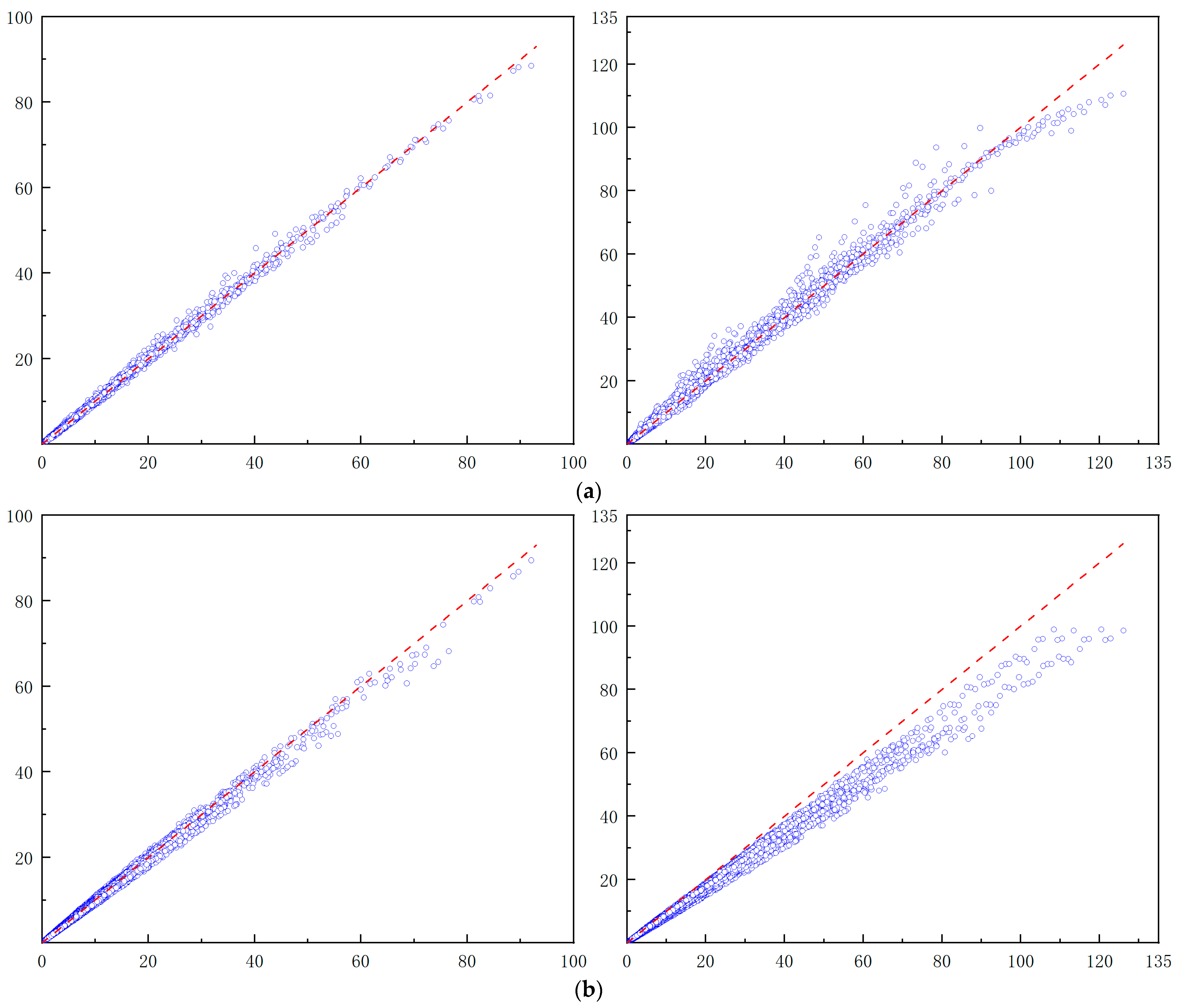
Use common deep learning loss functions and evaluation metrics to assess and fine-tune the model.
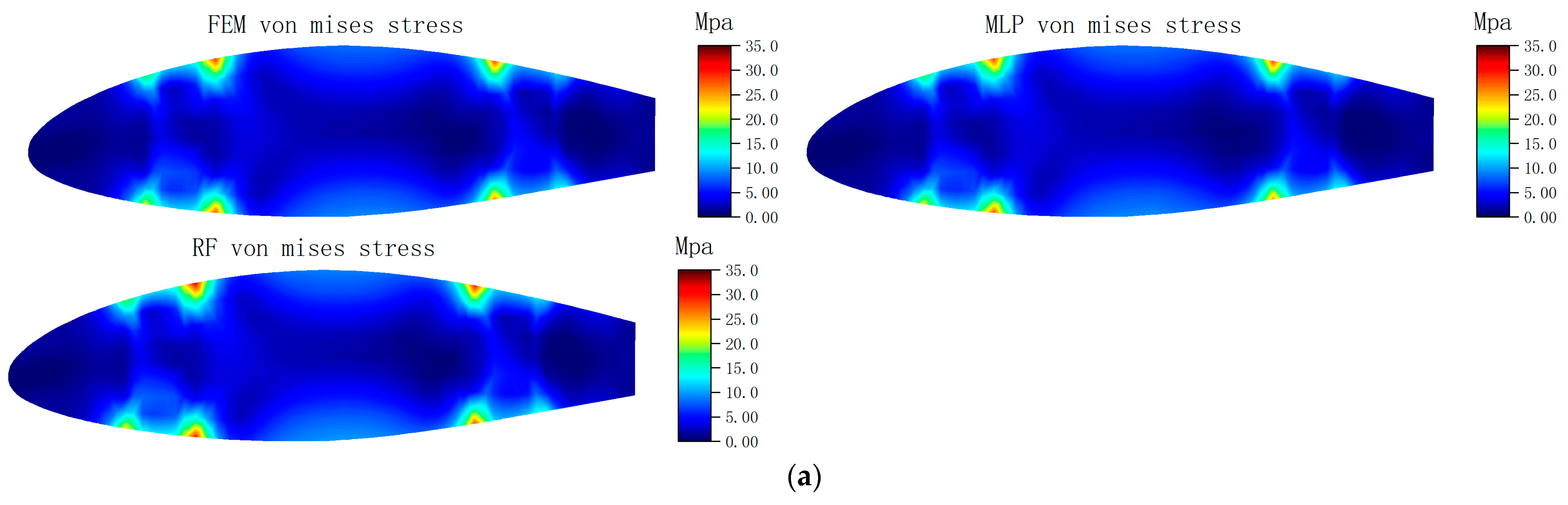
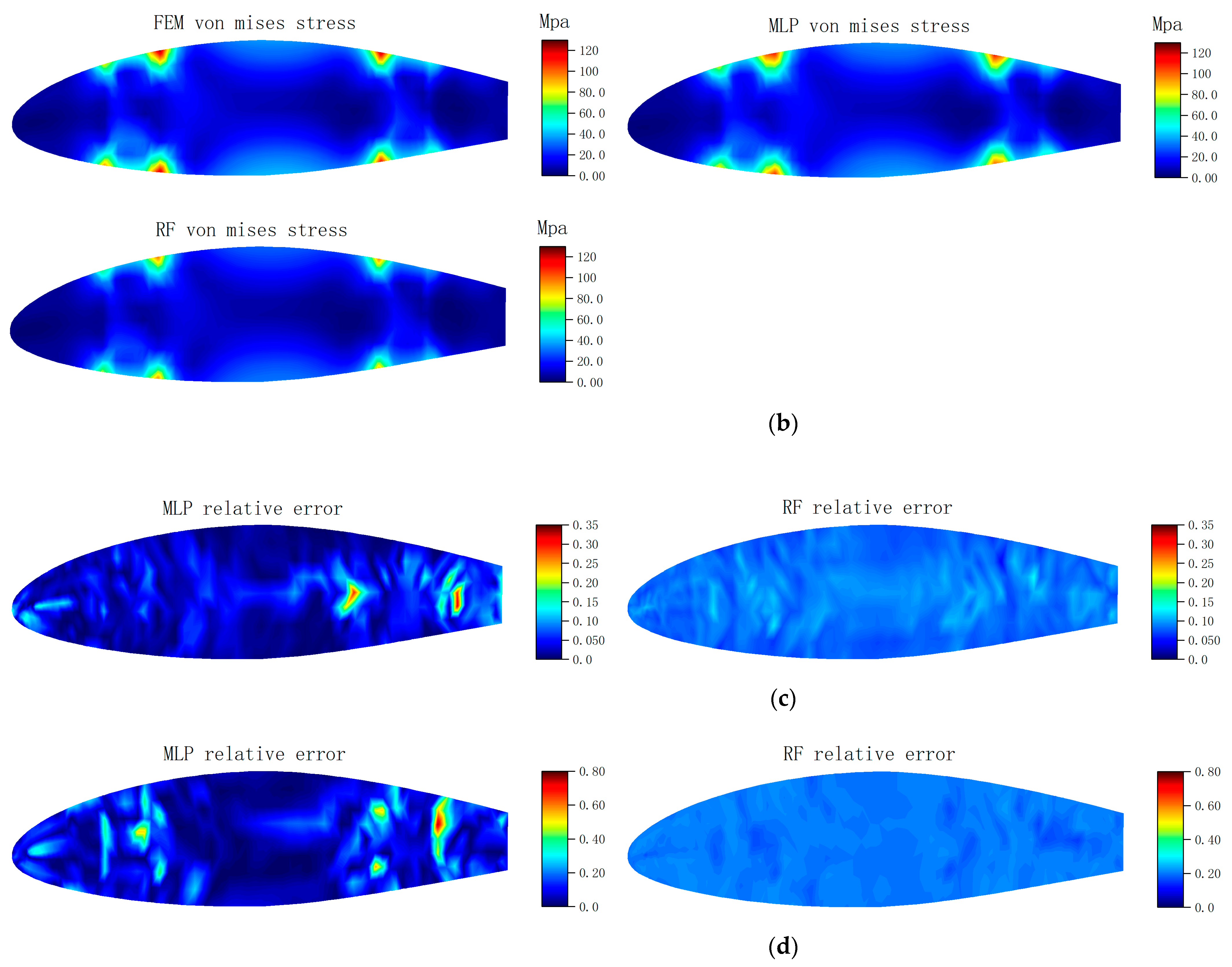
Train the model and compare the predictions of the trained model with those of the RF model for further analysis.
2. Finite Element Modeling and Static Aeroelasticity Calculation for Airfoils
The finite element software Nastran is employed to perform static aerodynamic elasticity calculations on the wing of a composite fixed-wing aircraft currently in the design phase [
24,
25]. The wing’s design parameters are as follows: a chord length of 1.45 meters, a wingspan of 10.46 meters, and a total airfoil area of 15.167 square meters. According to the design requirements for the air-to-air aircraft, under ultimate load conditions, the vertical displacement of the wing tip must not exceed 6% of the wingspan, and the stress around the bolt holes at the root of the wing beam must not exceed 60% of the material’s compressive strength [
26,
27].
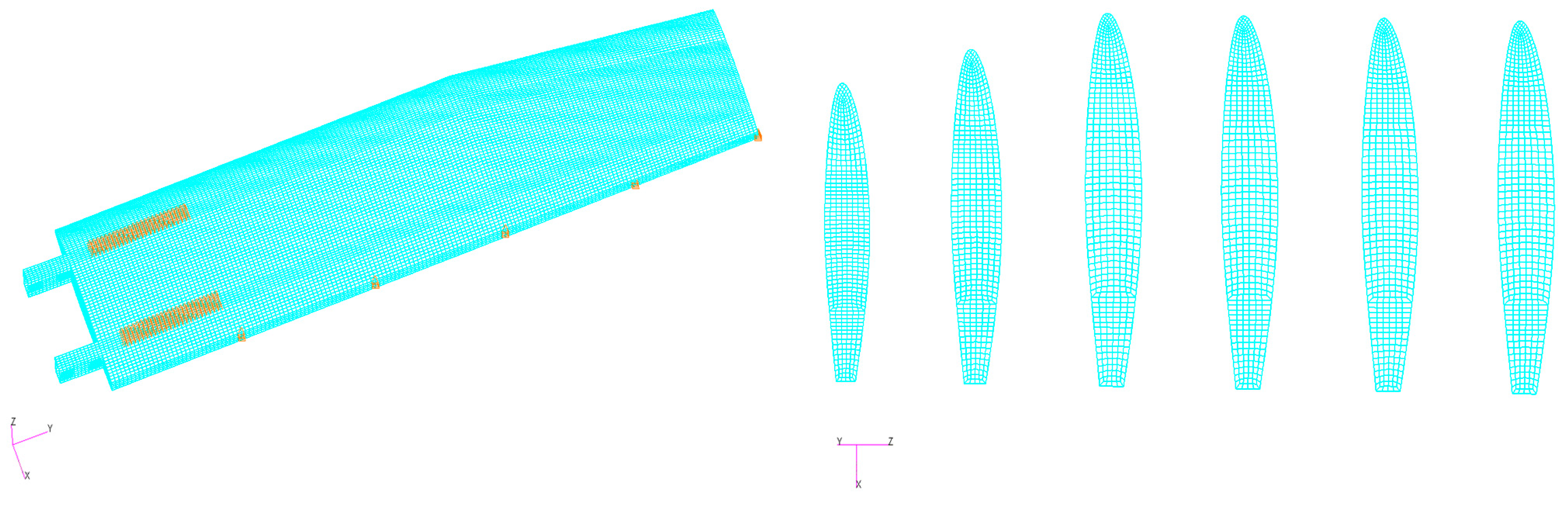
A 3D finite element model of the wing and the wing ribs is shown in
Figure 2. Fixed constraints are applied to the bolt holes at the beam root. The wing is meshed using quadrilateral shell cells for the airfoil, wing ribs, and beam. To ensure calculation accuracy, grid independence was verified during the initial design stage using 18,000, 32,000, and 56,000 meshes, with equivalent stress used as the evaluation criterion. For a flight condition of zero altitude, a flight speed of 150 km/h, and an angle of attack of 0°, the grid correlation verification results are shown in
Table 1. The findings reveal that the maximum equivalent stress difference between 18,000 and 56,000 grids is less than 2%, indicating that grid independence has been achieved. To reduce computational cost, 32,000 grids are selected for further numerical simulations. The detailed grid cell distribution is presented in
Table 2, with the airfoil containing 19,040 cells, the wing ribs containing 3048 cells, and the beam containing 8716 cells. The maximum cell size for the entire wing grid is 27 mm, while the minimum cell size is 2 mm. Based on the design specifications of the aircraft, with flight conditions at zero altitude, a speed range of 150 to 240 km/h, and an angle of attack range of 1 to 10 degrees, the wing stresses are solved under varying conditions.
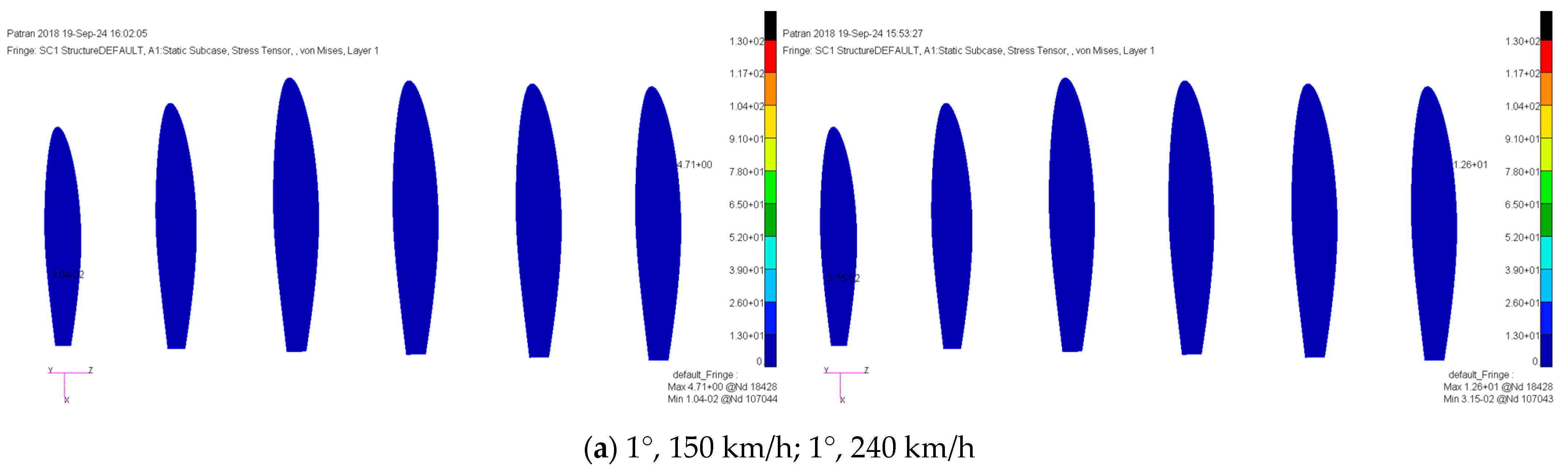
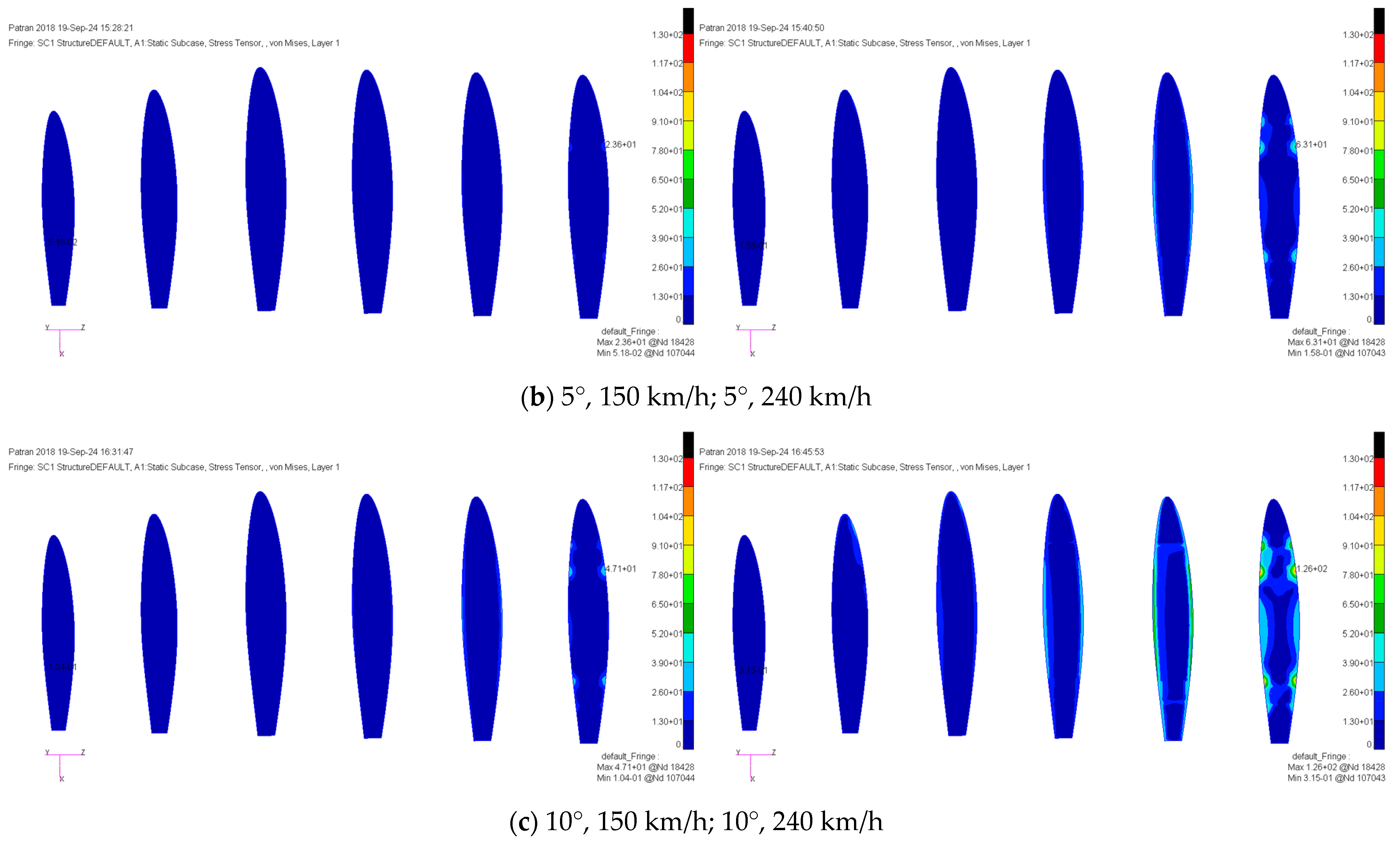
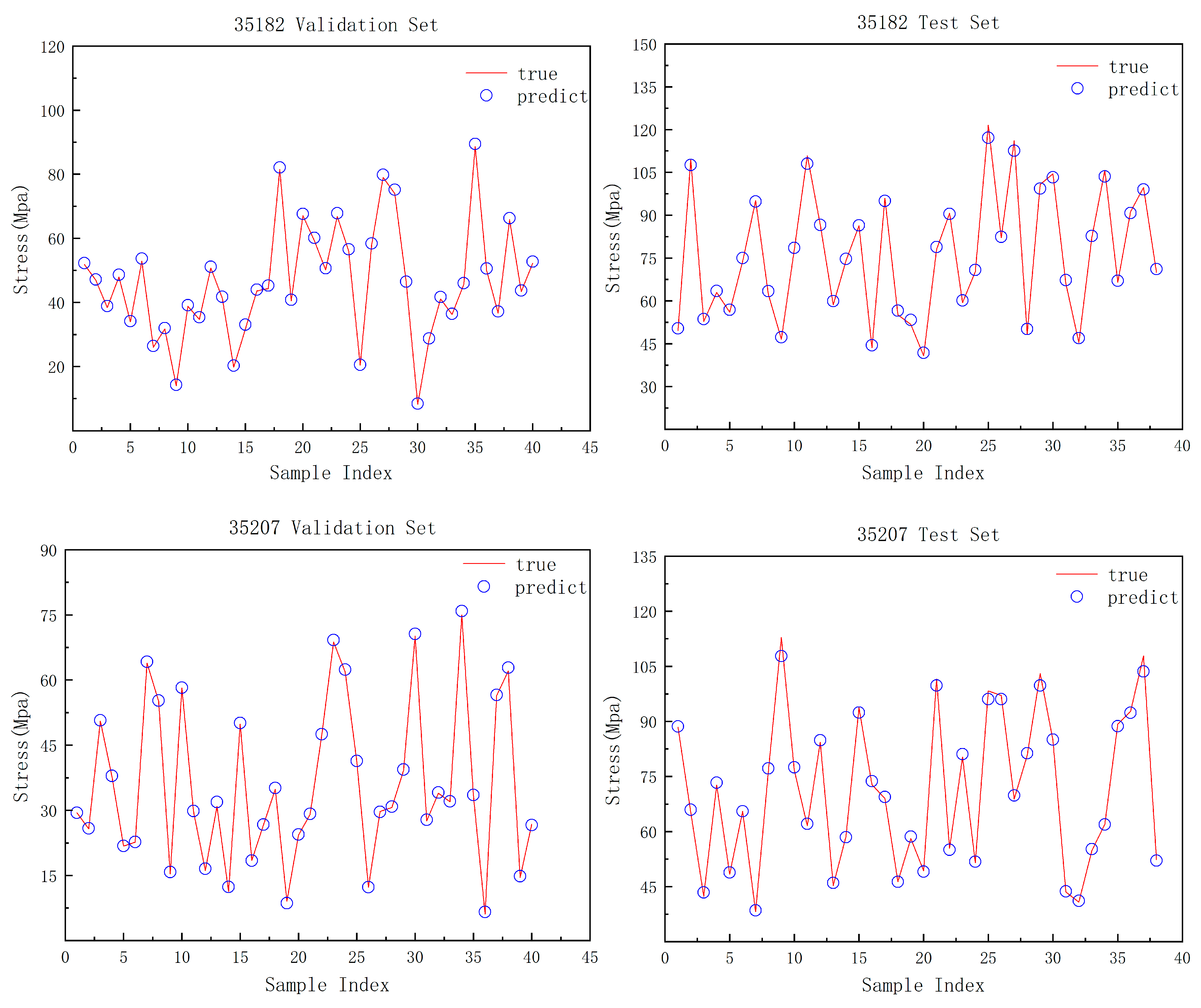
The results for typical working conditions were analyzed, with
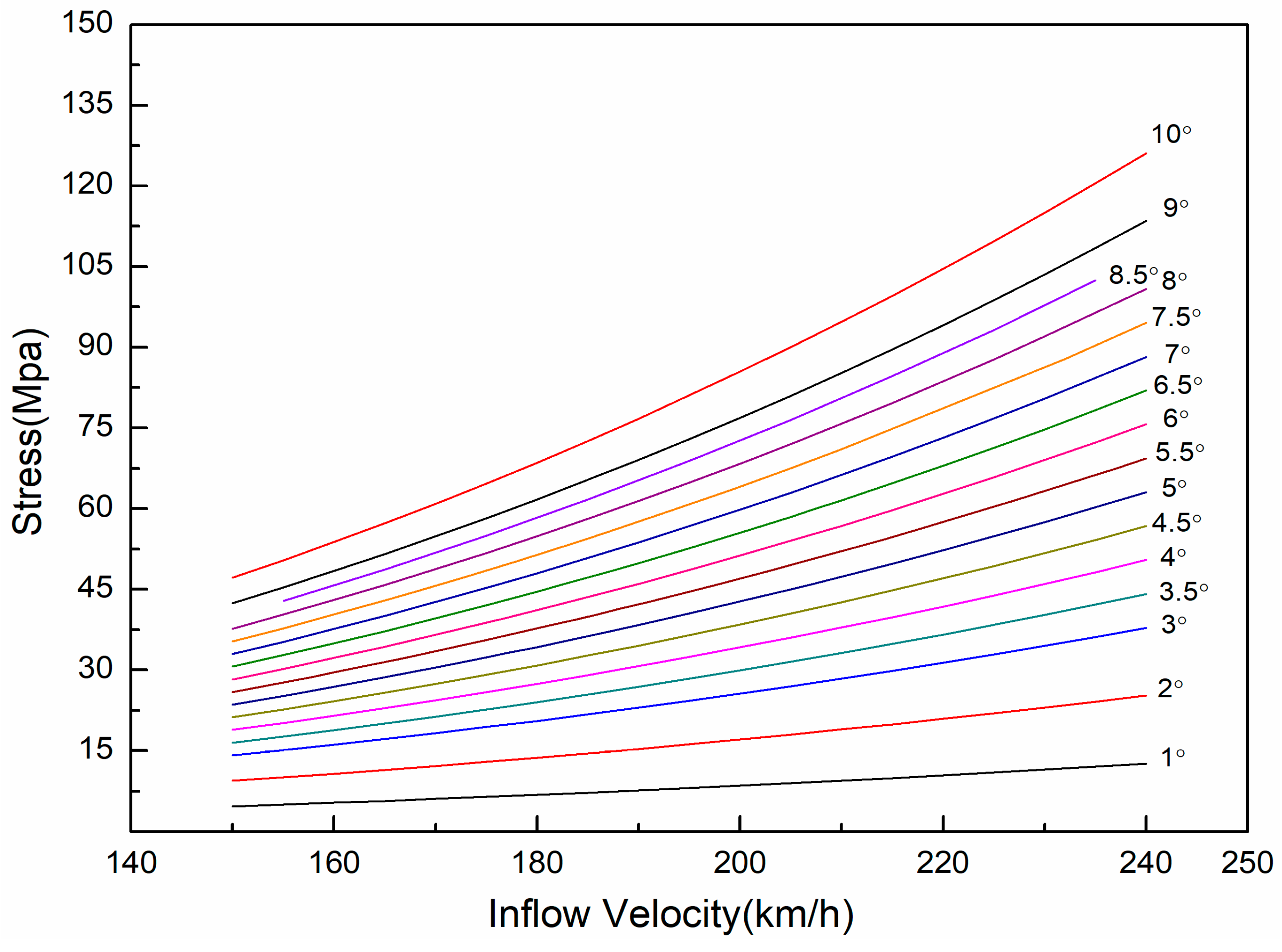
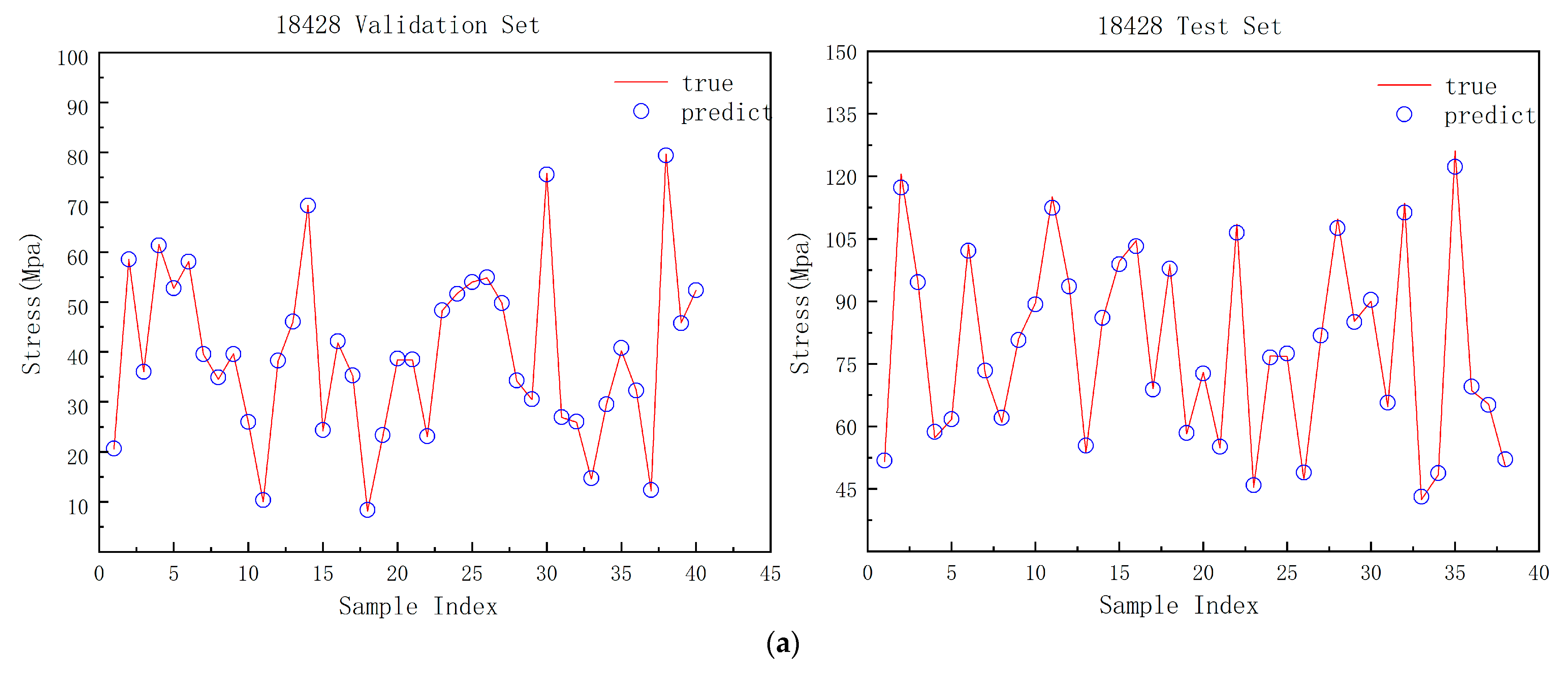
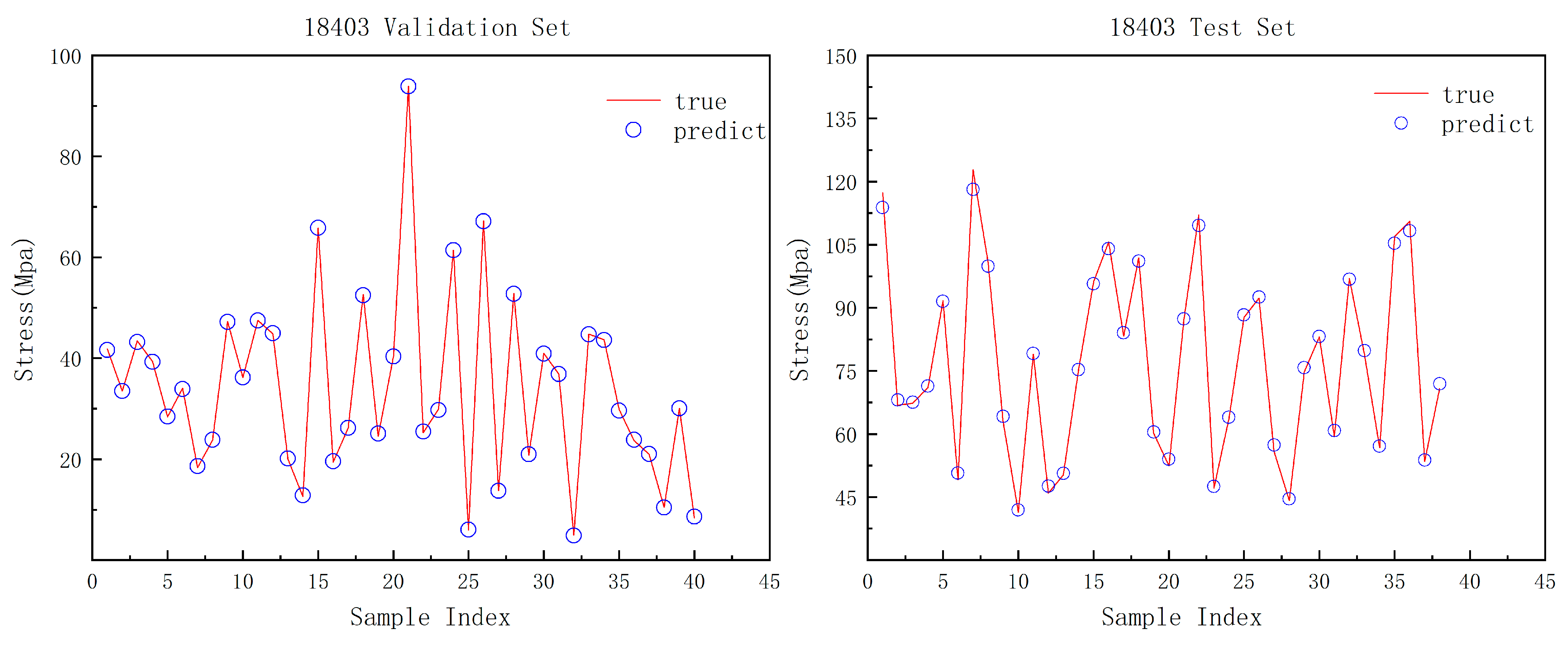
Figure 3 illustrating the equivalent stress distribution for different angles of attack and flow velocities. The stress distribution in the wing rib is significantly affected by changes in angle of attack and inflow velocity. As these parameters change, the equivalent stress tends to concentrate at the contact points where the wing rib meets the skin and the beam. Stress values increase closer to the wing root, particularly at the contact area between the wing rib, skin, and beam. The peak stress node for the wing rib is at node 18,428 of the first wing rib.
Figure 4 shows the stress variation at this node with respect to angle of attack and inflow velocity. At a constant inflow velocity, the equivalent stress at this node increases nonlinearly with the angle of attack. For a fixed angle of attack, the equivalent stress at this node rises with increasing inflow velocity, following an upward trend consistent with observed trends.