Research on the Identification of Rock Mass Structural Planes and Extraction of Dominant Orientations Based on 3D Point Cloud
Abstract
1. Introduction
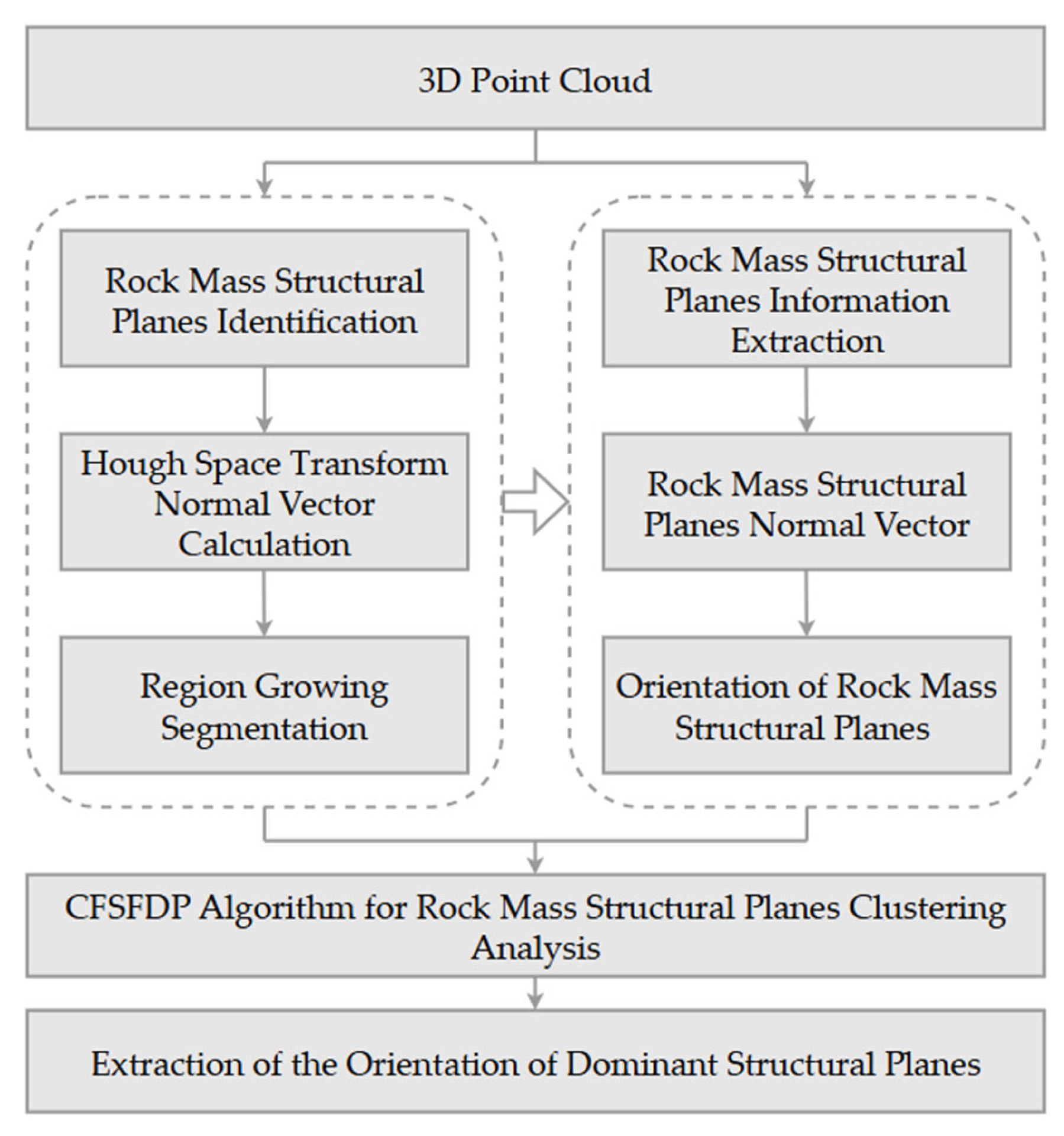
2. Methods
2.1. Identification and Information Extraction of Rock Mass Structural Planes
2.1.1. Rock Mass Structural Planes Identification
- Selection of Seed Points
- 2.
- Feature Judging Criteria
- 3.
- Stopping Conditions for Growth
- (1)
- Set the neighborhood size , calculate the surface variation of the point cloud, sort the point cloud data in ascending order by , and select the point with the smallest as the initial seed point.
- (2)
- Randomly select two points from the neighborhood and the current seed point to form a plane . Calculate the normal vector of the plane , then vote all normal vectors into the corresponding storage container. Region growing stops when the combination satisfies and the confidence level is met. The mean of the normal vectors in the container with the highest vote count is selected as the final normal vector for the point.
- (3)
- Set the normal vector angle threshold , calculate the angle between the normal vector of the neighboring point and the current seed point. If , the neighboring point is added to the current region.
- (4)
- Set the surface variation threshold , calculate the difference between the surface variation of the neighboring point and the current seed point. If , remove the current seed point and designate the neighboring point as the new seed point, continuing the growth process with the new seed point.
- (5)
- Repeat steps (3) and (4). If the number of clustered points is less than , the region growing process for that area is complete, and the region is added to the cluster array.
- (6)
- Repeat step (5) until all points are traversed.
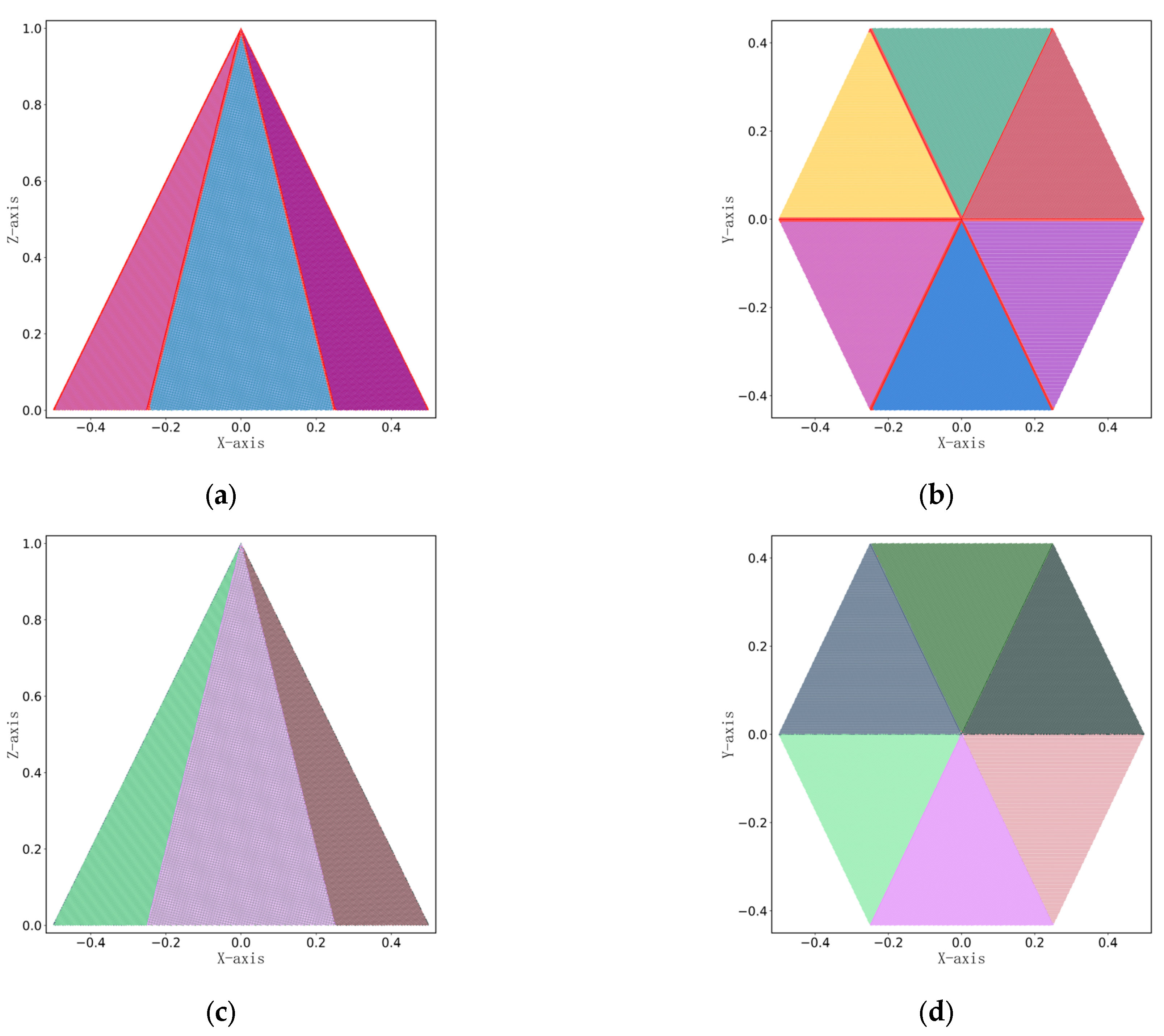
2.1.2. Extraction of Rock Mass Structural Planes Information
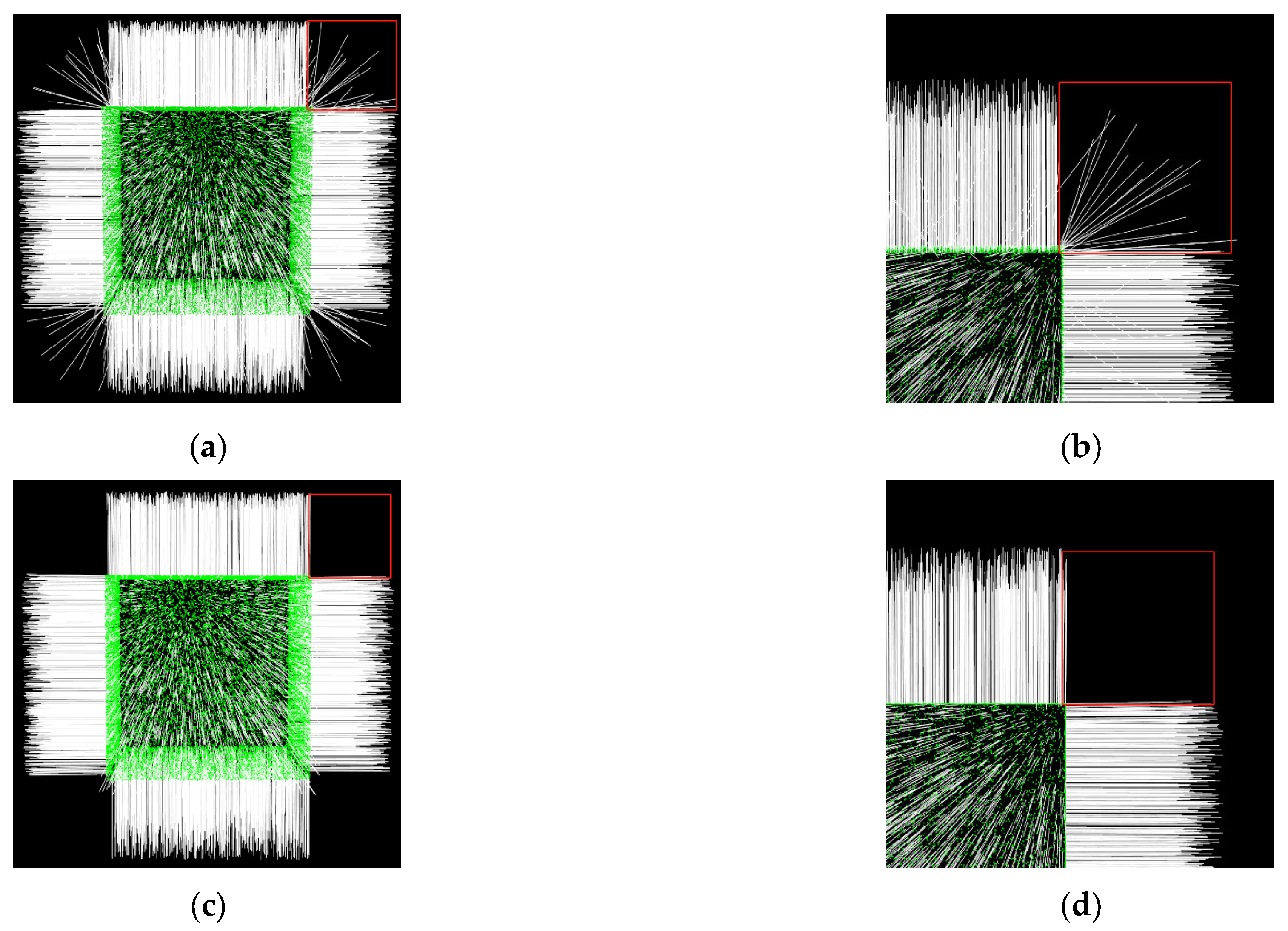
2.1.3. Application Analysis of Rock Mass Structural Planes Identification and Information Extraction
- 4.
- Visualization Analysis of Normal Vectors
- 5.
- Analysis of Region Growing Results
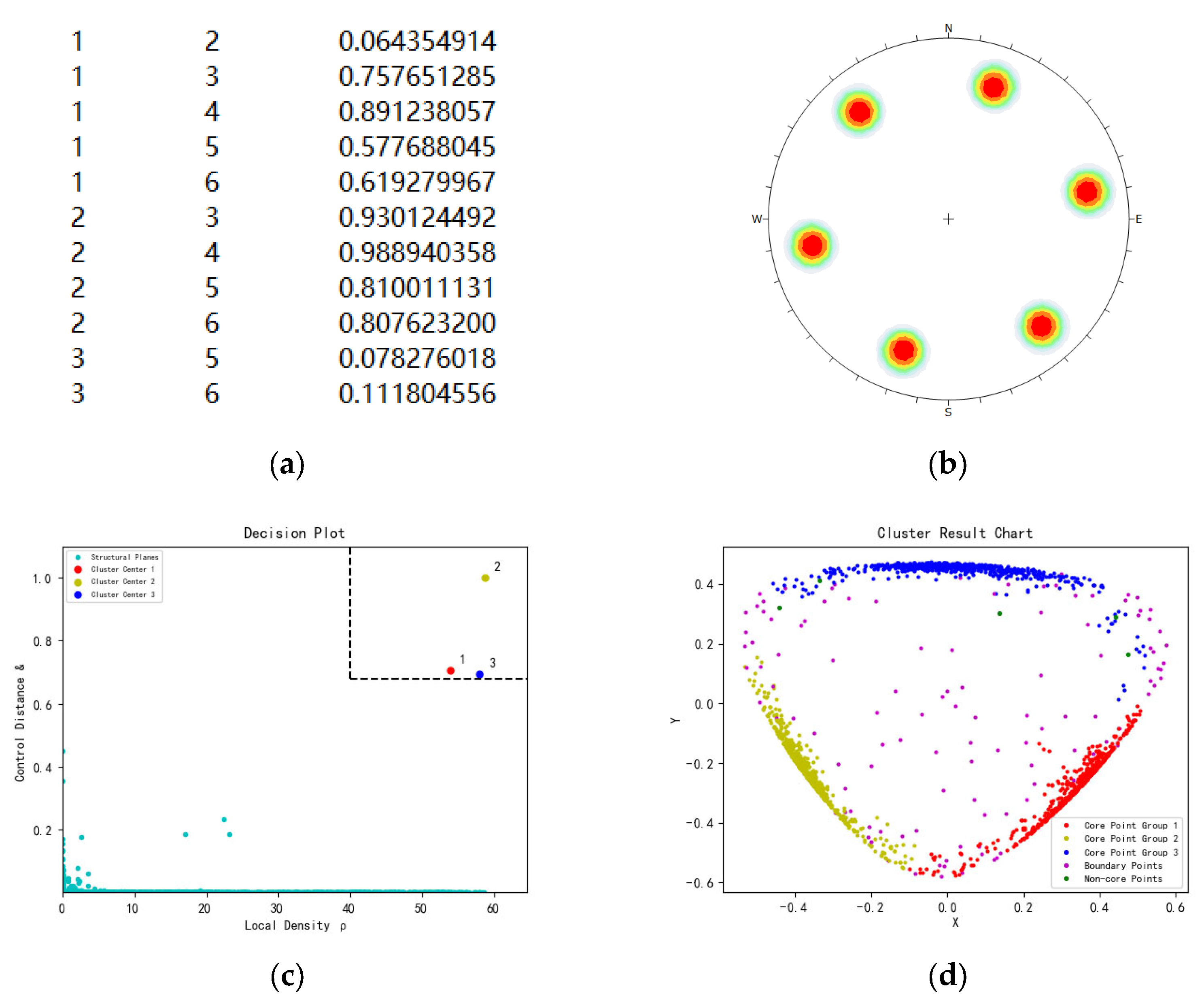
2.2. Cluster Analysis of Rock Mass Structural Planes
- Calculate the sine square value of the angle between the normal vectors of different structural planes, which serves as the clustering distance ;
- Set the cutoff distance and calculate the local density , which can effectively identify outlier structural planes;
- Arrange the local density in descending order and calculate the control distance ;
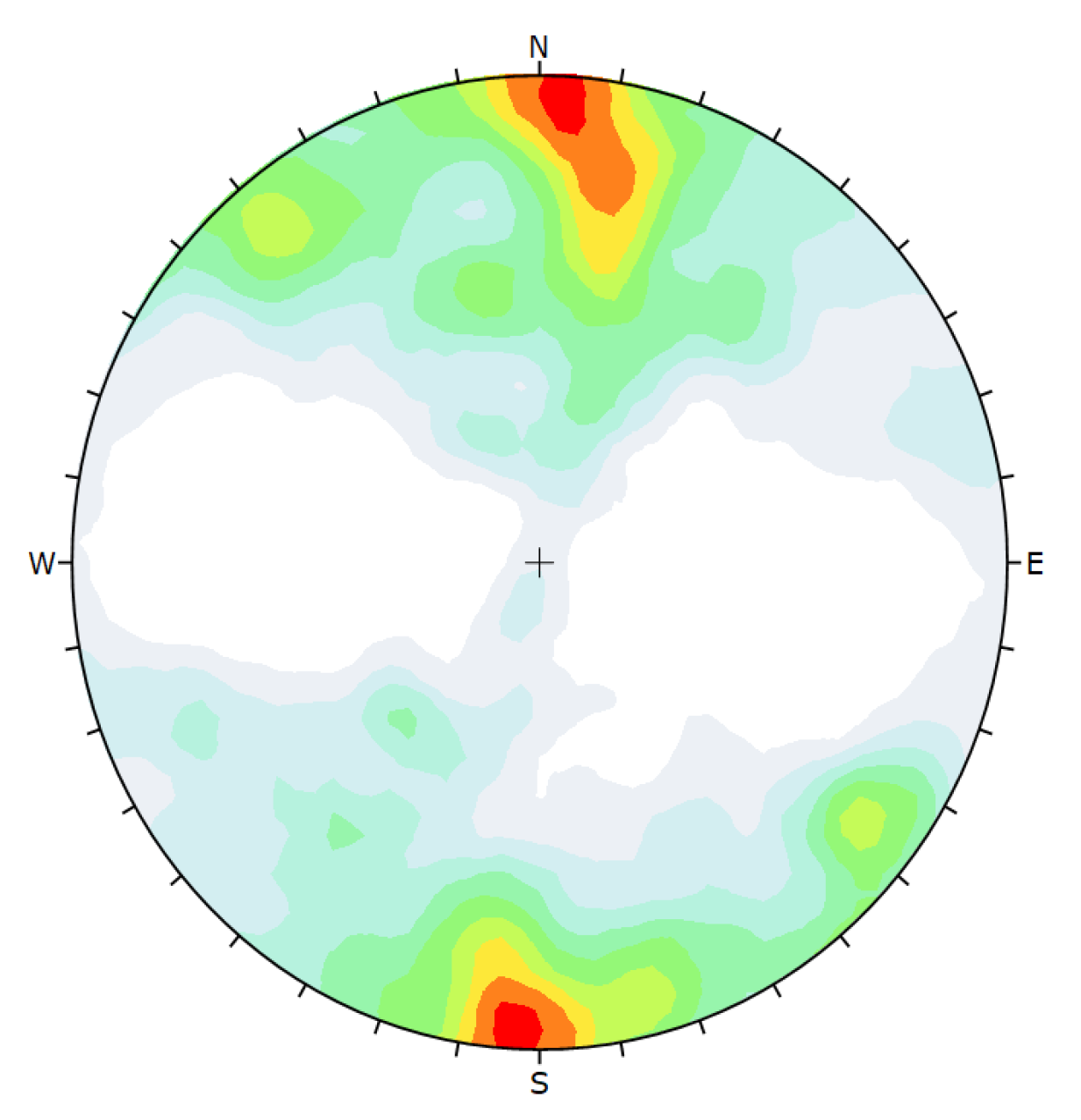
- Plot the decision graph using the local density as the horizontal axis and the control distance as the vertical axis and identify the cluster centers and the number of clusters;
- Assign the remaining points (non-central points) to the nearest category with a higher density than the point, completing the assignment of all non-central points in one iteration;
- Set the local density percentage, calculate the boundary density, and divide the structural planes into core and boundary points to identify outliers, thus improving clustering accuracy.
3. Example Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, H.H.; Pan, B.G.; Wu, W.; Yong, H.; Liu, J.; Li, H.M. Review on Collection and Extraction Methods of Rock Mass Discontinuity Information. J. Basic Sci. Eng. 2023, 31, 1339–1360. [Google Scholar]
- Sun, G.Z. On the Theory of Structure-Controlled Rock Mass. J. Eng. Geol. 1993, 1, 14–18. [Google Scholar]
- Ge, Y.F.; Tang, H.M.; Huang, L.; Wang, L.Q.; Sun, M.J.; Fan, Y.J. A New Representation Method for Three-Dimensional Joint Roughness Coefficient of Rock Mass Discontinuities. Chin. J. Rock Mech. Eng. 2012, 31, 2508–2517. [Google Scholar]
- Wu, X.; Wang, F.Y.; Wang, M.C.; Zhang, X.Q.; Wang, Q.; Zhang, S. A New Method for Automatic Extraction and Analysis of Discontinuities Based on TIN on Rock Mass Surfaces. Remote Sens. 2021, 13, 2894. [Google Scholar] [CrossRef]
- Wang, F.Y.; Chen, J.P.; Fu, X.H.; Shi, B.F. Study on Geometrical Information of Obtaining Rock Mass Discontinuities Based on VirtuoZo. Chin. J. Rock Mech. Eng. 2012, 33, 169–175. [Google Scholar]
- Wang, S.H.; Mu, J.J.; Zhang, H.; Zhang, S.C. Spatial Modeling of Refined Structural Plane of Rock Mass and Block Stability Analysis. J. Northeast. Univ. (Nat. Sci.) 2019, 40, 1186–1189. [Google Scholar]
- Li, S.C.; Liu, H.L.; Li, L.P.; Shi, S.S.; Zhang, Q.Q.; Sun, S.Q.; Hu, J. A Quantitative Method for Rock Structure at Working Faces of Tunnels Based on Digital Images and Its Application. Chin. J. Rock Mech. Eng. 2017, 36, 1–9. [Google Scholar]
- Hoppe, H.; DeRose, T.; Duchamp, T.; McDonald, J.; Stuetzle, W. Surface Reconstruction from Unorganized Points. In Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1 July 1992; pp. 71–78. [Google Scholar]
- Slob, S.; Van Knapen, B.; Hack, R.; Turner, K.; Kemeny, J. Method for Automated Discontinuity Analysis of Rock Slopes with Three-Dimensional Laser Scanning. Transp. Res. Rec. 2005, 1913, 187–194. [Google Scholar] [CrossRef]
- Gigli, G.; Casagli, N. Semi-Automatic Extraction of Rock Mass Structural Data from High Resolution LIDAR Point Clouds. Int. J. Rock Mech. Min. Sci. 2011, 48, 187–198. [Google Scholar] [CrossRef]
- Ge, Y.F. Intelligent Identification and Extraction of Geometric Properties of Rock Discontinuities Based on Terrestrial Laser Scanning. J. Rock Mech. Eng. 2017, 36, 3050. [Google Scholar]
- Chen, N.; Cai, X.M.; Xia, J.W.; Zhang, S.; Jiang, Q.; Shi, C. Intelligent Interpretation of Rock Mass Discontinuity Based on Three—Dimensional Laser Point Cloud. Earth Sci. 2021, 46, 2351–2361. [Google Scholar]
- Kong, X.L.; Xia, Y.H.; Wu, X.Q.; Wang, Z.H.; Yang, K.H.; Yan, M.; Li, C.; Tai, H.Y. Discontinuity Recognition and Information Extraction of High and Steep Cliff Rock Mass Based on Multi-Source Data Fusion. Appl. Sci. 2022, 12, 11258. [Google Scholar] [CrossRef]
- Guo, J.T.; Liu, S.J.; Zhang, P.N.; Wu, L.X.; Zhou, W.H.; Yu, Y.A. Towards Semi-Automatic Rock Mass Discontinuity Orientation and Set Analysis from 3D Point Clouds. Comput. Geosci. 2017, 103, 164–172. [Google Scholar] [CrossRef]
- Gao, F.; Chen, D.P.; Zhou, K.P.; Niu, W.J.; Liu, H.W. A Fast-Clustering Method for Identifying Rock Discontinuity Sets. KSCE J. Civ. Eng. 2019, 23, 556–566. [Google Scholar] [CrossRef]
- Cui, X.J.; Yan, E.C.; Chen, W. Cluster analysis of discontinuity occurrence of rock mass based on improved genetic algorithm. Rock Soil Mech. 2019, 40, 374–380. [Google Scholar]
- Chen, J.Q.; Zhu, H.H.; Li, X.J. Automatic Extraction of Discontinuity Orientation from Rock Mass Surface 3D Point Cloud. Comput. Geosci. 2016, 95, 18–31. [Google Scholar] [CrossRef]
- Wang, S.H.; Ren, Y.P.; Chen, J.Z.; Zhang, Z.S. An Improved Fish Swarm Clustering Algorithm for Structural Grouping. J. Northeast. Univ. (Nat. Sci.) 2019, 40, 420. [Google Scholar]
- Kong, D.H.; Wu, F.Q.; Saroglou, C. Automatic Identification and Characterization of Discontinuities in Rock Masses from 3D Point Clouds. Eng. Geol. 2020, 265, 105442. [Google Scholar] [CrossRef]
- Daghigh, H.; Tannant, D.D.; Daghigh, V.; Lichti, D.D.; Lindenbergh, R. A Critical Review of Discontinuity Plane Extraction from 3D Point Cloud Data of Rock Mass Surfaces. Comput. Geosci. 2022, 169, 105241. [Google Scholar] [CrossRef]
- Hu, L.; Xiao, J.; Wang, Y. Efficient and Automatic Plane Detection Approach for 3-D Rock Mass Point Clouds. Multimed. Tools Appl. 2020, 79, 839–864. [Google Scholar] [CrossRef]
- Zhang, J.H. Intelligent Identification of Rock Mass Structural Plane and Stability Analysis of Rock Slope Block. Sci. Rep. 2022, 12, 16745. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.D.; Liu, J.; Zhang, H.X.; You, W.; Liu, F.T. Rock mass Structural Plane Digital Recognition and Stope Stability Classification Based on the Photographic Surveying Method. J. Min. Saf. Eng. 2014, 31, 127. [Google Scholar]
- Sheng, Y.; Song, T.J.; Chen, J.P.; Zhang, W. Clustering Analysis of Dominative Attitudes of Rock Mass Structural Plane Based on Firefly Algorithm. J. Northeast. Univ. (Nat. Sci.) 2015, 36, 284. [Google Scholar]
- Feng, Y.; Ma, F.S.; Gong, C.C.; Guo, J.; Wang, S.F.; Liu, Z.C. Data Analysis Method for Optimized and Dominant Orientations of Joints in Rock Mass. J. Eng. Geol. 2011, 19, 887–892. [Google Scholar]
- Ai, C.M.; Lu, Y.; Sun, P.P. Dynamic Cluster Grouping Analysis of Occurrence of Structural Plane in Natural Rock Mass. J. Yangtze River Sci. Res. Inst. 2023, 40, 106. [Google Scholar]
- Song, J.L.; Huang, R.Q.; Pei, X.J. Particle swarm optimization algorithm based fuzzy c-means cluster analysis for discontinuities occurrence in rock mass. J. Eng. Geol. 2012, 20, 591–598. [Google Scholar]
- Deng, J.H.; Chen, B.L.; Wu, X.M.; Xie, G.H. Self-Organized Cluster Analysis on Texture Plane Occurrence of Rock Mass. J. Yangtze River Sci. Res. Inst. 2011, 28, 50. [Google Scholar]
- Guo, G. Study on Rock Mass Structural Plane Identification and Rock Mass Integrity Evaluation Based on 3D Laser Scanning Technology. Master’s Thesis, Three Gorges University, Yichang, China, 2023. [Google Scholar]
- Dong, X.J. The Three-Dimensional Laser Scanning Technique and Research on Its Engineering Application. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2007. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by Fast Search and Find of Density Peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Slob, S. Automated Rock Mass Characterization Using 3-D Terrestrial Laser Scanning; ResearchGate: Berlin, Germany, 2010. [Google Scholar]

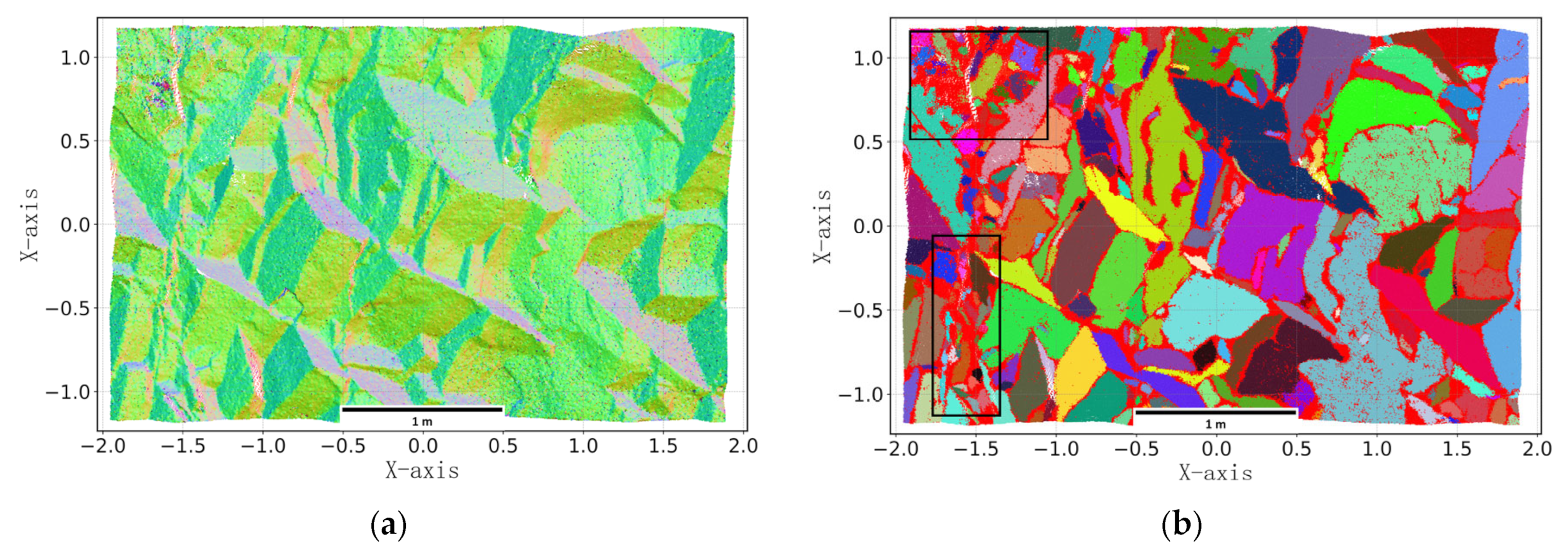

| Structural Plane ID | Total Points (Count) | Identified Points (Count) | Unidentified Points (Count) | Identification Rate (%) | |||
|---|---|---|---|---|---|---|---|
| PCA | Hough | PCA | Hough | PCA | Hough | ||
| J1 | 28,559 | 27,218 | 28,459 | 1341 | 100 | 95.30 | 99.65 |
| J2 | 28,479 | 27,142 | 28,356 | 1337 | 123 | 95.31 | 99.57 |
| J3 | 25,292 | 23,889 | 25,070 | 1403 | 222 | 94.45 | 99.12 |
| J4 | 21,995 | 21,095 | 21,853 | 900 | 142 | 95.91 | 99.35 |
| J5 | 21,475 | 20,880 | 21,378 | 595 | 97 | 97.23 | 99.55 |
| J6 | 21,113 | 20,099 | 20,935 | 1014 | 178 | 95.20 | 99.16 |
| Total | 146,913 | 140,323 | 146,051 | 6590 | 862 | 95.51 | 99.41 |
| Method | J1 | J2 |
|---|---|---|
| Dip Direction < Dip Angle | Dip Direction < Dip Angle | |
| RocScience Dips 7.0 | 182.76° < 81.07° | 282.42° < 33.13° |
| Proposed Method | 183.08° < 82.32° | 284.65° < 33.95° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Xia, Y.; Wang, B.; Yang, Z.; Yang, K. Research on the Identification of Rock Mass Structural Planes and Extraction of Dominant Orientations Based on 3D Point Cloud. Appl. Sci. 2024, 14, 9985. https://doi.org/10.3390/app14219985
Zhu J, Xia Y, Wang B, Yang Z, Yang K. Research on the Identification of Rock Mass Structural Planes and Extraction of Dominant Orientations Based on 3D Point Cloud. Applied Sciences. 2024; 14(21):9985. https://doi.org/10.3390/app14219985
Chicago/Turabian StyleZhu, Jiarui, Yonghua Xia, Bin Wang, Ziliang Yang, and Kaihua Yang. 2024. "Research on the Identification of Rock Mass Structural Planes and Extraction of Dominant Orientations Based on 3D Point Cloud" Applied Sciences 14, no. 21: 9985. https://doi.org/10.3390/app14219985
APA StyleZhu, J., Xia, Y., Wang, B., Yang, Z., & Yang, K. (2024). Research on the Identification of Rock Mass Structural Planes and Extraction of Dominant Orientations Based on 3D Point Cloud. Applied Sciences, 14(21), 9985. https://doi.org/10.3390/app14219985





