Study of the Impact of Acquisition Parameters on Fault Feature Identification Based on Magnetotelluric Modeling
Abstract
1. Introduction
2. MT Forward Modeling and Parameter Setting
2.1. Fault Model Setup
2.2. Finite Element Modeling
2.3. Forward Modeling Parameters Setting
3. MT Synthetic Data Inversion
4. Discussion
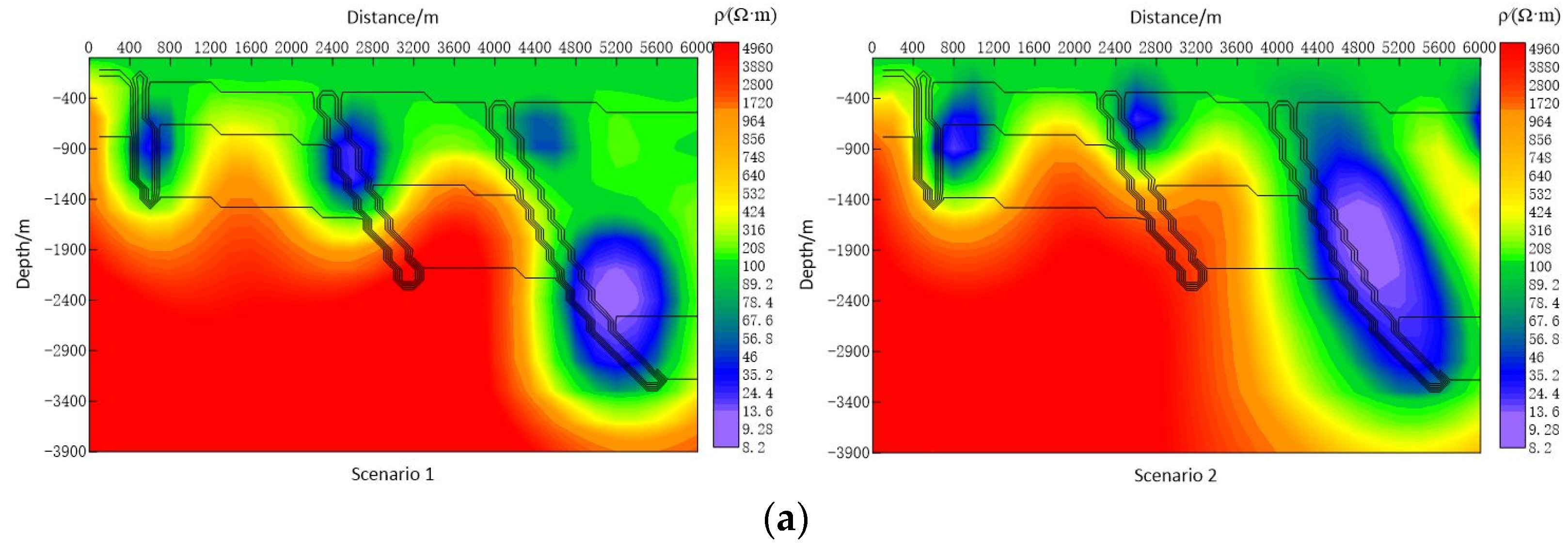
4.1. Effect of Station Spacing on Fault Imaging
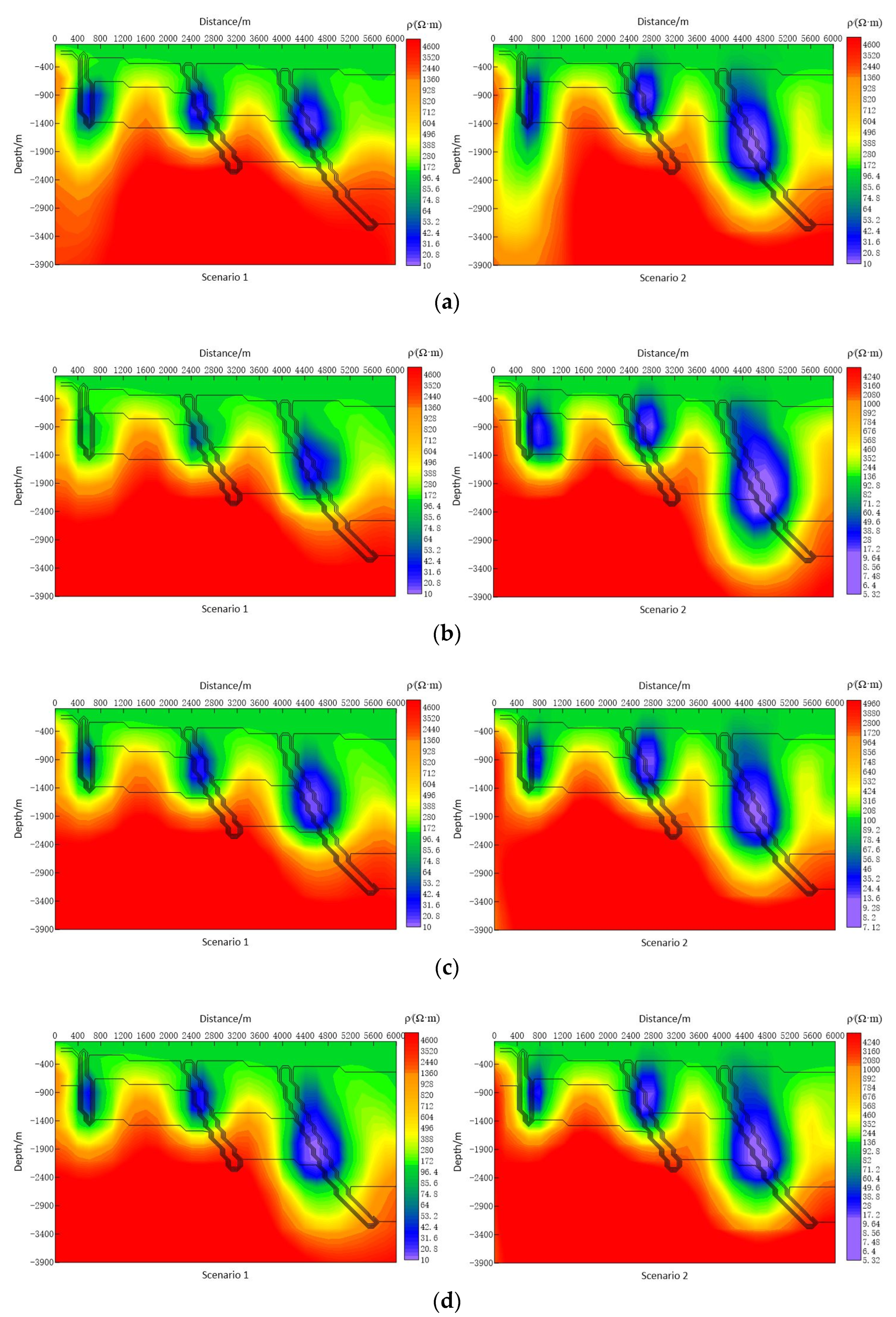
4.2. Effect of Survey Length on Fault Imaging
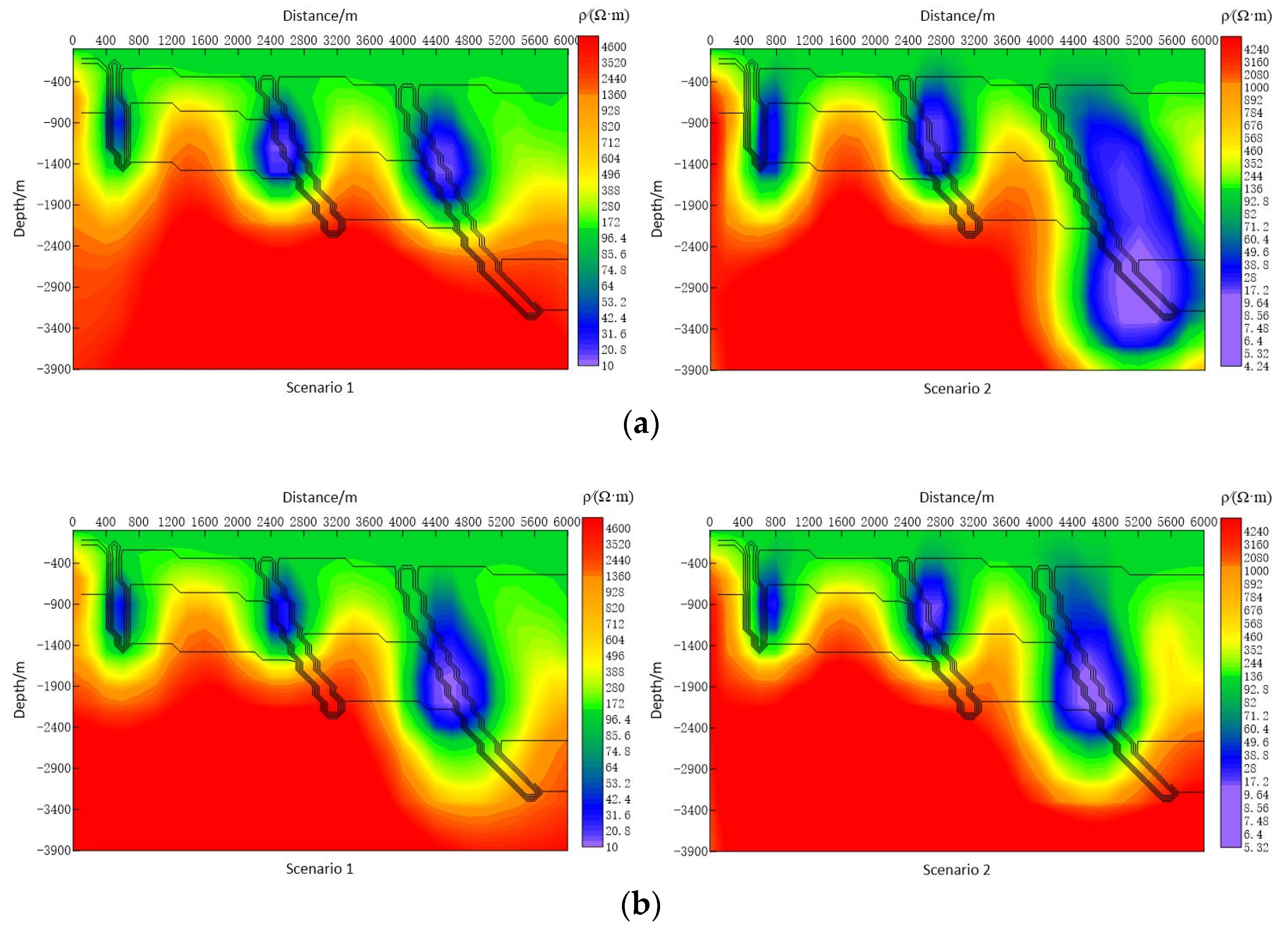
4.3. Effect of Observation Frequency Bands on Fault Imaging
5. Conclusions
- (1)
- Forward modeling results show that a station spacing of 400 m effectively resolves fault zones and transverse conductive fault zones ranging from 100 m to 400 m in width. However, reducing station spacing offers no significant advantage in accurately determining their extent and morphology. In contrast, larger station spacing impacts fault boundary localization and increases deviations from the actual geological model. Specifically, in Scenario 2, when station spacing exceeds 400 m, the imaging of both the F1 and F3 faults deteriorates, with lateral errors increasing from 0.1 km to as much as 1.2 km. These findings emphasize the need for tighter station spacing, particularly in complex geological regions, to achieve accurate fault localization.
- (2)
- In this study’s geological model, using a 400 m station spacing, a survey length of 12 km or more yields optimal imaging accuracy for fault boundaries (F1 and F3), especially for narrower faults (Scenario 1), enhancing localization accuracy and inversion depth. For wider faults (Scenario 2), increasing the survey length does not significantly improve the clarity of the deeper faults. In both scenarios, the F1 fault is best imaged with a survey length of 12 km, where the lateral error in fault positioning decreases from 1.0 km to less than 0.3 km. For the F3 fault, a 12 km survey reduces its positional error from 1.5 km to 0.2 km. In contrast, the F2 fault consistently shows a shallower inversion depth, with reduced low-resistivity anomalies and an average depth discrepancy of 1.0 km across all survey lengths.
- (3)
- With a 400 m station spacing, broadband measurements do not significantly improve the clarity of shallow fault structures compared to regular measurements. This limitation may result from insufficient resolution of narrow fault structures in broadband data at a 400 m station spacing. Therefore, acquiring lower frequency and broader bandwidth data through long-period measurements is essential to improve the resolution of deep fault structures.
- (4)
- The inversion results in this study show a shallower inversion depth compared to the true depth, resulting in poor resolution of the faults’ vertical extent. Additionally, the inversion results suggest that due to the limitations of MT inversion, resistivity models derived from MT data should be interpreted with caution, especially without support from other geophysical methods, as this may affect resource estimation. For instance, the F2 fault zone appears the smallest in the inversion results, with the resistivity model showing the poorest conductivity, contradicting its true characteristics but not diminishing its exploration potential. The forward modeling in this study has been optimized for a two-dimensional observation system, with simplifications made regarding subsurface structures and conductive materials. However, real-world conditions are likely more complex, requiring consideration of factors such as fault connectivity, variations in fault zones across planes, and the types of conductors involved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McLeod, J.; Ferguson, I.; Craven, J.; Roberts, B.; Giroux, B. Pre-injection magnetotelluric surveys at the Aquistore CO2 sequestration site, Estevan, Saskatchewan, Canada. Int. J. Greenh. Gas Control 2018, 74, 99–118. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, X.B.; Tang, J.; Cui, T.F.; Sun, X.Y.; Wang, P.J.; Liu, Z.Y. Three-dimensional modeling of magnetotelluric data from the Hefei-Suqian segment of the Tanlu Fault Zone, Eastern China. Chin. J. Geophys. 2022, 65, 1336–1353. (In Chinese) [Google Scholar]
- Heinson, G.; Didana, Y.; Soeffky, P.; Thiel, S.; Wise, T. The crustal geophysical signature of a world-class magmatic mineral system. Sci. Rep. 2018, 8, 10608. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.P.; Duan, J.M.; Michael, D.; Andrew, C.; Anthony, S.; Brodie, R.C.; Goodwin, J. Application of Multi-Scale Magnetotelluric Data to Mineral Exploration: An Example from the East Tennant Region, Northern Australia. Geophys. J. Int. 2021, 229, 1628–1645. [Google Scholar] [CrossRef] [PubMed]
- Niu, P.; Han, J.T.; Zeng, Z.F.; Hou, H.S.; Liu, L.J.; Ma, G.Q.; Guan, Y.W. Deep controlling factors of the geothermal field in the northern Songliao basin derived from magnetotelluric survey. Chin. J. Geophys. 2021, 64, 4060–4074. (In Chinese) [Google Scholar]
- Zhang, J.F.; Sun, N.Q.; Liu, Z.L.; Qi, Z.P. Electromagnetic methods in the detection of water hazards in coal mines: A review. Coal Geol. Explor. 2023, 51, 301–316. [Google Scholar]
- Nikiforov, V.M.; Varentsov, I.M.; Shkabarnya, G.N.; Kaplun, V.B.; Zhukovin, A.Y.; Cuong, D.H. Long-period (10 < T < 20,000 s) Magnetotelluric Studies in Northern Vietnam. Russ. Geol. Geophys. 2020, 61, 1036–1055. [Google Scholar]
- He, J.S. Wide field electromagnetic sounding methods. J. Cent. South Univ. (Sci. Technol.) 2010, 41, 1065–1072. [Google Scholar]
- Cai, J.T.; Chen, X.B.; Fang, L.H.; Qi, H.; Wang, P.J.; Zhang, Y.Y.; Liu, Z.Y.; Xie, X.B.; Zhou, L. Study on the seismotectonic environment in Bengbu city using the dense magnetotelluric array. Chin. J. Geophys. 2023, 66, 638–658. (In Chinese) [Google Scholar]
- Zhang, J.H.; Zhao, G.Z.; Xiao, Q.B.; Xia, Q.B.; Tang, J. Analysis of electric structure of the central Tan-Lu fault zone (Yi-Shu fault zone, 36°N ) and seismogenic condition. Chin. J. Geophys. 2010, 53, 605–611. (In Chinese) [Google Scholar]
- Han, J.T.; Kang, J.Q.; Liu, C.; Liu, W.Y.; Zhang, Y.C.; Wang, T.Q.; Guo, Z.Y.; Yuan, T.M.; Liu, L.J. Characteristics of the asthenosphere structure beneath the eastern segment of the Central Asia orogenic belt inferred from a long-period magnetotelluric survey. Chin. J. Geophys. 2019, 62, 1148–1158. (In Chinese) [Google Scholar]
- Qiao, Y.; Zhang, H. Methodology and Application of Deep Geothermal Sounding in Low-Resistance Cover Areas. Appl. Geophys. 2023; Early Access. [Google Scholar]
- Zhang, H.; Sui, S.Q.; Qian, L.R. The application of multiple non-seismic methods to geothermal exploration in Qihe Shandong Province. Geophys. Geochem. Explor. 2020, 44, 727–733. [Google Scholar]
- Patro, P.K. Magnetotelluric Studies for Hydrocarbon and Geothermal Resources: Examples from the Asian Region. Surv. Geophys. 2017, 38, 1005–1041. [Google Scholar] [CrossRef]
- Geiermann, J.; Schill, E. 2-D Magnetotellurics at the geothermal site at Soultz-sous-Forets: Resistivity distribution to about 3000 m depth. Comptes Rendus Geosci. 2010, 342, 587–599. [Google Scholar] [CrossRef]
- Pospeeva, E.V.; Potapov, V.V. Deep Structure of the Junction Zones of the Chuya Tectonic Depression and Its Mountainous Frame in Gorny Altai according to Magnetotelluric Studies. Russ. Geol. Geophys. 2021, 62, 474–485. [Google Scholar] [CrossRef]
- Avdeev, D.B. Three-dimensional electromagnetic modeling and inversion from theory to application. Surv. Geophys. 2005, 26, 767–799. [Google Scholar] [CrossRef]
- Zhou, R.F.; Wand, X.B.; Qin, C.; Xu, Y.C.; Zhang, J.T.; Wang, R. Comprehensive utilization of NLCG and OCCAM in two-dimensional magnetotelluric inversion. Prog. Geophys. 2016, 31, 2306–2312. [Google Scholar]
- Chen, M.S. Analysis of some problems on the detecting depth of frequency electromagnetic sounding. Coal Geol. Explor. 2012, 40, 67–70. [Google Scholar]
- Zhang, H.; Nie, F. Magnetotelluric Forward Modeling Using a Non-Uniform Grid Finite Difference Method. Mathematics 2024, 12, 2984. [Google Scholar] [CrossRef]
- Gallardo, G.E.U.; Ruiz, A.D. High order edge-based elements for 3D magnetotelluric modeling with unstructured meshes. Comput. Geosci. 2022, 158, 104971. [Google Scholar] [CrossRef]
- Klaus, S. Electromagnetic Modeling Using Adaptive Grids—Error Estimation and Geometry Representation. Surv. Geophys. 2023, 45, 227–314. [Google Scholar]
- Tong, X.Z.; Sun, Y.; Zhang, B.Y. An efficient spectral element method for two-dimensional magnetotelluric modeling. Front. Earth Sci. 2023, 11, 1183150. [Google Scholar] [CrossRef]
- Jahandari, H.; Bihlo, A. Forward modelling of geophysical electromagnetic data on unstructured grids using an adaptive mimetic finite-difference method. Comput. Geosci. 2021, 25, 1083–1104. [Google Scholar] [CrossRef]
- Erdogan, E.; Candansayar, M.E. The conductivity structure of the Gediz Graben geothermal area extracted from 2D and 3D magnetotelluric inversion: Synthetic and field data applications. Geothermics 2017, 65, 170–179. [Google Scholar] [CrossRef]
- Zainalpour, A.; Kamali, G.; Moradzadeh, A. Optimal selection of regularization parameter in magnetotelluric data inversion. Acta Geod. Geophys. 2022, 57, 245–263. [Google Scholar] [CrossRef]
- Wang, P.J.; Chen, X.B.; Zhang, Y.Y. Synthesizing magnetotelluric time series based on forward modeling. Front. Earth Sci. 2023, 11, 1086749. [Google Scholar] [CrossRef]
- Tomassi, A.; Trippetta, F.; de Franco, R.; Ruggieri, R. How petrophysical properties influence the seismic signature of carbonate fault damage zone: Insights from forward-seismic modelling. J. Struct. Geol. 2023, 167, 104802. [Google Scholar] [CrossRef]
- Kirkby, A.; Doublier, M.P. Synthetic magnetotelluric modelling of a regional fault network—Implications for survey design and interpretation. Explor. Geophys. 2022, 55, 617–628. [Google Scholar] [CrossRef]
- Dmitriev, V.I.; Mershchikova, N.A. Mathematical Modeling of the Influence of the Coastal Effect on Marine Magnetotelluric Soundings. Izv.-Phys. Solid Earth 2010, 46, 717–721. [Google Scholar] [CrossRef]
- Zhang, M.L.; Li, Y.G. Efficient magnetotelluric data acquisition using irregular stations and compressive sensing reconstruction. J. Appl. Geophys. 2023, 217, 105169. [Google Scholar] [CrossRef]
- Batista, J.D.; Sampaio, E.E.S. Magnetotelluric inversion of one- and two-dimensional synthetic data based on hybrid genetic algorithms. Acta Geophys. 2019, 67, 1365–1377. [Google Scholar] [CrossRef]
- Arun, S.; Rahul, D.; Pravin, K.G.; Israil, M. A MATLAB based 3D modeling and inversion code for MT data. Comput. Geosci. 2017, 104, 1–11. [Google Scholar]
- Mackie, R.L.; Smith, J.T.; Madden, T.R. Three-Dimensional electromagnetic modeling using finite-difference equations-the magnetotelluric example. Radio Sci. 1994, 29, 923–935. [Google Scholar] [CrossRef]
- Rodi, W.; Mackie, R.L. Nonlinear conjugate gradients algorithm for 2D magnetotelluric inversion. Geophysics 2001, 66, 174–187. [Google Scholar] [CrossRef]
- Kelbert, A.; Egbert, G.D.; Schultz, A. Non-linear conjugate gradient inversion for global em induction: Resolution studies. Geophys. J. Int. 2008, 173, 365–381. [Google Scholar] [CrossRef]
- Miensopust, M.P.; Queralt, P.; Jones, A.G. Magnetotelluric 3-D inversion- a review of two successful workshops on forward and inversion code testing and comparison. Geophys. J. Int. 2013, 193, 1216–1238. [Google Scholar] [CrossRef]


| Station Spacing (m) | Survey Length (km) | Frequency Band (Hz) | No of Air Layers | No of Vertical Cell | Horizontal Cell Size (Scenario 1) (m) | Horizontal Cell Size (Scenario 2) (m) |
|---|---|---|---|---|---|---|
| 200 | 14 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 400 | 14 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 600 | 14 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 800 | 14 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 400 | 12 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 400 | 10 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 400 | 8 | 0.001–1000 | 8 | 25 | 100 | 200 |
| 400 | 14 | 0.01–100 | 8 | 25 | 100 | 200 |
| Station Spacing (m) | Survey Length (km) | Frequency Band (Hz) | No. of Air Layers | No. of Vertical Cell | RMS Misfit (Scenario 1) | RMS Misfit (Scenario 2) |
|---|---|---|---|---|---|---|
| 200 | 14 | 0.001–1000 | 8 | 25 | 0.82 | 1.51 |
| 400 | 14 | 0.001–1000 | 8 | 25 | 1.27 | 1.38 |
| 600 | 14 | 0.001–1000 | 8 | 25 | 1.42 | 1.50 |
| 800 | 14 | 0.001–1000 | 8 | 25 | 1.64 | 1.59 |
| 400 | 12 | 0.001–1000 | 8 | 25 | 1.29 | 1.40 |
| 400 | 10 | 0.001–1000 | 8 | 25 | 1.26 | 1.44 |
| 400 | 8 | 0.001–1000 | 8 | 25 | 1.26 | 1.49 |
| 400 | 14 | 0.01–100 | 8 | 25 | 1.41 | 1.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Nie, F. Study of the Impact of Acquisition Parameters on Fault Feature Identification Based on Magnetotelluric Modeling. Appl. Sci. 2024, 14, 9720. https://doi.org/10.3390/app14219720
Zhang H, Nie F. Study of the Impact of Acquisition Parameters on Fault Feature Identification Based on Magnetotelluric Modeling. Applied Sciences. 2024; 14(21):9720. https://doi.org/10.3390/app14219720
Chicago/Turabian StyleZhang, Hui, and Fajian Nie. 2024. "Study of the Impact of Acquisition Parameters on Fault Feature Identification Based on Magnetotelluric Modeling" Applied Sciences 14, no. 21: 9720. https://doi.org/10.3390/app14219720
APA StyleZhang, H., & Nie, F. (2024). Study of the Impact of Acquisition Parameters on Fault Feature Identification Based on Magnetotelluric Modeling. Applied Sciences, 14(21), 9720. https://doi.org/10.3390/app14219720






