Abstract
The construction time of concrete structures in hydraulic tunnels is long, the construction environment is complex, and there are many influencing factors. The requirements for construction quality are high not only to meet the strength requirements but also to meet the design requirements of erosion resistance, crack resistance, and seepage resistance according to its specific operating environment. Therefore, evaluating the construction quality of concrete structures in hydraulic tunnels is of great significance. Considering the randomness and fuzziness of factors affecting the construction quality of concrete structures in hydraulic tunnels, this paper proposes a comprehensive evaluation model based on combined weighting (CWM) and uncertainty measurement theory (UM). The improved analytic hierarchy process (IAHP) and the CRITIC method are used to determine the subjective and objective weights of evaluation indicators. Combined weighting is based on the principle of minimum entropy, and the UM method is used to evaluate the construction quality level. Finally, taking a hydraulic tunnel as an example, its construction quality grade is calculated to be III, according to the evaluation model proposed in this paper, which matches the engineering reality, and a comparative study is made with the mixture element topology theory at the same time. It is verified that the evaluation model can scientifically and reasonably evaluate the construction quality level of concrete structures in hydraulic tunnels.
1. Introduction
China is a vast country with abundant water resources, but they are unevenly distributed in space, with large differences between the north and the south, and the shortage of water resources restricts the development of some cities and agriculture. For this reason, China has built a series of water diversion projects such as the South-to-North Water Diversion, the Diversion of River to Huaihuai, the Diversion of Yellow to Qingdao, etc., which basically involve the construction of a large number of hydraulic tunnels. The construction of concrete structures in hydraulic tunnels is characterized by its multi-stage, multi-level, and multi-factor nature, and the construction processes are closely connected and interact with each other, which not only have to meet the strength requirements, but also the design requirements of erosion resistance, cracking resistance, seepage resistance, impact resistance and wear resistance according to the specific operation environment. Therefore, it is of great significance to improve the service life of hydraulic tunnels by reasonably evaluating the construction quality level of the concrete structure in hydraulic tunnels and taking scientific and effective measures to maintain it in time.
There have been a number of studies conducted on tunnel concrete structures. You Zhemin et al. [1] focused on highway tunnels and proposed methods to handle quality problems such as collapse, water gushing, large deformation of surrounding rock and cracking of supports that may occur during their construction. Wu Jiming [2] conducted a systematic analysis for the construction quality control of hydraulic concrete structures in terms of selection and inspection of raw materials for hydraulic concrete, structural design, the determination of mixing ratios, control of structural deformation, and pouring and vibration during construction. Lan Xiaofeng [3] collaborated with Jimingyi Tunnel to study the quality control of winter construction, selected the appropriate concrete ratio and raw materials, and adopted the appropriate temperature during concrete mixing and transportation to ensure the quality of concrete construction and maintenance. Hu et al. [4] studied the fast slope surface data acquisition and pre-processing technology based on the high slope excavation process of a water conservancy project and established the slope quality control index analysis model and real-time feedback flow, which were applied to the quality control of actual slope excavation projects. Cheng Lili [5] combined the PDCA cycle method and construction project quality control for construction quality control in the Pandawling Tunnel, establishing a construction quality control process based on the PDCA cycle and discussing, in detail, the application of the process in the preparation stage, construction stage and quality inspection stage. Qian et al. [6] set up settlement and deformation observation points in the middle of the tunnel and on both sides of the elevated arch and buried the observation elements according to the specified scheme and monitored the roadbed settlement after the construction of the railroad tunnel, proposing the curve regression method to evaluate and predict the settlement of the tunnel foundation. Arends B.J. [7] proposed a method based on probabilistic risk assessment to evaluate tunnel safety based on three major aspects: economic, personal and social risk, and applied it to a real case study of a tunnel project in the Netherlands. Manchao et al. [8] concluded that large deformation phenomenon occurs in tunnels during or after excavation due to poor geology, design defects, etc., and for this reason, an MPM method based on finite element analysis software was introduced to simulate the deformation of materials. An evaluation technique incorporating Bayesian neural networks was further proposed for the case where significant deformation occurs in tunnels. Hussain et al. [9] assessed the rock quality in excavated tunnels by combining practical experience with numerical analysis and analyzed the stability of the tunnels before and after excavation. Zong Dachao et al. [10] established a new model of fuzzy comprehensive judgment of the risk level of existing tunnels based on the cloud model and applied it to the evaluation of the risk level of tunnels of the Guangzhou–Shenzhen–Hong Kong Express Railway, verifying the feasibility of the new model by comparing the results with those of the traditional method as well as the inspection data of the actual project. Sheng Tanjie et al. [11] proposed a small-clearance tunnel construction risk assessment model based on an entropy weight-normal cloud model for small-clearance tunnels traversing rockpile bodies and demonstrated the feasibility and unique advantages of applying the model in the quantitative assessment of small-clearance tunnel construction risk by taking an actual tunnel project as an example. Jiang Pengfei et al. [12] took Yunnan Xishanying Tunnel as an example and established a combined weight calculation method based on the entropy weight and hierarchical analysis methods, constructing an evaluation model for the quality of tunnel peripheral rock by using gray correlation analysis, which accurately evaluates the stability of the tunnel peripheral rock, reducing the risk in the excavation process. Chen Guofang et al. [13] constructed an evaluation model based on EW-AHP and uncertainty measurement theory to evaluate the tunnel gas risk based on the Yudu No. 2 Tunnel Project of Xingquan Railway. Zhou Hang et al. [14] constructed an evaluation model based on combined empowerment and unconfirmed measurements to evaluate the rockburst hazard of deep-buried tunnels in complex mountainous areas, taking the Sangzhuling Tunnel in the Sichuan–Tibet transportation corridor as an example.
At present, the research on tunnel condition mainly focuses on railroad and highway tunnels, while relatively few studies have been conducted on hydraulic tunnels, which remain in a water environment for extended periods; the research mainly focuses on construction quality control and safety risks in tunnels but ignores the evaluation of the construction quality grade. Additionally, the research methods cannot comprehensively take into account the actual situation of the project, making it difficult to solve the randomness and ambiguity of the quality of tunnel construction in a better way. Compared with highway tunnels, the concrete structure of hydraulic tunnels remains in a complex water environment for extended periods, which makes it susceptible to erosive ions, acidic substances, carbonization, penetration pressure and other factors, resulting in a series of quality problems. The construction period of concrete structures in hydraulic tunnels is long, the construction environment is complex, and there are many influencing factors. The construction quality requirements are high, not only to meet the strength requirements, but also according to its specific operating environment to achieve erosion resistance, crack resistance, seepage resistance, impact wear resistance and other design requirements. The quality of construction affects compactness, strength, water seepage, cracking, corrosion of reinforcing steel and other conditions of the concrete structure in hydraulic tunnels. Therefore, there is an urgent need for a set of scientific and reasonable construction quality evaluation index systems and an evaluation model for the construction of concrete structures in hydraulic tunnels, which can effectively assess construction quality conditions, guide actual project construction, and ensure the quality and durability of construction.
In summary, this paper proposes a set of new methods for evaluating the construction quality level of concrete structures in hydraulic tunnels. The subjective and objective weights of the evaluation indexes are calculated using the IAHP method and the CRITIC method, respectively, and the comprehensive weights of the evaluation indexes are calculated using the principle of minimum entropy (MIE). The construction quality level is evaluated by combining the uncertainty measurement evaluation model, and finally, a comprehensive evaluation model based on CWM-UM theory is established. Relevant calculations are carried out with a hydraulic tunnel as the research background to verify the reasonableness and scientificity of the model in evaluating the construction quality grade of concrete structures in hydraulic tunnels. Through the combination of evaluation indexes, not only can we avoid the one-sidedness of weight calculation, but we can also consider the subjective intention of the decision-maker and the objective attributes of the data itself, which improves the reasonableness and reliability of the evaluation indexes of the quality of tunnel construction, making the evaluation results more in line with reality. The construction quality of concrete structures in hydraulic tunnels is a complex evaluation system. Some of the information in its evaluation is uncertain due to subjective or objective reasons, and this uncertainty of the information will lead to subjective cognitive uncertainty for the evaluator at the same time. The uncertainty measurement evaluation model can solve this type of information uncertainty. The model is simple to calculate, the results are reliable, and the existing information is fully utilized to reduce human subjective errors to a certain extent, so as to make the results of the structural safety evaluation of the diversion tunnel lining more comprehensive and objective, and at the same time, it has a certain degree of operability.
2. The Establishment of CWM-UM Evaluation Modeling
2.1. Determination of Index Weight
2.1.1. IAHP Method to Determine the Subjective Weight
In this paper, the IAHP method [15] is used to determine the subjective weights of the construction quality evaluation indexes of hydraulic tunnels. Hierarchical analysis has a strong advantage in addressing multi-factor problems, as it can split different factors, determine the corresponding level, and then construct a hierarchical relationship model between the factors to calculate their subjective weights. In this paper, the judgment matrix is established based on the theory of four scales, as shown in Equation (1), and the scale of the matrix is shown in Table 1.
where, ; is the result of the importance of comparing the two evaluation indicators and in guideline A, .

Table 1.
Numerical values and significance relationships.
Construct the antisymmetric matrix B of the judgment matrix A. The values of the matrix B and its element can be calculated by Equation (2).
Construct the optimal transfer matrix C of the antisymmetric matrix B. The values of the elements in the matrix C can be calculated by Equation (3).
Construct the proposed good agreement matrix of the judgment matrix A. The values of the element in the matrix can be calculated by Equation (4).
Normalize the proposed good agreement matrix by columns. The values of the elements in the normalized matrix can be calculated by Equation (5).
The sum vector is calculated by adding rows, as shown in Equation (6):
The weight vector can be calculated by normalizing the sum vector through Equation (7).
The analytic hierarchy process (AHP) [16] is used to determine the weights of evaluation indicators, consistency tests are needed to ensure that the indicators are harmonized. This paper optimizes the hierarchical analysis method through the optimal matrix method, which enables the calculation results to meet the consistency requirement by itself.
2.1.2. CRITIC Method to Determine the Objective Weight
The CRITIC method is a technique that uses the standard deviation and correlation coefficient to calculate objective weights, which comprehensively takes into account the variability and conflict between indicators. It can be more reasonable and comprehensive for the assignment of weights, and the calculation process is as follows [17,18]:
Assuming that there are m evaluation objects and n construction quality evaluation indicators, the value for the evaluation object to the indicator is recorded as ().
The evaluation data can be standardized using Equation (8).
Calculate the variability among indicators using Equation (9).
where, is the coefficient of variation of the th indicator; is the standard deviation of the i-th indicator; and is the mean of the i-th indicator.
The conflict between indicators can be calculated using Equations (10) and (11).
where is the correlation coefficient between indicators and ; and is the value of the quantitative indicator of conflictiveness for indicator .
The amount of information for the i-th indicator can be calculated using Equation (12).
The objective weight values of construction quality evaluation indicators are calculated using Equation (13).
2.1.3. The Method of Calculating Combination Weight
- (1)
- Rationality analysis of combination weighting
Before combining the subjective weight and the objective weight , their rationality should be analyzed to ensure the scientific and rational weights of the construction quality evaluation indicators for concrete structures in hydraulic tunnels. The specific process is as follows:
The subjective and objective weights of evaluation indicators are sorted, as shown in Table 2, where is the sorted value of and is the sorted value of . The sorting values range from 1 to n. The index with the largest weight value is sorted as 1, and the index with the smallest weight value is sorted as n.

Table 2.
Sorting result of indicator weights.
The correlation between the two sets of variables can be tested using Spearman’s consistency coefficient [19] as shown in Equation (14).
where the value range of is . When , it means that there is a lack of consistency between subjective and objective weights; when , it means that the correlation between subjective and objective weights is 0; and when , it indicates that there is consistency between subjective and objective weights, which can be combined and assigned.
- (2)
- Calculating the combination weights
The weights of evaluation indexes calculated based on the IAHP method and the CRITIC method are and , respectively. In order to make the combination weight as close as possible to and , the combination weights are calculated based on the MIE principle. The calculation model is as follows [20]:
By solving this optimization model based on the Lagrange’s algorithm, the combination weights can be obtained as follows:
2.2. Uncertainty Measure Evaluation Model
This paper uses uncertainty measurement theory to evaluate the construction quality of hydraulic tunnels. The uncertainty measurement theory mainly includes two parts: single-indicator and multiple-indicator uncertain measurements. The evaluation method and corresponding calculation formula are as follows [21,22]:
- (1)
- Uncertainty measures for single indicators
Let the evaluation objects form the object space of . For each object to be evaluated , there exist n indicators , then is called the evaluation space. is the measured value of the th indicator for the th object to be evaluated , and the indicator is classified into levels , where is the th evaluation level . If the effect of class is better than that of class , denoted as , then is the ordered segmentation class on evaluation space C [23]. is used to indicate that the measured value belongs to the range of the th evaluation grade , and the following conditions must be met:
Equation (17) represents non-negative boundedness, Equation (18) represents normalization, and Equation (19) represents additivity. When z satisfies all three of these formulas at the same time, z is said to be an uncertain measure.
Construct the uncertainty measurement function for each evaluation index, substitute the measurement value , and calculate the uncertainty measurement value , which can form the single-indicator measurement evaluation matrix shown in Equation (20).
- (2)
- Uncertainty measures for multiple indicators
If represents the degree to which the th evaluation object belongs to the th evaluation level , then:
where satisfies , and . Then is the evaluation vector of ’s multi-index comprehensive measure [24].
- (3)
- Confidence identification criteria
The calculation results are analyzed according to the confidence identification criteria, and the confidence is set as [25]. If satisfies Equation (22), it can be determined that the evaluation object belongs to the th evaluation level .
3. Construction Quality Evaluation Process of Concrete Structure in Hydraulic Tunnel
The construction quality evaluation of concrete structures in hydraulic tunnels analyzes the factors that affect construction quality, employs appropriate methods to organize and evaluate these factors, and determines the grade of tunnel construction quality. This paper first defines the concrete structures in hydraulic tunnels to be evaluated and constructs the construction quality evaluation index system based on six aspects: construction measurement, tunnel excavation, support construction, anti-drainage construction, secondary lining concrete construction and tunnel grouting. The IAHP method and the CRITIC method are used to determine the subjective and objective weights of evaluation indicators, respectively, and combined weights are given based on the principle of minimum entropy. The uncertain measure function and matrix of single indices are constructed, and the uncertain measure vector of multiple indices is calculated. Finally, the construction quality grade of concrete structures in hydraulic tunnels is determined based on the confidence criterion. The specific evaluation process is shown in Figure 1.
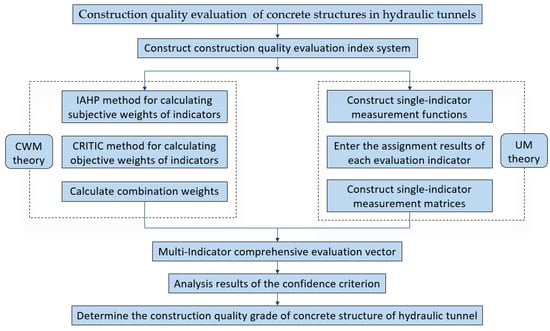
Figure 1.
Construction quality evaluation process of concrete structures in hydraulic tunnels based on CWM-UM modeling.
4. Examples of Engineering Applications
In order to verify the rationality and scientificity of the method, a hydraulic tunnel is applied in this paper. According to the characteristics and general construction procedures of concrete structures in hydraulic tunnels, they can be divided into six main stages: construction survey, tunnel excavation, support construction, anti-drainage construction, secondary lining concrete construction and tunnel grouting.
4.1. Reasons Affecting Construction Quality
The construction process of concrete structures in hydraulic tunnels is complex, and there are numerous uncertainty factors affecting construction quality, which can be basically summarized as five aspects: personnel, materials, machinery, methods and environment according to quality management theory. Therefore, according to the actual situation of the project and the existing literature, this paper adopts the fishbone diagram method [26] to carry out a hierarchical analysis of the aspects of people, materials, machines, methods and environment to summarize the reasons affecting construction quality.
- (1)
- In the process of construction measurement, due to the unskilled surveyors and the unfavorable influence of the environmental factors, such as heavy rain, gales, high temperatures, etc., there will be quality problems, such as horizontal penetration errors, vertical penetration errors and marking the wrong direction of digging.
- (2)
- In the process of tunnel excavation, due to unskilled tunneling operators and the low level of construction site management and monitoring, there will be quality problems, such as uneven excavation surfaces, groundwater seepage caused by excavation, and tunnel over-excavation and under-excavation.
- (3)
- In the process of support construction, the low business level of the constructor and poor inspection and management causes problems such as collapsed holes, deviation of the position and direction of anchor holes, low stability of steel arches, insufficient thickness of sprayed concrete and lagging of the sprayed concrete construction surface.
- (4)
- In the process of anti-drainage construction, the performance and laying of waterproof materials are not qualified due to non-timely testing; improper treatment of construction joints and deformation joints due to insufficient construction technology levels; and the drainage system is unreasonable due to the lack of scientific planning.
- (5)
- In the process of secondary lining concrete construction, the performance of concrete materials and mixing ratios does not meet the design requirements due to the lack of timely testing, insufficient maintenance of concrete, low strength of concrete demolding and inadequate concrete pouring and vibration due to the low level of construction management and poor construction environment, along with other quality problems. In addition, the quality of secondary lining concrete construction will also be affected by factors such as non-standardized concrete pouring, failure to clean the surface of the formwork in time, insufficient reinforcement of the formwork and incomplete assembly.
- (6)
- In the process of tunnel grouting, due to unskilled construction personnel, it is impossible to strictly control key parameters such as hole diameter, hole position, verticality, etc., resulting in irrational disposal of the drilled holes; due to the lack of advance hydrogeological and engineering geological exploration, it is not possible to effectively predict the ambient temperature of the construction area, which results in the grouting temperature being too high or too low; and irregularities in the grouting test result in too high or too low a grouting pressure being selected.
In summary, the fishbone diagram of the quality problems of concrete structure construction of hydraulic tunnels is shown in Figure 2.
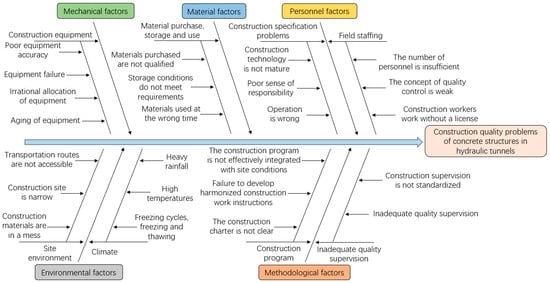
Figure 2.
Fishbone diagram of construction quality problems of concrete structures in hydraulic tunnels.
4.2. Selection of Construction Quality Evaluation Indicators
By investigating the construction site and combing the contents in Section 4.1, as well as combining the research results of relevant scholars [27,28], this paper summarizes 21 factors affecting the construction quality of concrete structures in hydraulic tunnels according to six main construction procedures: construction survey, tunnel excavation, supporting construction, waterproof and drainage construction, secondary lining concrete construction and tunnel grouting, and analyzes the types of their causes. The results are shown in Table 3.

Table 3.
Summary of factors affecting construction quality.
According to Table 3, the construction process and the construction quality problems of each process are taken as primary and secondary evaluation indexes respectively. The construction quality evaluation index system is constructed to evaluate the construction quality of concrete structures in hydraulic tunnels.
4.3. Construction Quality Grading
To evaluate the construction quality of concrete structures in hydraulic tunnels reasonably, it is necessary to divide the evaluation results into appropriate grades. At present, China has not issued relevant specifications for concrete structures in hydraulic tunnels. This paper refers to the Technical Procedure for Detection and Evaluation of Defects in Hydraulic Concrete Buildings (DL/T5251-2010) [29], the Code for Design of Hydraulic Tunnels (SL279-2016) [30], and the research achievements of relevant scholars [27,31]. The relevant design requirements for tunnel support and lining, tunnel grouting, seepage prevention and drainage, and the quality grade classification of hydraulic tunnel concrete structure construction by relevant scholars can be consulted. Therefore, the construction quality condition of the concrete structures in hydraulic tunnels is categorized into five grades: Grade I indicates that the quality of tunnel construction is excellent, with few or no quality problems, and only normal inspection of the construction process is required; Grade II indicates that the quality of tunnel construction is good, with relatively small problems, and the construction process needs to be strengthened to prevent; Grade III indicates that the quality of tunnel construction is qualified, with relatively more problems, and the construction process needs to formulate the appropriate monitoring and management system; Grade IV indicates that the quality of tunnel construction is basically qualified, with more problems but still within the permissible range, but the construction needs to be strictly prevented from proceeding, and the quality problems can be corrected using appropriate means; Grade V means that the construction quality of the tunnel is unqualified—there are many problems, and the construction process must put forward targeted quality control and corrective measures for the quality problems to avoid quality and safety incidents.
Due to the large number of tunnel construction processes, each quality indicator is defined in a different range, and it is impossible to carry out an accurate quantitative description; therefore, this paper suggests that the indicators and grades should be evaluated by the percentage standard, and the division of evaluation criteria is shown in Table 4.

Table 4.
Tunnel construction quality evaluation grading.
4.4. Construction Quality Evaluation Process of Concrete Structures in Hydraulic Tunnels
This paper takes a concrete structure of a hydraulic tunnel as an example to carry out construction quality evaluation research. Indicator grading and grading standards are shown in Table 4. In order to ensure the validity and accuracy of the evaluation results, this paper assigns values to the construction quality indicators by inviting five experts in different aspects, including design units, construction units, supervisory units and scientific research institutes, with the score range of [0,100], and the better the quality control of the indicators, the larger the score. The results of the assigned values are shown in Table 5.

Table 5.
Assigned results of quality indicators.
4.4.1. IAHP Method to Determine the Subjective Weight
- (1)
- Combined with expert opinions and similar literature, the importance of the construction process of concrete structures in hydraulic tunnels is ranked. According to the provisions of Table 1, the evaluation indexes of the construction quality of hydraulic tunnels are compared two by two to quantify their relative importance, and the judgment matrix of the evaluation indexes is established as shown below:
The judgment matrix of the construction quality index layer of hydraulic tunnels is as follows:
The judgment matrix of the construction measurement indicator layer is as follows:
The judgment matrix of the tunnel excavation index layer is as follows:
The judgment matrix of the support construction indicator layer is as follows:
The judgment matrix of the anti-drainage construction indicator layer is as follows:
The judgment matrix of the secondary lining concrete construction index layer is as follows:
The judgment matrix of the tunnel grouting index layer is as follows:
- (2)
- According to Equations (2)–(7), the subjective weight value of each indicator is calculated, as shown in Table 6.
 Table 6. Subjective weighting values of evaluation indicators.
Table 6. Subjective weighting values of evaluation indicators.
4.4.2. CRITIC Method to Determine the Objective Weight
According to the assignment results of quality indicators in Table 5, it is standardized through Equation (8) to obtain a standardized matrix. Then, according to Equations (9)–(13), the variability, conflict, information content and weight values of evaluation indicators can be calculated by writing MATLAB code in turn, as shown in Table 7.

Table 7.
The calculated result of the CRITIC method.
4.4.3. Calculate Combination Weights
- (1)
- Rationality analysis of combined weights
According to the subjective and objective weights calculated by the above IAHP method and CRITIC method, the weights are sorted, as shown in Table 8.

Table 8.
Ranking results of weight values for evaluation indicators.
The consistency coefficient can be calculated from Equation (14) as . The calculation shows that the weights calculated using the IAHP method and the CRITIC method satisfy the consistency requirements and can be combined and assigned.
- (2)
- Calculate combination weights
Finally, the MIE principle is utilized to eliminate the subjective and objective weight bias, and by substituting the calculation results into Equation (16), the final combined weight calculation results can be obtained, as shown in Table 9.

Table 9.
The result of calculating the combined weights of evaluation indicators.
4.4.4. Construct Uncertain Measure Function and Matrix of Single Index
In the process of using an unascertained measure theory to evaluate construction quality, it is necessary to construct uncertain measure function and matrix of a single index scientifically and reasonably.
The evaluation level space must conform to a certain order; that is, or , where represents the th evaluation level, and its corresponding grading standard is represented as . Then conforms to or . Assuming that the measured value of the indicator at belongs to level , when the measured value changes from to , its state value at level gradually changes from 1 to 0, and its state value at level gradually changes from 0 to 1.
The unconfirmed function constructed according to the above method only obtains non-zero values on two adjacent intervals, and the values are zero everywhere else. It is obvious that the unconfirmed function constructed according to the above method meets the requirements of its definition, i.e., satisfies the non-negativity, additivity and normalization, which is one of the biggest differences between the unconfirmed measurement function and the fuzzy affiliation function. In practical problems, the uncorroborated function can be expressed in different forms at different level intervals, and the decision-maker can choose different function forms according to the specific situation. The common forms of the uncertain measure function are mainly four types: straight line, parabola, exponential curve and sinusoidal curve type [32], of which the more widely used is the straight line type, and its function expression is shown in Equation (23).
Based on the classification standard of tunnel construction quality in Table 4 and the expression of the unascertained measure function in Equation (23), the unascertained measure function of the index can be determined as follows:
Based on the evaluation results of quality evaluation indicators in Table 5, the expected value of five experts’ scores for each indicator is taken as the measurement value, as shown in Table 10. It is put into the unascertained measure function, and the unascertained measure matrix of a single indicator can be calculated as follows:

Table 10.
Expected value of evaluation indicators.
4.4.5. Calculate Multi-Index Unascertained Measure Vector
According to the combined weights of the evaluation indicators in Table 9 and the unascertained measure matrix of the single index mentioned above, the multi-index unascertained measure vector of the construction quality of the hydraulic tunnel can be calculated by Equation (21):
Construction measurement:
Tunnel excavation:
Support construction:
Anti-drainage construction:
Secondary lining concrete construction:
Tunnel grouting:
Total weight value:
4.4.6. Construction Quality Evaluation of Concrete Structures in Hydraulic Tunnels
According to the multi-indicator unconfirmed measurement vector of hydraulic tunnel construction quality in Section 4.4.5, set the confidence level , and the quality evaluation results of each stage and the whole in the tunnel construction process can be obtained from Equation (22), which is shown in Table 11.

Table 11.
Construction quality evaluation grade of concrete structures in hydraulic tunnels.
From the above results, it can be seen that the overall construction quality of the concrete structure in the hydraulic tunnel is grade III, i.e., the overall construction quality of this section of the tunnel is qualified, and there are relatively more problems. Therefore, the construction process needs to formulate a corresponding monitoring and management system to strictly control the construction quality. At the same time, it can also be concluded that the quality level of tunnel excavation, support construction and secondary lining concrete construction is grade II, and the construction quality level of construction measurement, anti-drainage construction and tunnel grouting is grade III. This is conducive to the construction personnel controlling the construction quality of the concrete structure in hydraulic tunnel from the details of the construction process and making the corresponding measures to improve, thus ensuring the overall construction quality of the tunnel.
4.5. Comparative Study
In order to illustrate the science and rationality of the method, this paper adopts the matter-element extension theory to evaluate the construction quality of hydraulic tunnels, which is used as a comparative study with the above. No further explanation about the matter-element extension theory is given, and specific reference can be made to the literature [33,34]. The focus here is on the calculation of the correlation function value of the matter-element grade of hydraulic tunnels to be evaluated.
- (1)
- Correlation of evaluation indicators
The correlation of the construction quality level t of the hydraulic tunnel to be evaluated is shown in Equation (24):
where
where is the th construction quality evaluation index; is the magnitude range of the th index divided by the evaluation grade ; is the magnitude range of the th index divided under each level; and is the interval length.
- (2)
- Determine the construction quality evaluation grade of the hydraulic tunnel
By combining the weights of the indicators and the value of the correlation function, the comprehensive correlation of the evaluation object can be calculated; see Equation (27). If , the evaluation object belongs to level .
where is the comprehensive correlation degree of with respect to grade ; and takes the objective weight value of the CRITIC method.
According to the grading standards of each evaluation index in Section 4.3, the classical domain and node domain of the construction quality evaluation index of the hydraulic tunnel can be determined, as shown in Table 12.

Table 12.
Classical domain and node domain of the construction quality evaluation indicators of the hydraulic tunnel.
Based on the expected value of each evaluation indicator in Table 11, the correlation degree matrix of the evaluation indicators of hydraulic tunnel construction quality can be obtained from Equations (24)–(26):
The weight value of each secondary index calculated using the CRITIC method is as follows:
(0.2937, 0.2196, 0.1930, 0.2937); (0.2603, 0.2405, 0.2088, 0.2904); (0.3903, 0.3303, 0.2794); (0.3475, 0.2852, 0.3674);
(0.2383, 0.2275, 0.3172, 0.2169); (0.2850, 0.3569, 0.3580).
According to Equation (27), the comprehensive correlation degree of the evaluation level t for the construction quality of the hydraulic tunnel can be calculated as follows:
Construction measurement:
Tunnel excavation:
Support construction:
Anti-drainage construction:
Secondary lining concrete construction:
Tunnel grouting:
The weight values of the primary indicators calculated using the CRITIC method are as follows: (0.1723, 0.1890, 0.1818, 0.1377, 0.2043, 0.1150). According to Equation (27), the comprehensive correlation degree of the target layer for hydraulic tunnel construction quality with respect to the evaluation level can be calculated as follows:
Overall Construction:
According to the principle of maximum affiliation, the construction quality evaluation grade of the hydraulic tunnel can be determined, as shown in Table 13.

Table 13.
Evaluation grade.
A comparative analysis of the evaluation results of Section 4.4 and Section 4.5 shows that the results of both are consistent. This paper adopts the IAHP method and the CRITIC method to calculate the subjective and objective weights of the evaluation indexes, respectively, which avoids the one-sidedness of the weight calculation, gives comprehensive consideration to the subjective intention of the decision-maker and the objective attributes of the data itself, and results in evaluation outcomes that are more scientific and reasonable. At the same time, the CWM-UM model constructed in this paper can calculate the combination weights of each indicator, calculate the unconfirmed measures of single and multiple indicators, and then determine the construction quality level based on the confidence identification criterion. The results obtained are consistent with part of the comparative study. In summary, the evaluation index system and evaluation model of concrete structure construction quality for hydraulic tunnels established in this paper are scientific and reasonable.
5. Conclusions
- (1)
- According to the analysis and summarization of the factors affecting the quality of tunnel construction, 21 factors, such as excessive horizontal penetration error, over-excavation of the tunnel, low stability of the steel arch, unreasonable drainage system and insufficient maintenance of the concrete, were selected from five aspects, including construction measurement, tunnel excavation, support construction, anti-drainage construction, concrete secondary lining construction and grouting of the tunnel. Constructing a more scientific and reasonable construction quality evaluation index system of concrete structures in hydraulic tunnels.
- (2)
- The subjective and objective weights calculated by the IAHP method and the CRITIC method are optimized and synthesized using the combination assignment method, which avoids the one-sidedness of weight calculation. The subjective intention of the decision-maker and the objective attributes of the data itself are considered comprehensively, which improves the reasonableness and reliability of the weights of the tunnel construction quality evaluation indexes and makes the evaluation results more in line with reality.
- (3)
- Taking a hydraulic tunnel as an example, the CWM-UM comprehensive evaluation model constructed in this paper is used to calculate its construction quality level, and the results are as follows: The quality level of tunnel excavation, support construction and secondary lining concrete construction are all grade II, and the quality level of construction measurement, anti-drainage construction, tunnel grouting and the overall construction of the hydraulic tunnel are all grade III. At the same time, a comparative study is conducted with the matter-element extension theory to verify the applicability and reasonableness of the model, thus providing a basis for subsequent construction.
- (4)
- Due to limited energy and time, there are still many problems that need to be further studied: evaluating the construction quality level of the concrete structure in hydraulic tunnels through a computer software system can not only simplify the calculation process, improve work efficiency and save manpower and material resources but also reduce the influence of human factors. Therefore, in the future, with the help of computer programming software, we can develop a software system for evaluating the construction quality of concrete structures in hydraulic tunnels, establishing a corresponding quality monitoring and evaluation management network, and grasping the construction quality dynamics of concrete structures in hydraulic tunnels in real time.
Author Contributions
L.Z.: Writing-Original Draft, Validation, Formal analysis, Visualization, Methodology. C.H.: Writing-Original Draft, Resources, Conceptualization, Data Curation, Investigation. Z.L.: Methodology, Writing-Review and Editing, Resources, Project administration, Investigation. Q.L.: Writing-Review and Editing, Project administration, Validation, Supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Since no new data link was created, the link supporting the report result data cannot be provided.
Conflicts of Interest
The authors declare no conflict of interest.
References
- You, Z.M.; Chen, J.P. Research on Controlling the Quality of Highway Tunnels: Taking Shi-Man Highway Tunnel for Example. Saf. Environ. Eng. 2009, 16, 111–114. [Google Scholar]
- Wu, J.M. Design of concrete structures for hydraulic buildings and their construction quality control. Tech. Superv. Water Resour. 2011, 19, 26–28. [Google Scholar]
- Lan, X.F. Quality control of winter construction of concrete in Jimingyi Tunnel of Dazhun Railway Additional Second Line. Railw. Eng. 2013, 26, 49–50. [Google Scholar]
- Hu, C.; Zhao, C.-J.; Zhou, Y.-H.; Pan, Z.-G. Excavation surface quality real-time control for high slope in hydropower engineering. Water Resour. Power 2017, 35, 125–128, 158. [Google Scholar]
- Cheng, L.L. Study on Quality Control of Pandaoling Tunnel Project Construction. Master’s Thesis, Liaoning Technical University, Fuxin, China, 2019. [Google Scholar]
- Jin, Q.; Yanhui, Z. Study on quality and safety monitoring scheme of tunnel construction based on 3D laser scanning. IOP Conf. Ser.: Earth Environ. Sci. 2021, 804, 022073. [Google Scholar]
- Arends, B.; Jonkman, S.; Vrijling, J.; Van Gelder, P. Evaluation of tunnel safety: Towards an economic safety optimum. Reliab. Eng. Syst. Saf. 2005, 90, 217–228. [Google Scholar] [CrossRef]
- Manchao, H.; Sousa, R.L.; Müller, A.; Vargas, E., Jr.; Sousa, L.R.; Xin, C. Analysis of excessive deformations in tunnels for safety evaluation. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2015, 45, 190–202. [Google Scholar] [CrossRef]
- Hussain, S.; Rehman, Z.U.; Mohammad, N.; Tahir, M.; Shahzada, K.; Khan, S.W.; Salman, M.; Khan, M.; Gul, A. Numerical modelling for engineering analysis and designing of optimum support systems for headrace tunnel. Adv. Civ. Eng. 2018, 2018, 7159873. [Google Scholar] [CrossRef]
- Zong, D.C.; Wu, F.J.; Li, X.L.; Zhao, Y.J.; Quan, Y.W. Fuzzy Comprehensive Evaluation Model of Existing Tunnel Risk Based on Cloud Modeling. Highway 2024, 69, 370–375. [Google Scholar]
- Sheng, D.J.; Tang, R.; Wang, K.; Dai, S.Q.; Tan, F. Risk assessment model of small clear distance tunnel construction based on entropy weight and normal cloud model. Saf. Environ. Eng. 2024, 31, 89–95. [Google Scholar]
- Jiang, P.F.; Du, F.X.; Wang, X.R.; Zhou, J.T. Evaluation of Tunnel Surrounding Rock Quality Based on Composite Weight Grey Relational Analysis. Pearl River 2021, 42, 112–116. [Google Scholar]
- Chen, G.F.; Wei, H. Tunnel gas risk assessment based on EW-AHP and unascertained measurement theory. Nonferrous Met. Sci. Eng. 2021, 12, 89–95. [Google Scholar]
- Zhou, H.; Liao, X.; Chen, S.; Feng, T.; Wang, Z. Rockburst Risk Assessment of Deep Lying Tunnels Based on Combination Weight and Unascertained Measure Theory: A Case Study of Sangzhuling Tunnel on Sichuan-Tibet Traffic Corridor. Earth Sci. 2022, 47, 2130–2148. [Google Scholar]
- Mao, X.; Hu, A.; Zhao, R.; Wang, F.; Wu, M. Evaluation and Application of Surrounding Rock Stability Based on an Improved Fuzzy Comprehensive Evaluation Method. Mathematics 2023, 11, 3095. [Google Scholar] [CrossRef]
- Li, Z.; Meng, X.; Liu, D.; Tang, Y.; Chen, T. Disaster Risk Evaluation of Superlong Highways Tunnel Based on the Cloud and AHP Model. Adv. Civ. Eng. 2022, 2022, 8785030. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Sun, L.; Xie, G.; Lou, Q. Research on the evaluation index system of “new energy cloud” operation mode based on CRITIC weighting method and AHP method. IOP Conf. Ser. Earth Environ. Sci. 2021, 831, 012017. [Google Scholar] [CrossRef]
- Wu, B.; Zhou, L.; Liu, C. Evaluation of Water-rich Soft Rock Mountain Ridge Tunnel Collapse Risk Based on Game-combination Empowerment-TOPSIS Method. Sci. Technol. Eng. 2023, 23, 1726–1733. [Google Scholar]
- Hu, Y.; Zhu, C. Credit evaluation model of road transportation enterprises based on the combination weighting method. Math. Probl. Eng. 2021, 2021, 6637164. [Google Scholar] [CrossRef]
- Qiu, D.; Chen, Q.; Xue, Y.; Su, M.; Liu, Y.; Cui, J.; Zhou, B. A new method for risk assessment of water inrush in a subsea tunnel crossing faults. Mar. Georesources Geotechnol. 2022, 40, 679–689. [Google Scholar] [CrossRef]
- Huang, C.; Tian, S.; Li, Q.; Huang, J. Evaluation of Rock Quality of Tunnel Wall Rock Based on Rough Set Theory and Unascertained Measurement Theory. Math. Probl. Eng. 2018, 2018, 3571028. [Google Scholar] [CrossRef]
- Jia, Q.; Wu, L.; Li, B.; Chen, C.; Peng, Y. The Comprehensive Prediction Model of Rockburst Tendency in Tunnel Based on Optimized Unascertained Measure Theory. Geotech. Geol. Eng. 2019, 37, 3399–3411. [Google Scholar] [CrossRef]
- Mu, C.L.; Huang, R.Q.; Pei, X.J.; Pei, Z.; Lu, J. Evaluation of rock stability based on combined weighting-unascertained measurement theory. Chin. J. Geotech. Eng. 2016, 38, 1057–1063. [Google Scholar]
- Li, X.; Jiangwen, Q.; Tang, J.; Pu, Q.S.; Xia, X.B.; Xu, K. Study on combination weighting method-TOPSIS methodbased risk assessment of water in-rush in construction of North Tianshan Mountain Tunnel. Water Resour. Hydropower Eng. 2019, 50, 114–119. [Google Scholar]
- Huang, R.; Zhang, F.X. Method of Comprehensively Evaluating Water Quality Based on Optimal Set Pair Analysis. J. Chang. River Sci. Res. Inst. 2016, 33, 6–10+17. [Google Scholar]
- Pi, S.L. Research on the PRS Integrated Fishbone Diagram and Its Application in Project Management. China Soft Sci. 2009, 19, 92–97. [Google Scholar]
- Yang, Y.H. Research on Highway Tunnel Construction Quality Inspection and Evaluation Methods. Master’s thesis, Southwest Jiaotong University, Chengdu, China, 2009. [Google Scholar]
- Lv, J.H. Analysis on influencing factors of tunnel construction and key points of supervision control. Constr. Mater. Decor. 2019, 1, 268–269. [Google Scholar]
- DL/T5251-2010; Technical Code for Detection and Evaluation of Hydraulic Concrete Structure. China Electric Power Press Co., Ltd.: Beijing, China, 2010.
- SL279-2016; Specification for Design of Hydraulic Tunnel. China Water Conservancy and Hydropower Press: Beijing, China, 2016.
- Ye, F. Study on Highway Tunnel Construction Quality Management. Master’s Thesis, Chang’an University, Xi’an, China, 2004. [Google Scholar]
- Chen, C.M. Research on Evaluation Method of Eco-city Construction Based on Unascertained Mesure Theory. Master’s Thesis, Tianjin University, Tianjin, China, 2013. [Google Scholar]
- Li, Q.; Zhou, H.D.; Zhang, H. Durability evaluation of highway tunnel lining structure based on matter element extension-simple correlation function method-cloud model: A case study. Math. Biosci. Eng. MBE 2021, 18, 4027–4054. [Google Scholar] [CrossRef]
- Sun, X.R. Safety evaluation of sluice based on matter-element extension theory. Harnessing Huaihe River 2018, 45, 19–21. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).