Device-Free Crowd Size Estimation Using Wireless Sensing on Subway Platforms

Featured Application

This work presents the use of device-free wireless sensing for crowd size estimation on subway platforms.

Abstract

Dense urban environments pose significant challenges when it comes to detecting and measuring crowd size due to their nature of being free-flow environments containing many dynamic factors. In this paper, we use a wireless sensor network (WSN) to perform device-free crowd size estimation in a subway station. Our sensing solution uses the change in attenuation of the communication links between sensor nodes to estimate the number of people standing on the platform. In order to achieve this, we use the same attenuation information coming from the WSN to detect the presence of a rail vehicle in the station and compensate for the channel fading caused by the introduced rail vehicle. We make use of two separately trained regression models depending on the presence or absence of a rail vehicle to estimate the people count. The detection of rail vehicles occurred with a near-perfect accuracy. When evaluating the resulting estimation model on our test set, we achieved a mean average error of 3.567 people, which is a significant improvement over 6.192 people when using a single regression model. This demonstrates that device-free sensing technologies can be successfully implemented in dynamic environments by implementing detection techniques and using different regression models depending on the environment’s state.

1. Introduction

The demand for crowd-monitoring solutions has increased significantly in the past decade as large-scale events increase in size and frequency [1]. Another important use case for crowd monitoring is in improving the safety and efficiency of large cities. As of 2018, The United Nations reports that 4.2 billion people are living in urban areas, with a projected increase to 6.7 billion people by 2050 [2].

Performing crowd management in cities has its own set of challenges. Large-scale events such as music festivals and soccer games tend to be held in demarcated areas with designated entrances and exits. This allows for the use of gate-counting solutions, such as ticket scans, turnstile gates, and down-facing counting cameras. In cities, people move freely without passing through such bottlenecks at which the aforementioned people-counting techniques can be utilized. We cannot give every individual a tracking device to collect data regarding their movement throughout the city, and it is no longer possible to rely on people carrying personal devices, such as cellphones, that transmit identifiable Wi-Fi or Bluetooth signals due to the fact that efforts are being made to prevent such messages from being used for tracking purposes by randomizing identifiable information [3,4,5].

Metro and train stations are similarly challenging environments. While these types of environments have entrances that can be equipped with gate-counting solutions, they can only be installed at certain locations. In practice, counting people who are rapidly embarking and disembarking from railway vehicles is largely infeasible. This limitation effectively makes significant parts of these environments free-flow environments.

An important distinction can be made between direct and indirect measurement solutions. Gate counting is a form of indirect counting. In order to obtain a value for the number of people in the environment, one has to take the difference between the ’in’ and ’out’ counts. This leads to the important requirement that such a system needs to be running for the full period of time when people are able to enter or leave the environment of interest. Even a short downtime of the system will lead to an offset error in the data. In contrast, direct methods, such as counting cameras [6,7] or Wi-Fi counting [8,9], are capable of estimating the number of people in the area directly from a single sample or short period of measurement.

An emerging technology for directly estimating the crowd density at events and in urban areas consists of using device-free wireless sensing (DFWS) [10]. The DFWS technique makes use of a set of wireless nodes that are placed in and around the environment of interest. These nodes periodically transmit messages to each other, creating a mesh of links for which we are able to collect signal strength values. Prior research has established a strong correlation between the signal strength attenuation and the crowd density in the environment [11]. This estimation technique is an application derived from the field of Radio Tomographic Imaging (RTI), which is a popular technique for device-free localization applications [12]. The ability of RTI to detect the presence and location of dynamic obstacles such as road vehicles is demonstrated in [13].

A regression model describing the relation between signal strength and crowd density can be trained based on collected ground-truth data. A simple regression model, such as linear or polynomial regression, expects a static environment. When big changes in the environment take place, e.g., a metal fence is removed or a car stops in the environment, the resulting changes regarding line-of-sight propagation, as well as multipath propagation, will affect the relationship between the measured signal strength and the number of people present in the environment, rendering the trained model inaccurate.

The use of multiple models in time-series analysis is commonly referred to as regime switching. A common example of such a regime change is in the scope of economic growth and decline, as first demonstrated by Hamilton in [14].

In our crowd context, we encounter situations containing periodically introduced changes to the environment in subway stations, where a rail vehicle will enter or leave the station, thereby creating huge temporary changes to the environment from a signal strength perspective. In prior research [15], a solution was proposed to detect the arrival of rail vehicles in the environment by using a Time-of-Flight (ToF) sensor-based solution. In this paper, we will demonstrate a system using only a DFWS network to both estimate the number of people present in the environment and detect changes in the environment. Based on the measured environment’s state, we switch the active model between two trained models in order to provide a more reliable crowd size estimation.

In this study, we aim to address the following research question: Can the accuracy of DFWS-based crowd size estimation systems be improved by incorporating a switching model to mitigate the impact of dynamic environmental factors?

This paper makes the following novel contributions:

• We demonstrate the use of Received Signal Strength Indicator (RSSI) values in a wireless sensor network to detect the presence of a rail vehicle in a subway station.
• We demonstrate the use of two separately trained polynomial regression models, when a rail vehicle is present and absent, in order to perform crowd size estimation using the change in the RSSI between wireless sensor nodes in the different environment states.
• We evaluated our proposed switching model in an uncontrolled environment and used a single DFWS network to perform the detection of the environment’s state and switch between models accordingly.

This paper is structured as follows: In Section 2, we will provide a brief overview of related research. We will dedicate Section 3 to describing the system and the chosen parameters for our experiments. In Section 4, we will discuss the algorithms used to detect the presence of a rail vehicle in the environment, as well as the models used for crowd size estimation. In Section 5, we present the achieved accuracy of both the independent components and the full system and discuss these results. Finally, in Section 6, we conclude this paper.

2. Related Research

In recent years, different solutions have been proposed to perform crowd counting in dynamic public transportation environments. Within the field of DFWS, efforts have been made to improve Radio Frequency (RF) sensing, making it more robust to environmental changes.

Bartoletti et al. proposed a backscattering framework using wideband signals to estimate the number of people (called targets in their work) in the environments [16]. They proposed two different methods to achieve this. The first is an individual-centric method, and the second is a crowd-centric method. The individual-centric method makes use of the additional reflections caused by the introduced targets in order to estimate the positions of the reflections. A people count can be derived from the vector of predicted positions. The crowd-centric method uses feature extraction to extract relevant features from the change in the energy pattern received by the receivers to estimate the number of people in the environment. For the crowd-centric method, energy detector (ED) feature extraction has the best performance and results in a counting error below 2 targets in 88% of cases within a numerical analysis of up to 30 targets. The individual-centric method using a maximum likelihood algorithm resulted in a Root Mean Square Error (RMSE) of 1, outperforming the best algorithm used for the crowd-centric method, ED, resulting in an RMSE of 2 to 10 targets for a spatial density of 0.1 targets per square meter.

In [17], a method is proposed for estimating the occupancy of an environment derived from the measured Doppler spectrum. The more people in the environment, the higher the spread in the Doppler spectrum. The relationship between the Doppler spectrum-derived feature and the number of people is not dependent on the environment, and thus, once trained, the model can be used in different environments. The paper demonstrates this system in three different rooms with 0 to 7 people present. Their model was trained using the data from one environment and tested on the other two environments. They achieved an average accuracy of 73% and 63% for classification into five levels.

Xu et al. demonstrated the use of radio link RSSI fingerprinting to perform localization in cluttered indoor environments [18]. In the first environment, a one-bedroom apartment (5 m × 8 m), they used eight transmitters and eight receivers, leading to a cell size of 0.75 m by 0.75 m, and achieved a cell classification accuracy of 97.2% and an average localization error distance of 0.36 m. The second environment was a commercial office space (10 m × 15 m), where they employed 13 transmitters and 9 receivers and achieved a classification accuracy of 93.8% and an average localization error distance of 1.4 m.

The degradation of wireless sensing due to changes in the environment has been explored in the context of device-free localization (DFL) by Mager et al. [19]. They performed an analysis of the degradation of fingerprint-based DFL in changing indoor environments. They performed their experiments on the main floor of a house (approximately 84 m²) by changing the locations of objects (e.g., chairs, tables, plants) in the environment. They tested different classification algorithms and concluded that the random forest classifier was most robust to changes in the environment during the evaluation phase. Furthermore, they examined the use of multiple radio channels and the option to select channels that improve the robustness to a changing environment and found that using two out of the eight measured channels that had the highest correlation during training further improved the localization accuracy.

In [20], Lei et al. improved on the work in [19] by allowing the channel selection to be decided during operation. If a higher Pearson correlation coefficient is found between a pair of channels in the currently received data, the new pair of channels containing the higher correlation will be used. If no higher correlation is found, the channel pair containing the highest correlation in the training set is used. The second contribution is the use of a logistic regression classifier on the resulting RSSI data. The proposed method was tested on the dataset collected by Mager et al. in [19]. Both the use of channel correlation on the test set as well as the use of a logistic regression classifier improved the robustness to environmental changes.

Pištek et al. proposed the use of a Passive Infrared (PIR) sensor array above the entrance and exits of buses to count the number of people entering and leaving the bus in order to estimate the total number of people present [21]. The accuracy of their implementation was assessed at $95.5$ % when one person was passing under the sensor, but this accuracy was reduced to 70% when four people were entering together.

In [22], a solution was proposed to perform people counting in waiting lines using a modular system containing RF transceivers placed on top of retractable belt stanchions, creating small zones (1 m × 1 m) of four nodes holding between 0 and 4 people. They achieved a classification accuracy of 98% in a single zone. This accuracy can statistically be extrapolated to 93% for a queue of six units.

Choi et al. demonstrated the use of an Impulse Radio Ultra-Wideband (IR-UWB) radar sensor to count people in a subway station [23]. The system uses two narrow beam-width radars in order to detect people crossing two Fields of View, enabling the detection of the direction of travel. They reported an error below 10% for most cases.

A vision-based crowd density solution for use in narrow tram and metro environments was proposed by Zhao et al. [24]. They proposed a novel Convolutional Neural Network (CNN) model named Coordinate Deformable Net (CDNet) using four sections: feature extraction, a Coordinate Attention Module (CAM), a Deformable Scale-aware Module (DSM), and an output section of dilated convolution layers constructing the crowd density map. They validated their proposed solution using their own collected dataset comprising high-resolution images collected inside tram carriages, as well as the open ShanghaiTech dataset. Their proposed algorithm outperformed common density map algorithms and object detection algorithms in estimating the number of people on both datasets.

Our proposed solution differs from the related works in the sense that, rather than trying to compensate for the impact that the presence of a railway vehicle has on our measurements, we aim to identify whether the impact exists and switch between separately trained models accordingly. This approach is more suitable for the use case encountered in public transportation environments, such as subway stations, since the impact of rail vehicles is larger than simply moving a chair. This requires a new selection of links to obtain the new optimal accuracy of the system. This work is the first to validate the use of solely a DFWS system to perform crowd size estimation in public transportation platform environments.

3. Experimental Setup

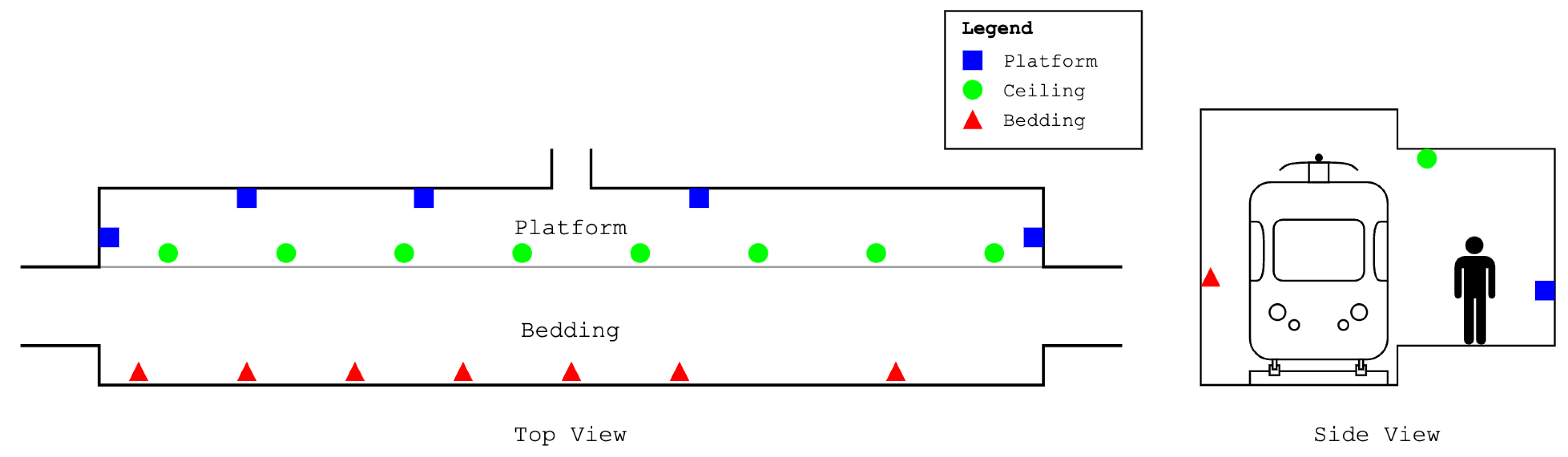
We demonstrate our solution in a subway station in Antwerp, Belgium. We mounted sensor nodes on both the walls and the ceiling above the edge of the platform, as shown in Figure 1. This allowed us to make separate virtual sensor networks for crowd size estimation depending on the state of the environment. The nodes were separated into three groups: 5 “platform nodes’’ were mounted at waist height on the walls of the platform, 8 “ceiling nodes’’ were mounted on the ceiling near the edge of the platform at a height of $2.7$ $\mathrm{m}$, and 7 “bedding nodes’’ were mounted at waist height as well but on the opposite wall across from the platform.

The number and placement of the nodes are based on the available hardware and the spatial limitations of the environment (e.g., furniture, timetables, platform width, …). As the optimization of node placement is not within the scope of this work, we aimed to distribute the nodes as evenly as possible throughout the environment. Three nodes disappeared or malfunctioned over the course of the experimental measurement period and were omitted from this work.

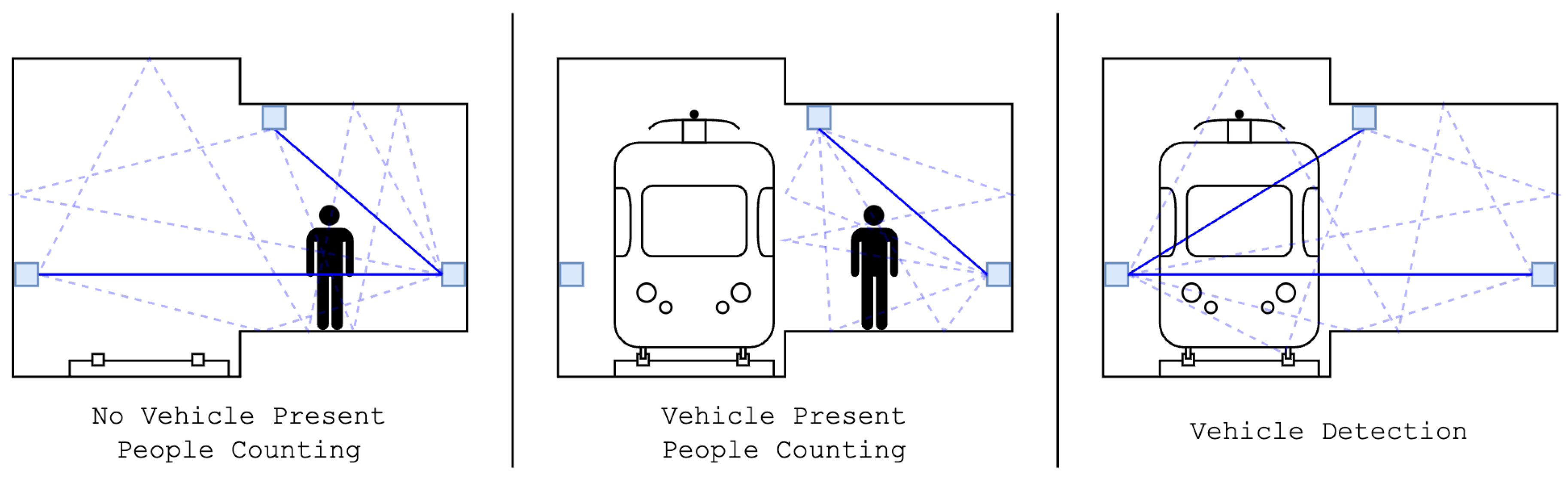
We combined these three groups of nodes to make three virtual sensor networks, as shown in Figure 2. The nodes and links to be used for each scenario were selected based on training and evaluating each scenario on the training and test sets for all 64 possible combinations with 3 node groups.

When no rail vehicle is present, we use all nodes, but we exclude the links between ceiling nodes and bedding nodes, as well as the links in between the different bedding nodes. This results in 20 nodes forming 113 unique links.

When a rail vehicle is present in the environment, we only use the ceiling nodes and the platform nodes, containing all links involving any of these nodes. In total, this virtual sensor network contains 13 nodes, resulting in 78 unique links. We empirically determined that the large RSSI variances resulting from the obstruction of the line of sight (LoS) led to a lower correlation between the crowd size and the RSSI values. When excluding the nodes mounted against the bedding wall, we saw an improvement in the correlation and the subsequent estimation accuracy.

For the detection of the rail vehicles, we use all nodes, but we exclude the links between the ceiling and the platform wall, as well as the links formed between the platform wall nodes and those formed between the bedding wall nodes. This virtual sensor network contains 20 nodes and 119 unique links after link exclusion. This combination of links proved to maximize the correlation between attenuation values and vehicle presence or absence.

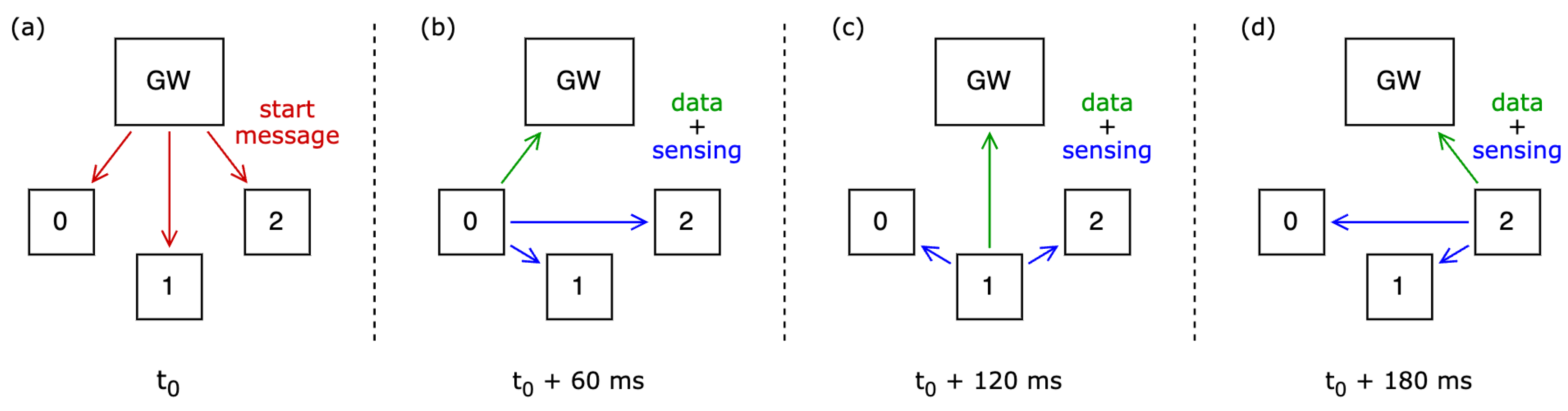
The communication sequence in the network is displayed in Figure 3. After receiving the initialization message from the gateway (Figure 3a), all nodes will transmit a message consecutively (Figure 3b–d). These messages are received by the other nodes, which measure the RSSI value with which this communication is received. The recorded values will be the data body of the message in the next cycle. This allows the gateway that is receiving the messages to also collect the data and forward them to the back-end for processing. The frequency of this measurement cycle is dictated by the gateway. In our experiment, we used a sample rate of a cycle every 10 s. The used sensor nodes are WizziLab Wolt-XL nodes containing custom firmware. All communication in the network happens using DASH7 messages in the 868 MHz Short-Range Devices (SRD) band. The deployed network communicates on a single Hi-Rate channel with a bandwidth of 150 kHz and a baud rate of 166.667 kbit/s [25]. The nodes transmit using an Effective Radiated Power (ERP) of 14 dBm.

In order to be able to adjust for static changes in the environment, we do not directly use the RSSI values but convert them to attenuation values relative to the empty environment. We call this process the calibration step, which occurs every night at a fixed time when the subway station is closed. When calibrating, we measure the RSSI values of every link in the network during a 15 min window and average them to obtain a stable value for every link in the environment. These values are stored in the back-end and are subtracted from the collected RSSI data when the system is in operation to become the attenuation vector per cycle used for further processing. Storing the full vector is required in order to allow for calculating the mean attenuation value based on the selected virtual network. The mean attenuation is what is used to feed into the input of our regression models, as we will discuss in detail in the following sections.

To train and evaluate the system, we performed 3 ground-truth measurements, in which we manually collected ground-truth data on the number of people standing on the platform, as well as the arrival and departure of rail vehicles in the station. All three of these collection periods had a duration of approximately 1 h and occurred on separate days in order to remove as much bias as possible between the training and test sets. We also added a single 30 min window at 03.00 a.m. at night to the training set. This allowed for collecting many samples where the platform was empty and no trams were present. For all results that we will be presenting in the next sections, we used the first collection period and the nightly period for training and the last two periods for evaluation.

4. Materials and Methods

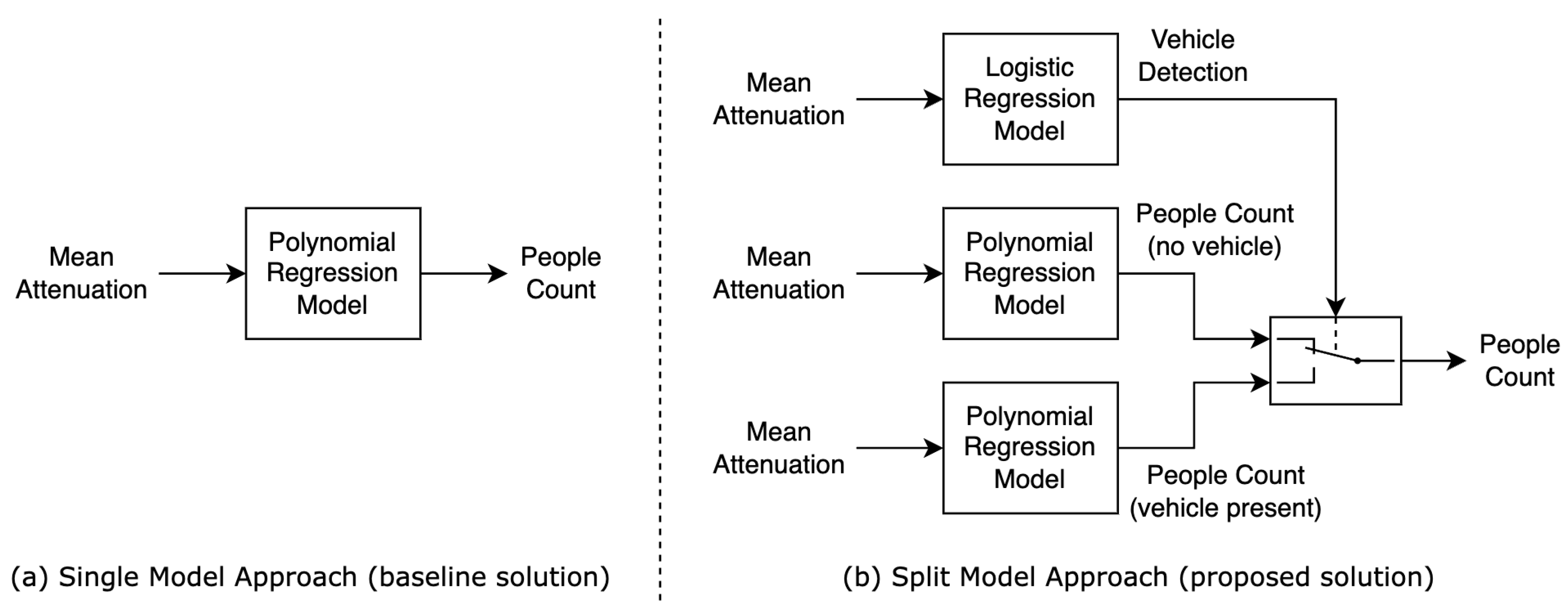
Figure 4 presents two block diagrams of the implemented methods that will be compared in the result section. In (a), the baseline implementation is depicted, using a single model to estimate a people count based on the mean attenuation of a single virtual sensor network. In (b), we propose to expand on this by splitting the people count estimation into two separate models based on whether a rail vehicle is present or not. To be able to switch between these model outputs, we use a logistic regression model to predict the presence of a rail vehicle. All three of the models in the proposed solution (b) use a mean attenuation from a different virtual sensor network, selected to optimize the accuracy of the model.

4.1. Vehicle Detection

In order to know which combination of sensor nodes and estimation model we need to use for people counting, we need to be able to detect whether a vehicle is present in the environment or not. By using the links crossing the rail bedding or close to it, we obtain a strong correlation between the presence of a rail vehicle and the measured signal strength. This allows us to perform binary classification using a logistic regression model. The advantage of using a simpler model for detection, such as a logistic regression model, is that it allows for training the model using a limited amount of data and reduces the risk of overfitting the model to specific unrelated environmental factors. However, this requires a careful selection of links, as a strong correlation needs to be present based on the user’s manually selected virtual sensor network.

When collecting ground-truth data, timestamps of the arrival and departure of rail vehicles were stored. The collected attenuation data within this time span are labeled as “present’’, while samples outside of the spans when no rail vehicle was present are labeled as “not present’’. This binary labeling of samples allows for the training of a binary classification model:

$$\widehat{y}=\sigma (w_2{\overline{\mathbf{a}}}^2+w_1\overline{\mathbf{a}}+b)with\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(1)

The model that is used is shown in Equation (1). In this mathematical representation, $\overline{\mathbf{a}}$ is the input variable and is the arithmetic mean attenuation of the links of the virtual sensor network in dB. $w_2$, $w_1$, and b are the parameters of the model, namely, the curvature (or 2nd-order weight), slope (or 1st-order weight), and intercept (or bias), respectively. A sigmoid function $\sigma$ is applied after the quadratic scaling of the input variable as defined, resulting in an output between 0 and 1. The output of the sigmoid function $\widehat{y}$ represents the predicted likelihood of the presence of a rail vehicle. This predicted likelihood can be rounded to the nearest integer when deployed in order to obtain the predicted label.

The model was implemented using the LogisticRegression and PolynomialFeatures classes provided by the scikit-learn Python library [26], which provide an established implementation for the logistic regression model and polynomial feature transformation, respectively.

When evaluating this model on the test set, we used two different metrics to measure the accuracy of the trained model.

The first metric we used is a sample-based comparison between the labeled samples in the test set and the labels for the same samples predicted by our trained model.

The second metric is an event-based comparison between the ground-truth spans (“entering’’ and “leaving’’ timestamps) and spans derived from the sample-based predictions, taking the timestamps from the first and last samples in which a vehicle was predicted. The metric comprises two values: “false positives’’ and “misses’’. In order to calculate the false positives, we compare, for every predicted span, whether there is an overlap with the ground-truth span, and if this is not the case, we increment the false positive count. When there is an overlap, we associate the ground-truth span with the predicted span. We only allow a single association per ground-truth span, so if a prediction span is broken into two spans, the false positive value will be incremented as well. In order to calculate the misses, we determine, for every ground-truth span, whether there is any overlap with a predicted span. If none of the predicted spans overlaps with the current ground-truth span, it is counted as a “miss’’.

We trained the model on approximately one hour of ground-truth data containing 25 vehicles. This corresponds to 366 samples, of which 242 samples are labeled 0 and 124 samples are labeled 1. We also included a window of 30 min during the night in the training set, as during that time period, the station sees no activity from either vehicles or people, and the environment is completely stable. These data add 168 samples labeled 0 to the training set.

As previously explained, for the evaluation, we used data that were captured on two different days, containing 43 vehicles in total. This results in a test set containing 395 samples labeled 0 and 203 samples labeled 1.

4.2. Crowd Size Estimation

The main goal of our application is to obtain an accurate estimate regarding the number of people present on the platform. Previous research [10,11] has demonstrated that a linear or polynomial relationship can be obtained between the mean measured attenuation within a stable environment and the number of people present. This relationship, once learned by a model, can be utilized to calculate the real-time number of people present from the measured mean attenuation.

However, when a rail vehicle is introduced into the environment, it obstructs the LoS of links, causing shadow fading as well as changing the reflection paths. This change in reflections results in significant changes in constructive and destructive interference called multipath fading. The fading caused by the rail vehicle is significant enough to alter the relationship between the mean attenuation and people count. This change in relationship causes the model to become unreliable for making accurate predictions of people count.

In order to compensate for the changed environment, we split the model for crowd size estimation into two separate models: one model for use when the obstruction (rail vehicle) is not present and one for the situation when the obstruction is present.

To demonstrate this hypothesis, we compare the Pearson correlation coefficients and Spearman’s rank correlation coefficients of the training set’s ground truth and the corresponding attenuation values of the full set, as well as for separated sets. We do so for scenarios both with and without a vehicle present. The results are shown in

Table 1. Correlation coefficient comparison.

	Pearson	Spearman
No split	0.774	0.819
Without vehicle	0.904	0.908
With vehicle	0.921	0.889

. Both the Pearson correlation coefficients and Spearman’s rank correlation coefficients show improvements when splitting the training set based on the presence of a rail vehicle. To calculate these correlations, we only used the data collected during the day, as these data have a more even distribution over different crowd densities. This improves the reliability of the resulting correlation coefficients. The improvement in the Pearson correlation coefficients indicates an increase in linearity when splitting the dataset, while Spearman’s rank correlation coefficients indicate an increase in monotonicity.

The model used when no rail vehicle is present uses the measured attenuation values from the virtual sensor network containing all nodes, as described in Section 3. We trained the model on the collected training data when no vehicle was present in the environment.

The model used when a rail vehicle is present uses the nodes mounted on the ceiling and the platform wall and was trained on the data collected when a vehicle was present.

The regression model we used for both models is a polynomial regression model, as depicted in Equation (2). Similar to the model used for vehicle detection, we use the arithmetic mean attenuation (in dB) of the links in the virtual sensor network $\overline{\mathbf{a}}$ as an input variable. $w_2$, $w_1$, and b are the parameters of the model, namely, the curvature (or 2nd-order weight), slope (or 1st-order weight), and intercept (or bias), respectively. The output variable $\widehat{p}$ represents the predicted number of people present in the environment.

$$\widehat{p}=w_2{\overline{\mathbf{a}}}^2+w_1\overline{\mathbf{a}}+b$$

(2)

Similar to the logistic regression model discussed before, this model was implemented using the LinearRegression and PolynomialFeatures classes provided by the scikit-learn Python library [26], which provide an established implementation for the linear regression model and polynomial feature transformation, respectively.

The ground-truth people counts used for training the crowd size estimation models were manually collected together with the vehicle detection data. The samples that were collected contain the manually counted number of people present together with the timestamp of submission. At regular intervals, the person training the system counted the number of people present in the environment and submitted the resulting count through a training smartphone app, which automatically timestamped the sample. By simultaneously collecting data on people counts and vehicle presence, it becomes straightforward to split the samples based on whether a vehicle is present or not in order to train and evaluate both models. This resulted in a training set of 304 training samples without a vehicle present and 24 training samples with a vehicle present.

The evaluation of both models was performed on a test set comprising two one-hour periods of manually collected ground-truth data. This set contained 162 test samples without a vehicle and 40 test samples with a vehicle. The metric used for evaluating the crowd size estimation models is based on a combination of the median, Mean Absolute Error (MAE), RMSE, and Cumulative Distribution Function (CDF) plots displaying the cumulative error expressed in the number of people.

5. Results and Discussion

5.1. Vehicle Detection

We trained the model in Equation (1) on the labeled samples. Equation (3) shows the resulting logistic regression model. The output is a likelihood value between 0 and 1, with the threshold at $0.5$:

$$\begin{array}{cc}\hfill \widehat{y}& =\sigma (w_2{\overline{\mathbf{a}}}^2+w_1\overline{\mathbf{a}}+b)with\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}\hfill \\ \hfill \widehat{y}& =\sigma (0.082·{\overline{\mathbf{a}}}^2+1.246·\overline{\mathbf{a}}-5.056)\hfill \end{array}$$

(3)

We evaluated the significance of the estimated parameters $w_2$, $w_1$, and b by calculating the corresponding p-values, which were $0.987$, $5.377·{10}^{-3}$, and $6.563·{10}^{-12}$, respectively. The low parameter value and large p-value for the second-order term show that it does not contribute to the function, and the model effectively fits a first-order logistic regression in performing the classification.

We evaluated the vehicle detection model on the test set, as described in Section 4. The results of the sample-based comparison can be found in

Table 2. Confusion matrix vehicle detection (samples).

		Ground Truth
		Not Present	Present
Prediction	Not Present	385	28
	Present	11	174

and

Table 3. Confusion matrix vehicle detection (percentage).

		Ground Truth
		Not Present	Present
Prediction	Not Present	$97.2$ %	$13.9$ %
	Present	$2.8$ %	$86.1$ %

. For the event-based evaluation, the results are 0 misses and 0 false positives. Because of the perfect event-based metric, the sample-based errors can be explained by a potential misalignment between the collected ground-truth vehicle windows and the predicted windows. A vehicle is, on average, inside a station for 51.3 s based on the ground-truth data. A single sample mismatch due to human inconsistency during data collection translates to a 20% error for that vehicle event in the sample error rate. As a sample period of 10 s is used, an average vehicle event takes five samples. A comparison between the prediction (black line) and the collected ground-truth data (green spans) is shown in Figure 5.

5.2. Crowd Size Estimation

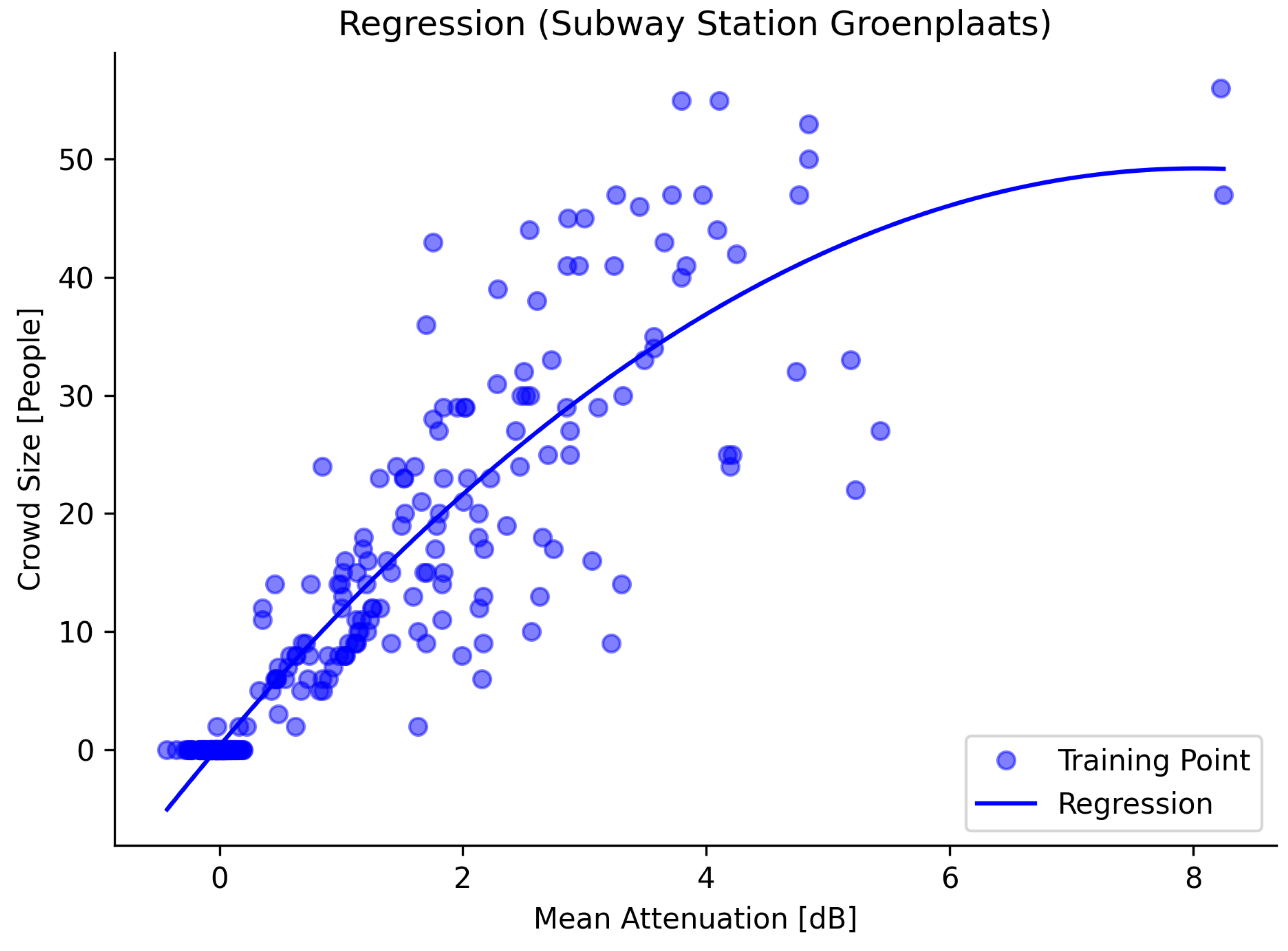
As a benchmark, we trained the single regression model depicted in Equation (2) on the complete dataset regardless of whether a rail vehicle was present or not. Equation (4) shows the resulting regression model:

$$\begin{array}{cc}\hfill \widehat{p}& =w_2{\overline{\mathbf{a}}}^2+w_1\overline{\mathbf{a}}+b\hfill \\ \hfill \widehat{p}& =-0.757·{\overline{\mathbf{a}}}^2+12.171·\overline{\mathbf{a}}+0.311\hfill \end{array}$$

(4)

We evaluated the significance of the estimated parameters $w_2$, $w_1$, and b by calculating the corresponding p-values, which were $38.84·{10}^{-15}$, $1.475·{10}^{-78}$, and $0.451$, respectively. The low parameter value and large p-value for the intercept term show that it does not contribute to the function. The function passes through the origin, which is expected given that we use attenuation values relative to the empty environment.

To test for autocorrelation, we calculated the Durbin–Watson statistic, which was 0.903. This value indicates significant autocorrelation between the residuals. This can be explained by the fact that consecutive ground-truth samples are often taken in very similar situations; more precisely, the locations at which people are standing will be similar to the previous ground-truth sample. The location at which a person is standing will impact the amount of attenuation they cause on the links. This difference in attenuation can result in an error that remains consistent across multiple evaluation samples.

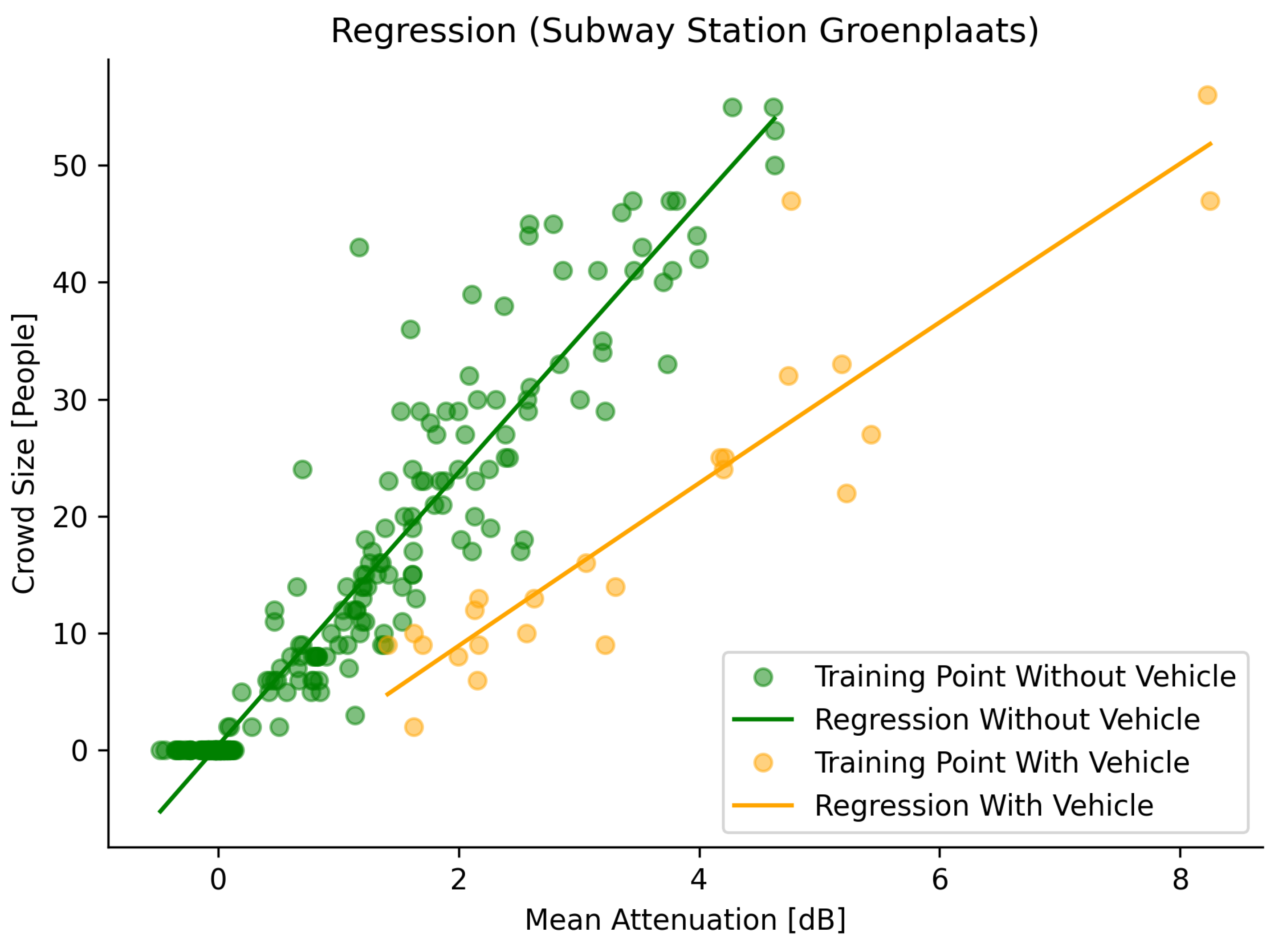
We trained the model in Equation (2) for both environment states using the corresponding training sets. Equation (5) shows the resulting regression model when no rail vehicle was present in the environment. Equation (6) shows the resulting regression model when a vehicle is present in the environment.

$$\begin{array}{cc}\hfill \widehat{p}& =w_2{\overline{\mathbf{a}}}^2+w_1\overline{\mathbf{a}}+b\hfill \end{array}$$

$$\begin{array}{cc}\hfill \widehat{p}& =-0.033·{\overline{\mathbf{a}}}^2+11.735·\overline{\mathbf{a}}+0.417\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \widehat{p}& =-0.021·{\overline{\mathbf{a}}}^2+7.082·\overline{\mathbf{a}}-5.155\hfill \end{array}$$

(6)

We evaluated the significance of the estimated parameters $w_2$, $w_1$, and b for both models by calculating the corresponding p-values. For Equation (5), we obtain p-values of $0.834$, $0.295·{10}^{-63}$, and $0.151$, respectively. For Equation (6), we obtain p-values of $0.941$, $0.016$, and $0.350$, respectively. For both models, we observe low values and high p-values for the second-order parameter, indicating that the data mainly fit a first-order trend. The p-values for the intercept of both models indicate they are not significant.

To test for autocorrelation, we calculated the Durbin–Watson statistic. For Equation (5), we obtain a value of 0.786, indicating a strong positive autocorrelation between the residuals. This can be explained, as above, by consecutive samples representing fairly similar environment states with their corresponding error. For Equation (6), we obtain a value of 2.063, indicating practically no autocorrelation. This can be explained by the fact that we only took a single sample when a rail vehicle stopped; this causes more time and differences between consecutive samples.

Figure 6 and Figure 7 show the correlation between the used training samples for both approaches, together with the resulting polynomial regression models. These graphs visually show the advantage of using separate models depending on the environment’s state.

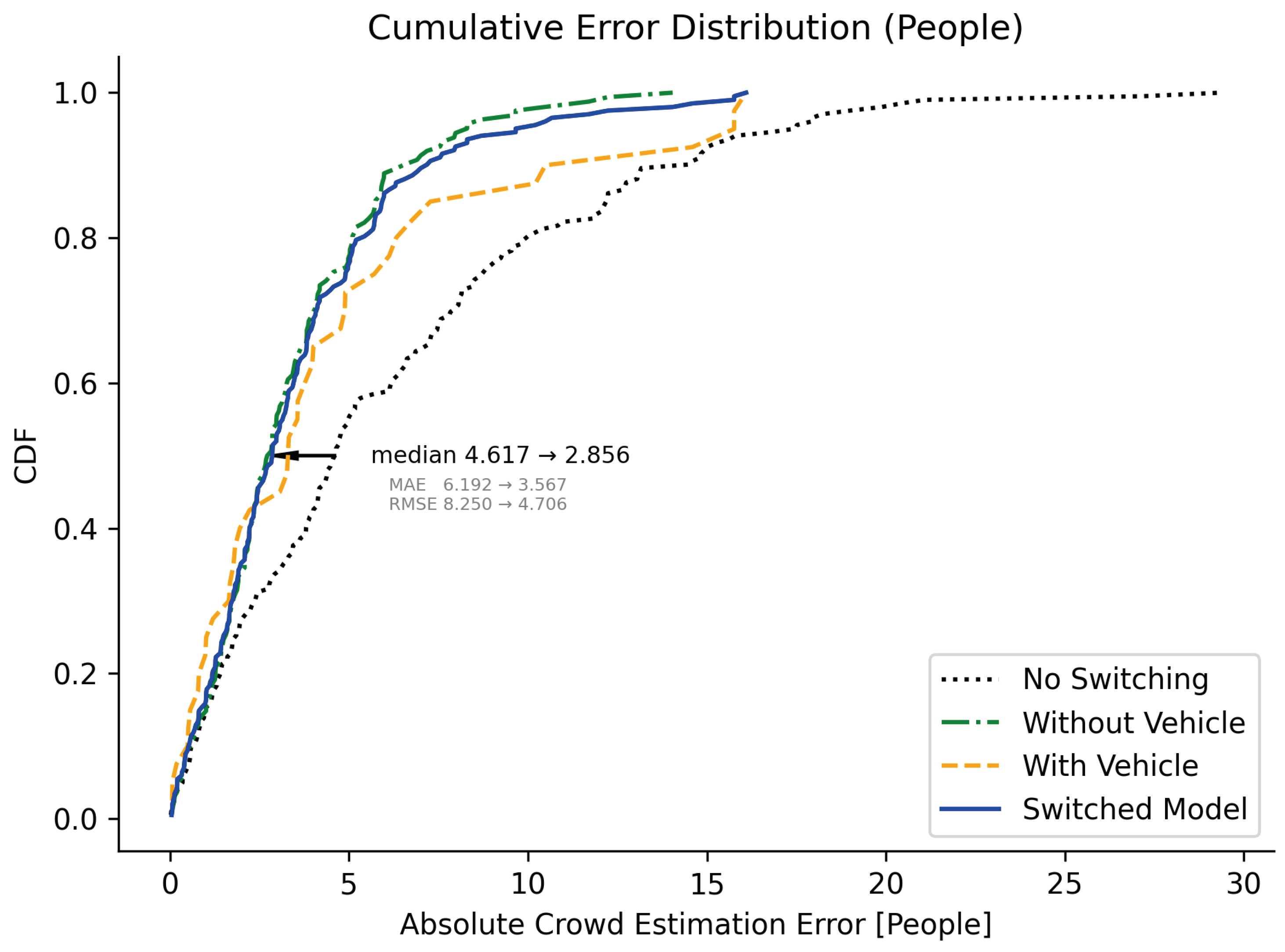
When evaluating the crowd size estimation with no vehicle present, a median error of 2.769 people is observed, along with an MAE of 3.342 people and an RMSE of 4.211. The CDF plot is shown in Figure 8 as a green dash-dotted line.

When evaluating the crowd size estimation when a vehicle is present, a median error of 3.304 people is observed, along with an MAE of 4.478 people and an RMSE of 6.326. The CDF plot is shown in Figure 8 as an orange dashed line.

5.3. Combined Model

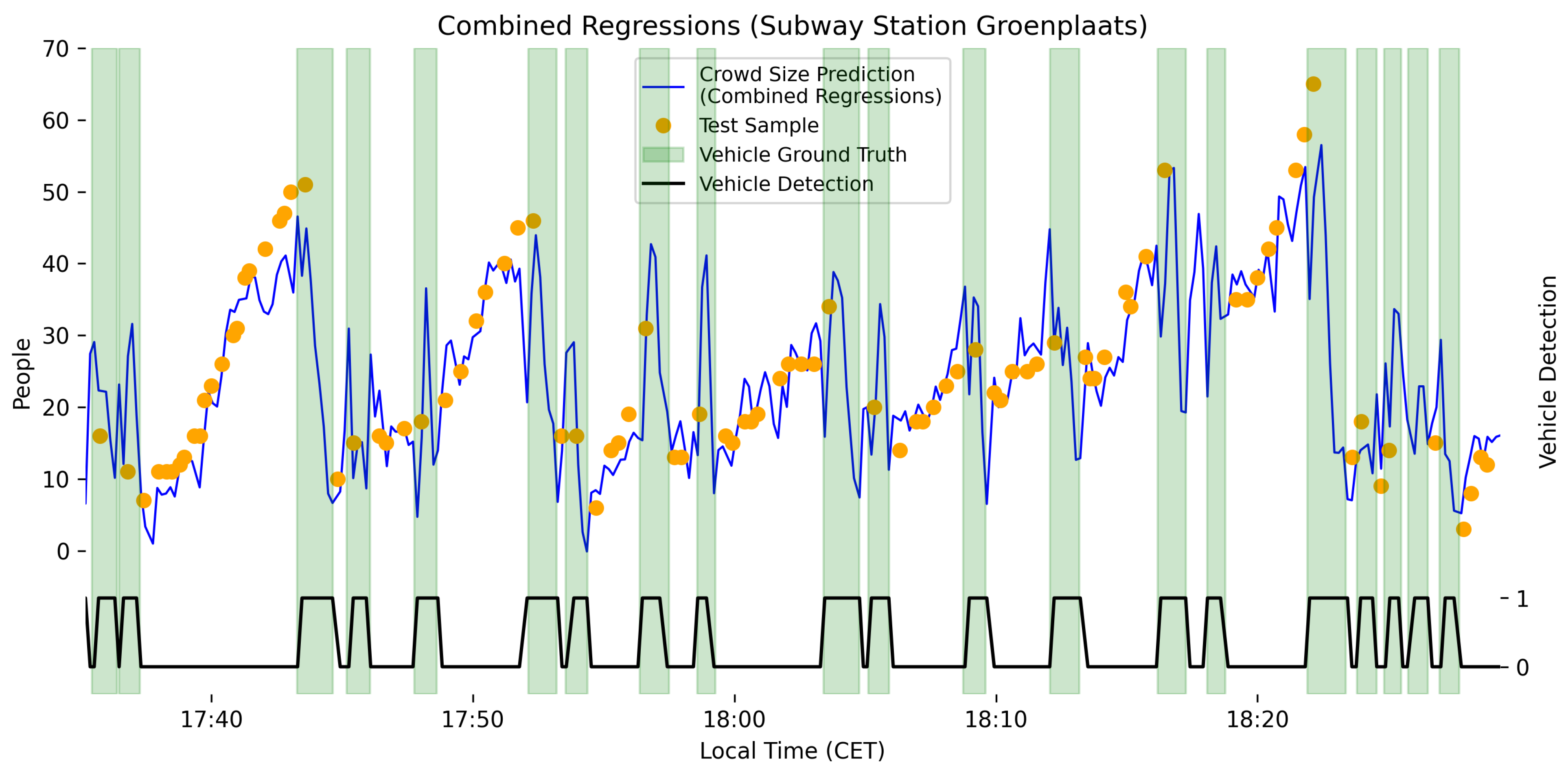
The use of a reliable vehicle detection system and two separately trained models for the two environment states enables us to combine both models in a real-time environment. When we overlay the output of the combined model with the ground-truth data, we obtain the graph shown in Figure 5. The trend and magnitude of the predicted crowd size have a clear correlation with the trend that can be observed in the test data.

When we look at more statistical metrics, we obtain a median error of 2.856 people, an MAE of 3.567 people, and an RMSE of 4.706. These numbers are a clear improvement over the use of a single polynomial regression model trained on both states, which results in a median error of 4.617 people, an MAE of 6.192 people, and an RMSE of 8.250.

If we calculate the F-test and p-value between absolute errors of the proposed switching model and the non-switching model, we achieve an F-test value of 35.394 and a p-value of $5.861·{10}^{-9}$, confirming the statistical significance of this improvement.

The data as presented are the raw output of the regression models and are not yet filtered or smoothed in any way. Due to the lack of filtering, the movement of people in the environment causes fluctuations based on their positions and movement patterns. Since the data used within this paper were collected during busy periods in an uncontrolled environment, we obtained a thorough benchmark on how the system will perform in similar environments.

Switching between models when not perfectly aligned with changes in the environment can result in discontinuities in the combined output. These discontinuities can become visible as upward or downward spikes in the final graphs during the arrival or departure of rail vehicles.

Another important note is that the ground-truth samples for both training and testing are combined with the closest measurement sample collected every 10 s. This allows for a mismatch of up to 5 s between the ground-truth samples and the corresponding attenuation values. In a very lively public transportation environment, large changes in the number of people and their location can occur in the time between collecting the ground truth and the measurement by the system. An example of this is people disembarking the rail vehicle and walking to the exit. These short events of 10 to 20 s can result in a significant increase in crowd size for the duration of only one or two samples. This poses challenges in collecting reliable training data during these periods.

6. Conclusions

In this paper, we discuss the use of a battery-powered wireless sensor network to perform device-free wireless sensing of a crowd’s size in a subway station by detecting the presence of rail vehicles. Simultaneous rail vehicle detection and crowd size estimation allows for switching between multiple pre-trained regression models, reducing the impact caused by the changing environment.

We demonstrated the capability of using attenuation within a wireless sensor network for reliably detecting the presence of rail vehicles. We achieved perfect detection when looking at the event-based metric. On a sample basis, we achieved an overall accuracy of $93.5$ % on the test set.

We improved the level of accuracy for crowd size estimation by using two separately trained polynomial regression models depending on whether a rail vehicle is present or not in comparison to a single regression model. Switching between the two models improved the MAE from 6.192 people to 3.567 people for the entire test set. When no rail vehicle was present, we achieved an MAE of 3.342 people on the test set. When a rail vehicle was present, we achieved an MAE of 4.478 people on the test set.

To obtain our full model, we combined both regression models based on the output of the vehicle detection model. This full model is able to perform real-time predictions on a per-sample basis for both environment states. The final results reflect trends and magnitudes that are very similar to those observed in the ground-truth data.

6.1. Limitations

Despite the clear improvements achieved in the experiment used in this study, there are limitations to consider for implementing the proposed solution in practical applications.

Sufficient training data need to be available or collected for every scenario that requires a separate model. By using first- or second-order polynomial models, a limited amount of training data can suffice to perform training.

The different environment states need to reoccur in a stable way. This is the case with a rail vehicle in a station but can be more challenging with more flexible scenarios; for example, for different parked cars, a small car compared to a large truck could have a different impact on the attenuation. Evaluating the trained model on unseen data can provide insight into how well the model will behave in multiple scenarios.

In the presented experimental setup, we mounted a multitude of sensors on the walls and ceiling of the subway station. This is possible in indoor environments, but outdoor environments often offer fewer options for mounting sensors. This will require more thought to find a suitable combination of nodes that minimizes the impact created by the dynamic environmental factor.

6.2. Future Work

Future work needs to be conducted to extend the validation scope to other bistable environments besides subway stations. Outdoor environments offer a different set of challenges than indoor environments. Examples of these are changing weather conditions, limitations on sensor placement, and vehicular traffic.

Other regression models or techniques to enable the DFWS system to handle environmental changes should be investigated as well. Machine learning models incorporating multiple layers, such as multilayer perceptron networks, could be used to learn patterns in the data automatically. However, as model complexity increases, a larger amount of training data is required, compared to simpler polynomial models, in order to mitigate unwanted behavior, such as overfitting.

Finding ways to optimize the number of sensor nodes and their placement in the environment could further improve the reliability and efficiency of the system.

Finally, further investigation into the effects of limited training data on the estimation accuracy should be conducted.