Query Optimization in Distributed Database Based on Improved Artificial Bee Colony Algorithm

Abstract

Query optimization is one of the key factors affecting the performance of database systems that aim to enact the query execution plan with minimum cost. Particularly in distributed database systems, due to the multiple copies of the data that are stored in different data nodes, resulting in the dramatic increase in the feasible query execution plans for a query statement. Because of the increasing volume of stored data, the cluster size of distributed databases also increases, resulting in poor performance of current query optimization algorithms. In this case, a dynamic perturbation-based artificial bee colony algorithm is proposed to solve the query optimization problem in distributed database systems. The improved artificial bee colony algorithm improves the global search capability by combining the selection, crossover, and mutation operators of the genetic algorithm to overcome the problem of falling into the local optimal solution easily. At the same time, the dynamic perturbation factor is introduced so that the algorithm parameters can be dynamically varied along with the process of iteration as well as the convergence degree of the whole population to improve the convergence efficiency of the algorithm. Finally, comparative experiments conducted to assess the average execution cost of Top-k query plans generated by the algorithms and the convergence speed of algorithms under the conditions of query statements in six different dimension sets. The results demonstrate that the Top-k query plans generated by the proposed method have a lower execution cost and a faster convergence speed, which can effectively improve the query efficiency. However, this method requires more execution time.

1. Introduction

Due to the continuous development of the information age, people’s daily production of data and lifetime data volume have resulted in explosive growth, and the traditional centralized database has been unable to meet the massive data storage and computational processing needs [1,2,3]; therefore, distributed databases have emerged. Compared with centralized databases, distributed databases have more powerful storage and computation performance. In general, a distributed database cluster includes a coordinated control site and multiple data storage sites, and the stored data are sliced and distributed in different data storage sites through a certain rule [4,5]. Meanwhile, in order to ensure the high availability of the distributed database cluster, the data shardings usually have several backups that are distributed across different sites [6,7,8,9]. Therefore, a query statement has multiple corresponding query execution plans (QEPs), and the query execution cost of each query plan is different [10,11]. In order to reduce the execution overhead of retrieving data and to speed up the query response, it is important to choose an appropriate query execution plan. When it comes to high-dimensional join queries, the space of the feasible query plans will also be very huge [12], and it is impossible to calculate the query execution cost for each query plan. Therefore, the core goal of distributed database query optimization is to find the one with the lowest execution cost among many query execution plans [13,14].

As an NP (non-deterministic polynomial) problem, the process of query optimization for distributed databases can be transformed into the problem of exhaustive search [15] and hence can be solved by heuristic-based techniques such as the ant colony optimization algorithm [16,17,18], greedy algorithms, particle swarm optimization algorithms [19], the genetic algorithm [20,21,22,23] and random search algorithms [24,25,26].

Ozger et al. [27] proposed a discrete artificial bee colony (dABCSPARQL) algorithm based on a novel heuristic approach for reordering SPARQL queries. The method first performs syntax tree parsing on the query statements to classify them into chained, star, cyclic, and chain-star queries; converts the statements into pre-ordered vectors based on different types of queries; and then further optimizes them using the discrete artificial bee colony algorithm to obtain a better execution plan. Although this algorithm performs well with the small number of relations, this situation is inverted when the query has more relations and requires excess memory and processor consumption. Moreover, this method increases the runtime.

Kumar et al. [28] proposed a distributed database query optimization method based on the ant colony algorithm by simulating the process of ants searching for food by iterating the pheromone mechanism left on the pathway that ants search for food to carry out optimal pathway planning. This has a certain optimization effect, but it consumes more computation time when the query involves a larger number of data sites. At the same time, there exists the problem of falling into the local optimal solution.

Zhou et al. [29] proposed a distributed database query optimization method based on the multi-ant colony genetic algorithm. The method first uses the characteristics of rapid convergence of the genetic algorithm to obtain a set of relatively optimal query execution plans, and then the execution plan is transformed into the initial routing pheromone value of the multi-ant colony algorithm. This improves the overall algorithm’s computational efficiency, but the method reduces the computation time due to the two algorithms of the parallel computation greatly increasing the cost of the computer’s computation.

Mohsin et al. [30] designed a quantum-inspired ant colony-based algorithm to optimize large join queries and improve the cost of query joins in distributed databases. Quantum computing has the ability to diversify and scale so that a larger query search space can be covered in the search. In this way, it speeds up convergence and helps to avoid falling into local optima. With such a strategy, the algorithm aims to determine an optimal order of connections to reduce the total execution time. Experimental results show that the convergence speed is higher using this method. However, for relatively small queries, it performs terribly and easy to precocity.

Zheng et al. [31] proposed an adaptive genetic algorithm based on double entropy for distributed database query optimization. The two types of entropy are genotype entropy and phenotype entropy. Genotype entropy is used to optimize the distribution of the initial population, ensuring a diverse set of initial solutions. Phenotype entropy, on the other hand, optimizes the genetic strategy and consists of individual entropy and population entropy. The algorithm improves the diversity of the population to prevent the algorithm from falling into local optima easily, but the algorithm lacks local search capability, which leads to slower convergence at a later stage.

Ragmani et al. [32] proposed a hybrid fuzzy ant colony optimization algorithm (FACO) for distributed database query optimization. The proposed FACO algorithm incorporates a fuzzy module that uses historical information to calculate the pheromone value and select the appropriate ACO parameters while maintaining optimal computing time. The algorithm sets different algorithm parameters for different input query statements by leveraging the advantages of ant colony optimization and fuzzy logic. This improves the query efficiency, but the use of a single search algorithm means that the method still has the problem of easily falling into local optimum.

Table 1 shows some of the advantages and limitations of the related works.

Table 1. A side-by-side comparison of the discussed join query optimization mechanisms.

Mechanism	Approach	Advantages	Weaknesses
Ozger et al. [27]	Proposed a discrete artificial bee colony algorithm based on a novel heuristic approach.	•Performing well with a small number of relations	•Terrible performance for a large query •Excess memory and processor consumption
Kumar et al. [28]	Proposed an ant colony algorithm optimization for query optimization.	•Improving the average •Quality of query plan	•High overhead •High response time
Zhou et al. [29]	Proposed a multi-ant colony genetic algorithm.	•Increasing the convergence speed •Low execution time	•Low variety population •Drop to local optima
Mohsin et al. [30]	Designed a quantum-inspired ant colony-based algorithm.	•High convergence speed •High effectiveness	•Terrible performance for a smaller query •Easy to precocity
Zheng et al. [31]	Proposed an adaptive genetic algorithm based on double entropy.	•High population diversity •Avoiding getting stuck in local minima	•Low convergence speed •Suffers from long execution time
Ragmani et al. [32]	Proposed a hybrid fuzzy ant colony optimization algorithm.	•Decreasing the time •High efficiency	•Easily falls into local optimum for large join query

As the cluster size of distributed databases continues to expand, the data shardings and storage nodes will also increase, resulting in exacerbating the complexity of data query in distributed databases and further leading to the current query optimization algorithms suffering from problems of low optimization efficiency and easy to precocity in the face of high-dimensional join queries. Therefore, in this paper, a dynamic perturbation artificial bee colony algorithm combined with genetic operators is proposed to solve the distributed database problem. The main contributions of this paper are as follows:

(1) A new artificial bee colony algorithm optimization strategy is used to solve the optimization problem of discrete feasible domains without the concept of distance;

(2) A dynamic perturbation factor is proposed so that the parameters of the algorithm can change dynamically with the iterative process and the convergence degree of the whole population in order to improve the convergence efficiency of the algorithm;

(3) The global search ability of the artificial bee colony algorithm is improved by combining the selection, crossover, and mutation operators of the genetic algorithm to overcome the problem of falling into the local optimal solution easily.

The remainder of this paper is organized as follows: The design of the cost function and the proposed algorithm are expressed in Section 2. The data and results of the experiment are delivered in Section 3. Finally, Section 4 demonstrates conclusions and future work.

2. Proposed Method

Distributed databases usually include a coordinator site and multiple data sites. The data are sliced and distributed to different sites according to certain rules, usually using the consistent hashing method according to the keyword of tuples to balance the data storage capacity of each site. The query execution plan determines the selection and join order of sites. In a distributed database, the query execution cost mainly consists of the resource cost of the site’s local disk data scanning and the network communication expense of data transmission between different sites. Due to the current limitations of the network bandwidth, the data transmission communication expense between sites is much larger than the resource expense of the local data scanning, so the optimal query execution plan for a distributed database is that which has the minimum communication cost. The four main phases of query optimization applied to distributed databases are shown in Figure 1.

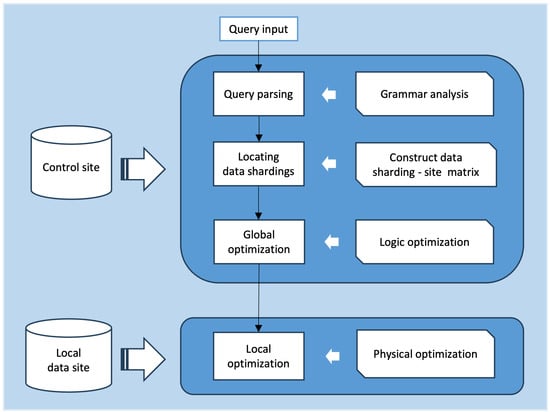
Figure 1. Query execution process in a distributed database.

The first stage is query decomposition: receive query requests submitted by users and parse the query, then recognize the syntactic structure and semantics of the query. Then, transform the query statement (e.g., SQL statements) into a corresponding parse tree. The second stage is data retrieval: determine the data tables involved in the query by analyzing the parse tree, retrieve the location of the sites where the required data are located via a metadata table, and construct a storage site matrix. The third stage is global optimization: the query optimizer generates the query execution plan from the parse tree as well as the data storage matrix. Since a statement can have multiple equivalent execution plans, a cost function is needed to find the least costly query execution plan. The cost of the query plan is calculated using the cost function (CPU cost + I/O cost + communication cost), and the optimal order of query operations is calculated based on the calculation. If it is in a wide-area network, the communication cost will be large and is called the trade-off factor. Then, the query is decomposed into multiple subqueries based on the query-optimized execution plan and distributes the decomposed subqueries to various distributed sites for execution. The fourth stage is local optimization: after the query request is assigned to the local processing site according to the upper layer, it is equivalent to a centralized database environment. Therefore, at this time, the centralized database method can be used for query optimization. Finally, the results of the subqueries executed on each site are merged and return the final merged query results to the user. In this paper, we focus on the third stage of global optimization, using the cost function to calculate the execution cost of the query plan, and find the query plan with the smallest query cost as the optimal query plan.

2.1. Improved Artificial Bee Colony Algorithm

The bees in the artificial bee colony (ABC) algorithm are categorized into three groups [33,34,35] including leader bees, follower bees, and scout bees. Half of the colony consists of leader bees, and the other half consists of follower bees. Leader bees are responsible for finding available food sources, collecting information, and passing food information to the follower bees. The follower bees select good food sources from the information passed on by the leader bees to further search for food. When the quality of a food source does not improve by a predetermined number of iterations, the corresponding leader bee abandons the food source, and then the leader bee becomes a scout bee and starts searching for a new food source in a location farther away. The location of a food source corresponds to a possible solution to the optimization problem, which in this paper is a feasible query execution plan (QEP), whereas the amount of food from each food source represents the quality (fitness) of the solution in question. Meanwhile, the number of leader bees is equal to the number of food sources. The specific steps are as follows:

The first step is data preprocessing. The input to the algorithm is the data sharding-site matrix (DSM) generated from the metadata table of the database system during the query process. However, this input matrix is not yet directly usable by the algorithm, so it also needs to be de-zeroed and transposed to generate a search domain matrix executable by the artificial bee colony algorithm. As shown in Figure 2, in the data sharding-site matrix, “1” represents that the data sharding exists in the corresponding site, and “0” is the opposite. In the feasible domain matrix, each row represents the site number that stores a certain data sharding; for example, the first row shows that the sites that store data sharding 1 are site 1, site 2, and site 5.

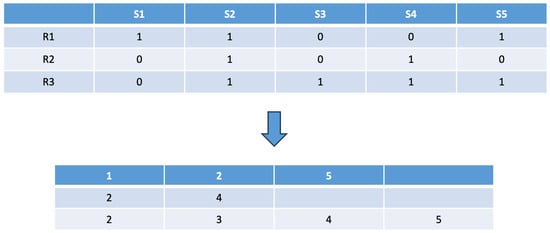
Figure 2. Data preprocessing.

In the second step, each leader bee searches for a food source. The initial position of the food source X${}_i$ = {X${}_{i1}$, X${}_{i2}$, …, X${}_{id}$} is randomly generated in the search domain matrix according to the equation below:

$$X_{id}=Random\left(L_d\right)$$

(1)

where d = 0, 1, 2 …D, with D being the dimension of the feasible solution. In this paper, D represents the data site where one of the required data shardings of a feasible query execution plan is located; Random(L${}_d$) denotes the random selection of a data site with the d-th data sharding in the row where the d-th data sharding is located in the search domain matrix.

The fitness value of a food source is measured as the execution cost of a feasible query execution plan. In distributed databases, the cost of a query is mainly the communication cost incurred by the transmission of data among sites. In order to minimize the cost of a query, the transmission of data among sites should be minimized. Therefore, the concentration of data sites selected in the query execution plan should be as high as possible, as expressed in equation below:

$$Fit=\sum _{i=1}^M\frac{S_i}{N}(1-\frac{S_i}{N})$$

(2)

where M is the number of sites involved in the query plan, N is the number of data shardings involved in the query plan, S${}_i$ is the number of times the i-th site is used in the query plan, and the query cost Fit between 0 and (N − 1)/N. 0 means optimal, that is to say, that the query plan involves data shardings in the same site, with no need to carry out the site-to-site data transfer. Additionally, (N − 1)/N; that is to say, the data shardings involved in query plan are all from different sites, and all the data need to carry out the transmission of site-to-site transfer.

The traditional artificial bee colony algorithm starts the searching phase with leader bees searching around the food source X${}_i$ according to Equation (3) to produce a new food source Y${}_i$ = Y${}_{i1}$, Y${}_{i2}$, …, Y${}_i{}_d$:

$$Y_{id}=X_{id}+\delta ·(X_{id}-X_{jd})$$

(3)

where d is a random integer in [1, D], denoting a dimension of the random selection search by the leader bees; j ⊆ 1, 2, …, N, j ≠ i, denotes a random selection of a food source not equal to i among the current N food sources; and $\delta$ = [−1, 1] is a uniformly distributed random number that determines the magnitude of the random selection perturbation.

However, in this study, the problem to be solved by query optimization is to find a query execution plan with the fewest number of sites involved, which is equivalent to the highest site concentration, and where each dimension in each food source X only represents the label of a data site, with no size. Therefore, there is no concept of distance between food sources in this problem. Following the traditional search method, it is equivalent to re-performing a random search at each iteration, which leads to an algorithm without directional optimization, making the convergence speed extremely slow. In this paper, a greedy artificial bee colony algorithm in the face of a discrete feasible domain without the concept of distance is proposed to improve the optimization strategy of the traditional artificial bee colony algorithm.

The strategy for leader bees to generate a new food source Y${}_i$ based on food source X${}_i$ in the search initiation phase of the improved artificial bee colony algorithm is as follows: first, calculating and sorting the number of times that the sites involved in the food source X${}_i$ were used. The sites with a high number of use times are retained according to the perturbation coefficient $\delta$ by using the greedy idea, and the sites with a low number of use times are perturbed. Then, the data shardings corresponding to the lesser-used sites re-select data sites according to Equation (1). Finally, the obtained new food source Y${}_i$ is compared with X${}_i$. If the fitness value of Y${}_i$ is better than X${}_i$, then replace X${}_i$ with Y${}_i$; otherwise, keep X${}_i$ unchanged. The details are shown in Algorithm 1:

Algorithm 1 Improved Optimization Strategy Logical Pseudo-Code

Input: X${}_i$ and $\delta$   ▹ A food source in the population and the perturbation coefficient Output: Y${}_i$                ▹ A new food source generated by X${}_i$ 1: N← the number of sites used in X${}_i$; 2: (n${}_1$, n${}_2$, …, n${}_N$) ← the number of each site used in X${}_i$ ▹ Calculate the number of times each site is used 3: sort(n${}_1$, n${}_2$, …, n${}_N$);             ▹ sort them from largest to smallest 4: N’ ←$[N·\delta ]$; ▹ the number of sites that need to be updated is calculated as based on the perturbation coefficient $\delta$ 5: re-select (N’ sites); ▹ reselect the $[N·\delta ]$ sites for data shardings corresponding to sites with smaller usage counts in X${}_i$ by Equation (1), and the rest remain unchanged 6: Y${}_i$← the new food source; 7: return Y${}_i$

For example, suppose a food source X = {1, 1, 1, 1, 1, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5, 5, 5, 6} is a query plan involving 15 data shardings across 6 sites, and the number of times each site has been used is sorted in descending order as {S${}_1$:4; S${}_5$:4; S${}_3$:3; S${}_4$:2; S${}_2$:1; S${}_6$:1}, with the perturbation coefficient $\delta$ = 0.5. Then, retain the three most used sites (S${}_1$, S${}_5$, S${}_3$), perturb the remaining three sites (S${}_4$, S${}_2$, S${}_6$), and re-select the used sites in the corresponding search domains for the data shardings using the perturbed nodes according to Equation (1). In this way, the lesser-used sites are perturbed in each iteration in order to increase the site concentration of the query plan.

Meanwhile, a dynamic perturbation factor $\eta$ is proposed so that the perturbation coefficient changes dynamically with the change in the whole population state during the iteration of the algorithm. Since the fitness values of food sources in the population are converging as the population iteration progressing, i.e., the concentration of sites in each query plan is increasing, a food source with a better fitness value for the population should be updated using a lower perturbation coefficient. If the perturbation coefficient is too large, the sites that are originally used more may be re-randomized as well, which is detrimental to the optimization of the food source. The specific dynamic perturbation factor $\eta$ is shown in Equation (4):

$$\eta =1+(Fi{t}_i-Fi{t}_{best})·\frac{L-t}{L}$$

(4)

where L is the parameter for the maximum number of iterations of the algorithm, t is the current number of iterations, Fit${}_i$ is the fitness value of honey source X${}_i$ in the population under the current number of iterations, and Fit${}_{best}$ is the fitness value of the best honey source in the population under the current number of iterations. The perturbation coefficient $\delta$ for each specific food source is obtained as in Equation (5):

$$\delta ={\delta }^{\prime }·\eta$$

(5)

where ${\delta }^{\prime }$ is the perturbation coefficient set during the initialization of the algorithm, and $\eta$ is the perturbation factor of the current food source calculated according to the Equation (4).

The third step is the follower bee search phase. Based on the food source information shared by the leader bees, the probability that the leader bees are followed by the follower bees is calculated by Equation (6):

$$P_i=\frac{Fi{t}_i}{{\displaystyle \sum _i^N}Fi{t}_i}$$

(6)

where Fit${}_i$ is the fitness value of the i-th food source. Then, the follower bees adopt the roulette method to follow a leader bee. Equivalently, a uniformly distributed random number r is generated in [0, 1] and, if P${}_i$ is greater than r, this follower bee generates a new food source based on the food source i according to Algorithm 1. Then, the retained food source is determined by the greedy selection method used in the leader bee phase.

The fourth step is the scout bee search phase. When a leader bee searches for a food source X${}_i$, if the food source is not updated, the number of searches for this food source trail is recorded, plus 1. If the food source X${}_i$ reaches the threshold limit after trial iterations of search and no better food source is found, then this food source X${}_i$ will be abandoned, and the corresponding leader bee will be changed to a scout bee. The scout bee will generate a new food source Z${}_i$ based on this food source X${}_i$, according to Algorithm 1, but with a larger perturbation coefficient. The same greedy selection method will be used to determine the retained food source, while the number of searches of this food source is reset to 0, as shown in the equation below:

$$X_i^{t+1}=\left\{\begin{array}{c}Algorithm1(X_i,\delta ·1.5),tria{l}_i>limit\hfill \\ {X_i}^t,tria{l}_i<limit\hfill \end{array}\right.$$

(7)

where t is the current number of iterations and trial${}_i$ is the number of times the food source X${}_i$ has been searched for.

2.2. Genetic Operators

In this paper, the three operators of selection, crossover, and mutation in the genetic algorithm [36] are introduced to overcome the problem that the traditional artificial bee colony algorithm has a slow convergence speed and easily falls into local optimization. The chromosome in the genetic algorithm consists of “genes”, in which the chromosome and the food source in the artificial bee colony algorithm are consistent, both representing a feasible solution, i.e., a query execution plan. The genes represent the sites where the data shardings are located in the query; the value of the genes represents the location of the sites where the data are located; and the length of the chromosome represents the length of the data shardings involved in the from statement in the query.

Selection operator: this operation is based on the selection rate to determine the individuals to be subjected to crossover and mutation operations. In this method, the parameters will be initialized at the beginning of the algorithm, where P${}_{select}$ is the selection rate. In the leader bee and follower bee search phase, for the food source X${}_i$ currently being searched, a uniformly distributed random number r is generated in [0, 1], and the crossover and mutation operations are performed on the food source X${}_i$ if P${}_{select}$ is greater than r.

Crossover operator: the crossover operation is the key to improving the global search capability of the overall algorithmic model, which can improve the diversity of the solution set to avoid falling into local optimal solutions. This operation randomly selects multiple crossover points in the two chromosomes, and crossover interchanges the two chromosomes according to the gene values corresponding to the selected positions in order to generate two new chromosomes. Shown in Figure 3 is the two-point crossover operation, and the number of specific selections of crossover positions is obtained from Equation (8):

$$N_{cross}=P_{cross}·Len\left(X\right)$$

(8)

where N${}_{cross}$ is the number of crossover points in the crossover operation, P${}_{cross}$ is the crossover rate, and Len(X) is the length of the chromosome, i.e., the food source.

Figure 3. Two-point cross-operator example.

Mutation operator: this operation changes the values of multiple random genes in a chromosome to produce a new chromosome. Shown in Figure 4 is a two-point mutation operation, with the number of crossover points obtained from Equation (9):  

$$N_{\mathrm{mutation}}=P_{\mathrm{mutation}}·Len\left(X\right)$$

(9)

where N${}_{mutation}$ is the number of variant points in the mutation operation,P${}_{mutation}$ is the mutation rate, and Len(X) is the length of the chromosome. The mutation operation is shown in Equation (10):

$${X_{id}}^{\prime }=Random(L_d-X_{id}).$$

(10)

Figure 4. Two-point mutation operator example.

In the equation, d is the mutation point position selected for the food source X${}_i$, X${}_{id}$ is the value of the corresponding mutation point, X${}_{i{d}^{\prime }}$ is the value of this point after the mutation operation, and Random(L${}_d$−X${}_{id}$) denotes that a data site with this data sharding that is not equal to X${}_{id}$ is randomly selected in the row where the d-th data sharding is located in the search domain matrix.

Similarly, the selection rate, crossover rate, and mutation rate of the genetic operator corresponding to each food source dynamically change with the iterative process of the overall population, as shown in Table 2:

Table 2. Probability value of genetic operators.

Operator	Probability Value
Selection	P${}_{select}$·$\eta$
Crossover	P${}_{crossover}$·$\eta$
Mutation	P${}_{mutation}$·$\eta$

In the table, P${}_{select}$, P${}_{crossover}$, and P${}_{mutation}$ are the selection, crossover, and mutation rates set at initialization, respectively, and $\eta$ is the dynamic perturbation factor of the current food source.

Example: D1, D2, D3, D4, D5, and D6 are the data shardings that need to be accessed in the query. Assume that these six shardings are distributed in nine sites as S1, S2, S3, S4, S5, S6, S7, S8, and S9. Then, the data sharding-site matrix is shown in Figure 5, and the query statement is as follows:

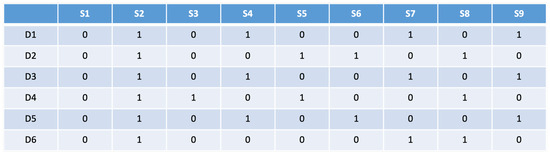
Figure 5. Data sharding-site matrix.

Select F1, F2, F3

From D1, D2, D3, D4, D5, D6

Where D1.F1 = D2.F1 AND

R3.F2 = D4.F2 AND

R5.F3 = D6.F3.

In a query plan, access sites are randomly assigned to the required data shardings according to the DSM of Figure 5. Figure 6 illustrates the five randomly generated alternative query execution plans. Let the i-th food source in the current population be X${}_i$, where X${}_i$ = (2, 2, 2, 2, 4, 2) is the current execution plan; Y${}_i$ = (2, 2, 2, 3, 2, 6) is a food source generated by X${}_i$ through Algorithm 1; Z${}_i$ = (2, 2, 7, 8, 9, 8) is a food source obtained by X${}_i$ through the mutation operation; and X${}_{best}$ = (2, 2, 2, 2, 2, 2) is a food source that, under the current number of iterations, is the solution with the highest fitness value in the population. As shown in Figure 7, these food sources are considered parents, and all of them are subjected to two-by-two crossover operations to produce offspring. In this way, the food sources are kept diversified by crossover and mutation operations to solve the problem that the artificial bee colony algorithm easily falls into local optimality.  

Figure 6. Several alternative query plans.

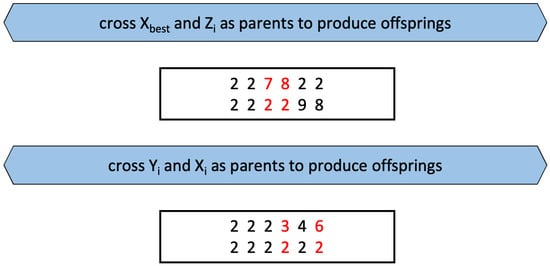
Figure 7. Crossover operation example.

2.3. A Hybrid Model of the Dynamic Artificial Bee Colony Algorithm Combined with Genetic Operators

The hybrid model proposed in this paper (dynamic disturbance artificial bee colony algorithm–genetic operator, DYABC-GO) aims to perform large join queries with less data communication between data sites to reduce the query cost and optimize the distributed database join query. Figure 8 shows the logical flowchart of the overall model, and Algorithm 2 is the logical pseudo-code of the overall model.

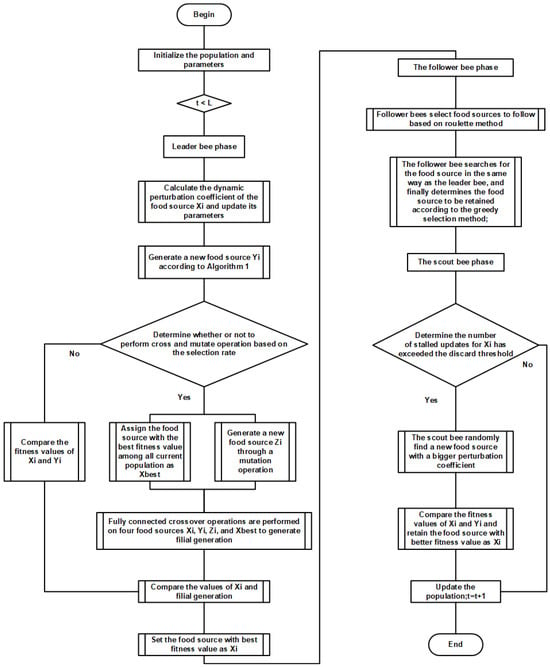
Figure 8. The flowchart of overall algorithm.

2.4. Time and Space Complexity of the Hybrid Model

Time complexity: The DYABC-GO algorithm has a time complexity of O(n${}^2$) for the initialization phase; O(n${}^2$) for the leader bees to search for food sources; O(n) for calculating the fitness values and selecting the food sources according to the greedy method, as well as for calculating the probability of selection of the follower bees; O(n${}^2$) for the follower bees to search for food sources; and O(n) for the scout bee phase. Thus, the total time complexity of the algorithm is O(n${}^2$) + O(n${}^2$) + O(n) + O(n) + O(n${}^2$) + O(n), which can be simplified to O(n${}^2$), or the same as that of the traditional artificial bee colony algorithm.

Space complexity: The DYABC-GO algorithm performs evolutionary search by maintaining a population. The population contains multiple individuals, each of which needs to store a data structure representing the food source or combination of its genes. Therefore, the size of the population storage space is related to the size of the population, the gene lengths of the individuals, and the data structures used. In general, the complexity of the population storage space is O(N · L), where N is the population size and L is the gene length of the individuals.

Algorithm 2 DYABC-GO Logical Pseudo-Code

Input: Data sharding-site matrix (DSM) for query statement and the number of output query plans k Output: Top-k query execution plans and their query execution costs 1: Initialize X${}_i$; set N, P${}_{select}$, P${}_{crossover}$, and P${}_{mutation}$ ▹ Initialize each food source; set the parameters: population size, selection rate, crossover rate, and mutation rate 2: Initialize $\delta$’, L, Limit, t = 1;   ▹ Initialize the perturbation coefficient as well as the maximum number of iterations and the food source abandonment threshold; current number of iterations 3: while t < L do 4:     The leader bee phase: 5:     for i = 0:N do 6:         ${\eta }_i$← Equation (3) [X${}_i$] and search X${}_i$;    ▹ Assign a leader bee to food source X${}_i$ and calculate the dynamic perturbation factor ${\eta }_i$ for food source X${}_i$ according to Equation (4) 7:         Recalculate perturbation coefficient, selection rate, crossover rate, and mutation rate based on dynamic perturbation factor ${\eta }_i$; 8:         Y${}_i$← a new food source;    ▹ Generate a new food source Y${}_i$ according to Algorithm 1 9:         Determine whether or not to perform cross and mutate operation based on the selection rate; if yes, proceed to step 10, otherwise go directly to step 13; 10:         X${}_i$← Mutation(X${}_i$); ▹ Food source X${}_i$ generates a new food source Z${}_i$ through a mutation operation 11:         X${}_{best}$← best food source; ▹ Assign the food source with the best fitness value among all current populations as X${}_{best}$ 12:         12 new food sources ← Crossover (X${}_i$, Y${}_i$, Z${}_i$, X${}_{best}$); ▹ Fully connected crossover operations are performed on four food sources, X${}_i$, Y${}_i$, Z${}_i$, and X${}_{best}$, to generate 12 new food sources and calculate their fitness values 13:         X${}_i$← best food source of 12 new food sources; ▹ Assign the food source with best fitness value as X${}_i$ according to the greedy selection method 14:         The scout bee phase: 15:         if The number of times of stalled update for X${}_i$ > Limit then 16:            Scout bee ← Leader bee; ▹ The corresponding leader bee become a scout bee, and the scout bee randomly finds a new food source according to Equation (7) 17:         else 18:            Go to step 21; 19:         end if 20:     end for 21:     The follower bee phase: 22:     for i = 0:N do 23:         Calculate the probability that a food source is followed in the population by Equation (6); 24:         The follower bee selects a food source according to the roulette method, searches for it in the same way as the leader bee, and finally determines the food source to be retained according to the greedy selection method; 25:         t = t + 1; 26:     end for 27: end while 28: return Top-k optimal solutions

3. Experiment Results and Analysis

3.1. Experimental Parameters and Data

In order to verify the effectiveness of the method proposed in this paper, experiments were conducted on a computer with CPU core i5 and 4G memory capacity. Using this method in comparison with other algorithms, the simulation dataset consists of six query statements involving up to 200 data sites, and the query length involves up to 85 data shardings [37]. DYABC-GO is the dynamic artificial bee colony algorithm incorporating genetic operators proposed in this paper; DYABC is the artificial bee colony algorithm that only introduces a dynamic perturbation factor; ABC-GO is the artificial bee colony algorithm that only incorporates a genetic manipulation operator; GA is the genetic algorithm; and ABC is the traditional artificial bee colony algorithm. The algorithm’s initialization parameters are set as shown in Table 3:

Table 3. Experimental parameters.

Argument\Method	DYABC-GO	DYABC	ABC-GO	ABC	GA
Maximum iterations	400
Population size	Data sharding quantity/2
Leader bee population	Data sharding quantity/2				/
Follower bee population	Data sharding quantity/2				/
Food source abandonment threshold	5				/
Perturbation coefficient	0.25				/
Selection rate	0.5			/	0.5
Crossover rate	0.25			/	0.25
Mutation rate	0.1			/	0.1

3.2. Results and Discussion

Figure 9 shows the Top-1 optimal query plan execution cost obtained by this method and other comparative methods in the cases involving S = 100, 150, 200 data sites and DS = 55, 85 data shardings. From the figure, it can be seen that, as the number of sites and the number of data shardings involved in the query increase, the query execution cost also increases. In contrast, the increase in the number of data shardings has more impact on the query execution cost. According to the results, the optimal query plan generated by the DYABC-GO algorithm and ABC-GO have a smaller query cost compared to the other comparative algorithms. The optimal query plans produced by these two algorithms are very close in cost for join queries with low dimensionality. However, when faced with higher dimensional join queries, DYABC-GO produces a more significant reduction in the cost of the query execution plan. Therefore, the DYABC-GO algorithm is able to produce a better quality Top-1 query execution plan than other algorithms.

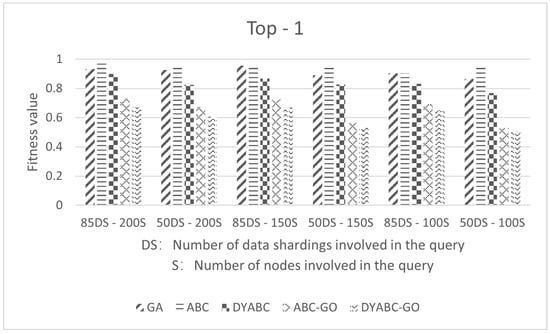
Figure 9. The Top-1 optimal query plan execution cost.

Figure 10 and Figure 11 show the average execution cost of the final Top-10 and Top-20 query plans involving S = 100, 150, 200 data sites and DS = 55, 85 data shardings. As can be seen from the figures, the average execution cost of the Top-10 and Top-20 query plans generated by DYABC-GO is still better than that of other algorithms. In the DSM matrices of 85 × 200, 50 × 200, 85 × 150, and 50 × 150, the average execution cost of Top-1, Top-10, and Top-20 generated by DYABC-GO are the same, which indicates that the proposed method has almost completely converged within the number of iterations, further proving that the proposed method in this paper is able to generate better quality query plans and improve the query efficiency.

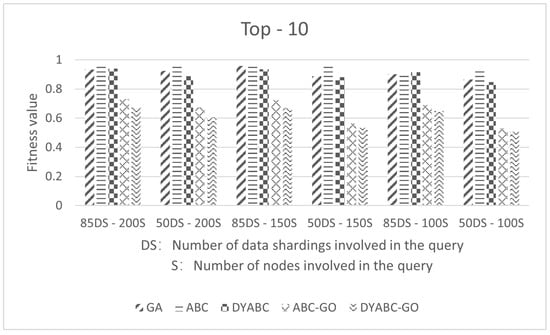
Figure 10. The average execution cost of the final Top-10 query plans.

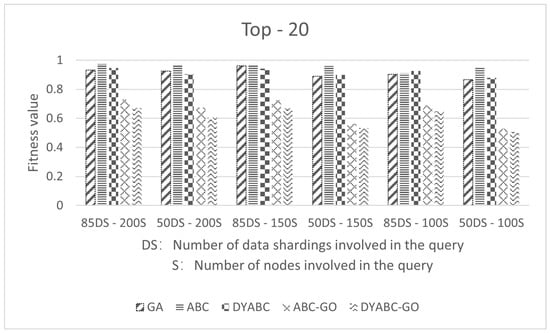
Figure 11. The average execution cost of the final Top-20 query plans.

Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show the comparison of the iterative convergence efficiency of the algorithms in cases involving different numbers of sites and data shardings. As shown in the figures, GA and ABC always plateau early in the iteration and have difficulty converging further in subsequent iterations. Since GA and ABC use traditional search strategies, and since the query optimization problem addressed in this paper is to find the execution plan with the highest concentration of sites, this leads to a very poor optimization performance of these two methods in the face of the spaceless conceptual problem, equivalent to blindly evolving randomly at each iteration instead of evolving in a better direction. According to the results, the model convergence speeds of DYABC-GO and ABC-GO are much faster than the other methods, which proves the effectiveness of the optimization search strategy of the new artificial bee colony algorithm proposed in this paper.

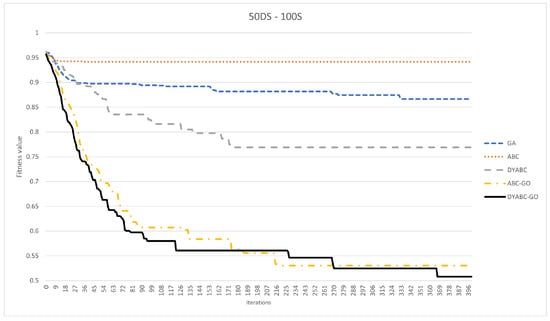
Figure 12. The iterative convergence efficiency of each method when DSM is 50 × 100.

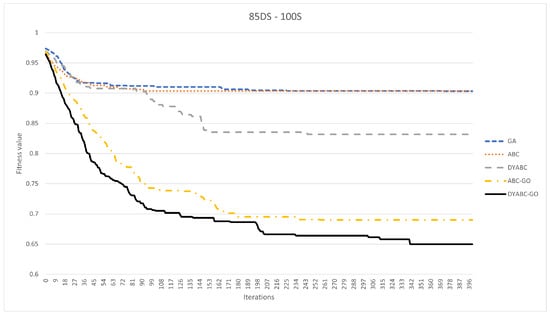
Figure 13. The iterative convergence efficiency of each method when DSM is 85 × 100.

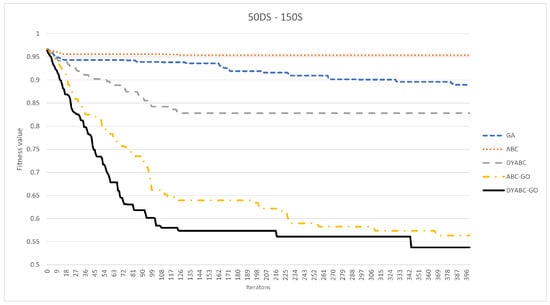
Figure 14. The iterative convergence efficiency of each method when DSM is 50 × 150.

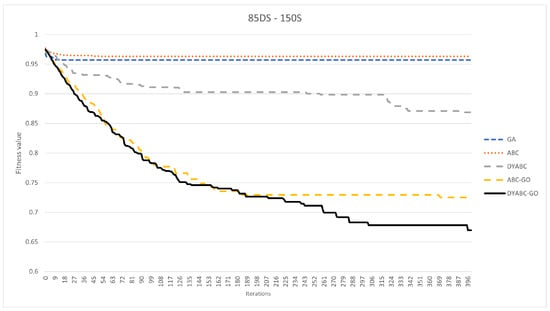
Figure 15. The iterative convergence efficiency of each method when DSM is 85 × 150.

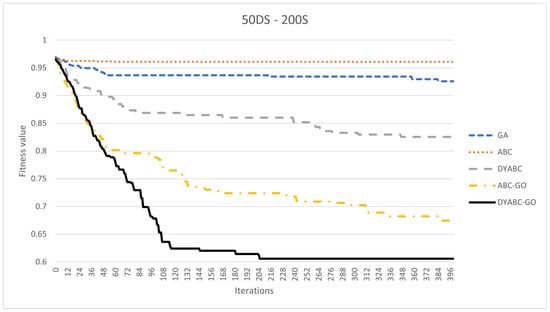
Figure 16. The iterative convergence efficiency of each method when DSM is 50 × 200.

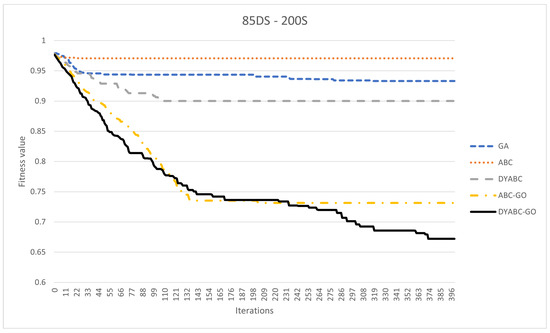
Figure 17. The iterative convergence efficiency of each method when DSM is 85 × 200.

DYABC has a better convergence speed than GA and ABC and has a certain probability of jumping out of the local optimum in subsequent iterations. However, it is difficult to maintain the diversity of the population, which means that the final convergence of the algorithm is not ideal. DYABC is the method that uses a dynamic perturbation operator without incorporating genetic operators. Thus, it can be found that this method is very prone to premature maturation, although it can evolve populations in a more optimal direction. DYABC-GO and ABC-GO are two methods that combined with selection, crossover, and mutation operations of the genetic algorithm. According to the results, these two approaches end up generating query plans with a lower execution cost, which proves that the combination of selection, crossover, and mutation operations of the genetic algorithm can increase the diversity of the population and improve the global search capability of the overall algorithm, preventing the algorithm from falling into the local optimum.

Although both DYABC-GO and ABC-GO have efficient convergence speeds, in the later iterations of the algorithm, DYABC-GO can generate plans with better fitness values than ABC-GO, thus proving that the introduction of dynamic perturbation factors can enhance the local search ability of the algorithm in the later stages. The use of smaller perturbation coefficients in the later stages of the algorithm when the skillfulness of the algorithm is more mature can enhance the convergence effect more effectively.

Figure 18 demonstrates the experimental results of the cost of the optimal execution plan between the present method and recently published related methods. Figure 19 shows the execution time of each algorithm. In Figure 18 and Figure 19, MACGA is the multi-ant colony genetic algorithm [29], and DEGA is the adaptive genetic algorithm based on double entropy [31]. As the figures show, compared to the other two methods, the proposed method in this paper is able to find less costly execution plans for queries of different lengths and with the same iteration limitations. However, DYABC-GO and DEGA require more algorithmic execution time.

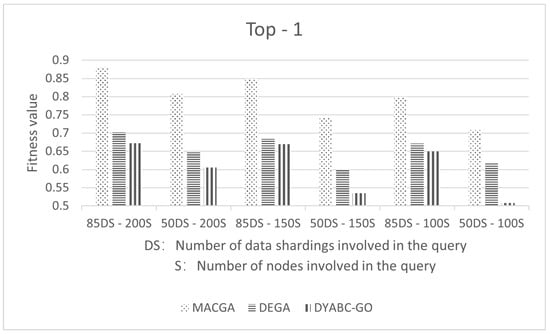
Figure 18. The best query plan execution cost.

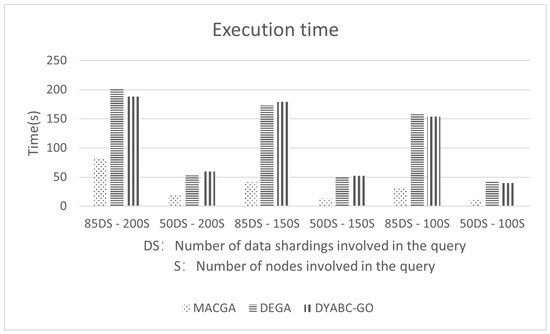
Figure 19. Comparing three algorithms in terms of time metrics.

MACGA is a hybrid algorithm that combines a genetic algorithm and an ant colony algorithm in a serial fashion, wherein the rapid convergence of the genetic algorithm is first used to generate a relatively optimal population, and then the ant colony algorithm is used to further search for the optimal solution. Although this method has a very short execution time and produces less costly query execution plans in the case of shorter join queries, the cost of the resulting execution plans is very high in the face of longer join queries. DEGA introduces two types of entropy into the genetic algorithm to increase the diversity of the population and to prevent the algorithm from falling into a local optimum. This makes the algorithm really effective in the face of high-dimensional connectivity queries but, due to the fact that the entropy value has to be computed for a different individual in each iteration, this makes the algorithm need more execution time and overly maintains the diversity of the population, which makes the algorithm worse in lower connectivity queries. The method proposed in this paper has the possibility to perform crossover and mutation operations during each iteration, which can effectively avoid the problem of the algorithm falling into a local optimum; however, it also increases a certain amount of computation, leading to an increase in execution time. In contrast, although both DYABC-GO and DEGA increase the execution time to a certain extent, the method in this paper introduces a dynamic perturbation factor to achieve better performance in the face of different dimensions of the join query, thus further proving the effectiveness of the method proposed in this paper.

4. Conclusions and Future Work

The query optimization problem for large-scale distributed databases is an NP-hard problem. The complexity of query optimization increases with the increase in the number of data shardings and data nodes involved in the query. In this paper, we solve the distributed database query optimization problem by combining the artificial bee colony algorithm and genetic manipulation operators (e.g., crossover and mutation). We then introduced a dynamic perturbation factor so that the control parameters of each individual in the population change dynamically according to the iteration process and the fitness values of the whole population. With the increase in the number of algorithmic iterations, the whole population keeps converging; then, the use of smaller perturbation coefficients at the later stage of the iteration can improve the optimization effect. Finally, by experimentally comparing the quality of the query execution plans generated under six different dimensional queries, it is proved that the Top-k query execution plan generated by the DYABC-GO algorithm not only has a lower query cost, but also has a higher algorithmic convergence speed, which in turn improves the efficiency of the distributed query optimization.

Although the method proposed in this paper has improved the effectiveness of query optimization, the increase in the complexity of the algorithm has led to an increase in the computational volume of the algorithm, making the running time of the algorithm increase. Therefore, in subsequent work, the optimization algorithm can be executed by parallel computing or heterogeneous computing to improve computational efficiency [38,39]; however, the distribution and integration of tasks in the optimization algorithm need further research. At the same time, in the case of databases deployed in a local area network (LAN), the query optimization also needs to consider local resource scheduling overhead so that the query optimization for a LAN distributed database can be taken as a multi-objective optimization [40,41].