Monte Carlo Sampling of Inverse Problems Based on a Squeeze-and-Excitation Convolutional Neural Network Applied to Ground-Penetrating Radar Crosshole Traveltime: A Numerical Simulation Study
Abstract
1. Introduction
2. Methods
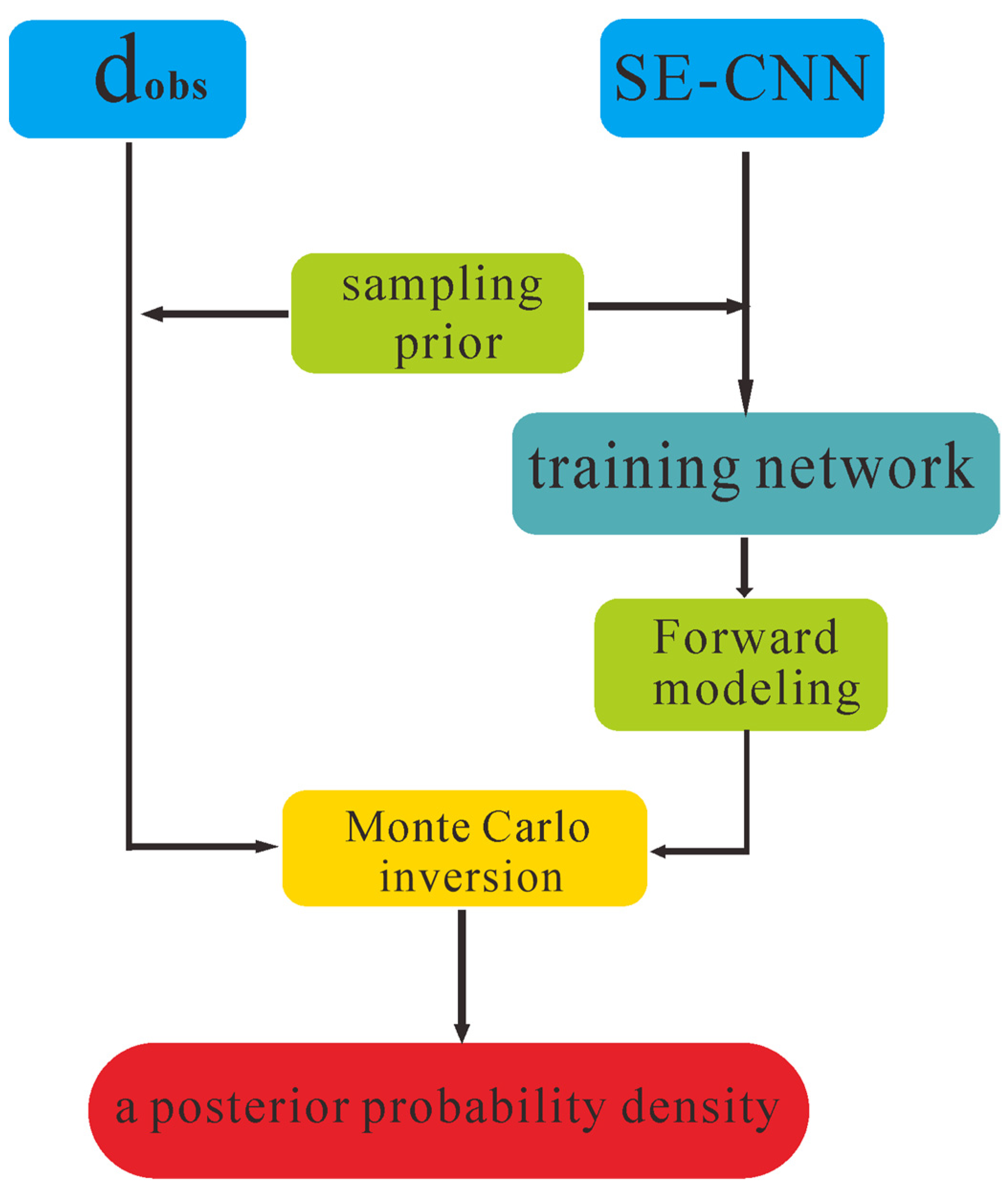
2.1. The Theory of Probability Inversion
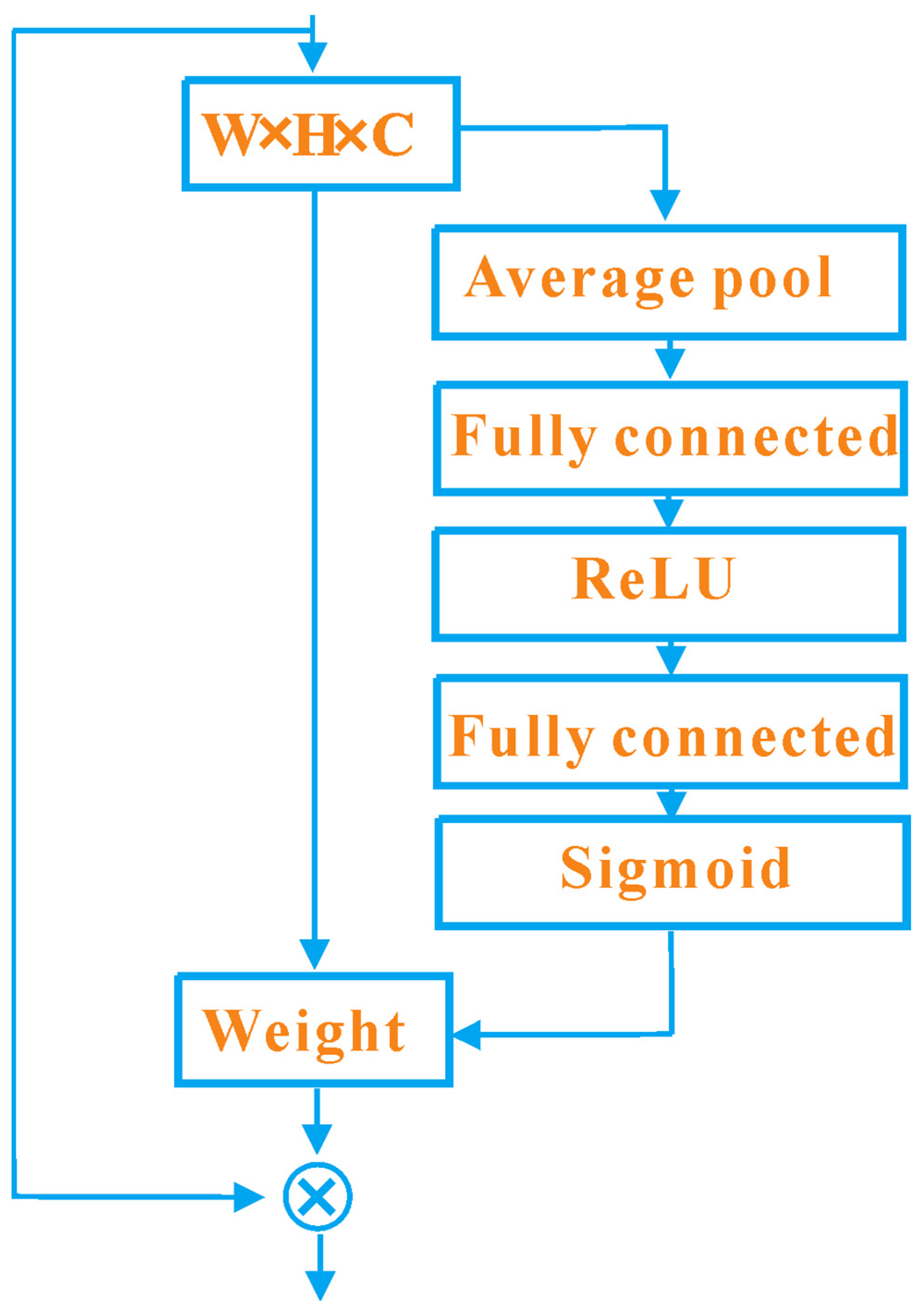
2.2. SE Attention Module
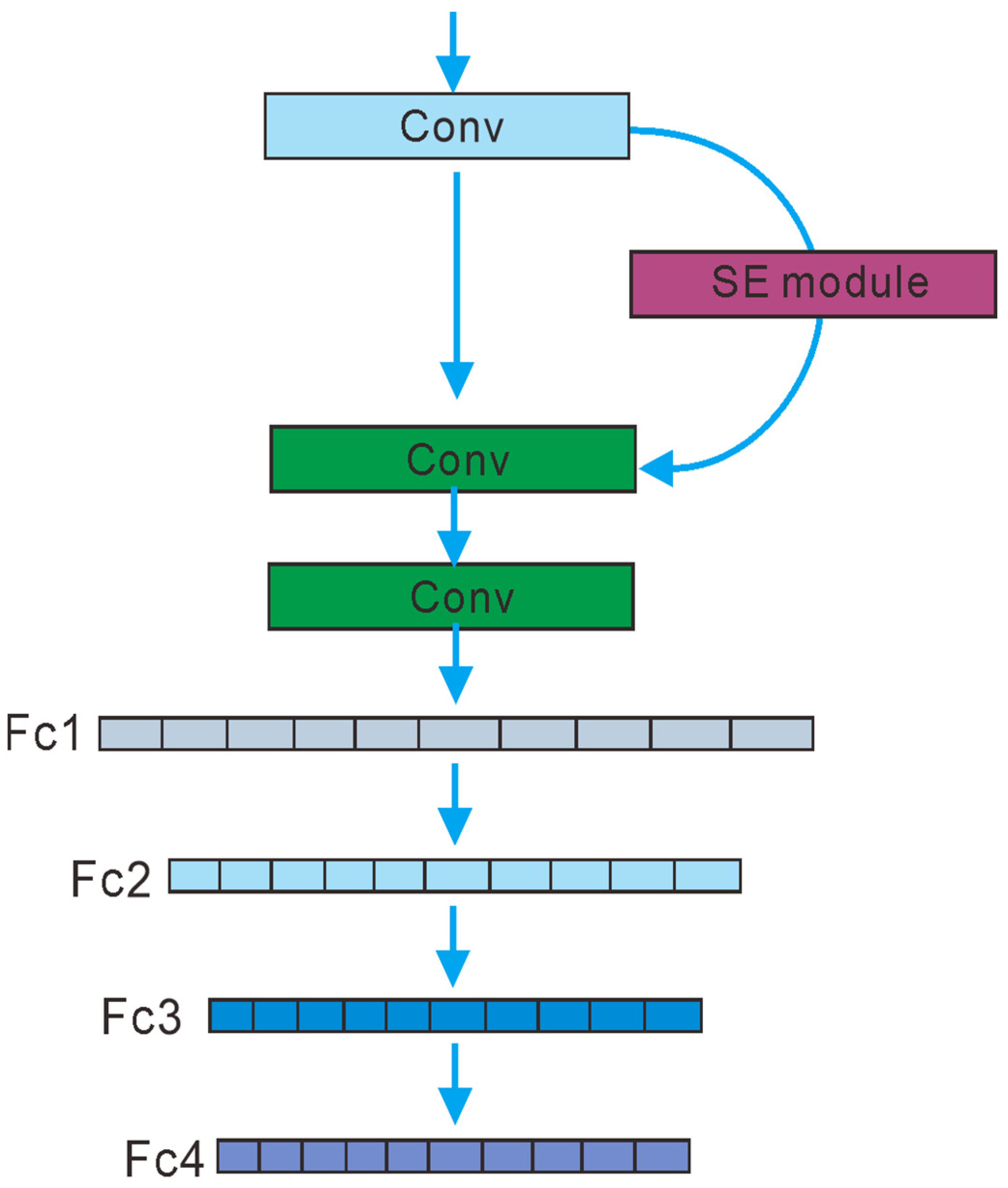
2.3. SE-CNN
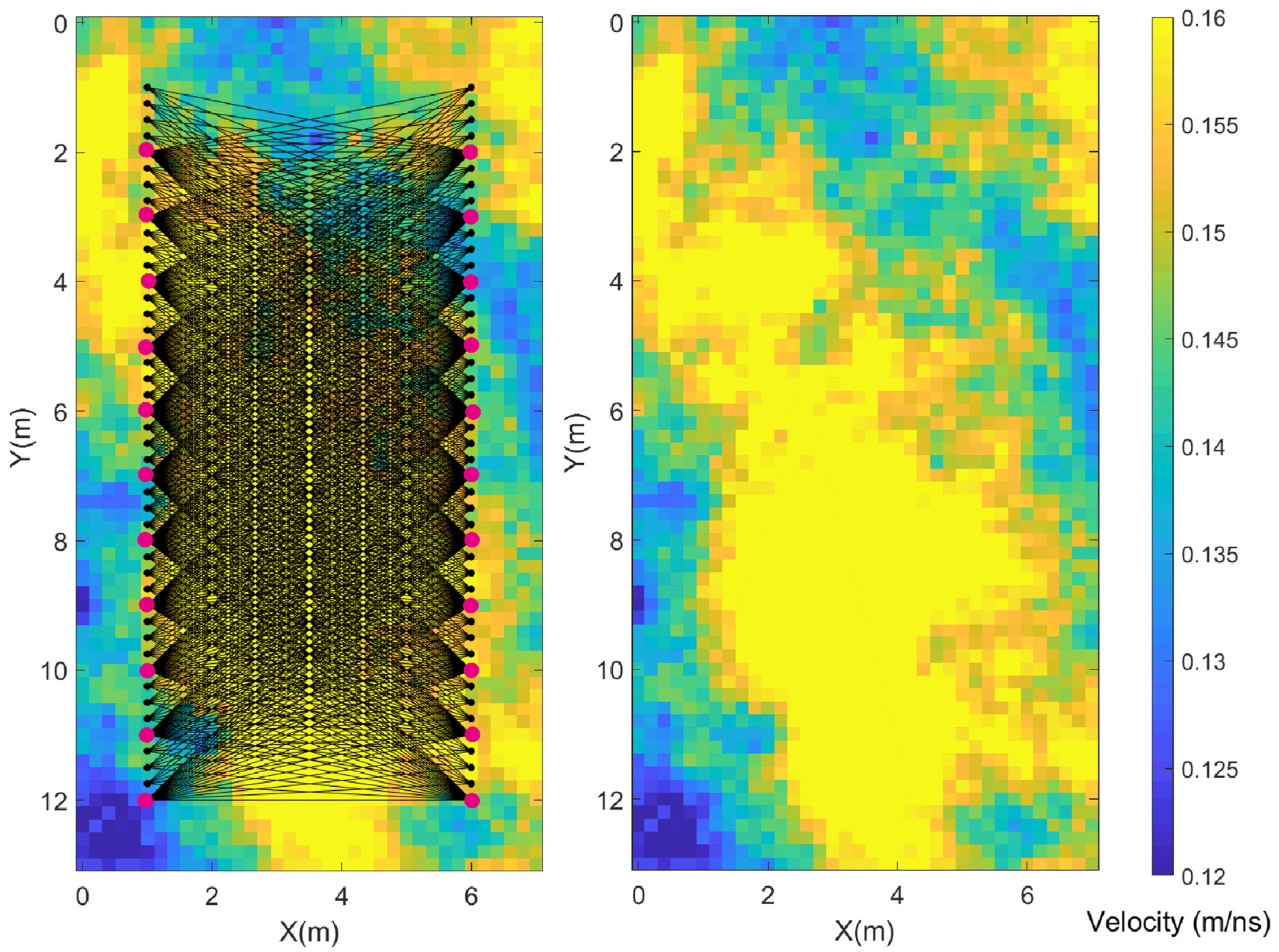
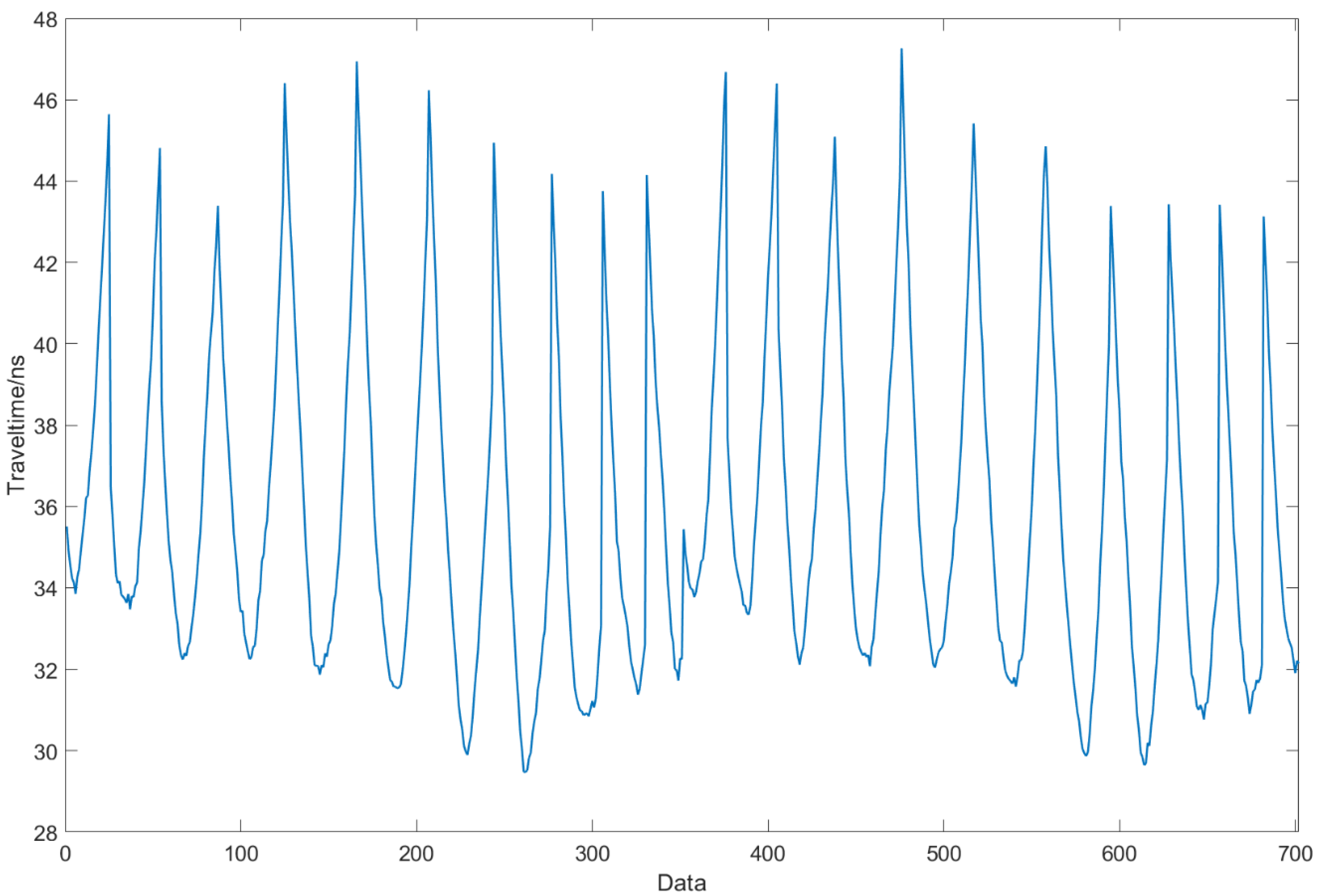
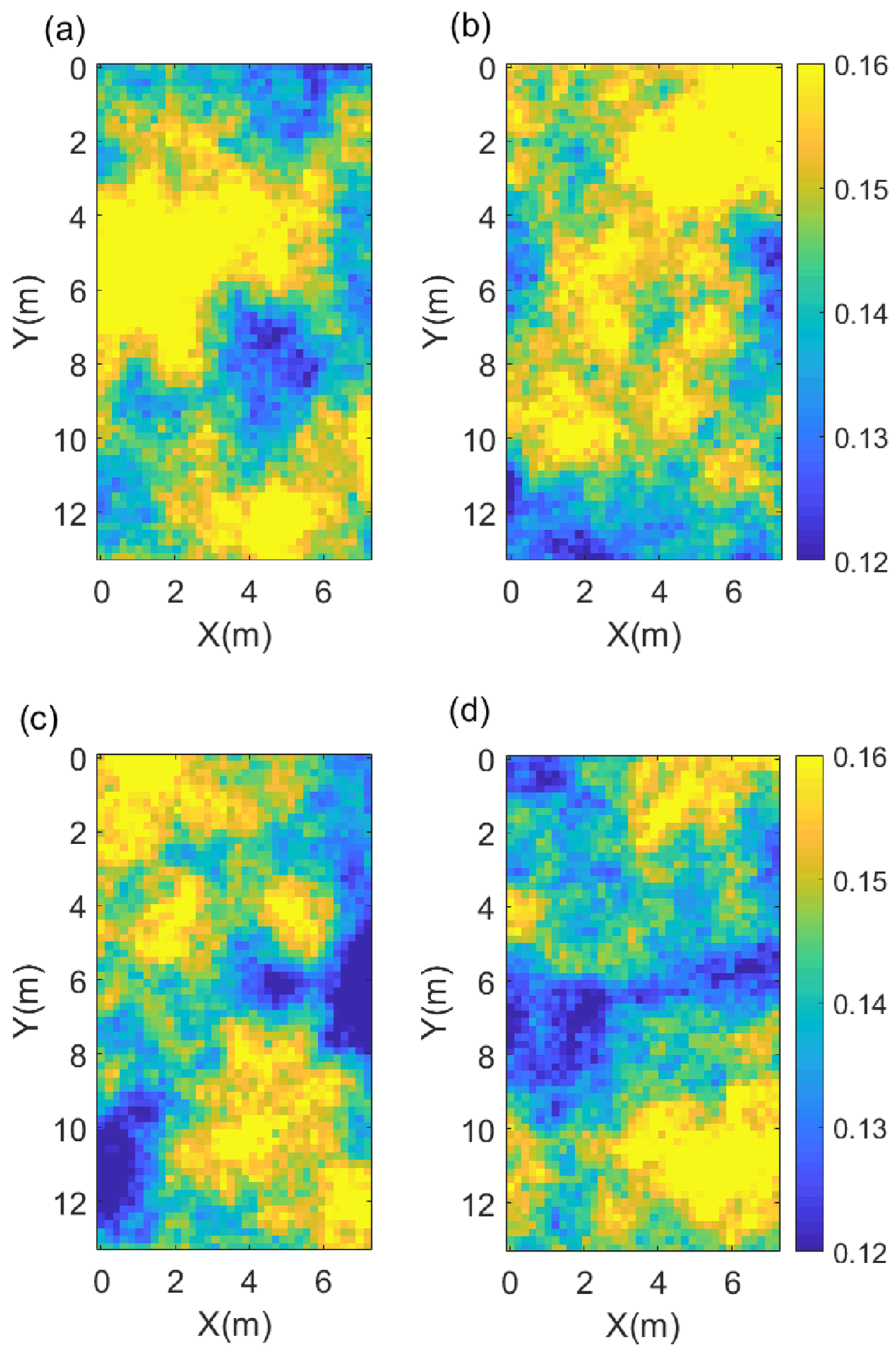
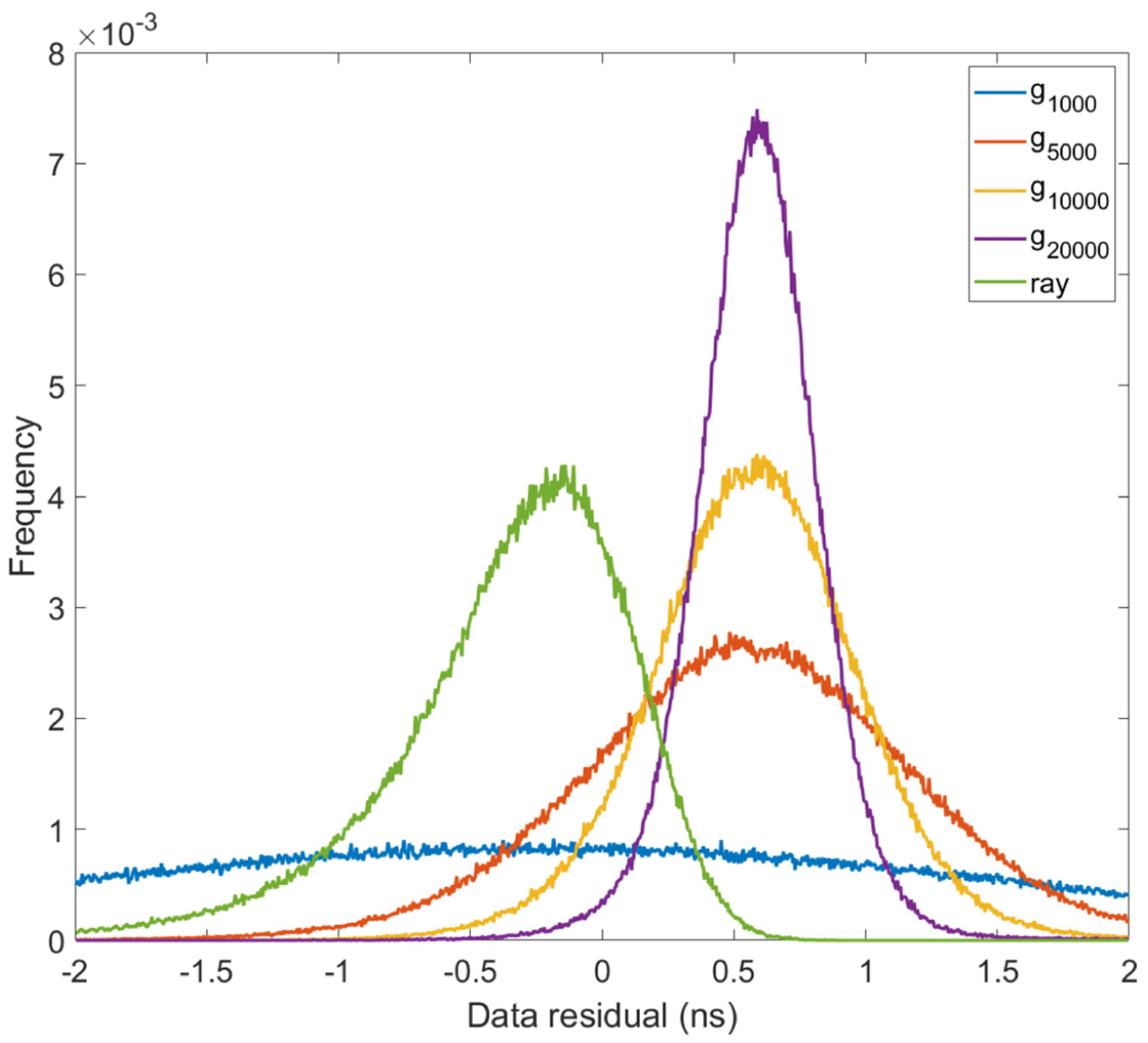
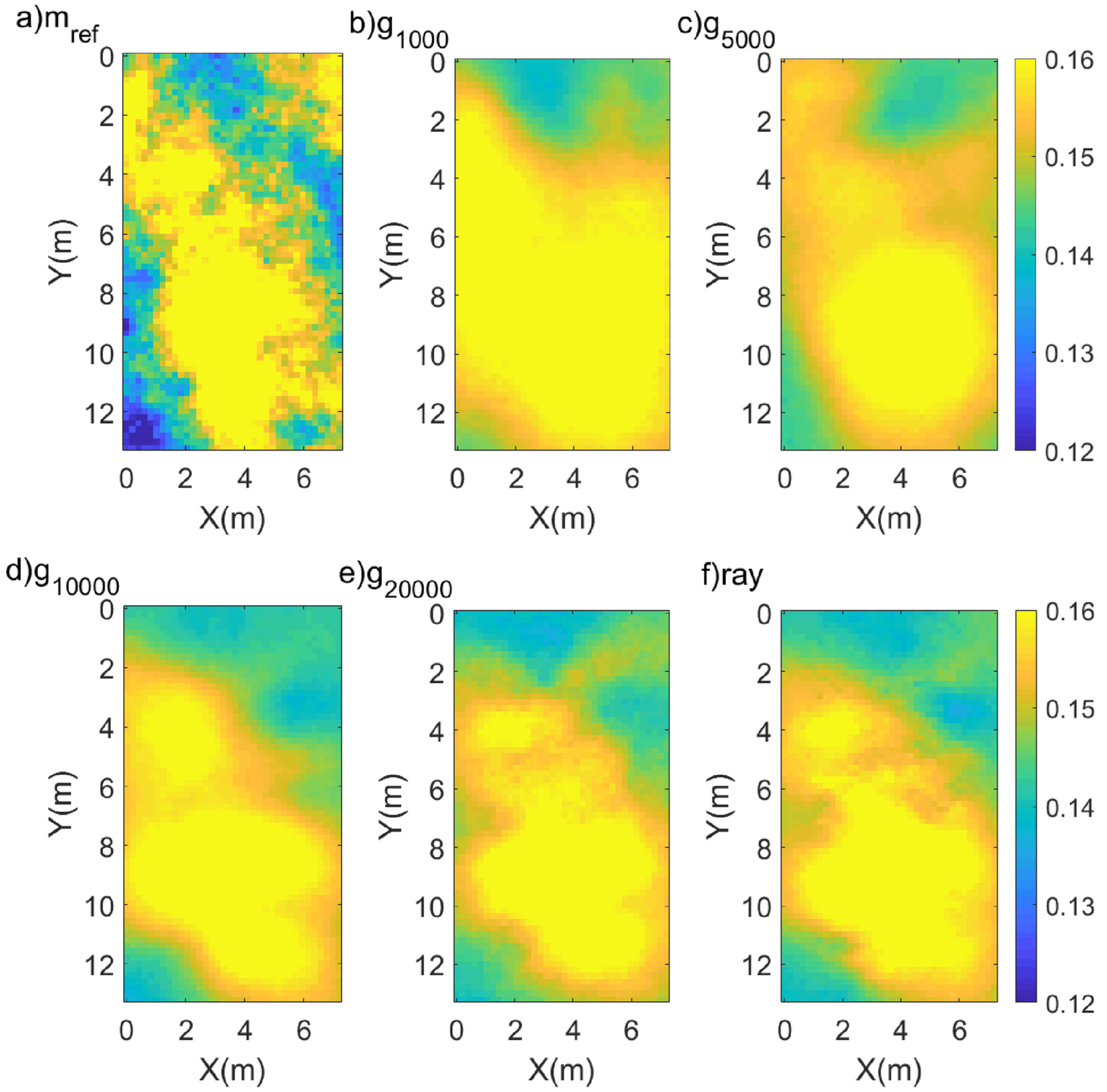
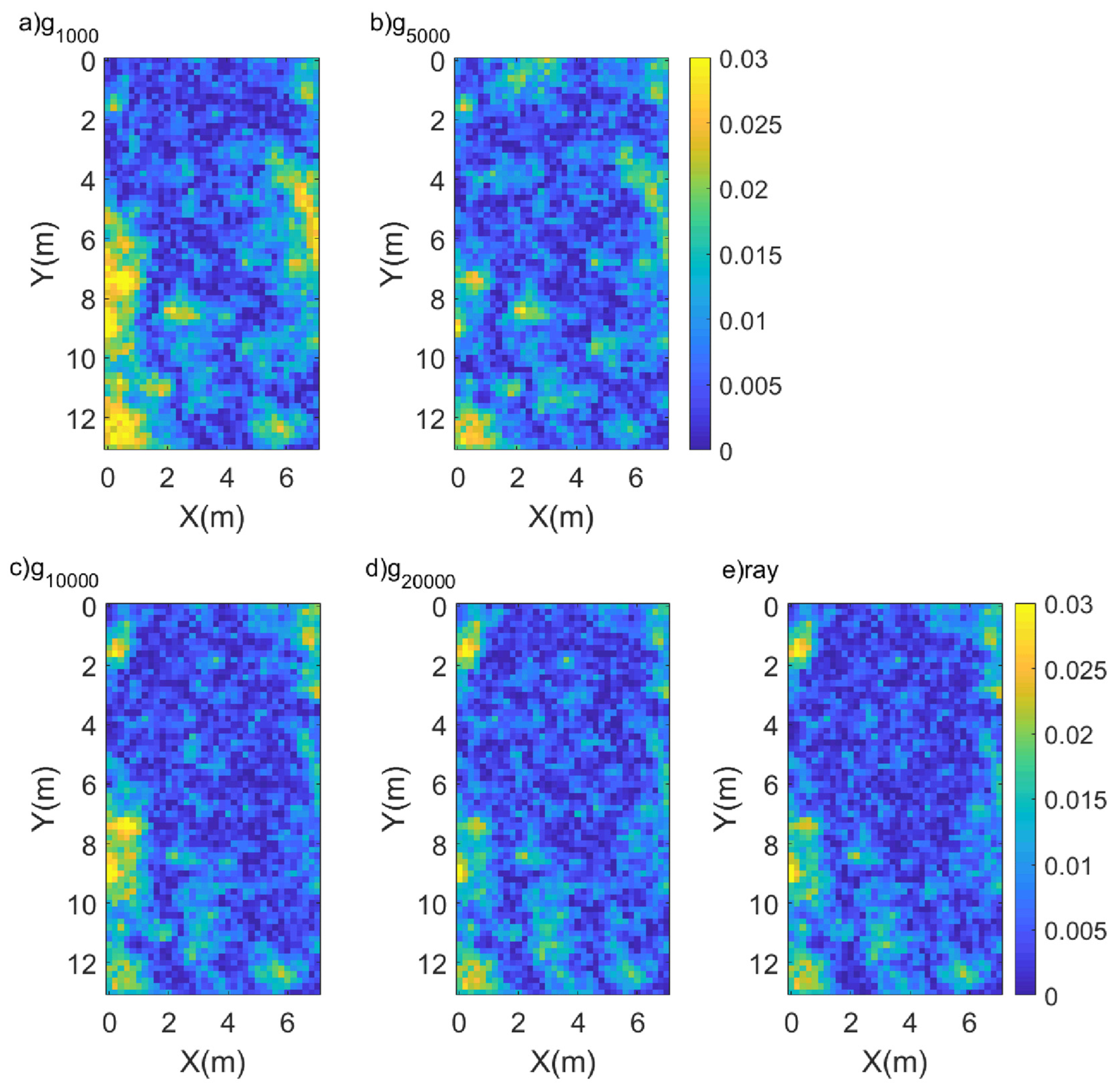
3. Experimental Validation
4. Discussion and Future Work
- (1)
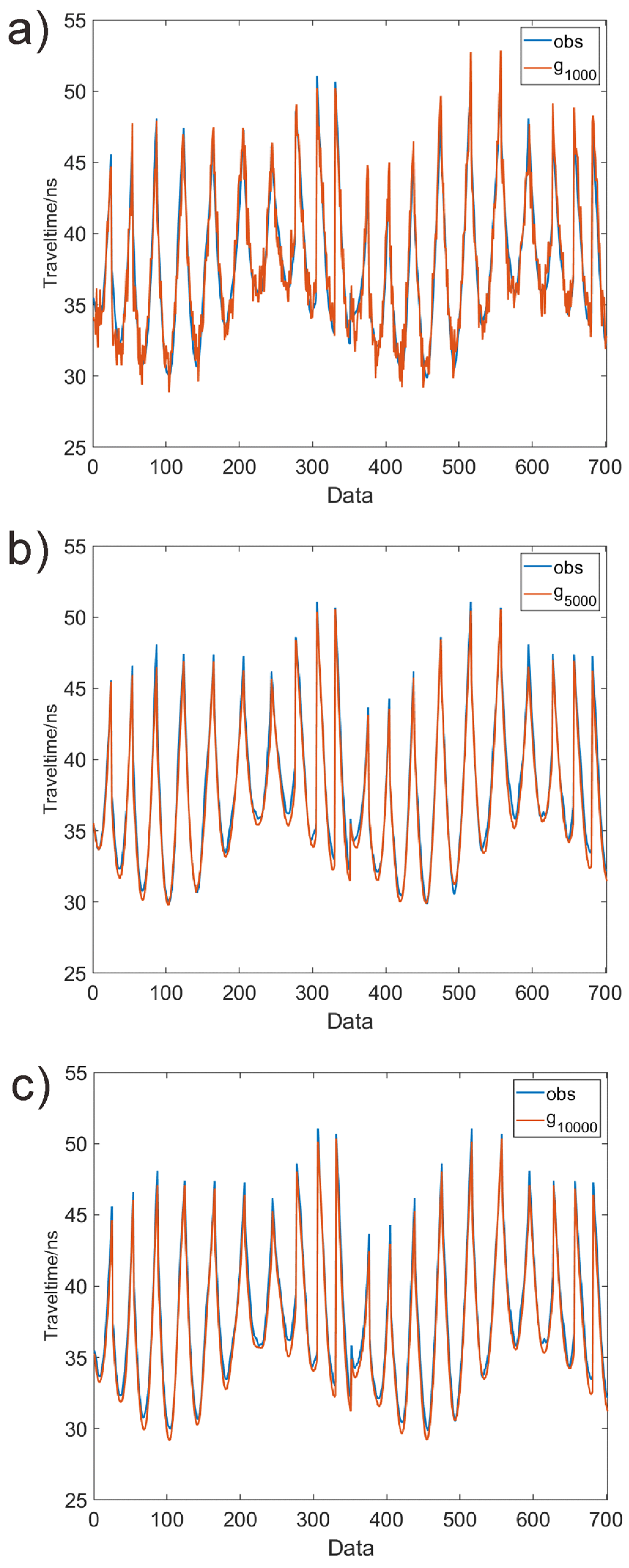
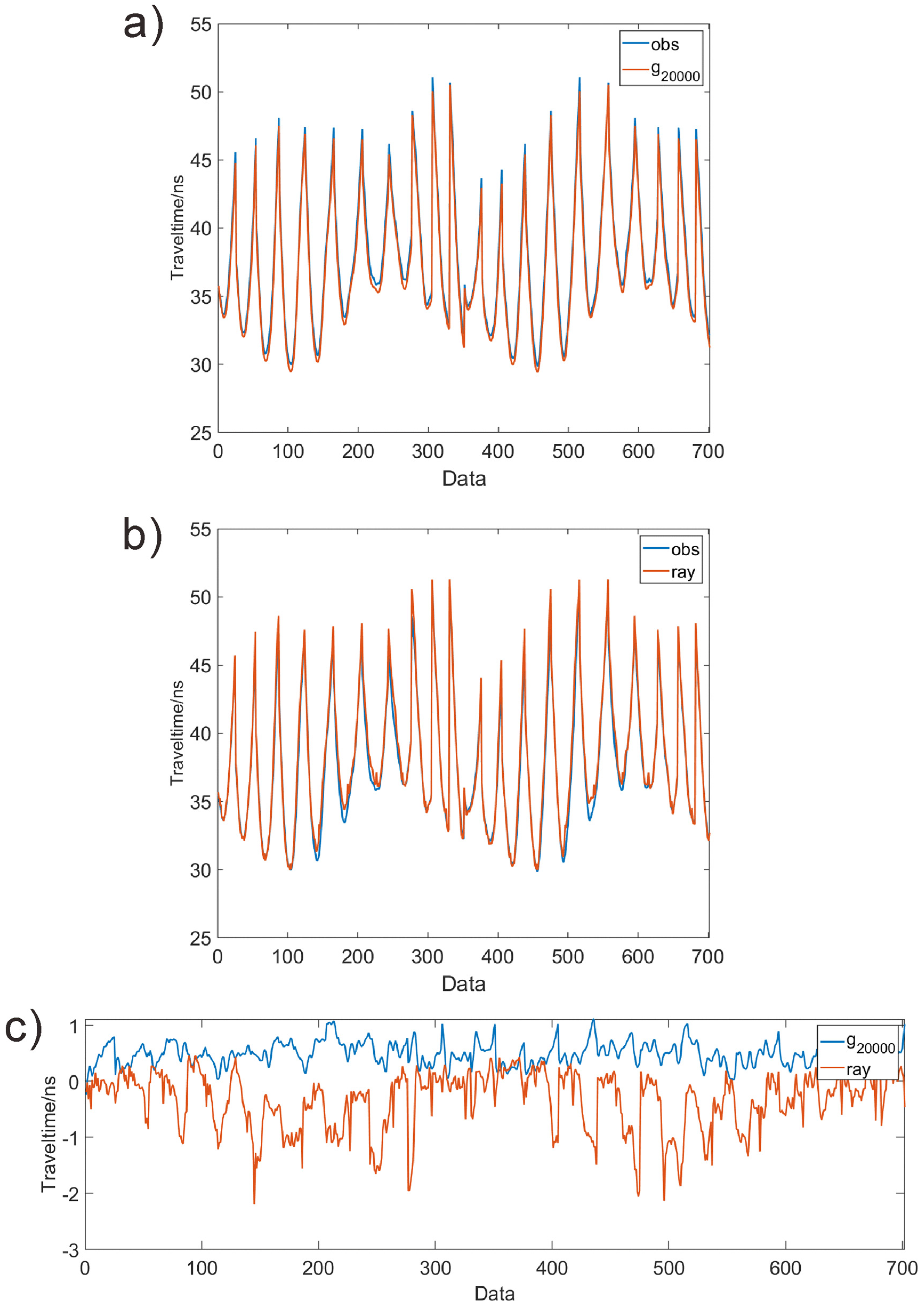
- The advantage of an SE-CNN network is that as the training size increases, the number of model errors gradually decreases. A high-precision forward model can be obtained by increasing the training size. The disadvantage is that as the training size increases, the computational cost also increases. Compared with traditional ray methods, the computational efficiencies of both methods are similar, but the model errors of SE-CNN method are smaller when the training size exceeds 20,000.
- (2)
- At present, the methods of using neural networks for MCMC inversion mainly focus on processing simulated data. The field data quality may not be ideal due to factors such as terrain, geometry systems, and noise. The targeted optimization of network structures is needed. To achieve the application conditions of field data, a large number of field cases need to be analyzed and tested, and this endeavor is a challenge to be addressed in our future research work.
- (3)
- The attention modules used in this article are SE attention modules. Currently, with the development of neural networks, various attention modules have sequentially emerged. We can try to introduce more types of attention modules into the network model and test their effectiveness. In response to the MCMC inversion problem, the introduction of attention modules not only improves the accuracy of the network but also ensures that the neural network maintains high computational efficiency. Therefore, the design of attention modules and network structures is very important and will be one of the focuses of future research.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Daniels, D. Ground Penetrating Radar, 2nd ed.; IEE: London, UK, 2004. [Google Scholar]
- Giannopoulos, A. Modelling ground penetrating radar by GprMax. Construct. Building Mater. 2005, 19, 755–762. [Google Scholar] [CrossRef]
- Meles, G.; Greenhalgh, S.; der Kruk, J.V.; Green, A.; Maurer, H. Taming the non-linearity problem in GPR full-waveform inversion for high contrast media. J. Appl. Geophys. 2012, 78, 31–43. [Google Scholar] [CrossRef]
- Liu, S.; Lei, L.; Fu, L.; Wu, J. Application of pre-stack reverse time migration based on FWI velocity estimation to ground penetrating radar data. J. Appl. Geophys. 2014, 107, 1–7. [Google Scholar] [CrossRef]
- Xue, M. Inversion of Common Offset Ground Penetrating Radar Data Based on Ray Theory. Master’s Thesis, Jilin University, Changchun, China, 2021. [Google Scholar]
- Zhou, H.; Chen, H.; Li, Q.; Wang, J.; Zhang, Q. Ground Penetrating Radar Waveform Inversion Method without Extracting Excitation Pulses. J. Geophys. 2014, 57, 1968–1976. [Google Scholar]
- Yang, F.; Du, C.; Liang, Y.; Xu, X. Simulation of Metal Mining Exploration Based on Ground Penetrating Radar Wave Velocity Tomography. Prog. Geophys. 2014, 29, 1332–1336. [Google Scholar]
- Meincke, P. Linear GPR conversion for loose soil and a planar air soil interface. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2713–2721. [Google Scholar] [CrossRef]
- Mosegaard, K.; Tarantola, A. Monte Carlo sampling of solutions to inverse problems. J. Geophys. Res. 1995, 100, 431–447. [Google Scholar] [CrossRef]
- Hansen, T.M.; Mosegaard, K.; Cordua, K.S. Using geostatisticsto describe complex a priori information for inverse problems. In VIII International Geostatistics Congress; Ortiz, J.M., Emery, X., Eds.; Geostatistics; University of Chile: Region Metropolitana, Chile, 2008; Volume 1. [Google Scholar]
- Hansen, T.M.; Mosegaard, K.; Cordua, K.S. Inverse problems with non-trivial priors: Efficient solution through sequential Gibbs sampling: Computational. Geosciences 2012, 16, 593–611. [Google Scholar] [CrossRef]
- Hansen, T.M.; Cordua, K.S.; Jacobsen, B.H.; Mosegaard, K. Accounting for imperfect forward modeling in geophysical inverse problems-exemplified for crosshole tomography. Geophysics 2014, 79, H1–H21. [Google Scholar] [CrossRef]
- Zhao, Y. CNN Based Inversion of Ground Penetrating Radar Data and Automatic Recognition of Road Diseases. Master’s Thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Ji, Y. Research on Dielectric Constant Inversion of Ground Penetrating Radar Images Based on Deep Learning. Master’s Thesis, Shandong University, Ji’nan, China, 2021. [Google Scholar]
- Liu, T.; Su, Y.; Huang, C. Inversion of ground penetrating radar data based on neural networks. Remote Sens. 2018, 10, 730. [Google Scholar] [CrossRef]
- Liu, B.; Ren, Y.; Liu, H.; Xu, H.; Wang, Z.; Cohn, A.G.; Jiang, P. GPRInvNet: Deep learning based ground penetrating radar data conversion for tunnel liners. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8305–8325. [Google Scholar] [CrossRef]
- Hansen, T.M.; Cordua, K.S. Efficient Monte Carlo sampling of inverse problems using a neural network-based forward—Applied to GPR crosshole traveltime inversion. Geophys. J. Int. 2017, 211, 1524–1533. [Google Scholar] [CrossRef]
- Yang, F.; Ma, J. Deep-learning inversion: A next-generation seismic velocity model building methodDL for velocity model building. Geophysics 2019, 84, R583–R599. [Google Scholar] [CrossRef]
- Luo, S.; Ren, Q.; Wang, C.; Song, Q.; Lei, W. GPR time-frequency domain joint electromagnetic inversion method based on deep learning. J. Radio Wave Sci. 2022, 37, 555–567. [Google Scholar]
- Wang, H.; Ouyang, X.; Liu, Q.; Liao, K.; Zhou, L. Structural Feature Detection Method for Ground Penetrating Radar 2D Profile Image Based on Deep Learning. J. Electron. Inf. Technol. 2022, 44, 1284–1294. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2019. [Google Scholar]
- Ba, J.; Mnih, V.; Kavukcuoglu, K. Multiple objectrecognition with visual attention. arXiv 2014, arXiv:1412.7755. [Google Scholar]
- Tarantola, A.; Valette, B. Inverse problems = quest for information. J. Geophys. 1982, 50, 159–170. [Google Scholar]
- Bording, R.P.; Gersztenkorn, A.; Lines, L.R.; Scales, J.A.; Treitel, S. Applications of seismic travel-time tomography. Geophys. J. Int. 1987, 90, 285–303. [Google Scholar] [CrossRef]
- Schuster, G.T.; Quintus-Bosz, A. Wave path eikonal traveltime inversion: Theory. Geophysics 1993, 58, 1314–1323. [Google Scholar] [CrossRef]
- McMechan, G.A. Seismic tomography in boreholes. Geophys. J. Int. 1983, 74, 601–612. [Google Scholar]
- Hansen, T.; Cordua, K.; Looms, M.; Mosegaard, K. SIPPI: A Matlab toolbox for sampling the solution to inverse problems with complex prior information: Part 2, Application to cross hole GPR tomography. Comput. Geosci. 2013, 52, 481–492. [Google Scholar] [CrossRef]
- Ernst, J.; Green, A.; Maurer, H.; Holliger, K. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data. Geophysics 2007, 72, J53–J64. [Google Scholar] [CrossRef]
- Ernst, J.R.; Maurer, H.; Green, A.G.; Holliger, K. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of Maxwell’s equations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2807–2828. [Google Scholar] [CrossRef]
- Cordua, K.S.; Hansen, T.M.; Mosegaard, K. MonteCarlofullwave-form inversion of crosshole GPR data using multiple-point geostatistical a priori information. Geophysics 2012, 77, H19–H31. [Google Scholar] [CrossRef]

| Forward Model | ||||||
|---|---|---|---|---|---|---|
| Calculation Time(s) | 1015.8 | 2.03 | 1.97 | 1.94 | 1.92 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, H.; Liu, C.; Wang, S. Monte Carlo Sampling of Inverse Problems Based on a Squeeze-and-Excitation Convolutional Neural Network Applied to Ground-Penetrating Radar Crosshole Traveltime: A Numerical Simulation Study. Appl. Sci. 2024, 14, 618. https://doi.org/10.3390/app14020618
Qiao H, Liu C, Wang S. Monte Carlo Sampling of Inverse Problems Based on a Squeeze-and-Excitation Convolutional Neural Network Applied to Ground-Penetrating Radar Crosshole Traveltime: A Numerical Simulation Study. Applied Sciences. 2024; 14(2):618. https://doi.org/10.3390/app14020618
Chicago/Turabian StyleQiao, Hanqing, Cai Liu, and Shengchao Wang. 2024. "Monte Carlo Sampling of Inverse Problems Based on a Squeeze-and-Excitation Convolutional Neural Network Applied to Ground-Penetrating Radar Crosshole Traveltime: A Numerical Simulation Study" Applied Sciences 14, no. 2: 618. https://doi.org/10.3390/app14020618
APA StyleQiao, H., Liu, C., & Wang, S. (2024). Monte Carlo Sampling of Inverse Problems Based on a Squeeze-and-Excitation Convolutional Neural Network Applied to Ground-Penetrating Radar Crosshole Traveltime: A Numerical Simulation Study. Applied Sciences, 14(2), 618. https://doi.org/10.3390/app14020618





