Abstract
This paper deals with the design of a calibration device for measuring the residual torque of the vehicle brake. It informs about the problems and purpose of the brakes, requirements placed on the brake system, and the design of vehicle brake systems. The practical part of the research contains the design of four versions of the calibration device and the 3D model of the proposed calibration device. There is also a new calibration methodology and calculation of the theoretical fault of the calibration device. An analysis and comparison of the original and new torque sensor calibration methods are presented at the end of this paper. By comparing the original and new calibration methods, it was revealed that the deviations from the required torque value compared to the original calibration version decreased from an average value of 0.154 Nm to 0.0047 Nm, and the variance of the measured values decreased on average from 0.00276 Nm to 2.07 × 10−6 Nm. The proposed new torque sensor calibration method has shown a positive contribution to the accuracy of torque sensor calibration, which as a result will significantly increase the reliability and accuracy of measuring the residual torque of automobile brakes and shorten the measurement time.
1. Introduction
More than 130 years have passed since the world’s first car with a gasoline engine was produced. Whether it was a car of the distant past or the cars of today, they all need to stop at the right time and in the right place, which requires brakes. Constantly increasing demands for ecological and environmental sustainability have increased the demands for the operation of cars and, ultimately, for the brakes themselves. The current trend is to reduce fuel consumption as much as possible, influence the amount of emissions from the combustion of hydrocarbon fuels, and reduce the particle of matter emissions from the wear of brake friction materials and vehicle tires. As stated [1], particulate matter (PM) is one of the world’s most problematic pollutants in terms of harm to the environment and human health. Brake dust emissions represent on average 21% of PM emissions in the air, while their share increases near the edges of roads and at intersections, or other places where it is necessary to adjust the traffic speed [2,3,4,5,6]. The statistics show that motor vehicle exhaust emissions have a decreasing trend, while the amount of non-exhaust emissions gradually increases [7,8,9,10]. Several tests demonstrated that PM emissions significantly increased at the brake temperature of 130 °C and higher during long-term or intensive braking [11]. With the increasing dimensions of cars, the increasing weight of vehicles, and the increasing payloads of vehicles, there is a higher production of PM emissions. The amount of these emissions also affects the technical condition of vehicles, or their braking systems [12]. A lot of research work has been conducted on the production and distribution of brake particulate matter [13]. Based on PM size distribution from brake wear, 84% of total PM emissions are considered as PM1, i.e., smaller than 1 μm [1,14]. Kukutschova et al. [15] report that minimal knowledge about the morphology, chemical composition, and toxicity of nano- and micro-sized particles released from automotive brakes is alarming due to the fact that brake manufacturers are currently not required to develop eco-friendly formulations, particularly when over 70% of the U.S. and only a slightly smaller amount of European brake linings are being imported, which makes it more difficult to control all aspects of these imported brake linings. The authors of refs. [16,17] pointed out that the different kinds of friction materials, LM, SM, and NAO, behave differently considering the differences that can be observed in the friction layer’s morphology, resulting from the different wear mechanisms.
Apart from PM, squeal is another harmful effect of the operation of a brake system. Squeal is generated due to the contact of the friction couple during braking and with the related high frequency of the vibration of the brake system components [18]. However, there are many cases, in which the residual torque after braking leads to unpleasant noise, which is given off during vehicle movement [19,20]. This residual torque not only causes squeals but also negatively contributes to the drag [21,22,23].
Based on the facts described above, there are efforts to minimize the residual torque of the brake system of vehicles. The issue is to determine the value of this residual torque. It is possible to find it experimentally by means of a suitable calibration device [24,25].
In all cases, a strict relationship exists between the composition of the friction layer forming on the mating surfaces and the composition of the emitted particles. The residual torque of the brake plays a significant role in this issue. This is the torque that is created by the contact of the brake element with the disc after the brake is released. For the measurement results of this torque to be as accurate as possible, it is necessary to ensure the high accuracy of the entire measuring device, especially the torque sensor. For the values measured by the sensor to be as accurate as possible, it is necessary to calibrate it at regular intervals and verify its correctness and function with a suitable calibration device. Such a device is equipped with a torque sensor and other needed components [26,27,28]. The designed device is detailed as described below. This issue is currently highly relevant due to the upcoming arrival of the latest emission standard, EURO 7, in 2026, which will regulate emissions from brakes and tires for the first time.
2. Brake System
The brake system is one of the most important parts of the vehicle in terms of active safety. The main brake systems of road vehicles [29,30,31] and rail vehicles [32,33,34] work on the friction principle when friction couples are in contact and generate brake force. These systems contain friction parts, whose main tasks are to slow down the vehicle, stop it, as well as secure the stationary vehicle from starting on its own. A system consists of brake and control mechanisms and is based on criteria such as the purpose of use, energy source, braking force transmission, and the control mechanism. Brake systems are divided into four main groups:
- Service brakes, the main feature of which is foot control. During operation, they must act on all vehicle wheels and vehicle sets and their effect must be variable. They must ensure a reduction in speed or a complete stop of the vehicle while maintaining the desired direction.
- Emergency brakes, which, unlike service brakes, do not have to act on every single wheel of the vehicle or set of vehicles. In case of failure, they replace the service brakes, and it is important that they act on at least one wheel on each side. Emergency brakes often work with less effect than service brakes.
- Parking brakes, the main task of which is to prevent a stationary vehicle from moving off a slope even if there is no driver in the vehicle.
- Auxiliary brakes, which are characterized by maintaining a constant speed of the vehicle, but also by reducing it. In this way, they increase the effect of the service brake while lightening it, thereby extending its service life [35].
2.1. Types of Brake Systems
Two basic types of brake systems are used in today’s cars, which differ in their construction and have their own advantages and disadvantages:
- Drum brakes—use drum-shaped housing where the brake shoes are pressed against the inner surface to create friction. They are durable and cost-effective for rear wheels.
- Disc brakes—use a disc-shaped rotor that rotates with the wheel and the brake pads press against it to brake. Due to better heat dissipation and stopping power, they are usually used in front-wheel and high-performance vehicles.
The advantages and disadvantages of this solution are introduced in Table 1.

Table 1.
The advantages and disadvantages of drum brakes and disc brakes [36].
Another criterion for the division of brake systems involves the method of their control. According to this criterion, brake systems are divided into conventional brake systems and electronic brake systems. Conventional braking systems are controlled by the driver’s power, while the driver not only determines the magnitude of the braking pressure with his foot but also the magnitude of the braking moments on the wheels of the car. The force of the driver creates hydraulic pressure in the master brake cylinder, which is transmitted to the wheel brakes with the help of brake fluid. In most light commercial vehicles and passenger cars, this hydraulic pressure is increased by means of a brake booster. The basic essence of generating braking force in electronic braking systems is based on the same principle as in conventional braking systems. The difference lies in the so-called “intelligent braking”, where the braking effect is achieved through hydraulic and electronic parts of the system [35]. The use of intelligent braking and electronic safety elements using the brake system leads to much more frequent braking and, thus, longer periods of contact between the lining and the friction surface of the brake disc compared to conventional braking. The result is greater wear of the friction material. Therefore, the development is directed toward the optimization of brake systems and their parts, as well as the increase in energy recuperation [37,38,39]. The most common types of brake systems used in passenger cars are direct-acting fluid brakes. These brakes are based on Pascal’s law, which refers to the uniform spread of pressure in liquids in all possible directions. The rule applies that pressure in a liquid propagates at the speed of sound. With this rule, the braking start-up time and the braking distance itself will be shortened. An important property of the working fluid is its incompressibility at normal pressures in the system. Equalizing and distribution devices, which are necessary for mechanical brakes, can be replaced with working fluid. Fluid brakes consist of the brake pedal, brake master cylinder, brake booster, pipe system, brake caliper with brake rollers, and brake effect limiter.
The main principle of braking is the creation of a braking force by means of friction, which causes the kinetic energy of the vehicle to be hindered. With disc brakes (which are the most widely used today and which this article deals with), friction is caused by pressing the brake pads against the braking surface of the brake disc using pistons controlled by the pressure of the liquid in the brake system.
Nowadays, several designs of disc brakes are used. These types are distinguished from each other mainly due to the different construction of the brake caliper. The most widespread are disc brakes with fixed calipers (Figure 1) and disc brakes with floating calipers. The advantages and disadvantages of such disc brakes are shown in Table 2.

Figure 1.
Disc brake with a fixed caliper [40].

Table 2.
The advantages and disadvantages of disc brakes.
2.2. Residual Torque
Today, vehicles are subject to strict emission standards that began to be applied as early as 1992 (EURO 1). For this reason, vehicle manufacturers place great emphasis on the gradual reduction of emissions. All periods of validity for individual standards and permissible values for CO and particulate matter (PM) emissions referenced in this article are listed in Table 3, where one can see how significantly they are restricted. Currently, the EURO 7 standard is applied to eliminate the majority of undesirable substances that affect the overall air quality, and for the first time, sets limits for the production of emissions from parts of the vehicle other than the engine, specifically particulate matter emissions from brakes and tires. Brake emissions are in the range of PM10 with a diameter of 10 microns or less, or PM 2.5, which is fine dust with a diameter of 2.5 microns or less [41]. Brake dust production occurs at the greatest extent during braking, but thanks to the residual moment of the brake, it also forms after braking. The residual torque of the brake is created when the pressure in the brake system is released (when the brake pad is still in contact with the brake disc). With a fixed caliper design, this contact is less than that with a floating caliper. This is because the plate with the pistons on both sides is pulled back due to the deformation of the sealing ring and the release of pressure in the system. Backlash due to disc vibrations is minimal in this case. In the construction solution with a floating caliper, it is obvious that the pistons are only on one side. After the pressure is released and due to the deformation of the sealing ring, the brake pad retracts on only one side. The pad, on the other side, is imprinted only by the influence of vibrations and some throwing on the disc. Here, there is significantly greater contact between the brake pad and the disc, which adversely affects the vehicle’s operating parameters. Contact creates increased friction, which, in addition to the formation of brake dust, also leads to increased fuel consumption, which is reflected in increased production of gas emissions.

Table 3.
Development of emission standards [41,42,43].
3. Description of the Measuring Device
The measuring device intended for measuring the residual torque on the disc brake enables the performance of functional static tests of hydraulic brake calipers. It is a fully automated device that is constructed from several electrical, hydraulic, and pneumatic circuits. The device is used for performing tests on hydraulic brakes with fixed or floating calipers. The device consists of the following parts, which are shown in Figure 2:
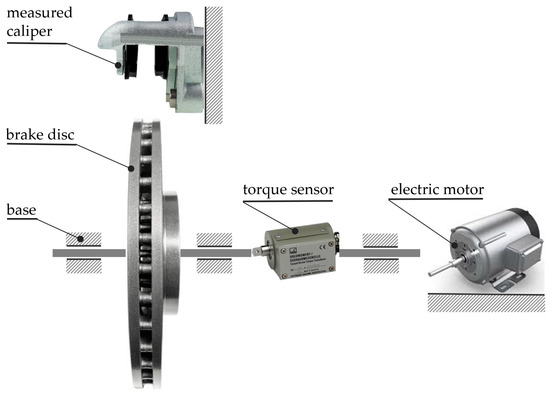
Figure 2.
Measuring chain for the measurement of residual torque.
- Bases 1 and 2 serve to fix the universal plate and the brake disc. Base 2 is equipped at one end with a simple mechanism for clamping the torque sensor.
- A universal plate serves to fasten the measured brake caliper.
- A brake disc is used for measurements. It is fixed through the flange on base 2.
- Gearbox system with an el. motor, which serves to rotate the brake disc.
- Torque sensor, which is used to measure the residual torque on the brake disc.
The torque sensor is the most important part of the entire measuring chain, and its accuracy has the greatest influence on the accuracy of the entire measuring device. For this reason, it was necessary to design an accurate, simple, and reliable calibration device that would introduce errors into the measured values as little as possible.
Figure 3 shows a used torque sensor from HBM. To measure the residual torque of the brake, a sensor with a nominal range of 10 Nm to 20 Nm is used.

Figure 3.
Torque sensor T4A from HBM.
Sensor parameters [44,45] are as follows:
- Type: T4A.
- Accuracy class: 0.1.
- Nominal (measuring) range: 10 Nm; 20 Nm.
- Nominal (measurement) sensitivity: 2 mV/V < ±0.2%.
- Amount of rotation at the nominal (measuring) torque: 0.9° for a 10 Nm sensor and 1.1° for a 20 Nm sensor.
4. Calibration Equipment Models
Four types of construction design of calibration devices are proposed; in three cases, a torque sensor was used as a standard, and in one case a calibrated weight was used as a standard. The CAD program Autodesk Inventor Professional 2023 was used to create the models.
4.1. Design of a Calibration Device with a Threaded Rod
Figure 4 shows the model of the calibration device, where the torque is induced using a threaded rod, and a torque sensor is used as a standard. In this version, the torque is generated in both directions of rotation. The disadvantages of this design involve the more time-consuming setting of the torque value using a threaded rod and the problematic axial setting of the torque sensor to the standard. In this design, the device contains bearings that would cause resistance during calibration and thereby introduce unwanted measurement errors into the calibration.
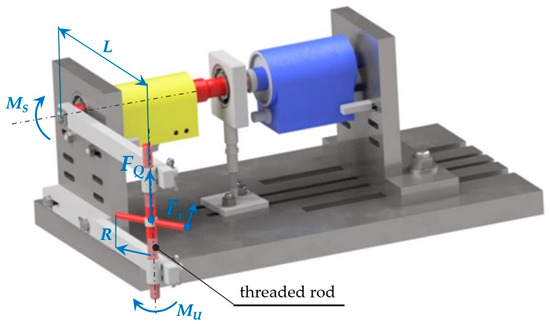
Figure 4.
Design of a calibration device with a threaded rod.
The wanted torque on the shaft with the torque sensor is given as follows:
where
- denotes the force in the treaded rod [N].
- denotes the distance between the shaft axis and the treaded rod axis (Figure 4).
Further, the force FQ is calculated by means of the known relations for a screw joint (Figure 5).
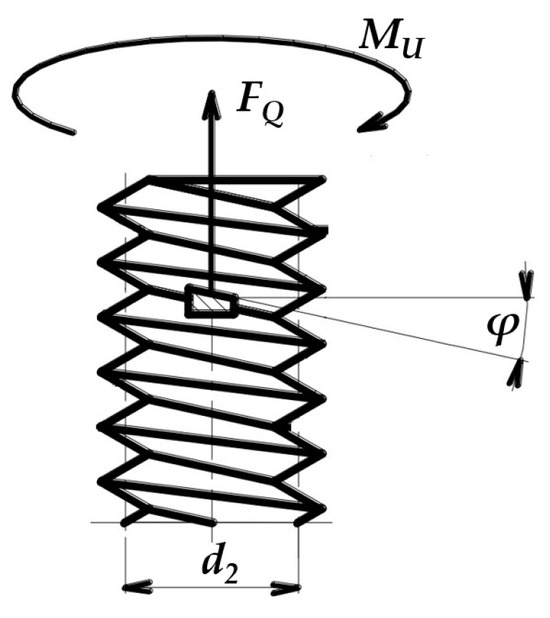
Figure 5.
A scheme of a screw joint.
The torque MU, which is caused by an operator, is calculated as follows:
where
- denotes the mean screw diameter [m].
- denotes the pitch angle of the thread [rad].
- denotes the friction angle [rad].
- denotes the friction coefficient in a thread.
- denotes the mean diameter of the contact surface [m].
- denotes the force on a handle of a threaded screw deduced by an operator [N].
- denotes the diameter of a threaded screw handle [m].
4.2. Design with the Angular Gearbox
With this design, the problematic and time-consuming settings of the torque were eliminated. This was achieved by replacing the threaded rod with an angle gear with a given gear ratio. The advantage is an easier and faster setting of the torque value, which could be set in both directions of rotation. The disadvantages include the problematic axial adjustment of the torque sensor to the standard and the introduction of errors due to the effect of rolling bearings. By using the gearbox, the built-in dimensions of the entire calibration device were increased, which significantly increased the entire weight of the device. A rather complicated gearbox with a high gear ratio and a self-locking mechanism meant that this device was not developed further. Figure 6 shows the model of this device.
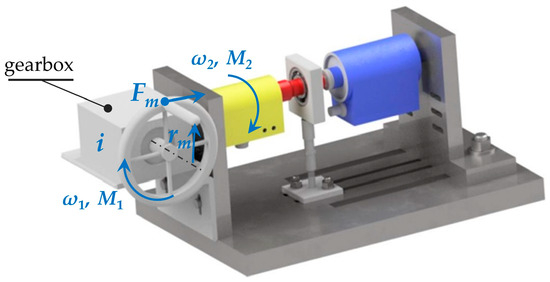
Figure 6.
Design of a calibration device with an angular gearbox.
The determination of torque M2 requires knowledge of torque M1. The wheel has a radius (rm) and includes a crank. An operator causes the force, Fm. Then, the torque in the gearbox input is given by the following formulation:
where
- denotes the torque on the gearbox input [Nm].
- denotes the force induced by an operator [N].
- denotes the wheel radius [m].
The gear ratio of gearbox i can be calculated based on the input and output angular velocities, and , as follows:
Then, torque is given by the following equation:
where
- denotes the mechanical efficiency of the gearbox.
Substituting Formulae (4) and (5) to Equation (6), torque is calculated as follows:
4.3. Design with Weight Carriers
In this case, a torque sensor is used as the standard. Weight carriers placed on an arm of a known length serve to store a set of weights that cause a moment of force on this arm. The advantages of this version include a simpler design and a lighter version compared to the version with an angular gearbox. The disadvantages include the errors introduced into the overall calibration due to the occurrence of rolling bearings and the problematic provision of the sensor’s axial position relative to the standard. With this design, there is an imperfect alignment of the system, which is caused by friction between the arm and the weight carriers. Figure 7 shows such a model with weight carriers.
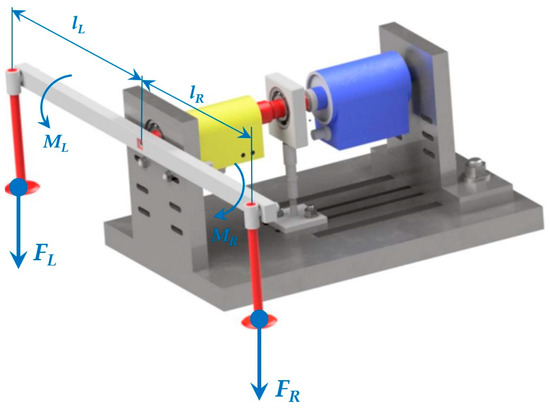
Figure 7.
Design of the calibration device with weight carriers.
The mathematical description of this device comes from the principle of the lever mechanism’s moment equilibrium, as follows:
where
- , denote the gravitational forces due to the weights [N].
- , denote the lengths of the arms that the weights act on [m].
4.4. Design with a Calibration Wheel
In previous designs, errors introduced by friction from rolling bearings, problematic settings of the measuring assembly, and relatively complex construction affected the calibration process; thus, it was necessary to eliminate these influencing factors. For this reason, a design solution was proposed, where a set of calibrated weights was used as a standard and the occurrence of rolling bearings was removed. This design, which is shown in Figure 8, minimized the influence of external factors affecting the calibration results and simplified the construction of the entire device, which resulted in a reduction of the total weight. Significant advantages include easy handling, good securing of the position of the calibration device on the measuring device, and reliable clamping of the sensor in this calibration device. The advantage of this device is that it can be used for all torque sensors used in the measuring laboratory. By using a calibration wheel with a given radius, it was ensured that after the steel strip with the weight carriers was established, the system was able to stabilize itself in an equilibrium position.
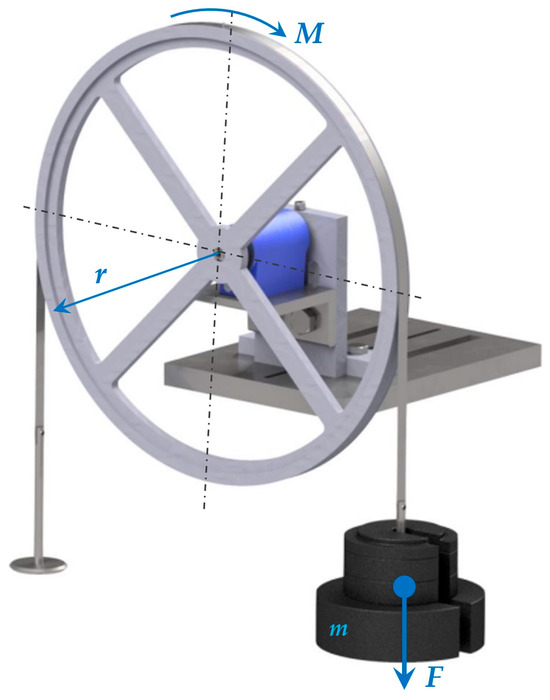
Figure 8.
Design of a calibration device with a calibration wheel.
This calibration device works on the principle of creating a moment of force according to the following relationship:
where
- denotes the force moment [Nm].
- denotes the force induced by the calibration weight [N].
- denotes the length of the arm on which the force F acts [m].
- denotes the weight of the weight [kg].
- denotes the local gravity acceleration [m/s2].
The calibration device with a calibration wheel works on the principle of creating a torque [Nm]. A force [N] acts on the calibration wheel with the radius r [m] representing the arm. This force F is induced using a set of calibration weights m, whose value is recalculated and determined in newtons based on the local gravity acceleration [m/s2]. The force, , induced by means of weights, acts on the arm (radius of the calibration wheel) and creates the required torque, which is necessary for the calibration of the torque sensors. The device is designed in such a way that it is possible to induce a moment of force in both the right and left directions of rotation. When designing the selected device, its load during operation was also taken into account. For this reason, the steel strip was determined as the weakest member of the system. This strip serves as a connecting member between the calibration wheel and the weight carriers and also as a holder for the weight carriers themselves. From this point of view, it was necessary to verify this steel strip for its maximum load. Verification was performed on a Zwick/Roell Z030 test rig. The condition for compliance was that the used steel strip with a thickness of h = 0.07 mm could withstand a load of at least = 80 N. After the test was completed, it was found that the beginning of the deformation occurred at a force of = 362.3 N, which in the case of the calibration device is satisfactory. Even a certain degree of oversizing was achieved.
Based on a comparison of the advantages and disadvantages with the previous three proposals of calibration devices, which are listed in Table 4, variant 4 (with a calibration wheel) was shown to be the most suitable solution; therefore, the next part of this paper is devoted to its use for the calibration of the torque sensor.

Table 4.
Comparison of designed calibration devices.
5. Calculation of the Calibration Device Error
In order to verify the possible error that arose due to the inaccurate production of the calibration wheel and inaccurate production of calibration weights, the theoretical error of the calibration device was calculated. For this reason, it was necessary to find out the manufacturing tolerance of the calibration weights given by the manufacturer and to find out the actual diameter of the calibration wheel. The calculation was based on known tolerance values for calibration weights given by the manufacturer, which are shown in Table 3, and the known value of the local gravitational acceleration, = 9.80853 m/s2, calculated by the weight manufacturer based on geographical coordinates. An important piece of information was the actual diameter of the calibration wheel, which was found using a 3D scanner, the value of which was ds = 400.1334 mm. Since the value of the weight was given in newtons, it was necessary to calculate the value of the mass of the weight using relation (10), as follows:
where
- is the mass of the given weight [kg].
- is the value of the given calibration weight [N].
- is the local gravitational acceleration [m/s2].
Subsequently, the weight tolerance value is added or subtracted from the weight value according to relation (11), as follows:
where
- is the mass of the weight increased or reduced by the tolerance value [kg].
- is the value of the mass of the given calibration weight [kg].
- is the tolerance value for the given weight [kg].
The calculation example for a weight of 2.5 is as follows:
In the next step, the values of the maximum and minimum forces induced by the weight with the given tolerance were calculated according to relation (12), as follows:
The values for other calibration weights were calculated in the same way and the results are shown in Table 5.

Table 5.
Table of calculated values.
Since the actual diameter of the calibration wheel detected by the 3D scanner, which measures with an uncertainty of U = ±1.2 μm, is ds = 400.1334 mm, it was necessary to add or subtract this uncertainty from the actual value of the diameter of the calibration wheel according to relation (13):
where
- is the actual diameter of the calibration wheel enlarged or reduced by the uncertainty of the 3D scanner [m].
- is the actual diameter of the calibration wheel [m].
- is the uncertainty of the 3D scanner [m].
Subsequently, the actual maximum and minimum values of the radius of the calibration wheel could be calculated, where half the thickness of the steel strip with a thickness of hp = 0.07 mm was added. This radius was calculated using relation (14), as follows:
where
- is the maximum or minimum radius of the calibration wheel [m].
- is the actual diameter of the calibration wheel enlarged or reduced by the uncertainty of the 3D scanner [m].
- is half the thickness of the steel strip [m].
After finding the actual maximum and minimum radii of the calibration wheel, the maximum and minimum values of the torque induced by the force of the weight on the given arm could be calculated according to relations (15) and (16):
where
- is the maximum or minimum value of the torque induced by the given weight [Nm].
- is the maximum or minimum value of the calibration weight [N].
- is the maximum or minimum value of the radius of the calibration wheel [m].
The calculation procedure for other calibration weights is the same as in the previous calculation and the results are shown in Table 6.

Table 6.
Calculated values of maximum and minimum torque values.
During calibration, the required torque values were achieved by combining calibration weights. Therefore, it was necessary to calculate the tolerance for each torque value (MM = 0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15) depending on the weight combination used. In this calculation, the law of propagation of uncertainties was applied, and the maximum and minimum tolerance values were calculated according to relations (17) and (18):
where
- is the sum of the maximum or minimum torque value induced for a given combination of calibration weights [Nm].
- is the maximum or minimum torque value induced by the given weight [Nm].
All the results of the maximum and minimum torque tolerance values for the given combinations of the calibrated weight are shown in Table 7.

Table 7.
Maximum and minimum torque tolerance values.
From these values, the range of changes in determined according was determined according to relation (19):
where
- is the range of deviations from the nominal value [Nm].
- is the sum of maximum torque values for a given combination of calibration weights [Nm].
- is the sum of the minimum torque values for the given combination of calibration weights [Nm].
The results of the calculations are shown in Table 8.

Table 8.
Calculated values of the range of deviation changes.
From the calculated results, the value necessary for the subsequent calculation of the standard uncertainty of the considered source uBz was subsequently determined according to relation (20), as follows:
where
- is the standard uncertainty of the considered source [Nm].
- is the range of deviations from the nominal value of torque [Nm].
- k is the value of the chosen approximation of the probability distribution, while for this type of approximation of the distribution, the uniform distribution was chosen.
The calculations for other required torque values are similar. The calculation results are shown in Table 9.

Table 9.
Calculated values of the standard uncertainty of the considered source.
Theoretical calculations revealed that the largest theoretical error reaches a standard uncertainty of = 0.000077235 Nm. This verified that the error introduced by the calibration due to the imprecise production of the calibrated weight and the imprecise production of the calibration wheel will only minimally affect the measured values during calibration. This statement is based on the fact that the values measured during calibration are measured to three decimal places, i.e., thousandths, and the largest theoretical error affects the measurement only in the fourth decimal place, i.e., ten-thousandths.
6. Calibration Measurements That Were Performed
After the theoretical calculations, calibration measurements were performed with the given calibration device (Figure 9). The torque sensor pulled from the measuring chain was inserted into the prepared calibration device together with the calibration wheel and weight carriers. After running the calibration program on the measuring computer, the sensor was loaded three times to its maximum value in the calibrated direction using a set of calibrated weights to ensure its mobility throughout the measurement range. Calibration was performed gradually from the smallest required value by a suitable combination of calibration weights that were added to the weight carrier. A torque was created on the arm of the calibration wheel, which was subsequently compared with the value displayed by the program on the measuring device. Calibration consisted of loading the sensor to preselected values with ten consecutive repetitions. Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 show the measured values for a torque of 1–5, 7 and 9 Nm.

Figure 9.
Calibration device with weights and the calibrated torque sensor.
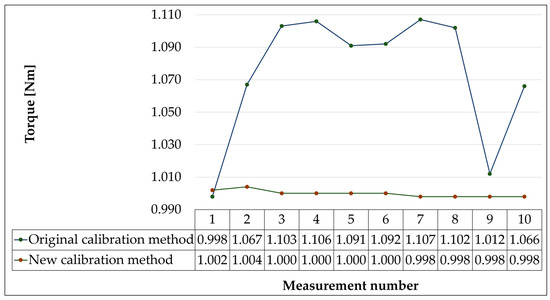
Figure 10.
Graph of measured values for the required torque value of 1 Nm.
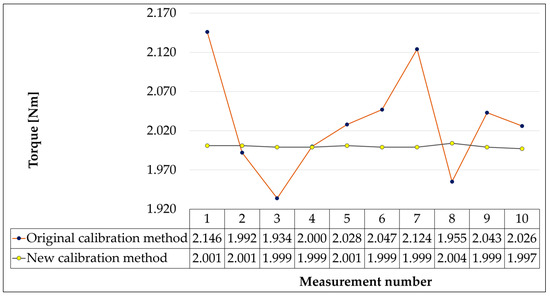
Figure 11.
Graph of measured values for the required torque value of 2 Nm.
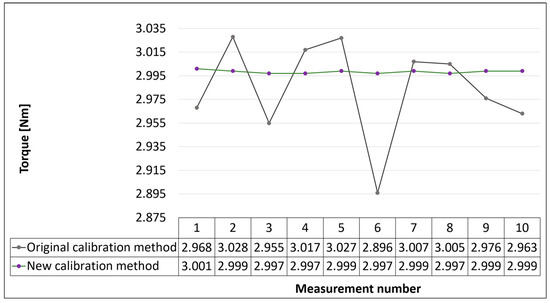
Figure 12.
Graph of measured values for the required torque value of 3 Nm.
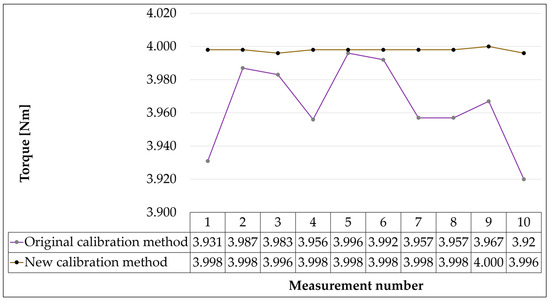
Figure 13.
Graph of measured values for the required torque value of 4 Nm.
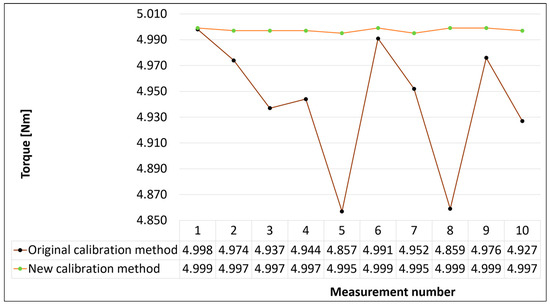
Figure 14.
Graph of measured values for the required torque value of 5 Nm.
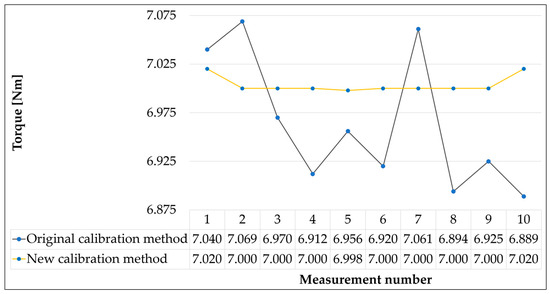
Figure 15.
Graph of measured values for the required torque value of 7 Nm.
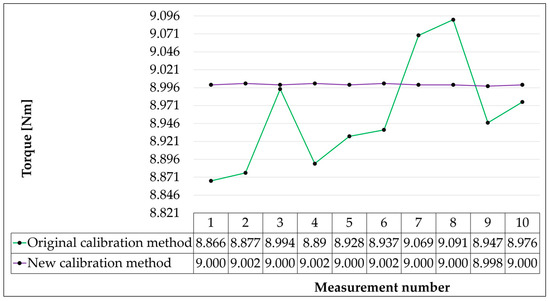
Figure 16.
Graph of measured values for the required torque value of 9 Nm.
During calibration, the measured values were read from the display of the measuring device to which the calibrated sensor was connected. The settings of the given measuring device made it possible to display the measured values in three decimal places.
After finishing the measurement by this method, the analysis of the measurement was carried out and the measurement was carried out with the original calibration device (Figure 17) using the standard torque sensor loaded by means of a lever. In this type of calibration, a Lorenz DR-12 torque sensor with a measuring range of ±25 Nm and an accuracy class of 0.1 was used as the standard. By carrying out both compared calibration measurements in a short time span, the same conditions were ensured for both measurements.
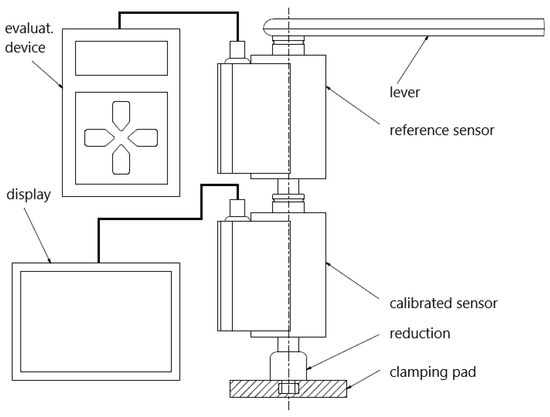
Figure 17.
Scheme of the original calibration device.
7. Discussion
As can be seen from Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, the original calibration method worked with relatively large differences between the measured values. The smallest differences were measured in the case of a required torque value of 4 Nm. The difference between the maximum and minimum deviation from the desired value was 0.076 Nm. On the contrary, the values at the required torque values of 2 and 9 Nm represented the largest differences, where the maximum and minimum torque values were 0.212 and 0.225 Nm. The distribution of the measured values in relation to the desired value also played a significant role. While in calibration values at 2, 3, 7, and 9 Nm, the measured values oscillated around the required torque values; with calibration at 1 Nm, almost all measured values were above the required value, and in the case of calibration at 4 and 5 Nm, all measured values were below the required value of the torque. The variance values of the measured torque values reached a maximum in the case of calibration at 9 Nm (0.00527 Nm) and a minimum in the case of calibration at 4 Nm (0.00059 Nm). On average, the variance of the original calibration method was 0.00275 Nm.
The new calibration method proved to be much more accurate. The differences between the maximum and minimum deviations of the measured values from the desired value were only from 0.004 to 0.007 Nm, with the highest differences found with calibration at torque 1 (0.006 Nm) and 2 Nm (0.007 Nm) and the smallest difference of 0.004 Nm in the remaining measurement moments. The variance values for the new method were very small; they ranged from 1.16 × 10−6 when calibrated to 7 Nm and to 3.56 × 10−6 when calibrated to 1 Nm. It can be seen from this that the measured values were very close to the required values and showed a high measurement stability.
The proposed new torque sensor calibration method has positively contributed to the accuracy of torque sensor calibration, which will significantly increase the reliability and accuracy of measuring the residual torque of automobile brakes. Due to the method’s simplicity, it can also be used when calibrating other torque sensors used for various purposes, of course when checking the stability of the calibration wheel strip for the expected load.
8. Conclusions
The studies showed a significant difference in the accuracy of the original calibration method compared to the new method.
Similarly, different accuracy values were measured for other verified torque values. It can be said that the new calibration device has increased the accuracy of the measuring device, which makes it possible to record even tiny values of the residual torque and enables even better detection of the causes of its occurrence. During the analysis of the original method, several factors were found that affected the results and accuracy of the calibration, namely the following:
- The necessity of exactly setting the torque sensor and the standard on “one axis” and maintaining the stability of this position.
- Ensuring the temperature stability of the measuring device.
- Selecting a suitable accuracy class for the reference sensor.
The new method simplified the operation and reduced the number of people required during calibration from two to one; thus, the efficiency of the calibration increased, and the measurement time was shortened.
Author Contributions
Conceptualization, D.B., S.K., J.D., and A.D.; methodology, D.B., S.K., J.D., and A.D.; formal analysis, D.B., S.K., J.D., and A.D.; investigation, D.B., S.K., J.D., and A.D.; data curation, D.B., S.K., J.D., and A.D.; writing—original draft preparation, D.B., S.K., J.D., and A.D.; writing—review and editing, D.B., S.K., J.D., and A.D.; visualization, D.B., S.K., J.D., and A.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
This publication was supported by the Cultural and Educational Grant Agency of the Ministry of Education of the Slovak Republic within the project KEGA 031ŽU-4/2023: Development of key competencies of the graduate of the study program Vehicles and Engines.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Songkitti, W.; Wirojsakunchai, E.; Aroonsrisopon, T. Identifying Factors that Affect Brake Wear PM Emissions during Real-World Test Conditions; SAE Technical Paper; SAE International: Pittsburgh, PA, USA, 2022; p. 2022-01-0570. [Google Scholar] [CrossRef]
- Amato, F. Non-Exhaust Emissions: An Urban Air Quality Problem for Public Health; Impact and Mitigation Measures, 1st ed.; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Grigoratos, T.; Martini, G. Brake wear particle emissions: A review. Environ. Sci. Pollut. Res. Int. 2015, 22, 2491–2504. [Google Scholar] [CrossRef] [PubMed]
- Harrison, R.M.; Jones, A.M.; Gietl, J.; Yin, J.; Green, D.C. Estimation of the contributions of brake dust, tire wear, and resuspension to nonexhaust traffic particles derived from atmospheric measurement. Environ. Sci. Technol. 2012, 46, 6523–6529. [Google Scholar] [CrossRef] [PubMed]
- Thorpe, A.; Harrison, R.M. Sources and properties of non-exhaust particulate matter from road traffic: A review. Sci. Total Environ. 2008, 400, 270–282. [Google Scholar] [CrossRef]
- Wahid, S.M.S. Automotive brake wear: A review. Environ. Sci. Pollut. Res. Int. 2018, 25, 174–180. [Google Scholar] [CrossRef]
- Timmers, V.R.J.H.; Achten, P.A.J. Non-exhaust PM emissions from electric vehicles. Atmos. Environ. 2016, 134, 10–17. [Google Scholar] [CrossRef]
- Beddows, D.C.S.; Harrison, R.M. PM10 and PM2.5 emission factors for non-exhaust particles from road vehicles: Dependence upon vehicle mass and implications for battery electric vehicles. Atmos. Environ. 2021, 244, 117886. [Google Scholar] [CrossRef]
- Jiang, R.; Liu, Y.; Hu, D.; Zhu, L. Exhaust and non-exhaust airborne particles from diesel and electric buses in Xi’an: A comparative analysis. Chemosphere 2022, 306, 135523. [Google Scholar] [CrossRef]
- Woo, S.-H.; Jang, H.; Lee, S.-B.; Lee, S. Comparison of total PM emissions emitted from electric and internal combustion engine vehicles: An experimental analysis. Sci. Total Environ. 2022, 842, 156961. [Google Scholar] [CrossRef]
- Gramstat, S.; Mertens, T.; Waninger, R.; Lugovyy, D. Impacts on brake particle emission testing. Atmosphere 2020, 11, 1132. [Google Scholar] [CrossRef]
- Kozuch, P.; Hujo, L.; Kaszkowiak, J.; Markiewicz-Patalon, M. Evaluation of service brake braking of selected group of vehicles depending on wear of brake system’s parts. Acta Technol. Agric. 2024, 27, 101–107. [Google Scholar] [CrossRef]
- Zhong, C.; Sun, J.; Liu, Z.; Niu, H.; Zhang, J.; Liang, X.; Yin, J.; Wu, L.; Peng, J.; Zhang, Q.; et al. Size distribution of brake wear particulate matter based on a brake dynamometer investigation. Front. Future Transp. 2024, 5, 1407660. [Google Scholar] [CrossRef]
- Mathissen, M.; Grochowicz, J.; Schmidt, C.; Vogt, R.; Hagen, F.H.F.; Grabiec, T.; Steven, H.; Grigoratos, T. A novel real-world braking cycle for studying brake wear particle emissions. Wear 2018, 414–415, 219–226. [Google Scholar] [CrossRef]
- Kukutschová, J.; Moravec, P.; Tomásek, V.; Matejka, V.; Smolík, J.; Schwarz, J.; Seidlerová, J.; Safárová, K.; Filip, P. On airborne nano/micro-sized wear particles released from low-metallic automotive brakes. Environ. Pollut. 2011, 159, 998–1006. [Google Scholar] [CrossRef] [PubMed]
- Straffelini, G.; Gialanella, S. Airborne particulate matter from brake systems: An assessment of the relevant tribological formation mechanisms. Wear 2021, 478–479, 203883. [Google Scholar] [CrossRef]
- Kozuch, P.; Hujo, L.; Muślewski, L.; Markiewicz-Patalon, M. Dynamic and stationary testing of vehicle braking systems. Acta Technol. Agric. 2023, 26, 238–243. [Google Scholar] [CrossRef]
- Otto, J.; Ostermeyer, G.P. High-frequency vibrations in the contact of brake systems. Facta Univ.-Ser. Mech. Eng. 2019, 17, 103. [Google Scholar] [CrossRef]
- Koch, S.; Gödecker, H.; von Wagner, U. On the interrelation of equilibrium positions and work of friction forces on brake squeal. Arch. Appl. Mech. 2022, 92, 771–784. [Google Scholar] [CrossRef]
- Koch, S.; Köppen, E.; Gräbner, N.; von Wagner, U. On the influence of multiple equilibrium positions on brake noise. Facta Univ.-Ser. Mech. Eng. 2021, 19, 613–632. [Google Scholar] [CrossRef]
- Kim, Y.; Kwon, T.; Lee, S. Analysis of the effect of the wedged type brake caliper piston on brake drag. In Proceedings of the 39th Annual Brake Colloquium and Exhibition, BRAKE 2021, Virtual Event, 17–20 October 2021. [Google Scholar] [CrossRef]
- Mohan, S.; Dake, P.; Mullapudi, D.; Ingole, S. A method to capture and analyze brake dynamic drag. In Proceedings of the 17th Symposium on International Automotive Technology, SIAT 2021, Virtual Event, 29 September–1 October 2021. [Google Scholar] [CrossRef]
- Synák, F.; Rievaj, V.; Kucera, M.; Sebök, M.; Skrúcany, T. Effect of repeated vehicle braking on the warming of selected parts of the vehicle. Sci. J. Silesian Univ. Technol.-Ser. Transp. 2020, 107, 183–196. [Google Scholar] [CrossRef]
- Vecchiato, L.; Vecchiato, L.; Negri, M.; Picci, G.; Viale, L.; Zaltron, G.; Giacometti, S.; Meneghetti, G. Design and development of a brake test bench for formula SAE Race Cars. Machines 2024, 12, 135. [Google Scholar] [CrossRef]
- Dixit, C.; Gaurkar, P.; Ramakrishnan, R.; Shankar Ram, C.S.; Vivekanandan, G.; Sivaram, S. Calibration of an inertial measurement unit and its impact on antilock braking system performance. In Proceedings of the 18th Symposium on International Automotive Technology, SIAT 2024, Pune, India, 23–25 January 2024. [Google Scholar] [CrossRef]
- Tawadros, P.; Awadallah, M.; Walker, P.; Zhang, N. Using a low-cost bluetooth torque sensor for vehicle jerk and transient torque measurement. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2020, 234, 095440701986161. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Z.P.; Chen, J.; Qiu, F.; Na, S.D. Design and research of a novel non-contact vertical inductive torque sensor. Measurements 2021, 177, 109252. [Google Scholar] [CrossRef]
- De Carvalho Pinheiro, H.; Sisca, L.; Carello, M.; Ferraris, A.; Airale, A.G.; Falossi, M.; Carlevaris, A. methodology and application on LOAD monitoring using strain-gauged bolts in brake calipers. In Proceedings of the SAE 2022 Annual World Congress Experience, WCX 2022, Virtual Event, 5–7 April 2022. [Google Scholar] [CrossRef]
- Wheatley, G.; Rubel, R.I. An autonomous braking control system for a 2017 Yamaha Grizzly 700. Sci. J. Silesian Univ. Technol.-Ser. Transp. 2022, 115, 211–226. [Google Scholar] [CrossRef]
- Jneid, M.S.; Harth, P. Integrated torque vectoring control using vehicle yaw rate and sideslip angle for improving steering and stability of all off wheel-motor drive electric vehicles. Acta Polytech. Hung. 2024, 21, 87–106. [Google Scholar] [CrossRef]
- Ishak, M.R.; Abu Bakar, A.R.; Belhocine, A.; Taib, J.M.; Omar, W.Z.W. Brake torque analysis of fully mechanical parking brake system: Theoretical and experimental approach. Measurements 2016, 64, 487–497. [Google Scholar] [CrossRef]
- Panchenko, S.; Gerlici, J.; Vatulia, G.; Lovska, A.; Ravlyuk, V.; Harusinec, J. Studying the load of composite brake pads under high-temperature impact from the rolling surface of wheels. EUREKA Phys. Eng. 2023, 2023, 155–167. [Google Scholar] [CrossRef]
- Panchenko, S.; Gerlici, J.; Lovska, A.; Vatulia, G.; Ravlyuk, V.; Rybin, A. Method for Determining the Factor of Dual Wedge-Shaped Wear of Composite Brake Pads for Freight Wagons. Commun.-Sci. Lett. Univ. Zilina 2024, 26, B31–B40. [Google Scholar] [CrossRef]
- Panchenko, S.; Gerlici, J.; Lovska, A.; Ravlyuk, V. The Service Life Prediction for Brake Pads of Freight Wagons. Commun.-Sci. Lett. Univ. Zilina 2024, 26, B80–B89. [Google Scholar] [CrossRef]
- Hu, C.; Pan, G.; Kong, L.; Yu, J. Research of brake by wire system. J. Phys.-Conf. Ser. 2023, 2479, 012051. [Google Scholar] [CrossRef]
- Testbook. 2023. Available online: https://testbook.com/mechanical-engineering/drum-brakes-vs-disc-brakes (accessed on 21 August 2024).
- Zhou, X.; Wu, G.; Wang, C.; Zhang, R.; Shi, S.; Zhao, W. Cooperative optimization of energy recovery and braking feel based on vehicle speed prediction under downshifting conditions. Energy 2024, 301, 131699. [Google Scholar] [CrossRef]
- Li, W.; Zheng, H.Y.; Zong, C.F. A brake pad wear control algorithm for electronic brake system. Adv. Mater. Res. 2013, 694–697, 2099–2105. [Google Scholar] [CrossRef]
- Gerlici, J.; Kravchenko, K.; Fomina, Y. Development of an innovative technical solution to improve the efficiency of rolling stock friction brake elements operation. In Transbaltica XII: Transportation Science and Technology; Springer: Berlin/Heidelberg, Germany, 2022; pp. 28–38. [Google Scholar]
- Ledbestov. 2020. Available online: https://ledbestov.live/product_details/9746208.html (accessed on 5 May 2024).
- SAE. 2024. Available online: https://www.sae.org/news/2023/05/brakes-sustainability-dust-regulations (accessed on 21 August 2024).
- ACEA. 2023. Available online: https://www.acea.auto/fact/euro-standards/ (accessed on 21 August 2024).
- Dieselnet. 2024. Available online: https://dieselnet.com/standards/eu/ld.php (accessed on 21 August 2024).
- NOTA, S. Design of a Device for Calibration Torque Sensor for Measuring Residual Brake Moment. Master’s Thesis, University of Žilina, Žilina, Slovensko, 2019. [Google Scholar]
- HBM. 2019. Available online: https://www.sensor-hbm.com/upload/product-file/b0591.pdf (accessed on 18 May 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).