Abstract
The multi-microwave sources reactor can significantly reduce energy consumption and processing time with broad application prospects in industrial processing. In order to optimize the temperature field of materials, this paper proposes the heating strategy of multi-microwave sources based on collaborative switching, particularly in distributed combined heat source networks with poor communication conditions. Firstly, simplifying system control variables to enhance the design of the microwave intelligent agent system, and optimizing the time-frequency characteristics of combined power output from multi-microwave sources to emphasize the process of energy partition. Meanwhile, an event-triggered strategy reduces communication frequency and energy consumption between agents. Secondly, a fixed positive lower limit is used in event-triggered to avoid Zeno behavior caused by DoS attacks. Finally, The finite element method was used with the time domain for thermal analysis. The simulation results of SiC show that the energy utilization efficiency of microwave heating equipment is increased by 4.3∼10.7%, temperature uniformity is improved by 25.6∼43.6%, and the results of the potato experiment simulation showed that the multi-microwave source collaborative switching heating strategy can effectively optimize the temperature field distribution of the material.
1. Introduction
Microwave heating has become a popular and efficient method for processing materials, food, ceramics [1,2], metallurgy [3,4], etc. The factors that influence the effectiveness of microwave heating equipment include the shape of the microwave heating chamber [5], the number of microwave sources, the frequency of the microwave source [6], the mode stirrer, and the electric turntable. Additionally, the material’s properties [7] can also impact the microwave heating process.
Some scholars have tried to mix materials for heating due to varying microwave absorption. Fan et al. [8] modified carbon materials using nitrogen doping technology and prepared biomass-based nitrogen-doped porous carbon with excellent microwave absorption performance. Radoiu et al. [9] explained the elements of microwave technology and the practical issues associated with processing using microwaves. These methods have excellent temperature uniformity but require specific material and morphology.
Researchers have optimized the microwave heating effect by designing the cavity shape [5] to control electromagnetic field distribution. Shi et al. [10] discussed that elliptical polarized microwave fields enhance microwave energy efficiency. The cost of projecting the microwave heating chamber design is relatively high, and it is mainly used in the particular processing industry. Taghian Dinani et al. [11] demonstrated that the uniformity of material temperature varies with different orientations and angles on the electric turntable, as well as with and without rotation of the electric turntable. Chen et al. [12] further demonstrated that different motion modes of electric turntables could improve the uniformity and thermal efficiency of microwave heating. The electric turntable enhances the uniform electromagnetic field distribution within the material, while the mode stirrer alters the electromagnetic field distribution within the microwave equipment through its rotation. In contrast, some researchers favor the mode stirrer. Zou et al. [13] optimized the uniformity of biodiesel temperature in a microwave reactor using the mode stirrer. Wang et al. [14] proposed the dual pendulum structure mode stirrer to improve microwave heating uniformity. Microwave energy loss occurs due to heat transfer between the electric turntable, the mode stirrer, and the material.
To avoid the drawbacks, some scholars have used multi-microwave sources to optimize power output and improve heating efficiency and temperature uniformity. Guan et al. [15] optimized the uniformity of microwave electromagnetic fields using multiple microwave sources. Yang et al. [16] optimized the temperature uniformity of materials by dynamically planning the power output state characteristics of multi-microwave sources. Yin et al. [17] found metal inserts have enabled a uniform distribution of electromagnetic fields in the multi-source microwave heating cavity. The above literature used multiple magnetrons to construct a multi-microwave sources intelligent agent system [2,16] but did not consider the multi-microwave sources intelligent agent network communication issue.
The event-triggered theory is widely used in network communication among multi-agent systems. Wang et al. [18] Based on the Lyapunov function, a new mechanism for triggering events was designed to establish the relationship between system switches and event-triggered and eliminate the Zeno phenomenon. Zhao et al. [19] A hybrid method based on static/exchange-oriented network sampling data has been discovered to achieve multi-agent consensus. In multi-source microwave network communication systems, network attacks are bound to occur. Denial-of-service (DoS) attacks represent standard network attack methods that block network communication. Deng et al. [20] developed an elastic model-free adaptive control method to resist communication delays and DoS attacks of a class of nonlinear multi-agent systems. Hu et al. [21] achieved global exponential stability and weighted H-infinity performance of switch systems under DoS attacks. More studies are still needed on the stability of switching systems under DoS attacks [22] and switching systems for microwave heating are even less common.
Compared with continuous heating [15,17], the significant advantages of intermittent heat supply are its energy efficiency and the better options for process control, the architecture of the multi-microwave sources switching control system is improved by simplifying the switching control system variables. Compared to triggering over time [2,16], event-triggered [18,19] in intelligent agent communication has more research value. When DoS attacks occur, the Zero-Order Hold (ZOH) maintains the system output and ensures that the multi-microwave source intelligent agents system always maintains closed-loop control. The innovations are as follows:
- (1)
- A microwave heating distributed architecture using multiple magnetrons is designed to reduce heating time, and a collaborative switching heating strategy for multi-microwave sources is constructed.
- (2)
- Using an event-triggered strategy to reduce the frequency of communication between intelligent agents.
- (3)
- Establishing stability conditions for a multi-microwave sources cooperative switching system under DoS attacks.
- (4)
- Developing a numerical heating model for multi-microwave sources using finite element analysis and evaluating the optimal collaborative switching heating strategy under various time-frequency distributions.
2. Materials and Methods
2.1. Multi-Microwave Sources Heating Model
The microwave heating model utilizes a rectangular cavity with six microwave sources distributed symmetrically on the three faces of the cavity. The cavity and WR340 standard waveguide are made of copper. The internal medium is air, and the initial temperature is 25 °C at a microwave frequency of 2.45 GHz. Numbers 0–5 in the subfigure (a) represent six microwave sources, the specific model parameters are sourced from reference [16]. Establishing a numerical heating model for multi-microwave sources using finite element analysis in COMSOL, as shown in Figure 1.
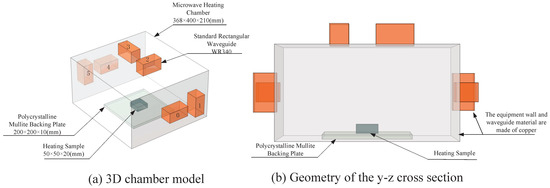
Figure 1.
3D geometrical model of the cavity with the multi-microwave sources distributions.
The cavity walls and waveguides are copper and can be considered perfect cavities with electromagnetic boundary conditions, . The natural thermal convection between the heated medium and air is expressed as:
where h is the heat transfer coefficient of air, and n is the unit normal vector of the cavity wall surface, T is the temperature for the medium. E and B denote the electric field intensity and the magnetic induction intensity, respectively. denotes the temperature of the air medium inside the reaction chamber. denotes the temperature gradient perpendicular to the surface of the temperature domain.
During microwave heating, the temperature of the medium is related to the dielectric loss and hysteresis loss [16], where is the vacuum permittivity and the denotes the frequency of the electromagnetic wave.
where Q, and denote microwave dissipation power, the imaginary part of dielectric constant, and the imaginary part of magnetic permeability, respectively.
The heat conduction equation for medium temperature is as follows:
where is the medium’s density, and another K and denote the thermal conductivity and specific heat capacity for the medium, respectively. By combining Equations (2) and (3) with , it can be concluded that:
From Equation (4), adjusting the electric field strength E and the electromagnetic wave frequency can optimize the temperature distribution. The E can vary based on microwave source power.
2.2. Experimental Material Selection
Two characteristic scales ( and ) [23,24], are used to measure the propagation of electromagnetic waves in the sample and the selection of heating materials.
where , f and c denote the microwave frequency and the speed of light, respectively. The parameter determines the number of waves formed inside the material under microwave heating. The penetration depth, denoted by , refers to the distance microwaves can travel through a material before being absorbed completely. Microwave absorbing materials such as SiC, carbon, and water can easily convert microwave energy into heat, their penetration depth is typically in the order of centimeters.
Let , [24], where , and have undergone de-unitization and normalization. Inspired by reference [24], materials can be categorized into four groups using parameters and , as illustrated in Table 1.

Table 1.
Groups of materials are categorized based on the magnitudes of and .
Two representative materials were selected for the experiment: Potato was chosen for the first group (), and SiC was chosen for the third group (). Potatoes are commonly used in the food processing industry and are a staple in daily life, in contrast, the SiC is primarily utilized in high-temperature materials research. Table 2 summarizes the relevant properties of the two materials.

Table 2.
Material parameters of the finite element analysis numerical calculation model.
Where
3. Theory
3.1. Theory of Consistency by Multi-Microwave Sources Event-Triggered
Generally, undirected graphs are used to represent information exchange between intelligent agents. In this article, is the undirected graph, , denote the node set and the edge set, respectively. denotes the agent label, and denotes the weight of the edge, , denote the adjacency matrices of the follower and the leader, respectively. When , agent i and j are neighbors to each other if . Let , , . The problem is as follows [25].
Let . denote the power state switching of microwave sources. Where and i, , denote the number, control strategy, and controller gain of the microwave intelligent agent. A signal of ∼ V represents the output power status of the microwave source , and denote the signal margin. Let , is the minimum eigenvalue of .
If there is a positive definite matrix in the Riccati inequality mentioned Equation (7). The gain of the controller in Equation (6) is constructed as .
Next, the event-triggered strategy is defined as follows:
where , , let . Where , t is the current time, denotes the previous triggering time of agent i, and denotes the lower bound of the triggering time, let . For the next triggering moment , let . is used to record the duration of and reset to at the next triggering moment , let .
When the microwave intelligent agent i triggers sampling at time , let ; otherwise, . For all agents i, the event-triggered times of the switching system were recorded as an event-triggered matrix .
3.2. Event-Triggered Consistency Theory of Multi-Microwave Sources under DoS Attacks
Typically, the energy of DoS attacks released by opponents is limited. Let represent the frequency of DoS attacks, and the denotes the duration of DoS attacks, where , and are constants, and the . The network can be located at any point in the feedback loop. Inspired by references [26], the network is positioned between the triggering mechanism and the controller in this paper.
As shown in Figure 2, when , the adversary initiates the DoS attacks to disrupt the communication between the controller network and the intelligent agent control system, if [26], it may decrease the system performance. To avoid this issue, ZOH generates a control signal that denotes the most recently even-triggered moment as shown in Figure 3.
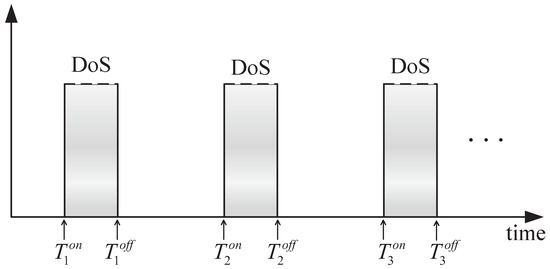
Figure 2.
Schematic of DoS attack signals.
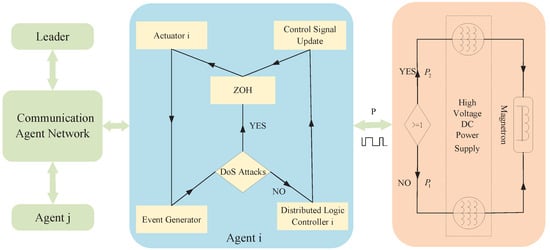
Figure 3.
Flowchart of network-based agent control.
On the other hand, when , if the event-triggered law form Equation (8), is updated and sent to agent j, using ZOH to save and send updated control signal to actuator i. When the value of , remains the same until the .
As shown in Figure 3, actuator i is controlled by control signal to output digital control signal p, which is then input into a comparator. When , the High Voltage DC Magnetron Power Supply drives the magnetron to output at high-power state , for , it outputs at low-power state , enabling the collaborative switching of high and low-power magnetrons. The leader’s state, denoted by , is generally not influenced by and changes over time through updates. When , the information exchange between microwave intelligent agents is reduced, achieving the uniform distribution of processor computing power.
Therefore, the parameter describes the impact of DoS attacks, and ZOH maintains a closed-loop system.
Then, Equation (6) can be rewritten as follows:
When switching system state transitions, the minimum event-triggered time [27,28] is introduced in an Event-triggered strategy to prevent Zeno behavior caused by DoS attacks. The definition of is as follows:
where , , and let , . is the minimum singular value, and is the maximum singular value of the independent matrix variable. Next, the following proves that the system does not exhibit Zeno behavior.
Define , and the derivative and inspired by [25], . Combining Equation (8), we then have:
Consequently, for any agent i, and ,
which means that the switching systems can avoid Zeno behavior [19,25].
For system consistency, first consider the absence of DoS attacks. let , . We have
let constructing Lyapunov function: . Inspired by [25] and Equation (7), Equation (9):
where be nonnegative and continuous function on , constant , denotes the positive definite matrix and then . According to Equation (16), Equation (17) and following the proof of result:
The existence of makes hold, Equation (18) means that the leader-following consensus can be exponentially implemented globally.
When their DoS attacks, for a single jump in the switching system, assuming is the switching moment of , and that exists, redesign Lyapunov function: , next we have:
Let denote the number of times the system state m switches, then there is as follows:
where , . denote the two states of the switching system, respectively, while denote the state switching rate parameter. Assuming a single heating cycle in the microwave switching system as a Markov jump system, let , and , , next we have , and let , combining Equation (19), Equation (20) and introducing important conclusions from reference [26,28]:
And then:
Taking expectations from both sides of Equation (22), combined with Equation (21):
where , when the DoS attacks satisfies , the closed-loop system Equation (11) can stably exist under DoS interference attacks [26,28].
4. Results and Discussion
4.1. Event-Triggered Collaborative Switching of Multi-Microwave Agents under DoS Attacks
This article uses six microwave sources symmetrically distributed pairwise. Assuming node 0 is the leader, and 1 to 5 denote followers. The adjacency matrix for followers and the adjacency matrix for leaders can be obtained from Figure 4.
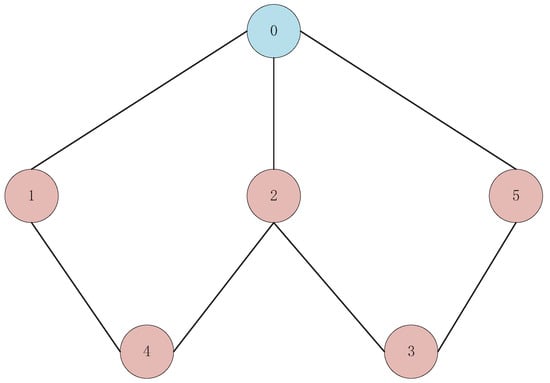
Figure 4.
Fixed communication topology of multi-source microwave intelligent agents.
The initial parameter settings are as follows:
As described in Section 3, let , , calculating , , and using the LMI Toolbox in Matlab (version number: 9.13.0.2049777 (R2022b)) as follows:
The proposed method only requires knowledge of the maximum values of and in Equation (20), as accurately measuring the transition rate during switching is difficult. So, ; therefore, in the experiment s. The leader switching trajectory is as follows:
Let , , , . The time for DoS attacks is set to s, followed by s of silence, and the cycle repeats every s, and assuming the system experiences the DoS attacks s. When , , there is a value of , and , make the satisfies the inequality.
During the no DoS attacks, the result of Equations (6) and (8) is shown in Figure 5a. The event-triggered frequency can be obtained from Equation (9), as shown in Figure 6.
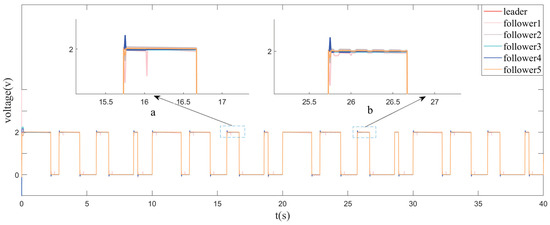
Figure 5.
Event-triggered multi-microwave sources intelligent agent consistency switching; (a) Event-triggered agents consistency switching without DoS attacks; (b) Event-triggered agent consistency switching under DoS attacks.
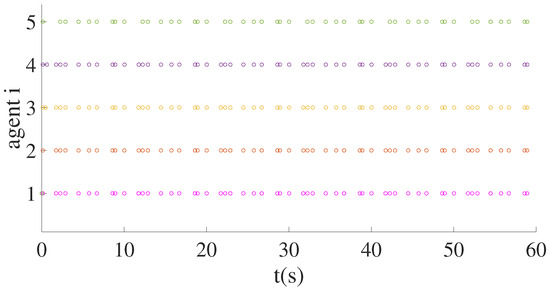
Figure 6.
Event-triggered time distribution of multi-microwave sources intelligent agents.
During the DoS attacks, the system state switching under the DoS attacks is shown in Figure 5b using the control law Equation (11) and event-triggered strategy Equation (8). Additionally, Figure 7 shows the time distribution of event-triggered for intelligent agents during the DoS attacks.
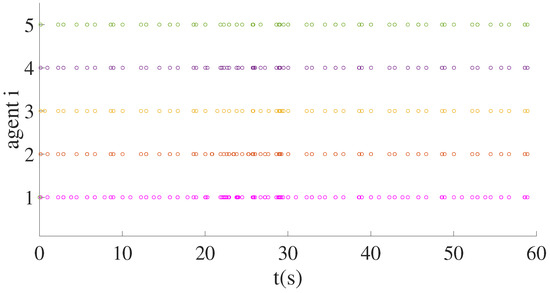
Figure 7.
Event-triggered time distribution of intelligent agents under DoS attacks.
When s, the DoS attack takes effect, and the error of the intelligent agent in the switching system increases, as shown in the comparison between Figure 5a,b, which leads to a rise in the number of event- triggered for the intelligent agent, illustrated in Figure 6 and Figure 7. While s, there is no DoS attack, and the switching system can maintain stability. As indicated in Table 3, for s, due to the existence of DOS attacks, there was an increase of 24, 15, 22, 18, and 10 in the number of event-triggered occurrences for agents 1–5, respectively. Noticeably, the frequency of event-triggered increases and the performance of system switching decreases when the system considers DoS attacks, as shown by comparing Figure 5a,b. Without the DoS attacks, and event-triggered strategy activation, the system control signal intervenes quickly until the state converges to the predetermined error range.

Table 3.
The number of event triggers is based on comparing the event and DoS attacks.
During the DoS attacks, control signals are blocked, information interaction is delayed, system errors increase, and intelligent agent states oscillate. An event-triggered strategy is activated, and the control signal intervenes quickly to help the system converge. However, the frequency of communication in the switching system rises during DoS attacks, causing additional state errors and reducing system stability. As a result, the convergence and divergence performance of the switching system is sacrificed to maintain the system state within an allowable error range, providing resistance to DoS attacks.
4.2. Multi-Microwave Sources Collaborative Switching Heating
A numerical simulation example in Section 4.1 demonstrates that the switching system has a specific resistance to DoS attacks. However, this performance improvement comes at the cost of sacrificing the system’s consistency convergence ability and increasing uncertainty. As shown in Figure 3, the High Voltage DC Power Supply driver controls the magnetron, assuming that the power output of the magnetron is stable and without time delay, using the event-triggered switching model described in Equation (11) in Section 3.2, the intelligent agent in the multi-microwave sources controls the High Voltage DC Power Supply driver to activate the magnetrons. By optimizing the power output frequency in the leader’s time domain, the follower can use control strategy Equation (11) to ensure a consistent switch between the high and low power of the magnetron.
The multi-microwave sources intelligent system feeds the same total energy into the cavity at w and t = 40 s. Eight experiments are conducted to compare different time-frequency distribution switching strategies by altering the leader state variables and . Control group (a) was heated with traditional constant power.
Figure 8 displays that the total power utilized in all experiments is unchanged. The heating cycles of four groups (b–e) are fixed for 10 s, with corresponding values of 0.8, 0.7, 0.6, and 0.5, respectively. Another four groups (f–i) have a fixed value of 0.5, but the heating cycles are set at 20 s, 10 s, 8 s, and 5 s, respectively.
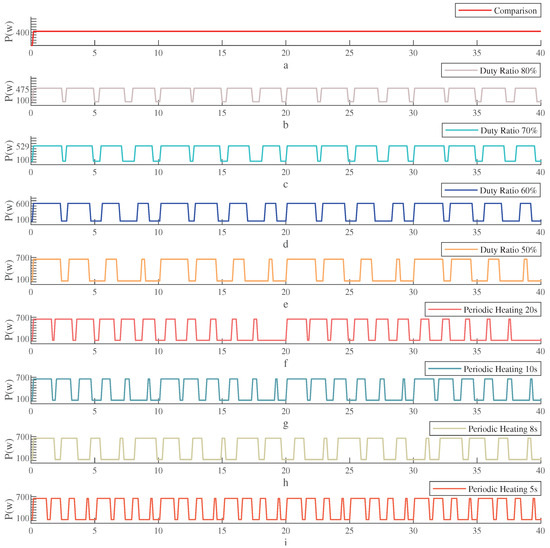
Figure 8.
Output power curve of multi-microwave sources under different switching strategies.
Using COMSOL software (version: COMSOL Multiphysics® 6.2) for finite element modeling and simulation experiments, the electromagnetic power loss density of the material is recorded. In order to evaluate the heating effect of materials in the microwave, the ratio of reflected power to input power and temperature variation coefficient are introduced [16,25].
Where and represent the electromagnetic power loss density and power value distribution in the time domain of the microwave source, respectively, n is the number of sampling points for material temperature, and the COMSOL built-in program selects the position and number of points used. denotes the temperature value of sampling point k, is the initial temperature of the material, and denotes the average temperature of the sampling points.
When the value of is smaller, the utilization efficiency of microwave energy is higher. The temperature distribution of the material becomes more uniform as the value of decreases. Calculate the temperature difference between the highest and lowest temperatures after SiC heating using ; the variables and denote the highest and lowest temperatures, respectively. Table 4 describes the value of , , and of SiC under different heating methods.

Table 4.
Heating effect parameters of SiC under different switching strategies in multi-microwave sources systems.
The heating effect of SiC under different switching strategies in the multi-microwave sources system is shown in Figure 9.
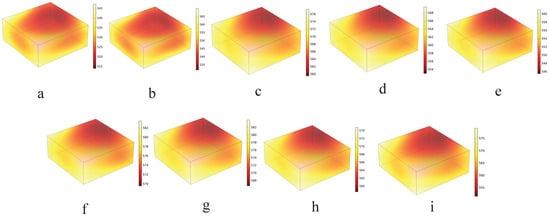
Figure 9.
Heating effect of SiC under different switching strategies in the multi-microwave sources system. (a) Heating effect of SiC under the Multi-microwave sources constant power strategy. (b–i) Heating effect of SiC under the multi-microwave sources collaborative switching heating strategies (methods of (b–i) in Figure 8).
Table 4 shows that the multi-microwave sources system maintains unchanged power fed into the cavity. Compared with constant power heating, eight different heating strategies have improved the uniformity of material temperature. The heating time for SiC in experimental groups (b–e) decreased from 32 s to 20 s, and the single source high-power state increased from 475 w to 700 w. Among them, the microwave utilization efficiency of switching strategy (c) reached 53.7%, which is 7% higher than that of constant power heating; the switching strategy (e) results in a more uniform temperature distribution of SiC, with a 43.6% improvement in temperature uniformity compared to constant power heating, the overall temperature difference of the heated SiC material is =15.502 °C, which is the lowest. The uniformity of material temperature may be affected to improve the efficiency of microwave energy utilization. The experimental group (f–i) has heating cycles of 20 s, 10 s, 8 s, and 5 s, respectively. The single source high-power state is fixed at 700 W. When maintaining uniform SiC heating temperature, switching strategy (f) has the highest microwave utilization efficiency, the energy utilization efficiency increased by 10.7% compared to constant power heating.
The experimental group (f–i) used higher microwave power, which caused a faster temperature rise, resulting in greater microwave energy utilization efficiency than the experimental group (b–e). When the total power remains constant, the energy input of the experimental group (f–i) is quickly concentrated, decreasing the uniformity of material temperature. High and low power complementarity and the self-organizing characteristics of material temperature can be utilized to suppress the generation of hotspots. To achieve better microwave energy utilization efficiency, sacrificing some uniformity in material temperature may be necessary.
In order to further emphasize the effectiveness and universal applicability of the multi-microwave sources collaborative switching heating strategy described in this article, we carried out four comparative heating experiments on potatoes based on reference [16,29], while keeping the total power supplied to the cavity constant:
- (i)
- Multi-microwave sources constant power strategy. The output power of six microwave sources in the experiment was set at 200 W.
- (ii)
- Multi-microwave sources consistent variable power (method of [29]). Inspired by reference [29], the microwave output power in the multi-microwave sources system varies over time, the output power curves of six microwave sources are set at .
- (iii)
- Group switching consistent variable power (method of [16]). The power output of the microwave varies over time. Following the example in reference [16], the power output curves for microwave sources 0, 3, and 5 are set to W, while the power output curves for microwave sources 1, 2, and 4 are set to W.
- (iv)
- The multi-microwave sources collaborative switching heating strategy (our method). The power output trajectory of the microwave source is denoted as , with a heating cycle of 20 s and duty cycle of ; the time-frequency distribution of the output power aligns with the switching strategy (f), as shown in Figure 8. Excessive microwave power can cause changes in material properties due to the differences between SiC and potato, therefore, let W, W. The heating effects of potatoes are shown in Figure 10.
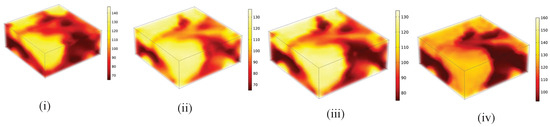 Figure 10. Compare the temperature distribution of potatoes in the heating model of the simulation experiment. (i) Heating effect of potato under the multi-microwave sources constant power strategy. (ii) Heating effect of potato under the multi-microwave sources consistent variable power. (iii) Heating effect of potato under the group switching consistent variable power. (iv) Heating effect of potato under the multi-microwave sources collaborative switching heating strategy.
Figure 10. Compare the temperature distribution of potatoes in the heating model of the simulation experiment. (i) Heating effect of potato under the multi-microwave sources constant power strategy. (ii) Heating effect of potato under the multi-microwave sources consistent variable power. (iii) Heating effect of potato under the group switching consistent variable power. (iv) Heating effect of potato under the multi-microwave sources collaborative switching heating strategy.
In Table 5, it is demonstrated that the multi-microwave sources collaborative switching heating strategy, as described in this article, achieves 64.17% microwave energy utilization efficiency for potatoes; this efficiency is 20.3% higher than that achieved by the multi-microwave sources constant power strategy and surpasses the methods outlined in references [16,29]. The heating strategy described in this article improves the potato’s temperature uniformity by 20.82% under constant power heating, however, compared to continuous power heating, this improvement is lower than the 50.34% achieved with the heating strategy in reference [29] and the 40.29% achieved with the heating strategy in reference [16].

Table 5.
Heating effect parameters of potatoes under different strategies in multi-microwave sources systems.
However, compared to references [16,29], this paper has the following advantages: (i) employing an event-triggered strategy to reduce system communication frequency and conserve system computing power. (ii) Optimizing the control architecture of the intelligent agent system to enhance its resistance to DoS attacks, the system should maintain stability even under uncertain communication conditions and improve the controller’s ability to withstand interference in high-frequency electromagnetic environments such as microwave heating systems. (iii) The heating strategy described in this article only has the magnetron’s high and low power states. It offers higher operability and more direct control than the time-varying power heating strategy. In comparison to reference [25], this article focuses on optimizing the control architecture of multi-agent systems, which provides stability conditions for intelligent agents operating under uncertain communication conditions, reduces control variables, and utilizes low-power states to prevent the magnetrons from operating at zero power, thus enhancing the energy utilization efficiency of materials.
The multi-microwave sources collaborative switching heating strategy improves material temperature uniformity compared to the traditional constant power heating model. However, the extent of this improvement is relatively small compared to references [16,29]. However, under the same conditions, the heating method described in this article has the highest energy utilization efficiency. Multi-microwave sources effectively improve energy utilization efficiency and reduce heating time. The main reasons are analyzed as follows: While ensuring the same total power input for heating, the microwave power is periodically switched; the high-power state of the switching system is mainly concentrated in the first half of the heating cycle, which causes the material temperature to increase rapidly. As the power gradually decreases, thermal conduction and radiation occur between the hot and cold regions of the material; this utilizes the self-organizing characteristics of heat to enhance heating uniformity. Meanwhile, the low-power state can ensure that the overall temperature does not decrease and no new hotspots are generated. Reasonable time-frequency allocation of power can effectively improve energy conversion rates and optimize the temperature distribution of materials.
5. Conclusions
A collaborative switching multi-microwave sources heating model is proposed to improve material temperature uniformity and energy utilization efficiency in microwave heating. We are optimizing the system control architecture to handle communication congestion caused by DoS attacks and adopting a fixed lower bound event-triggered scheme to prevent Zeno behavior resulting from DoS attacks. We used the distributed combined heating strategy of multi-microwave sources based on collaborative switching to balance the conflict between microwave heating efficiency and material temperature uniformity.
A numerical model of multi-microwave sources coordinated consistent switching heating is constructed using the finite element method. SiC has the best temperature uniformity distribution and energy utilization efficiency among the eight heating strategies, the minimum values for and are 0.0066 and 0.4449, respectively. The microwave energy utilization efficiency is increased by 4.3∼10.7%, and the temperature uniformity is improved by 25.6∼43.6% compared to constant power heating with multi-microwave sources. The numerical examples effectively demonstrated the proposed switching model can optimize the temperature field distribution during microwave heating.
Four comparative heating experiments were performed on potatoes to highlight the effectiveness and universal applicability of the multi-microwave sources collaborative switching heating strategy. The total power input of the cavity was kept constant throughout the experiments. The results demonstrated that the collaborative switching heating strategy improved the temperature uniformity of potatoes by 20.82% compared to the constant power strategy; it is important to note that this improvement was lower than heating strategies (ii) and (iii). However, in the four comparative heating experiments, the microwave energy utilization efficiency of the multi-microwave source collaborative switching heating strategy was the highest, reaching 64.17%.
The results above demonstrate that the distributed combined heating strategy of multi-microwave sources based on event-triggered collaborative switching can effectively optimize material temperature uniformity. We have also discovered an interesting phenomenon where there is a subtle balance between enhancing heating efficiency and improving temperature distribution uniformity. In the future, we will further study the diversity of group switch topology patterns and the temporal order of group switch topology modes throughout the heating period to better optimize the temperature field distribution, which will be an exciting area of focus.
Author Contributions
Conceptualization, B.Y. and Z.Z.; methodology, Z.Z.; software, Z.Z.; validation, B.Y., Z.Z. and H.Z.; formal analysis, Z.Z.; investigation, Y.C.; resources, B.Y.; data curation, B.Y.; writing—original draft preparation, Z.Z.; writing—review and editing, B.Y.; visualization, X.C.; project administration, B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62363019, 61863020).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gulisano, F.; Crucho, J.; Gallego, J.; Picado-Santos, L. Microwave healing performance of asphalt mixture containing electric arc furnace (EAF) slag and graphene nanoplatelets (GNPs). Appl. Sci. 2020, 10, 1428. [Google Scholar] [CrossRef]
- Cheng, C.; Yang, B.; Xiao, Q. Hierarchical Coordinated Predictive Control of Multiagent Systems for Process Industries. Appl. Sci. 2024, 14, 6025. [Google Scholar] [CrossRef]
- Li, B.; Fan, X.; Yu, S.; Xia, H.; Nong, Y.; Bian, J.; Sun, M.; Zi, W. Microwave heating of biomasswaste residues for sustainable bioenergy and biomass materials preparation: A parametric simulation study. Energy 2023, 274, 127347. [Google Scholar] [CrossRef]
- Li, W.; Ye, J.; Yang, Y.; Zhu, H. Double-ridged waveguide for efficiently heating ultrafine filament fibers. Int. J. Heat Mass Transf. 2023, 200, 123543. [Google Scholar] [CrossRef]
- Zhu, H.; Su, J.; Yang, F.; Wu, Y.; Ye, J.; Huang, K.; Yang, Y. Effect of lossy thin-walled cylindrical food containers on microwave heating performance. J. Food Eng. 2023, 337, 111232. [Google Scholar] [CrossRef]
- Du, M.; Zhang, Z.; Huang, J.; Zhu, H.; Yang, Y. Study of multi-frequency heating based on the nonlinear response characteristics of magnetron to improve uniformity. J. Microw. Power Electromagn. Energy 2023, 57, 71–88. [Google Scholar] [CrossRef]
- Acevedo, L.; Ferreira, G.; López-Sabirón, A.M. Exergy transfer principles of microwavable materials under electromagnetic effects. Mater. Today Commun. 2021, 27, 102313. [Google Scholar] [CrossRef]
- Fan, Q.; Song, C.; Fu, P. Regulating n-doping strategies to construct 3d interconnected abundant porous n-doped carbon for polarization loss-enhanced microwave absorbers: Theory, design, and experiments. J. Clean. Prod. 2024, 434, 140118. [Google Scholar] [CrossRef]
- Radoiu, M.; Mello, A. Technical advances, barriers, and solutions in microwaveassisted technology for industrial processing. Chem. Eng. Res. Des. 2022, 181, 331–342. [Google Scholar] [CrossRef]
- Shi, H.; Huang, K.; Liu, Y.; Gou, D. Multidirectional polarization impacts on microwave heating efficiency: A molecular dynamics research of microwave heating of common solvents. J. Phys. Chem. B 2023, 127, 970–979. [Google Scholar] [CrossRef]
- Taghian Dinani, S.; Jenn, A.; Kulozik, U. Effect of vertical and horizontal sample orientations on uniformity of microwave heating produced by magnetron and solid-state generators. Foods 2022, 10, 1986. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Gu, H.; Zhu, H.; Yang, Y. Multi-physics field computation for microwave heating of multi-mobile components based on transformation optics and implicit function. Appl. Sci. 2023, 14, 58. [Google Scholar] [CrossRef]
- Zou, P.; Jin, G.; Nie, G.; Song, C.; Cui, Z. Multi-physical simulation of stirring effect on heating uniformity in a microwave reactor with an interlayer. J. Therm. Sci. Eng. Appl. 2022, 14, 011002. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, X.; Qiu, Y. Double pendulum mode stirrer for improved multimode microwave heating performance. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22866. [Google Scholar] [CrossRef]
- Guan, C.; Zhan, L.; Yao, S. Finite element simulation and experimental research on uniformity regulation of microwave heating of composite materials. Polymers 2022, 14, 3484. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Wu, Z.; Gao, H.; Shi, Y.; Peng, F.; Huang, H.; Han, Z. Temperature field optimization for distributed combined heat of multi-microwave sources based on group consistency under time-varying communication topology. Appl. Therm. Eng. 2024, 241, 122302. [Google Scholar] [CrossRef]
- Yin, S. Effect of metal slots on the heating uniformity of multisource cavity microwave. Front. Energy Res. 2023, 10, 1007566. [Google Scholar] [CrossRef]
- Wang, Z.; He, W.; Sun, J.; Wang, G.; Chen, J. Event-triggered control of switched nonlinear time-delay systems with asynchronous switching. IEEE Trans. Cybern. 2024, 54, 4348–4358. [Google Scholar] [CrossRef]
- Zhao, G.; Hua, C. Leader-following consensus of multiagent systems via asynchronous sampled-data control: A hybrid system approach. IEEE Trans. Autom. Control 2022, 67, 2568–2575. [Google Scholar] [CrossRef]
- Deng, C.; Jin, X.Z.; Wu, Z.G.; Che, W.W. Data-driven-based cooperative resilient learning method for nonlinear mass under dos attacks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–10, early access. [Google Scholar] [CrossRef]
- Hu, S.; Yue, D.; Chen, X.; Cheng, Z.; Xie, X. Resilient h filtering for event-triggered networked systems under nonperiodic dos jamming attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1392–1403. [Google Scholar] [CrossRef]
- Wang, Y.-W.; Zeng, Z.-H.; Liu, X.-K.; Liu, Z.-W. Input-to-state stability of switched linear systems with unstabilizable modes under dos attacks. Automatica 2022, 146, 110607. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Basak, T. A review on the susceptor assisted microwave processing of materials. Energy 2016, 97, 306–338. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Basak, T. Role of metal inserts for targeted, uniform or controlled microwave heating objectives involving generalized sets of dielectrics (Group 1–4). Int. J. Heat Mass Transf. 2024, 222, 125133. [Google Scholar] [CrossRef]
- Yang, B.; Zhao, Z.; Wu, Z.; Liu, S.; Yang, Y.; Liu, B. Research on the optimisation of the temperature field distribution of a multi-source microwave agent system based on event-triggered. Chem. Eng. Process.-Process Intensif. 2024, 109727. [Google Scholar]
- Zeng, P.; Deng, F.; Liu, X.; Gao, X. Event-triggered resilientl control for markov jump systems subject to denial-of-service jamming attacks. IEEE Trans. Cybern. 2021, 52, 10240–10252. [Google Scholar] [CrossRef]
- Cheng, T.-H.; Kan, Z.; Klotz, J.R.; Shea, J.M.; Dixon, W.E. Event-triggered control of multiagent systems for fixed and time-varying network topologies. IEEE Trans. Autom. Control 2017, 62, 5365–5371. [Google Scholar] [CrossRef]
- Zeng, P.; Deng, F.; Gao, X.; Liu, X. Eventtriggered and self-triggered l control for markov jump stochastic nonlinear systems under dos attacks. IEEE Trans. Cybern. 2021, 53, 1170–1183. [Google Scholar] [CrossRef]
- Yang, B.; Wu, Z.; Gao, H.; Zhou, L.; Sun, J. Research on the optimisation of the temperature field distribution of a multi microwave source agent system based on group consistency. High Temp. Mater. Process. 2022, 41, 650–668. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).