Study of the Vibration Isolation Properties of a Pneumatic Suspension System for the Seat of a Working Machine with Adjustable Stiffness
Abstract
1. Introduction
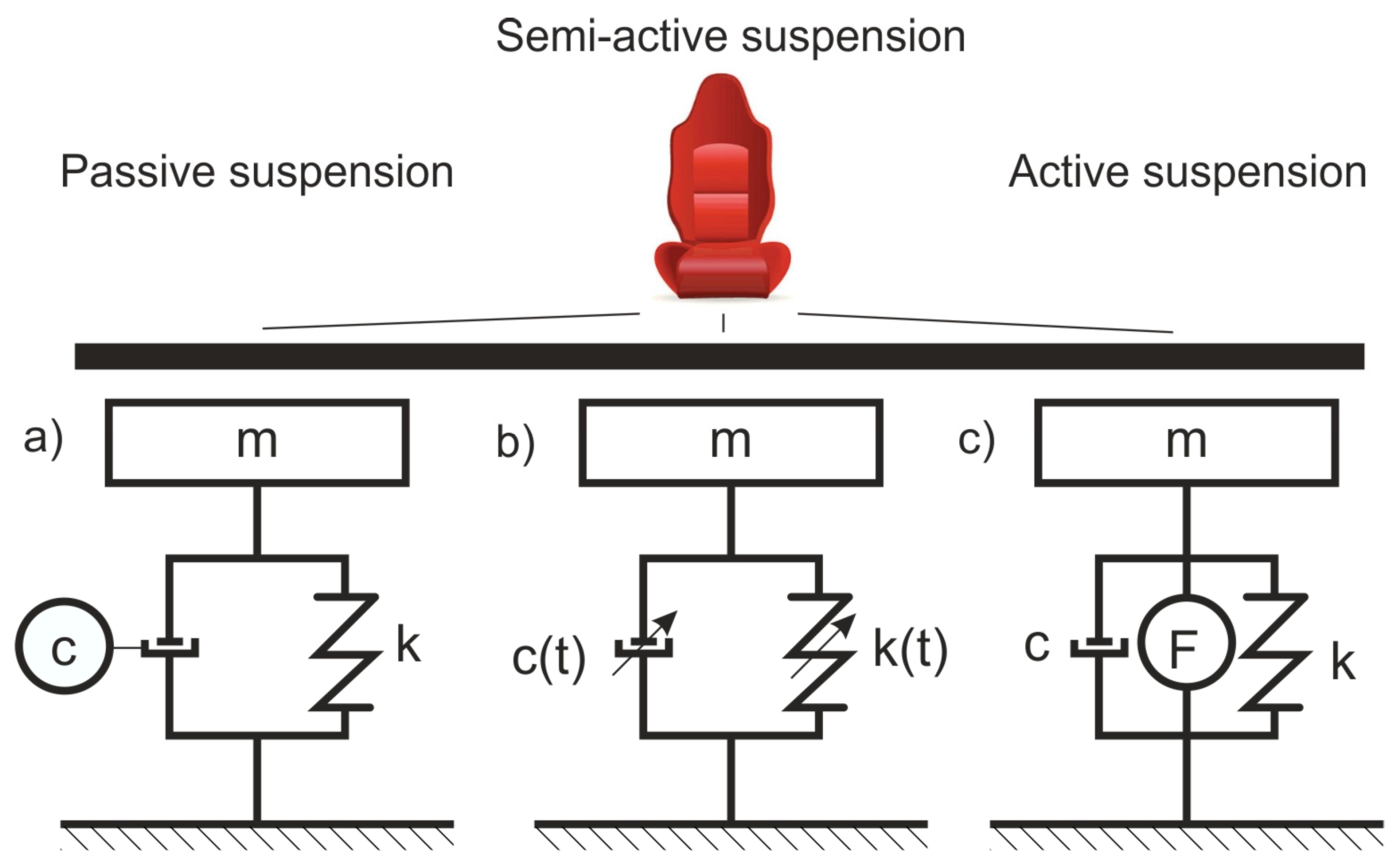
1.1. Suspension Types of Vehicle Driver Seats
- Semi-active damping allows the adjustment of damping to driving conditions, thus acting faster than traditional passive systems while enhancing vehicle comfort and handling;
- An adaptive damping system that adjusts itself to changing road conditions for improved comfort and control—it can also respond to irregularities on the road surface;
- Semi-active load-levelling, which maintains stability and vehicle height adjustment, especially while carrying heavy loads;
- Semi-active suspension control that offers control over damping—improving ride comfort and road friendliness.
1.2. Functionality of Semi-Active Suspension Systems
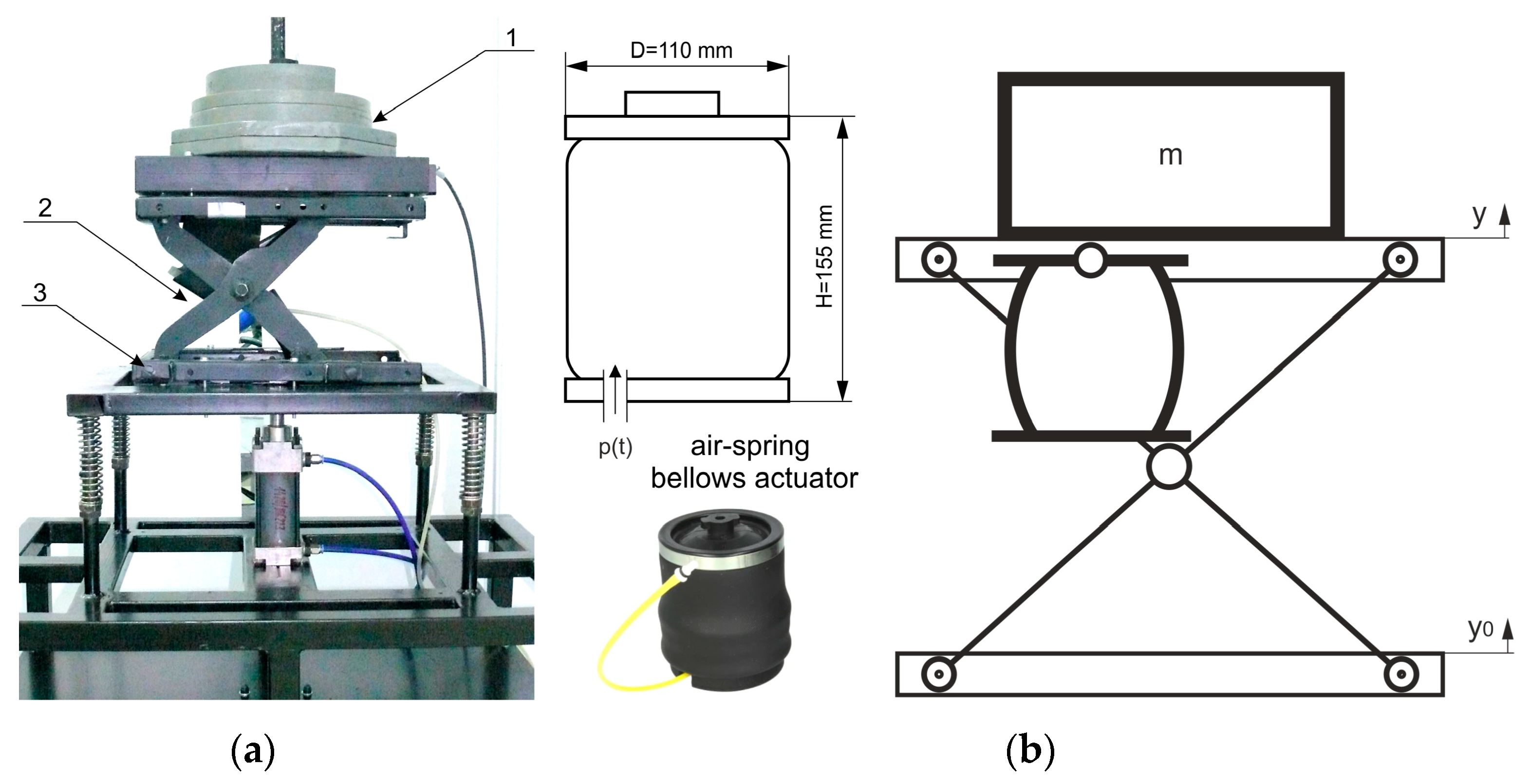
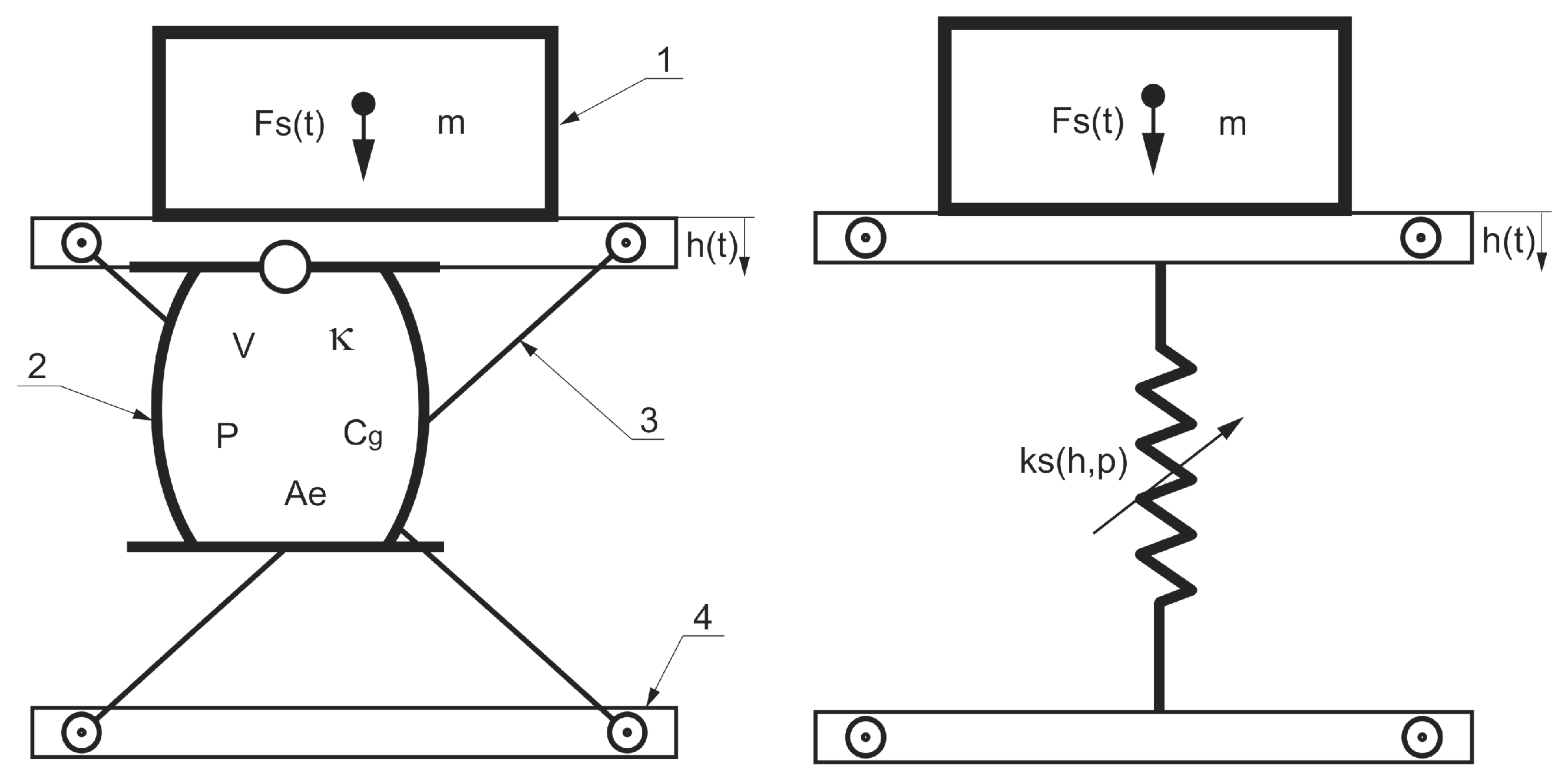
2. Test Stand Description
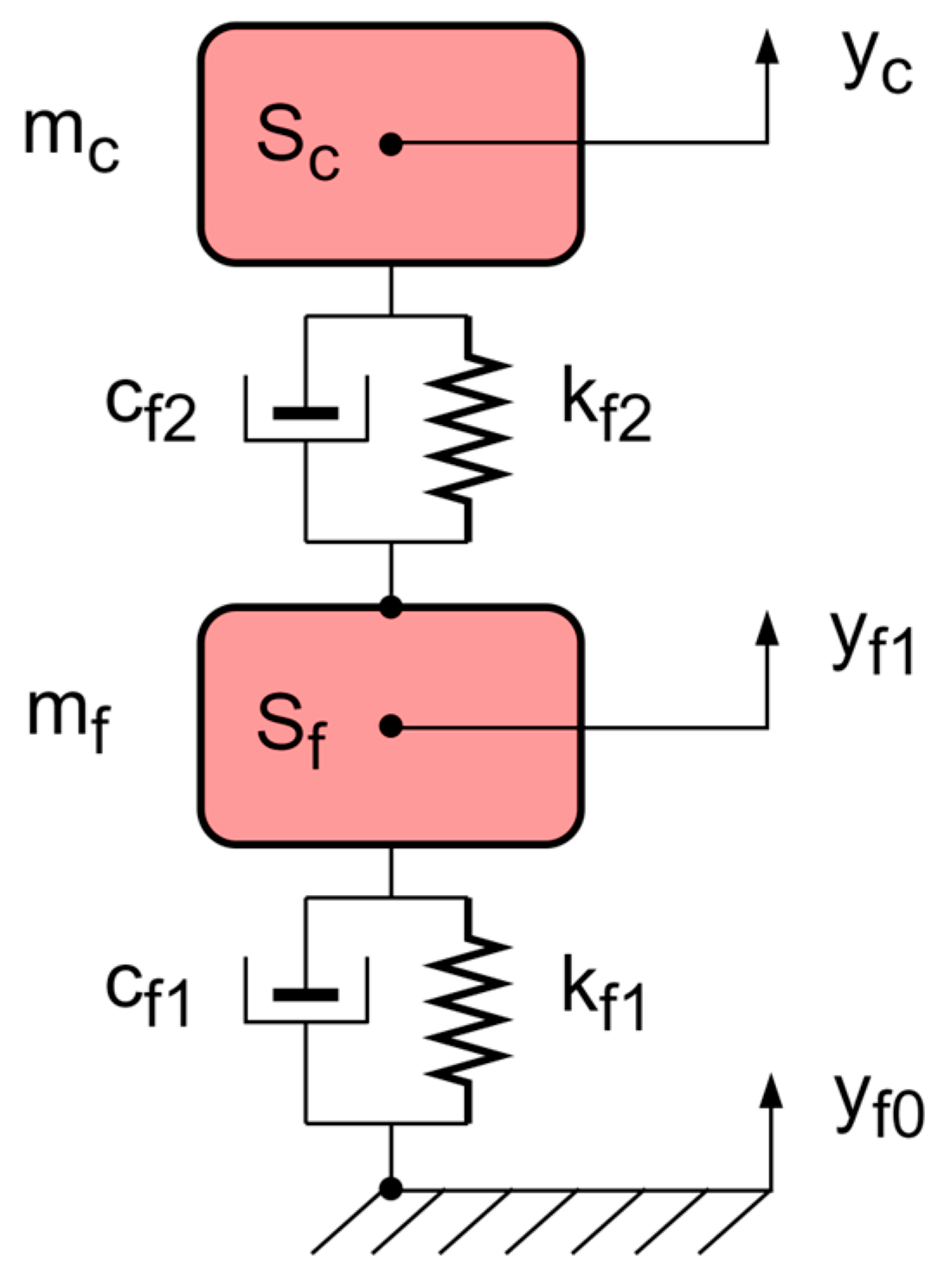
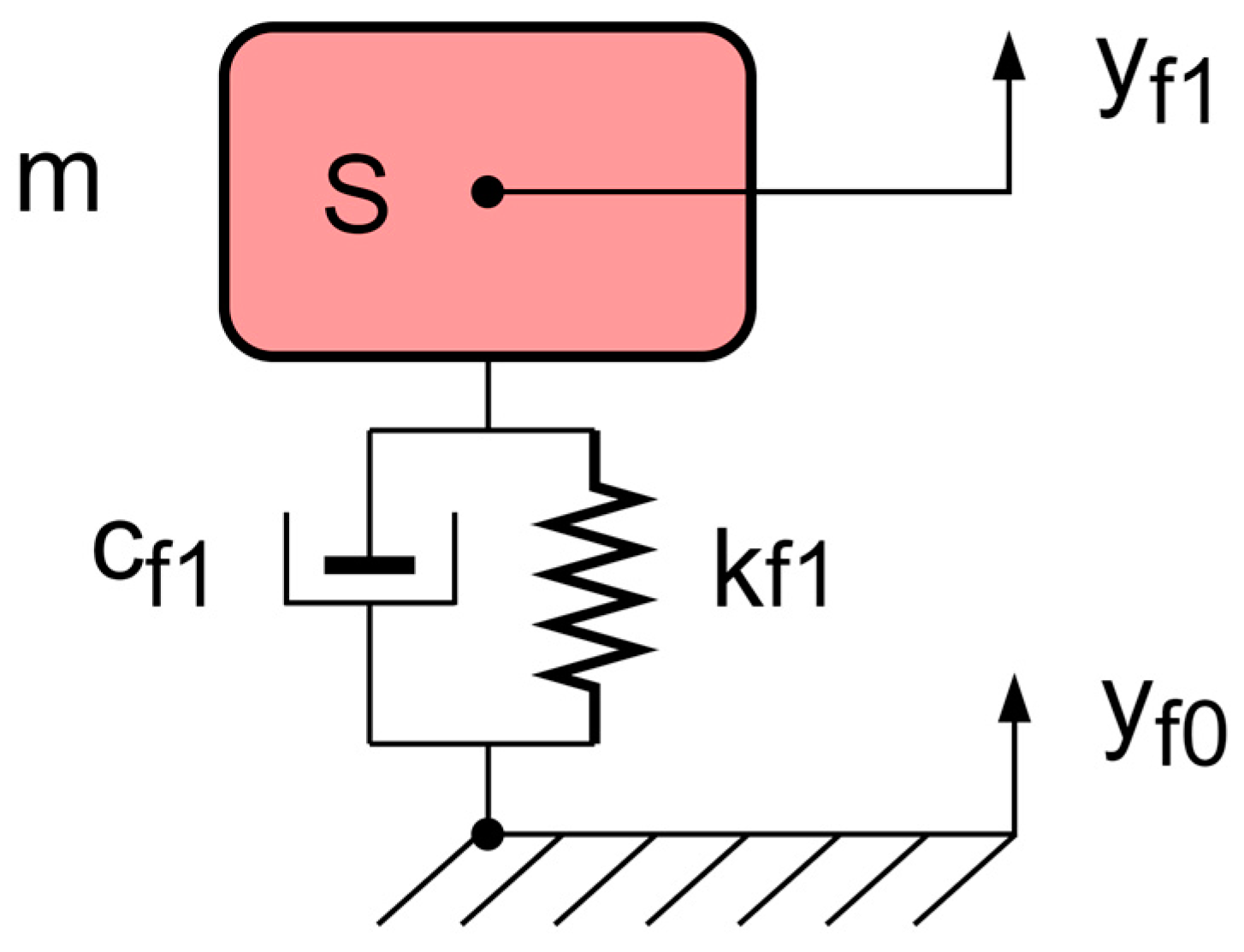
3. Physical and Mathematical Model of a Single-Degree-of-Freedom Seat Suspension
Results of the Theoretical and Experimental Analysis
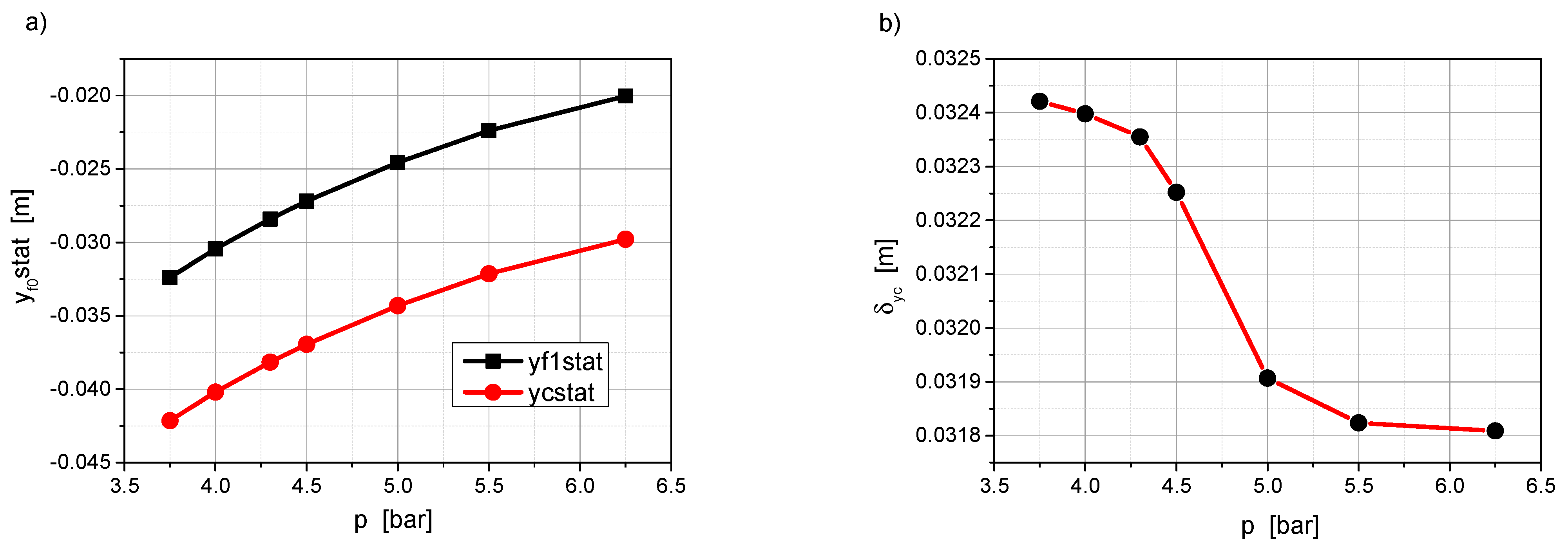
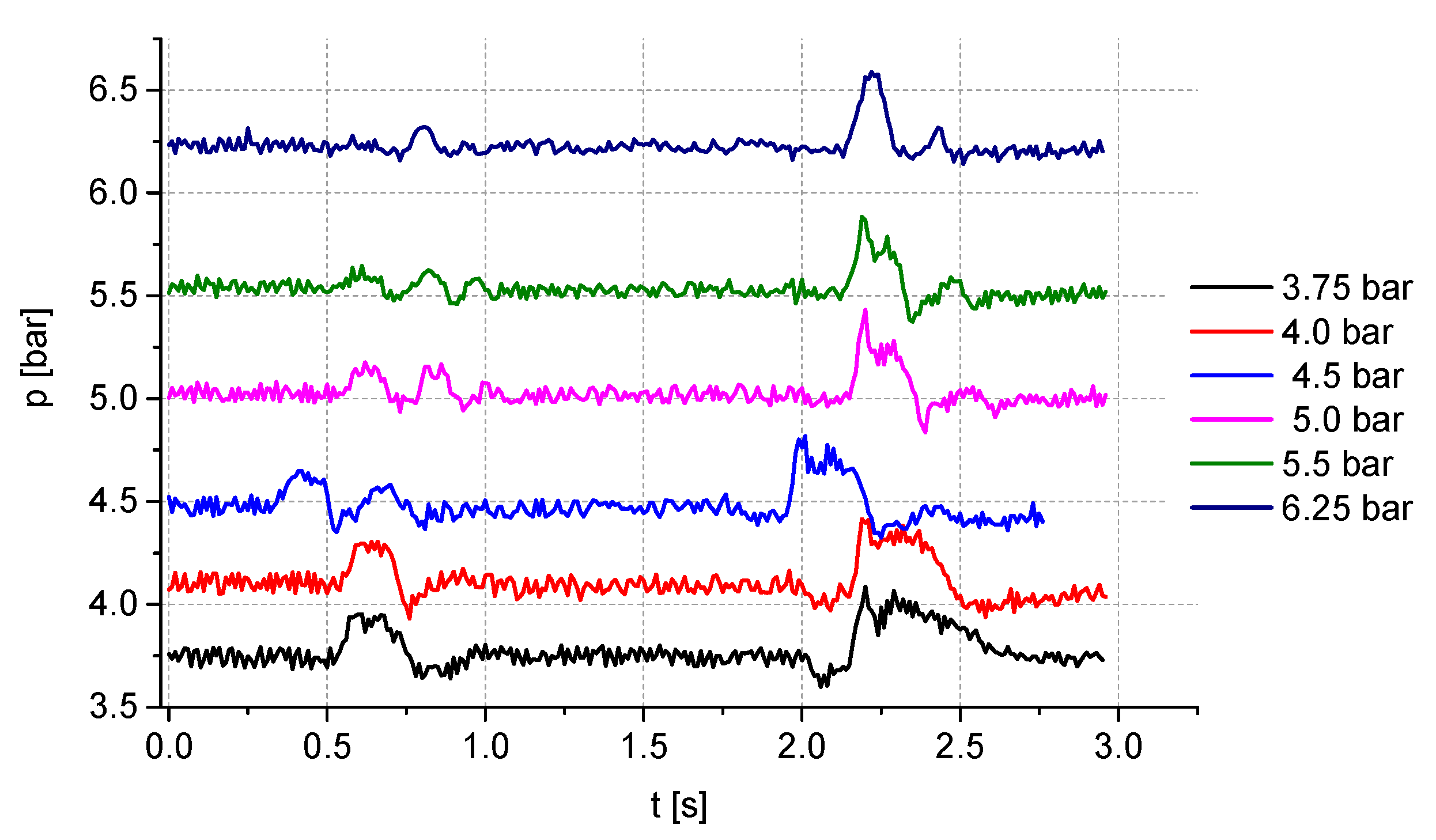
- The bellows are filled to the initial pressure specified by the pneumatic silencer manufacturer, as illustrated in Figure 9 for t = 0.0 s. The pressure value is set automatically by the system.
- The operator is seated on the seat, causing it to move. The displacement of this movement is automatically measured by the system. Thisdisplacementisstatic,.
- The weight of the operator is automatically determined by the system. There are two options for this determination. The first is to use the relationship from Figure 10b and approximate the mass value. The second is to use the relationship from Figure 9 for t = 0.0 s and calculate the mass from Equation (3). It is possible to use both options simultaneously and determine the average mass.
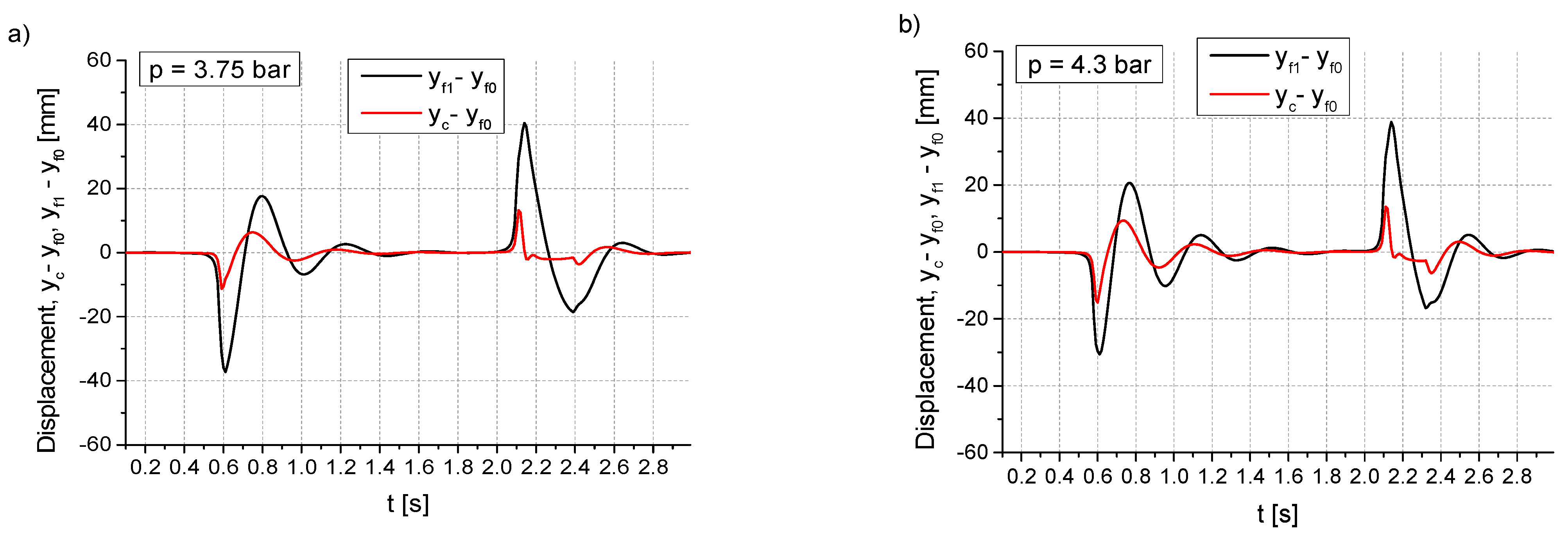
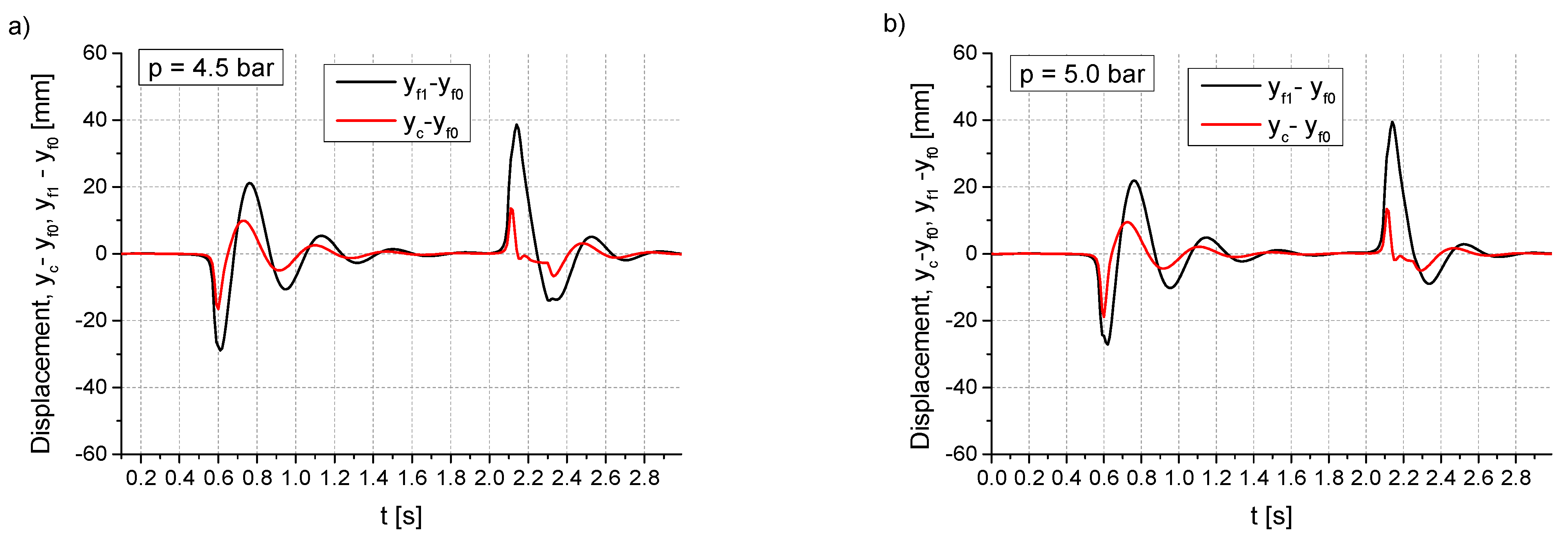
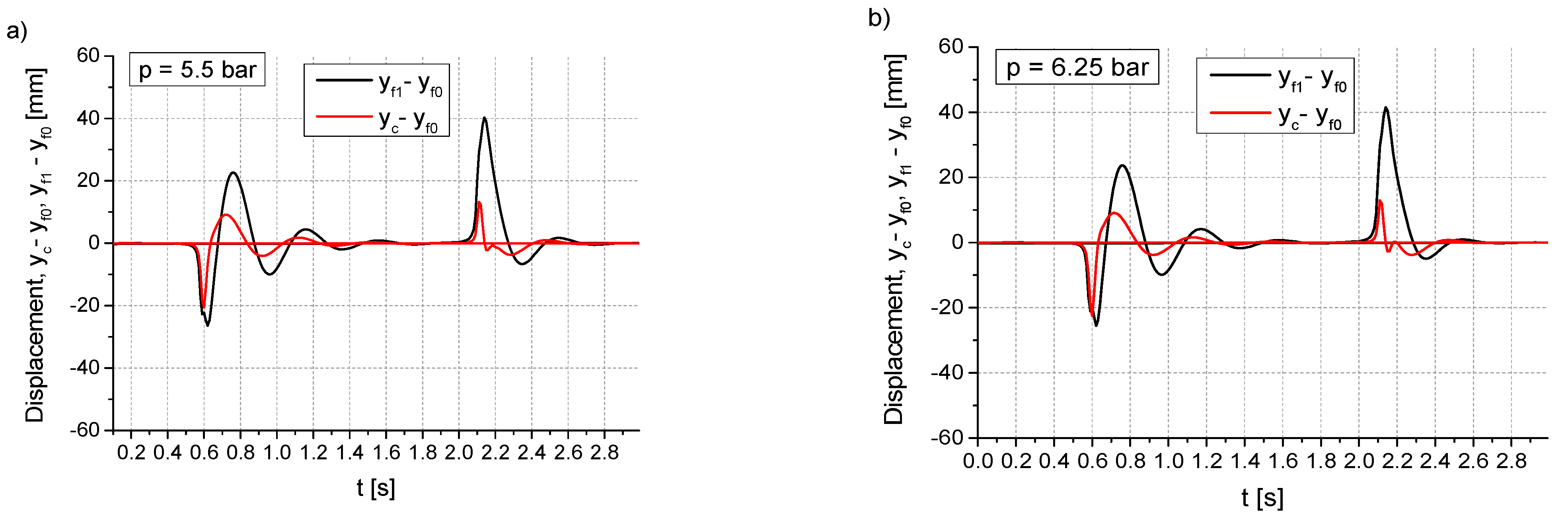
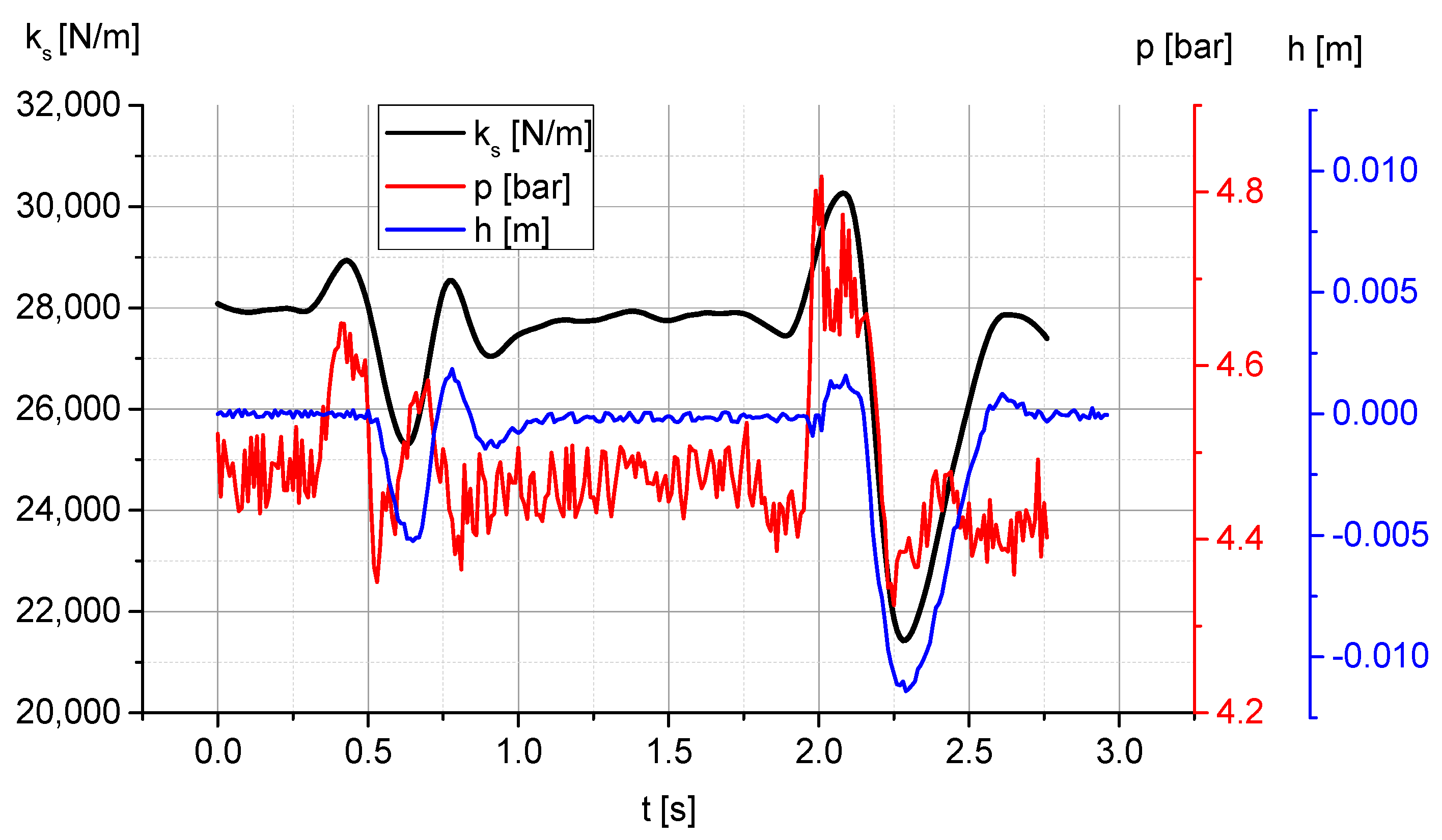
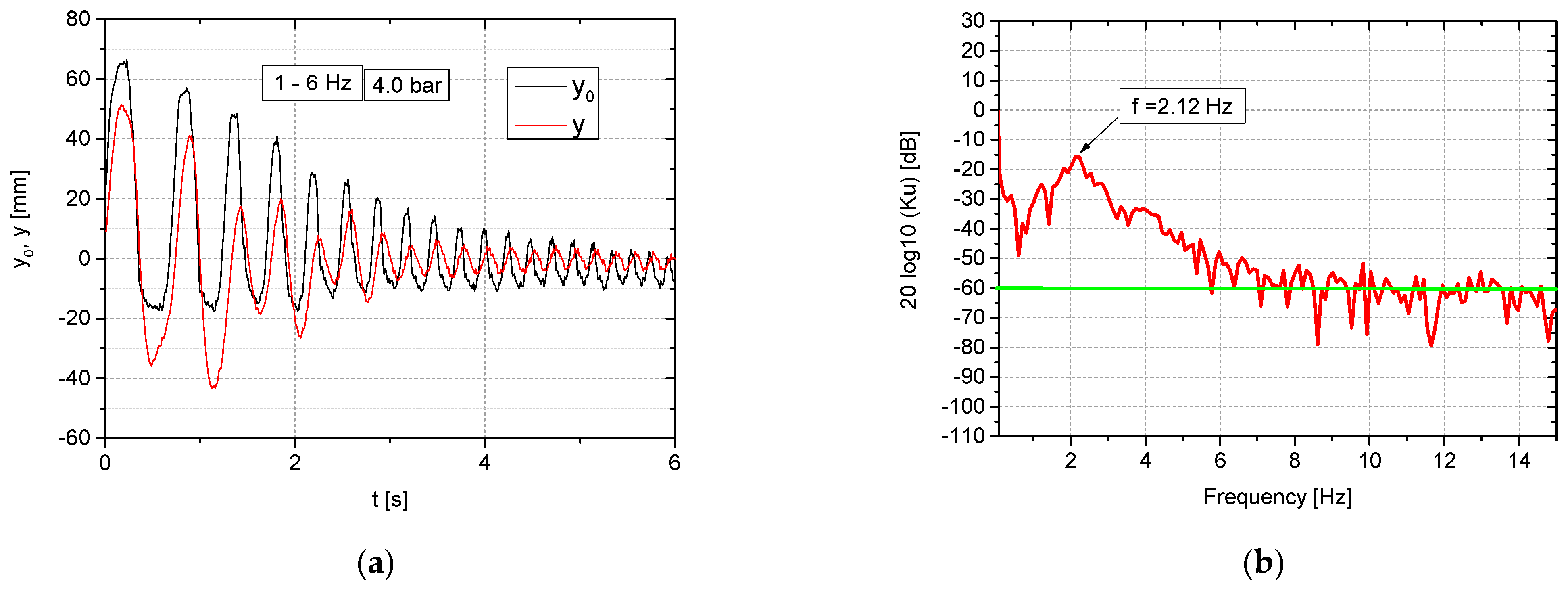
- The effective acceleration and the maximum relative displacement values , as determined by the system, can be found in Figure 12. The relative importance of these opposing vibration isolation quality criteria can be quantified by introducing weighting factors. It is necessary to decide which parameter is considered more important. The acceleration parameter can directly affect the human internal organs, while the displacement parameter can affect the perception of the activities performed.
- The values of the effective acceleration and maximum relative displacement , in conjunction with the current system weight, permit the determination of the bellows pressure at which the operator’s work will be performed.
4. AirSpring Equation
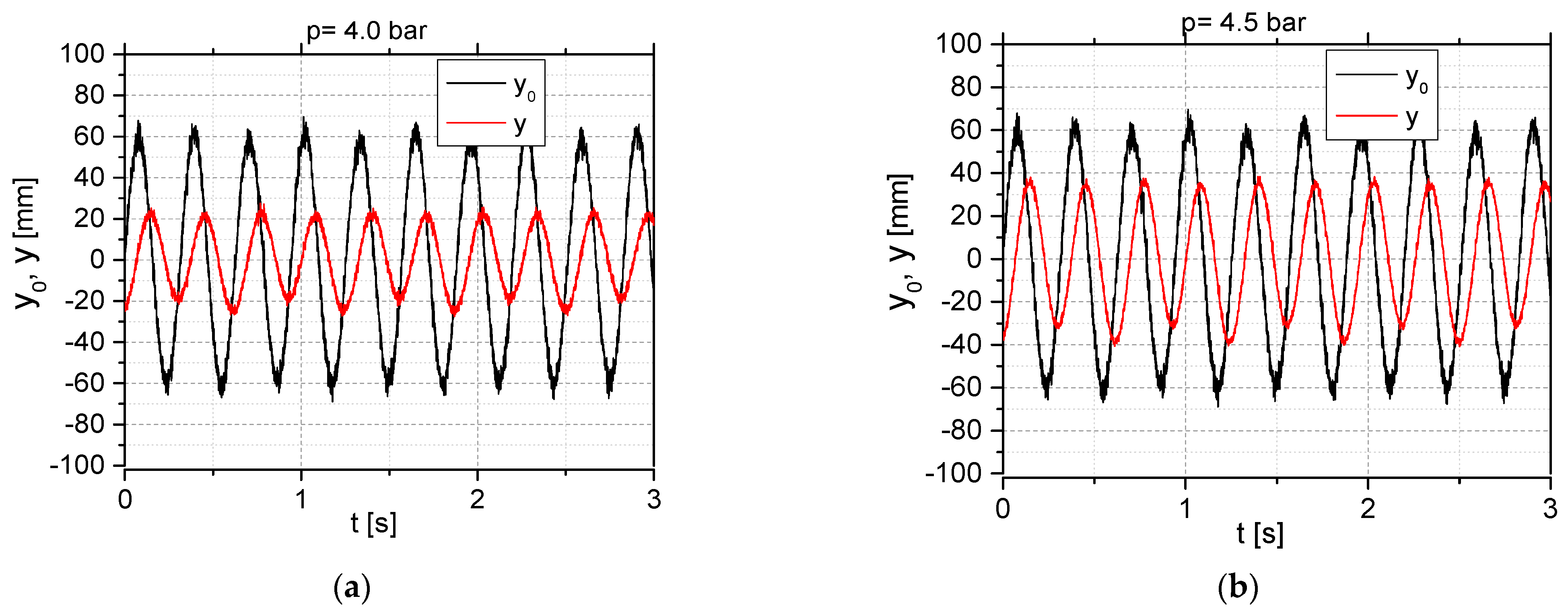
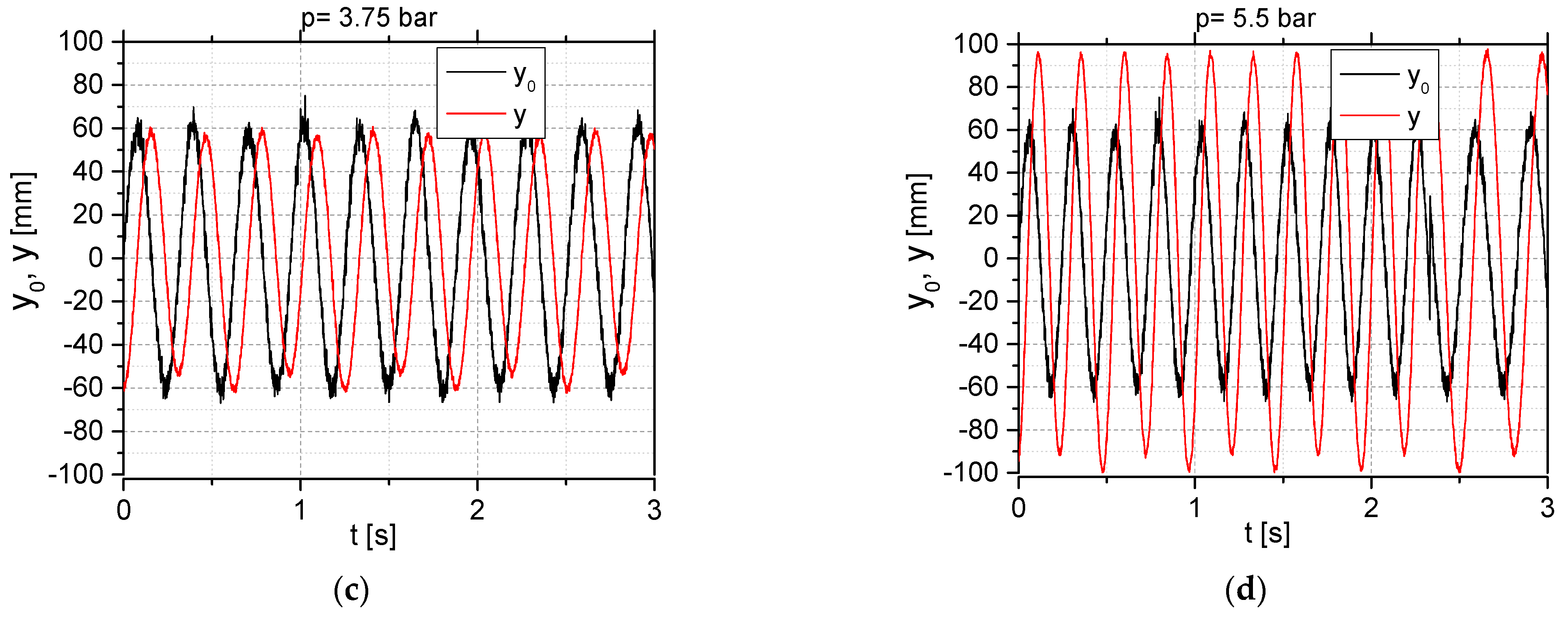
5. Experimental and Simulation Studies of the Harmonic Motion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Physical and Mathematical Model of a Human–Seat System with Two Degrees of Freedom
| p [bar] | [m] | ||
|---|---|---|---|
| 3.75 | |||
| 4.0 | |||
| 4.3 | |||
| 4.5 | |||
| 5 | |||
| 5.5 | |||
| 6.25 |
Appendix B. Simulation Parameters
| Symbol | Value | Unit | Quantity |
|---|---|---|---|
| p | 3.75–6.5 | bar | Pressure in the pneumatic bellows |
| H | 0.155 | m | Pneumaticbellowsheight |
| D | 0.11 | m | Pneumaticbellowsdiameter |
| V0 | 0.0013 | m3 | Initial volume in pneumatic bellows |
| Ae | 0.01 | m2 | Area of the pneumatic bellows |
| κ | 1.4 | Exponent of adiabatic | |
| 69.6 | kg | Mass of the person | |
| 8 | kg | Mass of the seat | |
| 9.81 | m/s2 | Acceleration of gravity | |
| 0.063 | m | Excitation amplitude | |
| 0.003 | Shape factor | ||
| 0.58 | s | The first-time extremes | |
| 2.1 | s | The second-time extremes | |
| s | Duration of forcing |
References
- Pellecchia, D.; Vaiana, N.; Spizzuoco, M.; Serino, G.; Rosati, L. Axial Hysteretic Behaviour of Wire Rope Isolators: Experiments and Modelling. Mater. Des. 2023, 225, 111436. [Google Scholar] [CrossRef]
- Desai, R.; Guha, A.; Seshu, P. A Comparison of Different Models of Passive Seat Suspensions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2585–2604. [Google Scholar] [CrossRef]
- Tu, L.; Ning, D.; Sun, S.; Li, W.; Huang, H.; Dong, M.; Du, H. A Novel Negative Stiffness Magnetic Spring Design for Vehicle Seat Suspension System. Mechatronics 2020, 68, 102370. [Google Scholar] [CrossRef]
- Hryciów, Z.; Krasoń, W.; Wysocki, J. Evaluation of the Influence of Friction in a Multi-Leaf Spring on the Working Conditions of a Truck Driver. Eksploat. i Niezawodn. 2021, 23, 422–429. [Google Scholar] [CrossRef]
- Na, W.; Dawei, G. Identification and Optimization of Vehicle Vibration and Noise. In Proceedings of the 8th International Conference on Electromechanical Control Technology and Transportation (ICECTT 2023), Hangzhou, China, 7 September 2023. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, R.; Yang, L.; Sun, Z.; Meng, X. Modelling and Control of a Semi-Active Dual-Chamber Hydro-Pneumatic Inerter-Based Suspension System. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2355–2370. [Google Scholar] [CrossRef]
- Bouvin, J.L.; Moreau, X.; Benine-Neto, A.; Hernette, V.; Serrier, P.; Oustaloup, A. Modelling and Design of a Pneumatic CRONE Suspension Architecture for Ride Comfort. Veh. Syst. Dyn. 2021, 59, 890–906. [Google Scholar] [CrossRef]
- Tan, X.; Chen, S.; Wang, B.; Tang, J.; Wang, L.; Zhu, S.; Yao, K.; Xu, P. Real-Time Tunable Negative Stiffness Mechanical Metamaterial. Extrem. Mech. Lett. 2020, 41, 100990. [Google Scholar] [CrossRef]
- Chen, L.; Ding, R.; Wang, R.; Meng, X. Research on the Mode Switching Control of Vehicle Electromagnetic Suspension Employing Linear Motor. Int. J. Veh. Syst. Model. Test. 2020, 14, 195. [Google Scholar] [CrossRef]
- Bian, Y.; Wang, Y.; Dong, M.; Kong, H. Research on Vertical Vibration Characteristics of Human Body under Standard Sitting Posture. In Proceedings of the Proc. SPIE 12612, International Conference on Artificial Intelligence and Industrial Design (AIID 2022), 126121B, Zhuhai, China, 14 April 2023. [Google Scholar] [CrossRef]
- Jiao, R.; Nguyen, V.; Le, V. Ride Comfort Performance of Hydro Pneumatic Isolation for Soil Compactors Cab in Low Frequency Region. J. Vibroengineering 2020, 22, 1174–1186. [Google Scholar] [CrossRef]
- Vo, N.Y.P.; Nguyen, M.K.; Le, T.D. Analytical Study of a Pneumatic Vibration Isolation Platform Featuring Adjustable Stiffness. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105775. [Google Scholar] [CrossRef]
- Tu, L.; Du, H.; Dong, M.; Ning, D.; Wu, Y.; Li, W.; Huang, H. Semiactively Controllable Vehicle Seat Suspension System with Negative Stiffness Magnetic Spring. IEEE/ASME Trans. Mechatron. 2021, 26, 156–167. [Google Scholar] [CrossRef]
- Nguyen, V.; Jiao, R.; Le, V.; Wang, P. Study to Control the Cab Shaking of Vibratory Rollers Using the Horizontal Auxiliary Damping Mount. Math. Model. Eng. 2020, 6, 57–65. [Google Scholar] [CrossRef]
- Liao, X.; Zhang, N.; Du, X.; Zhang, W. Theoretical Modeling and Vibration Isolation Performance Analysis of a Seat Suspension System Based on a Negative Stiffness Structure. Appl. Sci. 2021, 11, 6928. [Google Scholar] [CrossRef]
- Radhakrishnan, K.; Godwin Antony, A.; Rajaguru, K.; Sureshkumar, B. Torsional Vibration Analysis of Torsion Bar Spring for off Road Vehicle Driver Seat. Mater. Today Proc. 2020, 21, 669–672. [Google Scholar] [CrossRef]
- Liu, C. Vibration Isolation and Noise Reduction Design of Commercial Vehicle Cab Mounting System Based on Blind Source Separation. In Proceedings of the International Conference on Mechatronics Engineering and Artificial Intelligence (MEAI 2022), Changsha, China, 1 March 2023. [Google Scholar] [CrossRef]
- Davoodi, E.; Safarpour, P.; Pourgholi, M.; Khazaee, M. Design and Evaluation of Vibration Reducing Seat Suspension Based on Negative Stiffness Structure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4171–4189. [Google Scholar] [CrossRef]
- Wang, X.; Gong, H.; Liu, J. Design and Simulation of a Vibration Isolation Platform Based on Air Spring for Road Transportation Applications. In Proceedings of the 2nd International Conference on Internet of Things and Smart City (IoTSC 2022), Xiamen, China, 8 May 2022. [Google Scholar] [CrossRef]
- Liu, C.; Hemmatian, M.; Sedaghati, R.; Wen, G. Development and Control of Magnetorheological Elastomer-Based Semi-Active Seat Suspension Isolator Using Adaptive Neural Network. Front. Mater. 2020, 7, 171. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, J.; Zhang, Y. Dual-Chamber Pneumatically Interconnected Suspension: Modeling and Theoretical Analysis. Mech. Syst. Signal Process. 2021, 147, 107125. [Google Scholar] [CrossRef]
- Brijeshkumar, P.; Santhosh, B. Dynamics and Isolation Capabilities of a Magnetic Spring-Based Quasi-Zero Stiffness Vibration Isolation Mechanism for Passenger Vehicle Seat Isolation. In Advances in Industrial Machines and Mechanisms; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Cheng, C.; Hu, Y.; Ma, R. Enhanced Ride Comfort Using Nonlinear Seat Suspension with High-Static-Low-Dynamic Stiffness. Noise Vib. Worldw. 2020, 51, 63–76. [Google Scholar] [CrossRef]
- Woś, P.; Dindorf, R. Studies of Properties of the Seat Suspension System with Air Spring. EPJ Web Conf. 2019, 213, 02101. [Google Scholar] [CrossRef]
- Rakheja, S.; Afework, Y.; Sankar, S. An Analytical and Experimental Investigation of the Driver—Seat—Suspension System. Veh. Syst. Dyn. 1994, 23, 501–524. [Google Scholar] [CrossRef]
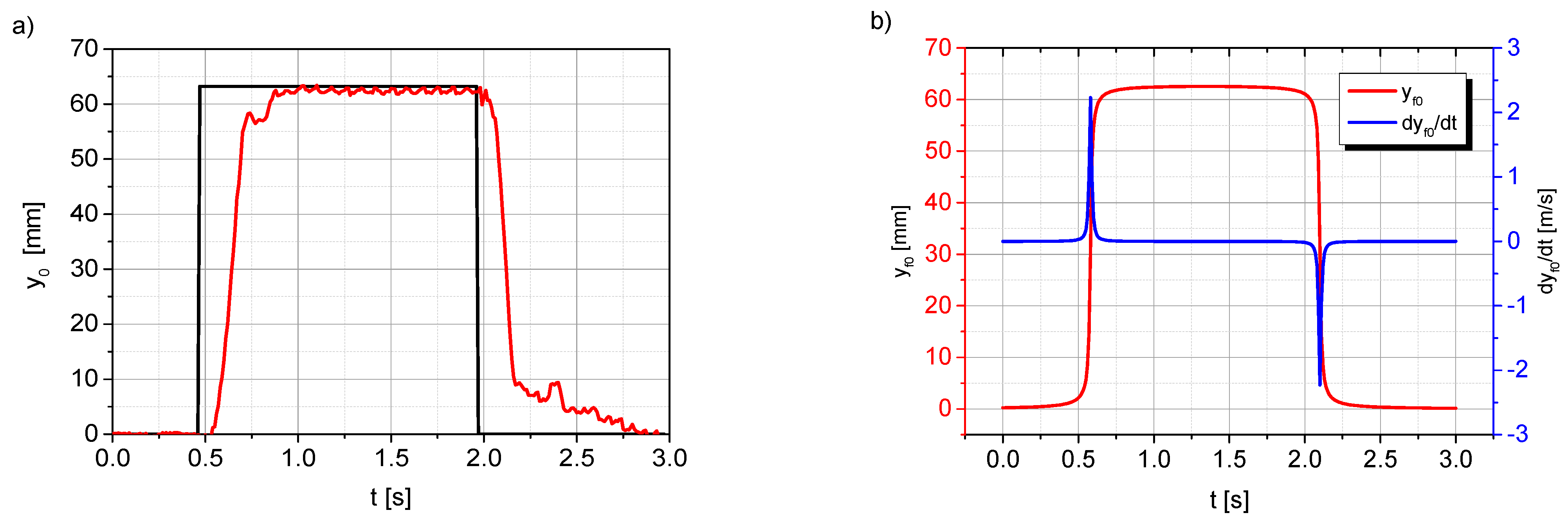
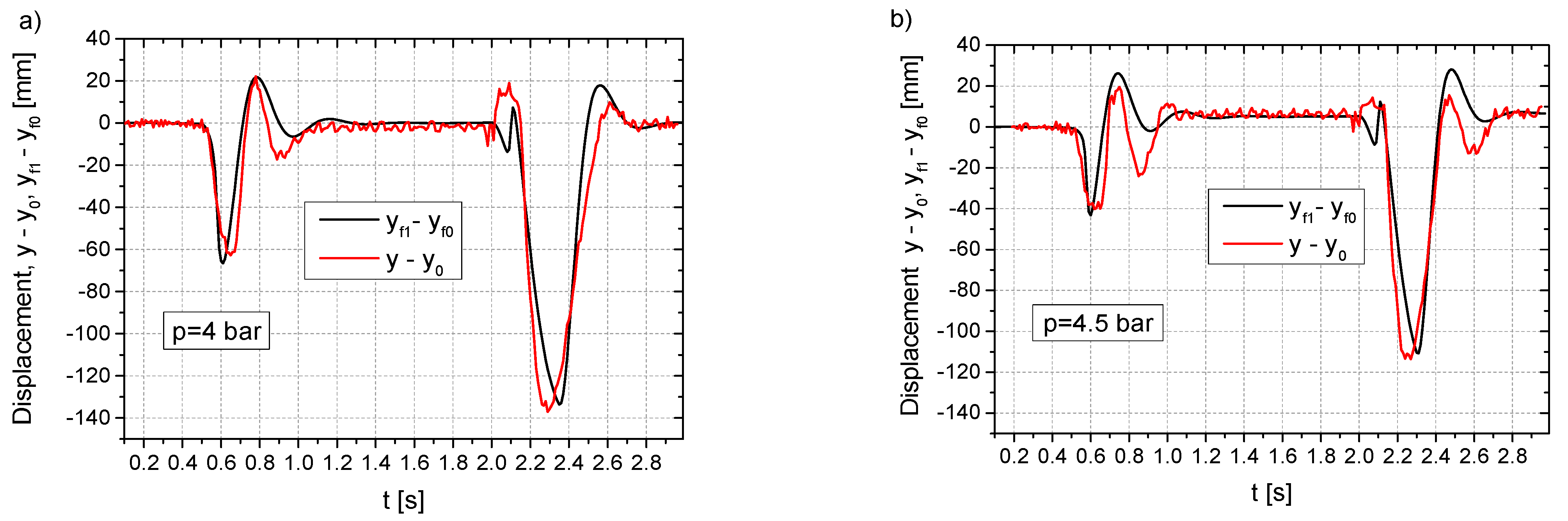

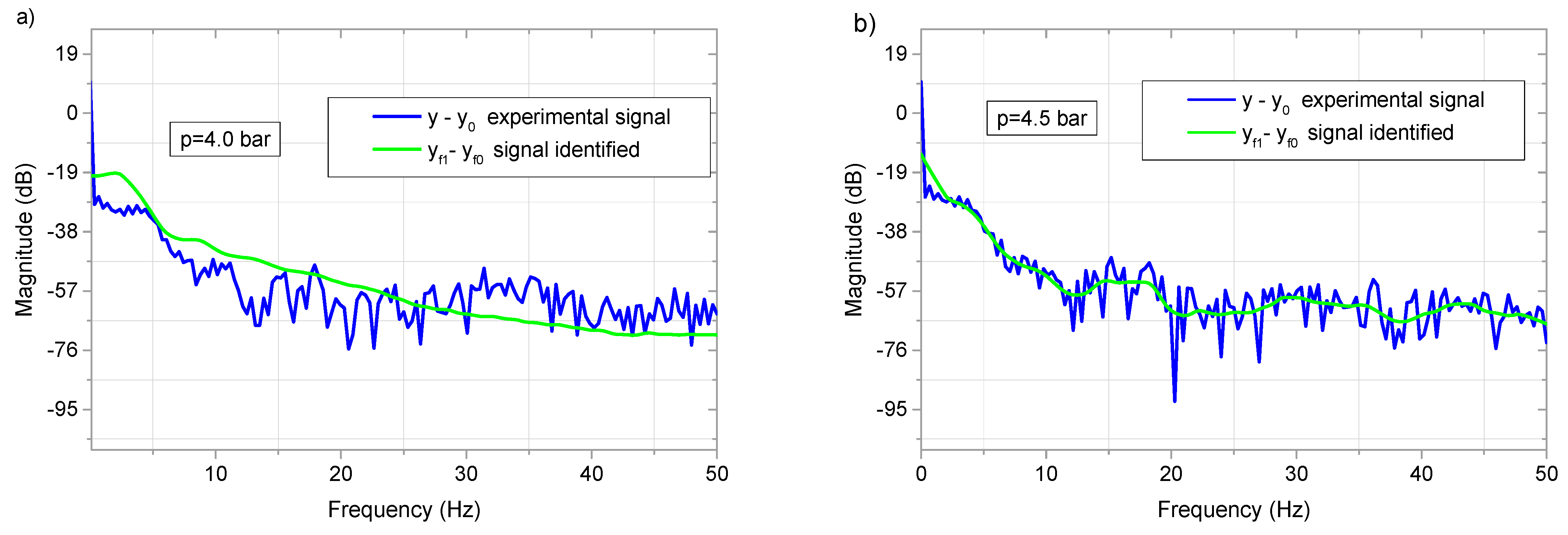
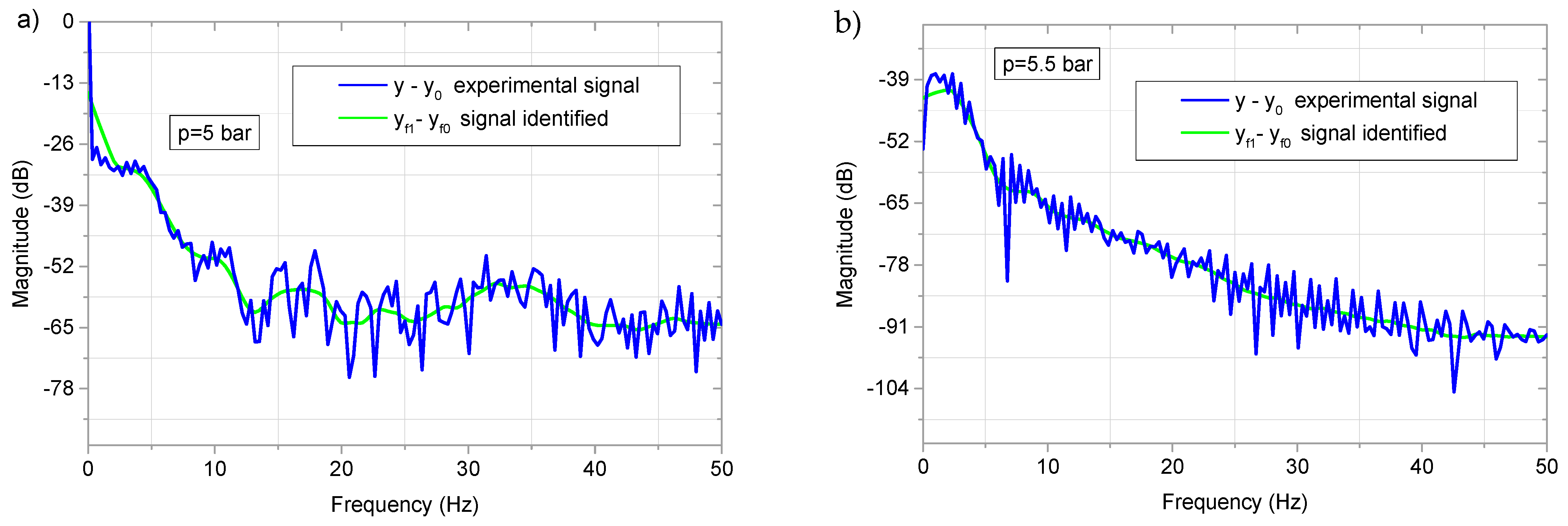
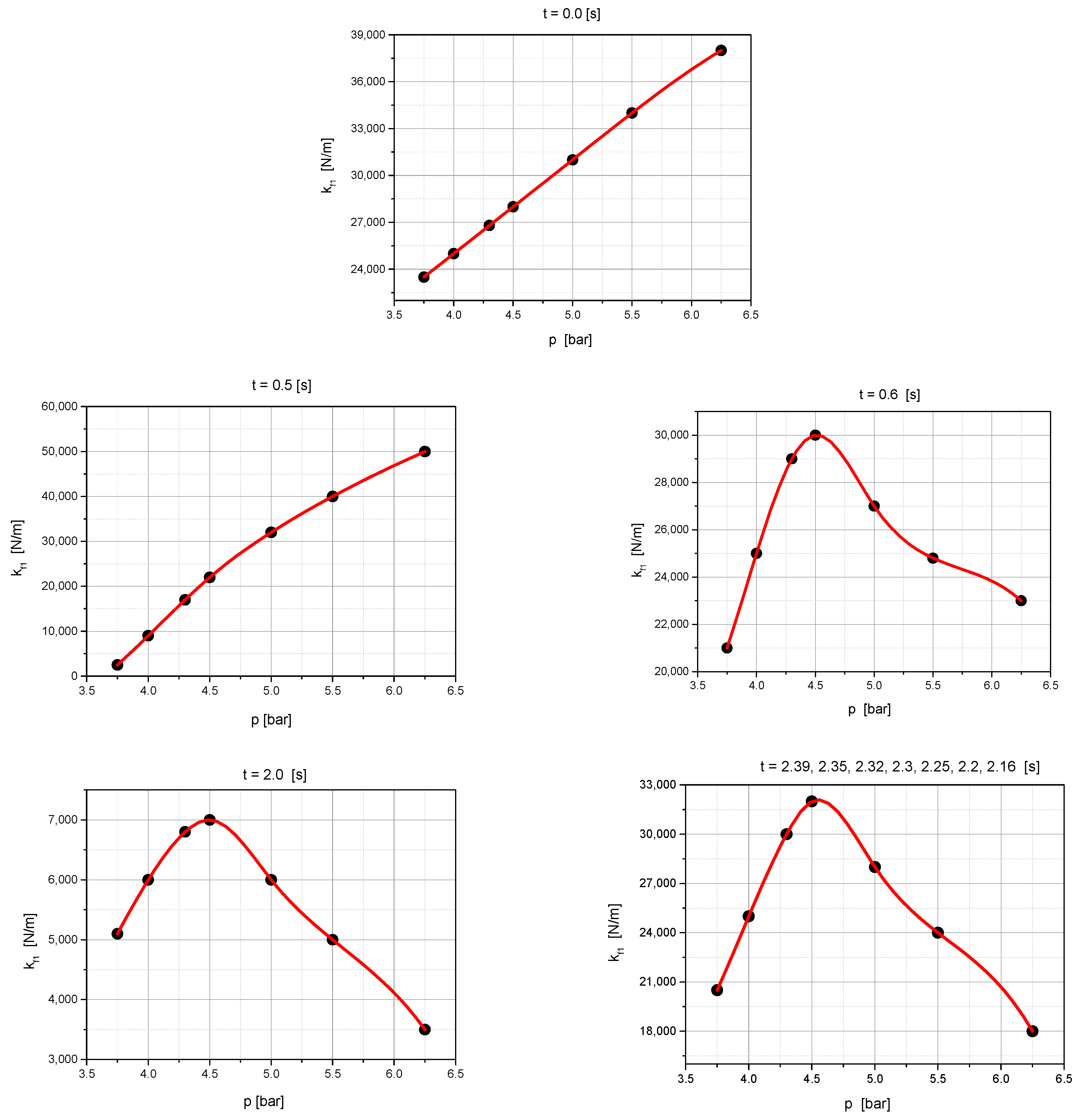
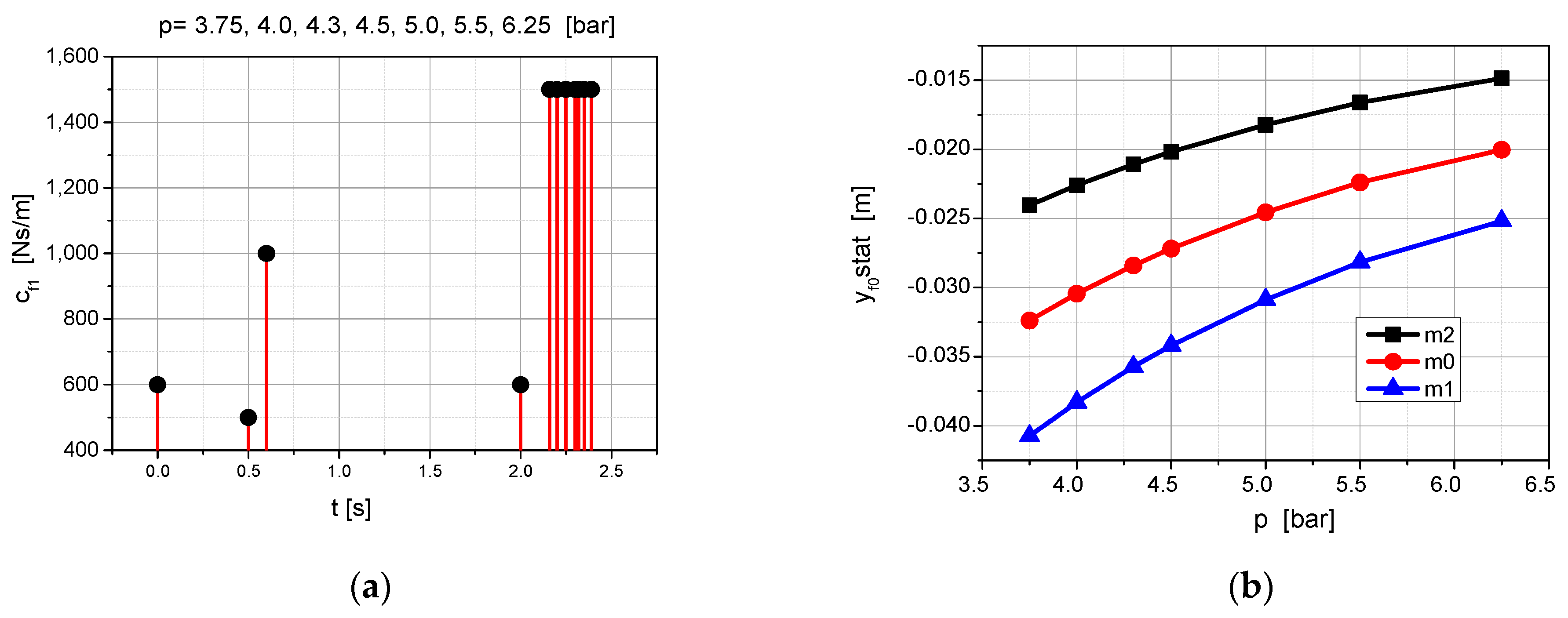

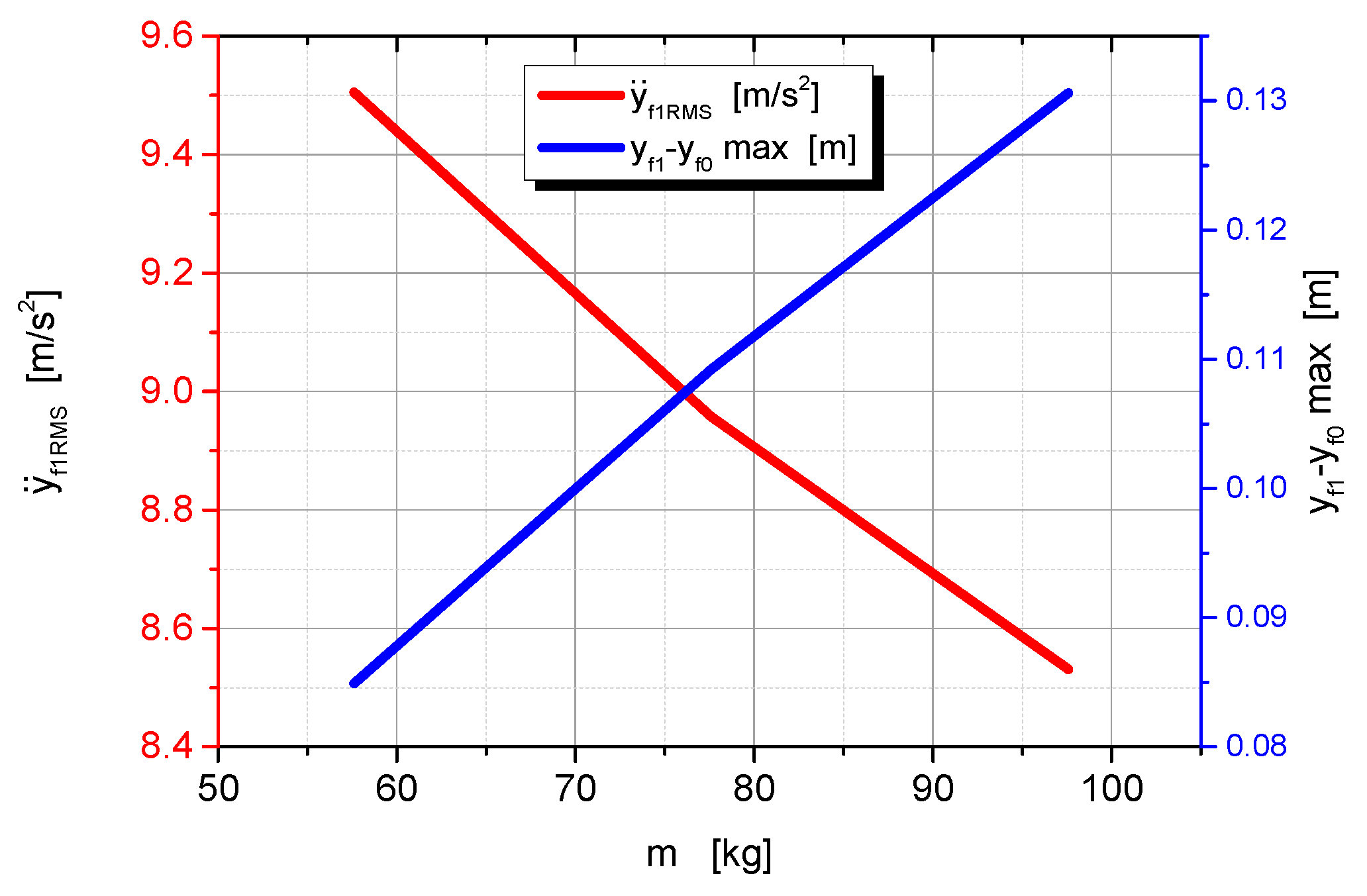

| 3.75 | 4.30 | 5.0 | 6.25 | |
|---|---|---|---|---|
| 0.0310 |
| Types of Seats | Pressure p [bar] | Amplification Coefficient Amplitudes for the Model Kfu | Amplification Coefficient Amplitudes Ku |
|---|---|---|---|
| Passive soft | 3.75 | 0.96 | 0.95 |
| Passive optimal 1 | 4.0 | 0.37 | 0.36 |
| Passive optimal 2 | 4.5 | 0.65 | 0.65 |
| Passive hard | 5.5 | 1.51 | 1.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wos, P.; Dziopa, Z. Study of the Vibration Isolation Properties of a Pneumatic Suspension System for the Seat of a Working Machine with Adjustable Stiffness. Appl. Sci. 2024, 14, 6318. https://doi.org/10.3390/app14146318
Wos P, Dziopa Z. Study of the Vibration Isolation Properties of a Pneumatic Suspension System for the Seat of a Working Machine with Adjustable Stiffness. Applied Sciences. 2024; 14(14):6318. https://doi.org/10.3390/app14146318
Chicago/Turabian StyleWos, Piotr, and Zbigniew Dziopa. 2024. "Study of the Vibration Isolation Properties of a Pneumatic Suspension System for the Seat of a Working Machine with Adjustable Stiffness" Applied Sciences 14, no. 14: 6318. https://doi.org/10.3390/app14146318
APA StyleWos, P., & Dziopa, Z. (2024). Study of the Vibration Isolation Properties of a Pneumatic Suspension System for the Seat of a Working Machine with Adjustable Stiffness. Applied Sciences, 14(14), 6318. https://doi.org/10.3390/app14146318





