Next-Generation Blockchain Technology: The Entropic Blockchain

Abstract

The storage, transmission, and processing of data become significant problems when large digital data files or databases are involved, as in the case of decentralized online global databases such as blockchain. Here, we propose a novel method that allows for the scalability of digital assets, including blockchain databases in the download, validation, and confidentiality processes, by developing a lightweight blockchain technology called Entropic Blockchain. This is a computer-implemented mathematical method by which to generate an information-entropic numerical barcode representation of a digital asset. Using this technique, a 1–2 Mb block of digital data can be represented by a few bytes, significantly reducing the size of a blockchain. The entropic barcode file can be utilized on its own or as an optically machine-readable entropic barcode for secure data transmission, processing, labeling, identification, and one-way encryption, as well as for compression, validation, and digital tamper-proof checks. The mathematics of this process and all the steps involved in its implementation are discussed in detail in this article.

1. Introduction

A blockchain is an online global database accessible to anyone via the Internet at any time [1]. In blockchain databases, the information is recorded, maintained, and shared by a community. The blocks within a blockchain contain information about transactions. A typical transaction is a data structure that defines a transfer of information or value. In this sense, a transaction can be the operation of storing information to the block, extracting information from the block, transferring value from one entity to another, a contract, and so on. Blockchain technology combines many other technologies, like cryptography, peer-to-peer networks, smart contracts, and consensus mechanisms, to make it nearly impossible to hack or tamper with the transactions and information stored within the blocks. Crypto currencies such as Bitcoin [2] are an application of the blockchain, which are related to day-to-day digital payment-based systems. In order to create a new block or to verify a transaction, computers must solve complicated math problems in a process called mining. The node that completes the mathematical puzzle the fastest receives a small Bitcoin reward and acquires the right to certify the transaction. Blocks are then appended to the blockchain in chronological order, i.e., as they are created.

The main issue with the blockchain technology is the ever-increasing size of the blockchain, which makes its storage and validation process more complicated. A single block in the Bitcoin blockchain is around 1–2 Mb in size, while the entire Bitcoin blockchain today is 578.48 Gb (on 12 June 2024), making it almost impossible to run on conventional laptops and desktops [3]. Moreover, its daily growth rate is around $0.04\%$, and its annual growth rate is $16.91\%$.

Another issue is the increasing computational power requirements of mining blocks and performing the validation. The proof-of-work consensus mechanism uses a lot of power. For example, the electricity consumption of Bitcoin is estimated to be 172.26 terawatt-hours (TWh) per year (on 12 June 2024), which amounts to 96.08 Mt CO₂ equivalent. The average energy consumption of Bitcoin per transaction is 766.64 kilowatt-hours (kWh), which has a carbon footprint of 427.60 kg CO₂ [4]. These huge numbers have a direct impact on the power requirements necessary to run the blockchains, and they also have a measurable environmental impact.

In this article, we propose a novel method that allows for the scalability of blockchain databases in the download, validation, and confidentiality process, developing a lightweight blockchain technology called Entropic Blockchain for simultaneous one-way data compression and encryption, while also facilitating a unique methodology for reaching consensus in real time. This novel method uses Shannon’s information entropy (IE) [5] to generate the entropic barcode of a dataset, and it is the subject of a recent patent application [6].

2. Calculating the Information Entropy

Let us assume that a given set X contains N characters, each chosen from a set with radix $U\ge 2$. Let $N_l$, where $l=1,2,3,\dots ,U$, be the number of $a_l$ characters in the set X. The fractions $p=\{p_1,p_2,\dots ,p_U\}$ can be defined for the set X, where $p_l=N_l/N$ is the fraction of the occurrence of a character $a_l$ within the set X. According to Shannon [5], the average information extracted per character, or the number of bits of information per character, or the information entropy of the set X, is

$$\mathrm{IE}=-\sum _{j=1}^U{p}_j·{log}_b\left(p_j\right),$$

(1)

where the base b gives the units of information (e.g., $b=2$ for bits), and the total bit content of the set is $N·\mathrm{IE}$.

For a given set, the maximum IE is obtained when the fractions are equal to each other (similarly as normal numbers); that is $p_j=1/U$, so

$$max\left(\mathrm{IE}\right)={log}_b\left(U\right).$$

(2)

The IE given by (1) is computed when the fractions refer to single characters within a set. However, a useful extrapolation could be the generalization of relation (1) to m-block information entropy [7]:

$${\mathrm{IE}}^{\left(m\right)}=-\sum _{j=1}^{\Omega }{p}_j^{\left(m\right)}·{log}_b\left(p_j^{\left(m\right)}\right),$$

(3)

where instead of single characters, combinations of m characters are used to define a new set of characters, called m-blocks. In this case, $p^{\left(m\right)}$ are the fractions of the m-block characters, and the summation extends over all possible combinations of distinct m-blocks. For a given set of N characters, each chosen from a set of radix U, the maximum number of distinct m-blocks of the newly constructed set of m-block characters is

$$\Omega =U^m.$$

(4)

The maximum value of the IE theoretically permitted for the new set of m-blocks is

$$max\left({\mathrm{IE}}^{\left(m\right)}\right)={log}_b(\Omega )={log}_b\left(U^m\right)=m{log}_b\left(U\right).$$

(5)

Combining (2) and (5), we deduce that $max\left({\mathrm{IE}}^{\left(m\right)}\right)=m·max\left(\mathrm{IE}\right)$, so using m-blocks increases the IE value by a factor of m relative to the set of single characters. In order to clarify the methodology proposed here, it is useful to show a few examples. Let us assume that a given set of characters contains characters form a set of radix $U=2$ (only two distinct single characters). Using bits, $b=2$ and relations (4) and (5), then the following apply:

If $m=1$, $\Omega =U^m=2$, indicating that we have two possible states, and each state encodes $\mathrm{IE}=1$ bit per character:

$$\{0,1\}.$$

If $m=2$, $\Omega =U^m=4$, indicating that we have four possible states, and each state encodes $\mathrm{IE}=2$ bits per character:

$$\{01,00,10,11\}.$$

If $m=3$, $\Omega =U^m=8$, indicating that we have eight possible states, and each state encodes $\mathrm{IE}=3$ bits per character:

$$\{000,001,011,101,110,100,111,010\}.$$

If $m=4$, $\Omega =U^m=16$, indicating that we have sixteen possible states, and each state encodes $\mathrm{IE}=4$ bits per character:

$$\{0000,0001,0011,0111,1111,1001,0100,0101,0111,0010,1100,1110,1101,1110,1000,0110\}.$$

If the set has N characters and we take $m=N$, then $\Omega =U^m=2^N$ is the number of possible states, and each state encodes $\mathrm{IE}=N$ bits per character.

3. Data Segmentation into Windows

Consider again our set of N characters $X=\{x_1,x_2,\dots ,x_N\}$. First, we create a subset called “window”, containing a number of characters called “window size” (WS). Taking a number of characters from $x_1$ to $x_{\mathrm{WS}}$, where $\mathrm{WS}\le N$, creates the first window. Starting from left to right, one slides the segment of WS across the whole set, where the position of each new window is obtained by sliding WS from left to right for a fixed number of characters, called “step size” (SS). In order to ensure that all sections of the set are captured by this process, the SS must be at least 1 and maximum WS, so $1<\mathrm{SS}\le \mathrm{WS}$. By doing this, a given set of N characters will result in a new set of $N_W$ windows, $\{W_1,W_2,\dots ,W_{Nw}\}$, given by the following formula:

$$N_W=1+{\displaystyle \frac{N-\mathrm{WS}}{\mathrm{SS}}}.$$

(6)

Ideally, the SS is taken to ensure the ratio $(N-\mathrm{WS})/\mathrm{SS}$ is an integer by selecting SS to satisfy the following relation:

$$N=A·\mathrm{SS}+\mathrm{WS},$$

(7)

where A is positive integer. However, in order to ensure that $N_W$ is an integer, another alternative is to augment the dataset by $N_P$ additional blank characters to cover the entire dataset with windows:

$$N_P=N_W·\mathrm{SS}+\mathrm{WS}-N.$$

(8)

The new augmented set has $\widehat{N}=N+N_P$ characters. Figure 1 shows this procedure applied to a set of bits. In the case illustrated in Figure 1, $\mathrm{WS}=20$ and $\mathrm{SS}=9$. Starting from left to right, the first window is formed, then sliding this to the right in terms of SS, the second window is obtained, and so on until the whole set is split into $N_W$ windows, forming a new set of $N_W$ elements.

The link between the index of a given j-th window and the index of the first character in the set corresponding to the j-th window is given by the following formula:

$$N_j=\mathrm{SS}·W_j-\mathrm{SS}+1,$$

(9)

where, $N_j=1,2,3,\dots ,N$ and $W_j=1,2,3,\dots ,W_{N_W}$, with $N_W$ given by relation (6).

4. Generating a Set of $\mathit{m}$-Blocks

We already established that a new set constructed using m-blocks from a given set of N single characters, containing U distinct characters, will have $\Omega =U^m$ distinct m-blocks/characters. We are now working out how many m-block elements will be in the newly formed set of m-blocks. Just as the “windows” segmentation of the set of N characters resulted in a new set containing $N_W$ windows, the same set could be transformed into a new set of m-blocks containing $N_m$ elements. The set of m-blocks is constructed using the same procedure used for generating the set of windows. However, instead of sliding the segment of WS from left to right, in step size (SS), where $1<\mathrm{SS}\le \mathrm{WS}$, we now slide the m-block segment from left to right in terms of SS, where the SS condition is now $1<\mathrm{ss}\le m$. When applied to each window, the newly formed set of m-block elements within a window of size (WS) contains a number of characters given by

$$N_m=1+{\displaystyle \frac{\mathrm{WS}-m}{\mathrm{ss}}}.$$

(10)

It is important to observe that the values of m and ss are selected so that the sliding procedure produces a set of $N_m$ integer elements. To clarify this procedure, let us again observe a few examples. Let us assume a random set of $N=16$ single characters (this could be a window with $\mathrm{WS}=16$) and U = 2:

$$\left\{0110101101011100\right\}.$$

Taking $\mathrm{ss}=1$ and $m=2$, we generate the new set of m-block characters by sliding the m-block segment of two single characters from left to right in steps of 1. This results in the following set, containing $N_m=15$ elements, as dictated by (10):

$$\{01,11,10,01,10,01,11,10,01,10,01,11,11,10,00\}.$$

Constructing another m-block set with $\mathrm{ss}=1$ and $m=3$, according to (10), we obtain the following set of $N_m=14$ elements:

$$\{011,110,101,010,101,011,110,101,010,101,011,111,110,100\}.$$

Using this procedure, a new set of any m-block size, with $m\le \mathrm{WS}$, can be generated. For sets of single characters, the window size has to satisfy the condition $\mathrm{WS}\ge U$ in order to ensure that the IE per window can take all possible values between zero and the maximum value theoretically permitted, ${log}_b\left(U\right)$. In the case of sets of m-blocks, to ensure that the IE per set can take all possible values between zero and the maximum value theoretically permitted, ${log}_b\left(U^m\right)$, the new imposed condition is $N_m\ge U^m$. Using (10) and solving for WS, we obtain the following:

$$\mathrm{WS}\ge \mathrm{ss}·U^m+m-1.$$

(11)

5. Generating the Entropic Barcode of a Digital File

Using the dataset windows segmentation procedure described above, together with the m-block procedure, the entropic barcode of a set is obtained by computing the information entropy IE value of each window and plotting the IE values as a function of the window index location within the new set. The IE of each window is computed identically using (1) for single-character sets, or (3) for sets of m-block characters, with each window containing WS characters, $X=\{x_1,x_2,\dots ,x_{\mathrm{WS}}\}$, and a number of U distinct characters. The entropic barcoding technology is the subject of a recent patent application (GB2404348.1) and allows for the conversion of the information contained within any dataset into a compressed numerical set that can be used for further data processing on its own or as a graphical optically readable barcode [8,9]. The generated entropic barcode is a representation of the dataset, which is irreversibly encrypted, and it has a massively compressed digital footprint size. In addition to the one-way encryption and data compression, the entropic barcode method offers a representation of the original dataset that could be used for data integrity checking, fraud detection, data labeling, and fast identification via laser barcode scanning. This technology is applicable to any dataset, including genomes, but one of the main applications of the entropic barcoding technology is to digital files. Any digital file is composed of 0s and 1s in machine code/binary language. This can be seen as a set of N characters containing two distinct characters, 0 and 1, so $U=2$, $a_l=\{0,1\}$, and fractions distributions are $p=\{p_0,p_1\}$. Using (1), the IE of the set can be easily calculated. To demonstrate this process, let us use a random set of $N=16$ bits:

$$\left\{0110101101011100\right\}.$$

If the bits within this set would occur with equal fractions ($p_j=1/2$), then the set would have $\mathrm{IE}=1$ and a total entropy of $N·\mathrm{IE}=16$ bits of information. However, counting the single bits, the above set has the following fractions:

$$p=\left\{p_0={\displaystyle \frac{7}{16}},p_1={\displaystyle \frac{9}{16}}\right\},$$

(12)

resulting in

$$\mathrm{IE}=-\left({\displaystyle \frac{7}{16}}{log}_2\left({\displaystyle \frac{7}{16}}\right)+{\displaystyle \frac{9}{16}}{log}_2\left({\displaystyle \frac{9}{16}}\right)\right)=0.989.$$

(13)

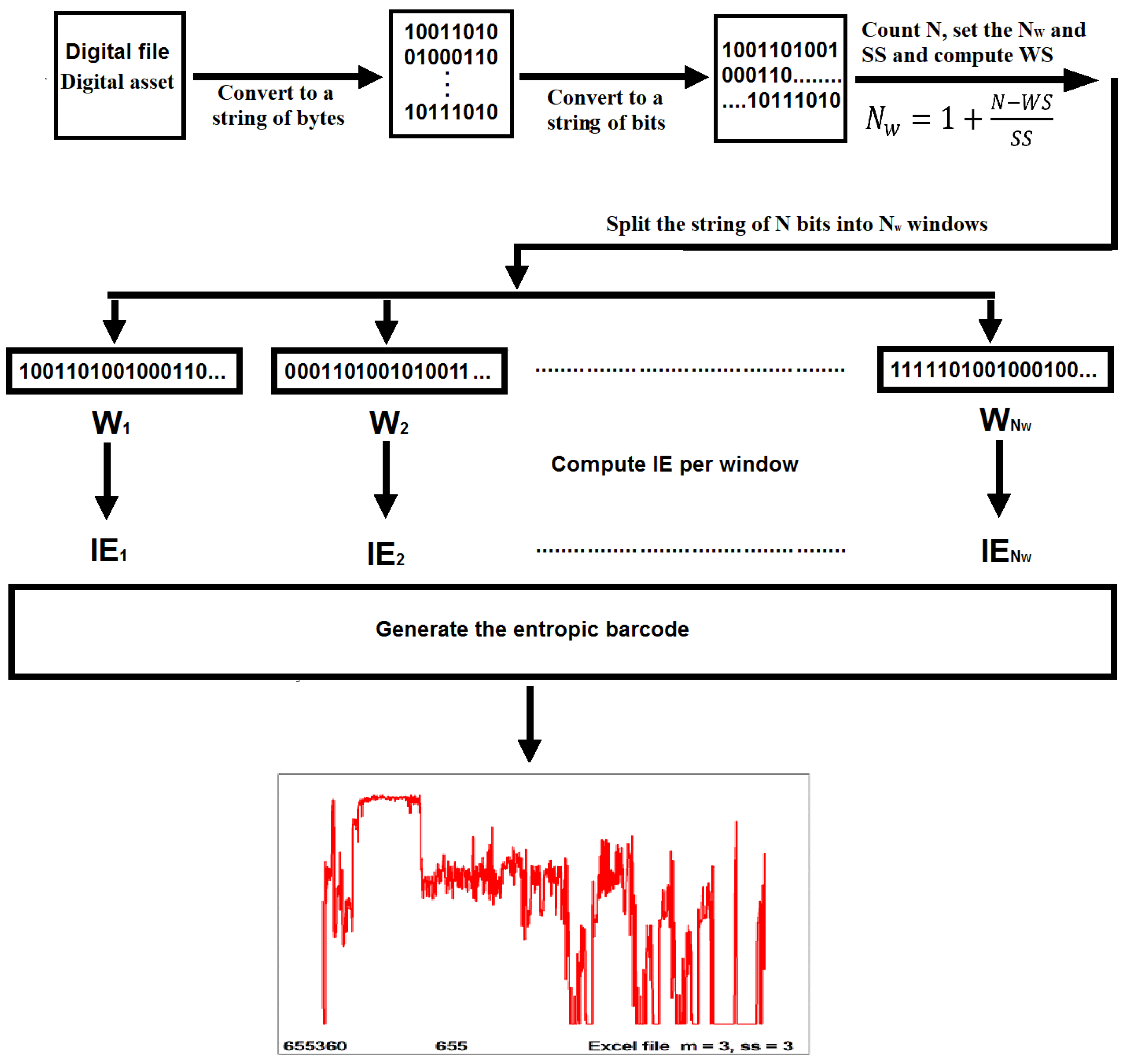
Hence, the IE of this binary set is 0.989 bits instead of 1 bit, and the total IE of the set is 15.84 bits instead of 16 bits. This is the basis of calculating the IE of each window within a set to generate an entropic barcode of the set, including a set of bits. The proposed entropic barcoding technology can only be implemented using fully automated computer software, and we created a proof-of-concept software called ENtropic BARCoding (ENBARC, version 1.a, M.M. Vopson), which is freely available and can be obtained by contacting the authors. For any given digital file, one can compute the entropic barcode representation of the original digital file by implementing the following steps:

• The file targeted for barcoding is decomposed from its own format into a string of bytes.
• The bytes are then converted into a text file containing a long string of bits, 0 s and 1 s. All other characters are removed.
• The string of 1 s and 0 s is split into windows.
• The IE per each window is calculated.
• The entropic barcode of the file is generated, which is a text file containing the IE values per window versus window location index.
• The graphical representation of the entropic barcode of the file is obtained by plotting the IE values per window versus window location index.

Figure 2 diagrammatically shows the proposed methodology with which to generate the entropic barcode of a digital file, including an example of a graphical entropic barcode representation.

6. Application to Blockchain–Entropic Blockchain

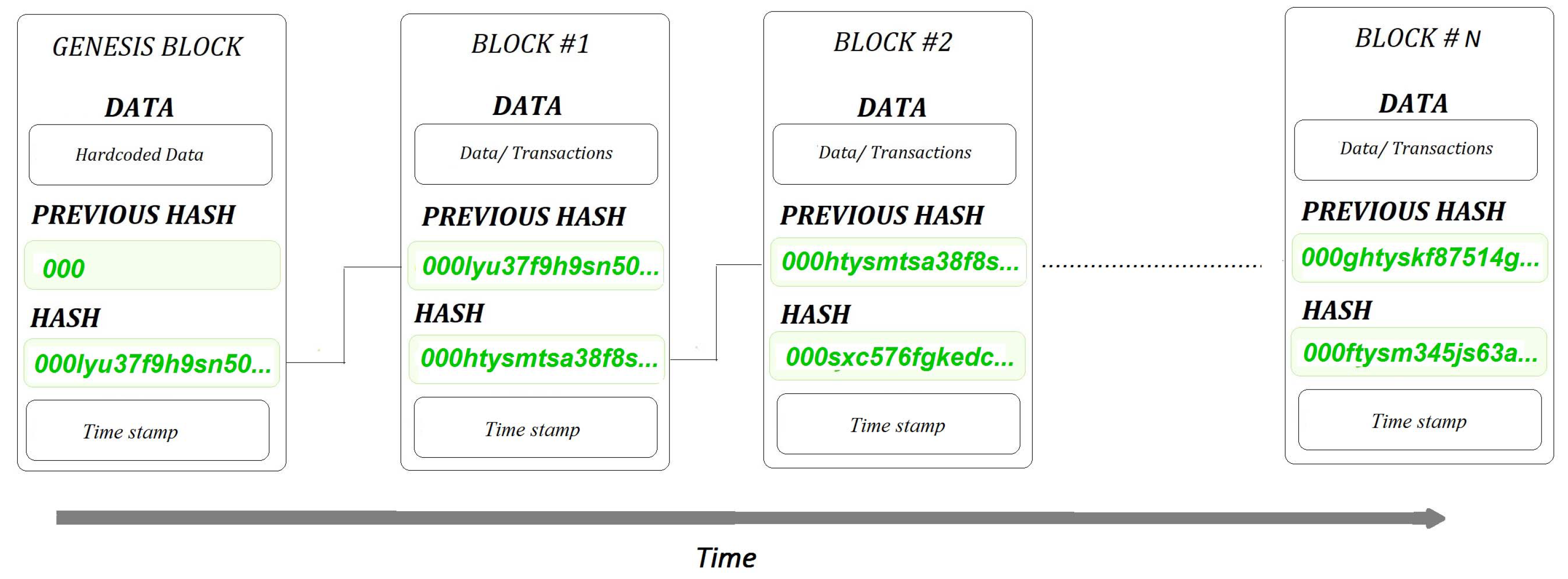
Blockchains are decentralized databases. The blocks within a blockchain contain data/transactions in digital format, as well as the hash keys and time stamps. Blocks are then appended to the blockchain in chronological order, i.e., sequentially as they are created. Figure 3 shows a diagrammatic representation of a blockchain.

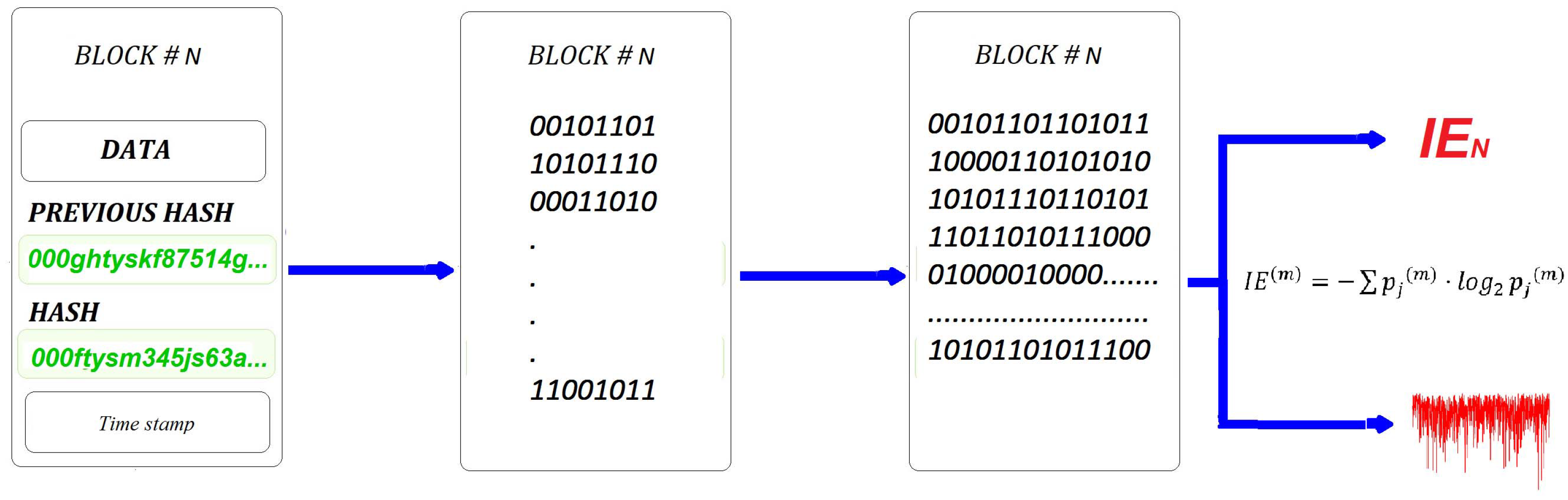
Since blockchains are composed of blocks of digital information, the entropic barcoding technology of a digital file described in the previous section can be applied to the blockchain databases, just as detailed in the Section 5. This process will be explained here, and the result is a superior blockchain, called an Entropic Blockchain. Although it is technically possible to retrofit the proposed Entropic Blockchain with the existing blockchains, this is not our objective. Instead, we hope that this research will stimulate the emergence of new blockchains built with the Entropic Blockchain technology. The method involves the conversion of all the blocks’ content into a string of bytes. The result is another block, which is a unique expression of the initial block, but its information content is expressed as a string of digital bytes. The block of bytes is then processed into a string of bits 0 s and 1 s. The result is a new block represented as a binary string, which is again a unique representation of the initial block’s content. At this stage, the method allows for two possible implementation options, as shown diagrammatically in Figure 4:

• Option 1: To compress the entire block’s information into a single IE numerical value by selecting the $\mathrm{WS}=N$ and calculating the IE value of the block.
• Option 2: To compress the entire block’s information into an Entropic Barcode.

Both proposed options result in massive one-way data compression and simultaneous encryption. However, the encryption achieved in this way is irreversible because there is no process of reconstructing the block’s information from the IE value or from the entropic barcode. In this sense, the IE value or the entropic barcode of the block are similar to a block’s Hash ke because any changes to the data inside the block will result in changes to the IE value or changes to its entropic barcode. 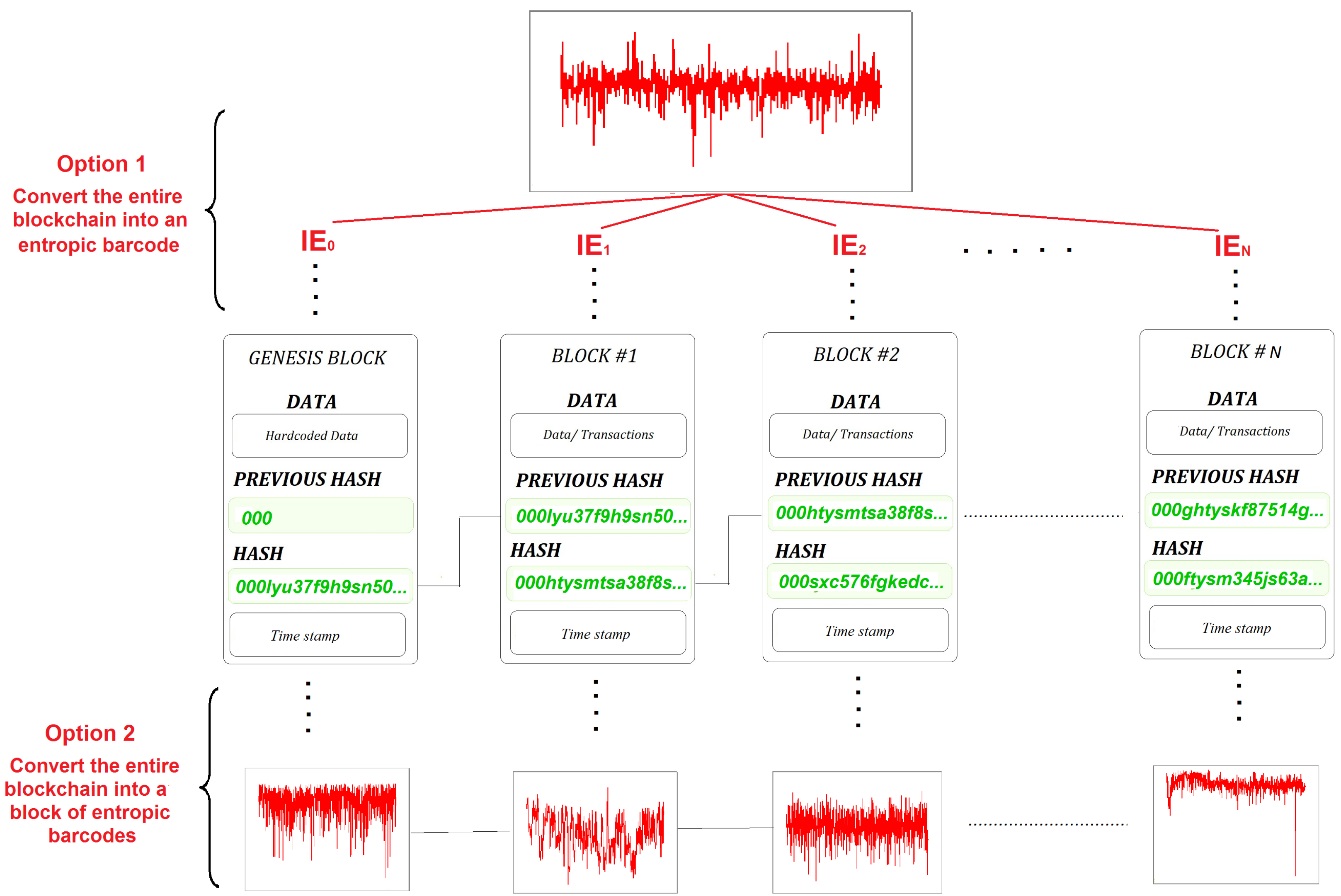Figure 5 shows diagrammatically the methodology proposed for the implementation of these two options to an entire blockchain database.

Repeating the procedure described in Figure 4 for the entire blockchain, i.e., for each block within the blockchain, Option 1 will produce an entropic barcode of IE values versus the block numbers, which is a unique 2D barcode of the entire blockchain. Deploying Option 2 will convert the entire blockchain into a chain of entropic barcodes, in which an entropic barcode represents each block, and a chain on N blocks will result in a chain of N entropic barcodes. Both proposed options drastically reduce the size of a blockchain while simultaneously encrypting its content. However, the new entropic barcode representation of the entire blockchain (Option 1) is particularly attractive because it could be used for fast peer-to-peer validation via the entropic differential barcoding technique (see Section 7). Using Option 1 as an example, a 1–2 Mb block would be represented by a decimal number and its index, taking only a few bytes of data. Assuming the Bitcoin blockchain is converted into a Bitcoin Entropic Blockchain, the entire Bitcoin blockchain of around 578 Gb size today would be represented by an entropic barcode of around 8.5 Mb. The details of mining are beyond the scope of this article and will not be discussed here, but essentially, each time a new block is created, a copy is sent to all nodes together with the information entropy value (Option 1) or the entropic barcode (Option 2) of the last block. The validation is performed on the entropic barcode of the blockchain (Option 1) or the chain of entropic barcodes (Option 2) instead of the entire blockchain.

Once the majority of the nodes agree on validating the Entropic Blockchain, the newly created block is added to the blockchain’s master copy, while the last IE value of the newly created block is added to the master blockchain’s entropic barcode (Option 1) or the last entropic barcode of the newly created block is added to the chain of entropic barcodes (Option 2). The benefit is that the newly created Entropic Blockchain is small enough to be emailed or transferred rapidly from terminal to terminal, and the validation process is extremely fast, saving time, energy, and data storage requirements. Hence, the proposed Entropic Blockchain technology offers solutions to the scalability of blockchain data, facilitating more effective download, transfer, validation, and confidentiality processes. However, some of the decentralized features of blockchain technology are lost because the Entropic Blockchain requires a blockchain master copy to be kept in a digital vault, while all operations are performed on its reduced Entropic Blockchain version. In a way, this is a semi-centralized blockchain, but there is still a degree of decentralization because all nodes must reach consensus on the Entropic Blockchain in order to validate it, while the keeper of the digital vault has zero ability to tamper with the blockchain.

7. Entropic Differential Barcode (EDB)

For any given digital asset, one can use the entropic barcode technology to generate an entropic barcode of the original asset, not only for the purpose of labeling, compressing, and encrypting but also for detecting any changes in it at later time. Detecting changes in the digital assets is a very powerful application because it allows one to check the integrity of a digital asset without accessing any information within it, maintaining full data privacy. Essentially, after the entropic barcode is generated, any changes to the original digital asset, as small as just one bit, will be easily detected regardless of its size. This method involves reconstructing the entropic barcode of the digital asset again and then comparing it to the original entropic barcode. The comparison between the two barcodes is performed via the entropic differential barcode (EDB), which is obtained by subtracting the two barcodes from each other. In a previous study using a similar method and applying it to genetic sequences, the entropic ratio was used instead of the entropic differential barcode to detect genetic mutations [10]. However, it is very possible that sections of the dataset might have IE = 0. This creates a problem when applying the ratio of the two spectra/barcodes as a number divided by zero is not computable. Hence, to avoid this problem, a better method based on the entropic differential barcode (EDB) is introduced. If the asset is unchanged, the EDB will be 0 everywhere. If the asset suffered any changes, the EDB will show deviations from 0 at the location where the changes occurred. This method could therefore be used to check the integrity of any digital asset and to detect any possible changes to it, however small. The applications are multifold and include validation of digital data files, blockchains, and crypto tokens. To demonstrate the method of entropic barcoding and entropic differential barcoding with respect to digital files, we will here provide an example.

Figure 6a shows an example of an Excel spreadsheet digital file for which we produced its unique entropic barcode representation (Figure 6b) of the original file. In this example, the Excel file has N = 655,360 bits. For this particular example, we imposed 1000 points of barcode size, i.e., the number of windows created equals 1000, $N_W=1000$, obtaining WS = 655. The SS has been taken equal to the WS; WS = SS = 655. The above example has been generated using an $m=3$ characters m-block with $\mathrm{ss}=m=3$. The maximum possible IE per window is therefore 3. The entire barcode contains data with maximum IE = 2.9765, minimum IE = 0, and average $〈\mathrm{IE}〉=1.5418$. For a 1000-points entropic barcode, the resulting spectrum text file is always 15 kilobytes (Kb), regardless of the type or size of the original file. Hence, this technique can achieve significant data compression from multiple gigabytes (Gb) to 15 Kb, while the entropic barcode is a true and unique representation of the original file, which does not disclose any of the file’s content.

After the barcode is generated, any changes or alterations to the original file, as small as just one bit, will be easily picked up. This method could be used to check for digital fraud and to determine the integrity of any digital file, including financial data files, banking records, image files, any type of document or software, blockchains, non-fungible tokens (NFTs), etc. Moreover, this method allows one to preserve the digital content of the file into this format while maintaining the full confidentiality of the file’s content, i.e., the entropic barcode does not reveal any information contained within the file. For example, one can have a digital copy of the entropic barcode of the spreadsheet Excel file analyzed here, and there would be no way of extracting any numerical or financial data contained in the file from the barcode itself. However, after the original file has been entropic barcoded, any future changes to the file itself can be detected by barcoding the file again and using the entropic differential barcode (EDB) method to check for the file’s integrity. To demonstrate this, we intentionally tampered with the file by changing a single bit (0 into 1), and we ran the EDB program to validate the file. Figure 7 shows the entropic barcodes of the original file, the 1-bit-altered file, and the EDB verification spectrum. The data clearly show that a single-bit alteration, which was a 0 changed into a 1, has been detected via the EDB validation check, showing a spectrum that contains a non-zero value at the location index 522. This means that the window index 522 contains a modification/alteration to the file. The original file’s IE value of the window index 522 was 1.831 bits. The change of a 0 into a 1 resulted in a change to the IE value from 1.831 bits to 1.847 bits, hence the non-zero spike in the EDB spectrum which indicates that the alteration has an absolute value of 0.016 bits. Any substantial changes to the file that result in a change in the total number of bits will show up as an EDB spectrum that is non-zero everywhere. This is a powerful technique that could be deployed to perform forensic verification of any form of digital file/asset, including performing financial audits and validating blockchains, crypto tokens, or NFTs.

8. Conclusions

Entropic barcoding technology facilitates the creation of new data processing tools with unique properties. The proposed method makes use of Shannon’s information theory to simultaneously one-way compress, encrypt, and barcode any dataset. Here, we proposed applying this technology to digital data files and blockchain databases to obtain next-generation blockchain technology, namely, Entropic Blockchains. Using entropic barcoding, the datasets are massively compressed in terms of their digital footprint, allowing for savings in digital data storage and transmission of data. At the same time, while condensing a whole dataset into an entropic barcode, the barcode acts as a one-way encryption of the data because there is no mechanism by which to reconstruct the set from its entropic barcode. For example, a window containing N bits in a string of 0 s and 1 s, for which we compute the IE value, would have $2^N$ possible combinations of the N bits. One would need to compute the IE value of all the possible combinations to guess the content of the window, which is impossible because different combinations can give the same IE value and because there are too many calculations to perform in the first place. A typical window of 1000 characters would have $2^{1000}$ possible arrangements, which is a number larger than all the particles in the universe, i.e., roughly $2^{256}$. This level of security assumes that no unauthorized access to the original data block files in the digital vault is possible. In order to mitigate possible security breaches upstream, a data encryption could be performed before the Entropic Blockchain procedure is deployed. When this method is combined with the differential entropic barcoding technique, also proposed here, the methodology allows for the fast detection of any change to the digital asset, facilitating an ultra-effective, fast, and energy-efficient blockchain validation method.

9. Patents

The entropic barcoding technology described in this study is the subject of the patent application GB2404348.1.