A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
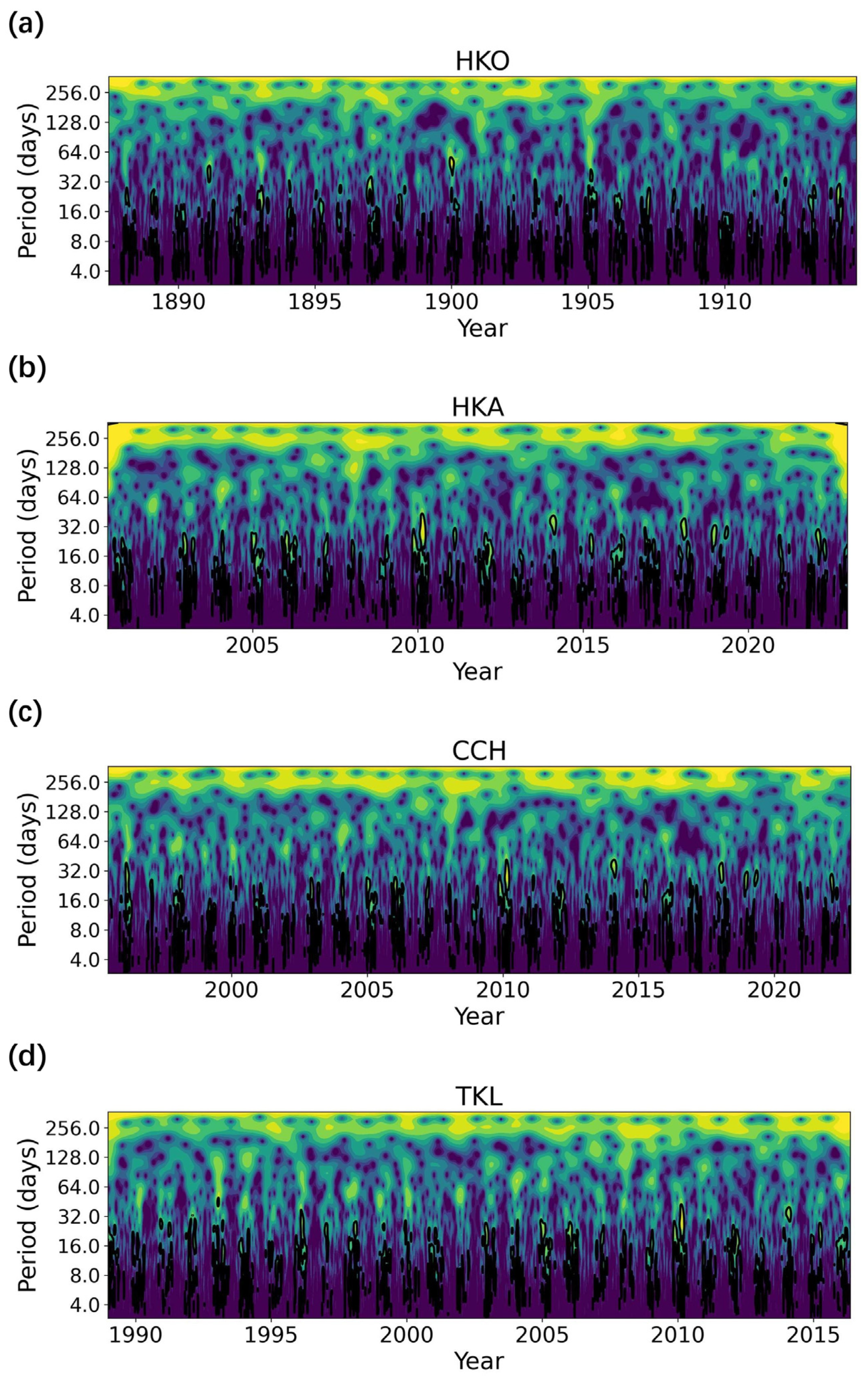
2.2.1. Wavelet Spectral Analysis
2.2.2. Lanczos Filter
2.2.3. Statistical Evaluation and Analysis Methods
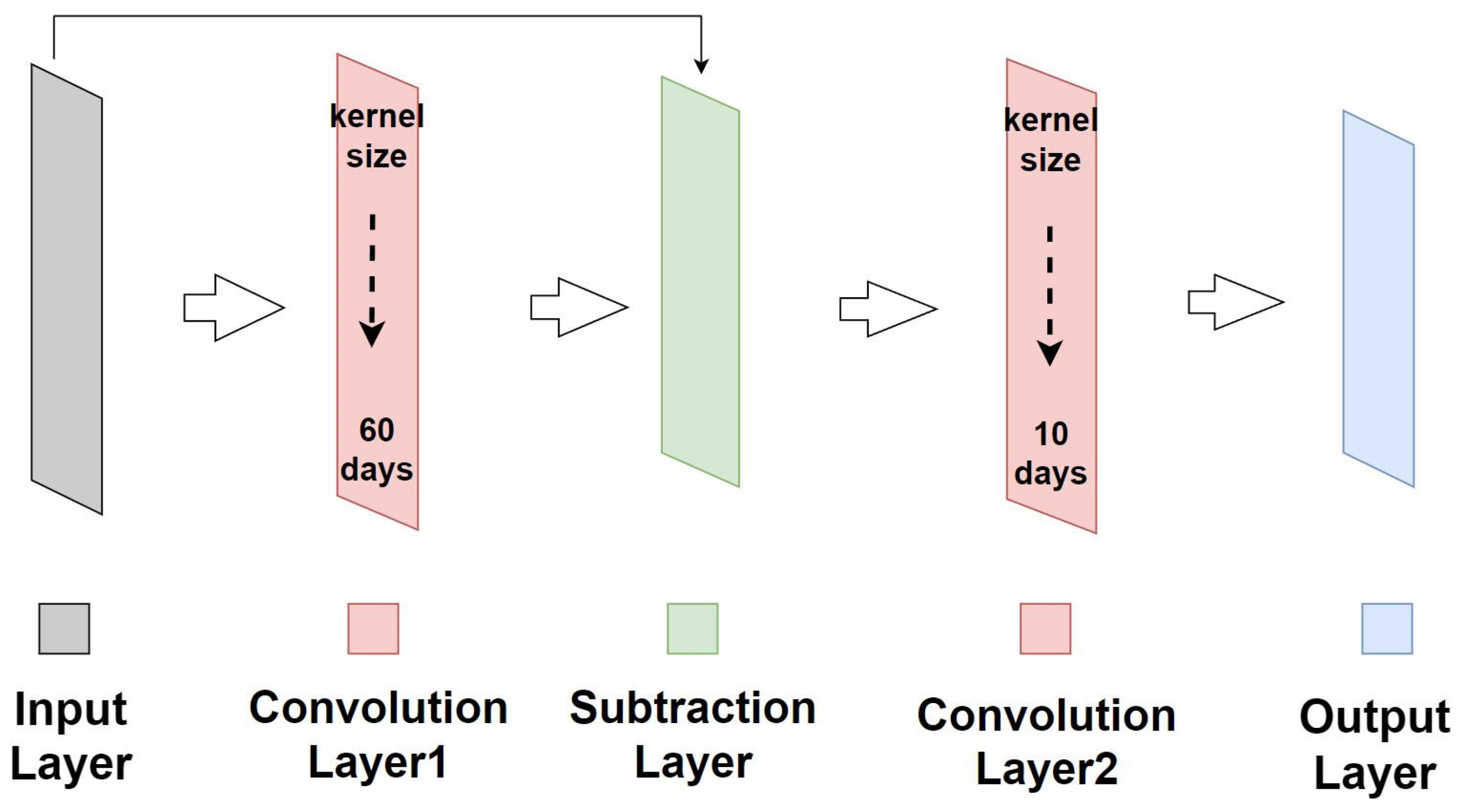
3. Design and Configuration of 1D-CNN Bandpass Filter
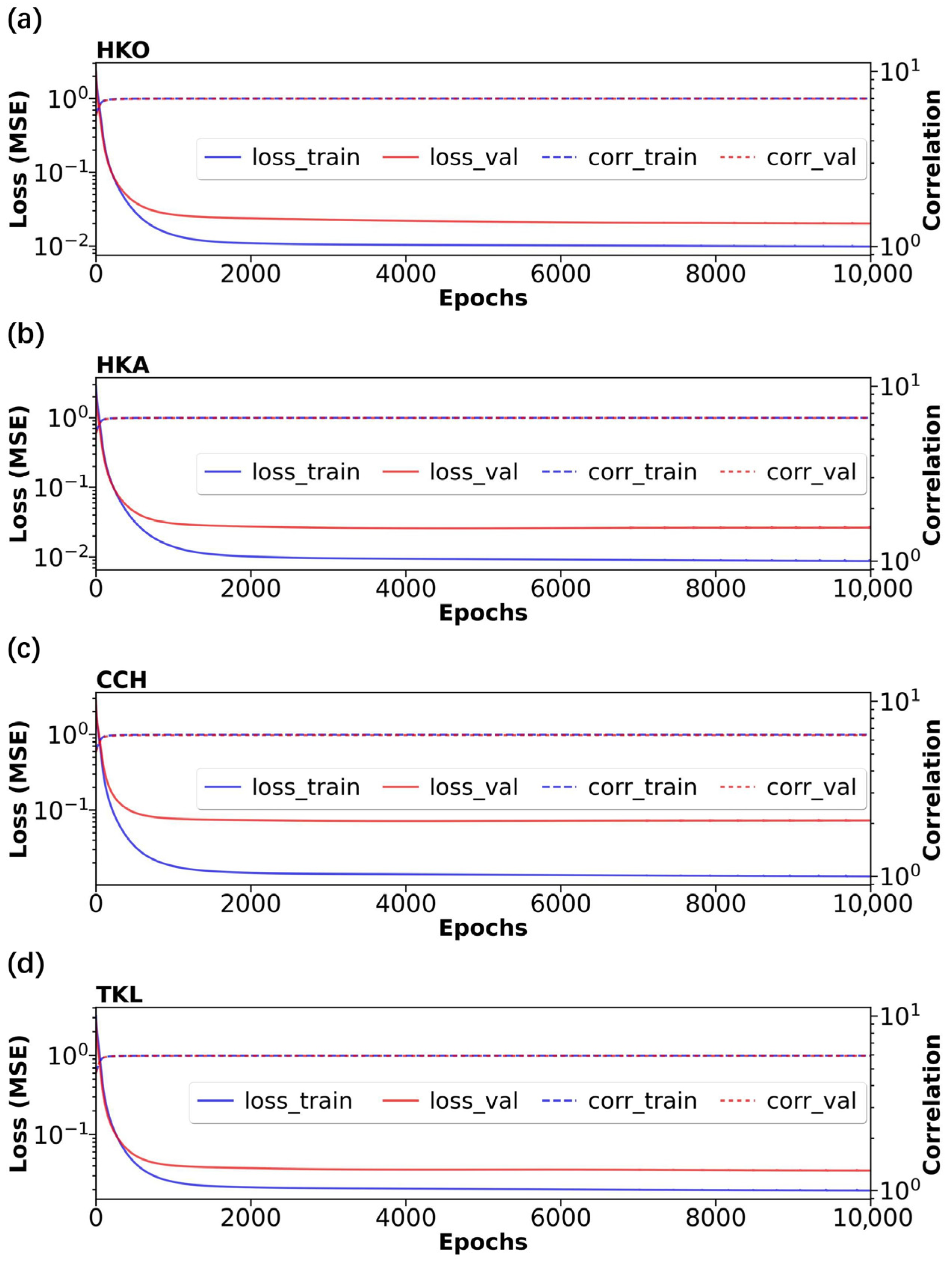
4. Validity of 1D-CNN Bandpass Filter
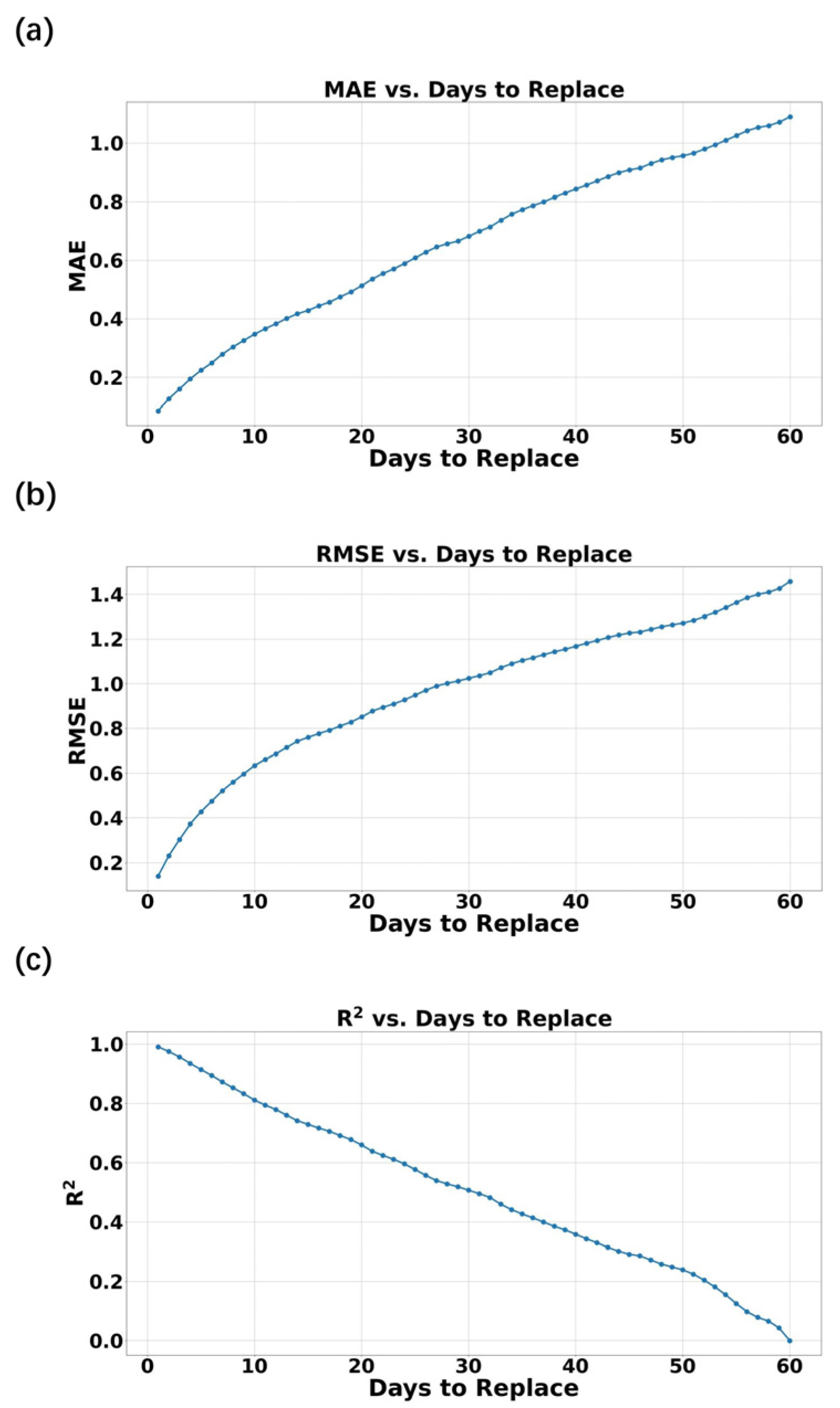
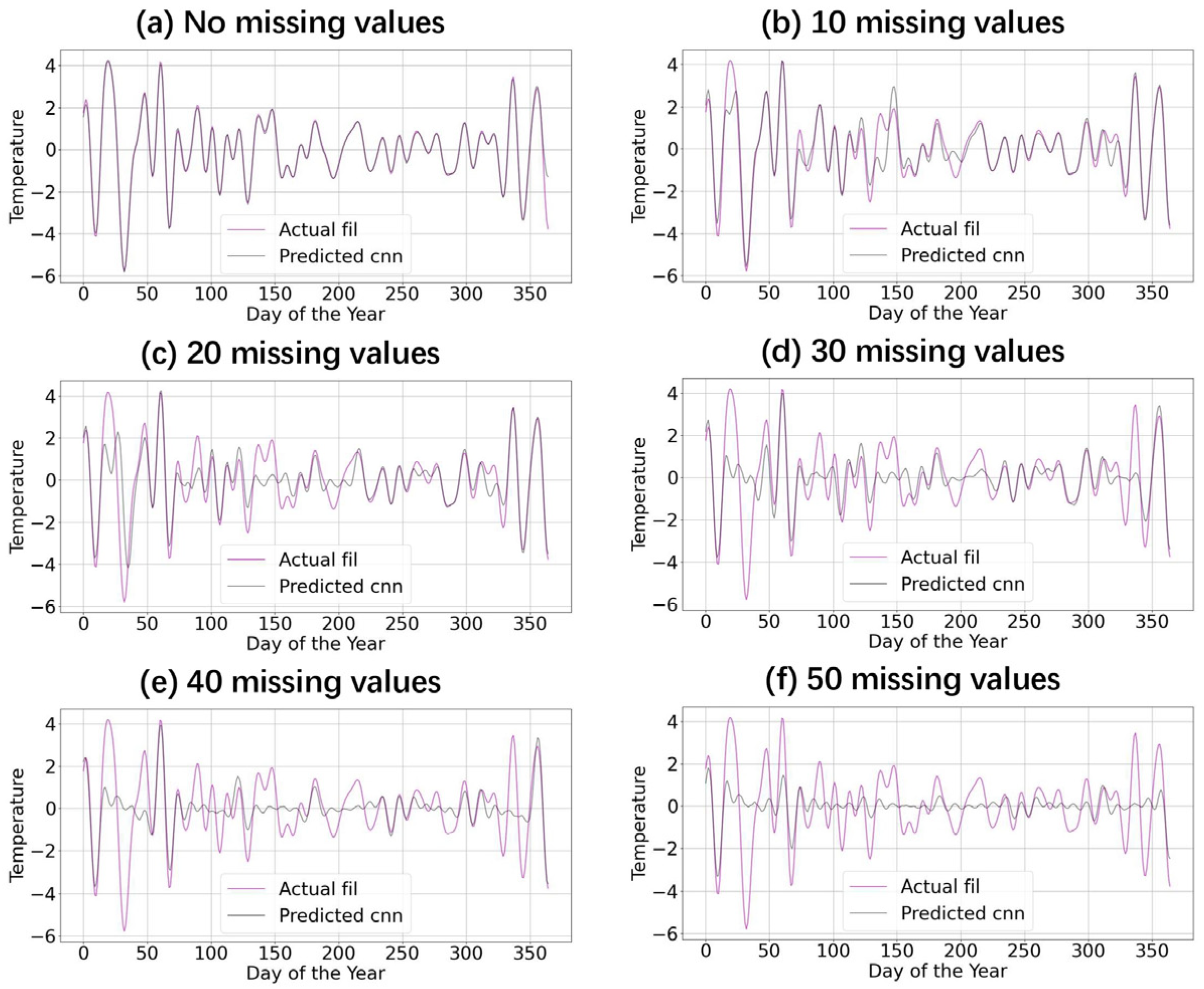
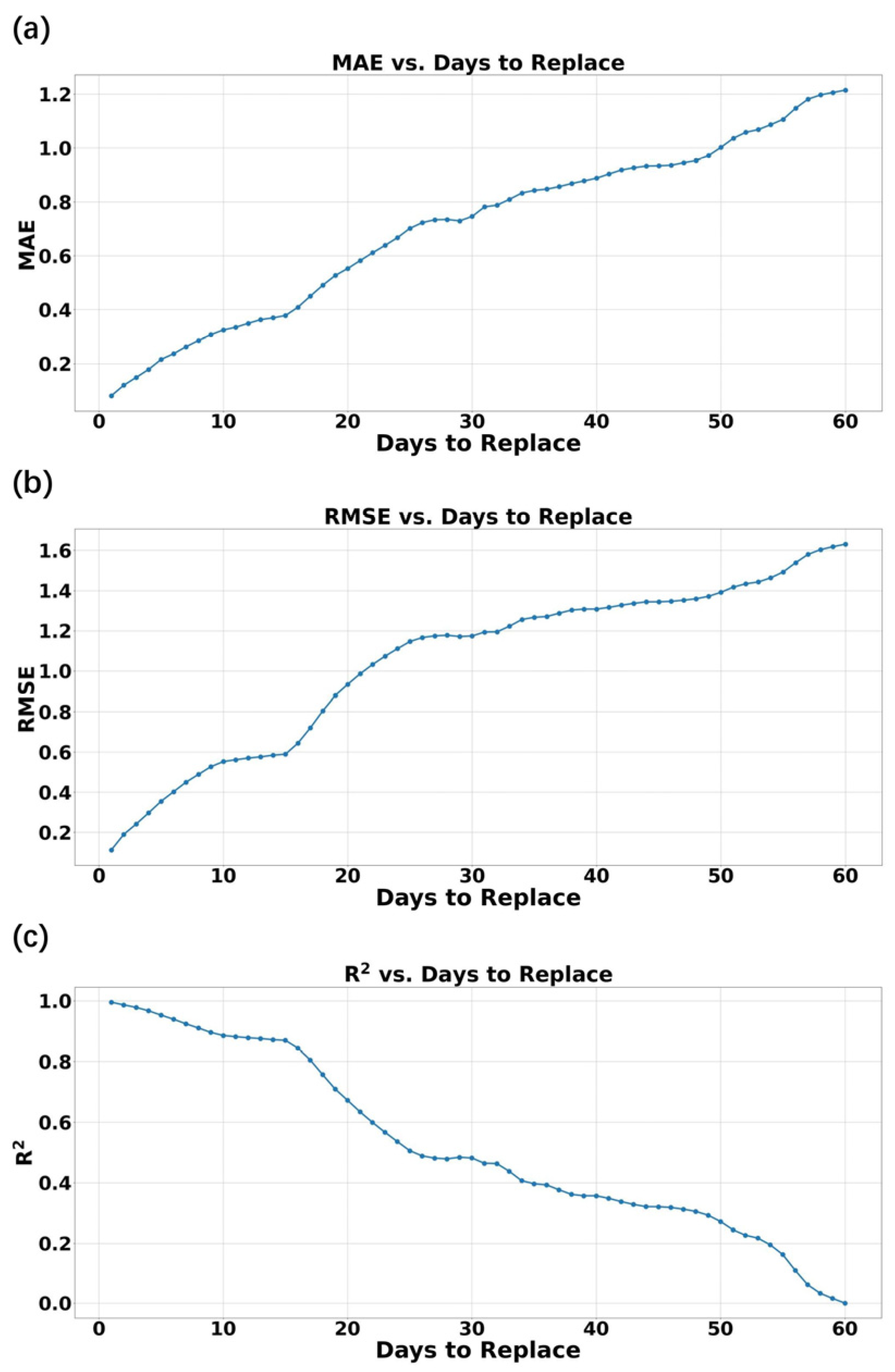
5. Application of 1D-CNN Bandpass Filter to Time Series with Missing Data Points
6. Conclusions and Discussion
- (1)
- A 1D-CNN temporal filter, which can be transformed into a highpass, bandpass, or lowpass filter, is developed.
- (2)
- The 1D-CNN filter is shown to be good at handling discontinuous time series.
- (3)
- The 1D-CNN filter allows a maximum number of missing data points that is approximately 16.67% of the filter window length. In other words, say, for a 100-day lowpass filter, the 1D-CNN filter is able to give relatively accurate filtered results even if there are ~17 missing values within a 100-day window.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Ding, Y.; Sikka, D. Synoptic systems and weather. In The Asian Monsoon; Springer: Berlin/Heidelberg, Germany, 2006; pp. 131–201. [Google Scholar]
- Sheridan, S.C.; Lee, C.C. Synoptic climatology and the general circulation model. Prog. Phys. Geogr. 2010, 34, 101–109. [Google Scholar] [CrossRef]
- Qian, W.; Leung, J.C.-H.; Ren, J.; Du, J.; Feng, Y.; Zhang, B. Anomaly based synoptic analysis and model prediction of six dust storms moving from Mongolia to northern China in spring 2021. J. Geophys. Res. Atmos. 2022, 127, e2021JD036272. [Google Scholar] [CrossRef]
- Loikith, P.C.; Pampuch, L.A.; Slinskey, E.; Detzer, J.; Mechoso, C.R.; Barkhordarian, A. A climatology of daily synoptic circulation patterns and associated surface meteorology over southern South America. Clim. Dyn. 2019, 53, 4019–4035. [Google Scholar] [CrossRef]
- Wang, J.; Guan, Y.; Wu, L.; Guan, X.; Cai, W.; Huang, J.; Dong, W.; Zhang, B. Changing lengths of the four seasons by global warming. Geophys. Res. Lett. 2021, 48, e2020GL091753. [Google Scholar] [CrossRef]
- Gan, Q.; Leung, J.C.-H.; Wang, L.; Zhang, B. Weakening seasonality of Indo-Pacific warm pool size in a warming world since 1950. Environ. Res. Lett. 2023, 18, 014024. [Google Scholar] [CrossRef]
- Santer, B.D.; Po-Chedley, S.; Zelinka, M.D.; Cvijanovic, I.; Bonfils, C.; Durack, P.J.; Fu, Q.; Kiehl, J.; Mears, C.; Painter, J.; et al. Human influence on the seasonal cycle of tropospheric temperature. Science 2018, 361, eaas8806. [Google Scholar] [CrossRef] [PubMed]
- Longandjo, G.-N.T.; Rouault, M. Revisiting the Seasonal Cycle of Rainfall over Central Africa. J. Clim. 2024, 37, 1015–1032. [Google Scholar] [CrossRef]
- Cai, W.; Santoso, A.; Collins, M.; Dewitte, B.; Karamperidou, C.; Kug, J.S.; Lengaigne, M.; McPhaden, M.J.; Stuecker, M.F.; Taschetto, A.S.; et al. Changing El Niño–Southern oscillation in a warming climate. Nat. Rev. Earth Environ. 2021, 2, 628–644. [Google Scholar] [CrossRef]
- Lin, J.; Qian, T. A new picture of the global impacts of El Nino-Southern oscillation. Sci. Rep. 2019, 9, 17543. [Google Scholar] [CrossRef]
- Cai, W.; Santoso, A.; Wang, G.; Yeh, S.-W.; An, S.-I.; Cobb, K.M.; Collins, M.; Guilyardi, E.; Jin, F.-F.; Kug, J.-S.; et al. ENSO and greenhouse warming. Nat. Clim. Chang. 2015, 5, 849–859. [Google Scholar] [CrossRef]
- Haines, A.; Lam, H.C. El Niño and health in an era of unprecedented climate change. Lancet 2023, 402, 1811–1813. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Madden–Julian oscillation: Bridging weather and climate. Bull. Am. Meteorol. Soc. 2013, 94, 1849–1870. [Google Scholar] [CrossRef]
- Liu, F.; Wang, B.; Ouyang, Y.; Wang, H.; Qiao, S.; Chen, G.; Dong, W. Intraseasonal variability of global land monsoon precipitation and its recent trend. NPJ Clim. Atmos. Sci. 2022, 5, 30. [Google Scholar] [CrossRef]
- Leung, J.C.-H.; Qian, W. Monitoring the Madden–Julian oscillation with geopotential height. Clim. Dyn. 2017, 49, 1981–2006. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43, RG2003. [Google Scholar] [CrossRef]
- Tanaka, H.L.; Ishizaki, N.; Kitoh, A. Trend and interannual variability of Walker, monsoon and Hadley circulations defined by velocity potential in the upper troposphere. Tellus A Dyn. Meteorol. Oceanogr. 2004, 56, 250–269. [Google Scholar] [CrossRef]
- Gan, Q.; Wang, L.; Leung, J.C.H.; Weng, J.; Zhang, B. Recent weakening relationship between the springtime Indo-Pacific warm pool SST zonal gradient and the subsequent summertime western Pacific subtropical high. Int. J. Climatol. 2022, 42, 10173–10194. [Google Scholar] [CrossRef]
- Crhová, L.; Holtanová, E. Temperature and precipitation variability in regional climate models and driving global climate models: Total variance and its temporal-scale components. Int. J. Climatol. 2019, 39, 1276–1286. [Google Scholar] [CrossRef]
- Liang, M.C.; Li, K.F.; Shia, R.L.; Yung, Y.L. Short-period solar cycle signals in the ionosphere observed by FORMOSAT-3/COSMIC. Geophys. Res. Lett. 2008, 35, L15818. [Google Scholar] [CrossRef]
- Russell, D.R. Development of a time-domain, variable-period surface-wave magnitude measurement procedure for application at regional and teleseismic distances, part I: Theory. Bull. Seismol. Soc. Am. 2006, 96, 665–677. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. Climatol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Liu, F. Inter-annual variability of boreal summer intra-seasonal oscillation propagation from the Indian ocean to the Western Pacific. Atmosphere 2019, 10, 596. [Google Scholar] [CrossRef]
- Ajayamohan, R.; Rao, S.A.; Luo, J.J.; Yamagata, T. Influence of Indian Ocean Dipole on boreal summer intraseasonal oscillations in a coupled general circulation model. J. Geophys. Res. Atmos. 2009, 114, D06119. [Google Scholar] [CrossRef]
- Arguez, A.; Bourassa, M.A.; O’Brien, J.J. Detection of the MJO signal from QuikSCAT. J. Atmos. Ocean. Technol. 2005, 22, 1885–1894. [Google Scholar] [CrossRef]
- Leung, J.C.-H.; Qian, W.; Zhang, P.; Zhang, B. Geopotential-based Multivariate MJO Index: Extending RMM-like indices to pre-satellite era. Clim. Dyn. 2022, 59, 609–631. [Google Scholar] [CrossRef]
- Roman-Stork, H.L.; Subrahmanyam, B.; Murty, V. Quasi-biweekly oscillations in the Bay of Bengal in observations and model simulations. Deep Sea Res. Part II Top. Stud. Oceanogr. 2019, 168, 104609. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, R.; Yang, S.; Li, W.; Wen, M. Quasi-biweekly oscillation of the South Asian high and its role in connecting the Indian and East Asian summer rainfalls. Geophys. Res. Lett. 2019, 46, 14742–14750. [Google Scholar] [CrossRef]
- Tong, Q.; Yao, S. The quasi-biweekly oscillation of winter precipitation associated with enso over southern China. Atmosphere 2018, 9, 406. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Gao, J.; Wang, W. Origins of quasi-biweekly and intraseasonal oscillations over the South China Sea and Bay of Bengal and scale selection of unstable equatorial and off-equatorial modes. J. Meteorol. Res. 2020, 34, 137–149. [Google Scholar] [CrossRef]
- Yan, X.; Yang, S.; Wang, T.; Maloney, E.D.; Dong, S.; Wei, W.; He, S. Quasi-biweekly oscillation of the Asian monsoon rainfall in late summer and autumn: Different types of structure and propagation. Clim. Dyn. 2019, 53, 6611–6628. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. Abrupt shift of the ITCZ over West Africa and intra-seasonal variability. Geophys. Res. Lett. 2000, 27, 3353–3356. [Google Scholar] [CrossRef]
- McNeall, D.; Halloran, P.R.; Good, P.; Betts, R.A. Analyzing abrupt and nonlinear climate changes and their impacts. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 663–686. [Google Scholar] [CrossRef]
- Stan, C.; Mantripragada, R.S.S. A deep learning filter for the intraseasonal variability of the tropics. Artif. Intell. Earth Syst. 2023, 2, e220079. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B. Monthly rainfall forecasting using one-dimensional deep convolutional neural network. IEEE Access 2018, 6, 69053–69063. [Google Scholar] [CrossRef]
- Sari, Y.R.; Djamal, E.C.; Nugraha, F. Daily rainfall prediction using one dimensional convolutional neural networks. In Proceedings of the 2020 3rd International Conference on Computer and Informatics Engineering (IC2IE), Yogyakarta, Indonesia, 15–16 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 90–95. [Google Scholar]
- Chen, W.; Ho, C.-H.; Yang, S.; Wu, Z.; Chen, H. Modulations of Madden–Julian Oscillation and Quasi-Biweekly Oscillation on Early Summer Tropical Cyclone Genesis over the Bay of Bengal and South China Sea. J. Clim. 2024, 37, 1951–1964. [Google Scholar] [CrossRef]
- Ge, Z. Significance tests for the wavelet power and the wavelet power spectrum. Ann. Geophys. 2007, 25, 2259–2269. [Google Scholar] [CrossRef]
- Chen, G.; Sui, C.H. Characteristics and origin of quasi-biweekly oscillation over the western North Pacific during boreal summer. J. Geophys. Res. Atmos. 2010, 115, D14113. [Google Scholar] [CrossRef]
- Allen, M.R.; Smith, L.A. Investigating the origins and significance of low-frequency modes of climate variability. Geophys. Res. Lett. 1994, 21, 883–886. [Google Scholar] [CrossRef]
- Gilman, D.L.; Fuglister, F.J.; Mitchell, J.M. On the power spectrum of “red noise”. J. Atmos. Sci. 1963, 20, 182–184. [Google Scholar] [CrossRef]
- Taquet, J.; Labit, C. Optimized decomposition basis using Lanczos filters for lossless compression of biomedical images. In Proceedings of the 2010 IEEE International Workshop on Multimedia Signal Processing, Saint-Malo, France, 4–6 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 122–127. [Google Scholar]
- Marmolin, H. Subjective MSE measures. IEEE Trans. Syst. Man Cybern. 1986, 16, 486–489. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Ozer, D.J. Correlation and the coefficient of determination. Psychol. Bull. 1985, 97, 307. [Google Scholar] [CrossRef]
- Haltiner, G.J. Numerical Weather Prediction; John Wiley and Sons: New York, NY, USA, 1971; 317p. [Google Scholar]

| Automatic Weather Station | Position | Length of Data Record | Number of Missing Values | |||
|---|---|---|---|---|---|---|
| Latitude N | Longitude E | Starting Date | Number of Data Points | Mean Temperature | Max/Min Temperature | |
| Ta Kwu Ling (TKL) | 22° 31′43″ | 114° 09′24″ | 14 October 1985 | 13,593 | 1091 | 1043 |
| Lau Fau Shan (LFS) | 22° 28′08″ | 113° 59′01″ | 16 September 1985 | 13,621 | 222 | 147 |
| Wetland Park (WLP) | 22° 28′00″ | 114° 00′32″ | 10 November 2005 | 6261 | 13 | 7 |
| Shek Kong (SEK) | 22° 26′10″ | 114° 05′05″ | 4 November 1996 | 9554 | 342 | 293 |
| Tai Mo Shan (TMS) | 22° 24′38″ | 114° 07′28″ | 1 December 1996 | 9527 | 231 | 179 |
| Sha Tin (SHA) | 22° 24′09″ | 114° 12′36″ | 1 October 1984 | 13,971 | 154 | 111 |
| Tate’s Cairn (TC) | 22° 21′28″ | 114° 13′04″ | 1 December 1997 | 9162 | 106 | 66 |
| King’s Park (KP) | 22° 18′43″ | 114° 10′22″ | 1 July 1992 | 11,141 | 25 | 7 |
| Hong Kong International Airport (HKA) | 22° 18′34″ | 113° 55′19″ | 1 June 1997 | 9345 | 0 | 31 |
| Hong Kong Observatory (HKO) | 22° 18′07″ | 114° 10′27″ | 1 April 1884 | 50,678 | 2557 | 2557 |
| Sha Lo Wan (SLW) | 22° 17′28″ | 113° 54′25″ | 25 February 1993 | 10,902 | 691 | 591 |
| Peng Chau (PEN) | 22° 17′28″ | 114° 02′36″ | 1 June 2004 | 6788 | 53 | 32 |
| Cheung Chau (CCH) | 22° 12′04″ | 114° 01′36″ | 30 March 1992 | 11,234 | 98 | 44 |
| Waglan Island (WGL) | 22° 10′56″ | 114° 18′12″ | 22 August 1989 | 12,185 | 811 | 665 |
| Automatic Weather Station | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|
| Ta Kwu Ling (TKL) | 0.066 | 0.012 | 0.111 | 0.996 |
| Lau Fau Shan (LFS) | 0.063 | 0.012 | 0.108 | 0.996 |
| Wetland Park (WLP) | 0.061 | 0.010 | 0.101 | 0.996 |
| Shek Kong (SEK) | 0.064 | 0.011 | 0.104 | 0.997 |
| Tai Mo Shan (TMS) | 0.059 | 0.012 | 0.107 | 0.995 |
| Sha Tin (SHA) | 0.058 | 0.008 | 0.092 | 0.997 |
| Tate’s Cairn (TC) | 0.062 | 0.011 | 0.104 | 0.996 |
| King’s Park (KP) | 0.055 | 0.009 | 0.093 | 0.996 |
| Hong Kong International Airport (HKA) | 0.057 | 0.009 | 0.094 | 0.997 |
| Hong Kong Observatory (HKO) | 0.053 | 0.007 | 0.085 | 0.997 |
| Sha Lo Wan (SLW) | 0.060 | 0.007 | 0.082 | 0.998 |
| Peng Chau (PEN) | 0.055 | 0.008 | 0.091 | 0.996 |
| Cheung Chau (CCH) | 0.055 | 0.008 | 0.091 | 0.996 |
| Waglan Island (WGL) | 0.053 | 0.008 | 0.092 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Kong, H.; Leung, J.C.-H.; Chan, P.W.; Fong, C.; Wang, Y.; Zhang, B. A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Appl. Sci. 2024, 14, 6289. https://doi.org/10.3390/app14146289
Yu D, Kong H, Leung JC-H, Chan PW, Fong C, Wang Y, Zhang B. A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Applied Sciences. 2024; 14(14):6289. https://doi.org/10.3390/app14146289
Chicago/Turabian StyleYu, Dan, Hoiio Kong, Jeremy Cheuk-Hin Leung, Pak Wai Chan, Clarence Fong, Yuchen Wang, and Banglin Zhang. 2024. "A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points" Applied Sciences 14, no. 14: 6289. https://doi.org/10.3390/app14146289
APA StyleYu, D., Kong, H., Leung, J. C.-H., Chan, P. W., Fong, C., Wang, Y., & Zhang, B. (2024). A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Applied Sciences, 14(14), 6289. https://doi.org/10.3390/app14146289








