A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Wavelet Spectral Analysis
2.2.2. Lanczos Filter
2.2.3. Statistical Evaluation and Analysis Methods
3. Design and Configuration of 1D-CNN Bandpass Filter
4. Validity of 1D-CNN Bandpass Filter
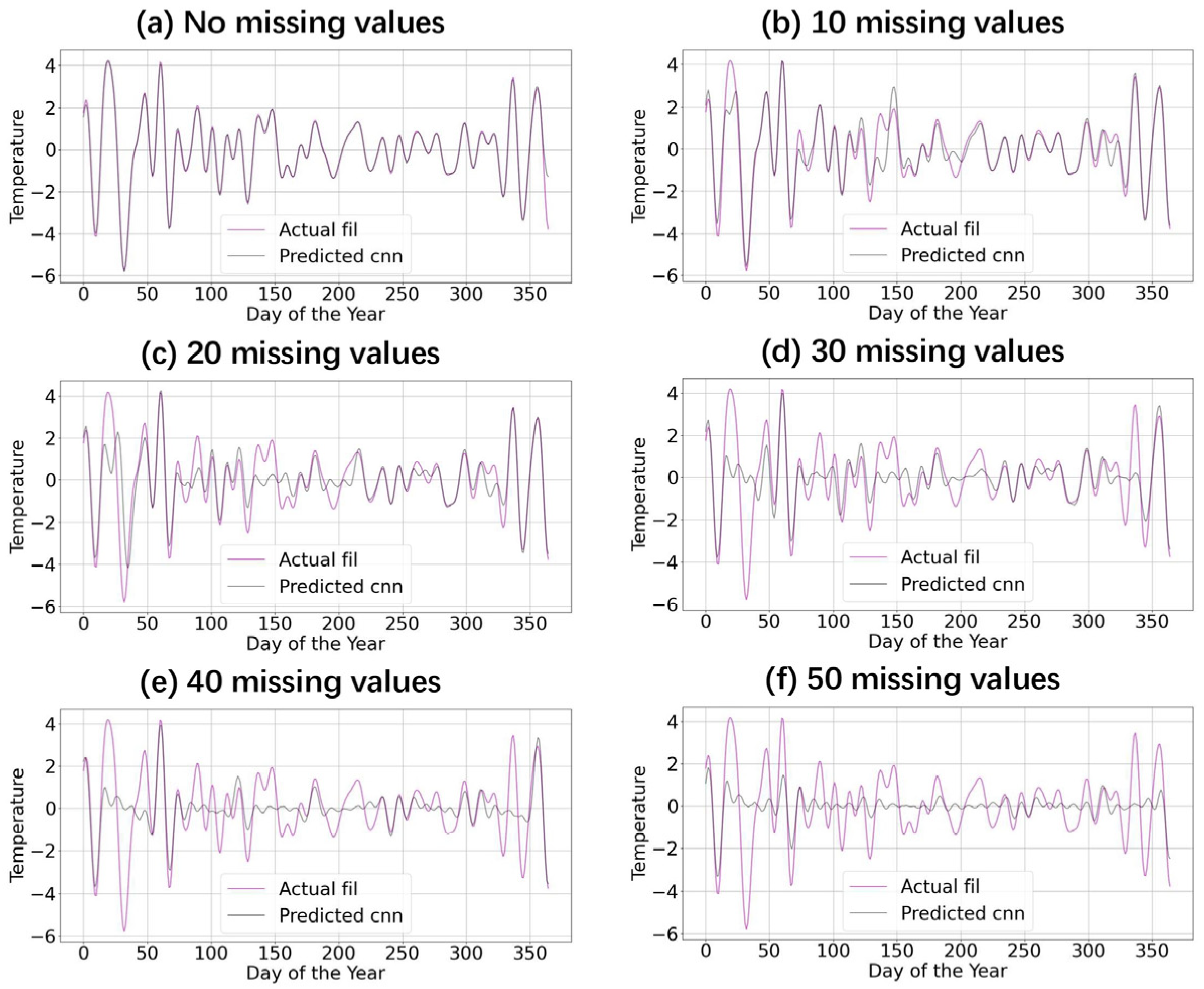
5. Application of 1D-CNN Bandpass Filter to Time Series with Missing Data Points
6. Conclusions and Discussion
- (1)
- A 1D-CNN temporal filter, which can be transformed into a highpass, bandpass, or lowpass filter, is developed.
- (2)
- The 1D-CNN filter is shown to be good at handling discontinuous time series.
- (3)
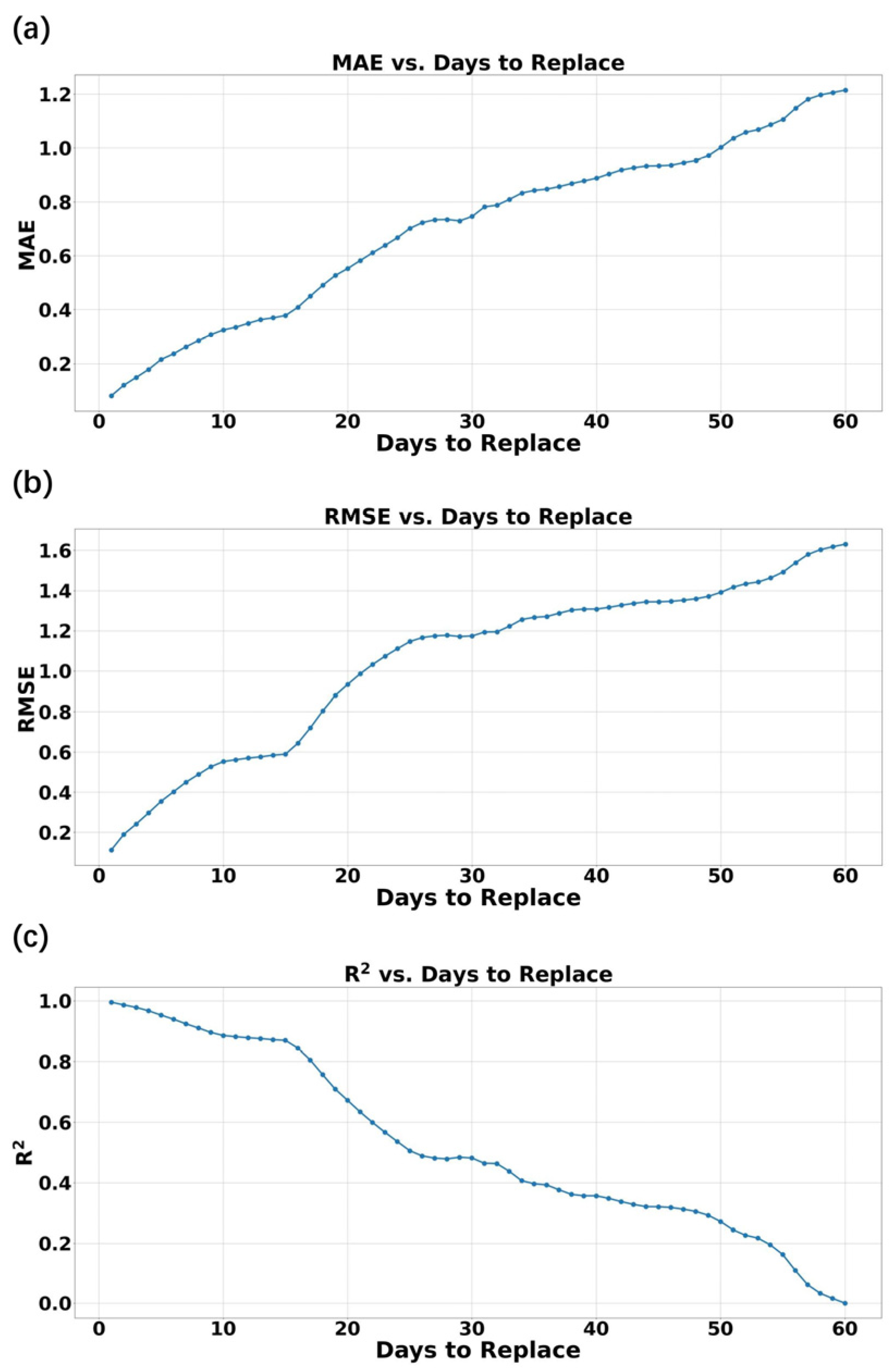
- The 1D-CNN filter allows a maximum number of missing data points that is approximately 16.67% of the filter window length. In other words, say, for a 100-day lowpass filter, the 1D-CNN filter is able to give relatively accurate filtered results even if there are ~17 missing values within a 100-day window.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, B.; Ding, Y.; Sikka, D. Synoptic systems and weather. In The Asian Monsoon; Springer: Berlin/Heidelberg, Germany, 2006; pp. 131–201. [Google Scholar]
- Sheridan, S.C.; Lee, C.C. Synoptic climatology and the general circulation model. Prog. Phys. Geogr. 2010, 34, 101–109. [Google Scholar] [CrossRef]
- Qian, W.; Leung, J.C.-H.; Ren, J.; Du, J.; Feng, Y.; Zhang, B. Anomaly based synoptic analysis and model prediction of six dust storms moving from Mongolia to northern China in spring 2021. J. Geophys. Res. Atmos. 2022, 127, e2021JD036272. [Google Scholar] [CrossRef]
- Loikith, P.C.; Pampuch, L.A.; Slinskey, E.; Detzer, J.; Mechoso, C.R.; Barkhordarian, A. A climatology of daily synoptic circulation patterns and associated surface meteorology over southern South America. Clim. Dyn. 2019, 53, 4019–4035. [Google Scholar] [CrossRef]
- Wang, J.; Guan, Y.; Wu, L.; Guan, X.; Cai, W.; Huang, J.; Dong, W.; Zhang, B. Changing lengths of the four seasons by global warming. Geophys. Res. Lett. 2021, 48, e2020GL091753. [Google Scholar] [CrossRef]
- Gan, Q.; Leung, J.C.-H.; Wang, L.; Zhang, B. Weakening seasonality of Indo-Pacific warm pool size in a warming world since 1950. Environ. Res. Lett. 2023, 18, 014024. [Google Scholar] [CrossRef]
- Santer, B.D.; Po-Chedley, S.; Zelinka, M.D.; Cvijanovic, I.; Bonfils, C.; Durack, P.J.; Fu, Q.; Kiehl, J.; Mears, C.; Painter, J.; et al. Human influence on the seasonal cycle of tropospheric temperature. Science 2018, 361, eaas8806. [Google Scholar] [CrossRef] [PubMed]
- Longandjo, G.-N.T.; Rouault, M. Revisiting the Seasonal Cycle of Rainfall over Central Africa. J. Clim. 2024, 37, 1015–1032. [Google Scholar] [CrossRef]
- Cai, W.; Santoso, A.; Collins, M.; Dewitte, B.; Karamperidou, C.; Kug, J.S.; Lengaigne, M.; McPhaden, M.J.; Stuecker, M.F.; Taschetto, A.S.; et al. Changing El Niño–Southern oscillation in a warming climate. Nat. Rev. Earth Environ. 2021, 2, 628–644. [Google Scholar] [CrossRef]
- Lin, J.; Qian, T. A new picture of the global impacts of El Nino-Southern oscillation. Sci. Rep. 2019, 9, 17543. [Google Scholar] [CrossRef]
- Cai, W.; Santoso, A.; Wang, G.; Yeh, S.-W.; An, S.-I.; Cobb, K.M.; Collins, M.; Guilyardi, E.; Jin, F.-F.; Kug, J.-S.; et al. ENSO and greenhouse warming. Nat. Clim. Chang. 2015, 5, 849–859. [Google Scholar] [CrossRef]
- Haines, A.; Lam, H.C. El Niño and health in an era of unprecedented climate change. Lancet 2023, 402, 1811–1813. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Madden–Julian oscillation: Bridging weather and climate. Bull. Am. Meteorol. Soc. 2013, 94, 1849–1870. [Google Scholar] [CrossRef]
- Liu, F.; Wang, B.; Ouyang, Y.; Wang, H.; Qiao, S.; Chen, G.; Dong, W. Intraseasonal variability of global land monsoon precipitation and its recent trend. NPJ Clim. Atmos. Sci. 2022, 5, 30. [Google Scholar] [CrossRef]
- Leung, J.C.-H.; Qian, W. Monitoring the Madden–Julian oscillation with geopotential height. Clim. Dyn. 2017, 49, 1981–2006. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43, RG2003. [Google Scholar] [CrossRef]
- Tanaka, H.L.; Ishizaki, N.; Kitoh, A. Trend and interannual variability of Walker, monsoon and Hadley circulations defined by velocity potential in the upper troposphere. Tellus A Dyn. Meteorol. Oceanogr. 2004, 56, 250–269. [Google Scholar] [CrossRef]
- Gan, Q.; Wang, L.; Leung, J.C.H.; Weng, J.; Zhang, B. Recent weakening relationship between the springtime Indo-Pacific warm pool SST zonal gradient and the subsequent summertime western Pacific subtropical high. Int. J. Climatol. 2022, 42, 10173–10194. [Google Scholar] [CrossRef]
- Crhová, L.; Holtanová, E. Temperature and precipitation variability in regional climate models and driving global climate models: Total variance and its temporal-scale components. Int. J. Climatol. 2019, 39, 1276–1286. [Google Scholar] [CrossRef]
- Liang, M.C.; Li, K.F.; Shia, R.L.; Yung, Y.L. Short-period solar cycle signals in the ionosphere observed by FORMOSAT-3/COSMIC. Geophys. Res. Lett. 2008, 35, L15818. [Google Scholar] [CrossRef]
- Russell, D.R. Development of a time-domain, variable-period surface-wave magnitude measurement procedure for application at regional and teleseismic distances, part I: Theory. Bull. Seismol. Soc. Am. 2006, 96, 665–677. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos filtering in one and two dimensions. J. Appl. Meteorol. Climatol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Liu, F. Inter-annual variability of boreal summer intra-seasonal oscillation propagation from the Indian ocean to the Western Pacific. Atmosphere 2019, 10, 596. [Google Scholar] [CrossRef]
- Ajayamohan, R.; Rao, S.A.; Luo, J.J.; Yamagata, T. Influence of Indian Ocean Dipole on boreal summer intraseasonal oscillations in a coupled general circulation model. J. Geophys. Res. Atmos. 2009, 114, D06119. [Google Scholar] [CrossRef]
- Arguez, A.; Bourassa, M.A.; O’Brien, J.J. Detection of the MJO signal from QuikSCAT. J. Atmos. Ocean. Technol. 2005, 22, 1885–1894. [Google Scholar] [CrossRef]
- Leung, J.C.-H.; Qian, W.; Zhang, P.; Zhang, B. Geopotential-based Multivariate MJO Index: Extending RMM-like indices to pre-satellite era. Clim. Dyn. 2022, 59, 609–631. [Google Scholar] [CrossRef]
- Roman-Stork, H.L.; Subrahmanyam, B.; Murty, V. Quasi-biweekly oscillations in the Bay of Bengal in observations and model simulations. Deep Sea Res. Part II Top. Stud. Oceanogr. 2019, 168, 104609. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, R.; Yang, S.; Li, W.; Wen, M. Quasi-biweekly oscillation of the South Asian high and its role in connecting the Indian and East Asian summer rainfalls. Geophys. Res. Lett. 2019, 46, 14742–14750. [Google Scholar] [CrossRef]
- Tong, Q.; Yao, S. The quasi-biweekly oscillation of winter precipitation associated with enso over southern China. Atmosphere 2018, 9, 406. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Gao, J.; Wang, W. Origins of quasi-biweekly and intraseasonal oscillations over the South China Sea and Bay of Bengal and scale selection of unstable equatorial and off-equatorial modes. J. Meteorol. Res. 2020, 34, 137–149. [Google Scholar] [CrossRef]
- Yan, X.; Yang, S.; Wang, T.; Maloney, E.D.; Dong, S.; Wei, W.; He, S. Quasi-biweekly oscillation of the Asian monsoon rainfall in late summer and autumn: Different types of structure and propagation. Clim. Dyn. 2019, 53, 6611–6628. [Google Scholar] [CrossRef]
- Sultan, B.; Janicot, S. Abrupt shift of the ITCZ over West Africa and intra-seasonal variability. Geophys. Res. Lett. 2000, 27, 3353–3356. [Google Scholar] [CrossRef]
- McNeall, D.; Halloran, P.R.; Good, P.; Betts, R.A. Analyzing abrupt and nonlinear climate changes and their impacts. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 663–686. [Google Scholar] [CrossRef]
- Stan, C.; Mantripragada, R.S.S. A deep learning filter for the intraseasonal variability of the tropics. Artif. Intell. Earth Syst. 2023, 2, e220079. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B. Monthly rainfall forecasting using one-dimensional deep convolutional neural network. IEEE Access 2018, 6, 69053–69063. [Google Scholar] [CrossRef]
- Sari, Y.R.; Djamal, E.C.; Nugraha, F. Daily rainfall prediction using one dimensional convolutional neural networks. In Proceedings of the 2020 3rd International Conference on Computer and Informatics Engineering (IC2IE), Yogyakarta, Indonesia, 15–16 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 90–95. [Google Scholar]
- Chen, W.; Ho, C.-H.; Yang, S.; Wu, Z.; Chen, H. Modulations of Madden–Julian Oscillation and Quasi-Biweekly Oscillation on Early Summer Tropical Cyclone Genesis over the Bay of Bengal and South China Sea. J. Clim. 2024, 37, 1951–1964. [Google Scholar] [CrossRef]
- Ge, Z. Significance tests for the wavelet power and the wavelet power spectrum. Ann. Geophys. 2007, 25, 2259–2269. [Google Scholar] [CrossRef]
- Chen, G.; Sui, C.H. Characteristics and origin of quasi-biweekly oscillation over the western North Pacific during boreal summer. J. Geophys. Res. Atmos. 2010, 115, D14113. [Google Scholar] [CrossRef]
- Allen, M.R.; Smith, L.A. Investigating the origins and significance of low-frequency modes of climate variability. Geophys. Res. Lett. 1994, 21, 883–886. [Google Scholar] [CrossRef]
- Gilman, D.L.; Fuglister, F.J.; Mitchell, J.M. On the power spectrum of “red noise”. J. Atmos. Sci. 1963, 20, 182–184. [Google Scholar] [CrossRef]
- Taquet, J.; Labit, C. Optimized decomposition basis using Lanczos filters for lossless compression of biomedical images. In Proceedings of the 2010 IEEE International Workshop on Multimedia Signal Processing, Saint-Malo, France, 4–6 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 122–127. [Google Scholar]
- Marmolin, H. Subjective MSE measures. IEEE Trans. Syst. Man Cybern. 1986, 16, 486–489. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Ozer, D.J. Correlation and the coefficient of determination. Psychol. Bull. 1985, 97, 307. [Google Scholar] [CrossRef]
- Haltiner, G.J. Numerical Weather Prediction; John Wiley and Sons: New York, NY, USA, 1971; 317p. [Google Scholar]
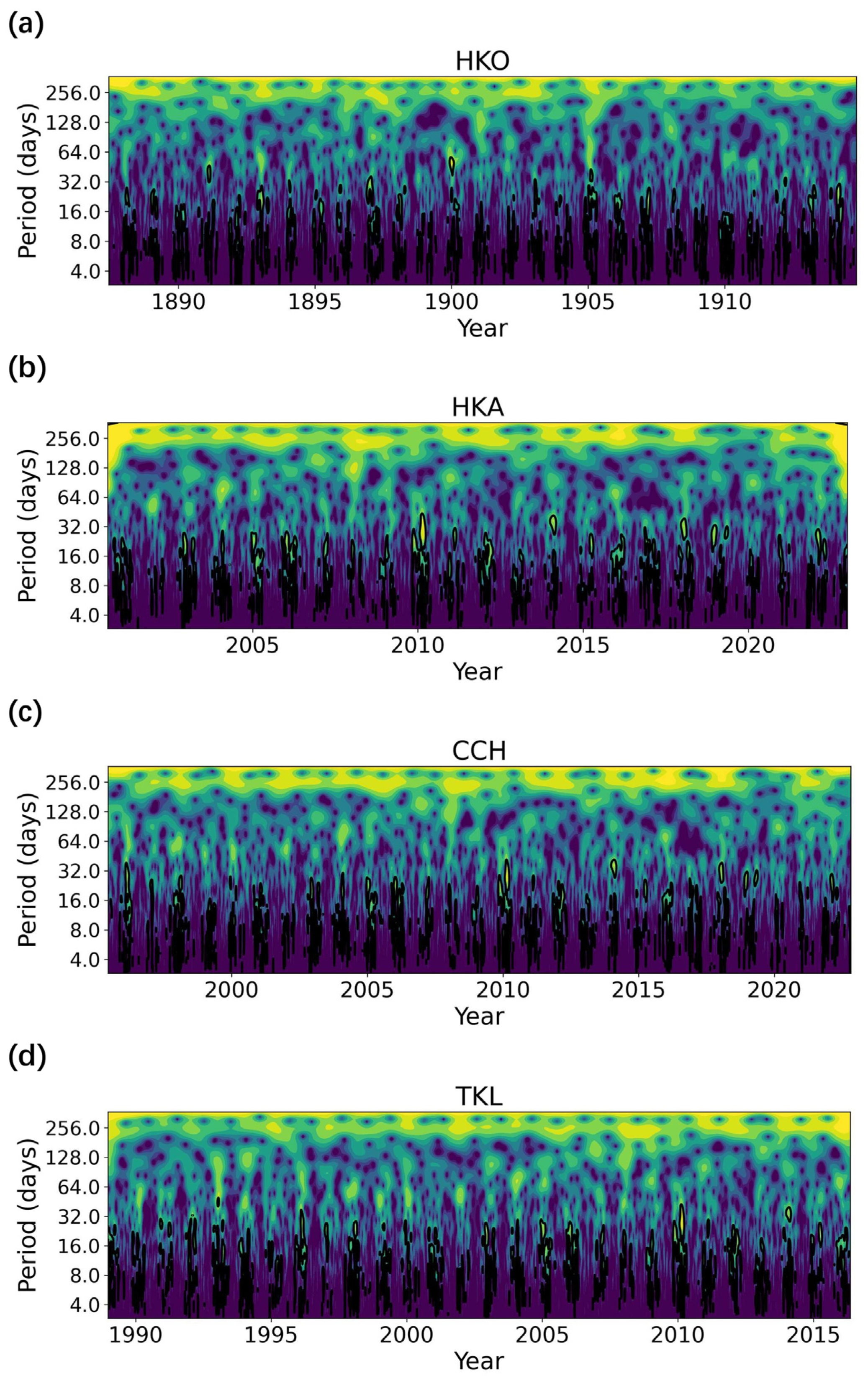
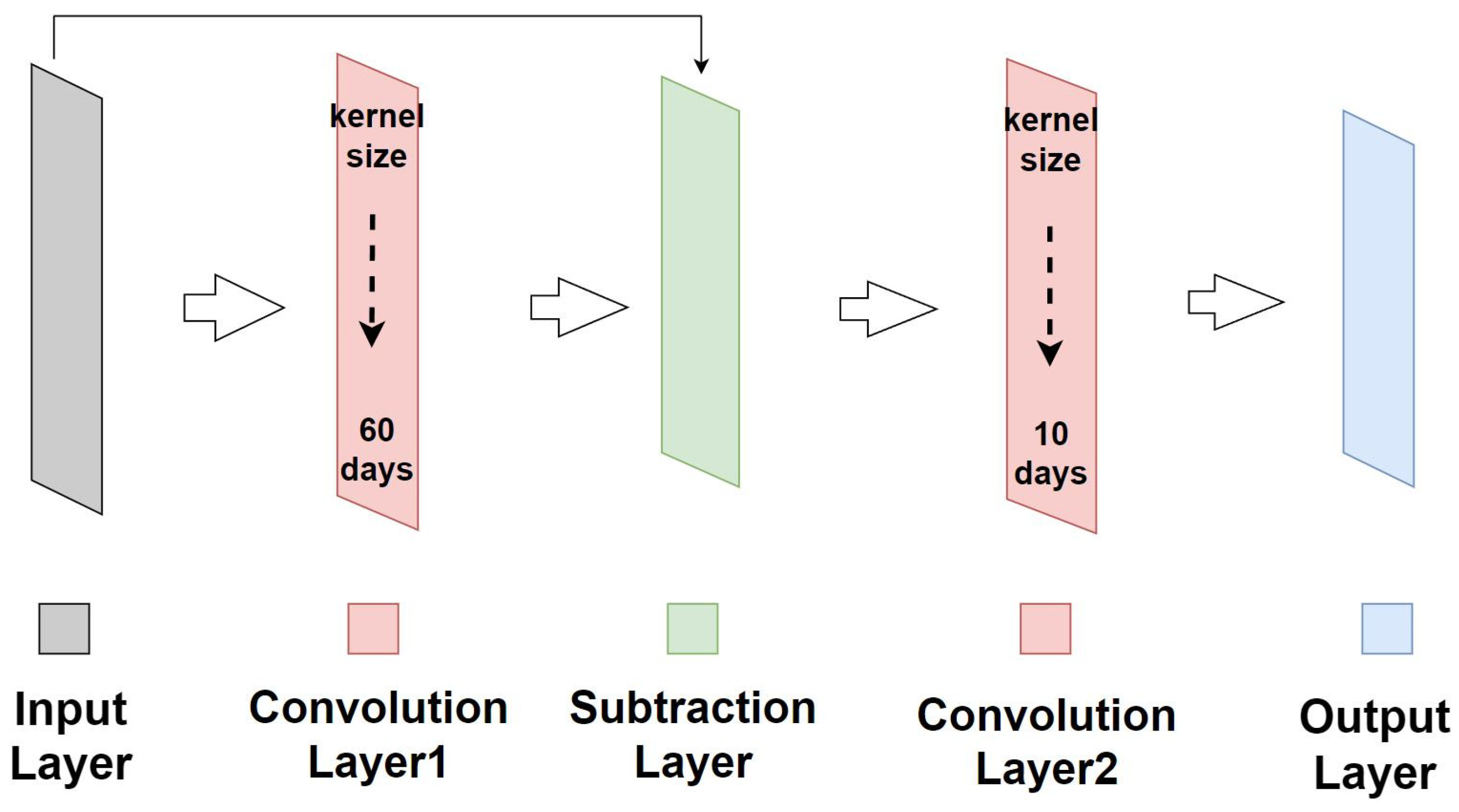
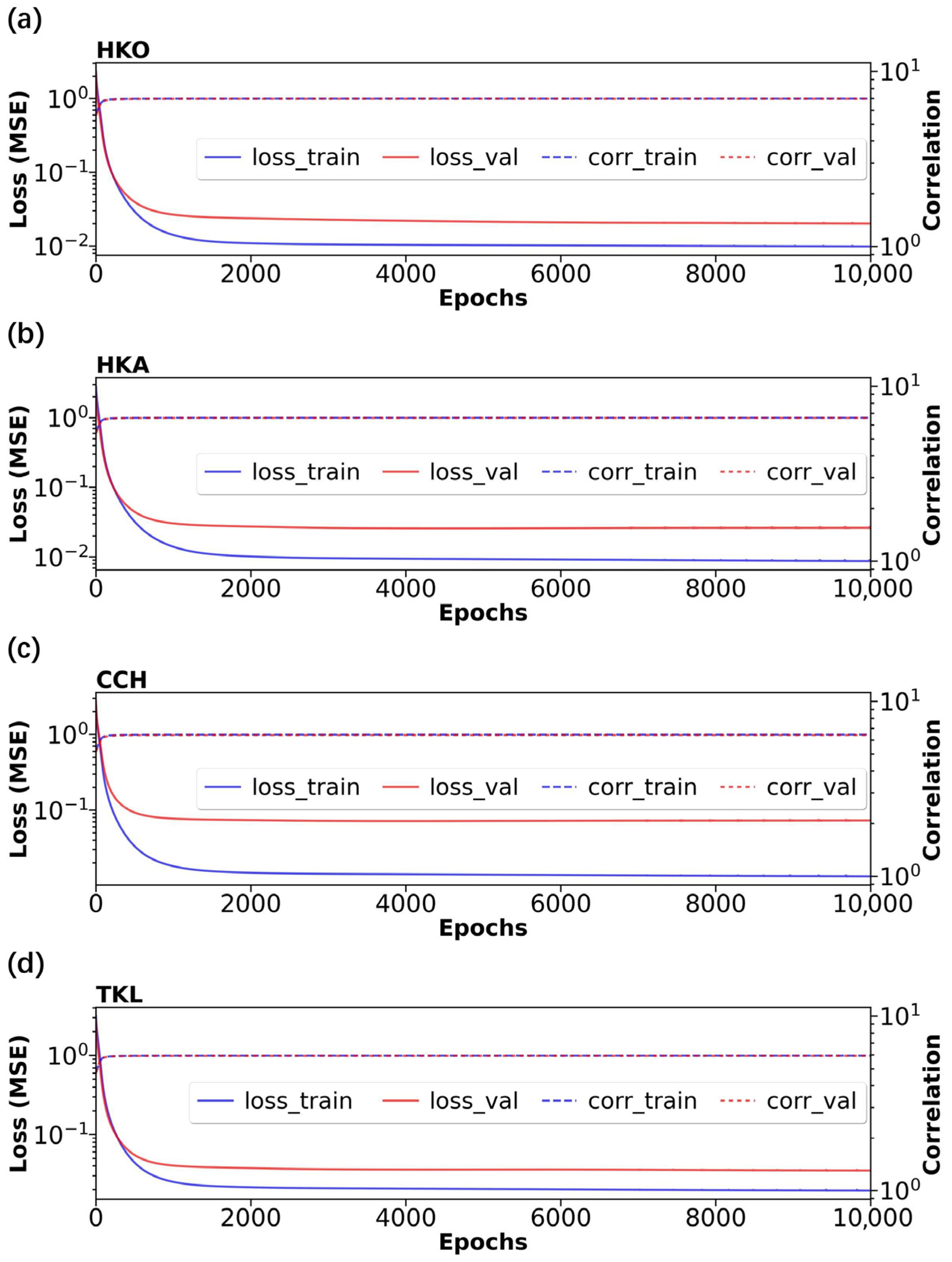

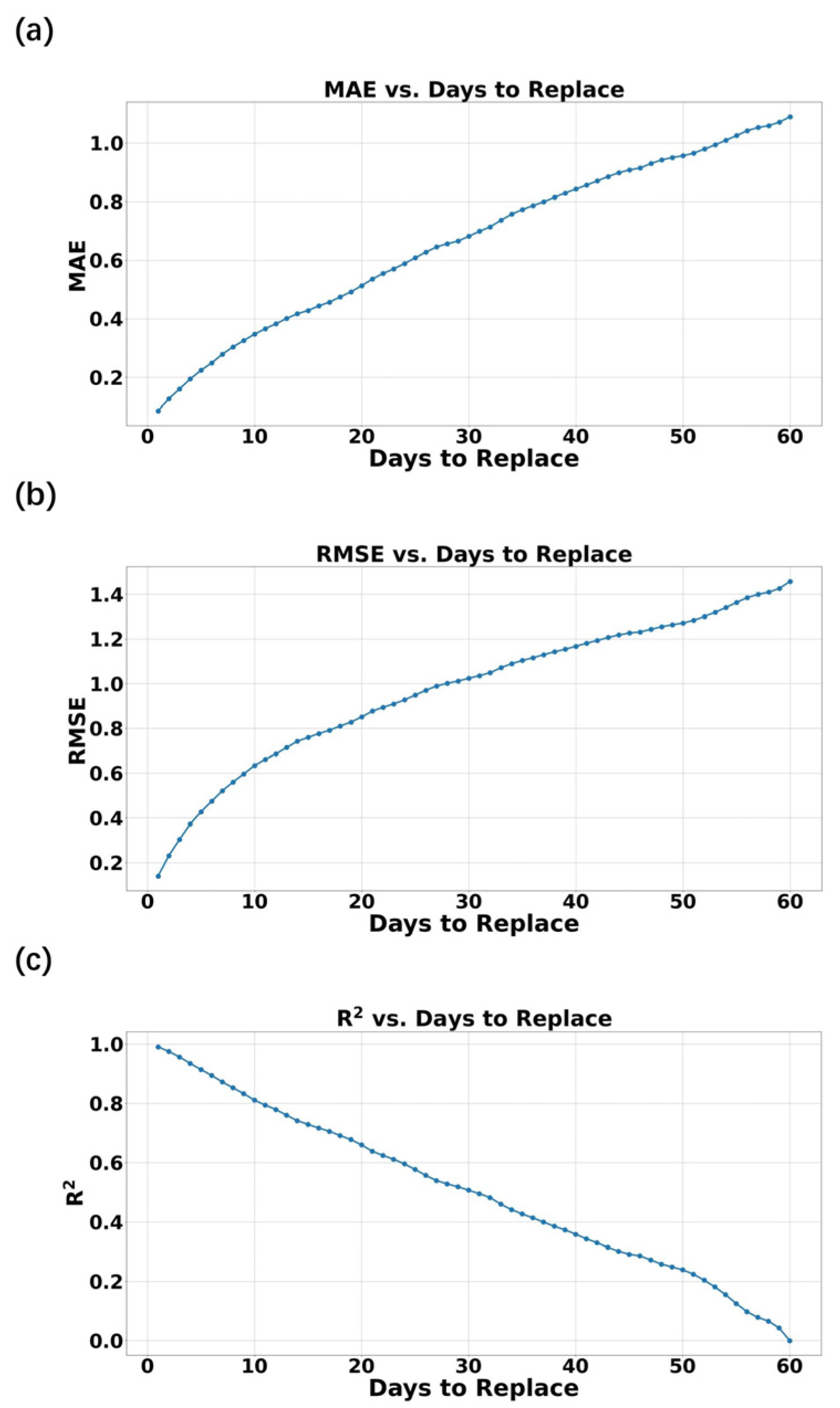
| Automatic Weather Station | Position | Length of Data Record | Number of Missing Values | |||
|---|---|---|---|---|---|---|
| Latitude N | Longitude E | Starting Date | Number of Data Points | Mean Temperature | Max/Min Temperature | |
| Ta Kwu Ling (TKL) | 22° 31′43″ | 114° 09′24″ | 14 October 1985 | 13,593 | 1091 | 1043 |
| Lau Fau Shan (LFS) | 22° 28′08″ | 113° 59′01″ | 16 September 1985 | 13,621 | 222 | 147 |
| Wetland Park (WLP) | 22° 28′00″ | 114° 00′32″ | 10 November 2005 | 6261 | 13 | 7 |
| Shek Kong (SEK) | 22° 26′10″ | 114° 05′05″ | 4 November 1996 | 9554 | 342 | 293 |
| Tai Mo Shan (TMS) | 22° 24′38″ | 114° 07′28″ | 1 December 1996 | 9527 | 231 | 179 |
| Sha Tin (SHA) | 22° 24′09″ | 114° 12′36″ | 1 October 1984 | 13,971 | 154 | 111 |
| Tate’s Cairn (TC) | 22° 21′28″ | 114° 13′04″ | 1 December 1997 | 9162 | 106 | 66 |
| King’s Park (KP) | 22° 18′43″ | 114° 10′22″ | 1 July 1992 | 11,141 | 25 | 7 |
| Hong Kong International Airport (HKA) | 22° 18′34″ | 113° 55′19″ | 1 June 1997 | 9345 | 0 | 31 |
| Hong Kong Observatory (HKO) | 22° 18′07″ | 114° 10′27″ | 1 April 1884 | 50,678 | 2557 | 2557 |
| Sha Lo Wan (SLW) | 22° 17′28″ | 113° 54′25″ | 25 February 1993 | 10,902 | 691 | 591 |
| Peng Chau (PEN) | 22° 17′28″ | 114° 02′36″ | 1 June 2004 | 6788 | 53 | 32 |
| Cheung Chau (CCH) | 22° 12′04″ | 114° 01′36″ | 30 March 1992 | 11,234 | 98 | 44 |
| Waglan Island (WGL) | 22° 10′56″ | 114° 18′12″ | 22 August 1989 | 12,185 | 811 | 665 |
| Automatic Weather Station | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|
| Ta Kwu Ling (TKL) | 0.066 | 0.012 | 0.111 | 0.996 |
| Lau Fau Shan (LFS) | 0.063 | 0.012 | 0.108 | 0.996 |
| Wetland Park (WLP) | 0.061 | 0.010 | 0.101 | 0.996 |
| Shek Kong (SEK) | 0.064 | 0.011 | 0.104 | 0.997 |
| Tai Mo Shan (TMS) | 0.059 | 0.012 | 0.107 | 0.995 |
| Sha Tin (SHA) | 0.058 | 0.008 | 0.092 | 0.997 |
| Tate’s Cairn (TC) | 0.062 | 0.011 | 0.104 | 0.996 |
| King’s Park (KP) | 0.055 | 0.009 | 0.093 | 0.996 |
| Hong Kong International Airport (HKA) | 0.057 | 0.009 | 0.094 | 0.997 |
| Hong Kong Observatory (HKO) | 0.053 | 0.007 | 0.085 | 0.997 |
| Sha Lo Wan (SLW) | 0.060 | 0.007 | 0.082 | 0.998 |
| Peng Chau (PEN) | 0.055 | 0.008 | 0.091 | 0.996 |
| Cheung Chau (CCH) | 0.055 | 0.008 | 0.091 | 0.996 |
| Waglan Island (WGL) | 0.053 | 0.008 | 0.092 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Kong, H.; Leung, J.C.-H.; Chan, P.W.; Fong, C.; Wang, Y.; Zhang, B. A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Appl. Sci. 2024, 14, 6289. https://doi.org/10.3390/app14146289
Yu D, Kong H, Leung JC-H, Chan PW, Fong C, Wang Y, Zhang B. A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Applied Sciences. 2024; 14(14):6289. https://doi.org/10.3390/app14146289
Chicago/Turabian StyleYu, Dan, Hoiio Kong, Jeremy Cheuk-Hin Leung, Pak Wai Chan, Clarence Fong, Yuchen Wang, and Banglin Zhang. 2024. "A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points" Applied Sciences 14, no. 14: 6289. https://doi.org/10.3390/app14146289
APA StyleYu, D., Kong, H., Leung, J. C.-H., Chan, P. W., Fong, C., Wang, Y., & Zhang, B. (2024). A 1D Convolutional Neural Network (1D-CNN) Temporal Filter for Atmospheric Variability: Reducing the Sensitivity of Filtering Accuracy to Missing Data Points. Applied Sciences, 14(14), 6289. https://doi.org/10.3390/app14146289








