Longitudinal Nonlinear Equivalent Continuous Model for Shield Tunnel under Coupling of Longitudinal Axial Force and Bending Moment
Abstract
1. Introduction
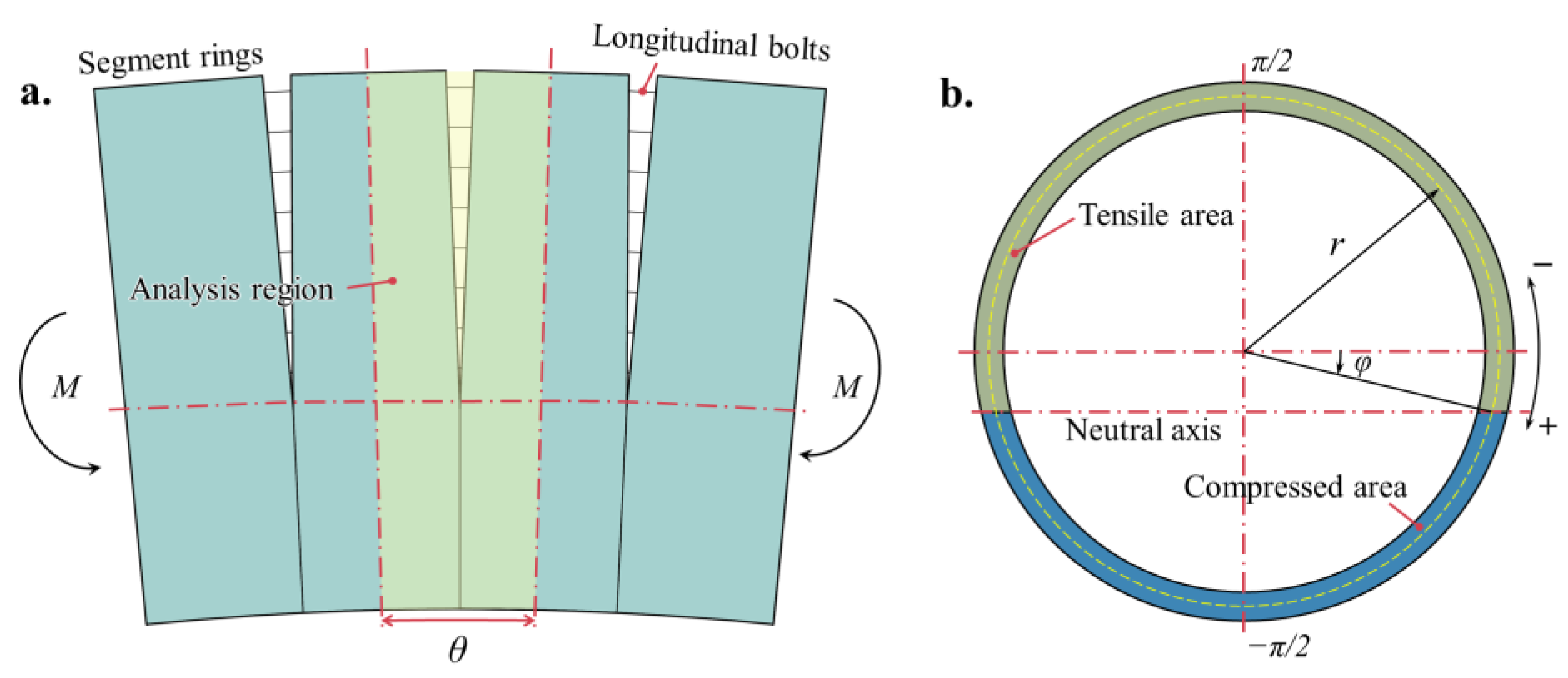
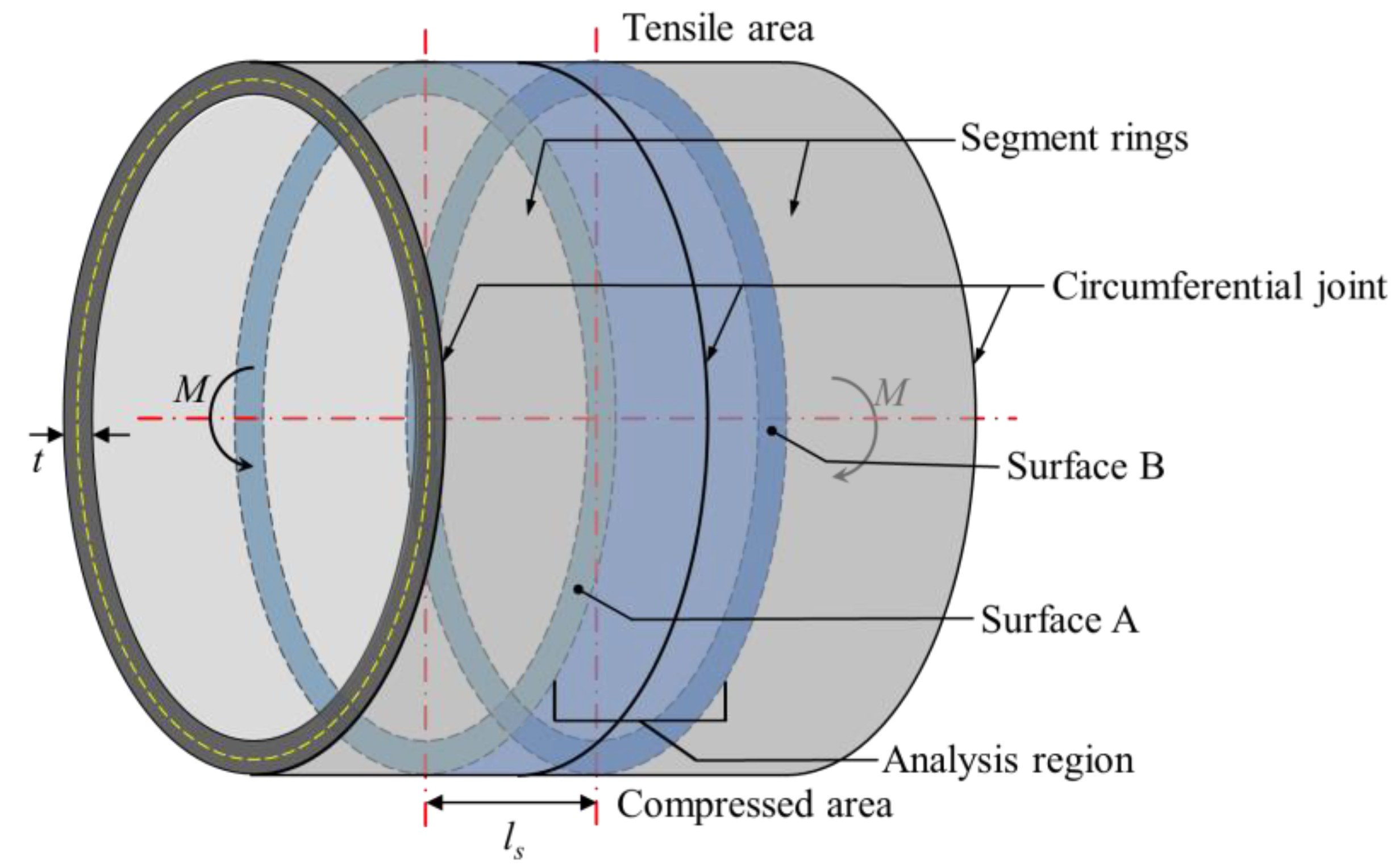
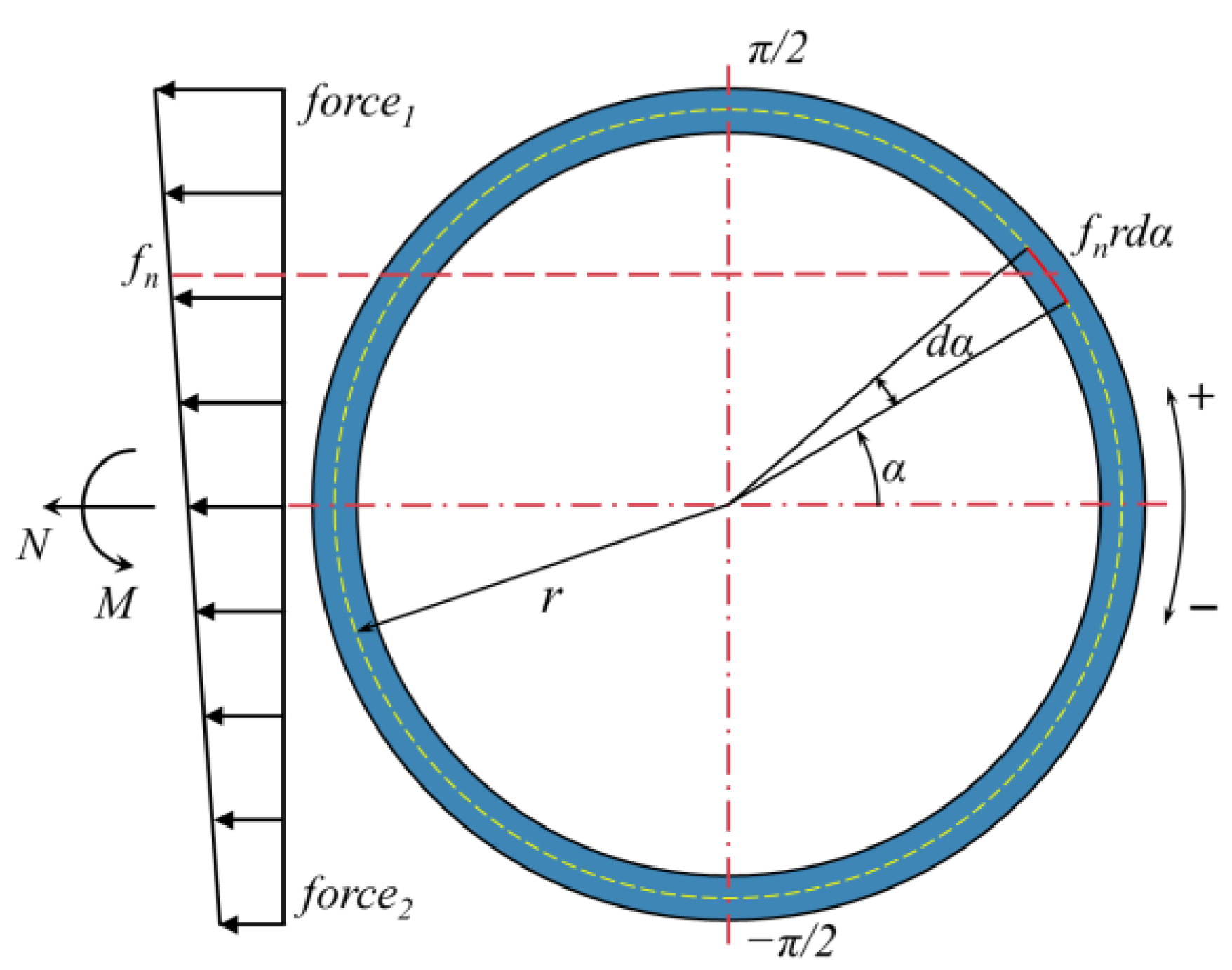
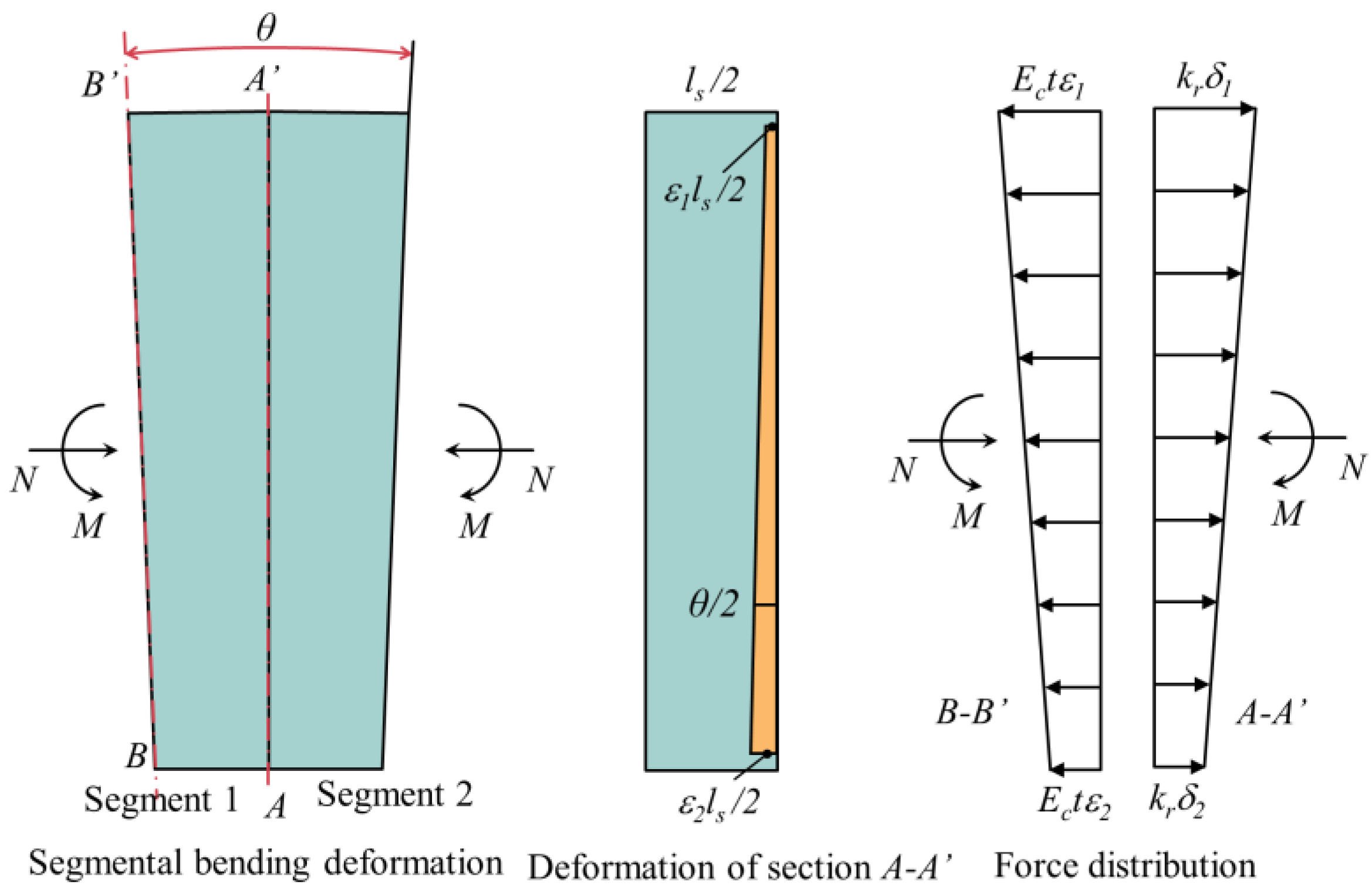
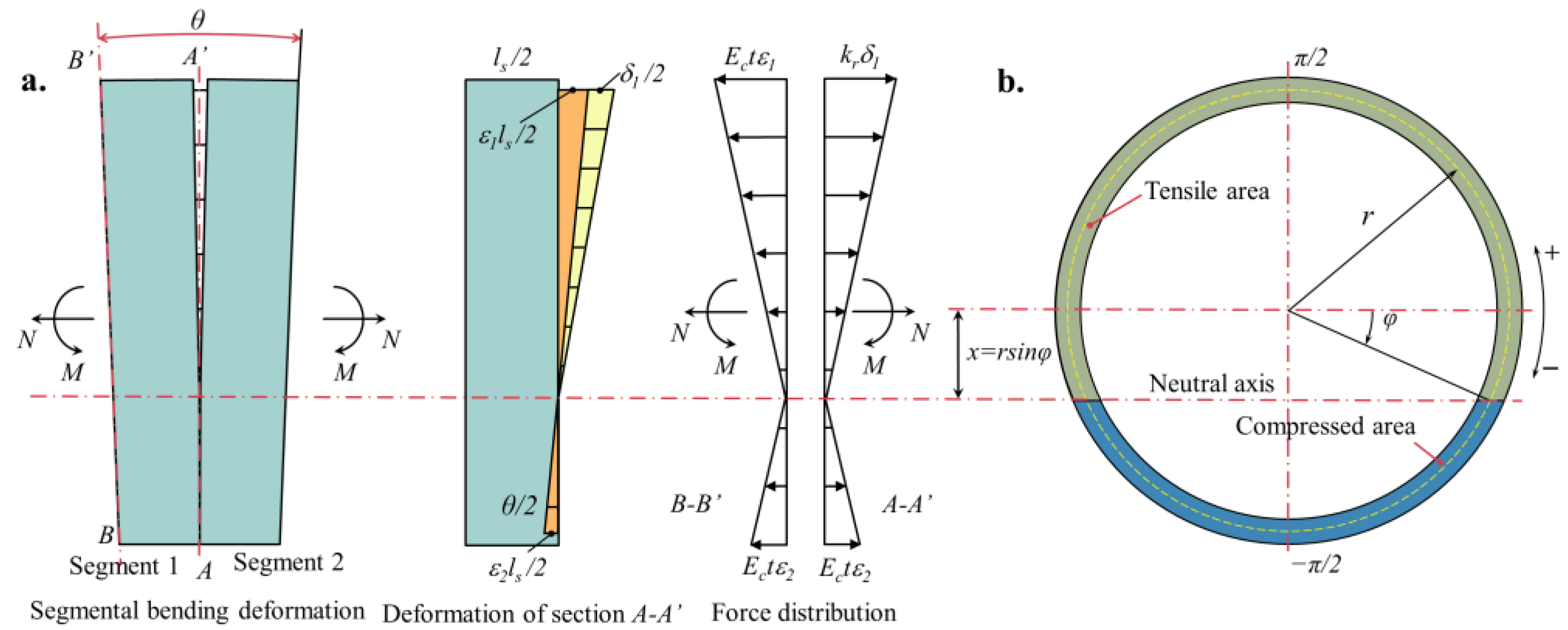
2. Longitudinal Equivalent Continuous Model
- (1)
- Flat cross-section assumption.
- (2)
- The relative position of the neutral axis in the cross-section does not change along the longitudinal direction.
- (3)
- The tensile side of the segmental ring and longitudinal bolts, together with the tensile force, only the compression side of the segmental ring is under pressure; longitudinal bolts are not stressed.
- (4)
- The preloading force of longitudinal bolts is not considered.
- (5)
- The discrete distribution of longitudinal bolts along the segmental ring is simplified to an equivalent continuous uniform distribution.
- (6)
- Both the segment and the bolts are in the elastic stage.
3. Longitudinal Nonlinear Equivalent Continuous Model
3.1. Mode 1
3.2. Mode 2
3.3. Mode 3
4. Theoretical Solution and Numerical Validation of Mechanical Parameters
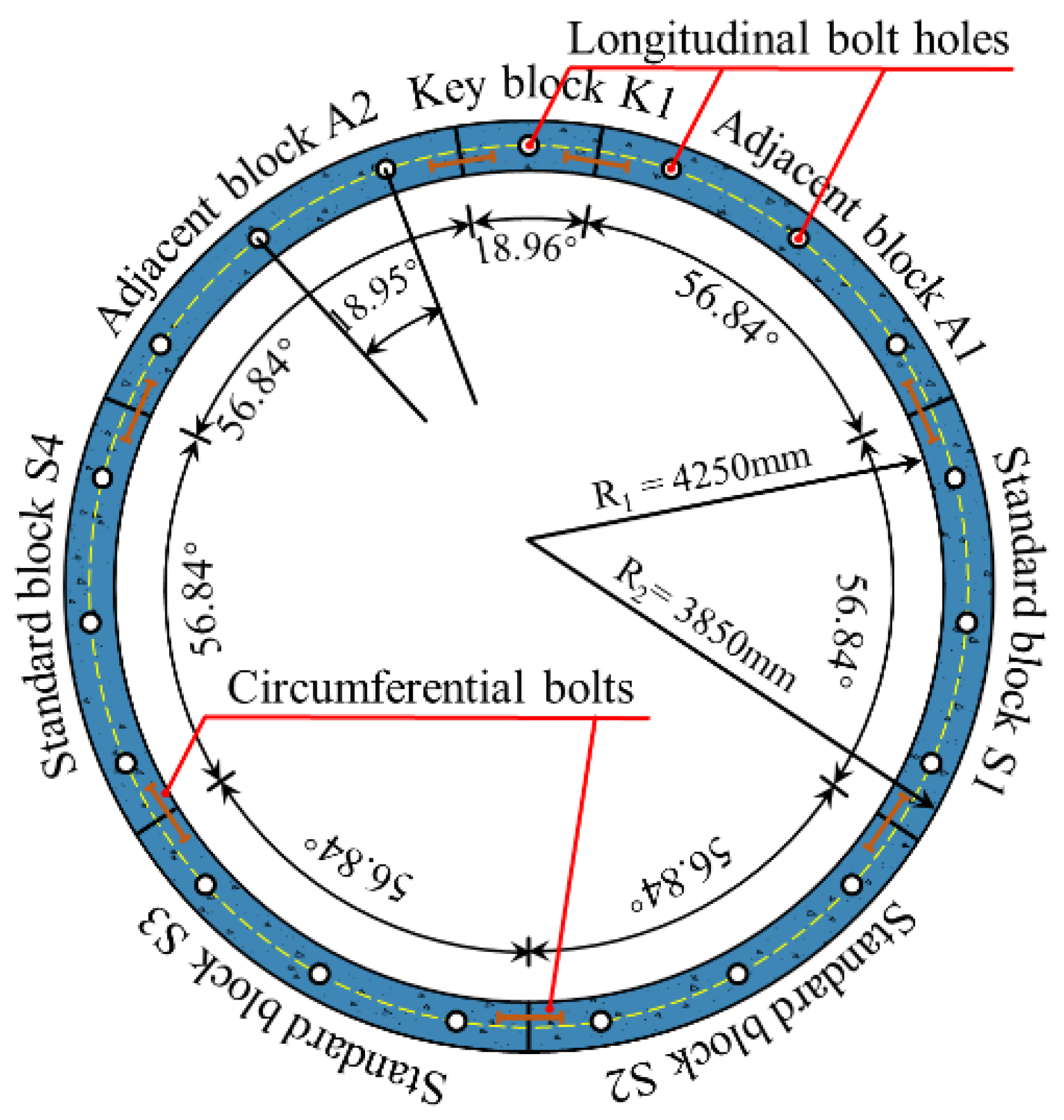
4.1. Engineering Background
4.2. Finite Element Modeling
4.3. Parameter Solving and Validation
4.3.1. Neutral Axis Angle
4.3.2. Longitudinal Equivalent Bending Stiffness
4.3.3. Longitudinal Equivalent Tensile and Compressive Stiffness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, G.; Geng, P.; Wang, T.; Meng, Q.; Huo, F.; Wang, X.; Wang, J. Seismic vulnerability of shield tunnels in interbedded soil deposits, Case study of submarine tunnel in Shantou Bay. Ocean. Eng. 2023, 286, 115500. [Google Scholar] [CrossRef]
- Zheng, J.; He, S.; Li, Y.; He, J.; He, J. Longitudinal Deformation of Deep Shield Tunnels Caused by Upper Load Reduction. Materials 2021, 14, 3629. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; He, C.; Qiu, Y.; Zhang, L.; Wang, W.; Xie, H.; Zhang, Y.; Cao, S. Full-scale tests on bending behavior of segmental joints for large underwater shield tunnels. Tunn. Undergr. Space Technol. 2018, 75, 100–116. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Liu, H. Measuring joint opening displacement between model shield-tunnel segments for reduced-scale model tests. Structures 2018, 16, 112–118. [Google Scholar] [CrossRef]
- Jin, H.; Yu, S.; Zhou, S.; Xiao, J. Research on Mechanics of Longitudinal Joint in Shield Tunnel by the Nonlinear Spring Equivalent Method. KSCE J. Civ. Eng. 2019, 23, 902–913. [Google Scholar] [CrossRef]
- Shiba, Y.; Kawashima, K.; Obinata, N.; Kano, T. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method. Proc. Civ. Soc. 1989, 1989, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Geng, P.; Wang, Q.; Chen, C.; Tang, R.; Yang, Q. Full-scale test on seismic performance of circumferential joint of shield-driven tunnel. Soil Dyn. Earthq. Eng. 2021, 151, 106957. [Google Scholar] [CrossRef]
- Zhang, J.; He, C.; Geng, P.; He, Y.; Wang, W.; Meng, L. Shaking table tests on longitudinal seismic response of shield tunnel through soft-hard stratum junction. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2017, 36, 68–77. [Google Scholar] [CrossRef]
- Wang, J.; Liu, H.; Liu, H.; Zou, Y. Centrifuge model study on the seismic responses of shield tunnel. Tunn. Undergr. Space Technol. 2019, 92, 103036. [Google Scholar] [CrossRef]
- Li, X.; Zhou, X.; Hong, B.; Zhu, H. Experimental and analytical study on longitudinal bending behavior of shield tunnel subjected to longitudinal axial forces. Tunn. Undergr. Space Technol. 2019, 86, 128–137. [Google Scholar] [CrossRef]
- Dong, Z.; Kuo, C.; Yin, J.; Wen, S.; Liu, G.; Gou, Y. Examination of Longitudinal Seismic Vulnerability of Shield Tunnels Utilizing Incremental Dynamic Analysis. Front. Earth Sci. 2021, 9, 779879. [Google Scholar] [CrossRef]
- Lu, Y.; Song, Y.; Wang, Y.; Yuan, J. Three-Dimensional Nonlinear Seismic Response of Shield Tunnel Spatial End Structure. Adv. Civ. Eng. 2021, 2021, 8441325. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Q.; Cao, W. Study on Stress and Deformation of Bolt Joints of Shield Tunnel under Static and Seismic Action. KSCE J. Civ. Eng. 2021, 25, 3146–3159. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, W.; Qi, J.; Niu, R.; Zhang, C. Seismic Response Analysis of Anchor Joint in Shield–Driven Tunnel Considering Soil–Structure Interaction. Appl. Sci. 2022, 12, 6362. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Yuan, Y.; Li, C.; Qiu, J. Experimental investigation of seismic performance of shield tunnel under near-field ground motion. Structures 2022, 43, 1407–1421. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, Y.; Bao, Z.; Yu, H.; Bilotta, E. Shaking table tests on shaft-tunnel junction under longitudinal excitations. Soil Dyn. Earthq. Eng. 2020, 132, 106055. [Google Scholar] [CrossRef]
- Guo, W.; Feng, K.; Lu, X.; Qi, M.; Liu, X.; Fang, Y.; He, C.; Xiao, M. Model test investigation on the longitudinal mechanical property of shield tunnels considering internal structure. Tunn. Undergr. Space Technol. 2023, 140, 105293. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Wang, Z.; Lei, M.; Zhao, D.; Cao, C. Damage mechanism modelling of shield tunnel with longitudinal differential deformation based on elastoplastic damage model. Tunn. Undergr. Space Technol. 2021, 113, 103952. [Google Scholar] [CrossRef]
- Wu, H.-N.; Shen, S.-L.; Yang, J.; Zhou, A. Soil-tunnel interaction modelling for shield tunnels considering shearing dislocation in longitudinal joints. Tunn. Undergr. Space Technol. 2018, 78, 168–177. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, R.; Wu, H.; Meng, F. A simplified method for estimating the longitudinal and circumferential behaviors of the shield-driven tunnel adjacent to a braced excavation. Comput. Geotech. 2020, 123, 103595. [Google Scholar] [CrossRef]
- Liu, D.; Tian, C.; Wang, F.; Hu, Q.; Zuo, J. Longitudinal structural deformation mechanism of shield tunnel linings considering shearing dislocation of circumferential joints. Comput. Geotech. 2021, 139, 104384. [Google Scholar] [CrossRef]
- Huang, W.M.; Wang, J.C.; Yang, Z.X.; Xu, R.Q. Analytical analysis of the longitudinal response of shield tunnel lining considering ring-to-ring interaction. Comput. Geotech. 2022, 146, 104705. [Google Scholar] [CrossRef]
- Zhang, J.; He, C.; Geng, P.; He, Y.; Wang, W. Improved longitudinal seismic deformation method of shield tunnels based on the iteration of the nonlinear stiffness of ring joints. Sustain. Cities Soc. 2019, 45, 105–116. [Google Scholar] [CrossRef]
- Geng, P.; Mei, S.; Zhang, J.; Chen, P.; Zhang, Y.; Yan, Q. Study on seismic performance of shield tunnels under combined effect of axial force and bending moment in the longitudinal direction. Tunn. Undergr. Space Technol. 2019, 91, 103004. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, C.; Gong, C.; Lei, M.; Liu, J.; Cao, C. An enhanced analytical model for predicting the nonlinear longitudinal equivalent bending stiffness of shield tunnels incorporating combined N-M actions. Tunn. Undergr. Space Technol. 2022, 126, 104567. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, R.; Wu, H.; Meng, F.; Yi, Y. General solutions for the longitudinal deformation of shield tunnels with multiple discontinuities in strata. Tunn. Undergr. Space Technol. 2021, 107, 103652. [Google Scholar] [CrossRef]
- Shiba, Y.; Kawashima, K.; Obinata, N.; Kano, T. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses. Doboku Gakkai Ronbunshu 1988, 1988, 319–327. (In Japanese) [Google Scholar] [CrossRef]


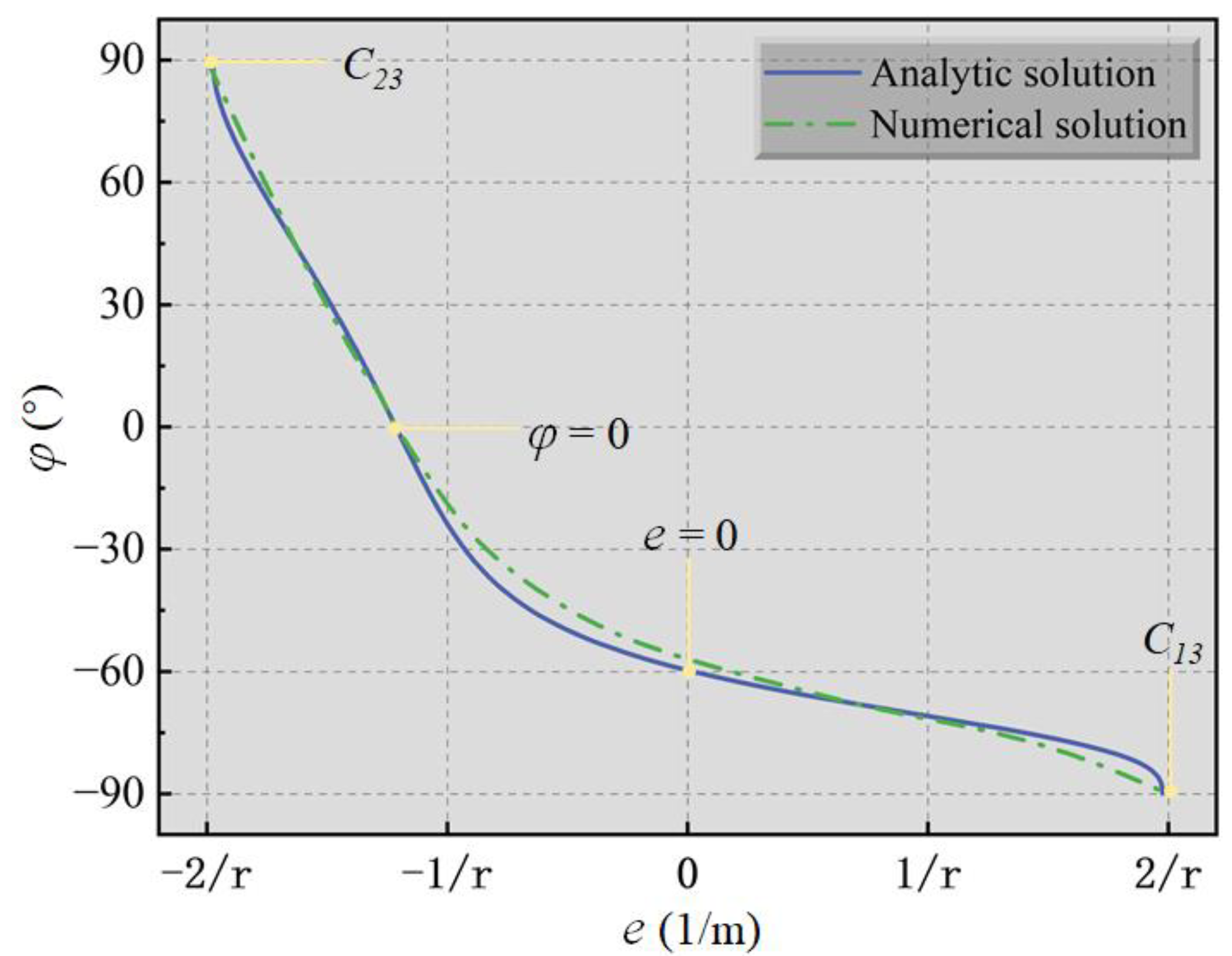
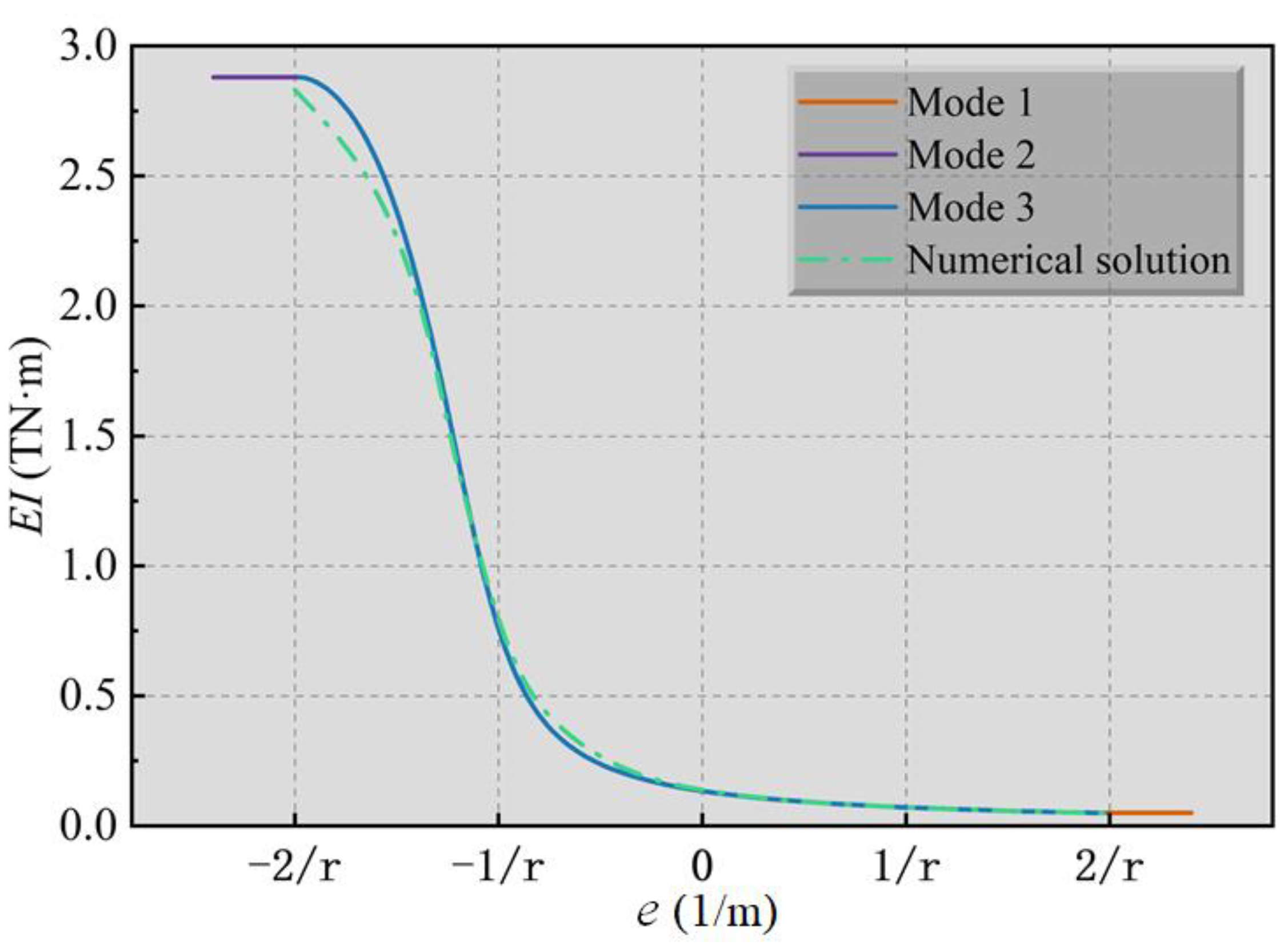


| Mode | Contact State | Bending Moment | Axial Force |
|---|---|---|---|
| 1 | Completely Separated | Small | Large, Tensile |
| 2 | Completely in Contact | Small | Large, Compressive |
| 3 | Partially in Contact | Large | Small, and either Tensile, Compressive, or Zero |
| Items | (GPa) |
|---|---|
| Segment (C50) | 34.5 |
| Longitudinal bolt (M30) | 210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Xu, Z.; Cai, Q.; Chen, C. Longitudinal Nonlinear Equivalent Continuous Model for Shield Tunnel under Coupling of Longitudinal Axial Force and Bending Moment. Appl. Sci. 2024, 14, 6261. https://doi.org/10.3390/app14146261
Guo X, Xu Z, Cai Q, Chen C. Longitudinal Nonlinear Equivalent Continuous Model for Shield Tunnel under Coupling of Longitudinal Axial Force and Bending Moment. Applied Sciences. 2024; 14(14):6261. https://doi.org/10.3390/app14146261
Chicago/Turabian StyleGuo, Xiangyu, Zhe Xu, Qipeng Cai, and Changjian Chen. 2024. "Longitudinal Nonlinear Equivalent Continuous Model for Shield Tunnel under Coupling of Longitudinal Axial Force and Bending Moment" Applied Sciences 14, no. 14: 6261. https://doi.org/10.3390/app14146261
APA StyleGuo, X., Xu, Z., Cai, Q., & Chen, C. (2024). Longitudinal Nonlinear Equivalent Continuous Model for Shield Tunnel under Coupling of Longitudinal Axial Force and Bending Moment. Applied Sciences, 14(14), 6261. https://doi.org/10.3390/app14146261






