Molecular Dynamics-Based Study of Graphene/Asphalt Mechanism of Interaction
Abstract
1. Introduction
2. Models Establishment and Simulation Methods
2.1. Molecule Models
2.1.1. Molecule Model for Virgin Asphalt
2.1.2. Molecule Model for Crumb Rubber
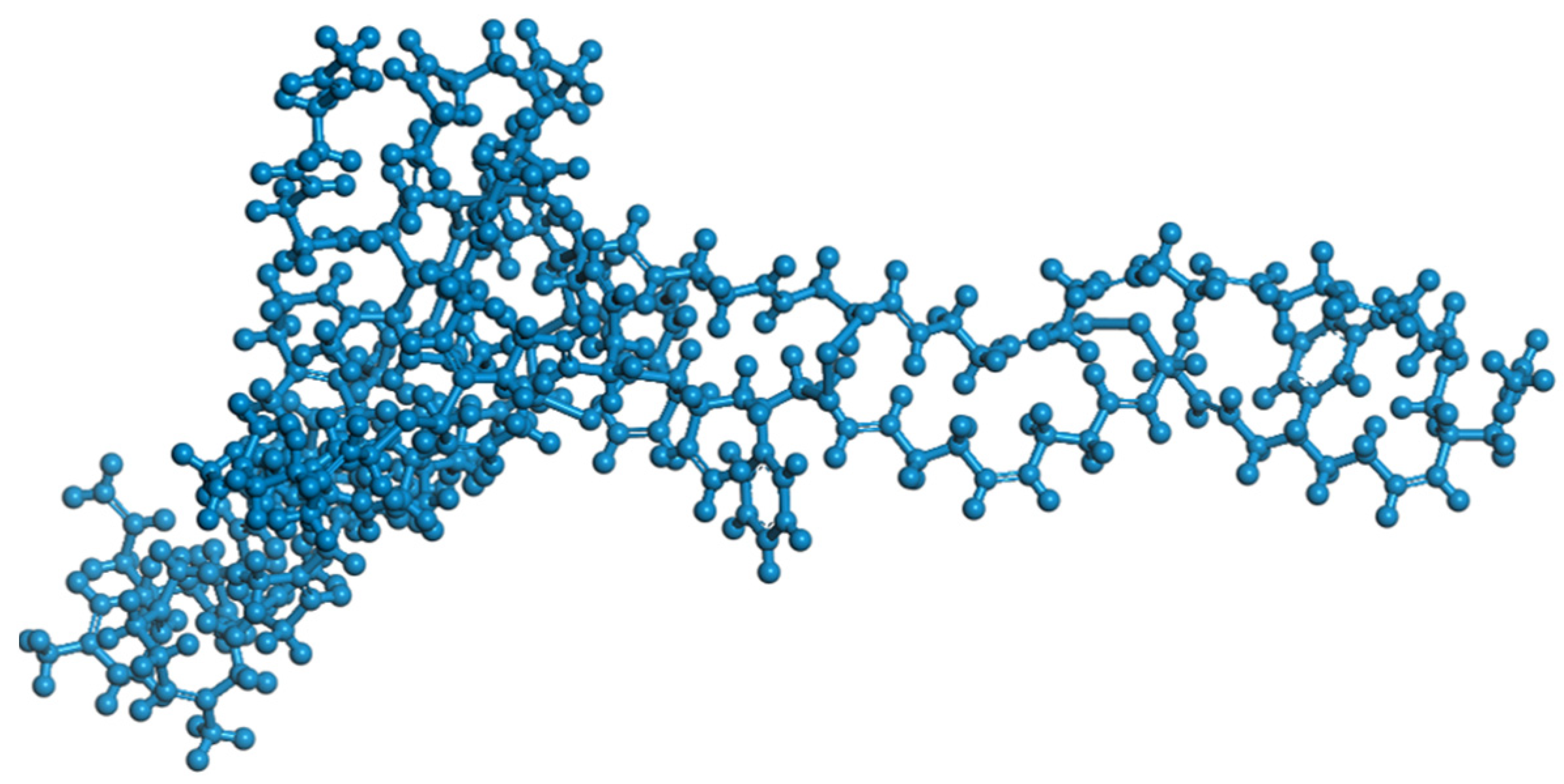
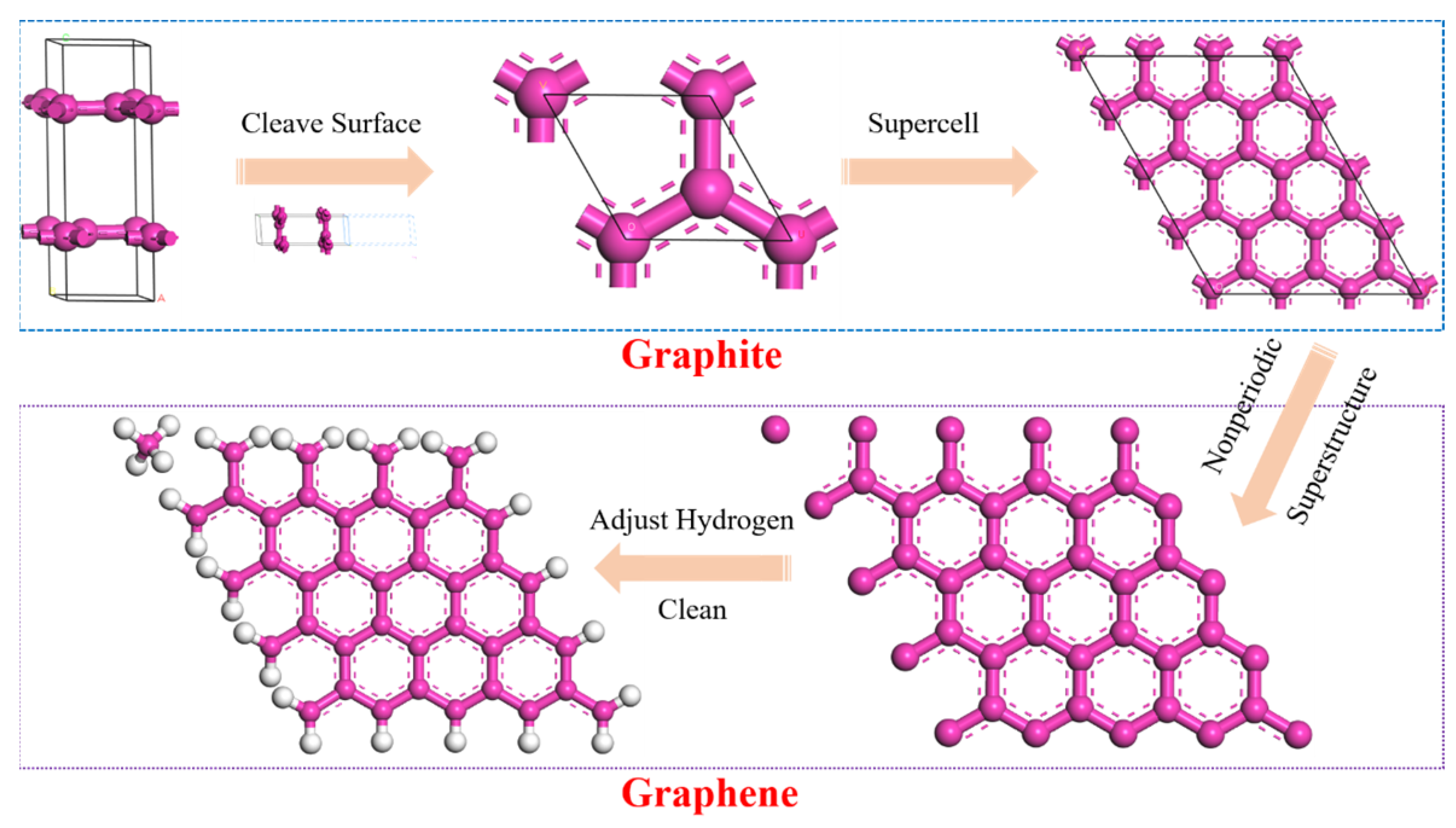
2.1.3. Molecule Model for GR
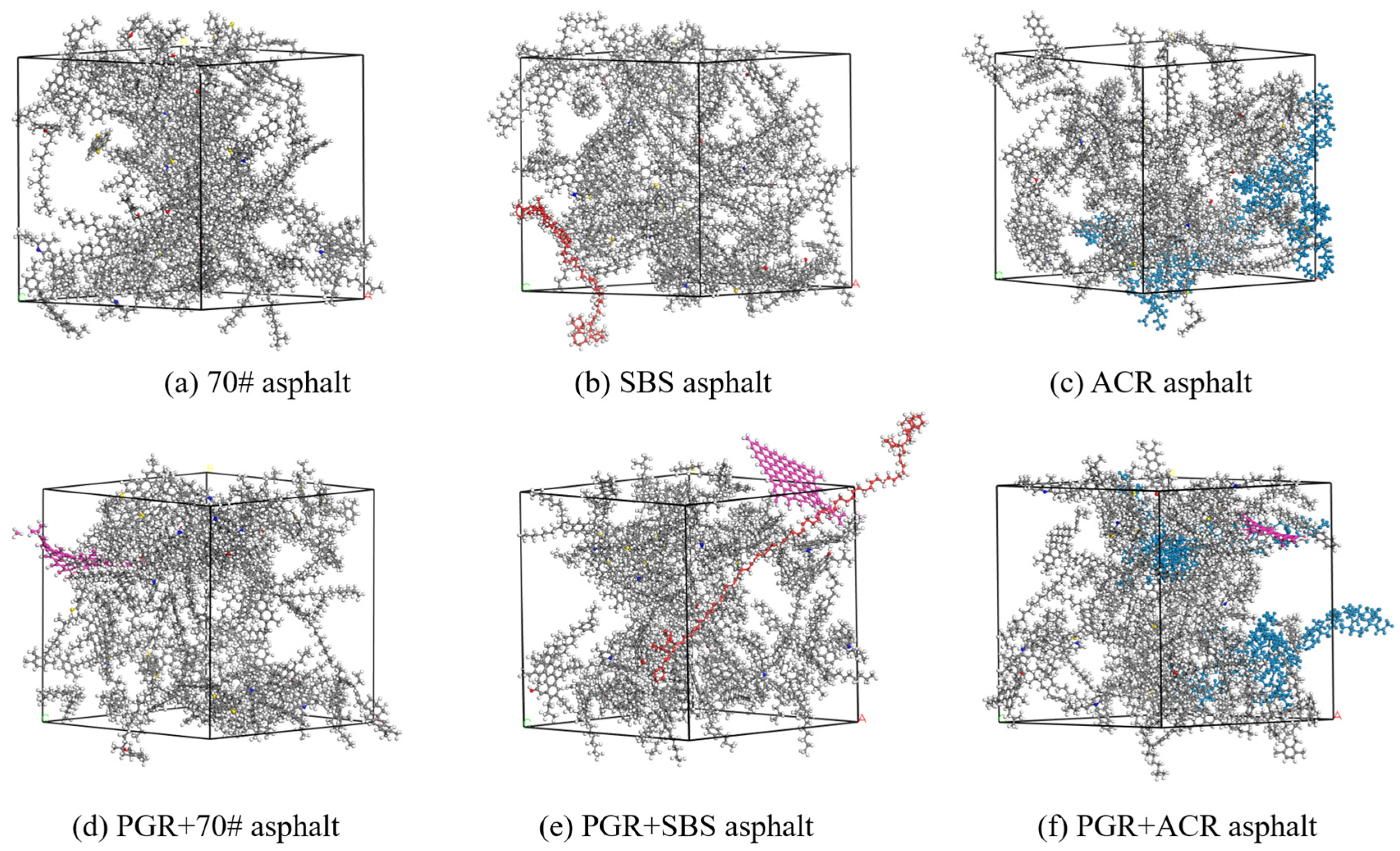
2.1.4. Construction of Asphalt Binder Bulks
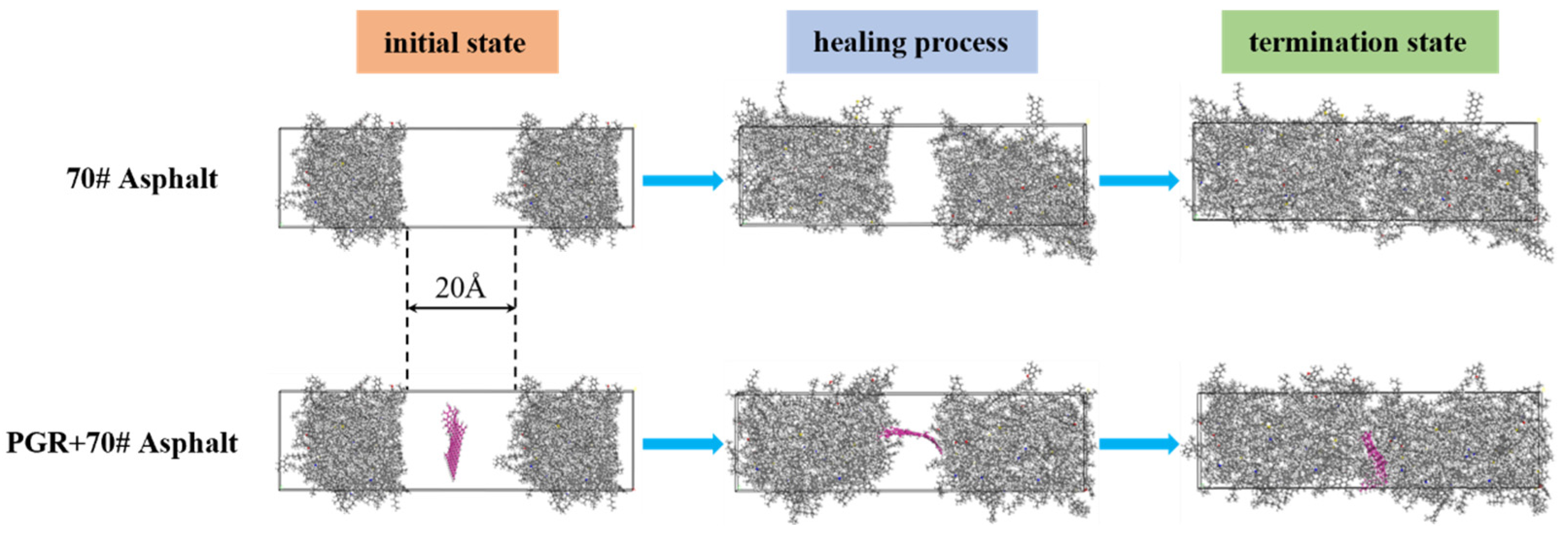
2.1.5. Modeling Molecular Self-Healing of Asphalt
2.1.6. Simulation of Self-Healing Processes
2.2. Molecular Dynamics Simulation Methods
2.2.1. Solubility Parameter
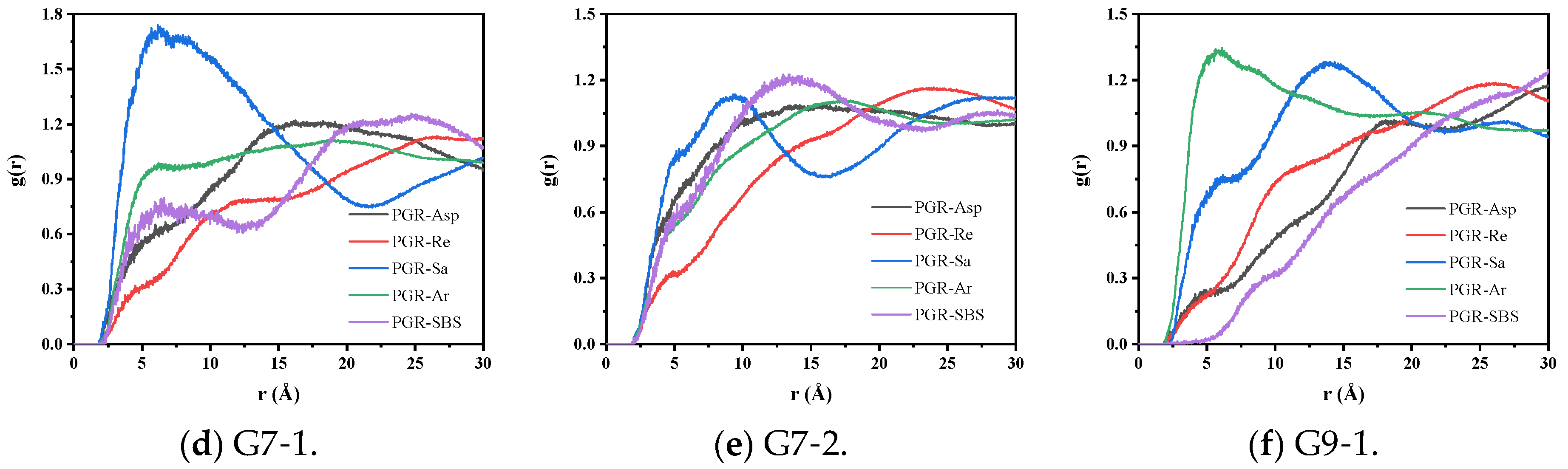
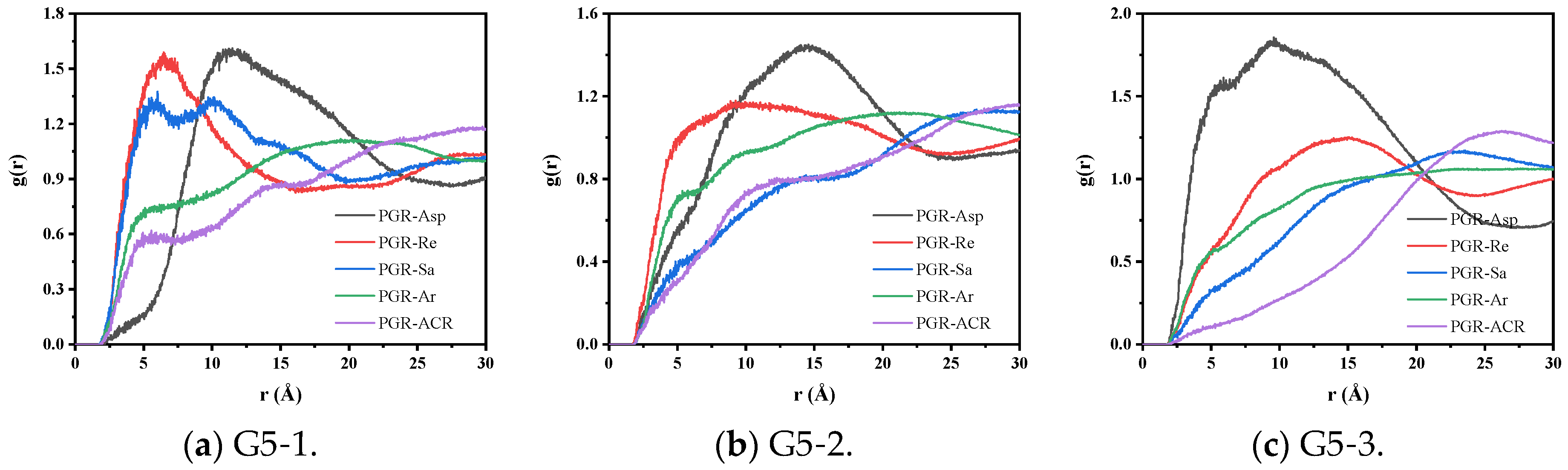
2.2.2. Radial Distribution Function (RDF)
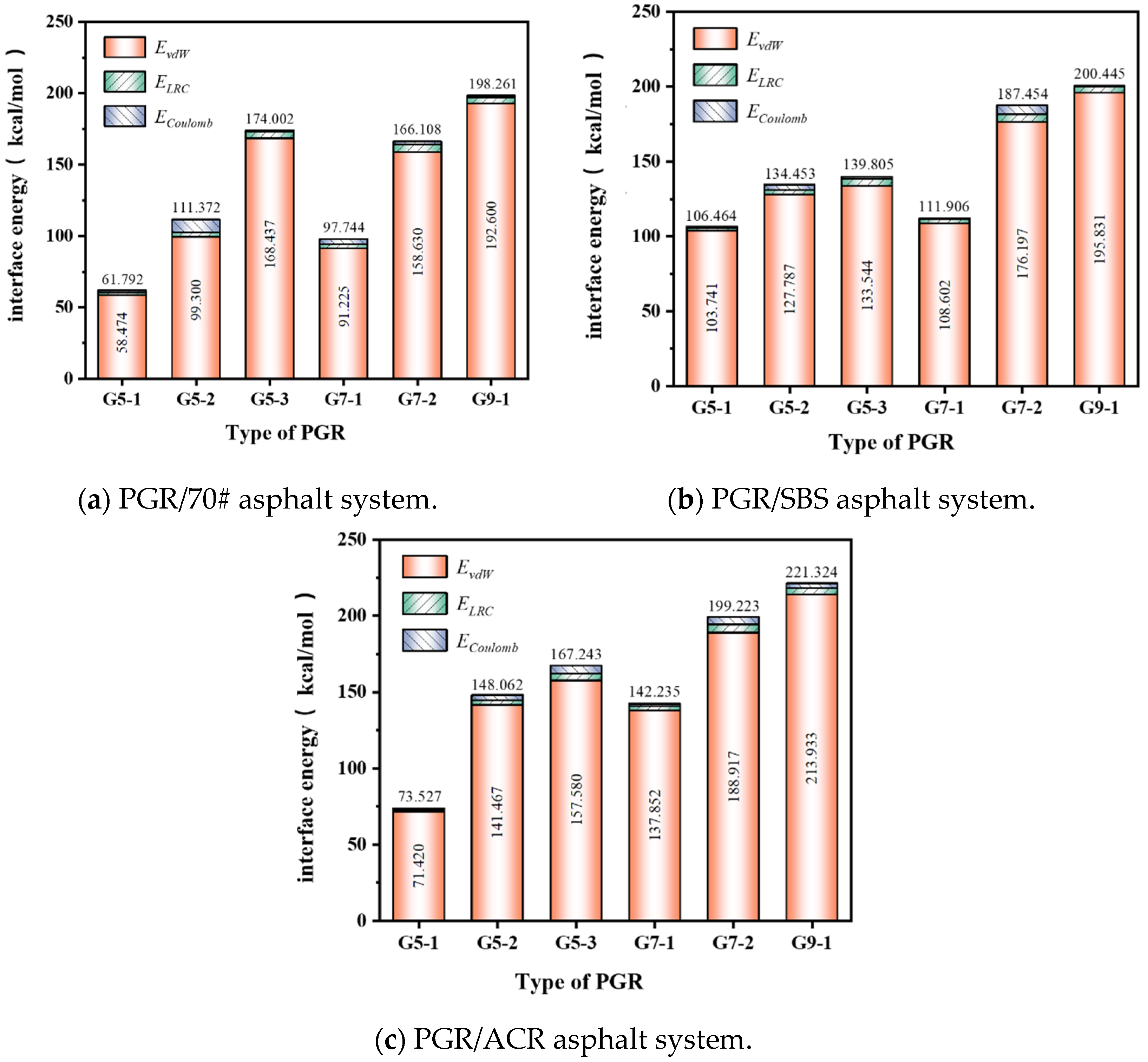
2.2.3. Binding Energy
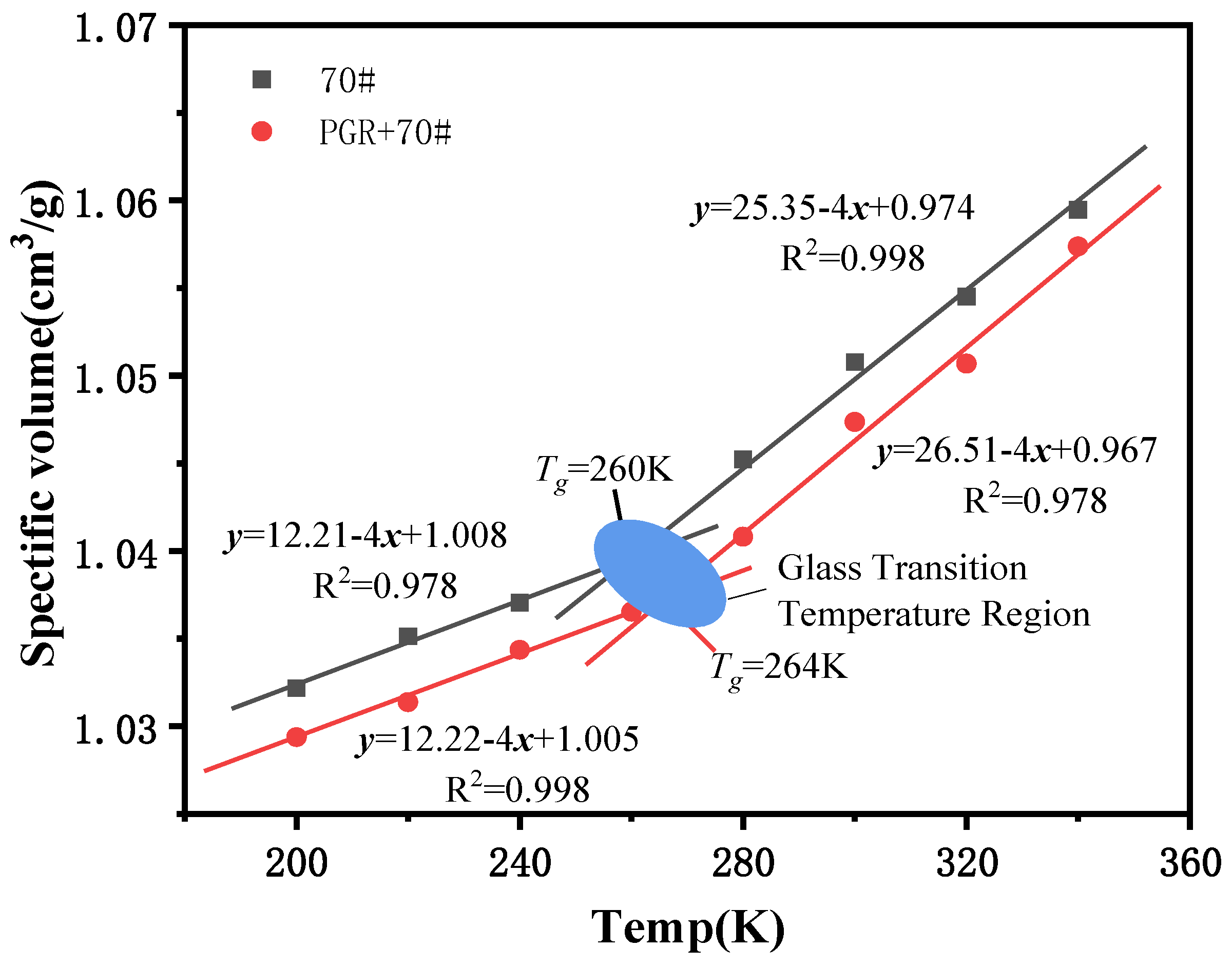
2.2.4. Glass Transition Temperature
2.2.5. Relative Concentration of Asphalt Molecules (RDF)
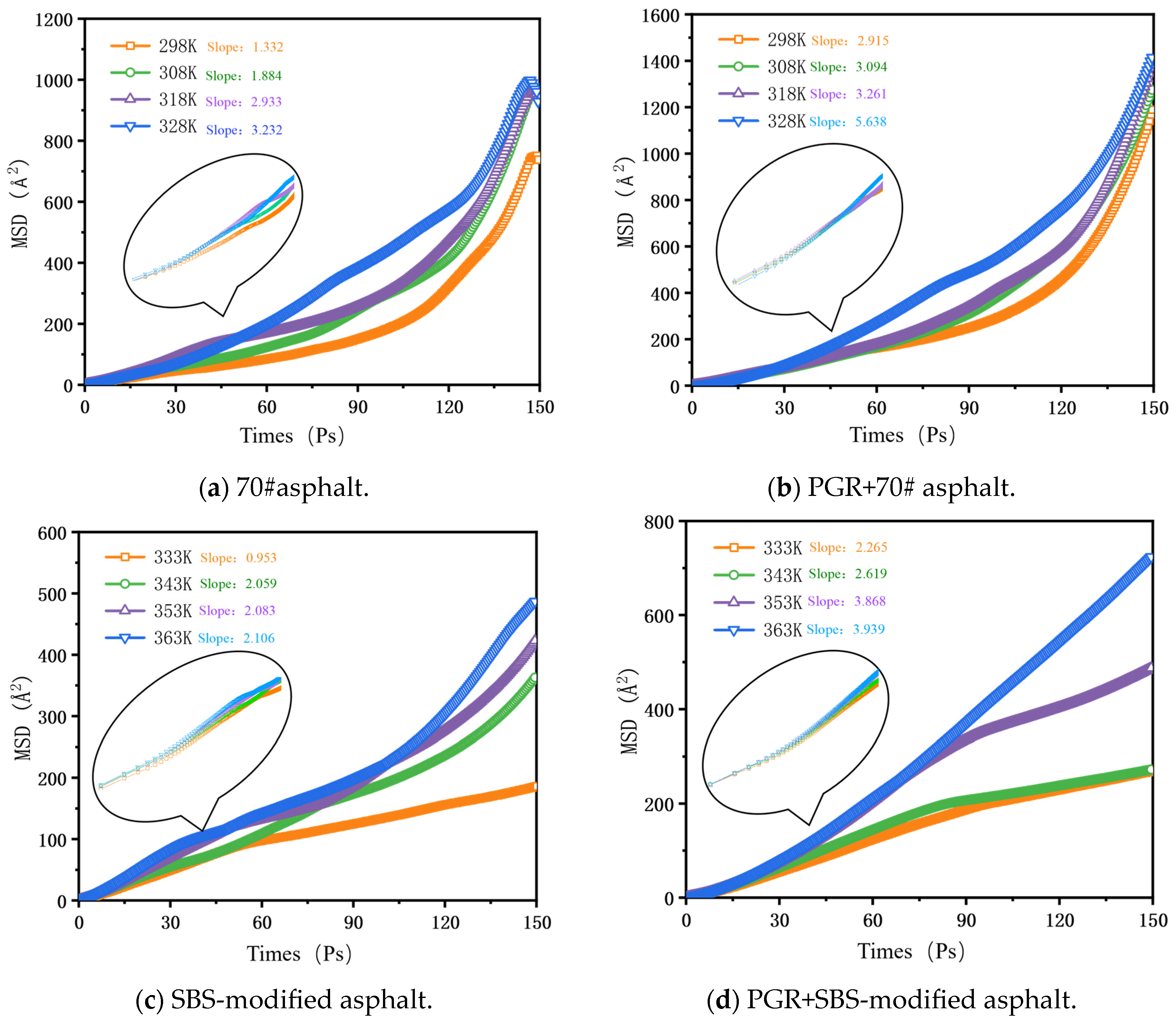
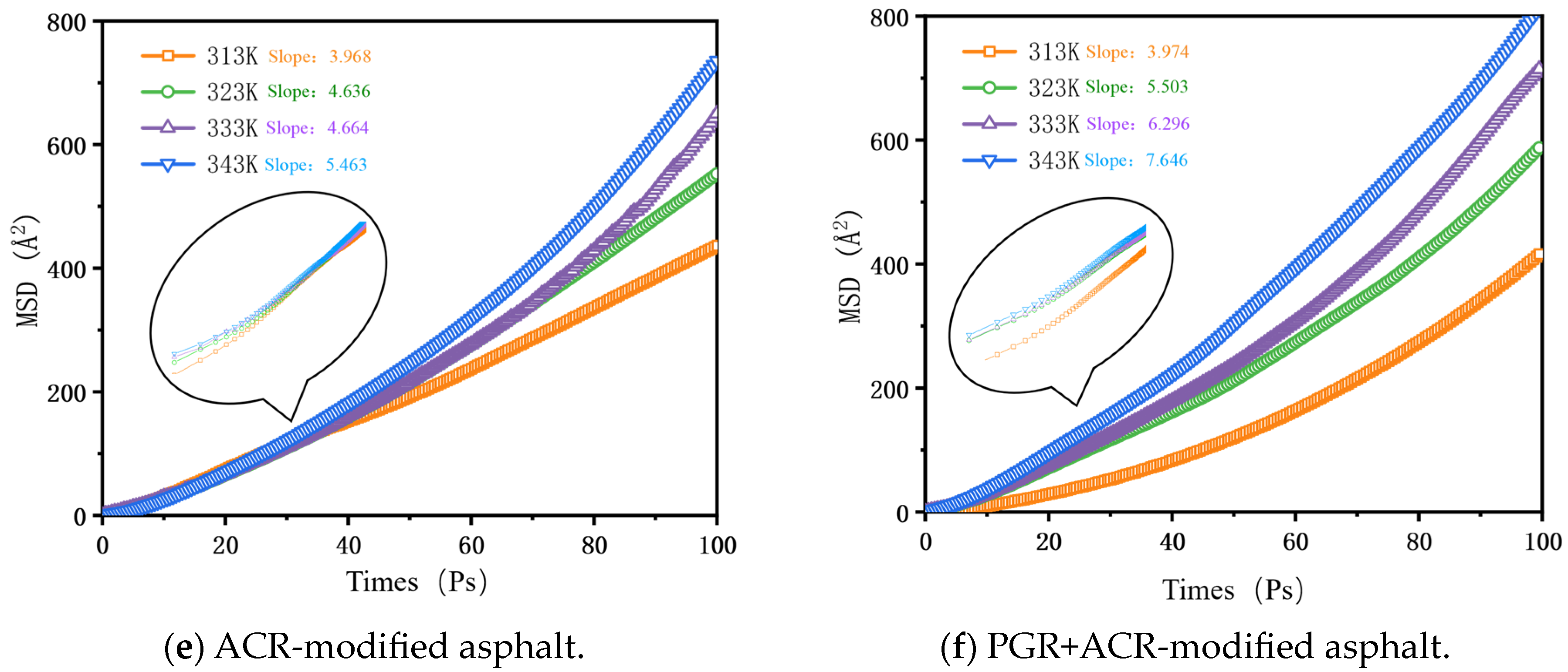
2.2.6. Mean Square Displacement
3. Results and Discussion
3.1. Verification for Binder Models
3.2. Interaction between Graphene and Asphalt Components
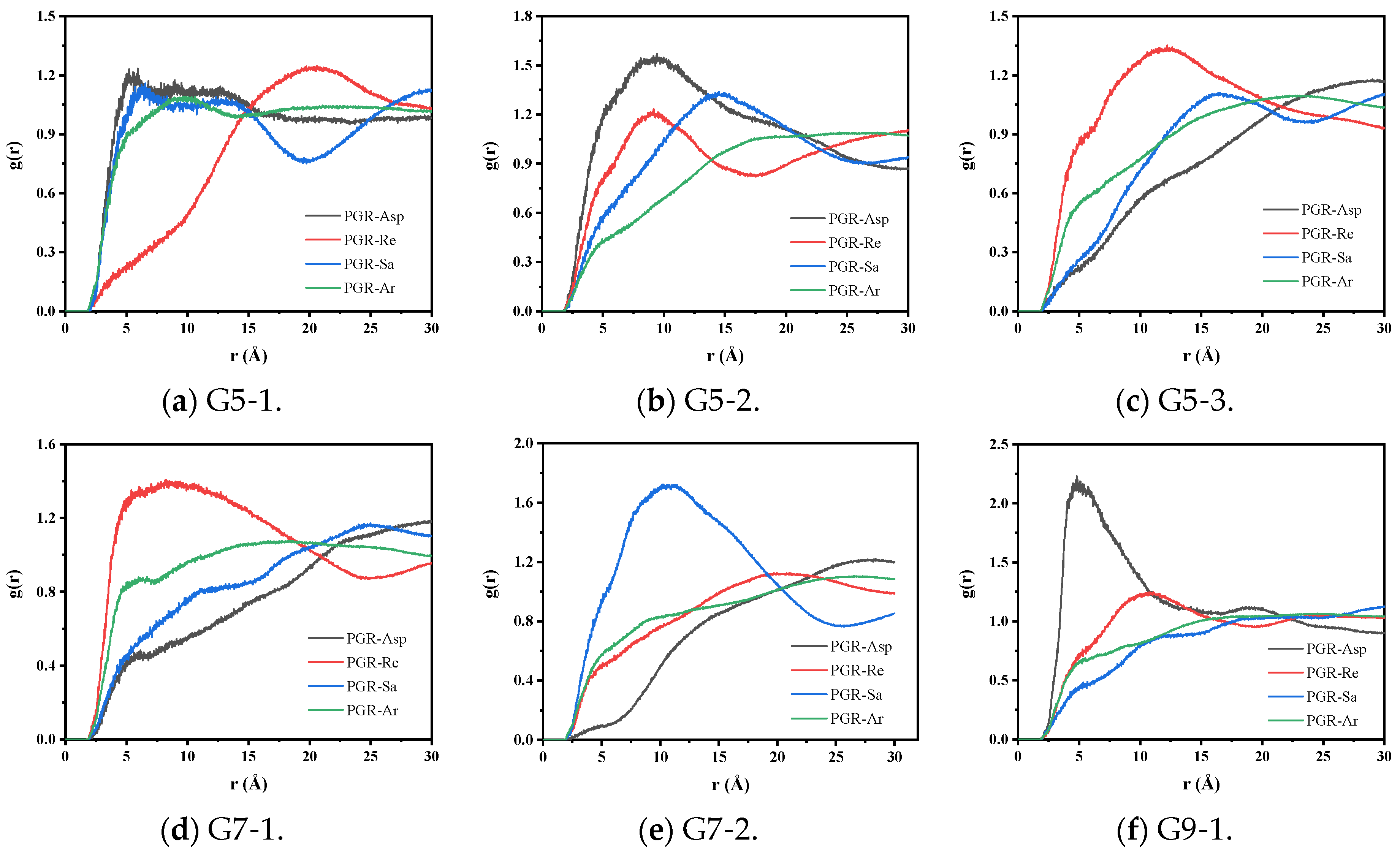
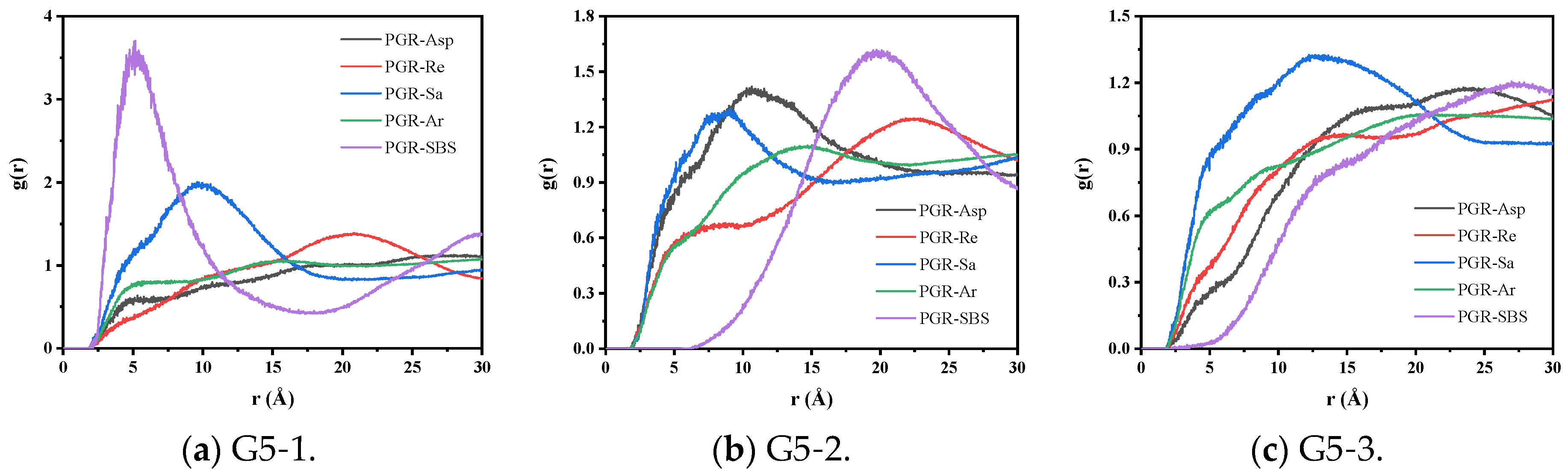
3.2.1. Radial Distribution Function Analysis
3.2.2. Binding Energy
3.2.3. Glass Transition Temperature
3.2.4. Relative Concentration of Asphalt Molecules
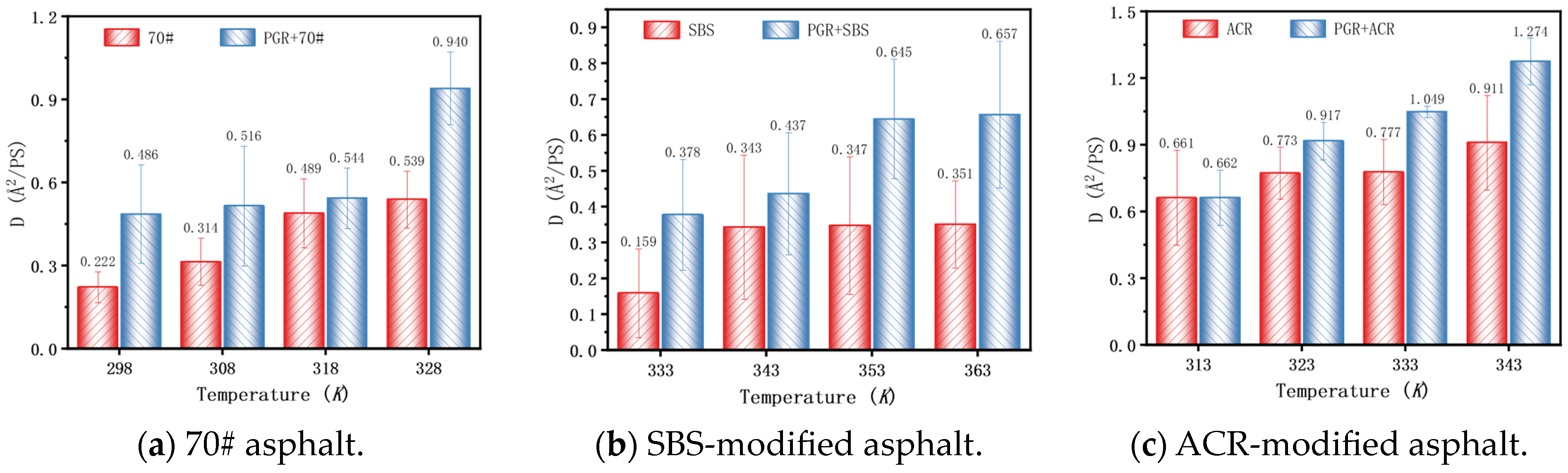
3.2.5. Mean Square Displacement and Diffusion Coefficient
4. Conclusions
- (1)
- The 4-component, 12-molecule model was used to construct the molecular model of matrix asphalt and polymerization-modified asphalt; the molecular model of graphene with different sizes and layers was successfully constructed by using cut graphite and supercrystalline constructions, etc., and the reasonableness of the model was verified by indexes such as energy, density, and solubility parameters.
- (2)
- The size and number of layers of PGR have a significant effect on its interaction with asphalt components, and the polar components in asphalt interact more strongly with PGR; when the size and number of layers of PGR are fixed, its interfacial binding with ACR-modified asphalt is the highest, followed by SBS-modified asphalt, and 70# matrix asphalt is the worst; the interfacial binding between PGR and asphalt mainly relies on the van der Waals interaction between interfacial molecules; multilayer graphene molecular modeling was successfully constructed with different sizes and numbers of layers, and the model was verified by energy, dissolution parameters, and other indicators. Van der Waals interaction: multilayer graphene on the mechanical properties of matrix asphalt strengthens the role of more apparent, and small-sized graphene is more suitable for enhancing the low-temperature performance of polymer-modified asphalt.
- (3)
- Based on the relative molecular concentration and MSD function, the self-healing process and mechanism of PGR-modified asphalt were comprehensively evaluated. PGR bridged asphalt molecules through rapid heat transfer and π-π stacking with aromatic ring-containing substances, which significantly improved the free diffusion ability of asphalt molecules, shortened the asphalt healing time, and enhanced the overall self-healing performance of asphalt.
- (4)
- Despite the above findings, the study may need to improve the realism of the simulation and the accuracy of the model construction. Future research could consider experimental validation of the simulation results and explore the effects of different modifiers and asphalt formulations on the self-healing ability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wu, S.; Amirkhanian, S. Investigation of the Graphene Oxide and Asphalt Interaction and Its Effect on Asphalt Pavement Performance. Constr. Build. Mater. 2018, 165, 572–584. [Google Scholar] [CrossRef]
- Shafabakhsh, G.; Mirabdolazimi, S.M.; Sadeghnejad, M. Evaluation the Effect of Nano-TiO2 on the Rutting and Fatigue Behavior of Asphalt Mixtures. Constr. Build. Mater. 2014, 54, 566–571. [Google Scholar] [CrossRef]
- Shafabakhsh, G.H.; Ani, O.J. Experimental Investigation of Effect of Nano TiO2/SiO2 Modified Bitumen on the Rutting and Fatigue Performance of Asphalt Mixtures Containing Steel Slag Aggregates. Constr. Build. Mater. 2015, 98, 692–702. [Google Scholar] [CrossRef]
- Sun, S.; Wang, Y.; Zhang, A. Study on Anti-Ultraviolet Radiation Aging Property of TiO2 Modified Asphalt. Adv. Mater. Res. 2011, 306–307, 951–955. [Google Scholar] [CrossRef]
- You, Z.; Mills-Beale, J.; Foley, J.M.; Roy, S.; Odegard, G.M.; Dai, Q.; Goh, S.W. Nanoclay-Modified Asphalt Materials: Preparation and Characterization. Constr. Build. Mater. 2011, 25, 1072–1078. [Google Scholar] [CrossRef]
- Liu, J.; Hao, P.; Jiang, W.; Sun, B. Rheological Properties of SBS Modified Asphalt Incorporated Polyvinylpyrrolidone Stabilized Graphene Nanoplatelets. Constr. Build. Mater. 2021, 298, 123850. [Google Scholar] [CrossRef]
- Yang, Q.; Qian, Y.; Fan, Z.; Lin, J.; Wang, D.; Zhong, J.; Oeser, M. Exploiting the Synergetic Effects of Graphene and Carbon Nanotubes on the Mechanical Properties of Bitumen Composites. Carbon 2021, 172, 402–413. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.-M.; Wu, Y.-L.; Wang, H.-R.; Chen, M.; Sun, H.-D.; Fan, L. Properties and Modification Mechanism of Asphalt with Graphene as Modifier. Constr. Build. Mater. 2021, 272, 121919. [Google Scholar] [CrossRef]
- Marasteanu, M.O.; Le, J.-L.; Turos, M. Graphene Nano-Platelet (GNP) Reinforced Asphalt Binders and Mixtures. In Proceedings of the 6th Eurasphalt & Eurobitume Congress, Prague, Czech Republic, 1–3 June 2016. [Google Scholar]
- Zhang, X. Research on Preparation of Graphene fou Pavement and Preformance of Graphene Modified Asphalt. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2021. [Google Scholar] [CrossRef]
- Nie, F.; Jian, W.; Lau, D. An Atomistic Study on the Thermomechanical Properties of Graphene and Functionalized Graphene Sheets Modified Asphalt. Carbon 2021, 182, 615–627. [Google Scholar] [CrossRef]
- Ashish, P.K.; Singh, D. Study on Understanding Functional Characteristics of Multi-Wall CNT Modified Asphalt Binder. Int. J. Pavement Eng. 2020, 21, 1069–1082. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Q.; Zhong, J.; Hong, B.; Wang, D.; Oeser, M. Rheological and Micro-Structural Characterization of Bitumen Modified with Carbon Nanomaterials. Constr. Build. Mater. 2019, 201, 580–589. [Google Scholar] [CrossRef]
- Guo, M.; Tan, Y.; Wei, J. Using Molecular Dynamics Simulation to Study Concentration Distribution of Asphalt Binder on Aggregate Surface. J. Mater. Civ. Eng. 2018, 30. [Google Scholar] [CrossRef]
- Xu, G.; Wang, H. Molecular Dynamics Study of Oxidative Aging Effect on Asphalt Binder Properties. Fuel 2017, 188, 1–10. [Google Scholar] [CrossRef]
- Sun, D.; Lin, T.; Zhu, X.; Tian, Y.; Liu, F. Indices for Self-Healing Performance Assessments Based on Molecular Dynamics Simulation of Asphalt Binders. Comput. Mater. Sci. 2016, 114, 86–93. [Google Scholar] [CrossRef]
- Shishehbor, M.; Pouranian, M.R.; Ramezani, M.G. Molecular Investigations on the Interactions of Graphene, Crude Oil Fractions and Mineral Aggregates at Low, Medium and High Temperatures. Pet. Sci. Technol. 2019, 37, 804–811. [Google Scholar] [CrossRef]
- Hu, K.; Yu, C.; Yang, Q.; Chen, Y.; Chen, G.; Ma, R. Multi–Scale Enhancement Mechanisms of Graphene Oxide on Styrene–Butadiene–Styrene Modified Asphalt: An Exploration from Molecular Dynamics Simulations. Mater. Des. 2021, 208, 109901. [Google Scholar] [CrossRef]
- Ramezani, M.G.; Rickgauer, J. Understanding the Adhesion Properties of Carbon Nanotube, Asphalt Binder, and Mineral Aggregates at the Nanoscale: A Molecular Dynamics Study. Pet. Sci. Technol. 2020, 38, 28–35. [Google Scholar] [CrossRef]
- Zeng, Q. Preparation and Mechanism analysis of Graphene Oxide/Asphalt Composites. Master’s Thesis, Changsha University of Science & Technology, Changsha, China, 2020. [Google Scholar] [CrossRef]
- Zhang, L.; Greenfield, M.L. Analyzing Properties of Model Asphalts Using Molecular Simulation. Energy Fuels 2007, 21, 1712–1716. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, Y.; Liao, M.; Li, Y.; Zhu, J.; Tian, W. Study on the Mechanism of the Effect of Graphene on the Rheological Properties of Rubber-Modified Asphalt Based on Size Effect. Constr. Build. Mater. 2023, 364, 129815. [Google Scholar] [CrossRef]
- Li, Y. Study on the Performance Enhancement Mechanism and Technical Characteristics of Dual-Response Oil-Carrying Fiber Self-Healing Asphalt Mixtures. Ph.D Thesis, Chang’an University, Xi’an, China, 2022. [Google Scholar]
- Guo, F.; Zhang, J.; Pei, J. Evaluation of the Compatibility between Rubber and Asphalt Based on Molecular Dynamics Simulation. Front. Struct. Civ. Eng. 2020, 14, 11. [Google Scholar] [CrossRef]
- Jiao, B.; Pan, B.; Che, T. Evaluating Impacts of Desulfurization and Depolymerization on Thermodynamics Properties of Crumb Rubber Modified Asphalt through Molecular Dynamics Simulation. Constr. Build. Mater. 2022, 323, 126360. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, Z.; Ma, F.; Zhao, P.; Hou, Y.; Jiang, X.; Peng, C. Effect of Water Molecular Behavior on Adhesion Properties of Asphalt-Aggregate Interface. Constr. Build. Mater. 2023, 402, 133028. [Google Scholar] [CrossRef]
- Ren, S.; Liu, X.; Lin, P.; Gao, Y.; Erkens, S. Review on the Diffusive and Interfacial Performance of Bituminous Materials: From a Perspective of Molecular Dynamics Simulation. J. Mol. Liq. 2022, 366, 120363. [Google Scholar] [CrossRef]
- Nie, F.; Jian, W.; Lau, D. Advanced Self-Healing Asphalt Reinforced by Graphene Structures: An Atomistic Insight. J. Vis. Exp. 2022, 183. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, H.; Wang, Y. Interaction of Asphalt and Water between Porous Asphalt Pavement Voids with Different Aging Stage and Its Significance to Drainage. Constr. Build. Mater. 2020, 252, 119085. [Google Scholar] [CrossRef]
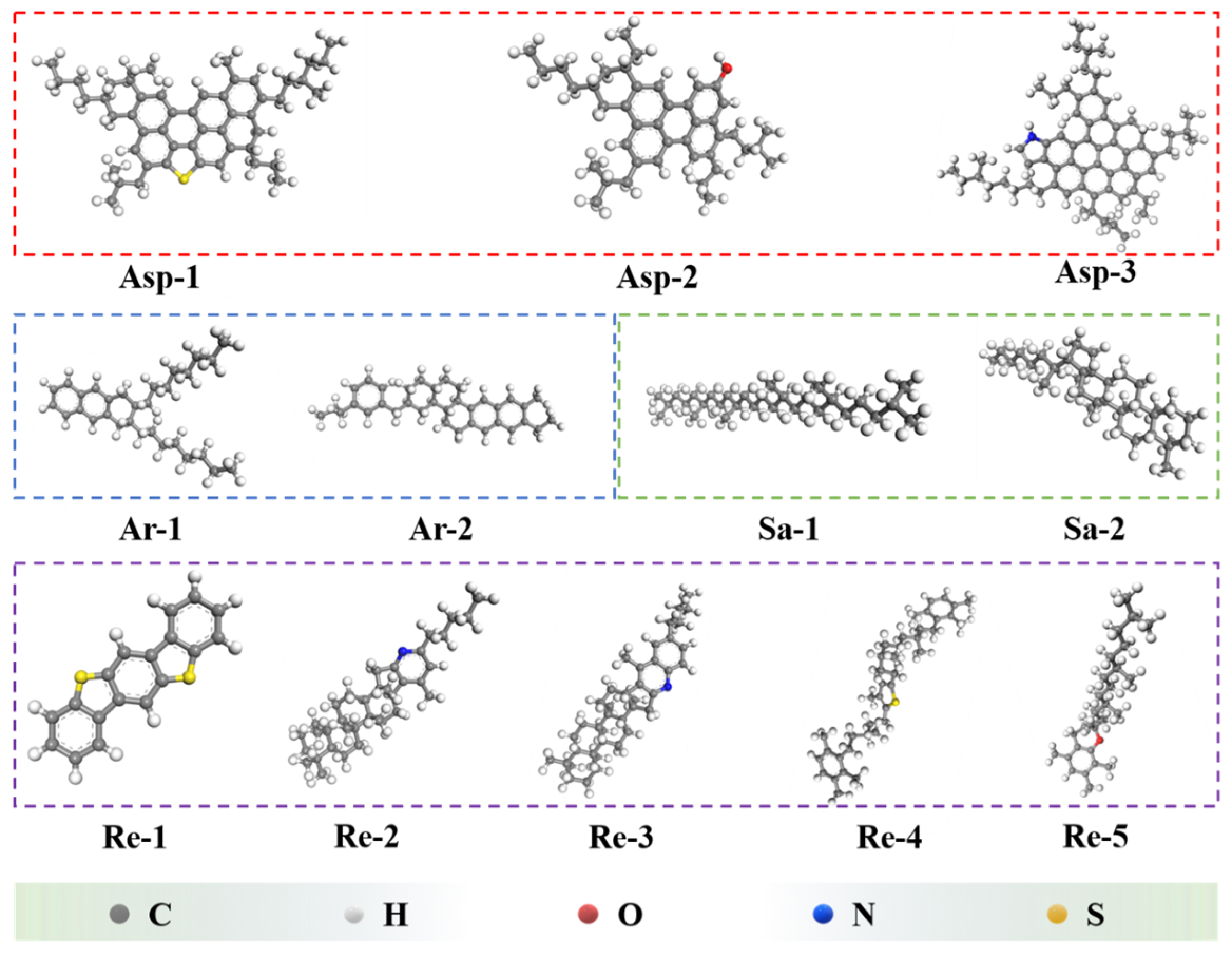
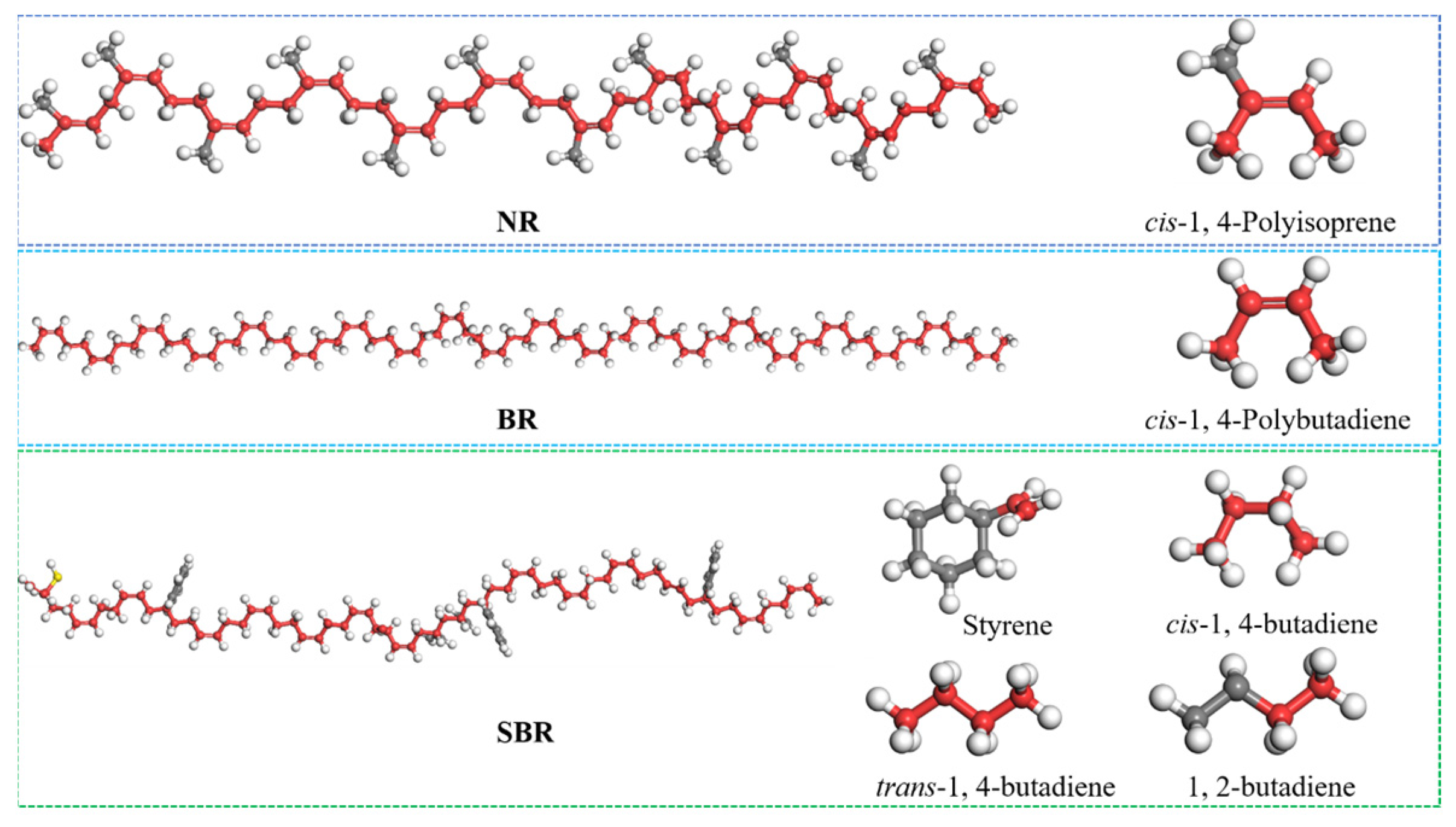





| Fraction | Encodings | Representation | Number | Simulated Content (%) | Measured Content (%) |
|---|---|---|---|---|---|
| Asphaltenes | Asp-1 | C51H62S | 2 | 12.78 | 12.78 |
| Asp-2 | C42H54O | 3 | |||
| Asp-3 | C66H81N | 2 | |||
| Saturates | Sa-1 | C30H62 | 6 | 12.87 | 12.89 |
| Sa-2 | C35H62 | 5 | |||
| Aromatics | Ar-1 | C30H46 | 22 | 52.26 | 52.47 |
| Ar-2 | C35H44 | 24 | |||
| Resins | Re-1 | C18H10S2 | 3 | 22.09 | 21.86 |
| Re-2 | C36H57N | 4 | |||
| Re-3 | C40H59N | 3 | |||
| Re-4 | C40H60S | 4 | |||
| Re-5 | C29H50O | 4 |
| Modifier Type | Number | Formula | Floors/Pieces | Mass (%) |
|---|---|---|---|---|
| PGR | G5-1 | C61H34 | 1 | 1.99 |
| G5-2 | C122H68 | 2 | 3.99 | |
| G5-3 | C183H102 | 3 | 5.98 | |
| G7-1 | C113H46 | 1 | 3.65 | |
| G7-2 | C226H92 | 2 | 7.30 | |
| G9-1 | C181H58 | 1 | 5.80 | |
| SBS | C107H176 | 1 | 3.80 | |
| ACR | C248H352S18 | 2 | 20.33 |
| Type of Asphalt | CED @ 298 K (J/m3) | δ @ 298 K ((J/cm3)0.5) | Solubility Parameter δ Range @ 298 K ((J/cm3)0.5) |
|---|---|---|---|
| 70# | 3.164 × 108 | 17.787 | 15.3~23.0 |
| PGR + 70# | 3.170 × 108 | 17.805 | |
| SBS | 3.162 × 108 | 17.783 | |
| PGR + SBS | 3.159 × 108 | 17.775 | |
| ACR | 2.998 × 108 | 17.315 | |
| PGR + ACR | 3.038 × 108 | 17.429 |
| Type of PGR | ∆EBinding (kcal/mol) | Non-Bonding Energy (kcal/mol) | ||
|---|---|---|---|---|
| EvdW | ELRC | ECoulomb | ||
| G5-1 | 61.79 | 58.47 | 1.58 | 1.74 |
| G5-2 | 111.37 | 99.30 | 3.08 | 8.99 |
| G5-3 | 174.00 | 168.44 | 4.54 | 1.03 |
| G7-1 | 97.74 | 91.23 | 2.77 | 3.75 |
| G7-2 | 166.11 | 158.63 | 5.34 | 2.14 |
| G9-1 | 198.26 | 192.60 | 4.26 | 1.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Sun, L.; Zhang, C.; Xu, J.; Liu, J.; Wang, C. Molecular Dynamics-Based Study of Graphene/Asphalt Mechanism of Interaction. Appl. Sci. 2024, 14, 6168. https://doi.org/10.3390/app14146168
Fan Y, Sun L, Zhang C, Xu J, Liu J, Wang C. Molecular Dynamics-Based Study of Graphene/Asphalt Mechanism of Interaction. Applied Sciences. 2024; 14(14):6168. https://doi.org/10.3390/app14146168
Chicago/Turabian StyleFan, Yinghua, Lijun Sun, Chenqi Zhang, Jinzhi Xu, Jingwen Liu, and Chun Wang. 2024. "Molecular Dynamics-Based Study of Graphene/Asphalt Mechanism of Interaction" Applied Sciences 14, no. 14: 6168. https://doi.org/10.3390/app14146168
APA StyleFan, Y., Sun, L., Zhang, C., Xu, J., Liu, J., & Wang, C. (2024). Molecular Dynamics-Based Study of Graphene/Asphalt Mechanism of Interaction. Applied Sciences, 14(14), 6168. https://doi.org/10.3390/app14146168






