A Method for Simulating the Positioning Errors of a Robot Gripper
Abstract
:1. Introduction
2. Materials and Methods
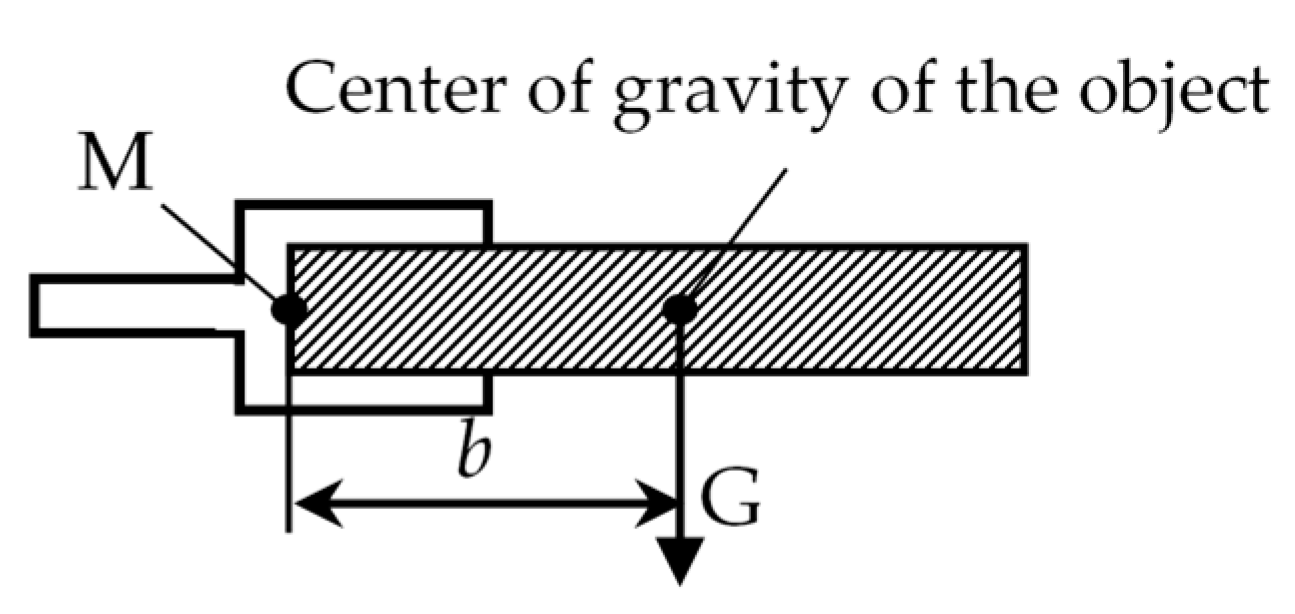
2.1. Elastic Static Deformations and Positioning Accuracy of the Manipulator
2.2. Geometric and Kinematic Errors of Robots
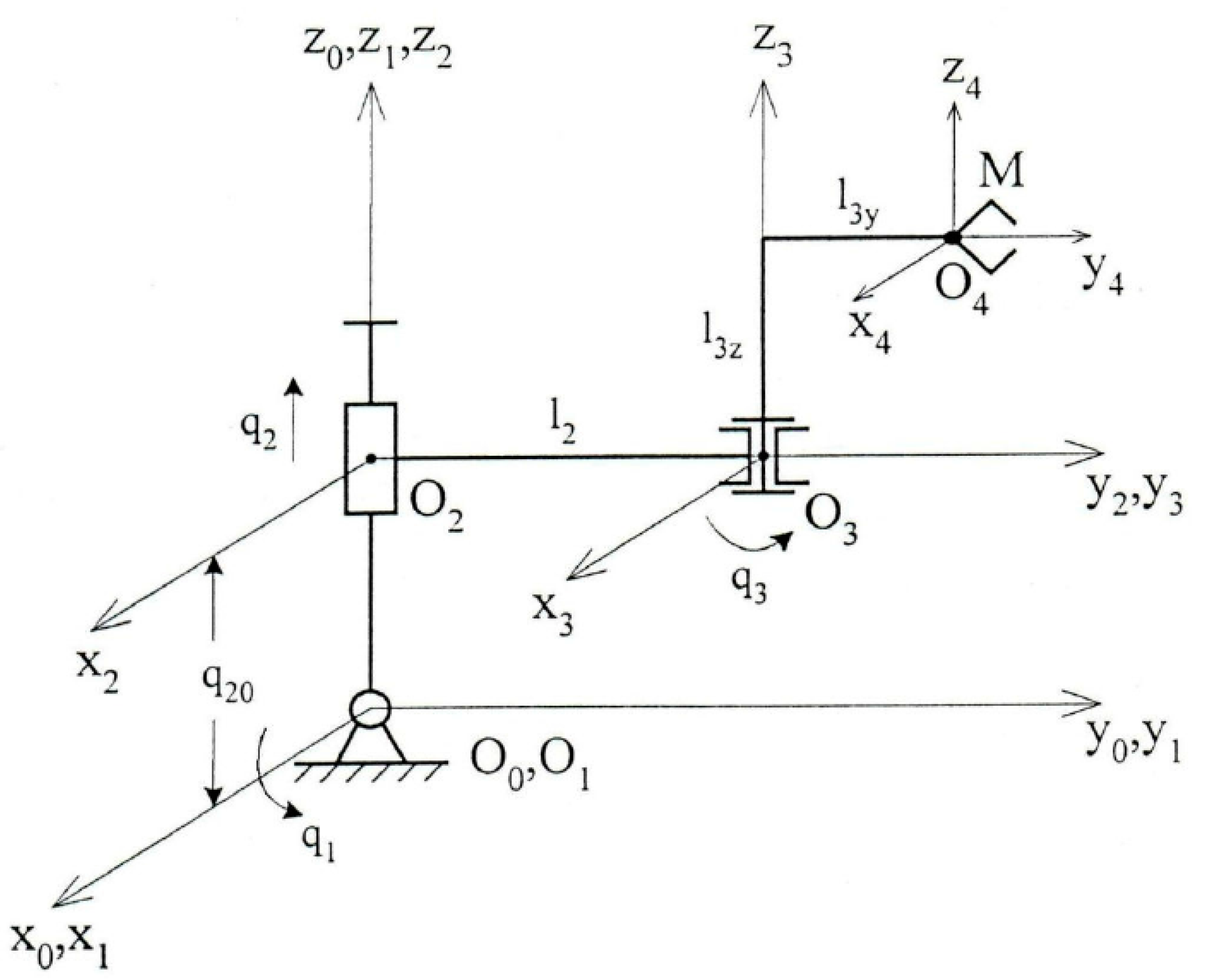
2.3. Elastic Static Deformations and Errors of Robot Manipulators
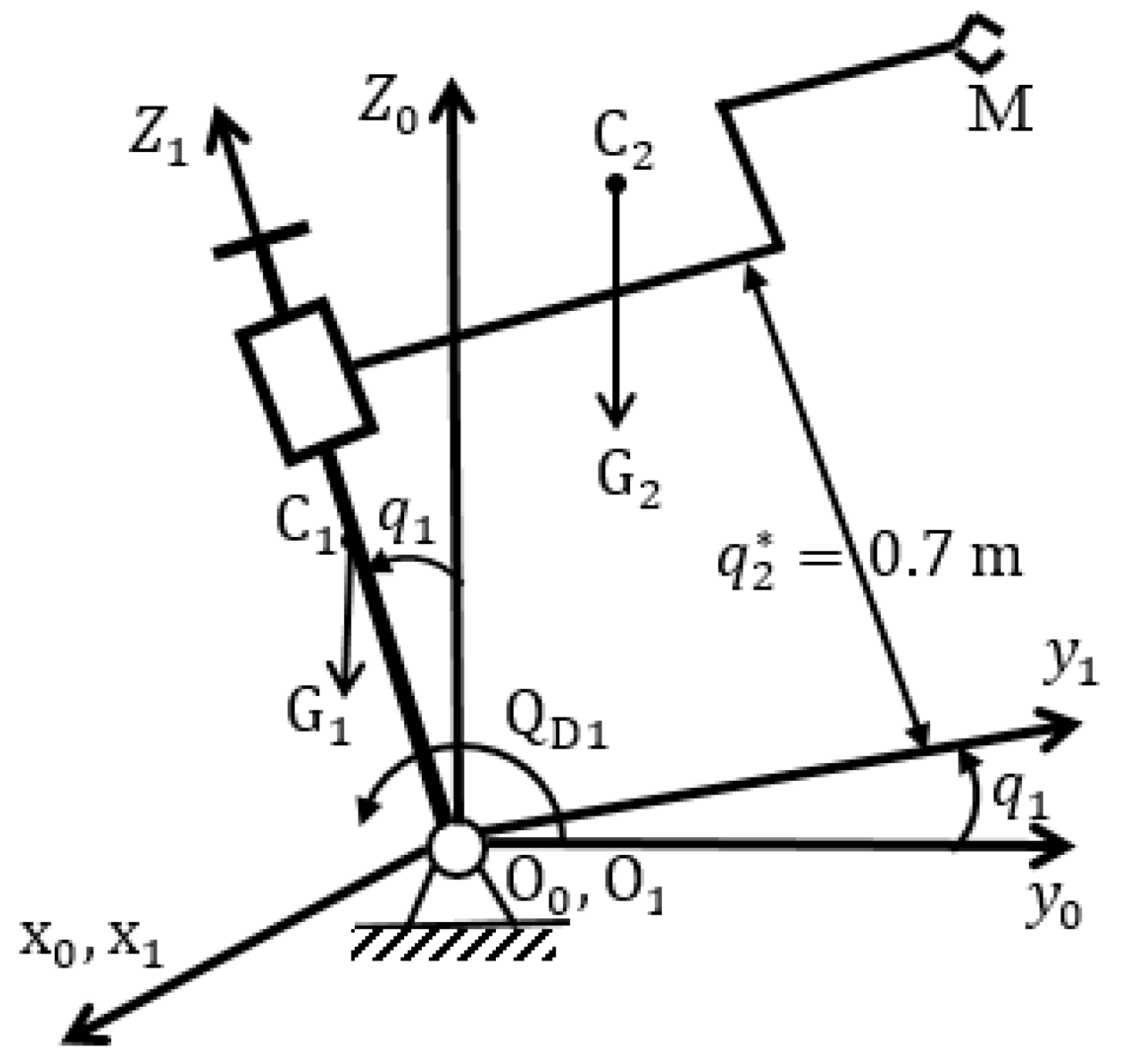
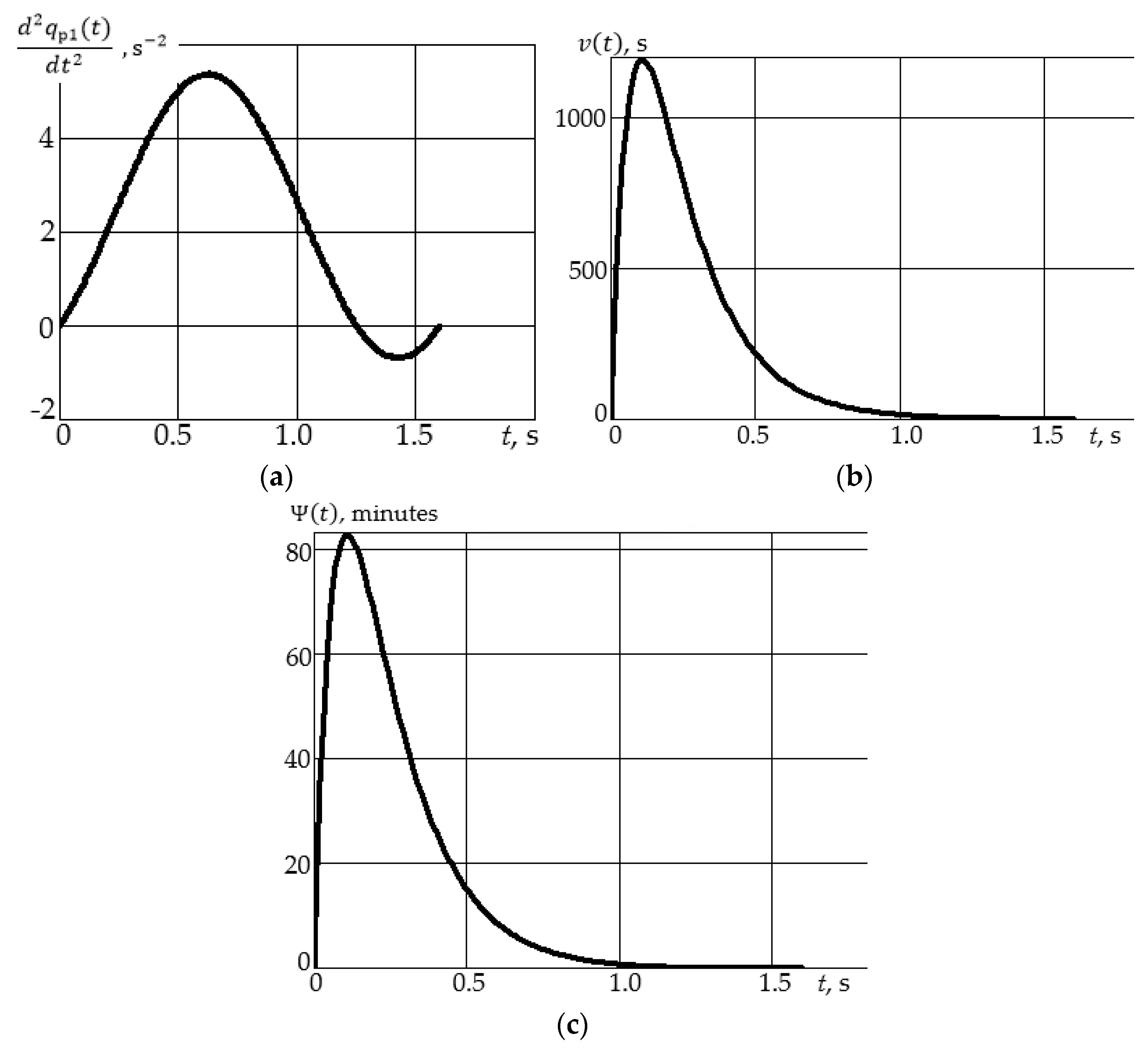
2.4. Dynamic Error in the Partial System of Motion of Robot Manipulator Links
- for the speedfor the acceleration we will differentiate Equation (50)
3. Results and Discussion
3.1. Modeling of the Position and Orientation Error of the Robot Gripper Due to the Temperature Deformation of the Manipulator Links
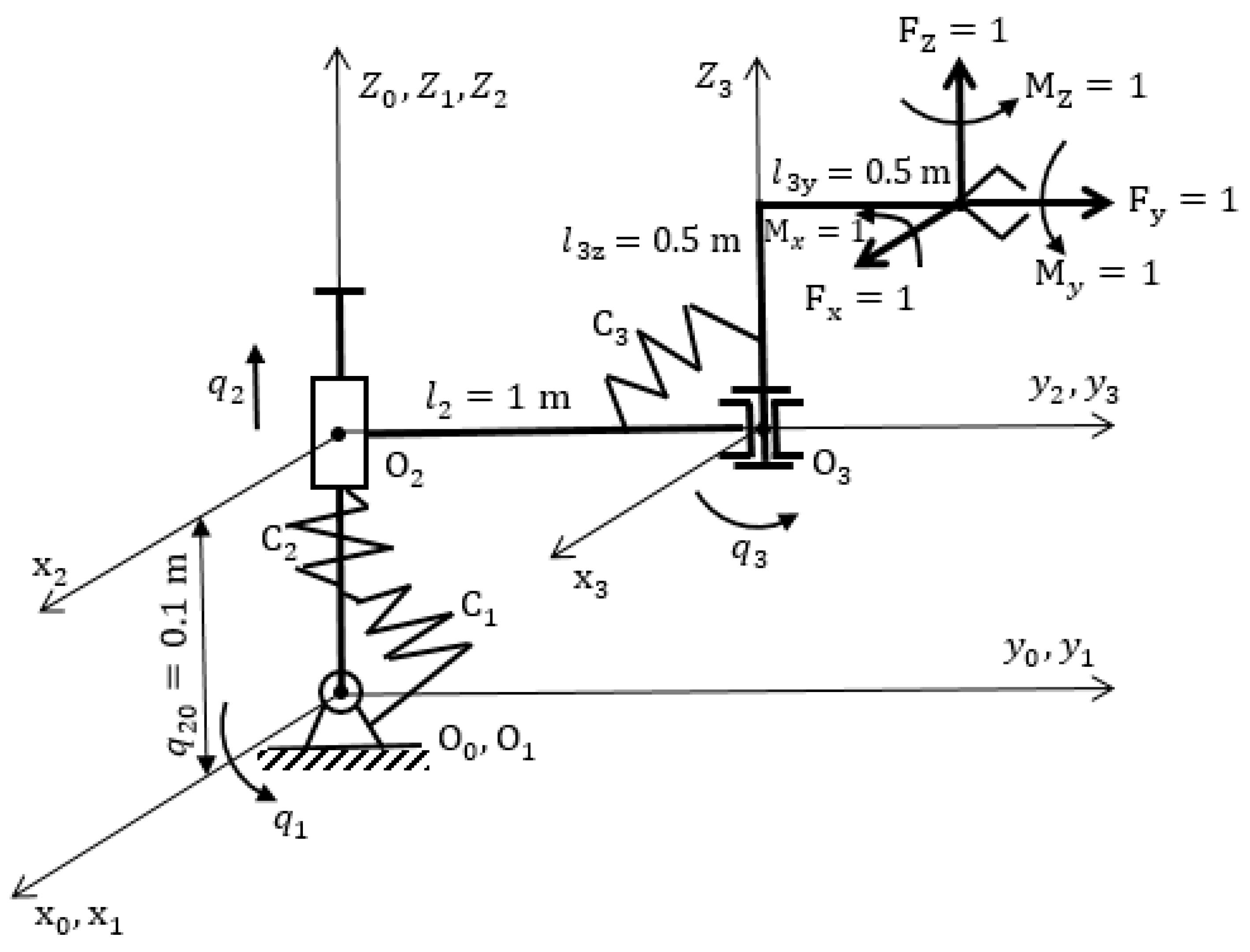
3.2. Modeling of Static Deformations and Manipulator Errors under Elastic Pliability of Robot Links
- Elements of the first column:
- Elements of the second column:
- Elements of the third column:
- Elements of the fourth column:
- All elements of the fifth column are zero; elements of the sixth column;
3.3. Modeling of Dynamic Errors in the Partial System of Motion of Robot Links
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beasley, R.A.; Howe, R.D. Increasing accuracy in image-guided robotic surgery through tip tracking and model-based flexion correction. IEEE Trans. Robot. 2009, 25, 292–302. [Google Scholar] [CrossRef]
- Cardoso, F.C.; Guimarâes, T.A.; de Sousa Dâmaso, R.; de Sousa Costa, E. Kinematic and dynamic behavior of articulated robot manipulators by two bars. ABCM Symp. Ser. Mechatron. 2012, 5, 1132–1141. [Google Scholar]
- Cheng, F.S. Calibration of robot reference frames for enhanced robot positioning accuracy. In New Technologies—Trends, Innovations and Research; Volosencu, C., Ed.; InTech: Rijeka, Croatia, 2012; Chapter 5; 19p, ISBN 978-953-51-0480-3. [Google Scholar]
- Conrad, K.L.; Shiakolas, P.S.; Yih, T.C. Robotic calibration issues: Accuracy, repetability and calibration. In Proceedings of the 8th Mediterranean Conference on Control & Automation (MED 2000), Patras, Greece, 17–19 July 2000. [Google Scholar]
- Jin, M.; Jin, Y.; Chang, P.H.; Choi, C. High-accuracy tracking control of robot manipulators using time delay estimation and terminal sliding mode. Int. J. Adv. Robot. 2011, 8, 65–787. [Google Scholar] [CrossRef]
- Hutsol, T.; Kutyrev, A.; Kiktev, N.; Biliuk, M. Robotic Technologies in Horticulture: Analysis and Implementation Prospects. Agric. Eng. 2023, 27, 113–133. [Google Scholar] [CrossRef]
- Çetinkaya, M.B.; Yildirim, K.; Yildirim, Ş. Trajectory Analysis of 6-DOF Industrial Robot Manipulators by Using Artificial Neural Networks. Sensors 2024, 24, 4416. [Google Scholar] [CrossRef]
- Maric, P.; Djalic, V. Improving accuracy and flexibility of industrial robots using computer vision. In New Technologies—Trends, Innovations and Research; Volosencu, C., Ed.; InTech: Rijeka, Croatia, 2012; Chapter 7; 26p, ISBN 978-953-51-0480-3. [Google Scholar]
- Meggiolaro, M.A.; Dubowsky, S.; Mavroidis, C. Geometric and elastic error calibration of a high accuracy patient positioning system. Mech. Mach. Theory 2005, 40, 415–427. [Google Scholar] [CrossRef]
- Oueslati, M.; Béaréea, R.; Gibaru, O.; Moraru, G. Improving the dynamic accuracy of elastic industrial robot joint by algebraic identification approach. In Proceedings of the First International Conference on Systems and Computer Science, Lille, France, 29–31 August 2012. [Google Scholar]
- Štrimaitis, M.; Urbanavičius, R.; Kilikevičius, A.; Jurevičius, M.; Striška, V.; Trumpa, A. Evaluation of dynamics and positioning of robotic system operating in heavy loaded high speed conditions. J. Meas. Eng. 2013, 1, 28–34. [Google Scholar]
- Zhang, J.; Cai, J. Error analysis and compensation method of 6-axis industrial robot. Int. J. Smart Sens. Intell. Syst. 2013, 6, 1383–1399. [Google Scholar] [CrossRef]
- Huinong, H.; Liansheng, H. Performance test progress of industrial robot. J. China Univ. Metrol. 2017, 2, 133–140. [Google Scholar]
- Cen, L.; Melkote, S.N. Effect of robot dynamics on the machining forces in robotic milling. Procedia Manuf. 2017, 10, 486–496. [Google Scholar] [CrossRef]
- Karim, A.; Corcione, E.; Verl, J.A. Experimental determination of compliance values for a machining robot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics AIM, Auckland, New Zealand, 9–12 July 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 1311–1316. [Google Scholar] [CrossRef]
- Sawyer, D.; Tinkler, L.; Roberts, N.; Diver, R. Improving Robotic Accuracy through Iterative Teaching; SAE Technical Papers, 2020-March; SAE International: Warrendale, PA, USA, 2020; p. 7. [Google Scholar] [CrossRef]
- Lattanzi, L.; Cristalli, C.; Massa, D.; Boria, S.; Lépine, P.; Pellicciari, M. Geometrical calibration of a 6-axis robotic arm for high accuracy manufacturing task. J. Adv. Manuf. Technol. 2020, 111, 1813–1829. [Google Scholar] [CrossRef]
- Sumanas, M.; Petronis, A.; Bucinskas, V.; Dzedzickis, A.; Virzonis, D.; Morkvenaite-Vilkonciene, I. Deep Q-learning in robotics: Improvement of accuracy and repeatability. Sensors 2022, 22, 3911. [Google Scholar] [CrossRef]
- Gharaaty, S.; Shu, T.; Xie, W.F.; Joubair, A.; Bonev, I.A. Accuracy enhancement of industrial robots by on-line pose correction. In Proceedings of the 2nd Asia-Pacific Conference on Intelligent Robot Systems ACIRS, Wuhan, China, 16–18 June 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2017; pp. 214–220. [Google Scholar] [CrossRef]
- Khort, D.; Kutyrev, A.; Kiktev, N.; Hutsol, T.; Glowacki, S.; Kuboń, M.; Nurek, T.; Rud, A.; Gródek-Szostak, Z. Automated Mobile Hot Mist Generator: A Quest for Effectiveness in Fruit Horticulture. Sensors 2022, 22, 3164. [Google Scholar] [CrossRef]
- Zu, H.; Chen, X.; Chen, Z.; Wang, Z.; Zhang, X. Positioning accuracy improvement method of industrial robot based on laser tracking measurement. Meas. Sens. 2021, 18, 100235. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, S.; Jing, F.; Tan, M. Parameter estimation survey for multi-joint robot dynamic calibration case study. Sci. China Inf. Sci. 2019, 62, 202203. [Google Scholar] [CrossRef]
- Trojanova, M.; Cakurda, T. Validation of the dynamic model of the planar robotic arm with using gravity test. MM Sci. J. 2020, 5, 4210–4215. [Google Scholar] [CrossRef]
- Park, K.-J. Flexible robot manipulator path design to reduce the endpoint residual vibration under torque constraints. J. Sound Vib. 2004, 275, 1051–1068. [Google Scholar] [CrossRef]
- Wu, K.; Krewet, C.; Kuhlenkötter, B. Dynamic performance of industrial robot in corner path with CNC controller. Robot. Comput. Manuf. 2018, 54, 156–161. [Google Scholar] [CrossRef]
- Sintov, A.; Shapiro, A. Dynamic regrasping by in-hand orienting of grasped objects using non-dexterous robotic grippers. Robot. Comput. Manuf. 2018, 50, 114–131. [Google Scholar] [CrossRef]
- Ponce-Hinestroza, A.N.; Castro-Castro, J.A.; Guerrero-Reyes, H.I.; Parra-Vega, V.; Olguín-Díaz, E. Cooperative redundant omnidirectional mobile manipulators: Model-free decentralized integral sliding modes and passive velocity fields. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016; pp. 2375–2380. [Google Scholar]
- Adamov, B.I. Influence of mecanum wheels construction on accuracy of the omnidirectional platform navigation (on example of KUKA youBot robot). In Proceedings of the 25th Saint Petersburg International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 28–30 May 2018; pp. 1–4. [Google Scholar]
- Huckaby, J.; Christensen, H.I. Dynamic Characterization of KUKA Light-Weight Robot Manipulators Technical Report GT-RIM-CR-2012-001; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- Mohamed, K.T.; Ata, A.; El-Souhily, B.M. Dynamic analysis algorithm for a micro-robot for surgical applications. Int. J. Mech. Mater. Des. 2011, 7, 17–28. [Google Scholar] [CrossRef]
- Urrea, C.; Pascal, J. Design, simulation, comparison and evaluation of parameter identification methods for an industrial robot. Comput. Electr. Eng. 2018, 67, 791–806. [Google Scholar] [CrossRef]
- Abele, E.; Weigold, M.; Rothenbücher, S. Modeling and Identification of an Industrial Robot for Machining Applications. CIRP Ann. 2007, 56, 387–390. [Google Scholar] [CrossRef]
- Sharifi, M.; Chen, X.; Pretty, C.; Clucas, D.; Cabon-Lunel, E. Modelling and simulation of a non-holonomic omnidirectional mobile robot for offline programming and system performance analysis. Simul. Model. Pract. Theory 2018, 87, 155–169. [Google Scholar] [CrossRef]
- Li, R.; Zhao, Y. Dynamic error compensation for industrial robot based on thermal effect model. Measurement 2016, 88, 113–120. [Google Scholar] [CrossRef]
- Shang, D.; Li, Y.; Liu, Y.; Cui, S. Research on the Motion Error Analysis and Compensation Strategy of the Delta Robot. Mathematics 2019, 7, 411. [Google Scholar] [CrossRef]
- Borisov, O.I.; Gromov, V.S.; Pyrkin, A.A.; Vedyakov, A.A.; Petranevsky, I.V.; Bobtsov, A.A.; Salikhov, V.I. Manipulation Tasks in Robotics Education. IFAC-PapersOnLine 2016, 49, 22–27. [Google Scholar]
- Wang, L.; Chen, L.; Shao, Z.; Guan, L.; Du, L. Analysis of flexible supported industrial robot on terminal accuracy. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418793022. [Google Scholar] [CrossRef]
- Mueggler, E.; Faessler, M.; Fontana, F.; Scaramuzza, D. Aerial-guided navigation of a ground robot among movable obstacles. In Proceedings of the 12th IEEE International Symposium on Safety, Security and Rescue Robotics, Hokkaido, Japan, 27–30 October 2014. [Google Scholar] [CrossRef]
- Sharma, S.; Kraetzschmar, G.K.; Scheurer, C.; Bischoff, R. Unified closed form inverse kinematics for the KUKA youBot. In Proceedings of the 7th German Conference on Robotics, ROBOTIK 2012, Munich, Germany, 21–22 May 2012; pp. 139–144. [Google Scholar]
- Bo, L.; Wei, T.; Zhang, C.; Fangfang, H.; Guangyu, C.; Yufei, L. Positioning error compensation of an industrial robot using neural networks and experimental study. Chin. J. Aeronaut. 2021, 35, 346–360. [Google Scholar]
- Cao, C.-T.; Do, V.-P.; Lee, B.-R. A Novel Indirect Calibration Approach for Robot Positioning Error Compensation Based on Neural Network and Hand-Eye Vision. Appl. Sci. 2019, 9, 1940. [Google Scholar] [CrossRef]
- Yuan, P.; Chen, D.; Wang, T.; Cao, S.; Cai, Y.; Xue, L. A compensation method based on extreme learning machine to enhance absolute position accuracy for aviation drilling robot. Adv. Mech. Eng. 2018, 10, 1687814018763411. [Google Scholar] [CrossRef]
- Dmytriv, V.T.; Dmytriv, I.V.; Lavryk, Y.M.; Krasnytsia, B.; Bubela, T.Z.; Yatsuk, V.O. Study of the pressure regulator work with a spring-damper system applied to milking machine. INMATEH Agric. Eng. 2017, 52, 61–67. [Google Scholar]
- Nazarova, O.; Osadchyy, V.; Hutsol, T.; Glowacki, S.; Nurek, T.; Hulevskyi, V.; Horetska, I. Mechatronic automatic control system of electropneumatic manipulator. Sci. Rep. 2024, 14, 6970. [Google Scholar] [CrossRef] [PubMed]
- Kutyrev, A.; Kiktev, N.; Jewiarz, M.; Khort, D.; Smirnov, I.; Zubina, V.; Hutsol, T.; Tomasik, M.; Biliuk, M. Robotic Platform for Horticulture: Assessment Methodology and Increasing the Level of Autonomy. Sensors 2022, 22, 8901. [Google Scholar] [CrossRef] [PubMed]

| Deformations | |||||||
|---|---|---|---|---|---|---|---|
| 0 | −1.2 | 3 | 2 | 0 | 0 | ||
| 0 | 0 | 4 | 0 | 0 | 0 | ||
| −1 | 0 | 0 | 0 | 0 | 2 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dmytriv, V.; Dmytriv, I.; Horodetskyy, I.; Hutsol, T.; Kukharets, S.; Cesna, J.; Bleizgys, R.; Pietruszynska, M.; Parafiniuk, S.; Kubon, M.; et al. A Method for Simulating the Positioning Errors of a Robot Gripper. Appl. Sci. 2024, 14, 6159. https://doi.org/10.3390/app14146159
Dmytriv V, Dmytriv I, Horodetskyy I, Hutsol T, Kukharets S, Cesna J, Bleizgys R, Pietruszynska M, Parafiniuk S, Kubon M, et al. A Method for Simulating the Positioning Errors of a Robot Gripper. Applied Sciences. 2024; 14(14):6159. https://doi.org/10.3390/app14146159
Chicago/Turabian StyleDmytriv, Vasyl, Ihor Dmytriv, Ivan Horodetskyy, Taras Hutsol, Savelii Kukharets, Jonas Cesna, Rolandas Bleizgys, Marta Pietruszynska, Stanislaw Parafiniuk, Maciej Kubon, and et al. 2024. "A Method for Simulating the Positioning Errors of a Robot Gripper" Applied Sciences 14, no. 14: 6159. https://doi.org/10.3390/app14146159
APA StyleDmytriv, V., Dmytriv, I., Horodetskyy, I., Hutsol, T., Kukharets, S., Cesna, J., Bleizgys, R., Pietruszynska, M., Parafiniuk, S., Kubon, M., & Horetska, I. (2024). A Method for Simulating the Positioning Errors of a Robot Gripper. Applied Sciences, 14(14), 6159. https://doi.org/10.3390/app14146159










