Coordinated Control Method for Unequal-Cycle Adjacent Intersections Using Vehicle–Road Collaboration
Abstract
1. Introduction
2. Architecture and Operational Analysis
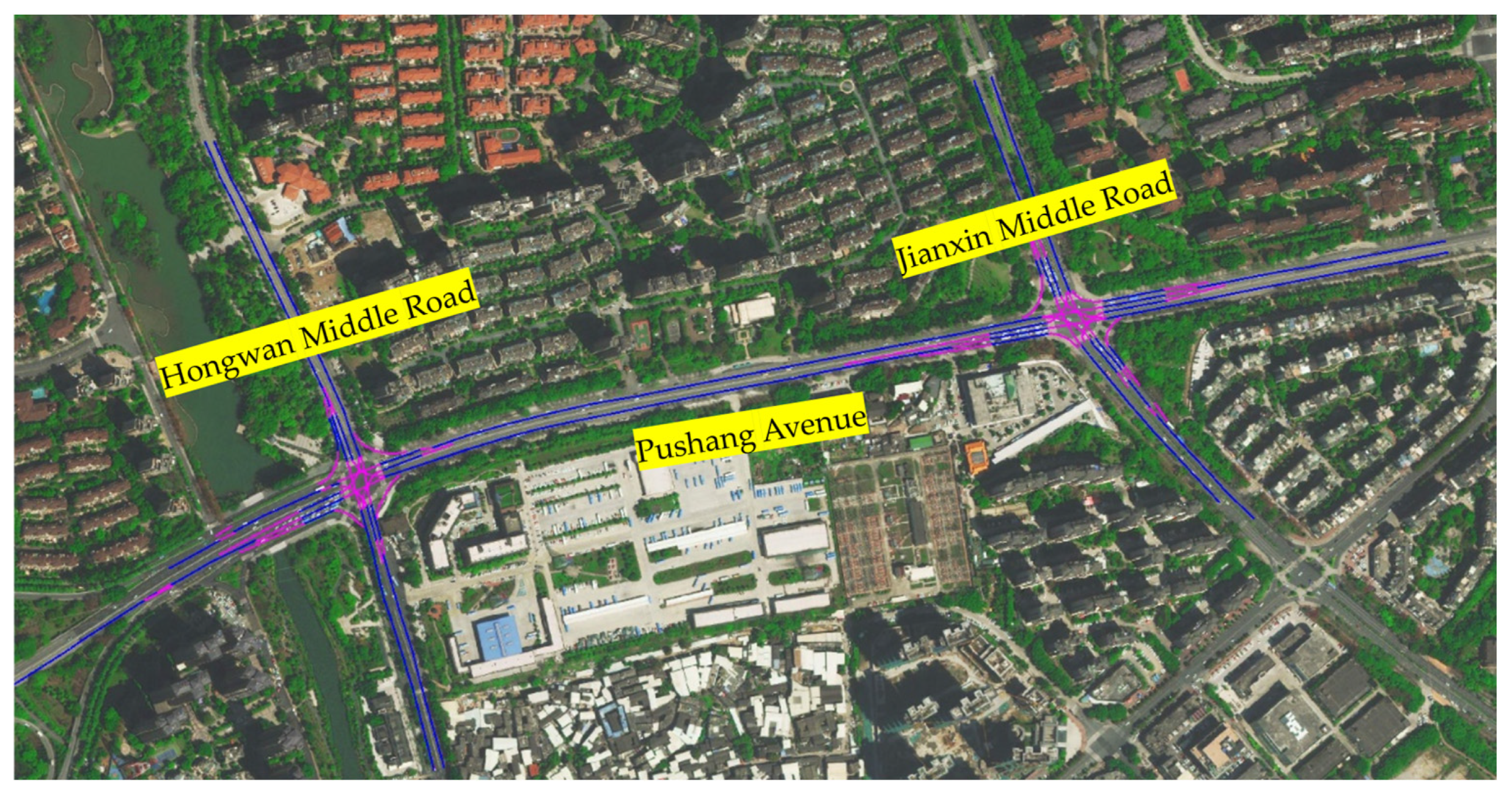
2.1. Architecture of Intersections
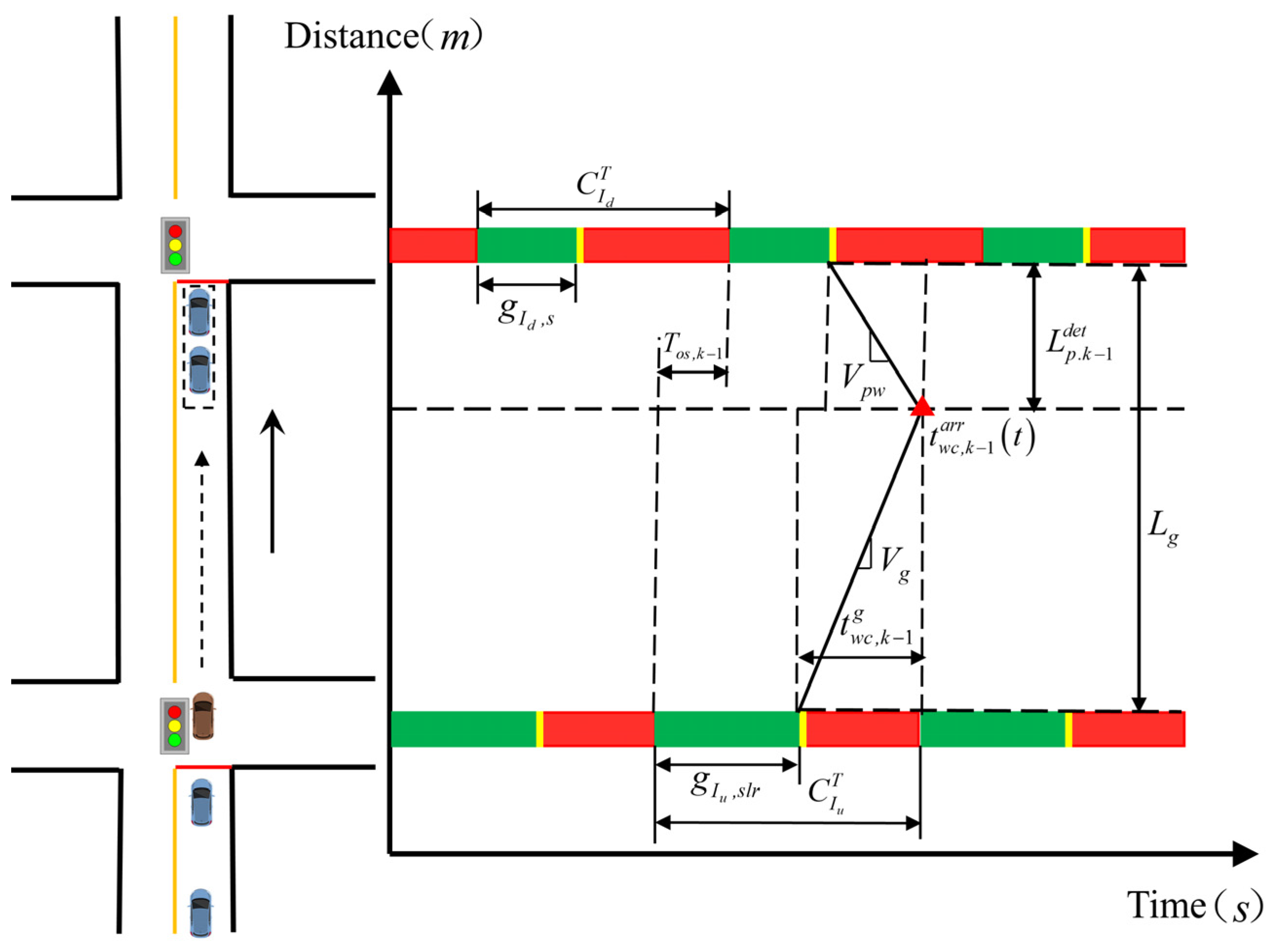
2.2. Periodic Offset Characteristics
2.3. Queue-Length Models
2.3.1. Model 1: Queue Length of Vehicles Delayed from Previous Cycle
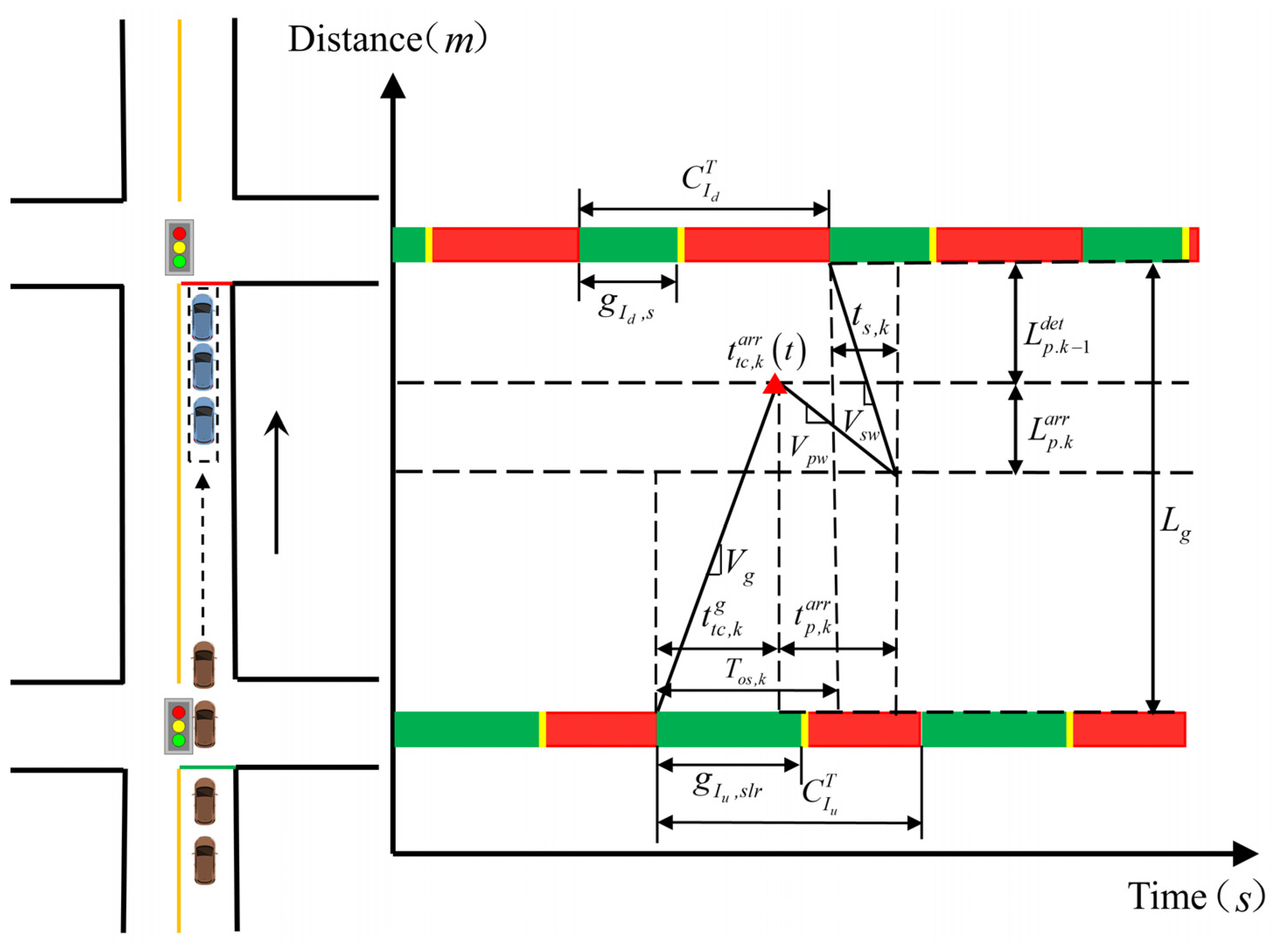
2.3.2. Model 2: Queue Length of Vehicles Arriving Ahead of Schedule in Current Cycle
2.3.3. Model 3: Maximum Queue Length in Current Cycle
2.4. Maximum Queue Length
3. Proposed Coordinated Control Method
3.1. Assumptions and Control Strategies
3.2. Strategy 1: Green Phase Extension Strategy
- (a)
- Determine the total amount of green phase time that can be reduced for each non-coordinated phase within the cycle while ensuring that the green phase time for each non-coordinated phase is not less than its minimum green time and the extended green phase time for the coordinated phase does not exceed the sum of the minimum green times for the non-coordinated phases plus the total available green phase time. That is,
- (b)
- Determine the extension time for a unit of green phase when the green phase time for the westbound through-coordinated phase at the downstream intersection reaches the initially pre-set green phase time, based on the detectors of the vehicle arrivals within the unit green extension time , determining the extension amount for the green phase time of the coordinated phase in cycle k. This value should not exceed the sum of the green phase time, which can be reduced. The green phase time for the coordinated phase after extension, , is given by
- (c)
- Sequentially reduce the green phase time for each non-coordinated phase by the time increments defined by until the total reduction matches the extension amount for the green phase time of the coordinated phase . Meanwhile, the following constraints ensure that the remaining green phase time for each non-coordinated phase does not fall below the minimum green time to balance the phase cycle duration:
3.3. Strategy 2: Dynamic Offset Adjustment Strategy
3.3.1. Determining Offset Adjustment
3.3.2. Determining Number of Phases Available for Adjustment
3.3.3. Determine Maximum Green Time Available for Adjustment
3.3.4. Updating Phase Signal Timing
3.4. Strategy 3: Queue-Speed Guidance Strategy for Transition Section
- ①
- If the downstream intersection’s coordinated phase is in the green signal state when the target queue approaches the guidance area, with sufficient remaining green time, or if it is in the red signal state with a relatively short remaining red time, and there are no vehicles ahead or any traffic that could affect the movement of the target queue, then the queue can be guided to travel at the maximum speed allowed by the road. Refer to Equation (17) for guidance speed and Figure 7a for the illustrative scenario.
- ②
- If the downstream intersection’s coordinated phase is in the green signal state with sufficient remaining green time when the target queue reaches the guidance area, and there is a stable-moving queue ahead, the target queue should be guided to catch up with the trailing vehicle of the preceding queue to form a platoon of vehicles. The target queue should closely follow the preceding queue to cross the intersection stop line. Refer to Equation (18) for guidance speed and Figure 7b for the illustrative scenario.
- ③
- If the downstream intersection’s coordinated phase is in the green signal state when the target queue arrives at the guidance area, and the queued vehicles ahead have not yet dispersed, or if it is in the red signal state with a significant remaining red time, to avoid the target queue from coming to a stop and waiting, the front vehicle of the target queue should be guided to drive to the rear of the queued vehicles in front. When the queue-starting wave reaches the last vehicle in the queue, the target queue can then closely follow the queued vehicles to cross the intersection stop line. Refer to Equation (19) for guidance speed and Figure 7c for the illustrative scenario.

4. Simulation Experiments
4.1. Experimental Design
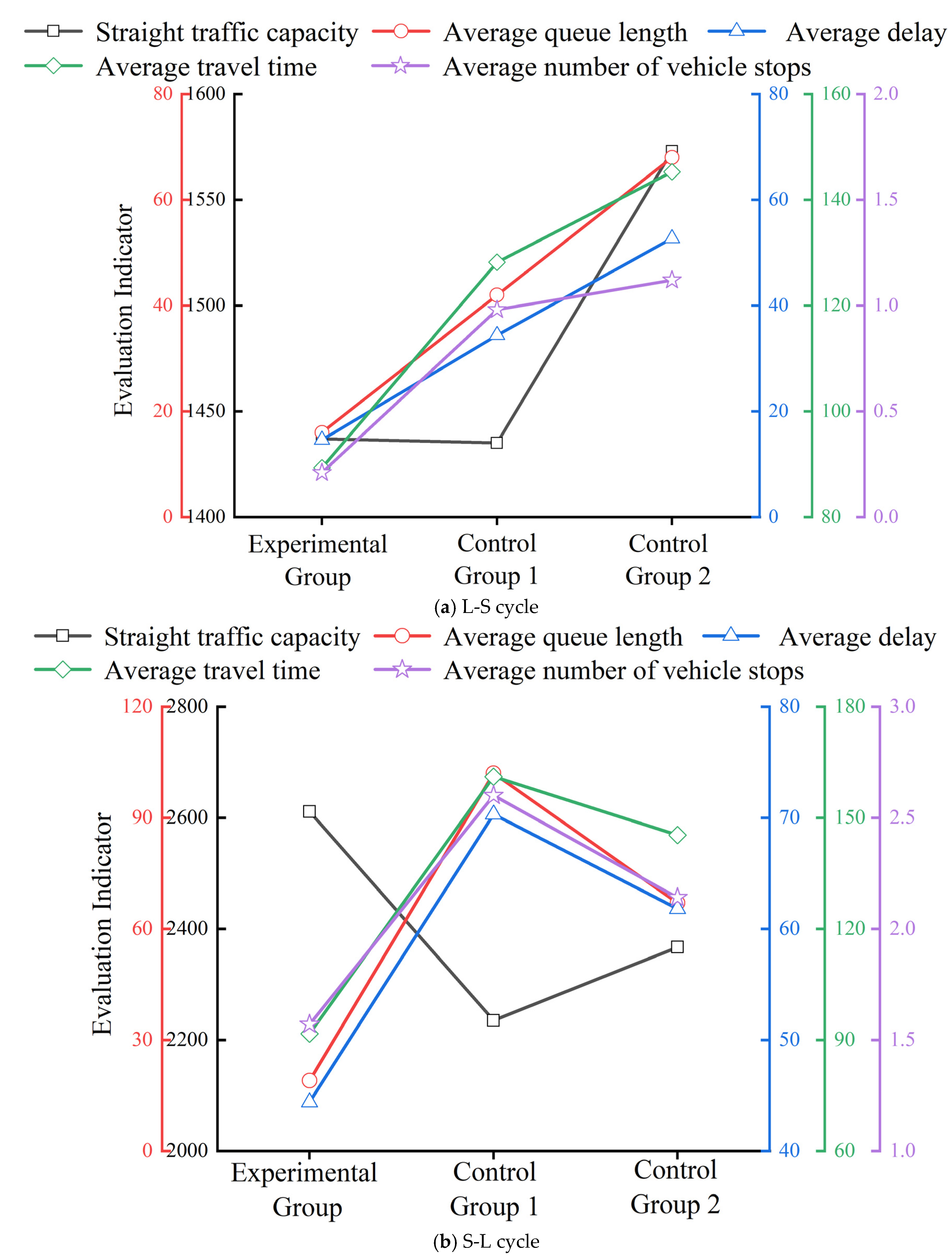
4.2. Analysis and Results
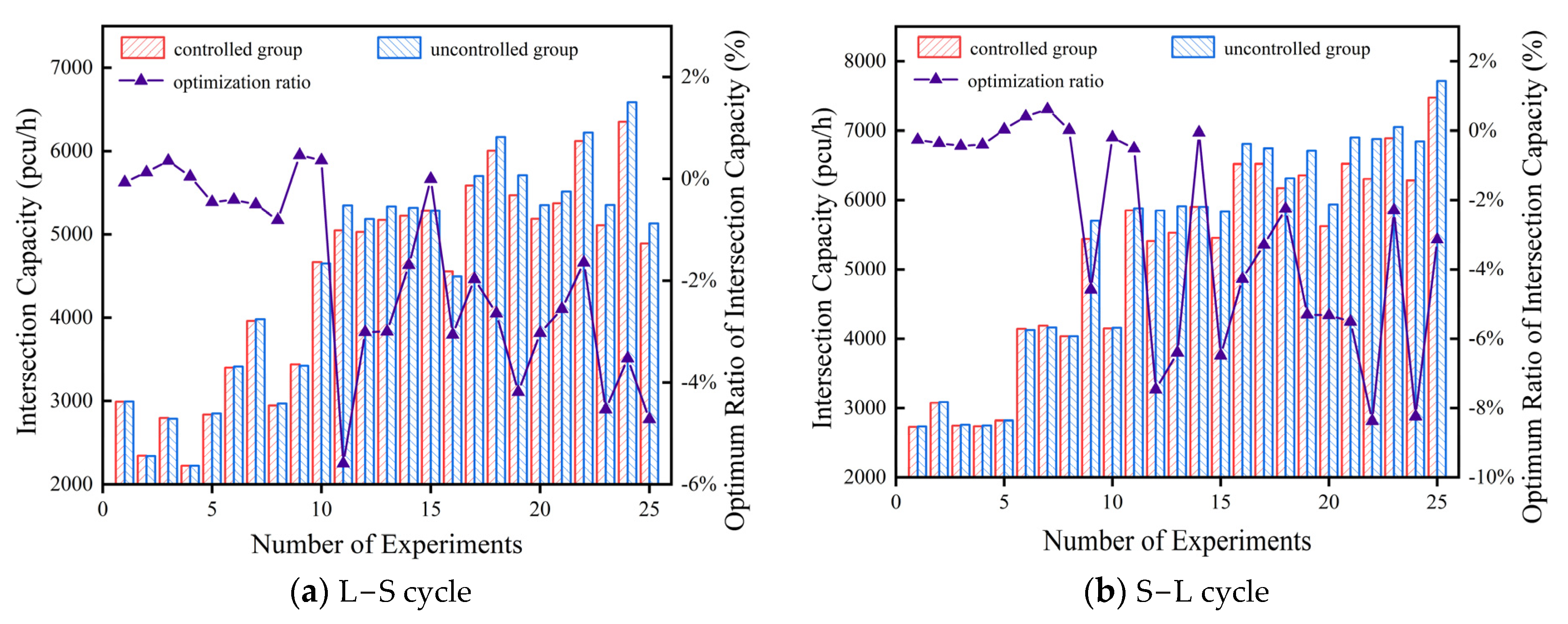
4.2.1. Analysis of Downstream Intersection Performance Intersection Capacity
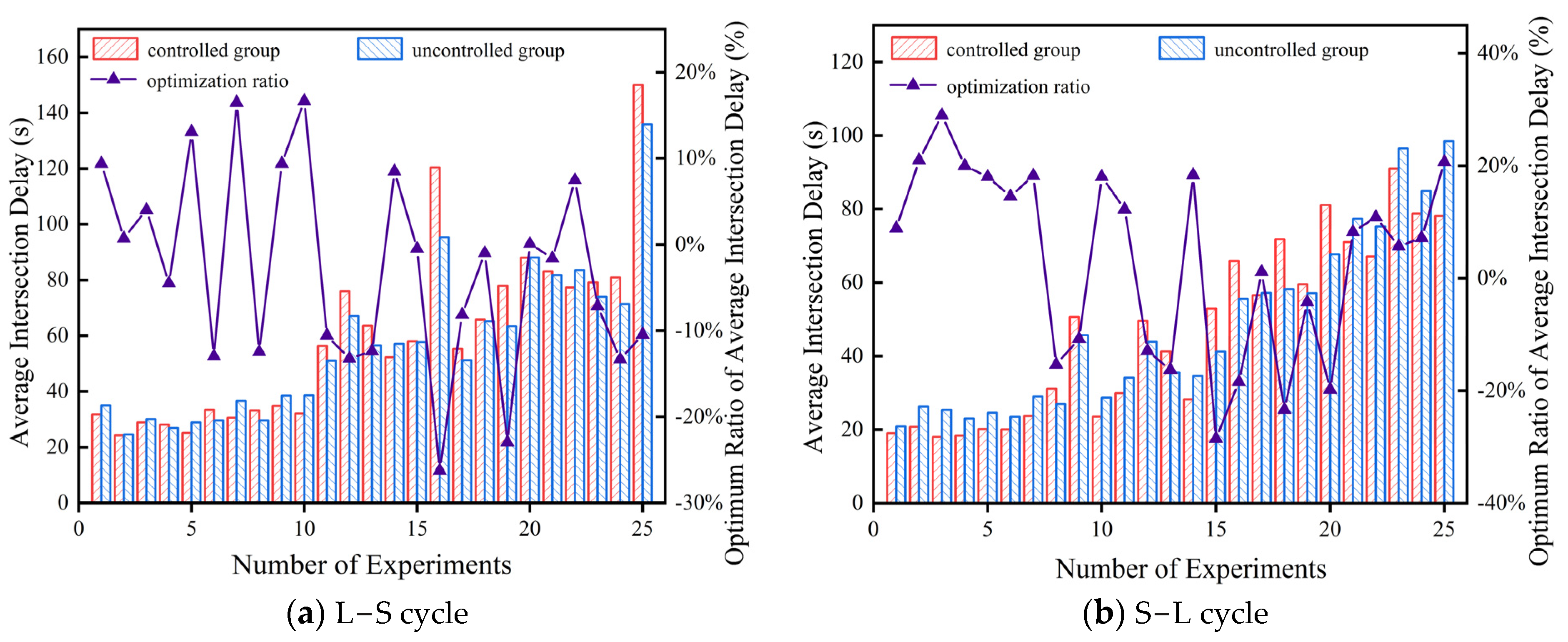
Intersection Average Vehicle Delay
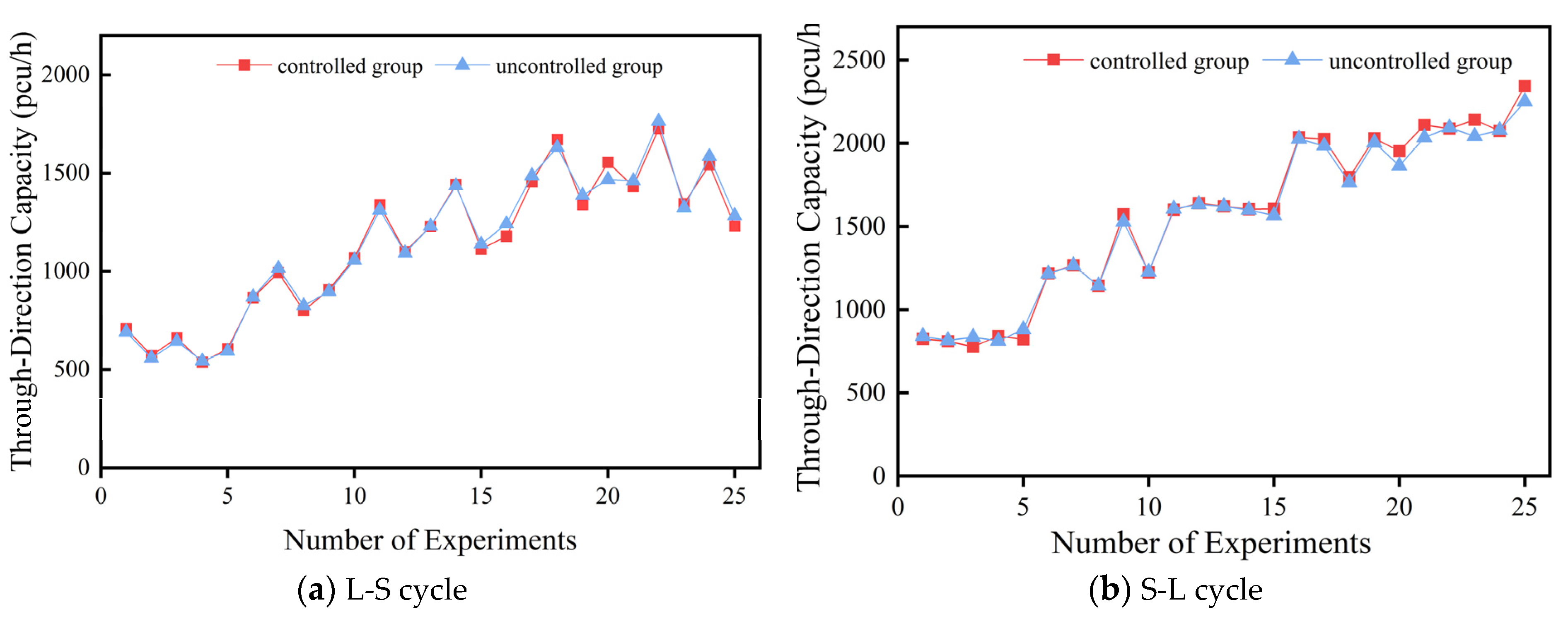
4.2.2. Analysis of Coordinated Through-Direction Performance Capacity
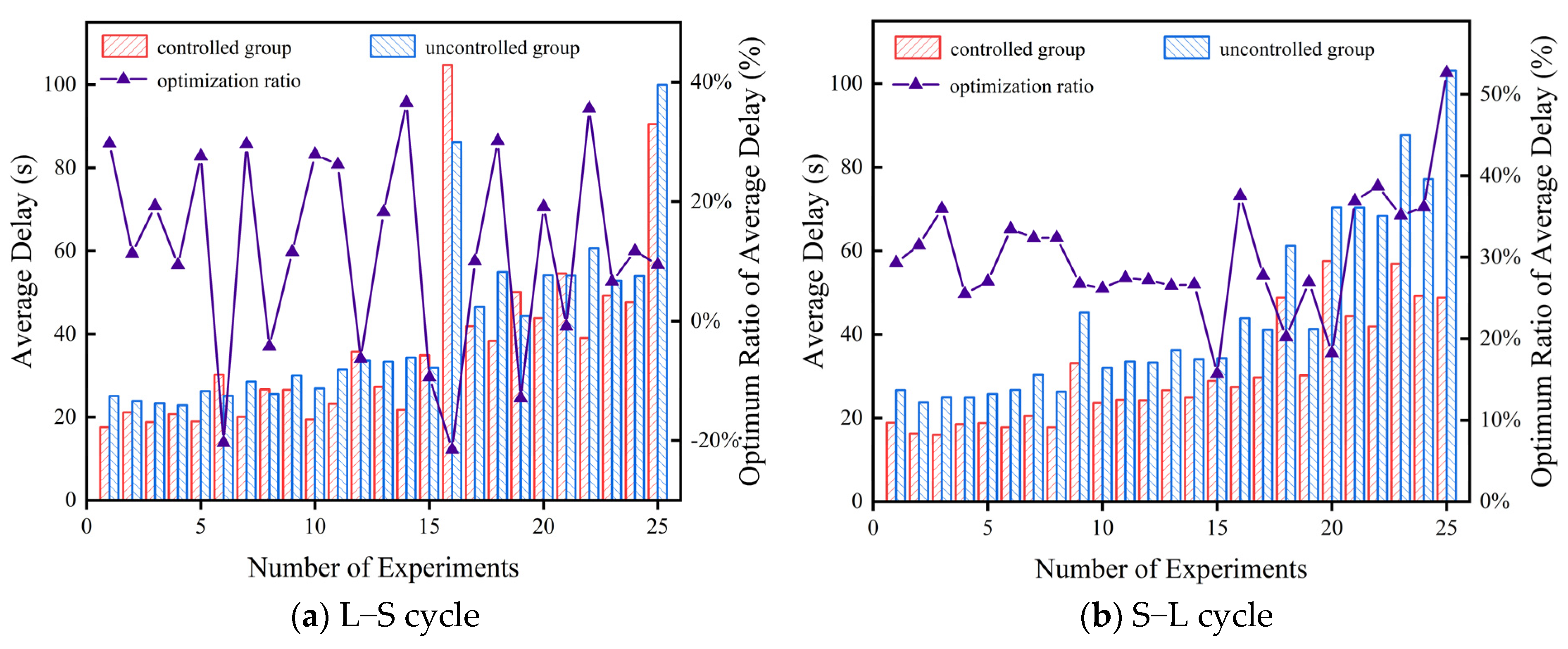
Average Delay
4.2.3. Orthogonal Analysis Results
4.2.4. Comparative Results
5. Conclusions
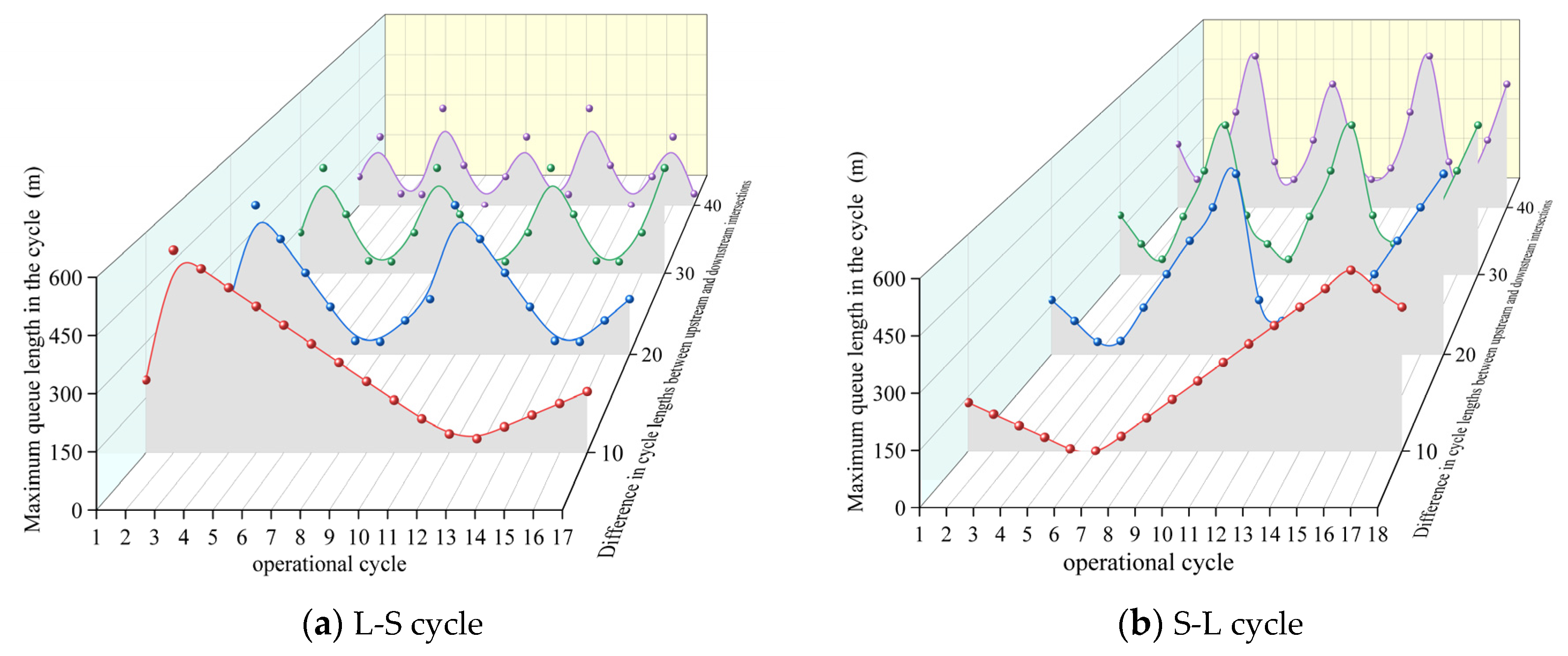
- The multi-strategy integrated method was validated using adaptive and comparative simulation experiments. The results showed that for an L-S cycle transition, the influencing factors are the following (ranked in decreasing order of importance): cycle length difference (10 s), inflow traffic volume (2000 pcu/h), transition segment length (1240 m), and desired speed (65 km/h), where the optimal values are shown in parentheses. For an S-L cycle transition, the influencing factors are inflow traffic volume (3000 pcu/h), desired speed (70 km/h), cycle length difference (50 s), and transition segment length (440 m).
- The proposed control strategies effectively reduce queue lengths, the number of stops, average vehicle delay time, and travel time for single-direction through lanes while improving the efficiency of the through traffic in the coordinated through direction between the adjacent intersections. This improvement is achieved while maintaining the original through traffic capacity.
- This study focuses on improving the passing efficiency for vehicles in one direction, and less attention was given to the coordinated control of the two-way traffic flow. It is hoped that the proposed methodology will be a valuable first step to optimizing the performance of two-way traffic flows at adjacent intersections with unequal cycles.
- The coordinated control method mentioned in this text requires pre-setting traffic signal control schemes, resulting in a lack of autonomy and flexibility in the optimization effect. Future research can incorporate optimization control algorithms within traffic signal controllers according to different optimization objectives, allowing intersections to automatically generate signal control schemes, thereby further enhancing the effectiveness of coordinated control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Steps for Determining Adjustment of Offset
References
- Ni, J.; Chen, J.; Xie, W.; Shao, Y. The impacts of the traffic situation, road conditions, and driving environment on driver stress: A systematic review. Transp. Res. Part F Traffic Psychol. Behav. 2024, 103, 141–162. [Google Scholar] [CrossRef]
- Fournier, N. Hybrid pedestrian and transit priority zoning policies in an urban street network: Evaluating network traffic flow impacts with analytical approximation. Transp. Res. Part A Policy Pract. 2021, 152, 254–274. [Google Scholar] [CrossRef]
- Ren, F.; Dong, W.; Zhao, X.; Zhang, F.; Kong, Y.; Yang, Q. Two-layer coordinated reinforcement learning for traffic signal control in traffic network. Export Syst. Appl. 2024, 235, 121111. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, Z.; Song, X.; Yun, Z.; Zhu, F. Coordinated perimeter control of urban road network based on traffic carring capacity model. Simul. Model. Pract. Theory 2023, 123, 102680. [Google Scholar] [CrossRef]
- Cao, J.; Hu, D.; Luo, Y.; Qiu, T.; Ma, Z. Exploring the impact of a coordinated variable speed limit control on congestion distribution in freeway. J. Traffic Transp. Eng. (Engl. Ed.) 2015, 2, 167–178. [Google Scholar] [CrossRef]
- Morgan, J.T.; Little, J.D.C. Synchronizing traffic signals for maximal bandwindth. Oper. Res. 1964, 12, 807–1051. [Google Scholar] [CrossRef]
- Gartner, N.H.; Assmann, S.F.; Lasaga, F.; Hous, D.L. Multiband—A Variable-Bandwidth Arterial Progression Scheme. Transp. Res. Rec. J. Transp. Res. Board 1990, 1287, 212–222. [Google Scholar]
- Hu, H.; Liu, H.X. Arterial offset optimization using archived high-resolution traffic signal data. Transp. Res. Part C Emerg. Technol. 2013, 37, 131–144. [Google Scholar] [CrossRef]
- Zhou, H.; Hawkins, H.G.; Zhang, Y. Arterial signal coordination with uneven double cycling. Transp. Res. Part A Policy Pract. 2017, 103, 409–429. [Google Scholar] [CrossRef]
- Brilon, W.; Wu, N.; Koenig, R. Delays and Queue Lengths at Traffic Signals with Two Greens in One Cycle. Transp. Res. Rec. 2022, 2677, 828–838. [Google Scholar] [CrossRef]
- Kesur, B. Optimization of Mixed Cycle Length Traffic Signals. J. Adv. Transp. 2024, 48, 431–442. [Google Scholar] [CrossRef]
- Mukhtar, H.; Adil, A.; Alahmari, S.; Yonbawi, S. CCGN: Centralized collaborative graphical transformer multi-agent reinforcement learning for multi-intersection signal free-corridor. Neural Netw. 2023, 166, 396–409. [Google Scholar] [CrossRef]
- Ducourthial, B.; Cherfaoui, V.; Fuhrmann, T.; Bonnet, S. Experimentation of a road hazard anticipation system based on vehicle cooperation. Veh. Commun. 2022, 36, 1000486. [Google Scholar] [CrossRef]
- Shi, Y.; Han, Q.; Shen, W.; Wang, X. A Multi-Layer Collaboration Framework for Industrial Parks with 5G Vehicle-to-Everything Networks. Engineering 2021, 7, 818–831. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J.; Sun, X.; Niu, J.; Zhao, X. A survey of vehicle group behaviors simulation under a connected vehicle environment. Phys. A Stat. Mech. Its Appl. 2022, 603, 127816. [Google Scholar] [CrossRef]
- Ma, X.; Ma, D.; Yuan, J.; Hao, S. Bandwidth optimisation and parameter analysis at two adjacent intersections based on set operations. IET Intell. Transp. Syst. 2019, 14, 684–692. [Google Scholar] [CrossRef]
- Münder, M.; Carbon, C. Howl, whirr, and whistle: The perception of electric powertrain noise and its importance for perceived quality in electrified vehicles. Appl. Acoust. 2022, 185, 108412. [Google Scholar] [CrossRef]
- Ayoub, J.; Yang, X.J.; Zhou, F. Modeling dispositional and initial learned trust in automated vehicles with predictability and explainability. Transp. Res. Part F Traffic Psychol. Behav. 2021, 77, 102–116. [Google Scholar] [CrossRef]
- Deng, J.; Wu, X.; Wang, F.; Li, S.; Wang, H. Analysis and Classification of Vehicle-Road Collaboration Application Scenarios. Procedia Comput. Sci. 2022, 208, 111–117. [Google Scholar] [CrossRef]
- Xing, Y.; Lv, C.; Cao, D.; Hang, P. Toward human-vehicle collaboration: Review and perspectives on human-centered collaborative automated driving. Transp. Res. Part C Emerg. Technol. 2021, 128, 103199. [Google Scholar] [CrossRef]
- Wu, W.; Li, P.; Zhang, Y. Modelling and simulation of vehicle speed guidance in connected vehicle environment. Int. J. Simul. Model. 2015, 14, 145–147. [Google Scholar] [CrossRef]
- Tiaprasert, K.; Zhang, Y.L.; Wang, X.B.; Zeng, X.S. Queue Length Estimation Using Connected Vehicle Technology for Adaptive Signal Control. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2129–2140. [Google Scholar] [CrossRef]
- Han, Y.; Yu, H.; Li, Z.; Xu, C.; Ji, Y.; Liu, P. An optimal control-based vehicle speedguidance strategy to improve traffic safety and efficiency against freeway jam waves. Accid. Anal. Prev. 2021, 163, 106429. [Google Scholar] [CrossRef]
- Agafonov, A.; Yumaganov, A.; Myasnikov, V. Cooperative Control for Signalized Intersections in Intelligent Connected Vehicle Environments. Mathematics 2023, 11, 1540. [Google Scholar] [CrossRef]
- Kim, S.; Habibie, A.; Williams, B.M.; Rouphail, N.W. Dynamic Bandwidth Analysis for Coordinated Arterial Streets. J. Intell. Transp. Syst. 2015, 20, 294–310. [Google Scholar] [CrossRef]
- Amirgholy, M.; Nourinejad, M.; Gao, H.O. Optimal traffic control at smart intersections: Automated network fundamental diagram. Transp. Res. Part B 2020, 137, 2–18. [Google Scholar] [CrossRef]
- Niu, D.; Sun, J. Eco-driving Versus Green Wave Speed Guidance for Signalized Highway Traffic: AMulti-vehicle Driving Simulator Study. Procedia Soc. Behav. Sci. 2013, 96, 1079–1090. [Google Scholar] [CrossRef]
- Song, L.; Li, R.; Wu, H. Intelligent control method for traffic flow at urban intersection based on vehicle networking. Int. J. Inf. Syst. Change Manag. 2020, 12, 35–52. [Google Scholar] [CrossRef]
- Peng, X.; Wang, H. Coordinated control model for arterials with asymmetric traffic. J. Intell. Transp. Syst. 2022, 27, 752–768. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Sun, J. Modeling and evaluation of speed guidance strategy in VII system. In Proceedings of the International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- He, Q.; Head, K.L.; Ding, J. Heuristic Algorithm for Priority Traffic Signal Control. Transp. Res. Rec. 2011, 2259, 1–7. [Google Scholar] [CrossRef]


| Influencing Factor | Range | Adjustment Step Size |
|---|---|---|
| Inflow traffic volume (pcu/h) | [1000, 3000] | 500 |
| Transition segment length (m) | [440, 1240] | 200 |
| Desired speed (km/h) | [30, 70] | 10 |
| Difference in cycle lengths (s) a | [10, 50] | 10 |
| Simulation Name | Value |
|---|---|
| Simulation duration (s) | 3600 |
| Maximum acceleration (m/s2) | 2.5 |
| Minimum acceleration (m/s2) | −2.5 |
| Response time (s) | 1.5 |
| Vehicle type | Car, HGV a, Bus |
| Percentage of vehicles | 0.7, 0.1, 0.2 |
| Lane width (m) | 3.5 |
| simulation.RandomSeed | 40 |
| Transition Type | Analysis Indicators | Influencing Factor | |||
|---|---|---|---|---|---|
| Inflow Traffic Volume (pcu/h) | Transition Section Length (m) | Desired Speed (km/h) | Difference in Cycle Lengths (s) | ||
| L-S cycle | Best level | 2000 | 1240 | 65 | 10 |
| Worst level | 2500 | 440 | 60 | 40 | |
| S-L cycle | Best level | 3000 | 440 | 70 | 50 |
| Worst level | 1500 | 1040 | 50 | 30 | |
| L-S cycle | 0.17 | 0.13 | 0.06 | 0.38 | |
| S-L cycle | 0.36 | 0.11 | 0.22 | 0.14 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, P.; Bao, R.; Zhang, K.; Easa, S.M.; Jiang, Z.; Chen, N. Coordinated Control Method for Unequal-Cycle Adjacent Intersections Using Vehicle–Road Collaboration. Appl. Sci. 2024, 14, 6151. https://doi.org/10.3390/app14146151
Lian P, Bao R, Zhang K, Easa SM, Jiang Z, Chen N. Coordinated Control Method for Unequal-Cycle Adjacent Intersections Using Vehicle–Road Collaboration. Applied Sciences. 2024; 14(14):6151. https://doi.org/10.3390/app14146151
Chicago/Turabian StyleLian, Peikun, Riyong Bao, Kangyi Zhang, Said M. Easa, Zhengyi Jiang, and Ning Chen. 2024. "Coordinated Control Method for Unequal-Cycle Adjacent Intersections Using Vehicle–Road Collaboration" Applied Sciences 14, no. 14: 6151. https://doi.org/10.3390/app14146151
APA StyleLian, P., Bao, R., Zhang, K., Easa, S. M., Jiang, Z., & Chen, N. (2024). Coordinated Control Method for Unequal-Cycle Adjacent Intersections Using Vehicle–Road Collaboration. Applied Sciences, 14(14), 6151. https://doi.org/10.3390/app14146151







