The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design and Procedures
2.3. Measures
2.4. Statistical Analyses
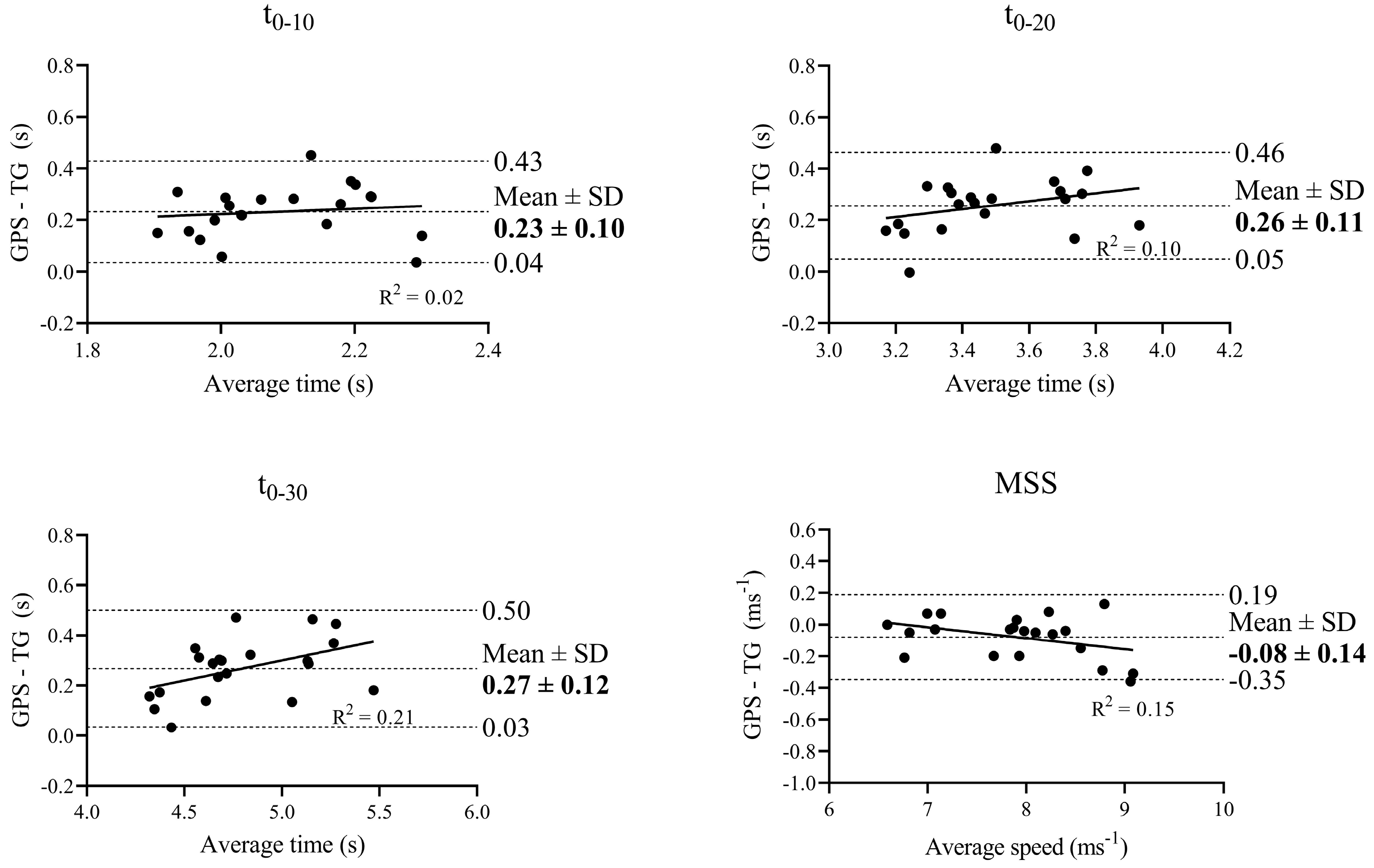
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haugen, T.; Tonnessen, E.; Hisdal, J.; Seiler, S. The role and development of sprinting speed in soccer. Int. J. Sports Physiol. Perform. 2014, 9, 432–441. [Google Scholar] [CrossRef] [PubMed]
- Caldbeck, P.; Dos’Santos, T. How do soccer players sprint from a tactical context? Observations of an English Premier League soccer team. J. Sports Sci. 2022, 40, 2669–2680. [Google Scholar] [CrossRef] [PubMed]
- Churchill, S.M.; Trewartha, G.; Bezodis, I.N.; Salo, A.I.T. Force production during maximal effort bend sprinting: Theory vs reality. Scand. J. Med. Sci. Sport. 2016, 26, 1171–1179. [Google Scholar] [CrossRef] [PubMed]
- Fílter, A.; Olivares, J.; Santalla, A.; Nakamura, F.Y.; Loturco, I.; Requena, B. New curve sprint test for soccer players: Reliability and relationship with linear sprint. J. Sports Sci. 2020, 38, 1320–1325. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.; Buchheit, M. Sprint Running Performance Monitoring: Methodological and Practical Considerations. Sport. Med. 2016, 46, 641–656. [Google Scholar] [CrossRef] [PubMed]
- Altmann, S.; Ringhof, S.; Becker, B.; Woll, A.; Neumann, R. Error-correction processing in timing lights for measuring sprint performance: Does it work? Int. J. Sports Physiol. Perform. 2018, 13, 1400–1402. [Google Scholar] [CrossRef] [PubMed]
- Haugen, T.A.; Tønnessen, E.; Svendsen, I.S.; Seiler, S. Sprint time deifferences between single- and dual-beam timing systems. J. Strength Cond. 2014, 28, 2376–2379. [Google Scholar] [CrossRef] [PubMed]
- Waldron, M.; Worsfold, P.; Twist, C.; Lamb, K. Concurrent validity and test–retest reliability of a global positioning system (gps) and timing gates to assess sprint performance variables. J. Sports Sci. 2011, 29, 1613–1619. [Google Scholar] [CrossRef] [PubMed]
- Zabaloy, S.; Freitas, T.T.; Alcaraz, P.E.; White, R.; Collins, N.; Ramirez-Lopez, C.; Pereira, L.A.; Loturco, I. The use of global positioning systems devices to measure maximum velocity in field-based team sport athletes: A narrative review. Strength Cond. J. 2023, 45, 13–28. [Google Scholar] [CrossRef]
- Clavel, P.; Leduc, C.; Morin, J.B.; Owen, C.; Samozino, P.; Peeters, A.; Buchheit, M.; Lacome, M. Concurrent Validity and Reliability of Sprinting Force-Velocity Profile Assessed with GPS Devices in Elite Athletes. Int. J. Sports Physiol. Perform. 2022, 17, 1527–1531. [Google Scholar] [CrossRef]
- Lacome, M.; Peeters, A.; Mathieu, B.; Marrier, B.; Piscione, J. Assessing sprinting performance in rugby sevens using GPS? A concurrent validity and between-device reliability study. Biol. Sport 2019, 36, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Scott, M.; Scott, T.; Kelly, V. The validity and reliability of global positioning systems in team sport: A brief review. J. Strength Cond. Res. 2015, 30, 1470–1490. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, M.W.; Baumgart, C.; Polglaze, T.; Freiwald, J. Validity and reliability of GPS and LPS for measuring distances covered and sprint mechanical properties in team sports. PLoS ONE 2018, 13, e0192708. [Google Scholar] [CrossRef] [PubMed]
- Thron, M.; Düking, P.; Woll, A.; Altmann, S. Assessing Anaerobic Speed Reserve: A Systematic Review on the Validity and Reliability of Methods to Determine Maximal Aerobic Speed and Maximal Sprinting Speed in Running-based Sports. Res. Sq. 2023, 19, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Arifin, W.N. A Web-based Sample Size Calculator for Reliability Studies. Educ. Med. J. 2018, 10, 67–76. [Google Scholar] [CrossRef]
- Loturco, I.; Pereira, L.A.; Fílter, A.; Olivares-Jabalera, J.; Reis, V.P.; Fernandes, V.; Freitas, T.T.; Requena, B. Curve sprinting in soccer: Relationship with linear sprints and vertical jump performance. Biol. Sport 2020, 37, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Altmann, S.; Ruf, L.; Fílter, A.; Härtel, S.; Naujoks, T.; Rauprich, M.; Seyler, C.; Baydoun, H.; Woll, A. Curved sprinting in soccer: The influence of radius. Int. J. Sport. Sci. Coach. 2023, 19, 1234–1239. [Google Scholar] [CrossRef]
- Zabaloy, S.; Freitas, T.T.; Carlos-Vivas, J.; Giráldez, J.C.; Loturco, I.; Pareja-Blanco, F.; Gálvez González, J.; Alcaraz, P.E. Estimation of maximum sprinting speed with timing gates: Greater accuracy of 5-m split times compared to 10-m splits. Sport. Biomech. 2021, 23, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Vescovi, J.D.; Jovanović, M. Sprint Mechanical Characteristics of Female Soccer Players: A Retrospective Pilot Study to Examine a Novel Approach for Correction of Timing Gate Starts. Front. Sport. Act. Living 2021, 3, 629694. [Google Scholar] [CrossRef]
- Jovanović, M.; Vescovi, J. An R Package for Modeling Short Sprints. Int. J. Strength Cond. 2022, 2, 1–23. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci. Sports Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, W.G. Spreadsheets for analysis of validity and reliability. Sportscience 2017, 21, 36–44. [Google Scholar]
- Bastida Castillo, A.; Gómez Carmona, C.D.; De La Cruz Sánchez, E.; Pino Ortega, J. Accuracy, intra- and inter-unit reliability, and comparison between GPS and UWB-based position-tracking systems used for time–motion analyses in soccer. Eur. J. Sport Sci. 2018, 18, 450–457. [Google Scholar] [CrossRef] [PubMed]
- Edwards, T.; Banyard, H.G.; Piggott, B.; Gregory Haff, G.; Joyce, C. Reliability and minimal detectable change of sprint times and force-velocity-power characteristics. J. Strength Cond. Res. 2022, 36, 268–272. [Google Scholar] [CrossRef] [PubMed]
- Buchheit, M.; Mendez-Villanueva, A.; Quod, M.; Quesnel, T.; Ahmaidi, S. Improving acceleration and repeated sprint ability in well-trained adolescent handball players: Speed versus sprint interval training. Int. J. Sports Physiol. Perform. 2010, 5, 152–164. [Google Scholar] [CrossRef] [PubMed]
- Shalfawi, S.A.I.; Ingebrigtsen, J.; Dillern, T.; Tønnessen, E.; Delp, T.K.; Enoksen, E. The effect of 40 m repeated sprint training on physical performance in young elite male soccer players. Serbian J. Sport. Sci. 2012, 6, 111–116. [Google Scholar] [CrossRef]
- Alphin, K.L.; Sisson, O.M.; Hudgins, B.L.; Noonan, C.D.; Bunn, J.A. Accuracy assessment of a gps device for maximum sprint speed. Int. J. Exerc. Sci. 2020, 13, 273–280. [Google Scholar] [PubMed]
- Paradisis, G.P.; Bissas, A.; Cooke, C.B. Effect of combined uphill-downhill sprint training on kinematics and maximum running speed in experienced sprinters. Int. J. Sport. Sci. Coach. 2015, 10, 887–897. [Google Scholar] [CrossRef]
- Altmann, S.; Spielmann, M.; Engel, F.A.; Neumann, R.; Ringhof, S.; Oriwol, D.; Haertel, S. Validity of single-beam timing lights at different heights. J. Strength Cond. Res. 2017, 31, 1994–1999. [Google Scholar] [CrossRef]



| Rep 1 | Rep 2 | Rep 3 | Relative | Absolute | ||
|---|---|---|---|---|---|---|
| Sprint Type | Variable | Mean (SD) | Mean (SD) | Mean (SD) | ICC (95% CI) | CV (95% CI) |
| CSL | t0–10 (s) | 2.32 (0.16) | 2.29 (0.14) | 2.26 (0.11) | 0.77 (0.57–0.89) | 2.8 (2.3–3.8) |
| t0–20 (s) | 3.92 (0.29) | 3.87 (0.26) | 3.87 (0.26) | 0.93 (0.86–0.97) | 1.8 (1.4–2.4) | |
| t0–30 (s) | 5.49 (0.41) | 5.45 (0.36) | 5.45 (0.37) | 0.96 (0.91–0.98) | 1.4 (1.3–1.9) | |
| MSS (m s−1) | 6.61 (0.46) | 6.53 (0.47) | 6.46 (0.48) | 0.96 (0.90–0.98) | 1.5 (1.2–2.0) | |
| CSR | t0–10 (s) | 2.28 (0.14) | 2.3 (0.14) | 2.29 (0.16) | 0.79 (0.60–0.90) | 2.9 (2.3–3.9) |
| t0–20 (s) | 3.86 (0.25) | 3.9 (0.27) | 3.88 (0.27) | 0.91 (0.81–0.96) | 2.1 (1.7–2.8) | |
| t0–30 (s) | 5.45 (0.37) | 5.49 (0.38) | 5.48 (0.38) | 0.94 (0.88–0.97) | 1.8 (1.4–2.3) | |
| MSS (m s−1) | 6.53 (0.48) | 6.48 (0.48) | 6.37 (0.48) | 0.95 (0.89–0.98) | 1.8 (1.5–2.4) | |
| LS | t0–10 (s) | 2.22 (0.14) | 2.26 (0.17) | 2.23 (0.14) | 0.70 (0.46–0.85) | 3.6 (2.9–4.8) |
| t0–20 (s) | 3.64 (0.26) | 3.67 (0.28) | 3.68 (0.26) | 0.92 (0.83–0.96) | 2.1 (1.7–2.8) | |
| t0–30 (s) | 4.98 (0.39) | 4.99 (0.41) | 5.01 (0.39) | 0.96 (0.91–0.98) | 1.6 (1.3–2.2) | |
| MSS (m s−1) | 7.85 (0.81) | 7.76 (0.79) | 7.64 (0.79) | 0.98 (0.95–0.99) | 1.5 (1.2–1.9) |
| Sprint Type | Variable | GPEXE lt Mean (SD) | TGs Mean (SD) | ICC (95 CI) | % Bias (SD) | p | ES | |
|---|---|---|---|---|---|---|---|---|
| CSL | t0–10 (s) | 2.26 (0.13) | 1.99 (0.14) | 0.66 (0.32–0.84) | 13.10 (5.54) | <0.001 | 2.40 | very large |
| t0–20 (s) | 3.84 (0.24) | 3.51 (0.25) | 0.85 (0.67–0.93) | 8.79 (3.71) | <0.001 | 2.47 | very large | |
| t0–30 (s) | 5.40 (0.33) | 5.01 (0.37) | 0.98 (0.78–0.96) | 7.65 (3.11) | <0.001 | 2.56 | very large | |
| MSS (m s−1) | 6.58 (0.43) | 6.73 (0.60) | 0.87 (0.70–0.94) | −2.19 (3.85) | 0.015 | −0.58 | small | |
| CSR | t0–10 (s) | 2.28 (0.15) | 1.97 (0.14) | 0.71 (0.41–0.87) | 14.60 (5.33) | <0.001 | 2.78 | very large |
| t0–20 (s) | 3.86 (0.27) | 3.51 (0.26) | 0.89 (0.75–0.95) | 9.73 (3.50) | <0.001 | 2.90 | very large | |
| t0–30 (s) | 5.45 (0.38) | 5.02 (0.39) | 0.93 (0.83–0.97) | 8.22 (2.89) | <0.001 | 3.00 | very large | |
| MSS (m s−1) | 6.50 (0.47) | 6.68 (0.54) | 0.96 (0.91–0.99) | −2.57 (2.09) | <0.001 | −1.29 | large | |
| LS | t0–10 (s) | 2.21 (0.14) | 1.98 (0.12) | 0.70 (0.40–0.87) | 11.10 (4.66) | <0.001 | 2.32 | very large |
| t0–20 (s) | 3.61 (0.24) | 3.36 (0.21) | 0.89 (0.75–0.95) | 7.31 (2.96) | <0.001 | 2.42 | very large | |
| t0–30 (s) | 4.93 (0.37) | 4.66 (0.32) | 0.94 (0.86–0.98) | 5.52 (2.34) | <0.001 | 2.25 | very large | |
| MSS (m s−1) | 7.86 (0.74) | 7.94 (0.79) | 0.98 (0.94–0.99) | −0.95 (1.62) | 0.015 | −0.58 | small | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sašek, M.; Miras-Moreno, S.; García-Ramos, A.; Cvjetičanin, O.; Šarabon, N.; Kavčič, I.; Smajla, D. The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests. Appl. Sci. 2024, 14, 6116. https://doi.org/10.3390/app14146116
Sašek M, Miras-Moreno S, García-Ramos A, Cvjetičanin O, Šarabon N, Kavčič I, Smajla D. The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests. Applied Sciences. 2024; 14(14):6116. https://doi.org/10.3390/app14146116
Chicago/Turabian StyleSašek, Matic, Sergio Miras-Moreno, Amador García-Ramos, Oskar Cvjetičanin, Nejc Šarabon, Iztok Kavčič, and Darjan Smajla. 2024. "The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests" Applied Sciences 14, no. 14: 6116. https://doi.org/10.3390/app14146116
APA StyleSašek, M., Miras-Moreno, S., García-Ramos, A., Cvjetičanin, O., Šarabon, N., Kavčič, I., & Smajla, D. (2024). The Concurrent Validity and Reliability of a Global Positioning System for Measuring Maximum Sprinting Speed and Split Times of Linear and Curvilinear Sprint Tests. Applied Sciences, 14(14), 6116. https://doi.org/10.3390/app14146116










