Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultrashort Laser Pulses
Abstract
:1. Introduction
2. Experimental Setup
3. Experimental Results
3.1. Increased Proton Energies
3.2. Improved Proton Beam Profile
3.3. X-ray Emission
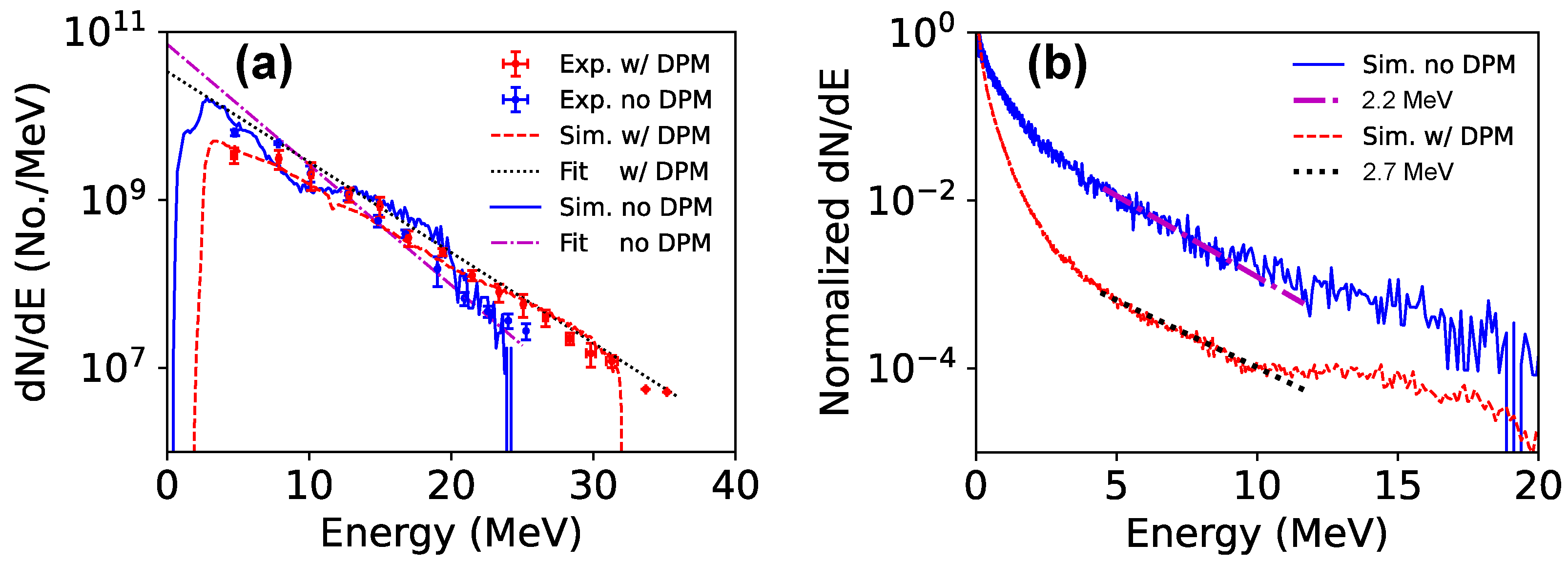
4. Numerical PIC Modeling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daido, H.; Nishiuchi, M.; Pirozhkov, A.S. Review of laser-driven ion sources and their applications. Rep. Prog. Phys. 2012, 75, 056401. [Google Scholar] [CrossRef] [PubMed]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751. [Google Scholar] [CrossRef]
- Zimmer, M.; Scheuren, S.; Ebert, T.; Schaumann, G.; Schmitz, B.; Hornung, J.; Bagnoud, V.; Rödel, C.; Roth, M. Analysis of laser-proton acceleration experiments for development of empirical scaling laws. Phys. Rev. E 2021, 104, 045210. [Google Scholar] [CrossRef] [PubMed]
- Schaeffer, D.B.; Bott, A.F.; Borghesi, M.; Flippo, K.A.; Fox, W.; Fuchs, J.; Li, C.; Séguin, F.H.; Park, H.S.; Tzeferacos, P.; et al. Proton imaging of high-energy-density laboratory plasmas. Rev. Mod. Phys. 2023, 95, 045007. [Google Scholar] [CrossRef]
- Bin, J.; Obst-Huebl, L.; Mao, J.H.; Nakamura, K.; Geulig, L.D.; Chang, H.; Ji, Q.; He, L.; De Chant, J.; Kober, Z.; et al. A new platform for ultra-high dose rate radiobiological research using the BELLA PW laser proton beamline. Sci. Rep. 2022, 12, 1484. [Google Scholar] [CrossRef] [PubMed]
- Lelasseux, V.; Söderström, P.A.; Aogaki, S.; Burdonov, K.; Chen, S.; Cvetinovic, A.; Dechefdebien, E.; Dorard, S.; Fazzini, A.; Gremillet, L.; et al. Experimental investigation of the effect of ionization on the 51V (p, n) 51Cr reaction. arXiv 2023, arXiv:2309.16340. [Google Scholar]
- Kroll, F.; Brack, F.E.; Bernert, C.; Bock, S.; Bodenstein, E.; Brüchner, K.; Cowan, T.E.; Gaus, L.; Gebhardt, R.; Helbig, U.; et al. Tumour irradiation in mice with a laser-accelerated proton beam. Nat. Phys. 2022, 18, 316–322. [Google Scholar] [CrossRef]
- Roth, M.; Jung, D.; Falk, K.; Guler, N.; Deppert, O.; Devlin, M.; Favalli, A.; Fernandez, J.; Gautier, D.; Geissel, M.; et al. Bright laser-driven neutron source based on the relativistic transparency of solids. Phys. Rev. Lett. 2013, 110, 044802. [Google Scholar] [CrossRef] [PubMed]
- Higginson, D.; Vassura, L.; Gugiu, M.; Antici, P.; Borghesi, M.; Brauckmann, S.; Diouf, C.; Green, A.; Palumbo, L.; Petrascu, H.; et al. Temporal narrowing of neutrons produced by high-intensity short-pulse lasers. Phys. Rev. Lett. 2015, 115, 054802. [Google Scholar] [CrossRef]
- Kleinschmidt, A.; Bagnoud, V.; Deppert, O.; Favalli, A.; Frydrych, S.; Hornung, J.; Jahn, D.; Schaumann, G.; Tebartz, A.; Wagner, F.; et al. Intense, directed neutron beams from a laser-driven neutron source at PHELIX. Phys. Plasmas 2018, 25, 053101. [Google Scholar] [CrossRef]
- Lelièvre, R.; Yao, W.; Waltenspiel, T.; Cohen, I.; Beck, A.; Cohen, E.; Michaeli, D.; Pomerantz, I.; Gautier, D.C.; Trompier, F.; et al. A Comprehensive Characterization of the Neutron Fields Produced by the Apollon Petawatt Laser. arXiv 2023, arXiv:2311.12653. [Google Scholar]
- Martinez, B.; Chen, S.; Bolaños, S.; Blanchot, N.; Boutoux, G.; Cayzac, W.; Courtois, C.; Davoine, X.; Duval, A.; Horny, V.; et al. Numerical investigation of spallation neutrons generated from petawatt-scale laser-driven proton beams. Matter Radiat. Extrem. 2022, 7, 024401. [Google Scholar] [CrossRef]
- Yogo, A.; Lan, Z.; Arikawa, Y.; Abe, Y.; Mirfayzi, S.; Wei, T.; Mori, T.; Golovin, D.; Hayakawa, T.; Iwata, N.; et al. Laser-driven neutron generation realizing single-shot resonance spectroscopy. Phys. Rev. X 2023, 13, 011011. [Google Scholar] [CrossRef]
- Hornỳ, V.; Chen, S.N.; Davoine, X.; Gremillet, L.; Fuchs, J. Quantitative feasibility study of sequential neutron captures using intense lasers. Phys. Rev. C 2024, 109, 025802. [Google Scholar] [CrossRef]
- Ziegler, T.; Göthel, I.; Assenbaum, S.; Bernert, C.; Brack, F.E.; Cowan, T.E.; Dover, N.P.; Gaus, L.; Kluge, T.; Kraft, S.; et al. Laser-driven high-energy proton beams from cascaded acceleration regimes. Nat. Phys. 2024, 1–6. [Google Scholar] [CrossRef]
- Wilks, S.; Langdon, A.; Cowan, T.; Roth, M.; Singh, M.; Hatchett, S.; Key, M.; Pennington, D.; MacKinnon, A.; Snavely, R. Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 2001, 8, 542–549. [Google Scholar] [CrossRef]
- Mora, P. Thin-foil expansion into a vacuum. Phys. Rev. E 2005, 72, 056401. [Google Scholar] [CrossRef] [PubMed]
- Mackinnon, A.; Borghesi, M.; Hatchett, S.; Key, M.; Patel, P.; Campbell, H.; Schiavi, A.; Snavely, R.; Wilks, S.; Willi, O. Effect of plasma scale length on multi-MeV proton production by intense laser pulses. Phys. Rev. Lett. 2001, 86, 1769. [Google Scholar] [CrossRef] [PubMed]
- McKenna, P.; Ledingham, K.; Yang, J.; Robson, L.; McCanny, T.; Shimizu, S.; Clarke, R.; Neely, D.; Spohr, K.; Chapman, R.; et al. Characterization of proton and heavier ion acceleration in ultrahigh-intensity laser interactions with heated target foils. Phys. Rev. E 2004, 70, 036405. [Google Scholar] [CrossRef]
- Fuchs, J.; Sentoku, Y.; Karsch, S.; Cobble, J.; Audebert, P.; Kemp, A.; Nikroo, A.; Antici, P.; Brambrink, E.; Blazevic, A.; et al. Comparison of laser ion acceleration from the front and rear surfaces of thin foils. Phys. Rev. Lett. 2005, 94, 045004. [Google Scholar] [CrossRef]
- Bolton, P.; Borghesi, M.; Brenner, C.; Carroll, D.; De Martinis, C.; Fiorini, F.; Flacco, A.; Floquet, V.; Fuchs, J.; Gallegos, P.; et al. Instrumentation for diagnostics and control of laser-accelerated proton (ion) beams. Phys. Med. 2014, 30, 255–270. [Google Scholar] [CrossRef]
- Fuchs, J.; Antici, P.; d’Humières, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.; Kaluza, M.; Malka, V.; Manclossi, M.; et al. Laser-driven proton scaling laws and new paths towards energy increase. Nat. Phys. 2006, 2, 48–54. [Google Scholar] [CrossRef]
- Dromey, B.; Coughlan, M.; Senje, L.; Taylor, M.; Kuschel, S.; Villagomez-Bernabe, B.; Stefanuik, R.; Nersisyan, G.; Stella, L.; Kohanoff, J.; et al. Picosecond metrology of laser-driven proton bursts. Nat. Commun. 2016, 7, 10642. [Google Scholar] [CrossRef]
- Ma, W.; Kim, I.J.; Yu, J.; Choi, I.W.; Singh, P.; Lee, H.W.; Sung, J.H.; Lee, S.K.; Lin, C.; Liao, Q.; et al. Laser acceleration of highly energetic carbon ions using a double-layer target composed of slightly underdense plasma and ultrathin foil. Phys. Rev. Lett. 2019, 122, 014803. [Google Scholar] [CrossRef]
- Danson, C.N.; Haefner, C.; Bromage, J.; Butcher, T.; Chanteloup, J.C.F.; Chowdhury, E.A.; Galvanauskas, A.; Gizzi, L.A.; Hein, J.; Hillier, D.I.; et al. Petawatt and exawatt class lasers worldwide. High Power Laser Sci. Eng. 2019, 7, e54. [Google Scholar] [CrossRef]
- Stockem Novo, A.; Kaluza, M.; Fonseca, R.; Silva, L. Optimizing laser-driven proton acceleration from overdense targets. Sci. Rep. 2016, 6, 29402. [Google Scholar] [CrossRef]
- Yan, X.; Lin, C.; Sheng, Z.M.; Guo, Z.; Liu, B.; Lu, Y.; Fang, J.; Chen, J. Generating high-current monoenergetic proton beams by a circularlypolarized laser pulse in the phase-stableacceleration regime. Phys. Rev. Lett. 2008, 100, 135003. [Google Scholar] [CrossRef]
- Qiao, B.; Zepf, M.; Borghesi, M.; Dromey, B.; Geissler, M.; Karmakar, A.; Gibbon, P. Radiation-pressure acceleration of ion beams from nanofoil targets: The leaky light-sail regime. Phys. Rev. Lett. 2010, 105, 155002. [Google Scholar] [CrossRef]
- Martin, P.; Ahmed, H.; Doria, D.; Cerchez, M.; Hanton, F.; Gwynne, D.; Alejo, A.; Fernández-Tobías, J.; Green, J.; Macchi, A.; et al. Narrow-band acceleration of gold ions to GeV energies from ultra-thin foils. Commun. Phys. 2024, 7, 3. [Google Scholar] [CrossRef]
- Yin, L.; Albright, B.; Hegelich, B.; Bowers, K.J.; Flippo, K.; Kwan, T.; Fernández, J. Monoenergetic and GeV ion acceleration from the laser breakout afterburner using ultrathin targets. Phys. Plasmas 2007, 14, 056706. [Google Scholar] [CrossRef]
- Palaniyappan, S.; Hegelich, B.M.; Wu, H.C.; Jung, D.; Gautier, D.C.; Yin, L.; Albright, B.J.; Johnson, R.P.; Shimada, T.; Letzring, S.; et al. Dynamics of relativistic transparency and optical shuttering in expanding overdense plasmas. Nat. Phys. 2012, 8, 763–769. [Google Scholar] [CrossRef]
- Chou, H.G.J.; Grassi, A.; Glenzer, S.H.; Fiuza, F. Radiation pressure acceleration of high-quality ion beams using ultrashort laser pulses. Phys. Rev. Res. 2022, 4, L022056. [Google Scholar] [CrossRef]
- Rehwald, M.; Assenbaum, S.; Bernert, C.; Brack, F.E.; Bussmann, M.; Cowan, T.E.; Curry, C.B.; Fiuza, F.; Garten, M.; Gaus, L.; et al. Ultra-short pulse laser acceleration of protons to 80 MeV from cryogenic hydrogen jets tailored to near-critical density. Nat. Commun. 2023, 14, 4009. [Google Scholar] [CrossRef]
- Antici, P.; Fuchs, J.; d’Humières, E.; Lefebvre, E.; Borghesi, M.; Brambrink, E.; Cecchetti, C.; Gaillard, S.; Romagnani, L.; Sentoku, Y.; et al. Energetic protons generated by ultrahigh contrast laser pulses interacting with ultrathin targets. Phys. Plasmas 2007, 14, 030701. [Google Scholar] [CrossRef]
- Lévy, A.; Ceccotti, T.; D’Oliveira, P.; Réau, F.; Perdrix, M.; Quéré, F.; Monot, P.; Bougeard, M.; Lagadec, H.; Martin, P.; et al. Double plasma mirror for ultrahigh temporal contrast ultraintense laser pulses. Opt. Lett. 2007, 32, 310–312. [Google Scholar] [CrossRef]
- Schumacher, D.W.; Zingale, A.; Czapla, N.; Nasir, D.; Cochran, G.E.; Poole, P.L. Liquid Crystal Targets and Plasma Mirrors for PW-Class Laser Experiments. In OSA High-Brightness Sources and Light-Driven Interactions Congress 2020 (EUVXRAY, HILAS, MICS); Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Huang, T.; Zhou, C.; Robinson, A.; Qiao, B.; Zhang, H.; Wu, S.; Zhuo, H.; Norreys, P.; He, X. Mitigating the relativistic laser beam filamentation via an elliptical beam profile. Phys. Rev. E 2015, 92, 053106. [Google Scholar] [CrossRef]
- Dollar, F.; Zulick, C.; Matsuoka, T.; McGuffey, C.; Bulanov, S.; Chvykov, V.; Davis, J.; Kalinchenko, G.; Petrov, G.; Willingale, L.; et al. High contrast ion acceleration at intensities exceeding 1021 Wcm−2. Phys. Plasmas 2013, 20, 056703. [Google Scholar] [CrossRef]
- Speicher, M.; Haffa, D.; Haug, M.A.; Bin, J.; Gao, Y.; Hartmann, J.; Hilz, P.; Kreuzer, C.; Lindner, F.H.; Ostermayr, T.M.; et al. Integrated double-plasma-mirror targets for contrast enhancement in laser ion acceleration. J. Phys. Conf. Ser. 2018, 1079, 012002. [Google Scholar] [CrossRef]
- Neely, D.; Foster, P.; Robinson, A.; Lindau, F.; Lundh, O.; Persson, A.; Wahlström, C.G.; McKenna, P. Enhanced proton beams from ultrathin targets driven by high contrast laser pulses. Appl. Phys. Lett. 2006, 89, 021502. [Google Scholar] [CrossRef]
- Antici, P.; Fuchs, J.; d’Humières, E.; Robiche, J.; Brambrink, E.; Atzeni, S.; Schiavi, A.; Sentoku, Y.; Audebert, P.; Pépin, H. Laser acceleration of high-energy protons in variable density plasmas. New J. Phys. 2009, 11, 023038. [Google Scholar] [CrossRef]
- Higginson, A.; Gray, R.; King, M.; Dance, R.; Williamson, S.; Butler, N.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J.; et al. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nat. Commun. 2018, 9, 724. [Google Scholar] [CrossRef]
- Poole, P.L.; Obst, L.; Cochran, G.E.; Metzkes, J.; Schlenvoigt, H.P.; Prencipe, I.; Kluge, T.; Cowan, T.; Schramm, U.; Schumacher, D.W.; et al. Laser-driven ion acceleration via target normal sheath acceleration in the relativistic transparency regime. New J. Phys. 2018, 20, 013019. [Google Scholar] [CrossRef]
- Burdonov, K.; Fazzini, A.; Lelasseux, V.; Albrecht, J.; Antici, P.; Ayoul, Y.; Beluze, A.; Cavanna, D.; Ceccotti, T.; Chabanis, M.; et al. Characterization and performance of the Apollon short-focal-area facility following its commissioning at 1 PW level. Matter Radiat. Extrem. 2021, 6, 064402. [Google Scholar] [CrossRef]
- Dover, N.; Nishiuchi, M.; Sakaki, H.; Kondo, K.; Alkhimova, M.; Faenov, A.Y.; Hata, M.; Iwata, N.; Kiriyama, H.; Koga, J.; et al. Effect of small focus on electron heating and proton acceleration in ultrarelativistic laser-solid interactions. Phys. Rev. Lett. 2020, 124, 084802. [Google Scholar] [CrossRef]
- Rusby, D.; Kemp, A.; Wilks, S.; Miller, K.; Sherlock, M.; Chen, H.; Simpson, R.; Mariscal, D.; Swanson, K.; Djordjević, B.; et al. Review and meta-analysis of electron temperatures from high-intensity laser–solid interactions. Phys. Plasmas 2024, 31, 040503. [Google Scholar] [CrossRef]
- Coury, M.; Carroll, D.; Robinson, A.; Yuan, X.; Brenner, C.; Burza, M.; Gray, R.; Quinn, M.; Lancaster, K.; Li, Y.; et al. Influence of laser irradiated spot size on energetic electron injection and proton acceleration in foil targets. Appl. Phys. Lett. 2012, 100, 074105. [Google Scholar] [CrossRef]
- Badziak, J.; Antici, P.; Fuchs, J.; Jabłoński, S.; Mancic, A.; Parys, P.; Rosiński, M.; Suchańska, R.; Szydłowski, A.; Wołowski, J. Laser-induced generation of ultraintense proton beams for high energy-density science. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2008; Volume 1024, pp. 63–77. [Google Scholar]
- Mirza, I.; Bulgakova, N.M.; Tomáštík, J.; Michálek, V.; Haderka, O.; Fekete, L.; Mocek, T. Ultrashort pulse laser ablation of dielectrics: Thresholds, mechanisms, role of breakdown. Sci. Rep. 2016, 6, 39133. [Google Scholar] [CrossRef]
- Burdonov, K.; Lelièvre, R.; Forestier-Colleoni, P.; Ceccotti, T.; Cuciuc, M.; Lancia, L.; Yao, W.; Fuchs, J. Absolute calibration up to 20 MeV of an online readout CMOS system suitable to detect high-power lasers accelerated protons. Rev. Sci. Instrum. 2023, 94, 083303. [Google Scholar] [CrossRef]
- Henig, A.; Steinke, S.; Schnürer, M.; Sokollik, T.; Hörlein, R.; Kiefer, D.; Jung, D.; Schreiber, J.; Hegelich, B.; Yan, X.; et al. Radiation-pressure acceleration of ion beams driven by circularly polarized laser pulses. Phys. Rev. Lett. 2009, 103, 245003. [Google Scholar] [CrossRef]
- Kar, S.; Kakolee, K.; Qiao, B.; Macchi, A.; Cerchez, M.; Doria, D.; Geissler, M.; McKenna, P.; Neely, D.; Osterholz, J.; et al. Ion acceleration in multispecies targets driven by intense laser radiation pressure. Phys. Rev. Lett. 2012, 109, 185006. [Google Scholar] [CrossRef]
- Brenner, C.M.; Robinson, A.; Markey, K.; Scott, R.; Gray, R.; Rosinski, M.; Deppert, O.; Badziak, J.; Batani, D.; Davies, J.; et al. High energy conversion efficiency in laser-proton acceleration by controlling laser-energy deposition onto thin foil targets. Appl. Phys. Lett. 2014, 104, 081123. [Google Scholar] [CrossRef]
- Wagner, F.; Bedacht, S.; Bagnoud, V.; Deppert, O.; Geschwind, S.; Jaeger, R.; Ortner, A.; Tebartz, A.; Zielbauer, B.; Hoffmann, D.; et al. Simultaneous observation of angularly separated laser-driven proton beams accelerated via two different mechanisms. Phys. Plasmas 2015, 22, 063110. [Google Scholar] [CrossRef]
- Zhuo, W.; Liu, W.; Huang, G.; Zhu, G.; Ma, G. Comparisons of dosimetric properties between GD-300 series of radiophotoluminescent glass detectors and GR-200 series of thermoluminescent detectors. Nucl. Sci. Tech. 2007, 18, 362–365. [Google Scholar]
- Faenov, A.Y.; Pikuz, S.A.; Erko, A.I.; Bryunetkin, B.A.; Dyakin, V.M.; Ivanenkov, G.V.; Mingaleev, A.R.; Pikuz, T.A.; Romanova, V.M.; Shelkovenko, T.A. High-performance X-ray spectroscopic devices for plasma microsources investigations. Phys. Scr. 1994, 50, 333–338. [Google Scholar] [CrossRef]
- Vyskočil, J.; Klimo, O.; Weber, S. Simulations of bremsstrahlung emission in ultra-intense laser interactions with foil targets. Plasma Phys. Controll. Fusion 2018, 60, 054013. [Google Scholar] [CrossRef]
- Ryazantsev, S.N.; Martynenko, A.S.; Sedov, M.V.; Skobelev, I.Y.; Mishchenko, M.D.; Lavrinenko, Y.S.; Baird, C.D.; Booth, N.; Durey, P.; Döhl, L.N.; et al. Absolute keV X-ray yield and conversion efficiency in over dense Si sub-petawatt laser plasma. Plasma Phys. Controll. Fusion 2022, 64, 105016. [Google Scholar] [CrossRef]
- Chen, M.; Sheng, Z.M.; Zheng, J.; Ma, Y.Y.; Bari, M.; Li, Y.T.; Zhang, J. Surface electron acceleration in relativistic laser-solid interactions. Opt. Express 2006, 14, 3093. [Google Scholar] [CrossRef]
- Serebryakov, D.; Nerush, E.; Kostyukov, I.Y. Near-surface electron acceleration during intense laser–solid interaction in the grazing incidence regime. Phys. Plasmas 2017, 24, 123115. [Google Scholar] [CrossRef]
- Thévenet, M.; Leblanc, A.; Kahaly, S.; Vincenti, H.; Vernier, A.; Quéré, F.; Faure, J. Vacuum laser acceleration of relativistic electrons using plasma mirror injectors. Nat. Phys. 2016, 12, 355–360. [Google Scholar] [CrossRef]
- Chung, H.K.; Chen, M.H.; Morgan, W.L.; Ralchenko, Y.; Lee, R.W. FLYCHK: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Phys. 2005, 1, 3–12. [Google Scholar] [CrossRef]
- Derouillat, J.; Beck, A.; Pérez, F.; Vinci, T.; Chiaramello, M.; Grassi, A.; Flé, M.; Bouchard, G.; Plotnikov, I.; Aunai, N.; et al. Smilei: A collaborative, open-source, multi-purpose particle-in-cell code for plasma simulation. Comput. Phys. Commun. 2018, 222, 351–373. [Google Scholar] [CrossRef]
- Grismayer, T.; Mora, P. Influence of a finite initial ion density gradient on plasma expansion into a vacuum. Phys. Plasmas 2006, 13, 032103. [Google Scholar] [CrossRef]
- Hornỳ, V.; Burdonov, K.; Fazzini, A.; Lelasseux, V.; Antici, P.; Chen, S.N.; Ciardi, A.; Davoine, X.; d’Humières, E.; Gremillet, L.; et al. A “lighthouse” laser-driven staged proton accelerator allowing for ultrafast angular and spectral control. arXiv 2024, arXiv:2404.11321. [Google Scholar]
- Favalli, A.; Aymond, F.; Bridgewater, J.S.; Croft, S.; Deppert, O.; Devlin, M.J.; Falk, K.; Fernandez, J.C.; Gautier, D.C.; Gonzales, M.A.; et al. Nuclear Material Detection by One-Short-Pulse-Laser-Driven Neutron Source; Technical Report; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 2015. [Google Scholar]
- Favalli, A.; Guler, N.; Henzlova, D.; Croft, S.; Falk, K.; Gautier, D.C.; Ianakiev, K.D.; Iliev, M.; Palaniyappan, S.; Roth, M.; et al. Characterizing laser-plasma ion accelerators driving an intense neutron beam via nuclear signatures. Sci. Rep. 2019, 9, 2004. [Google Scholar] [CrossRef]
- Yogo, A.; Mirfayzi, S.R.; Arikawa, Y.; Abe, Y.; Wei, T.; Mori, T.; Lan, Z.; Hoonoki, Y.; Golovin, D.O.; Koga, K.; et al. Single shot radiography by a bright source of laser-driven thermal neutrons and X-rays. Appl. Phys. Express 2021, 14, 106001. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, W.; Lelièvre, R.; Waltenspiel, T.; Cohen, I.; Allaoua, A.; Antici, P.; Beck, A.; Cohen, E.; Davoine, X.; d’Humières, E.; et al. Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultrashort Laser Pulses. Appl. Sci. 2024, 14, 6101. https://doi.org/10.3390/app14146101
Yao W, Lelièvre R, Waltenspiel T, Cohen I, Allaoua A, Antici P, Beck A, Cohen E, Davoine X, d’Humières E, et al. Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultrashort Laser Pulses. Applied Sciences. 2024; 14(14):6101. https://doi.org/10.3390/app14146101
Chicago/Turabian StyleYao, Weipeng, Ronan Lelièvre, Tessa Waltenspiel, Itamar Cohen, Amokrane Allaoua, Patrizio Antici, Arie Beck, Erez Cohen, Xavier Davoine, Emmanuel d’Humières, and et al. 2024. "Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultrashort Laser Pulses" Applied Sciences 14, no. 14: 6101. https://doi.org/10.3390/app14146101
APA StyleYao, W., Lelièvre, R., Waltenspiel, T., Cohen, I., Allaoua, A., Antici, P., Beck, A., Cohen, E., Davoine, X., d’Humières, E., Ducasse, Q., Filippov, E., Gautier, C., Gremillet, L., Koseoglou, P., Michaeli, D., Papadopoulos, D., Pikuz, S., Pomerantz, I., ... Fuchs, J. (2024). Enhanced Energy, Conversion Efficiency and Collimation of Protons Driven by High-Contrast and Ultrashort Laser Pulses. Applied Sciences, 14(14), 6101. https://doi.org/10.3390/app14146101





