Experimental Investigation on the Dynamic Characteristics of Bubble-in-Chain Near a Vertical Wall
Abstract
:1. Introduction
2. Materials and Methods
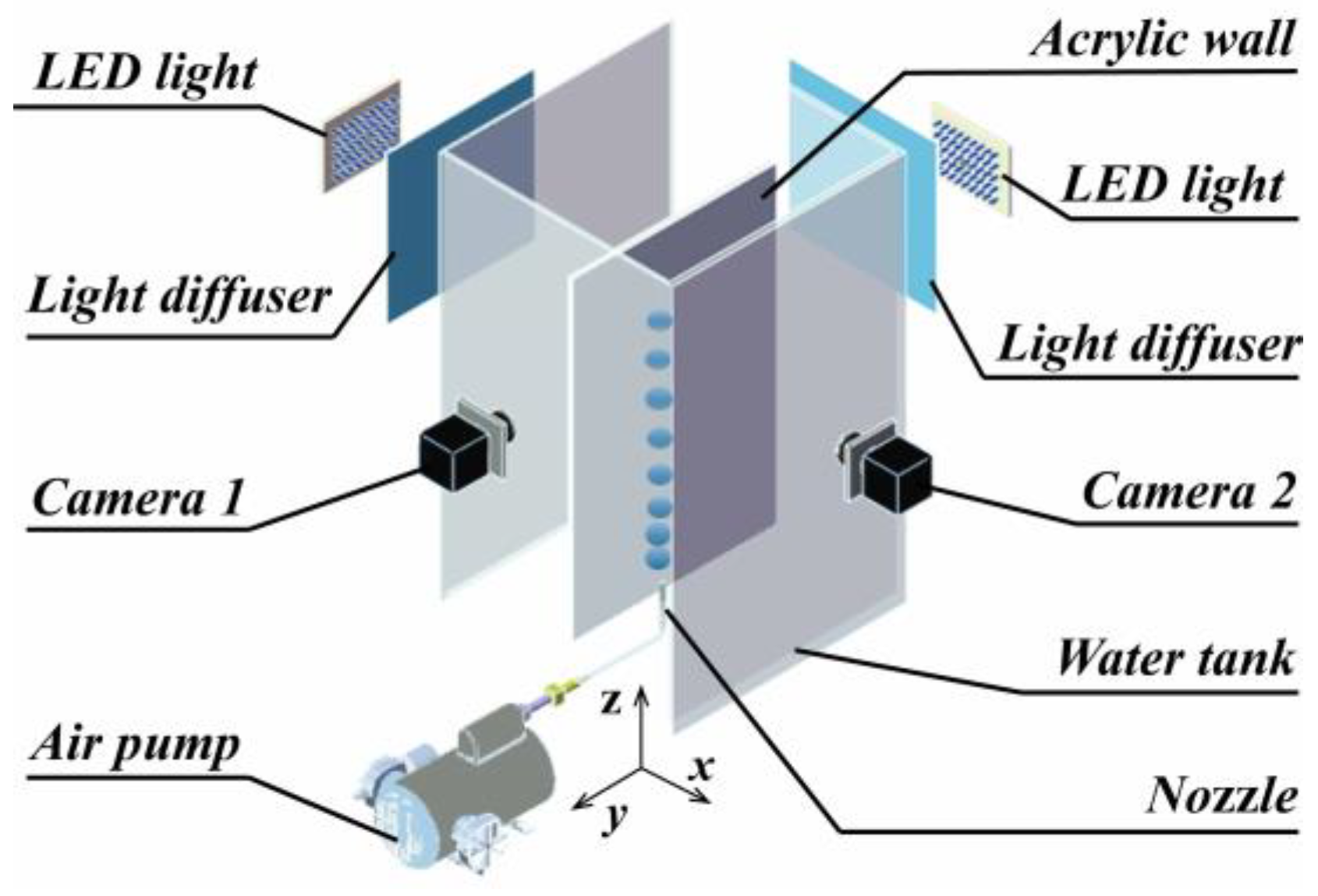
2.1. Experimental Setup
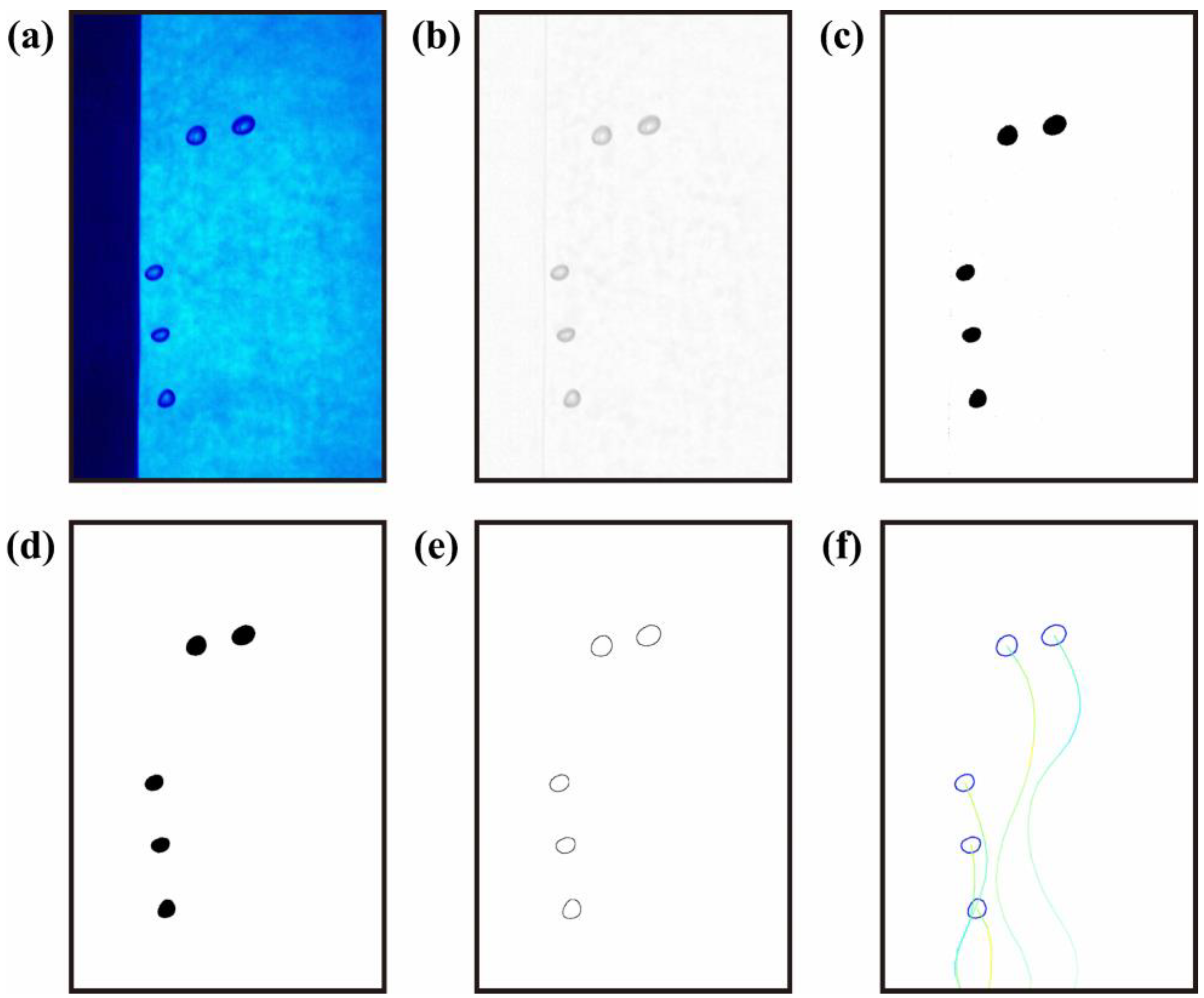
2.2. Bubble Tracking
3. Results
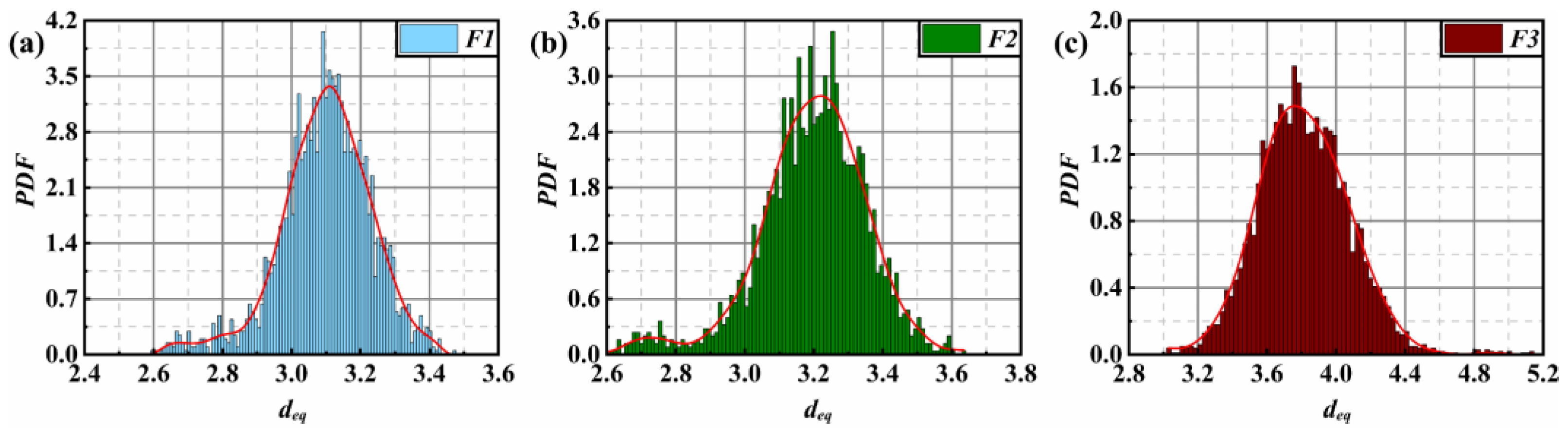
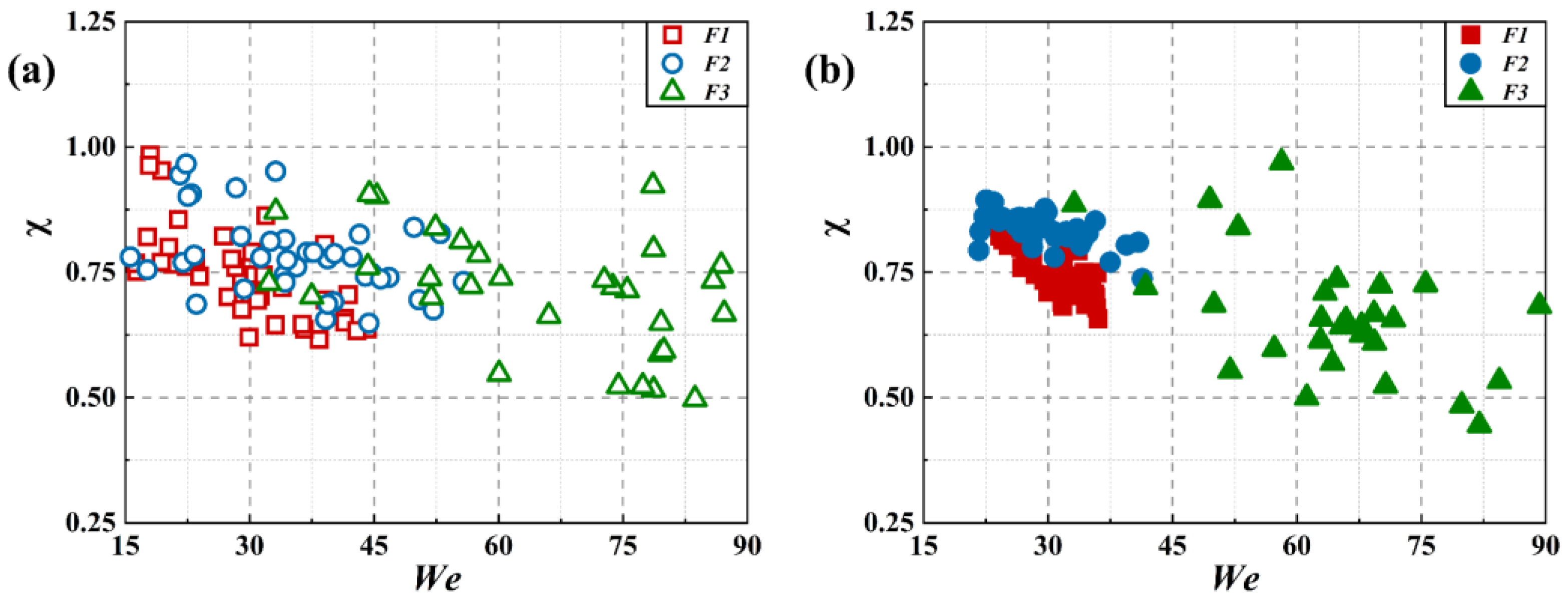
3.1. Statistical Characteristics of Bubble-in-Chain Near the Wall
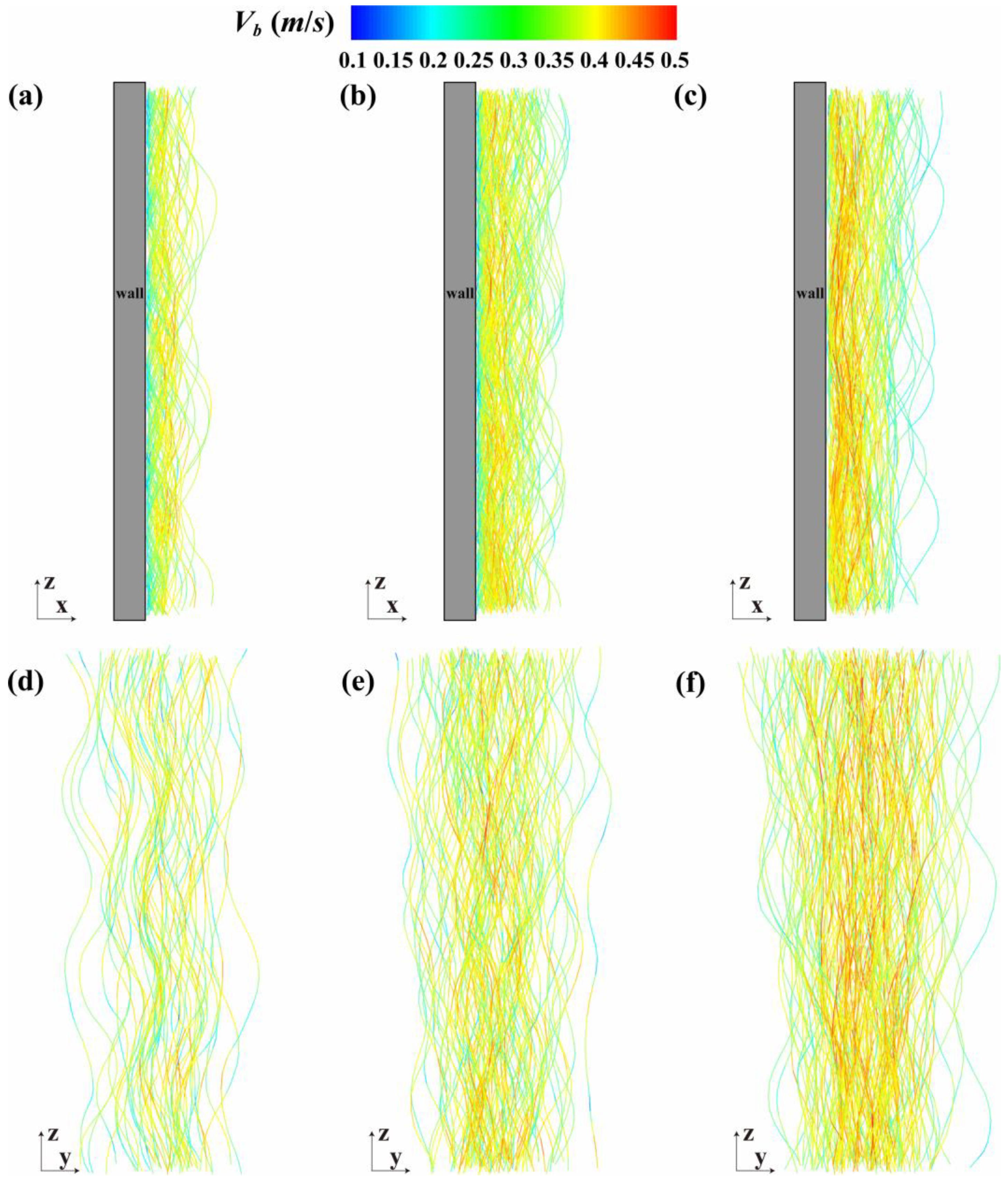
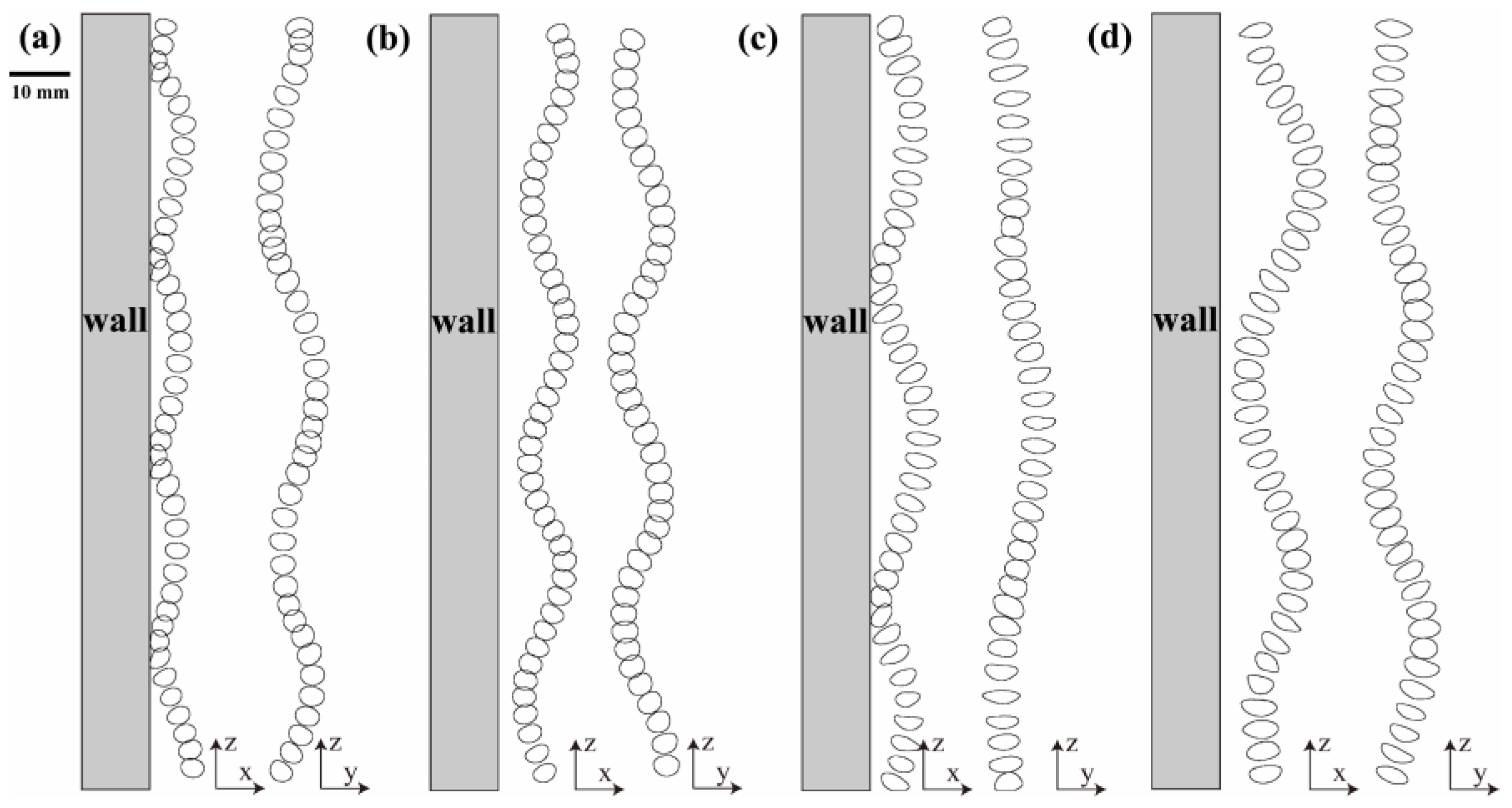
3.2. Motion Mode of the Bubble-in-Chain
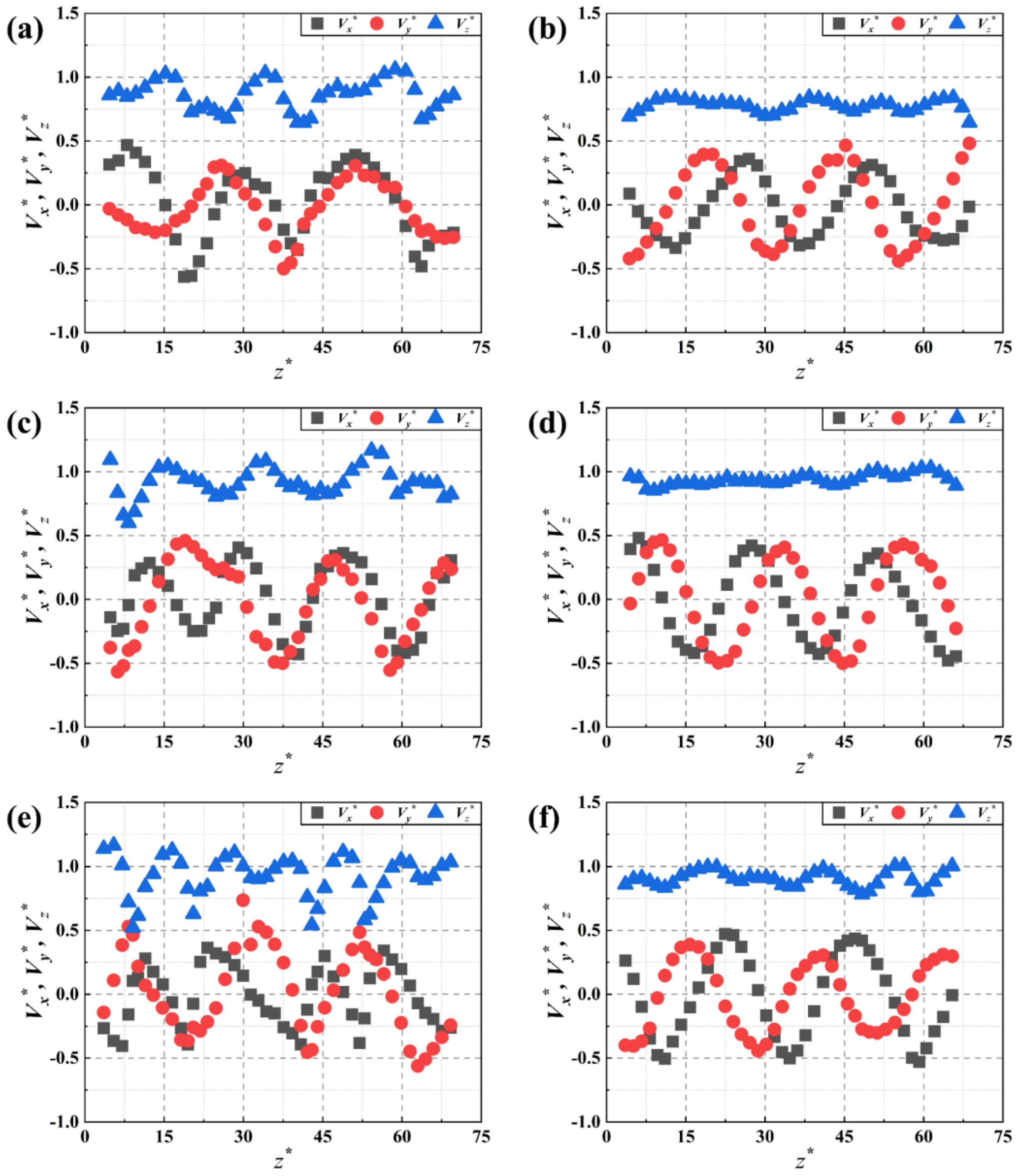
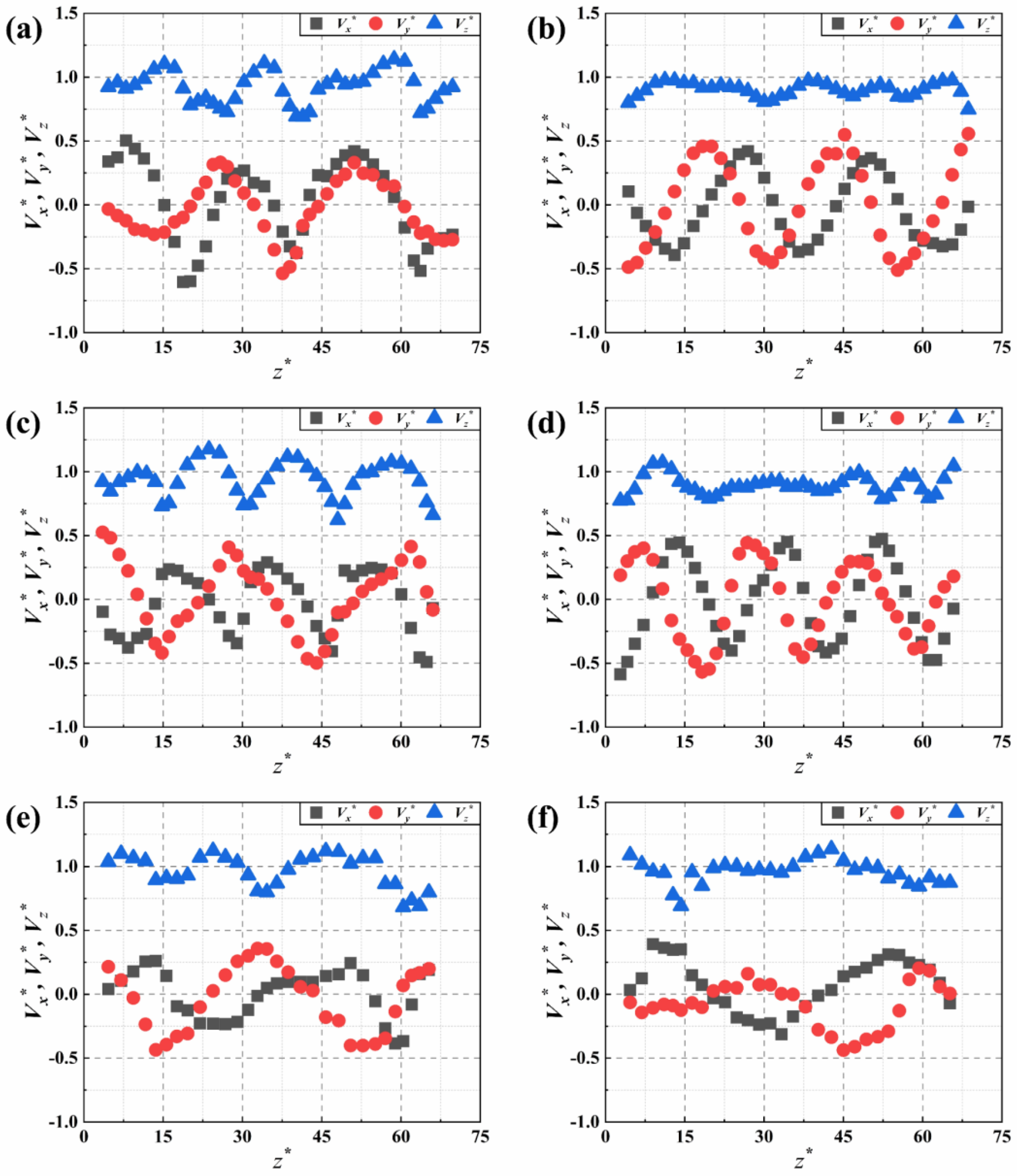
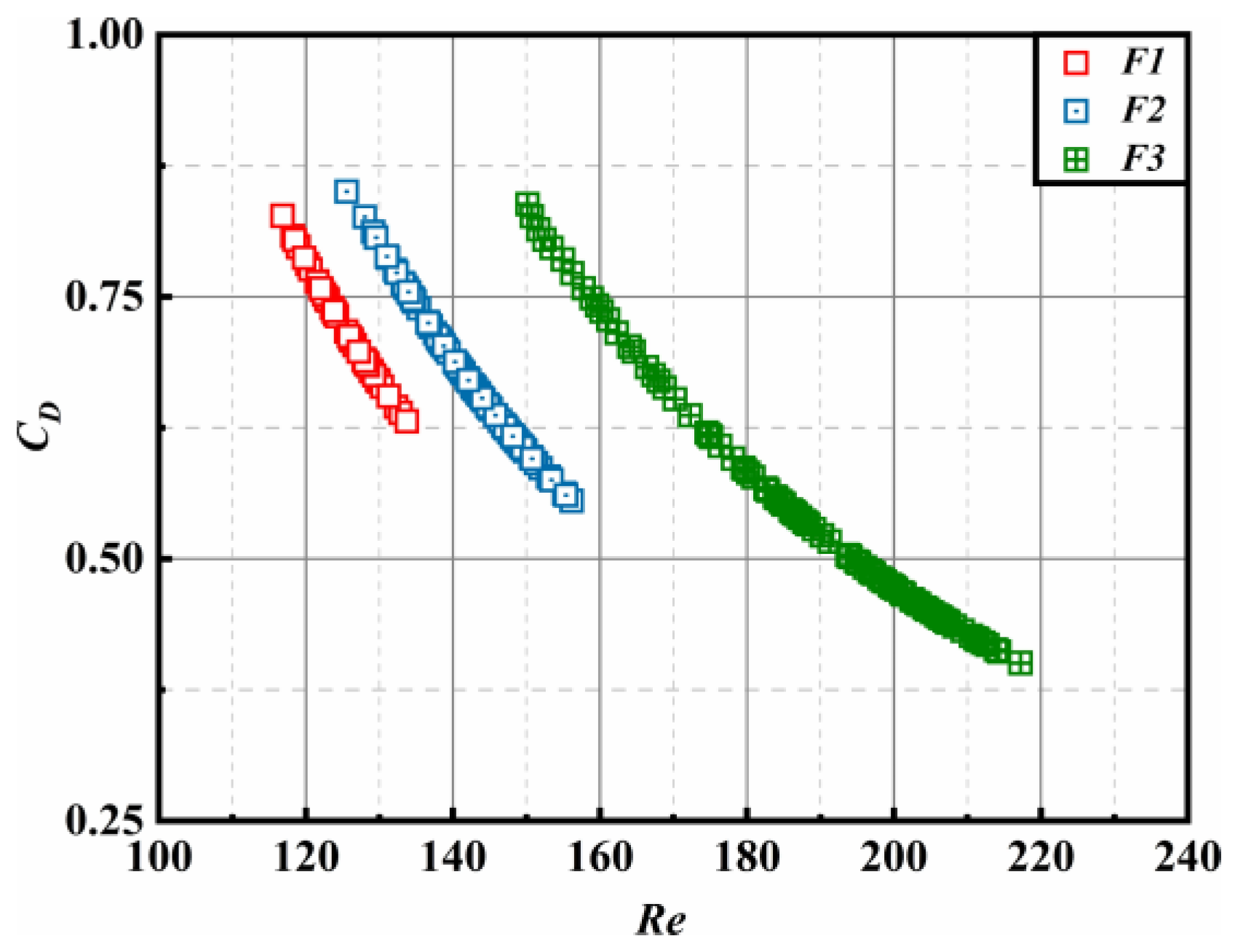
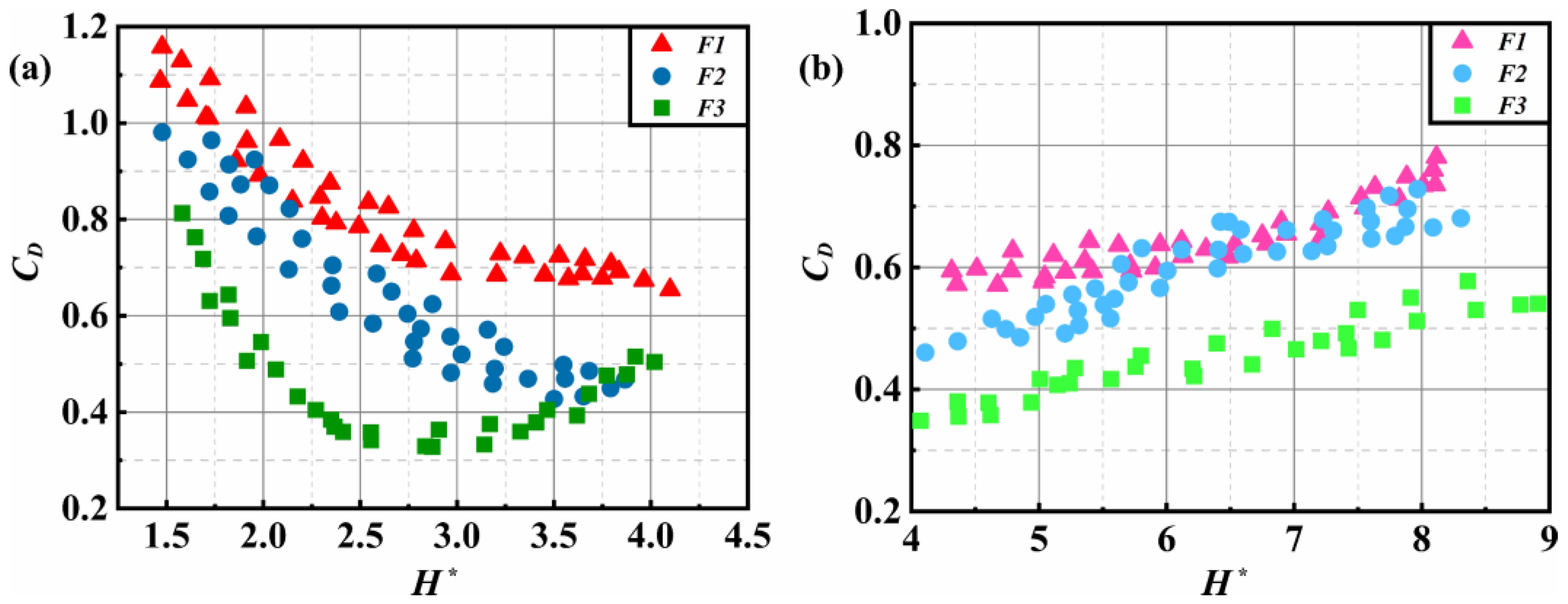
3.3. Dynamic Characteristics of the Bubble-in-Chain
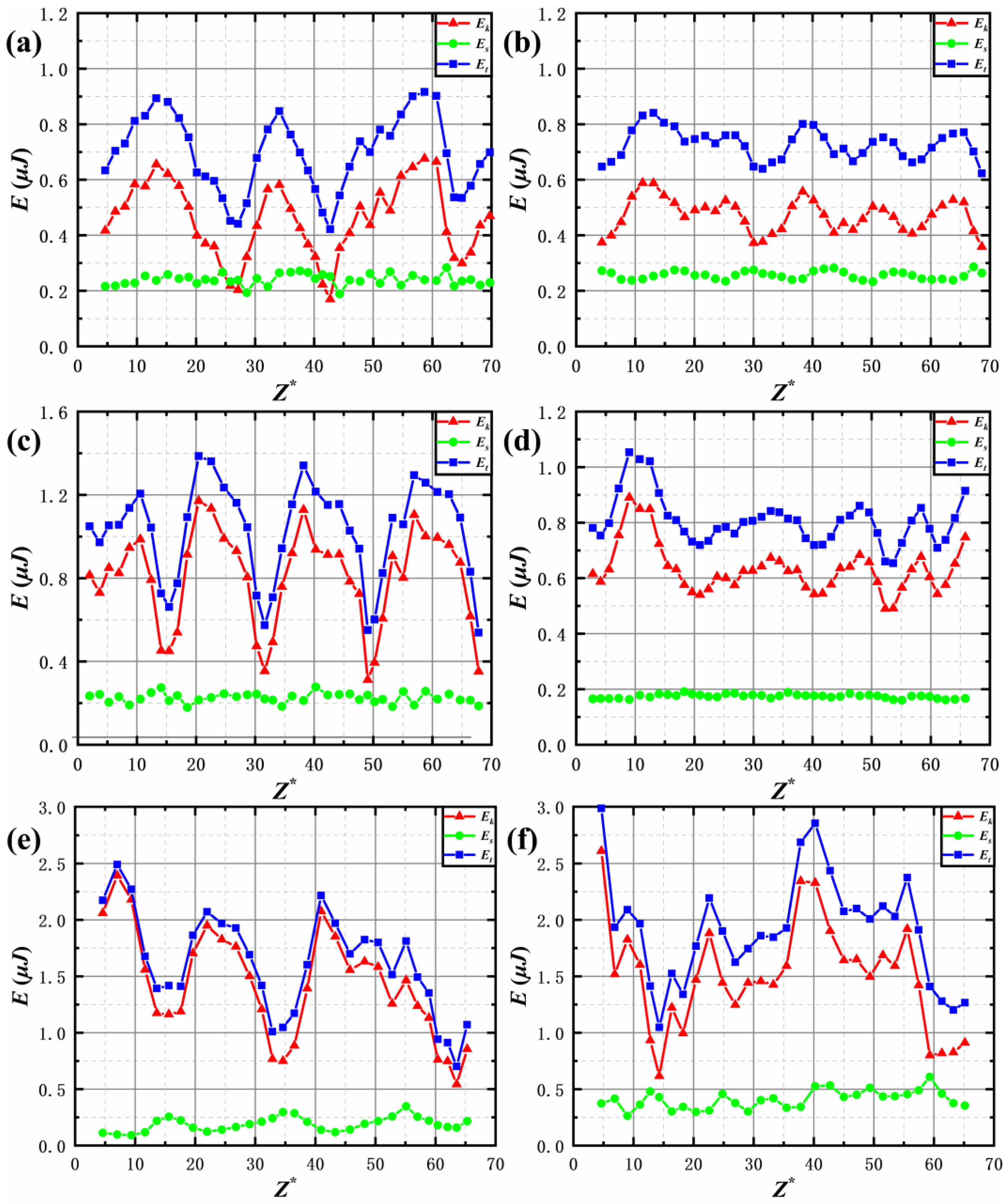
3.4. The Energy Variation of the Bubble-in-Chain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeong, H.; Park, H. Near-wall rising behaviour of a deformable bubble at high Reynolds number. J. Fluid Mech. 2015, 771, 564–594. [Google Scholar] [CrossRef]
- Métrailler, D.; Reboux, S.; Lakehal, D. Near-wall turbulence-bubbles interactions in a channel flow at Re τ = 400: A DNS investigation. Nucl. Eng. Des. 2017, 3213, 180–189. [Google Scholar] [CrossRef]
- Gong, Z.; Cai, J.; Lu, Q. Experiment characterization of the influence of wall wettability and inclination angle on bubble rising process using PIV. Eur. J. Mech./B Fluids 2020, 81, 62–75. [Google Scholar] [CrossRef]
- Yu, Q.; Ma, X.; Wang, G.; Zhao, J.; Wang, D. Thermodynamic Effect of Single Bubble Near a Rigid Wall. Ultrason. Sonochem. 2020, 71, 105396. [Google Scholar] [CrossRef]
- Zhang, Y.; Dabiri, S.; Chen, K.; You, Y. An initially spherical bubble rising near a vertical wall. Int. J. Heat Fluid Flow 2020, 85, 108649. [Google Scholar] [CrossRef]
- Maeng, H.; Park, H. An experimental study on the heat transfer by a single bubble wake rising near a vertical heated wall. Int. J. Heat Mass Transf. 2021, 165, 120590. [Google Scholar] [CrossRef]
- Yin, J.; Zhang, Y.; Zhu, J.; Lv, L.; Tian, L. An experimental and numerical study on the dynamical behaviors of the rebound cavitation bubble near the solid wall. Int. J. Heat Mass Transf. 2021, 177, 121525. [Google Scholar] [CrossRef]
- Yuan, J.; Weng, Z.; Shan, Y. Modelling of double bubbles coalescence behavior on different wettability walls using LBM method. Int. J. Therm. Sci. 2021, 168, 107037. [Google Scholar] [CrossRef]
- Yan, H.J.; Zhang, H.Y.; Zhang, H.M.; Liao, Y.X.; Liu, L. Three-dimensional dynamics of a single bubble rising near a vertical wall:Paths and wakes. Pet. Sci. 2023, 20, 1874–1884. [Google Scholar] [CrossRef]
- Khodayar, J.; Davoudian, S.H. Surface Wettability Effect on the Rising of a Bubble Attached to a Vertical Wall. Int. J. Multiphas. Flow. 2018, 109, 178–190. [Google Scholar] [CrossRef]
- Chen, Y.; Tu, C.; Yang, Q.; Wang, Y.; Bao, F. Dynamic behavior of a deformable bubble rising near a vertical wire-mesh in the quiescent water. Exp. Therm. Fluid. Sci. 2021, 120, 110235. [Google Scholar] [CrossRef]
- Sugiyama, K.; Takemura, F. On the lateral migration of a slightly deformed bubble rising near a vertical plane wall. Fluid Dyn. 2010, 662, 209–231. [Google Scholar] [CrossRef]
- Sugioka, K.-I.; Tsukada, T. Direct numerical simulations of drag and lift forces acting on a spherical bubble near a plane wall. Int. J. Multiphas. Flow. 2015, 71, 32–37. [Google Scholar] [CrossRef]
- Zeng, L.; Balachandar, S.; Fischer, P. Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid. Mech. 2005, 536, 1–25. [Google Scholar] [CrossRef]
- Moctezuma, M.F.; Lima-Ochoterena, R.; Zenit, R. Velocity fluctuations resulting from the interaction of a bubble with a vertical wall. Phys. Fluids. 2005, 17, 098106. [Google Scholar] [CrossRef]
- Zaruba, A.; Lucas, D.; Prasser, H.-M.; Höhne, T. Bubble-wall interactions in a vertical gas–liquid flow: Bouncing. sliding and bubble deformations. Chem. Eng. Sci. 2007, 62, 1591–1605. [Google Scholar] [CrossRef]
- Gonzales, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Pearson Prentice Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Tun, M.T.; Sugiura, Y.; Shimamura, T.J.J.O.S.P. Joint Training of Noisy Image Patch and Impulse Response of Low-Pass Filter in CNN for Image Denoising. J. Signal Process. 2024, 28, 1–17. [Google Scholar] [CrossRef]
- Li, S.Y.; Xu, Y.; Wang, J.J. Characteristics and Flow Dynamics of Bubble-in-Chain Rising in a Quiescent Fluid. Int. J. Multiphas. Flow. 2021, 143, 103760. [Google Scholar] [CrossRef]
- Celata, G.P.; D’Annibale, F.; Di Marco, P.; Memoli, G.; Tomiyama, A. Measurements of rising velocity of a small bubble in a stagnant fluid in one- and two-component systems. Exp. Therm. Fluid. Sci. 2007, 31, 609–623. [Google Scholar] [CrossRef]
- Lee, J.; Park, H. Wake structures behind an oscillating bubble rising close to a vertical wall. Int. J. Multiphas. Flow. 2017, 91, 225–242. [Google Scholar] [CrossRef]
- Sirino, T.; Mancilla, E.; Morales, R.E.M. Experimental Study on the Behavior of Single Rising Bubbles in a Confined Rectangular Channel. Int. J. Multiphas. Flow. 2019, 145, 103818. [Google Scholar] [CrossRef]
- Krishna, R.; Urseanu, M.I.; Baten, J.M.V.; Ellenberger, J. Wall effects on the rise of single gas bubbles in liquids. Int. Commun. Heat. Mass. 1999, 26, 781–790. [Google Scholar] [CrossRef]
- Cai, R.; Ju, E.; Chen, W.; Sun, J. Different modes of bubble migration near a vertical wall in pure water. Korean J. Chem. Eng. 2023, 40, 67–78. [Google Scholar] [CrossRef]
- Cai, R.; Sun, J.; Chen, W. Near-wall bubble migration and wake structure in viscous liquids. Chem. Eng. Res. Des. 2024, 202, 414–428. [Google Scholar] [CrossRef]
- Yan, X.; Zheng, K.; Jia, Y.; Miao, Z.; Wang, L.; Cao, Y.; Liu, J. Drag coefficient prediction of a single bubble rising in liquids. Ind. Eng. Chem. Res. 2018, 57, 5385–5393. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Dover Publications, Inc.: Mineola, NY, USA, 1978. [Google Scholar]
- Yan, X.; Jia, Y.; Wang, L.; Cao, Y. Drag coefficient fluctuation prediction of a single bubble rising in water. Chem. Eng. J. 2017, 316, 553–562. [Google Scholar] [CrossRef]
- Manica, R.; Klaseboer, E.; Chan, D.Y.C. The hydrodynamics of bubble rise and impact with solid surfaces. Adv. Colloid Interface 2016, 235, 214–232. [Google Scholar] [CrossRef]



| Liquid Type | Density (kg/m3) | Viscosity (Pa s) | Surface Tension (N/m) |
|---|---|---|---|
| 35% glycerin solution | 1071.6 | 6.6 × 10−3 | 64.14 × 10−3 |
| Frequency | F1 | F2 | F3 |
|---|---|---|---|
| Hz | 5 | 16 | 38 |
| Initial Distance | L1 | L2 | L3 |
|---|---|---|---|
| L* | 0.5 | 1.5 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, R.; Sun, J.; Chen, W. Experimental Investigation on the Dynamic Characteristics of Bubble-in-Chain Near a Vertical Wall. Appl. Sci. 2024, 14, 6076. https://doi.org/10.3390/app14146076
Cai R, Sun J, Chen W. Experimental Investigation on the Dynamic Characteristics of Bubble-in-Chain Near a Vertical Wall. Applied Sciences. 2024; 14(14):6076. https://doi.org/10.3390/app14146076
Chicago/Turabian StyleCai, Runze, Jiao Sun, and Wenyi Chen. 2024. "Experimental Investigation on the Dynamic Characteristics of Bubble-in-Chain Near a Vertical Wall" Applied Sciences 14, no. 14: 6076. https://doi.org/10.3390/app14146076
APA StyleCai, R., Sun, J., & Chen, W. (2024). Experimental Investigation on the Dynamic Characteristics of Bubble-in-Chain Near a Vertical Wall. Applied Sciences, 14(14), 6076. https://doi.org/10.3390/app14146076





