Non-Invasive Continuous Blood Pressure Estimation from Single-Channel PPG Based on a Temporal Convolutional Network Integrated with an Attention Mechanism
Abstract
1. Introduction
- (1)
- This paper introduces dilated convolution and causal convolution from TCN to effectively learn the temporal dependencies between blood pressure and PPG waveforms.
- (2)
- Integration of CBAM module: To further enhance the performance of feature extraction, this method incorporates the CBAM module into the one-dimensional convolutional module.
- (3)
- Experimental validation on large-scale public datasets: This study employs large-scale public datasets for experimental evaluation, aiming to ensure the robustness of continuous blood pressure estimation across diverse samples and scenarios.
2. Related Works
3. Materials
3.1. Dataset Introduction
3.2. Baseline Drift Elimination
3.3. Signal Segmentation
4. Methods
4.1. Dilated Causal Convolution
4.2. CBAM Module
4.2.1. Channel Attention Module
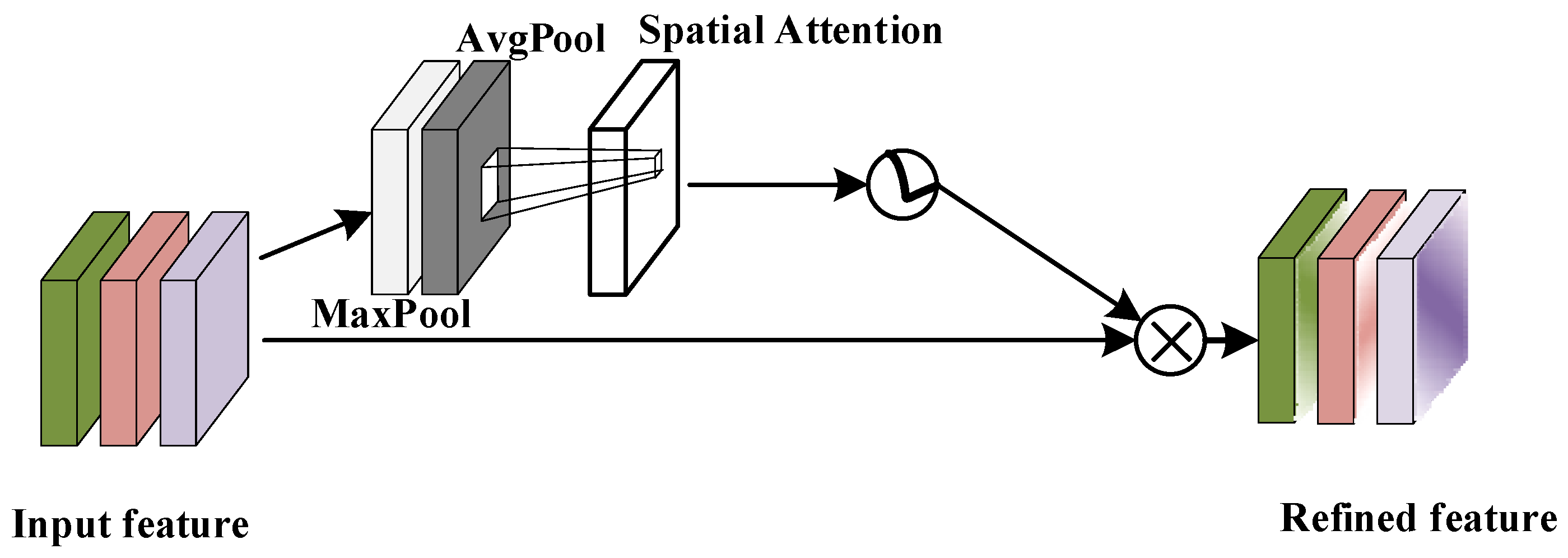
4.2.2. Spatial Attention Module
5. Results
5.1. Experimental Setup
5.2. Evaluation Metrics and Loss Functions
- (1)
- Mean Absolute Error
- (2)
- Standard Deviation
- (3)
- Mean Absolute Percentage Error
5.3. Comparison and Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Progn, V. Hypertension as a Medical and Social Problem and Ways to Solve it. Doctoral Dissertation, Scientific Repository of I.Horbachevsky Ternopil National Medical University, Ternopil, Ukraine, 2022. [Google Scholar]
- Picone, D.S.; Schultz, M.G.; Otahal, P.; Aakhus, S.; Al-Jumaily, A.M.; Black, J.A.; Bos, W.J.; Chambers, J.B.; Chen, C.H.; Cheng, H.M.; et al. Accuracy of cuff-measured blood pressure: Systematic reviews and meta-analyses. J. Am. Coll. Cardiol. 2017, 70, 572–586. [Google Scholar] [CrossRef]
- Corazza, I.; Zecchi, M.; Corsini, A.; Marcelli, E.; Cercenelli, L. Technologies for Hemodynamic Measurements: Past, Present and Future. In Advances in Cardiovascular Technology; Academic Press: Cambridge, MA, USA, 2022; pp. 515–566. [Google Scholar]
- El-Hajj, C.; Kyriacou, P.A. A review of machine learning techniques in photoplethysmography for the non-invasive cuff-less measurement of blood pressure. Biomed. Signal Process. Control 2020, 58, 101870. [Google Scholar] [CrossRef]
- Vidhya, C.M.; Maithani, Y.; Singh, J.P. Recent advances and challenges in textile electrodes for wearable biopotential signal monitoring: A comprehensive review. Biosensors 2023, 13, 679. [Google Scholar] [CrossRef] [PubMed]
- Rastegar, S.; GholamHosseini, H.; Lowe, A. Non-invasive continuous blood pressure monitoring systems: Current and proposed technology issues and challenges. Phys. Eng. Sci. Med. 2020, 43, 11–28. [Google Scholar] [CrossRef]
- Teng, X. Noninvasive and Cuffless Blood Pressure Measurement: The Effects of Contacting Force and Dynamic Exercise; The Chinese University of Hong Kong: Hong Kong, China, 2004. [Google Scholar]
- Kurylyak, Y.; Lamonaca, F.; Grimaldi, D. A Neural Network-based method for continuous blood pressure estimation from a PPG signal. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 280–283. [Google Scholar]
- Liu, M.; Po, L.M.; Fu, H. Cuffless blood pressure estimation based on photoplethysmography signal and its second derivative. Int. J. Comput. Theory Eng. 2017, 9, 202. [Google Scholar] [CrossRef]
- Maqsood, S.; Xu, S.; Springer, M.; Mohawesh, R. A benchmark study of machine learning for analysis of signal feature extraction techniques for blood pressure estimation using photoplethysmography (PPG). IEEE Access 2021, 9, 138817–138833. [Google Scholar] [CrossRef]
- Baek, S.; Jang, J.; Yoon, S. End-to-end blood pressure prediction via fully convolutional networks. IEEE Access 2019, 7, 185458–185468. [Google Scholar] [CrossRef]
- Su, P.; Ding, X.R.; Zhang, Y.T.; Liu, J.; Miao, F.; Zhao, N. Long-term blood pressure prediction with deep recurrent neural networks. In Proceedings of the 2018 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 323–328. [Google Scholar]
- Slapničar, G.; Mlakar, N.; Luštrek, M. Blood pressure estimation from photoplethysmogram using a spectro-temporal deep neural network. Sensors 2019, 19, 3420. [Google Scholar] [CrossRef]
- Schrumpf, F.; Frenzel, P.; Aust, C.; Osterhoff, G.; Fuchs, M. Assessment of non-invasive blood pressure prediction from ppg and rppg signals using deep learning. Sensors 2021, 21, 6022. [Google Scholar] [CrossRef] [PubMed]
- White, W.B.; Berson, A.S.; Robbins, C.; Jamieson, M.J.; Prisant, L.M.; Roccella, E.; Sheps, S.G. National standard for measurement of resting and ambulatory blood pressures with automated sphygmomanometers. Hypertension 1993, 21, 504–509. [Google Scholar] [CrossRef]
- Barna, I.; Keszei, A.; Dunai, A. Evaluation of Meditech ABPM-04 ambulatory blood pressure measuring device, according to the British Hypertension Society (BHS) protocol. Blood Press. Monit. 1998, 3, 363–368. [Google Scholar] [PubMed]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuff-less high-accuracy calibration-free blood pressure estimation using pulse transit time. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1006–1009. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Knai, K. Oscillations in Biological Signal. Doctoral Thesis, NTNU, Trondheim, Norway, 2020. [Google Scholar]
- Zhong, X.S. Research on Human Motion Partition Wall Detection and Localization Technology Based on UHF; North Central University: Minneapolis, MN, USA, 2021. [Google Scholar]
- Cheng, C.; Zhang, C.; Wei, Y.; Jiang, Y.G. Sparse temporal causal convolution for efficient action modeling. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 592–600. [Google Scholar]
- Zhang, X.; You, J. A gated dilated causal convolution based encoder-decoder for network traffic forecasting. IEEE Access 2020, 8, 6087–6097. [Google Scholar] [CrossRef]
- Ma, H.; Chen, C.; Zhu, Q.; Yuan, H.; Chen, L.; Shu, M. An ECG signal classification method based on dilated causal convolution. Comput. Math. Methods Med. 2021, 2021, 6627939. [Google Scholar] [CrossRef] [PubMed]
- Hamad, R.A.; Kimura, M.; Yang, L.; Woo, W.L.; Wei, B. Dilated causal convolution with multi-head self attention for sensor human activity recognition. Neural Comput. Appl. 2021, 33, 13705–13722. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Yang, J.; Jiang, J. Dilated-CBAM: An efficient attention network with dilated convolution. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 11–15. [Google Scholar]
- Chen, B.; Dang, Z. Fast PCB defect detection method based on FasterNet backbone network and CBAM attention mechanism integrated with feature fusion module in improved YOLOv7. IEEE Access 2023, 11, 95092–95103. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, D.; Zhang, Z.; Lin, S.; Dai, J. An empirical study of spatial attention mechanisms in deep networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, South Korea, 27 October–2 November 2019; pp. 6688–6697. [Google Scholar]
- Chen, B.; Huang, Y.; Xia, Q.; Zhang, Q. Nonlocal spatial attention module for image classification. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420938927. [Google Scholar] [CrossRef]
- Hu, M.; Guo, D.; Jiang, M.; Qian, F.; Wang, X.; Ren, F. rPPG-based heart rate estimation using spatial-temporal attention network. IEEE Trans. Cogn. Dev. Syst. 2021, 14, 1630–1641. [Google Scholar] [CrossRef]
- Kim, S.C. Analysis of Change Rate of SBP and DBP Estimation Fusion Algorithm According to PTT Measurement change PPG Pulse Wave Analysis. J. Korea Converg. Soc. 2020, 11, 35–40. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Lee, D.K.; In, J.; Lee, S. Standard deviation and standard error of the mean. Korean J. Anesthesiol. 2015, 68, 220. [Google Scholar] [CrossRef] [PubMed]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]







| Function Block | Hyperparameter | |
|---|---|---|
| Input layer | size: 3 × 1000 | |
| Dilated causal convolution residual block | Convolutional layer | Kernel size: 1 × 3 |
| Number of kernels: 64 | ||
| Dilation factor: 2i | ||
| Normalization layer | Method: batch normalization | |
| Activation layer | Activation function: ReLU | |
| Dropout layer | Dropout rate: 0.05% | |
| CBAM attention module | Channel attention layer | Feature reduction rate: 16 |
| Spatial attention layer | Kernel size: 1 × 7 | |
| Fully connected layer | First layer | Input dimensions: 64 |
| Output dimensions: 128 | ||
| Second layer | Input dimensions: 128 | |
| Output dimensions: 1 | ||
| Output Layer | Output size: 2 × 1 | |
| ≤5 mmHg | ≤10 mmHg | ≤15 mmHg | ||
|---|---|---|---|---|
| BHS | Grade A | 60% | 85% | 95% |
| Grade B | 50% | 75% | 90% | |
| Grade C | 40% | 65% | 85% | |
| TCN-CBAM Model test results | SBP Estimation error | 48.74% | 73.19% | 87.06% |
| DBP Estimation error | 38.62% | 88.73% | 97.29% |
| Model | SBP Estimation Error | DBP Estimation Error | ||||
|---|---|---|---|---|---|---|
| MAE | STD | MAPE | MAE | STD | MAPE | |
| Linear | 14.0665 | 17.9088 | 0.1097 | 4.5460 | 5.8711 | 0.0653 |
| SVR | 12.7897 | 16.3983 | 0.0990 | 4.5311 | 5.9229 | 0.0591 |
| MLP | 13.5818 | 17.3121 | 0.1039 | 4.3163 | 5.9181 | 0.0623 |
| XGBoost | 8.4072 | 11.9345 | 0.0656 | 2.9859 | 4.1835 | 0.0431 |
| RF | 7.1597 | 10.8400 | 0.0560 | 2.7073 | 3.9852 | 0.0391 |
| KNN | 7.3237 | 11.1455 | 0.0569 | 2.6817 | 4.0246 | 0.0386 |
| CNN | 8.2555 | 11.6321 | 0.0629 | 3.3077 | 4.3385 | 0.0336 |
| CNN-GRU | 5.6089 | 9.1172 | 0.0431 | 2.5339 | 3.7756 | 0.0368 |
| CNN-LSTM | 5.3837 | 9.0737 | 0.0420 | 2.5029 | 3.7069 | 0.0361 |
| TCN | 5.8680 | 8.8940 | 0.0405 | 2.3707 | 3.8023 | 0.0307 |
| TCN-CBAM | 5.3482 | 8.3410 | 0.0334 | 2.1190 | 3.1795 | 0.0240 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, D.; Ji, Z.; Wang, H. Non-Invasive Continuous Blood Pressure Estimation from Single-Channel PPG Based on a Temporal Convolutional Network Integrated with an Attention Mechanism. Appl. Sci. 2024, 14, 6061. https://doi.org/10.3390/app14146061
Dai D, Ji Z, Wang H. Non-Invasive Continuous Blood Pressure Estimation from Single-Channel PPG Based on a Temporal Convolutional Network Integrated with an Attention Mechanism. Applied Sciences. 2024; 14(14):6061. https://doi.org/10.3390/app14146061
Chicago/Turabian StyleDai, Dong, Zhaohui Ji, and Haiyan Wang. 2024. "Non-Invasive Continuous Blood Pressure Estimation from Single-Channel PPG Based on a Temporal Convolutional Network Integrated with an Attention Mechanism" Applied Sciences 14, no. 14: 6061. https://doi.org/10.3390/app14146061
APA StyleDai, D., Ji, Z., & Wang, H. (2024). Non-Invasive Continuous Blood Pressure Estimation from Single-Channel PPG Based on a Temporal Convolutional Network Integrated with an Attention Mechanism. Applied Sciences, 14(14), 6061. https://doi.org/10.3390/app14146061






