Floquet Modification of the Bandgaps and Energy Spectrum in Flat-Band Pseudospin-1 Dirac Materials

Abstract

In this paper, we investigate the so-called electronic dressed states, a unified quasiparticle resulting from the interaction between electrons in a two-dimensional material with an off-resonance optical dressing field. If the frequency of this field is much larger than all characteristic energies in the system, such as the Fermi energy or bandgap(s), the electronic band structure is affected by radiation so that some important properties of the electron dispersions could be modified in a way desirable for practical applications. For example, circularly polarized light can be used to vary the bandgap of Dirac materials: it opens a gap in graphene and other metallic and semimetallic lattices, or it modifies the magnitude of an existing gap. This will either enhance or reduce a gap, depending on its initial value as well as properties of a host material. Here, we consider gapped dice and Lieb lattices as samples, and we put forward a full theoretical model to reveal how these electronic states are deformed by elliptically-polarized irradiation with a focus on the generation and modification of a bandgap.

1. Introduction

Floquet theory, which was originally developed to solve partial differential equations [1], represents a unique tool for describing the electronic properties and behavior of a large number of diverse quantum systems [2,3,4] in the presence of high-frequency periodic dressing fields [5]. It has also advanced into the so-called Floquet engineering, a technique for obtaining the electronic dispersions and, specifically, bandgaps that are required for technical applications. This has quickly become one of the most promising research directions [6,7] in condensed matter physics [8,9,10] and photonics. Floquet engineering is primarily applied to two-dimensional (2D) materials or the surface states of three-dimensional lattices. Because of the recent experimental advances in laser and microwave optics, it has become possible to verify the theoretical predictions of condensed matter quantum optics in actual experiments and realize them in optoelectronic devices [11].

Floquet theory has been successfully applied to original [12,13,14,15,16,17], gapped [13,18] and Kekule-patterned graphene [19]. It has also entered into extensive studies on anisotropic [20] and tilted Dirac materials [21,22,23,24,25,26,27] as well as other structures [12,28,29,30,31,32]. Special interest has been given to the Floquet control of electronic transport properties of irradiated materials [33,34,35] in addition to indirect exchange interaction [36,37] and collective behaviors [38,39]. Its interests further extend to the fields of excitonic [40] and dissipative [9] Floquet systems, pseudospin textures, and nanoribbons [41,42,43,44,45]. In particular, an optical-dressing field was utilized to create localized trapped states [46], similarly to those in fullerenes [47,48,49,50].

In fact, the electron–photon interaction and its dressed states are only one part of an ongoing effort to investigate all electronic and collective properties in recently discovered Dirac materials. These efforts include establishing a Wentzel–Kramers–Brillouin (WKB) theory for taking into consideration semi-classical electronic states in $\alpha$-${\mathcal{T}}_3$, dice, and even Kekule-patterned graphene [51,52] in a way that is very similar to previously reported successful works on genuine graphene materials [53,54,55].

Additionally, Floquet engineering is utilized to alter the Bloch-electron states in Dirac materials with a flat band, such as a dice lattice [7,56,57]. The $\alpha$-${\mathcal{T}}_3$ model, which represents interpolation between a graphene and a dice lattice, is one of the most favorable and well-studied models for materials acquiring a flat band. A strong and ongoing interest on this $\alpha$-${\mathcal{T}}_3$ model is attributed to its unusual low-energy electronic band structure involving a regular graphene Dirac cone as well as a flat band. This actually makes $\alpha$-${\mathcal{T}}_3$ materials candidates for replacing graphene in modern electronic devices.

The atomic structure of the $\alpha$-${\mathcal{T}}_3$ materials consists of an additional atom at the center of a graphene-like honeycomb lattice (HCL). Therefore, the new hub-to-rim (and rim-to-hub) hopping coefficient can be related to an existing rim-to-rim hopping simply by a scaling parameter $\alpha$, which turns out to be a key factor for characterizing various $\alpha$-${\mathcal{T}}_3$ materials. For example, the case with $\alpha =1$ corresponds to a dice lattice, while $\alpha \to 1$ resembles graphene with a fully decoupled set of hub atoms at the center of each hexagon. Importantly, the electronic properties of the $\alpha$-${\mathcal{T}}_3$ model can be described by a pseudospin-1 Dirac-Weyl Hamiltonian which directly depends on an $\alpha$ parameter or, more specifically, on its phase $\varphi ={tan}^{-1}\alpha$.

The presence of an unusual band structure for the $\alpha$-${\mathcal{T}}_3$ model can lead to unique and unexpected features, including electronic [58,59,60], collective [61,62,63], magnetic [64], and optical properties [65,66,67,68,69], and even a phase transition [70]. These behaviors are very different from those of graphene. The major issue addressed by many researchers has been how these graphene-like properties will be modified by the presence of an additional flat band [71,72,73]. Already, a variety of materials, with their electronic properties described approximately by an $\alpha$-${\mathcal{T}}_3$ model, have already been identified and made by synthesis; meanwhile, the presence of such a stable flat-band in their energy spectrum has been experimentally verified. Particularly, the so-called Lieb lattice, which has already been demonstrated in a number of different systems and wave-guides [74,75,76], presents a new type of technologically promising pseudospin-1 Hamiltonian, and its corresponding inverted band structure reveals a finite bandgap as well as a flat band which lies within this bandgap but intersects the upper (valence) band at its bottom [77,78,79]. Apart from that, there are multiple applications of Dirac materials, such as a temperature-sensitive multi-band grating metamaterial absorption device [80] and a dual-tunable broadband metamaterial absorber using bulk Dirac semimetal in the terahertz frequency range [81].

The remaining part of this paper is organized as follows. In Section 2, we review the electronic properties, including energy band structure, and electronic states of $\alpha$-${\mathcal{T}}_3$ materials, a dice lattice, and a Lieb lattice. Specifically, we discuss the properties of an $\alpha$-${\mathcal{T}}_3$ model with a fixed finite bandgap induced by a dielectric substrate. Moreover, the electron dressed states due to an applied off-resonance circularly and, more generally, elliptically polarized irradiation, including related derivations, equations, and mathematical formalism, are all presented in Section 3. Section 4 is devoted to a detailed discussion on our numerical results and their connections to the band structure of electronic dressed states associated with different materials. Our concluding remarks are made in the final Section 5.

2. Low-Energy Electronic States of the Considered Materials

The electronic states of the $\alpha -{\mathcal{T}}_3$ model are described by the following low-energy $\varphi$-dependent pseudospin-1 Hamiltonian:

$${\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)=\hslash v_F\left\{\begin{array}{ccc}0& (\tau k_x-i{k}_y)cos\varphi & 0\\ (\tau k_x+i{k}_y)cos\varphi & 0& (\tau k_x-i{k}_y)sin\varphi \\ 0& (\tau k_x+i{k}_y)sin\varphi & 0\end{array}\right\},$$

(1)

where $k_{\pm }^{\tau }=\tau k_x\pm i{k}_y=\tau k{\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}$ depends on the valley index $\tau =\pm 1$, and $\mathit{k}=(k_x,k_y)$ is the two-dimensional wave vector, ${\theta }_{\mathbf{k}}={tan}^{-1}(k_y/k_x)$. Phase $\varphi$ is related to the relative hopping parameter $\alpha$ as $\alpha =tan\varphi$, and the Fermi velocity denoted by $v_F$ must be exactly equal to that in graphene $v_F=1.0·{10}^6$ m/s in order to enable a smooth transition between all the $\alpha -{\mathcal{T}}_3$ materials, including the limiting cases of graphene $(\varphi =0)$ and a dice lattice $(\varphi =\pi /4)$.

Remarkably, the Hamiltonian (1) could be presented in a generalized form

$${\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)=v_F\widehat{\mathit{S}}\left(\varphi \right)·{\mathbf{k}}^{\tau },$$

(2)

where vector ${\mathbf{k}}^{\tau }=(\tau k_x,k_y)$ depends on valley index $\tau =\pm 1$ and the $\varphi$-dependent matrices $\widehat{\mathit{S}}\left(\varphi \right)={\widehat{S}}_{x,y}\left(\varphi \right)$ represent a $3\times 3$ generalization of regular Pauli matrices.

$${\widehat{S}}_x\left(\varphi \right)=\left[\begin{array}{ccc}0& cos\varphi & 0\\ cos\varphi & 0& sin\varphi \\ 0& sin\varphi & 0\end{array}\right],$$

(3)

and

$${\widehat{S}}_y\left(\varphi \right)=i\left[\begin{array}{ccc}0& -cos\varphi & 0\\ cos\varphi & 0& -sin\varphi \\ 0& sin\varphi & 0\end{array}\right].$$

(4)

Hamiltonian (2) represents a general $\varphi$-dependent $\alpha -{\mathcal{T}}_3$ model. For $\varphi \to 0$, matrices (3) and (4) are reduced to the standard Pauli matrices. Hamiltonian (1) or (2) also becomes equivalent to that of graphene [82].

For the other limit, corresponding to a dice lattice with $\varphi =\pi /4$, expressions (3) and (4) accept a simplified and symmetric form of spin-1 Pauli matrices:

$${\widehat{\Sigma }}_x^{\left(1\right)}=\frac{1}{\sqrt{2}}\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 1\\ 0& 1& 0\end{array}\right],$$

(5)

and

$${\widehat{\Sigma }}_y^{\left(1\right)}=\frac{i}{\sqrt{2}}\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& -1\\ 0& 1& 0\end{array}\right].$$

(6)

Consequently, the Hamiltonian in Equation (1) could be rewritten as a symmetric and compact form, i.e.,

$${\widehat{\mathcal{H}}}_1\left(\mathit{k}\right|\tau )=\frac{\hslash v_F}{\sqrt{2}}\left[\begin{array}{ccc}0& k_{-}^{\tau }& 0\\ k_{+}^{\tau }& 0& k_{-}^{\tau }\\ 0& k_{+}^{\tau }& 0\end{array}\right]=\frac{\hslash v_F}{2}\sum _{\beta =\pm }{\widehat{\Sigma }}_{-\beta }^{\left(1\right)}{k}_{\beta }^{\tau },$$

(7)

where ${\widehat{\Sigma }}_{\pm }^{\left(1\right)}\equiv {\widehat{\Sigma }}_x^{\left(1\right)}\pm i{\widehat{\Sigma }}_y^{\left(1\right)}$.

The energy dispersions of an $\alpha -{\mathcal{T}}_3$ material, corresponding to Hamiltonian (1), are obtained as

$${\epsilon }_{\gamma }\left(\mathbf{k}\right)=\gamma \hslash v_{F}k,$$

(8)

where the three solutions (8) are related to the valence ($\gamma =-1$), conduction ($\gamma =+1$), and flat ($\gamma =0$) bands of the electronic structure. The energy dispersions (8) do not directly depend on $\alpha$ and, therefore, are also the same for a dice lattice.

The wave functions for the $\alpha -{\mathcal{T}}_3$ model, obtained as the eigenfunctions of Hamiltonian (1), are calculated as [57,69]

$${\mathbf{\Psi }}_{\gamma =\pm 1}\left(\mathit{k}\right|\tau ,\varphi )=\frac{1}{\sqrt{2}}\left\{\begin{array}{c}\tau cos\varphi {\mathtt{e}}^{-i\tau {\theta }_{\mathbf{k}}}\\ \gamma \\ \tau sin\varphi {\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}\end{array}\right\},$$

(9)

and

$${\mathbf{\Psi }}_{\gamma =0}\left(\mathit{k}\right|\tau ,\varphi )=\left\{\begin{array}{c}\tau sin\varphi {\mathtt{e}}^{-i\tau {\theta }_{\mathbf{k}}}\\ 0\\ -\tau cos\varphi {\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}\end{array}\right\}.$$

(10)

Unlike dispersions (8), wave functions (9) and (10) directly depend on phase $\varphi$ and valley index $\tau$.

For the case of a dice lattice, wave functions (9) and (10) are reduced to

$${\mathbf{\Psi }}_{\gamma =\pm 1}^{\left(d\right)}\left(\mathit{k}|\tau ,\frac{\pi }{4}\right)=\frac{1}{2}\left\{\begin{array}{c}{\mathtt{e}}^{-i\tau {\theta }_{\mathbf{k}}}\\ \sqrt{2}\tau \gamma \\ \tau {\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}\end{array}\right\},$$

(11)

and

$${\mathbf{\Psi }}_{\gamma =0}^{\left(d\right)}\left(\mathit{k}|\tau ,\frac{\pi }{4}\right)=\frac{1}{\sqrt{2}}\left\{\begin{array}{c}{\mathtt{e}}^{-i\tau {\theta }_{\mathbf{k}}}\\ 0\\ -{\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}\end{array}\right\}.$$

(12)

Such a symmetric form of wave functions (11) and (12) has a strong effect on several crucial electronic properties, such as Klein tunneling.

2.1. The $\alpha -{\mathcal{T}}_3$ Model with a Finite Gap

Importantly, an $\alpha -{\mathcal{T}}_3$ material could also acquire a finite gap in a complete analogy to graphene [83]. It could be induced either by a special type of a dielectric substrate, or by a circularly polarized dressing field.

In particular, we are very interested in investigating how an existing bandgap in an $\alpha -{\mathcal{T}}_3$ lattice created by a substrate would be modified or renationalized if a curricular polarized irradiation is also added. Therefore, we put a gapped $\alpha -{\mathcal{T}}_3$ model in the focus of our study.

The Hamiltonian of the gapped $\alpha -{\mathcal{T}}_3$ model is explicitly given as

$${\widehat{\mathcal{H}}}_{\tau }^{\left(\varphi \right)}\left(\mathit{k}\right|{\Delta }_0)=\left\{\begin{array}{ccc}{\Delta }_0{cos}^2\varphi & \hslash v_F{k}_{\tau }^{-}cos\varphi & 0\\ \hslash v_F{k}_{\tau }^{+}cos\varphi & -{\Delta }_{0}cos\left(2\varphi \right)& \hslash v_F{k}_{\tau }^{-}sin\varphi \\ 0& \hslash v_F{k}_{\tau }^{+}sin\varphi & -{\Delta }_0{sin}^2\varphi \end{array}\right\},$$

(13)

where ${\Delta }_0$ is the induced gap parameter.

Similarly to graphene, the Hamiltonian for the gapped $\alpha -{\mathcal{T}}_3$ model (13) is modified as

$${\widehat{\mathcal{H}}}_{\tau }^{\left(\varphi \right)}\left(\mathit{k}\right)⟶{\widehat{\mathcal{H}}}_{\tau }^{\left(\varphi \right)}\left(\mathit{k}\right|{\Delta }_0)={\widehat{\mathcal{H}}}_{\tau }^{\left(\varphi \right)}\left(\mathit{k}\right)+{\widehat{\mathcal{H}}}_a^{\left(\varphi \right)}\left({\Delta }_0\right),$$

(14)

meaning that Hamiltonian (1) receives an additional term

$$\begin{array}{ccc}\hfill & & {\widehat{\mathcal{H}}}_a^{\left(\varphi \right)}\left({\Delta }_0\right)=\frac{{\Delta }_0}{2}{\widehat{\Sigma }}_z\left(\varphi \right),\hfill \\ \hfill & & {\widehat{\Sigma }}_z^{\left(\varphi \right)}=-i\left[{\widehat{\Sigma }}_x\left(\varphi \right),{\widehat{\Sigma }}_y\left(\varphi \right)\right]\hfill \end{array}$$

(15)

which is explicitly given as

$${\widehat{\mathcal{H}}}_a^{\left(\varphi \right)}\left({\Delta }_0\right)=\frac{{\Delta }_0}{2}{\widehat{\Sigma }}_z\left(\varphi \right)={\Delta }_0\left\{\begin{array}{ccc}{cos}^2\varphi & 0& 0\\ 0& -cos2\varphi & 0\\ 0& 0& -{sin}^2\varphi \end{array}\right\}.$$

(16)

Here, ${\widehat{\Sigma }}_z\left(\varphi \right)$ is the $\varphi$-dependent generalization of the remaining Pauli matrix ${\widehat{\Sigma }}_z$.

We immediately discern that in the presence of a finite bandgap ${\Delta }_0$, the energy spectrum for the flat band of an $\alpha -{\mathcal{T}}_3$ material with $0<\alpha <1$ undergoes a special type of a deformation which results in a finite k-dispersion, i.e., the flat band is no longer flat. Finding the complete energy dispersions for the gapped $\alpha -{\mathcal{T}}_3$ model is a challenging problem, which involves solving a cubic equation [56,73]. However, it is relatively straightforward to verify that Hamiltonian (13) results in two inequivalent gaps between the conduction and flat, and the flat and the valence bands which depend on parameter $\alpha$ (or phase $\varphi$) and valley index $\tau$.

For a dice lattice with $\varphi \to \pi /4$, it is simplified as

$${\widehat{\Sigma }}_z^{\left(1\right)}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& -1\end{array}\right],$$

(17)

and Hamiltonian (13) is presented in the following form

$${\widehat{\mathcal{H}}}_d\left(\mathit{k}\right|\tau )=\frac{\hslash v_F}{\sqrt{2}}\left[\begin{array}{ccc}{\Delta }_0/\sqrt{2}& k_{-}^{\tau }& 0\\ k_{+}^{\tau }& 0& k_{-}^{\tau }\\ 0& k_{+}^{\tau }& -{\Delta }_0/\sqrt{2}\end{array}\right].$$

(18)

In contrast to the Hamiltonian (1) for the general $\alpha -{\mathcal{T}}_3$ model, the eigenvalue equation corresponding to Equation (18) results in a symmetric band structure with two equal bandgaps and an unaffected flat band right in the middle between the valence and conduction bands (see Figure 1). Therefore, the flat band is deformed and receives a finite k-dispersion for all $\alpha -{\mathcal{T}}_3$ materials with a finite gap, expect for a dice lattice with $\varphi =\pi /4$.

2.2. Lieb Lattice

Flat bands have also been realized in some other types of lattices, mostly optical Lieb and Kagome lattices. A Lieb lattice was observed in a number of existing systems and experimental setups: organic materials, optical lattices, and waveguides

A Lieb lattice is made of three displaced square sublattices. The Hamiltonian of a Lieb lattice is

$${\mathcal{H}}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })=\hslash v_F\left[\begin{array}{ccc}{k}_{\Delta }& q_x& 0\\ q_x& -k_{\Delta }& q_y\\ 0& q_y& k_{\Delta }\end{array}\right],$$

(19)

where

$$q_{x,y}=\frac{\pi }{a_0}+k_{x,y},$$

(20)

and $a_0$ is the lattice parameter.

The three energy dispersions, corresponding to Hamiltonian (19), are ${\epsilon }_{\gamma =\pm 1}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })=\gamma \sqrt{k_{\Delta }^2+q_x^2+q_y^2}$, and ${\epsilon }_{\gamma =0}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })=k_{\Delta }$, which could be written using a single unified expression

$${\epsilon }_{\gamma =\pm 1}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })=\hslash v_F\left\{{\delta }_{\gamma ,0}{k}_{\Delta }+\gamma v_F(1-{\delta }_{\gamma ,0})\sqrt{q_x^2+q_y^2+k_{\Delta }^2}\right\},$$

(21)

where ${\delta }_{\gamma ,0}$ is the Kronecker symbol. As a result, we have obtained three energy subbands. One of them is a flat band, while the other two have a finite dispersion, such as that shown in Figure 2c. In a Lieb lattice, the flat band is located at the finite energy $v_F{k}_{\Delta }$ right next to the lowest point of the conduction band, while for the case of a dice lattice with a finite gap, it is located symmetrically between the valence and conduction bands.

The corresponding wave functions are given by

$$\begin{array}{ccc}\hfill {\mathbf{\Psi }}_{\gamma =\pm 1}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })& =& {\left[2\left(k_{\Delta }^2+q_x^2+q_y^2+\gamma k_{\Delta }\sqrt{[k_{\Delta }^2+q_x^2+q_y^2}\right)\right]}^{-1/2}\hfill \\ & \times & \left\{\begin{array}{c}{q}_x\hfill \\ -k_{\Delta }-\gamma \sqrt{k_{\Delta }^2+q_x^2+q_y^2}\hfill \\ q_y\hfill \end{array}\right\}\hfill \end{array}$$

(22)

and

$${\mathbf{\Psi }}_{\gamma =0}^{\left(\mathrm{L}\right)}\left(\mathbf{k}\right|k_{\Delta })={\left(q_x^2+q_y^2\right)}^{-1/2}\left\{\begin{array}{c}-q_y\hfill \\ 0\hfill \\ q_x\hfill \end{array}\right\}$$

(23)

for the flat band.

3. Electron Dressed States: General Formalism

Let us now consider the changes in the energy dispersions of gapped $\alpha -{\mathcal{T}}_3$ when an off-resonance high-frequency irradiation is applied. It is known that the effects of such irradiation drastically depend on its polarization type: circularly polarized light modifies the existing energy bandgap, while a linearly polarized field induces an anisotropy of the electron energy dispersions in the direction of the light polarization. We shall examine the most general case of an elliptically-polarized dressing field. If the direction of the light polarization is aligned with the x-axis, its vector potential is given as

$$\mathit{A}\left(t\right)=\left[\begin{array}{c}{A}_x\left(t\right)\\ A_y\left(t\right)\end{array}\right]=\frac{{\mathcal{E}}_0}{\omega }\left[\begin{array}{c}cos\left(\omega t\right)\\ \beta sin\left(\omega t\right)\end{array}\right],$$

(24)

where ${\mathcal{E}}_0$ is the electric field of the imposed irradiation, so that its intensity is $I\backsim {\mathcal{E}}_0^2$, and $\omega$ is its frequency, meaning that for the high-frequency regime coefficient ${\mathcal{E}}_0/\omega$ represents only a small correction.

Parameter $\beta =sin{\Theta }_e$ is the ratio of field strengths (electric field amplitudes) along the two axes of the polarization ellipse. Equation (24) corresponds to the most general type of the light polarization. Thus, $\beta ⟶1$ results in a known expression

$${\mathit{A}}^{\left(C\right)}\left(t\right)=\left[\begin{array}{c}{A}_x^{\left(C\right)}\left(t\right)\\ A_y^{\left(C\right)}\left(t\right)\end{array}\right]=\frac{{\mathcal{E}}_0}{\omega }\left[\begin{array}{c}cos\left(\omega t\right)\\ sin\left(\omega t\right)\end{array}\right],$$

(25)

for the circularly polarized light, while a limit of $\beta ⟶0$ corresponds to the dressing light of a linear polarization

$${\mathit{A}}^{\left(L\right)}\left(t\right)=\left[\begin{array}{c}{A}_x^{\left(L\right)}\left(t\right)\\ A_y^{\left(L\right)}\left(t\right)\equiv 0\end{array}\right]=\frac{{\mathcal{E}}_0}{\omega }\left[\begin{array}{c}cos\left(\omega t\right)\\ 0\end{array}\right].$$

(26)

Thus, analyzing the general elliptical polarization of the imposed irradiation allows us immediately discern the results for these crucial situations as well.

It is well-known that the energy dispersions of the electron dress states due to an off-resonant dressing field are obtained by applying the canonical substitution

$$k_{x,y}\to k_{x,y}-\frac{e}{\hslash }{A}_{x,y}\left(t\right)$$

(27)

in the Hamiltonian (1), which corresponds to a non-irradiated material. Consequently, Equation (1)

$${\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)⟹{\widehat{\mathcal{H}}}^{\left(e\right)}(\mathit{k},t|\tau ,\varphi )\equiv {\widehat{\mathbb{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)+{\widehat{\mathcal{H}}}_A^{\left(e\right)}\left(t\right|\tau ,\varphi ),$$

(28)

receives an additional interaction Hamiltonian term

$$\begin{array}{ccc}\hfill & & {\widehat{\mathcal{H}}}_A^{\left(e\right)}\left(t\right|\tau ,\varphi )=-\frac{\tau c_0}{\sqrt{{cos}^2\omega t+{\left[\beta sin\omega t\right]}^2}}\hfill \\ \hfill & \times & \left\{\begin{array}{ccc}0& cos\varphi \mathtt{exp}\left[-i\tau \Phi (\beta ,t)\right]& 0\\ cos\varphi \mathtt{exp}\left[i\tau \Phi (\beta ,t)\right]& 0& sin\varphi \mathtt{exp}\left[-i\tau \Phi (\beta ,t)\right]\\ 0& sin\varphi \mathtt{exp}\left[i\tau \Phi (\beta ,t)\right]& 0\end{array}\right\},\hfill \end{array}$$

(29)

where

$$\Phi (\beta ,t)={tan}^{-1}\left[\beta tan\left(\omega t\right)\right]\underset{\beta \to 1}{\underbrace{⟹}}\omega t,$$

(30)

which corresponds to circularly polarized light. Parameter $c_0=e{\mathcal{E}}_0{v}_F/\omega$, which specifies the strength of the interaction between an electron and a photon, has a unit of energy. This interaction strength parameter is the same for irradiation with different types of polarization, meaning that the irradiation of a specific intensity and frequency affects the electronic band structure of graphene (and $\alpha -{\mathcal{T}}_3$ material) at the same level, regardless of its polarization. The way in which the dispersions are affected is obviously very different for the various types of polarizations. For our future calculations, we also need another type of coupling parameter ${\lambda }_0=c_0/\hslash \omega$, which is dimensionless in contrast to the previously considered $c_0$. For the considered off-resonance regime, we can assume ${\lambda }_0\ll 1$, which will be used later as a series expansion parameter.

To summarize, all our considered parameters could be presented in the following table.

Two-dimensional electron wave vector $\mathit{k}=(k_x,k_y)$, $k_{\pm }^{\tau }=\tau k_x\pm i{k}_y=\tau k{\mathtt{e}}^{i\tau {\theta }_{\mathbf{k}}}$, valley index $\tau =\pm 1$, ${\theta }_{\mathbf{k}}={tan}^{-1}(k_y/k_x)$, phase $\varphi$, relative hopping parameter $\alpha =tan\varphi$, Fermi velocity $v_F$	Related to the considered material/lattice
Electric field amplitude ${\mathcal{E}}_0$, irradiation frequency $\omega$	Related to the applied irradiation
Strength of the interaction between an electron and irradiation $c_0=e{\mathcal{E}}_0{v}_F/\omega$, dimensionless electron–photon coupling parameter ${\lambda }_0$	Combined

The key idea for using the Floquet–Magnus perturbation approach is as follows. First, we rewrite the interaction Hamiltonian term ${\mathbb{H}}_A^{\left(e\right)}\left(t\right|\tau ,\varphi )$ in the form of two time-independent complimentary conjugate terms:

$${\widehat{\mathbb{H}}}_A^{\left(e\right)}\left(t\right|\tau ,\varphi )={\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}{\mathtt{e}}^{i\omega t}+\mathrm{H}.\mathrm{c}.={\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}{\mathtt{e}}^{i\omega t}+{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}\right]}^{†}{\mathtt{e}}^{-i\omega t},$$

(31)

where +H.c. means Hermitian conjugate. Operator ${\widehat{\mathbb{O}}}_{\tau ,\varphi }$ and its Hermitian conjugate ${\widehat{\mathbb{O}}}_{\tau ,\varphi }^{†}$ are time-independent.

Comparing Hamiltonian (29) and representation (31), we can immediately derive the explicit form of the perturbation operator ${\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}$ as

$${\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}=-\frac{c_0}{2}\left[\begin{array}{ccc}0& cos\varphi (\tau -\beta )& 0\\ cos\varphi (\tau +\beta )& 0& sin\varphi (\tau -\beta )\\ 0& sin\varphi (\tau +\beta )& 0\end{array}\right].$$

(32)

Once this is completed, the effective time-independent Hamiltonian representing our dressed-state system is presented as

$$\begin{array}{ccc}\hfill & & {\widehat{\mathcal{H}}}_{\mathrm{eff}}^{\left(e\right)}(\mathit{k},t|\tau ,\varphi )={\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)\hfill \\ \hfill & +& \frac{1}{\hslash \omega }{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathbb{O}}}_{\tau ,\varphi }^{†}\right]}_{-}+\frac{1}{2{(\hslash \omega )}^2}\left\{{\left[{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)\right]}_{-},{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}\right]}_{-}+\mathrm{H}.\mathrm{c}.\right\}+\cdots ,\hfill \end{array}$$

(33)

where ${[\widehat{A},\widehat{B}]}_{-}\equiv \widehat{A}\widehat{B}-\widehat{B}\widehat{A}$ is a commutator. Since in our consideration of the off-resonance regime ${\lambda }_0\ll 1$, it is sufficient to take into consideration only the first few terms of expansion (33).

The matrix in Equation (32) is not Hermitian for any $\beta >1$, which is true for any type of light polarization except the linear one but includes circularly polarized irradiation corresponding to $\beta =1$. However, it is purely real for all types of Dirac materials with chiral terms $k_{\tau }^{\pm }=\tau k_x-i{k}_y$ in Hamiltonian (1), for both a zero or finite bandgap ${\Delta }_0$.

The zero-order term in expansion (33) must be equivalent to Hamiltonian (1) of an $\alpha -{\mathcal{T}}_3$ material in the absence of the dressing field. The next $\backsim c_0{\lambda }_0$ term is evaluated as

$$\frac{1}{\hslash \omega }{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathbb{O}}}_{\tau ,\varphi }^{†}\right]}_{-}=-c_0{\lambda }_0\tau \beta {\widehat{\Sigma }}_z\left(\varphi \right)=-c_0{\lambda }_0\tau \beta \left[\begin{array}{ccc}{cos}^2\varphi & 0& 0\\ 0& -cos2\varphi & 0\\ 0& 0& -{sin}^2\varphi \end{array}\right],$$

(34)

whose structure is equivalent to that of the bandgap term (16).

This unexpected result reveals a lot of interesting features of the electron dressed states for the circular and elliptical polarizations of the dressing field. Most importantly, we know that the term in Equation (34) mainly determines the bandgap of the radiated $\alpha -{\mathcal{T}}_3$ materials since it does not depend on the wave vector components $k_x$ and $k_y$. It represents the key contribution to the energy dispersions at $\mathbf{k}=0$ since the next term $\backsim {\lambda }_0^2$ would only result in a much smaller correction. Therefore, we find that for linearly polarized light with $\beta =0$, the bandgap remains completely unaffected by the dressing field.

The gap due to circular polarized light is mainly formed in the same way as the initial bandgap ${\Delta }_0$, which is induced by a specific substrate. However, there is a very important difference: the irradiation-induced bandgap in Equation (34) is proportional to the valley index $\tau =1$. Therefore, the total bandgap of the irradiated $\alpha -{\mathcal{T}}_3$ materials could be either increased or decreased, depending on whether we are considering the electronic states in the K or $K^{\prime }$ valley ($\tau =\pm 1$).

After carrying out the commutation relation in Equation (33), we arrive at the following expression for the effective perturbation Hamiltonian up to the order of $\mathcal{O}\left({\lambda }_0^2\right)$

$$\begin{array}{ccc}\hfill & & \frac{1}{2{(\hslash \omega )}^2}\left\{{\left[{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)\right]}_{-},{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}\right]}_{-}+\mathrm{H}.\mathrm{c}.\right\}\hfill \\ \hfill & =& -\frac{\tau }{4}\hslash v_F{\lambda }_0^2\left[\begin{array}{ccc}{d}_1^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )& h_{12}\left(\mathit{k}\right|\tau ,\varphi )& o_{\beta }\left({\Delta }_0\right|\varphi )\\ h_{12}^{*}\left(\mathit{k}\right|\tau ,\varphi )& d_2^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )& h_{23}\left(\mathit{k}\right|\tau ,\varphi )\\ o_{\beta }^{*}\left({\Delta }_0\right|\varphi )& h_{23}^{*}\left(\mathit{k}\right|\tau ,\varphi )& d_3^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )\end{array}\right],\hfill \end{array}$$

(35)

where

$$h_{12}\left(\mathit{k}\right|\tau ,\varphi )=cos\varphi \left[1+3cos\left(2\varphi \right)\right]({\beta }^2{k}_x-i\tau k_y),$$

(36)

$$h_{23}\left(\mathit{k}\right|\tau ,\varphi )=sin\varphi \left[1-3cos\left(2\varphi \right)\right]({\beta }^2{k}_x-i\tau k_y),$$

(37)

$$d_1^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )=\left(1+{\beta }^2\right){\Delta }_0{cos}^2\varphi \left[1+3cos\left(2\varphi \right)\right],$$

(38)

$$d_2^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )=-4\left(1+{\beta }^2\right){\Delta }_{0}cos\left(2\varphi \right),$$

(39)

$$d_3^{\left(\beta \right)}\left({\Delta }_0\right|\varphi )=-\left(1+{\beta }^2\right){\Delta }_0{sin}^2\varphi \left[1-3cos\left(2\varphi \right)\right],$$

(40)

and, finally,

$$o_{\beta }\left({\Delta }_0\right|\varphi )=-\frac{3}{4}\left(1-{\beta }^2\right){\Delta }_{0}sin\left(4\varphi \right),$$

(41)

which would vanish for a circularly polarized light $(\beta =1)$, as well as for graphene $(\varphi =0)$ and a dice lattice $(\varphi =\frac{\pi }{4})$.

Dressed States for a Lieb Lattice

We apply canonical substitution (27) so that Hamiltonian (19) has an additional interaction term

$${\widehat{\mathcal{H}}}_A^{\left(e\right)}\left(t\right|\tau ,\varphi )=-c_0\left[\begin{array}{ccc}0& cos\left(\omega t\right)& 0\\ cos\left(\omega t\right)& 0& sin\left(\omega t\right)\\ 0& sin\left(\omega t\right)& 0\end{array}\right],$$

(42)

Comparing the Hamiltonian in Equation (19) with the representation in Equation (31), we immediately derive an explicit form for the perturbation operator ${\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}$ as

$${\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}=-\frac{c_0}{2}\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& -i\\ 0& -i& 0\end{array}\right].$$

(43)

$$\frac{1}{\hslash \omega }{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathbb{O}}}_{\tau ,\varphi }^{†}\right]}_{-}=c_0{\lambda }_0\beta \left[\begin{array}{ccc}0& 0& 2i\\ 0& 0& 0\\ -2i& 0& 0\end{array}\right].$$

(44)

The second-order correction for a Lieb lattice is calculated in the following way:

$$\begin{array}{ccc}\hfill & & \frac{1}{2{(\hslash \omega )}^2}\left\{{\left[{\left[{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)},{\widehat{\mathcal{H}}}_{\tau }^{\varphi }\left(\mathit{k}\right)\right]}_{-},{\widehat{\mathbb{O}}}_{\tau }^{\left(\varphi \right)}\right]}_{-}+\mathrm{H}.\mathrm{c}.\right\}\hfill \\ \hfill & =& -\hslash v_F{\lambda }_0^2\left[\begin{array}{ccc}2k_{\Delta }& \frac{q_x}{2}& 0\\ \frac{q_x}{2}& -4k_{\Delta }& \frac{q_y}{2}\\ 0& \frac{q_y}{2}& 2k_{\Delta }\end{array}\right],\hfill \end{array}$$

(45)

Similar to the previously considered $\alpha -{\mathcal{T}}_3$ model, the term in Equation (45) represents a ${\lambda }_0^2$ correction, which is small in the off-resonance regime ${\lambda }_0\ll 1$.

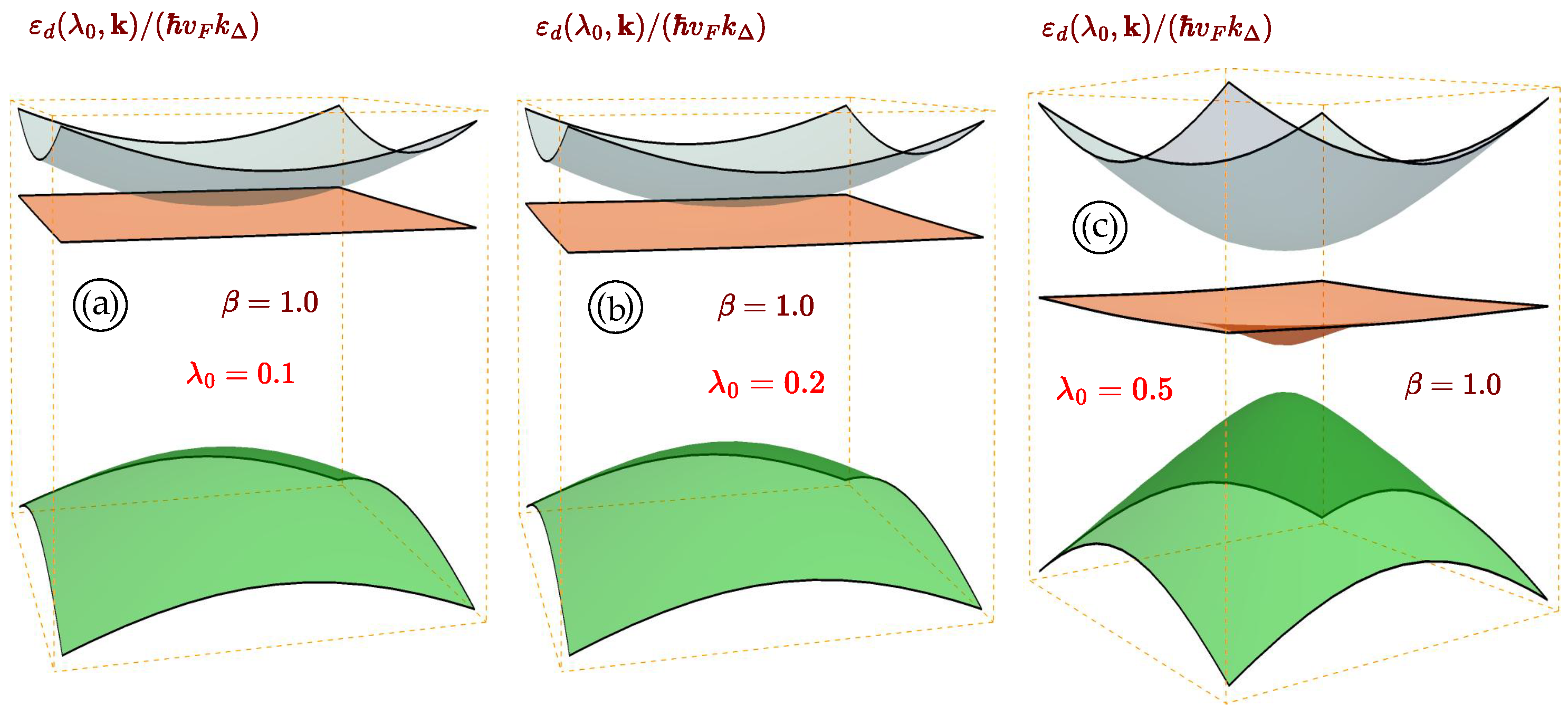
4. Results and Discussion

Our main goal is to investigate the band structure of the electron dressed states for the $\alpha -{\mathcal{T}}_3$ materials with a finite gap, i.e., to understand how the existing gaps are modified or renormalized due to the elliptically polarized dressing field.

First, we find that according to Equation (34), which demonstrates how in principle the bandgap is created for ${\lambda }_0\ll 1$, the structure of the gap induced by the dressing field is, like the existing gap, given by Equation (13). However, an important difference between the two types of gap is that the irradiation-induced gap directly depends on the valley index $\tau$, and it is opposite for the K and $K^{\prime }$ valleys. Therefore, the results of the two valleys are exactly opposite, and the same initial gap could be either decreased or increased depending on the value of $\tau =\pm 1$. This is exactly what we see when comparing the upper and the lower panels of Figure 3, Figure 4 and Figure 5.

In our calculations, the following system of units was employed. All the energy values, including bandgap ${\Delta }_0$, are measured in terms of a typical graphene Fermi energy $E_F^{\left(0\right)}$, which is obtained as $E_F^{\left(0\right)}=\hslash v_F{k}_F^{\left(0\right)}$. Here, $k_F^{\left(0\right)}$ is the corresponding Fermi momentum, which is also a reciprocal to our unit of length $1/\left[L_0\right]$; $n_0$ and $v_F$ denote the areal electron doping density and the Fermi velocity, respectively. Thus, for a typical density $n_0\backsim {10}^{11}$ cm⁻², we obtain $k_F^{\left(0\right)}\backsimeq 8.0\times {10}^7$ m⁻¹, $L_0\backsimeq {10}^{-8}$ m and $E_F^{\left(0\right)}\backsim 7.5\times {10}^{-21}J\backsimeq 50$ meV.

Our numerical results, which are presented in Figure 3, demonstrate how a finite bandgap is opened for an initially gapless $\alpha -{\mathcal{T}}_3$ material, as it is always expected due to the circularly polarized dressing field. In contrast, the change in the existing bandgap presented in Figure 4 substantially depends on the electron–light coupling parameter ${\lambda }_0$, the initial bandgap ${\Delta }_0$, phase $\varphi$, and the valley index $\tau$. We note that the bandgaps and the dispersions of the dressed state subbands could be modified in completely different ways, depending on the material parameters of a specific $\alpha -{\mathcal{T}}_3$ lattice.

Importantly, we also reveal a substantial dependence of the irradiation-induced bandgap on the phase $\varphi$. For the specific situation demonstrated in Figure 5 with the initial bandgap ${\Delta }_0=1.0$, we see that both gaps are significantly increased for the larger values of $\varphi$, just like the equivalence (the differences) between the two gaps.

The dressing field of elliptical polarization with $\beta <1$ (in contrast to circularly polarized light with $\beta =1$) is expected to induce finite anisotropy and an angular dependence of the initially isotropic dispersions with a circular constant-energy cut. This is exactly what we see in Figure 6. However, we also note that the obtained elliptical dispersions significantly depend on the phase $\varphi$. Both the shape and size of the constant-energy cut of the electron dressed state energy dispersions are changed more significantly for larger values of $\varphi$ or relative hopping parameter $\alpha$.

The way in which the energy dispersions of the dressed states are formed in a Lieb lattice is drastically different from that for the gapped $\alpha -{\mathcal{T}}_3$ materials. First, we have fewer parameters to consider here. The bandgap and the exact locations of the energy subbands of a non-irradiated lattice are fixed, and the main question here is whether once the dressing field is imposed, the flat band would remain flat, like in a dice lattice, or receive a finite curvature, just as we observed for the general $\alpha -{\mathcal{T}}_3$ model with $0<\alpha <1$.

Our numerical results, presented in Figure 7 and Figure 8, clearly demonstrate that the flat band receives a finite dispersion and its convex-concave type of curvature does not remain the same. Therefore, for any finite value of the coupling parameter ${\lambda }_0>0$, the subbands cannot be described by the parabolic dispersions obtained using a constant-mass approximation. Moreover, for a large $\lambda =0.9$, the former-flat band’s location is such that its energy could only decrease for larger values of the wave vector k (see Figure 8).

The degeneracy at $\mathbf{k}=\mathbf{0}$ is clearly lifted, and we observe three inequivalent bandgaps between the valence, flat, and conduction bands. The locations of the valence and conduction bands also change. Each of the two gaps is decreased, and the k-dependence becomes more significant. The situation becomes very different for a large $\lambda =0.9$, for which we find that all three subbands demonstrate low dispersions (reduced dependence on k), while each of the gaps is significantly modified.

5. Summary and Remarks

In this paper, we carried out a rigorous theoretical and numerical investigation into the effects arising from the electron–photon interaction. In particular, we examine the resulting electron dressed states for some specific types of Dirac cone materials. It is worth noting that their low-energy spectrum exhibits a flat band and a finite bandgap.

We consider that an electron in a two-dimensional material is irradiated with a high-frequency off-resonance dressing field. In this case, its interaction with the irradiation results in a specific unified quantum state with modified energy dispersions and bandgaps. The properties of the obtained dressed states strongly depend on the type of polarization of the imposed radiation. Whereas a linearly polarized dressing field is known to induce finite anisotropy, circularly polarized light is considered a tool to open or modify the existing energy gap.

Creating and analyzing new electronic states which appear as a consequence of electron–light interaction have significant applications in several areas of physics. Specifically, these include electron conductance and quantum transport. It is evident that a new type of electronic band structures and a new structure of electron transition between the valence, conduction, and middle bands lead to significantly novel electronic properties of a lattice and create several opportunities for device applications. It is of interest to examine the thermal dependence of the electronic conductivity and Boltzmann transport over certain temperature ranges. A novel electronic band structure may potentially lead to a smaller increase in the resistivity due to the temperature which is crucial for electronic nanodevices.

Our main goal was to consider the modification or renormalization of the existing bandgaps of pseudospin-1 Dirac cone materials with a flat band. Specifically, we focused on the gapped $\alpha -{\mathcal{T}}_3$ model, a dice lattice, and a Lieb lattice. Each of these materials has a very distinguished energy band structure. However, their common feature is the existence of a dispersionless flat band, as well as finite gaps between the valence, flat, and conduction bands.

We emphasize that our work is the suject of a theoretical and numerical study of the dressed states in a class of materials. We also present the derivation of several crucial analytical relations for the energy dispersions in the presence of circularly and elliptically polarized light. We have demonstrated that the existing bandgap could be either increased or decreased depending on several material parameters of the specific lattice and the valley index.

By applying circularly and elliptically polarized irradiation to various pseudospin-1 lattices with a flat band and finite bandgap, we achieved several very specific types of electron band structures. We found that the flat band could receive a finite dispersion, and its location also changes. The two remaining valence and conduction bands are also affected differently for each type of material. Either one or both bandgaps could be increased or decreased. Finite anisotropy could also be induced by elliptically polarized light. Therefore, we created and described absolutely new band structures and electron transitions. These could generate strong interest for researchers in different fields of physics and electronics.