Pore Water Pressure Prediction Based on Machine Learning Methods—Application to an Earth Dam Case
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
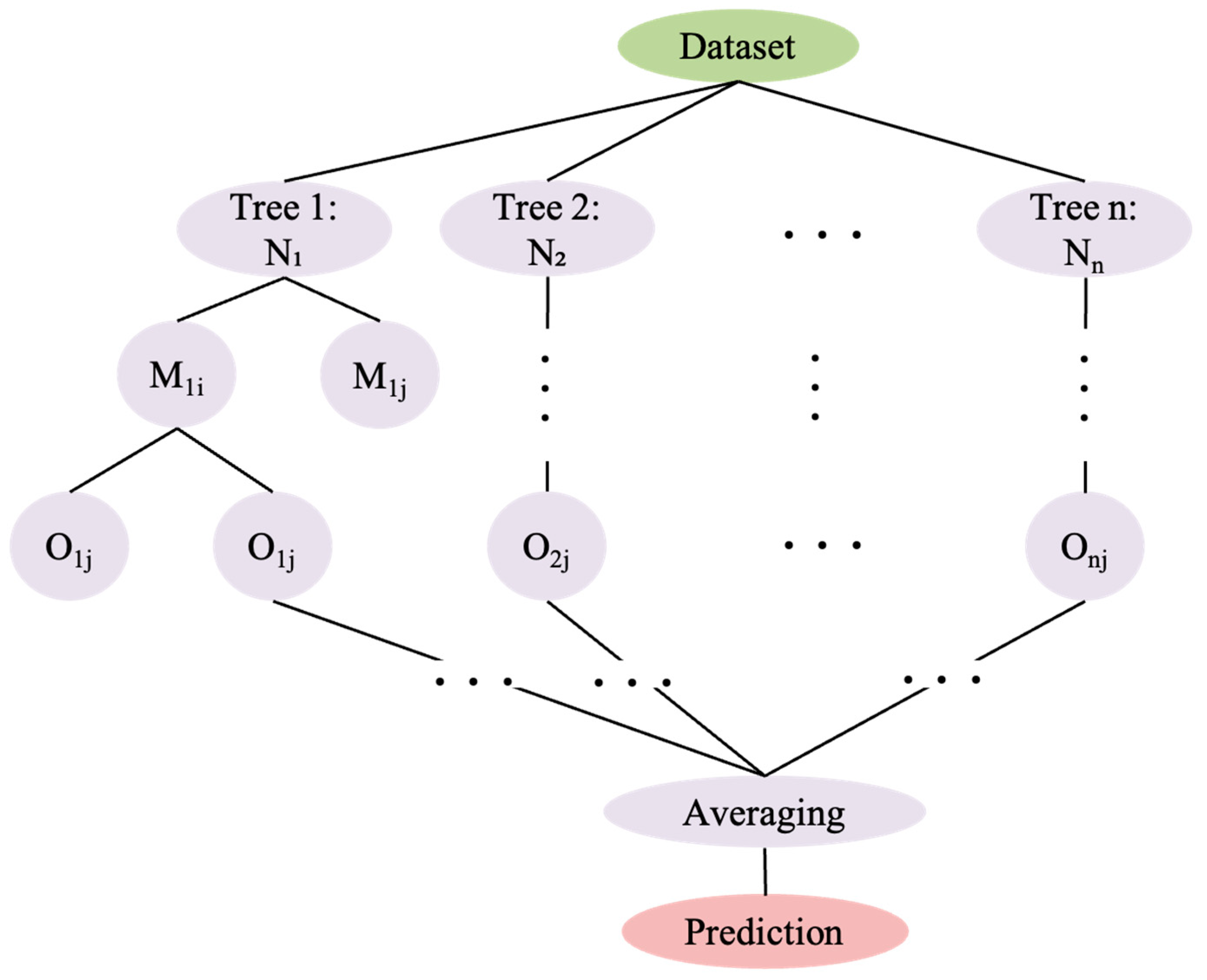
2.1. Random Forests Combined with Simulated Annealing
2.1.1. Random Forest
2.1.2. Simulated Annealing
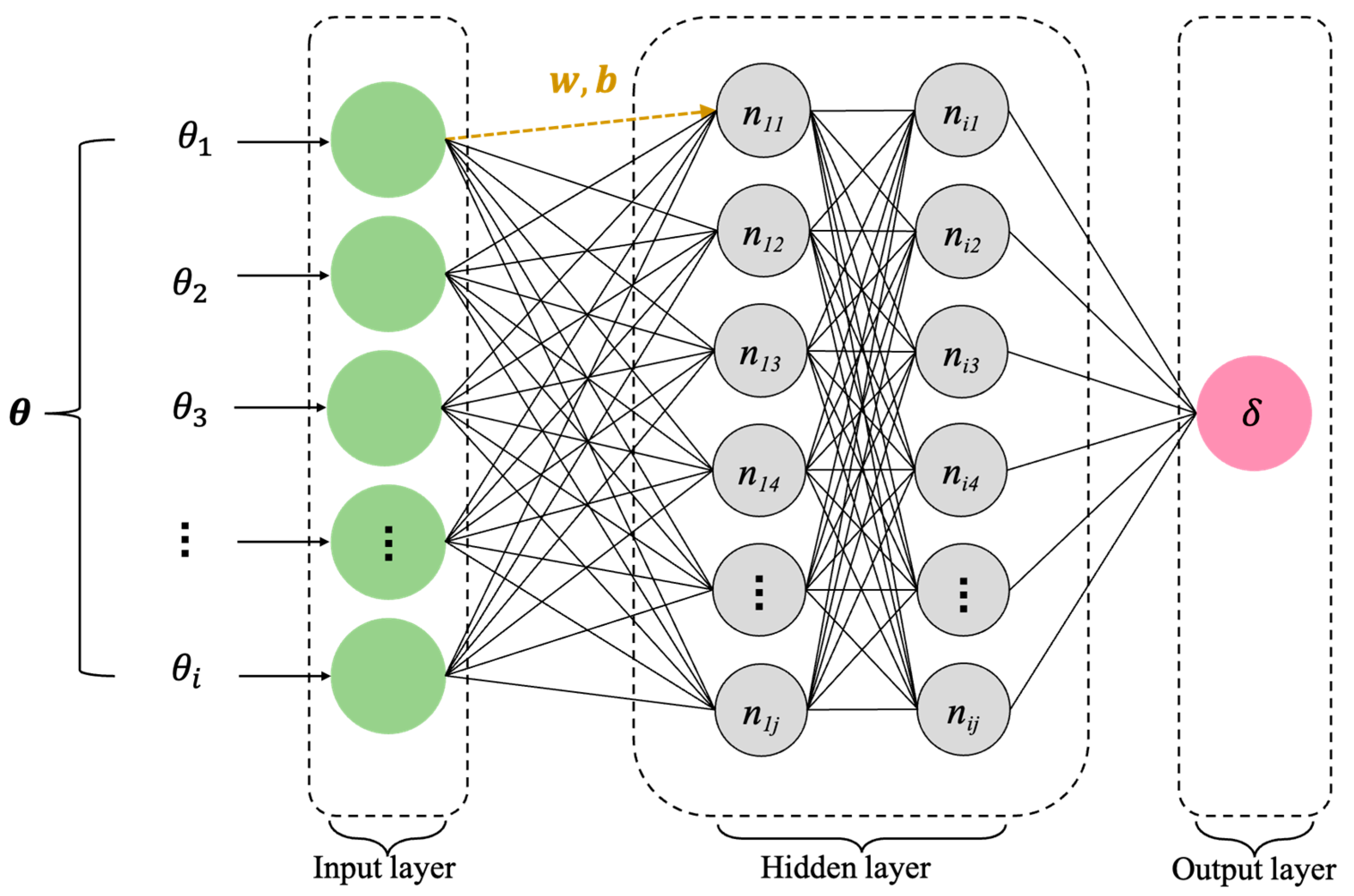
2.2. Artificial Neural Networks
2.2.1. Static Neural Network: Multilayer Perceptron
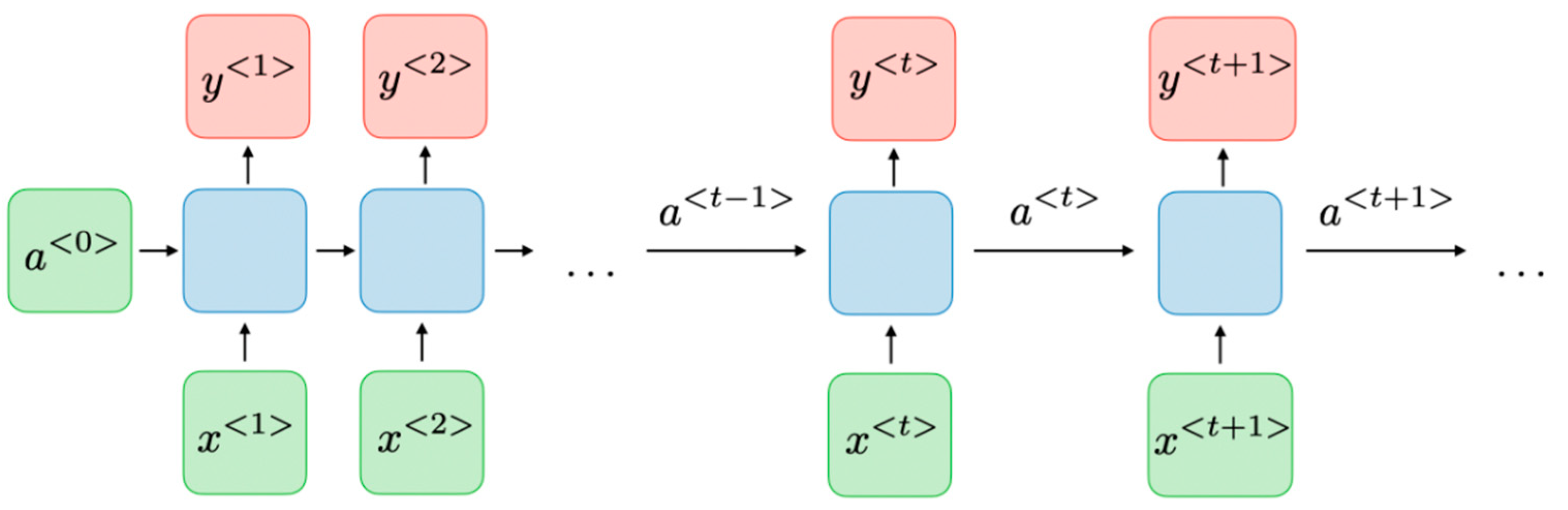
2.2.2. Dynamic Neural Network
The Standard Recurrent Neural Networks
The Gated Recurrent Unit
2.3. Optimization Methods
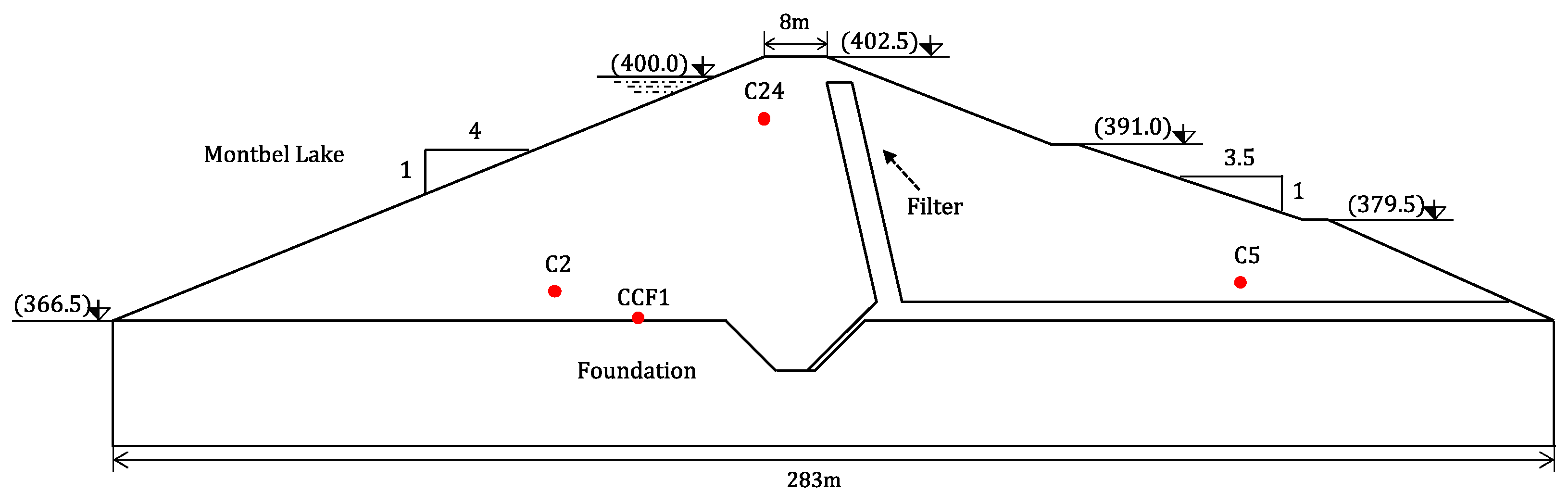
3. Application Case: Montbel Dam, an Existing Earth Dam
3.1. Description of the Case Study
3.2. Dataset Preparation
3.3. Development of Machine Learning Models
4. Results and Discussion
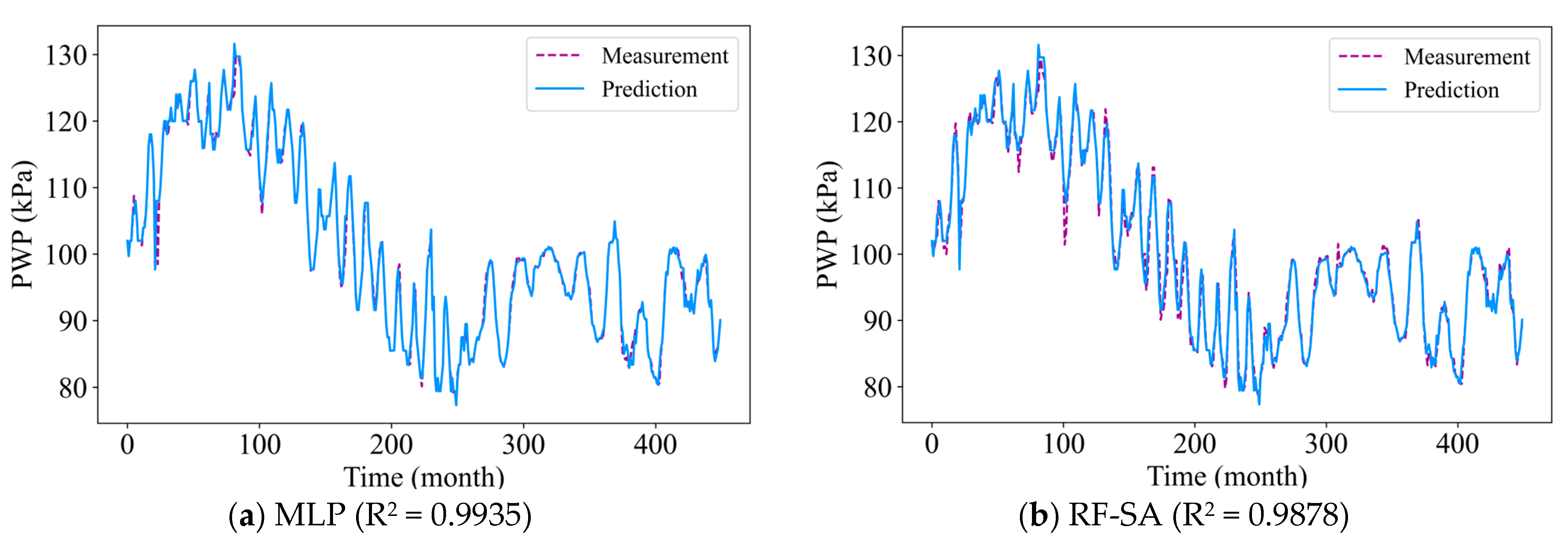
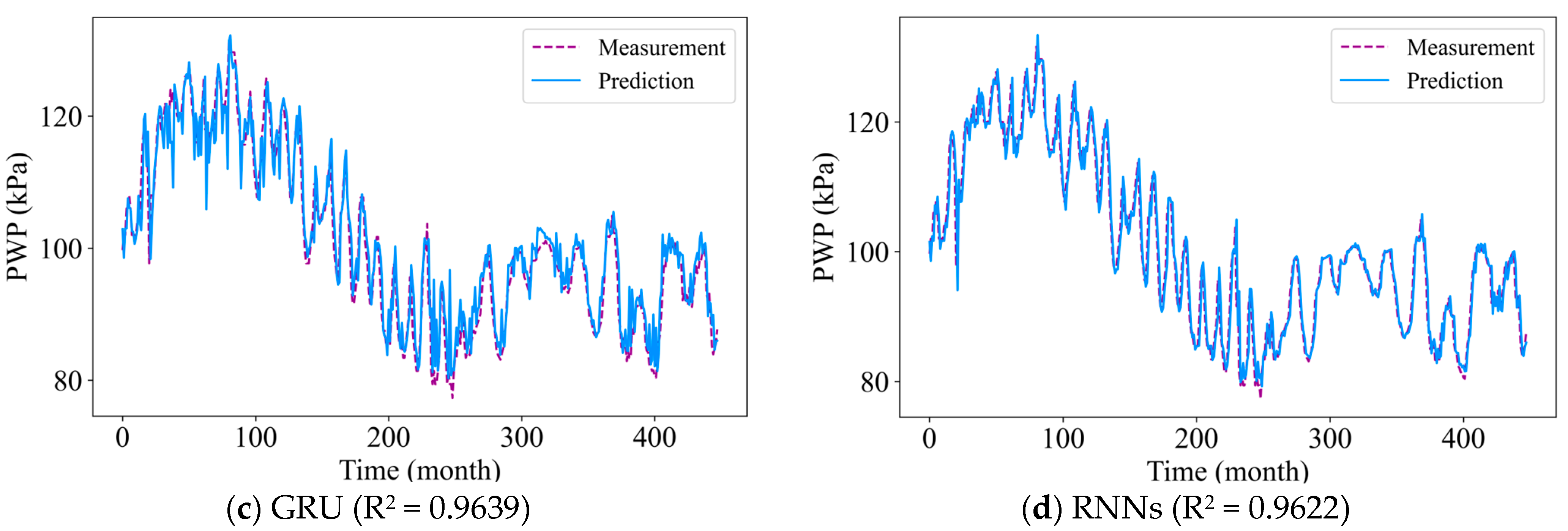
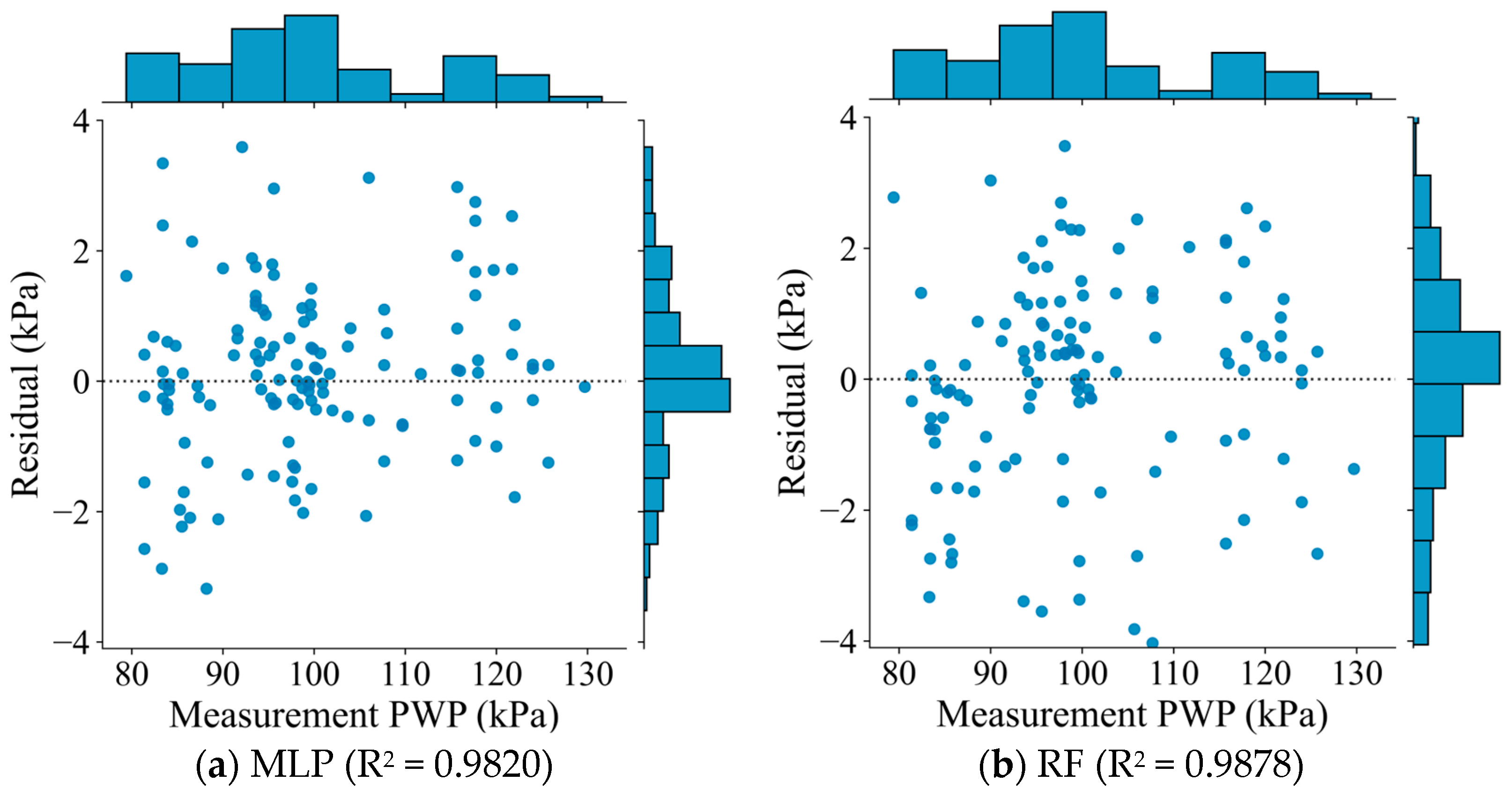
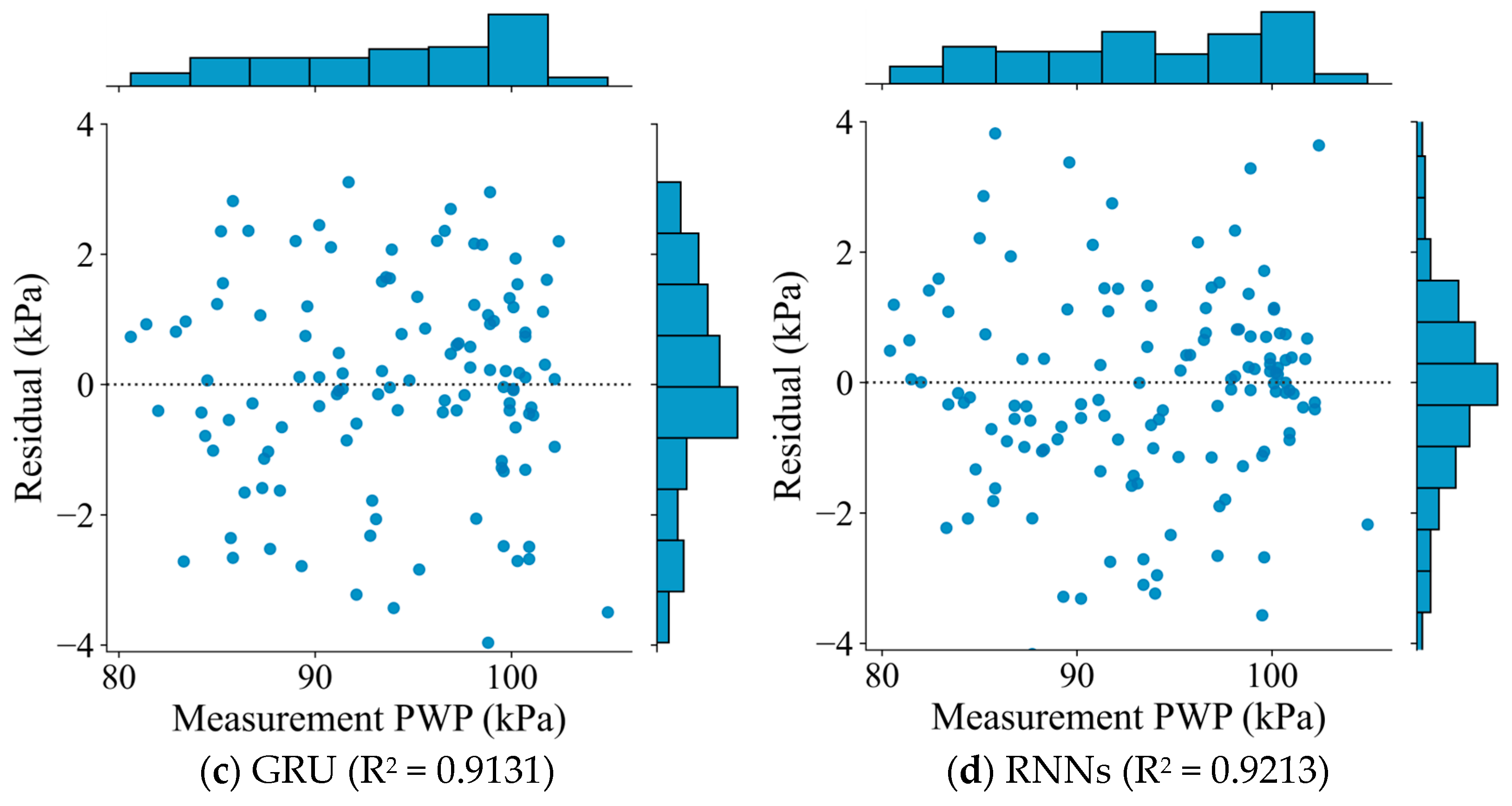
4.1. Model Performance and Comparison
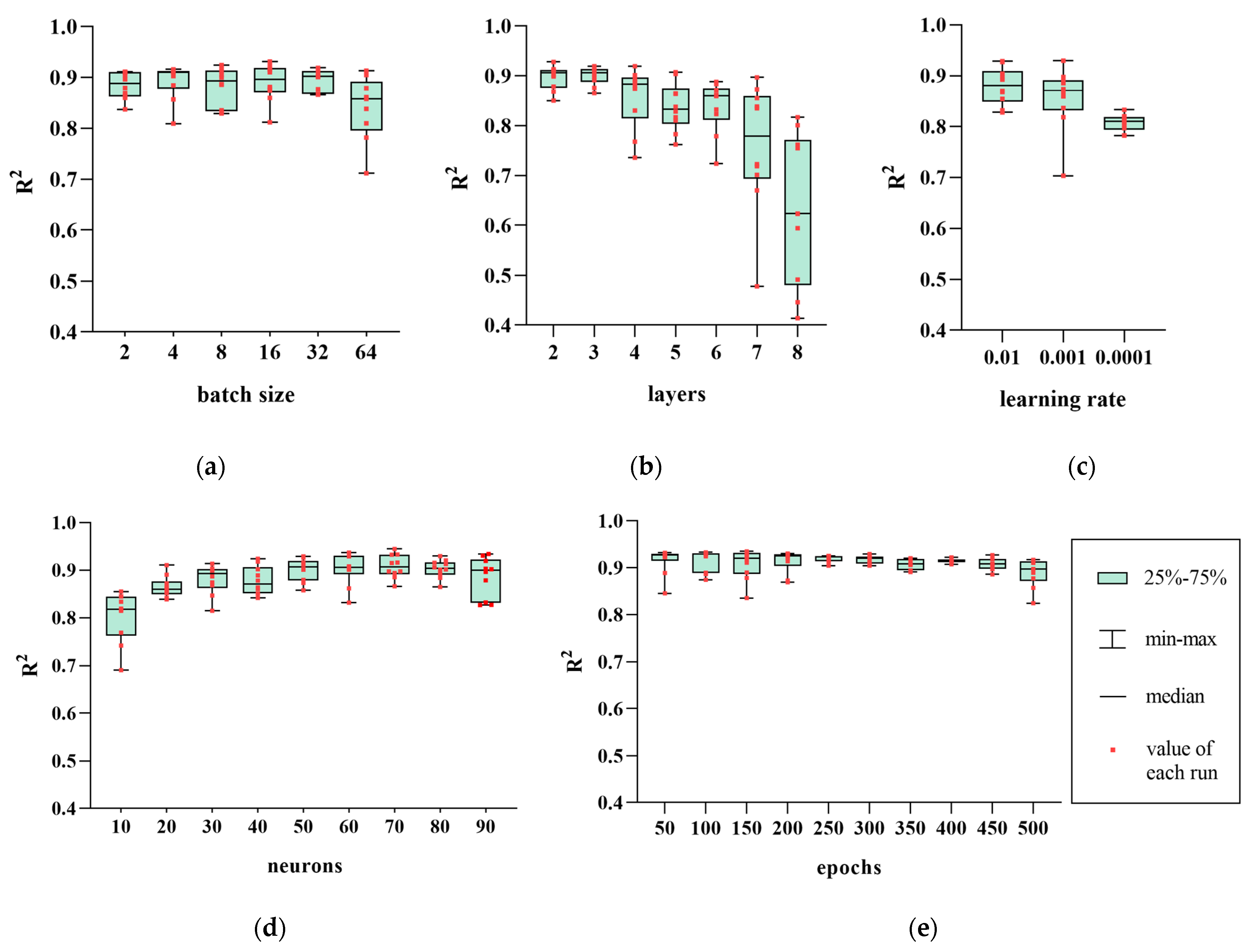
4.2. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdel-Ghaffar, A.M.; Scott, R.F. Analysis of Earth Dam Response to Earthquakes. J. Geotech. Eng. 1979, 105, 1379–1404. [Google Scholar] [CrossRef]
- Fattah, M.; Omran, H.; Hassan, M. Behavior of an Earth Dam during Rapid Drawdown of Water in Reservoir—Case Study. Int. J. Adv. Res. 2015, 3, 110–122. [Google Scholar]
- Wei, X.; Zhang, L.; Yang, H.-Q.; Zhang, L.; Yao, Y.-P. Machine learning for pore-water pressure time-series prediction: Application of recurrent neural networks. Geosci. Front. 2021, 12, 453–467. [Google Scholar] [CrossRef]
- Guo, X.; Baroth, J.; Dias, D.; Simon, A. An analytical model for the monitoring of pore water pressure inside embankment dams. Eng. Struct. 2018, 160, 356–365. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Liu, H.W.; Feng, S. Analytical solutions for calculating pore-water pressure in an infinite unsaturated slope with different root architectures. Can. Geotech. J. 2015, 52, 1981–1992. [Google Scholar] [CrossRef]
- Mouyeaux, A.; Carvajal, C.; Bressolette, P.; Peyras, L.; Breul, P.; Bacconnet, C. Probabilistic analysis of pore water pressures of an earth dam using a random finite element approach based on field data. Eng. Geol. 2019, 259, 105190. [Google Scholar] [CrossRef]
- Venkatesh, K.; Karumanchi, S.R. Distribution of pore water pressure in an earthen dam considering unsaturated-saturated seepage analysis. E3S Web Conf. 2016, 9, 19004. [Google Scholar] [CrossRef]
- Tufano, R.; Formetta, G.; Calcaterra, D.; De Vita, P. Hydrological control of soil thickness spatial variability on the initiation of rainfall-induced shallow landslides using a three-dimensional model. Landslides 2021, 18, 3367–3380. [Google Scholar] [CrossRef]
- de Granrut, M.; Simon, A.; Dias, D. Artificial neural networks for the interpretation of piezometric levels at the rock-concrete interface of arch dams. Eng. Struct. 2019, 178, 616–634. [Google Scholar] [CrossRef]
- Anello, M.; Bittelli, M.; Bordoni, M.; Laurini, F.; Meisina, C.; Riani, M.; Valentino, R. Robust Statistical Processing of Long-Time Data Series to Estimate Soil Water Content. Math. Geosci. 2024, 56, 3–26. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation. Eng. Geol. 2012, 133–134, 30–39. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Statistics of Free Surface Flow through Stochastic Earth Dam. J. Geotech. Eng. 1996, 122, 427–436. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Computat. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef]
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2020, 27, e2501. [Google Scholar] [CrossRef]
- Makasis, N.; Narsilio, G.A.; Bidarmaghz, A. A machine learning approach to energy pile design. Comput. Geotech. 2018, 97, 189–203. [Google Scholar] [CrossRef]
- Habibagahi, G.; Bamdad, A. A neural network framework for mechanical behavior of unsaturated soils. Can. Geotech. J. 2003, 40, 684–693. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, R.H.; Wang, W.; Wang, L.; Liu, H.L.; Zhang, W.G. Numerical study of the effects of groundwater drawdown on ground settlement for excavation in residual soils. Acta Geotech. 2020, 15, 1259–1272. [Google Scholar] [CrossRef]
- Huang, F.-K.; Wang, G.S. ANN-based Reliability Analysis for Deep Excavation. In Proceedings of the EUROCON 2007-The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 2039–2046. [Google Scholar] [CrossRef]
- Lu, Q.; Chan, C.L.; Low, B. Probabilistic evaluation of ground-support interaction for deep rock excavation using artificial neural network and uniform design. Tunn. Undergr. Space Technol. 2012, 32, 1–18. [Google Scholar] [CrossRef]
- Demirkaya, S.; Balcilar, M. The Contribution of Soft Computing Techniques for the Interpretation of Dam Deformation. In Proceedings of the FIG Working Week, Roma, Italy, 6–12 May 2012. [Google Scholar]
- Su, H.; Chen, Z.; Wen, Z. Performance improvement method of support vector machine-based model monitoring dam safety: Performance Improvement Method of Monitoring Model of Dam Safety. Struct. Control Health Monit. 2016, 23, 252–266. [Google Scholar] [CrossRef]
- Bouayad, D.; Emeriault, F. Modeling the relationship between ground surface settlements induced by shield tunneling and the operational and geological parameters based on the hybrid PCA/ANFIS method. Tunn. Undergr. Space Technol. 2017, 68, 142–152. [Google Scholar] [CrossRef]
- Puri, N.; Prasad, H.D.; Jain, A. Prediction of Geotechnical Parameters Using Machine Learning Techniques. Procedia Comput. Sci. 2018, 125, 509–517. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.; Santillan, D. Analysis of dam beaviour by statistical models: Application of the random forest approach. KSCE J. Civ. Eng. 2011, 23, 4800–4811. [Google Scholar] [CrossRef]
- Mata, J. Interpretation of concrete dam behaviour with artificial neural network and multiple linear regression models. Eng. Struct. 2011, 33, 903–910. [Google Scholar] [CrossRef]
- Mata, J.; Tavares de Castro, A.; Sa da Costa, J. Constructing statistical models for arch dam deformation. Struct. Control. Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Hellgren, R.; Malm, R.; Ansell, A. Performance of data-based models for early detection of damage in concrete dams. Struct. Infrastruct. Eng. 2021, 17, 275–289. [Google Scholar] [CrossRef]
- Tinoco, J.; de Granrut, M.; Dias, D.; Miranda, T.; Simon, A.G. Piezometric level prediction based on data mining techniques. Neural Comput. Appl. 2020, 32, 4009–4024. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, B.T. Prediction of relative crest settlement of concrete-faced rockfill dams analyzed using an artificial neural network model. Comput. Geotech. 2008, 35, 313–322. [Google Scholar] [CrossRef]
- Mustafa, M.R.; Rezaur, R.B.; Saiedi, S.; Rahardjo, H.; Isa, M.H. Evaluation of MLP-ANN Training Algorithms for Modeling Soil Pore-Water Pressure Responses to Rainfall. J. Hydrol. Eng. 2013, 18, 50–57. [Google Scholar] [CrossRef]
- Mohammed, M.; Watanabe, K.; Takeuchi, S. Grey model for prediction of pore pressure change. Environ. Earth Sci. 2010, 60, 1523–1534. [Google Scholar] [CrossRef]
- Tayfur, G.; Swiatek, D.; Wita, A.; Singh, V.P. Case Study: Finite Element Method and Artificial Neural Network Models for Flow through Jeziorsko Earthfill Dam in Poland. J. Hydraul. Eng. 2005, 131, 431–440. [Google Scholar] [CrossRef]
- Beiranvand, B.; Rajaee, T. Application of artificial intelligence-based single and hybrid models in predicting seepage and pore water pressure of dams: A state-of-the-art review. Adv. Eng. Softw. 2022, 173, 103268. [Google Scholar] [CrossRef]
- El Bilali, A.; Moukhliss, M.; Taleb, A.; Nafii, A.; Alabjah, B.; Brouziyne, Y.; Mazigh, N.; Teznine, K.; Mhamed, M. Predicting daily pore water pressure in embankment dam: Empowering Machine Learning-based modeling. Environ. Sci. Pollut. Res. 2022, 29, 47382–47398. [Google Scholar] [CrossRef]
- Qin, S.; Xu, T.; Zhou, W.-H. Predicting Pore-Water Pressure in Front of a TBM Using a Deep Learning Approach. Int. J. Geomech. 2021, 21, 04021140. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Bhanot, G. The Metropolis algorithm. Rep. Prog. Phys. 1988, 51, 429–457. [Google Scholar] [CrossRef]
- Freiman, M.H. Using Random Forests and Simulated Annealing to Predict Probabilities of Election to the Baseball Hall of Fame. J. Quant. Anal. Sports 2010, 6, 1–35. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Millar, D.L.; Clarici, E.; Calderbank, P.A.; Marsden, J.R. On the practical use of a neural network strategy for the modelling of the deformability behaviour of Croslands Hill sandstone rock. In International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1995; Volume 495, pp. 457–465. [Google Scholar]
- Bre, F.; Gimenez, J.M.; Fachinotti, V.D. Prediction of wind pressure coefficients on building surfaces using artificial neural networks. Energy Build. 2018, 158, 1429–1441. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Omlin, C.W.; Giles, C.L. Constructing deterministic finite-state automata in recurrent neural networks. J. ACM 1996, 43, 937–972. [Google Scholar] [CrossRef]
- Li, S.; Li, W.; Cook, C.; Zhu, C.; Gao, Y. Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5457–5466. [Google Scholar] [CrossRef]
- Restelli, F. Systemic Evaluation of the Response of Large Dams Instrumentation. In Proceedings of the ICOLD 2013 International Symposium, Seattle, WA, USA, 12–16 August 2013. [Google Scholar]
- Cho, S.E. Probabilistic stability analysis of rainfall-induced landslides considering spatial variability of permeability. Eng. Geol. 2014, 171, 11–20. [Google Scholar] [CrossRef]
- García, S.; Ramírez-Gallego, S.; Luengo, J.; Benítez, J.M.; Herrera, F. Big data preprocessing: Methods and prospects. Big Data Anal. 2016, 1, 9. [Google Scholar] [CrossRef]
- Cavalheiro, L.P.; Bernard, S.; Barddal, J.P.; Heutte, L. Random forest kernel for high-dimension low sample size classification. Stat. Comput. 2023, 34, 9. [Google Scholar] [CrossRef]


| Parameter | Min | Max | Mean | Unit |
|---|---|---|---|---|
| Hydrostatic (H) | 382.42 | 400.27 | 394.8 | m |
| Season (S) | 0 | 6.27 | 3.118 | radian |
| Time (T) | 0 | 10,939 | 6327 | day |
| Pore water pressure (PWP) | 77.3 | 131.6 | 100.8 | kPa |
| Hyperparameters | Meanings | Value |
|---|---|---|
| n_estimators | The number of trees in the forest. | 14 |
| max_depth | The maximum depth of the tree. | 18 |
| min_samples_leaf | The minimum number of samples required to be at a leaf node. | 1 |
| random_state | The number of random seeds to ensure the same results when inputting the same number. | 11 |
| Method | MSE (kPa2) | R2 | CPU Training Time (s) | |
|---|---|---|---|---|
| MLP | Mean | 0.0087 | 0.9949 | 8.14 |
| Max | 0.0091 | 0.9935 | 10.35 | |
| Min | 0.0066 | 0.9912 | 7.12 | |
| RF | Mean | 0.021 | 0.9801 | 52.13 |
| Max | 0.0259 | 0.9878 | 96.56 | |
| Min | 0.0194 | 0.9766 | 12.34 | |
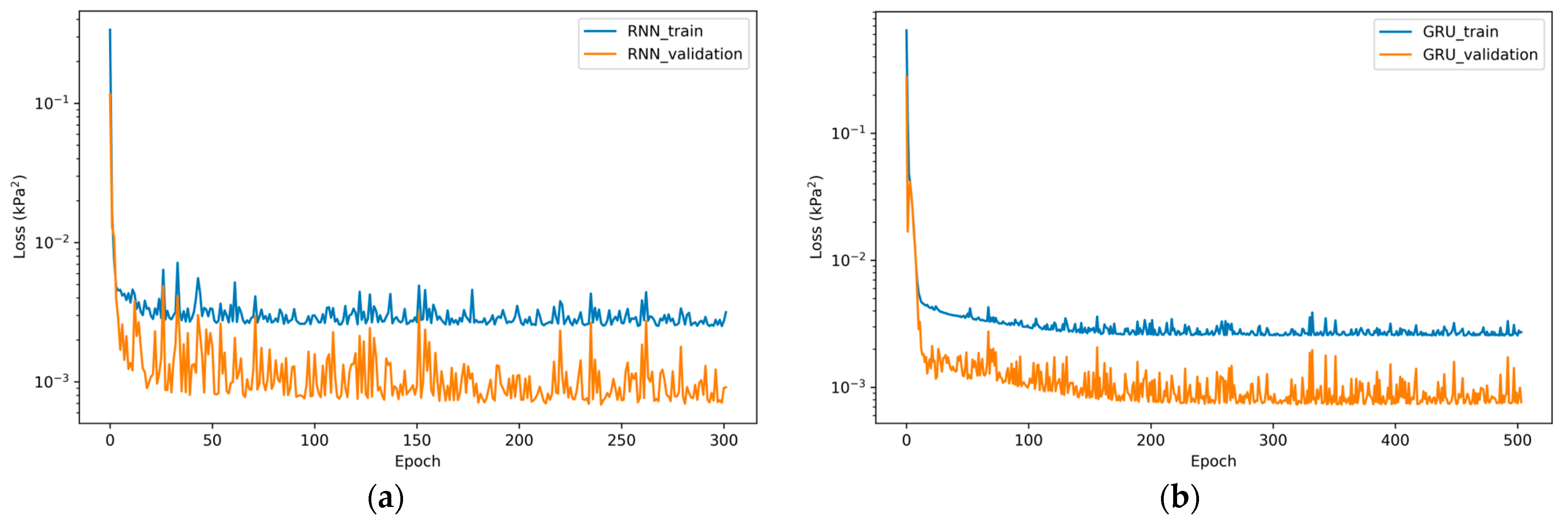
| RNNs | Mean | 0.0657 | 0.9601 | 7.22 |
| Max | 0.0799 | 0.9623 | 10.26 | |
| Min | 0.0511 | 0.9594 | 5.54 | |
| GRU | Mean | 0.0623 | 0.9689 | 27.16 |
| Max | 0.0746 | 0.9717 | 37.22 | |
| Min | 0.0435 | 0.9702 | 19.42 |
| Model | Sensor | MSE (kPa2) | R2 |
|---|---|---|---|
| 1 | C2 | 0.0292 | 0.9820 |
| 2 | C5 | 0.0051 | 0.9981 |
| 3 | C24 | 0.0040 * | 0.9034 |
| 4 | CCF1 | 0.0073 | 0.9925 |
| Hyperparameters | Meanings | Value |
|---|---|---|
| n_neurons | The number of neurons in hidden layer. | 50, 100, 150, 200, 250, 300 |
| n_layers | The number of layers in network (hidden layer and output layer). | 2, 3, 4, 5, 6, 7 |
| n_epochs | The times of the one forward pass and one backward pass of all the training examples. | 10, 20, 30, 40, 50, 60, 70, 80, 90 |
| learning_rate | The learning rate is a hyperparameter that controls how much to change the model in response to the estimated error each time the model weight is updated. | 0.01, 0.001, 0.0001 |
| batch_size | The number of training examples utilized in one iteration. | 2, 4, 8, 16, 32, 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, L.; Dias, D.; Carvajal, C.; Peyras, L.; Breul, P.; Jenck, O.; Guo, X. Pore Water Pressure Prediction Based on Machine Learning Methods—Application to an Earth Dam Case. Appl. Sci. 2024, 14, 4749. https://doi.org/10.3390/app14114749
An L, Dias D, Carvajal C, Peyras L, Breul P, Jenck O, Guo X. Pore Water Pressure Prediction Based on Machine Learning Methods—Application to an Earth Dam Case. Applied Sciences. 2024; 14(11):4749. https://doi.org/10.3390/app14114749
Chicago/Turabian StyleAn, Lu, Daniel Dias, Claudio Carvajal, Laurent Peyras, Pierre Breul, Orianne Jenck, and Xiangfeng Guo. 2024. "Pore Water Pressure Prediction Based on Machine Learning Methods—Application to an Earth Dam Case" Applied Sciences 14, no. 11: 4749. https://doi.org/10.3390/app14114749
APA StyleAn, L., Dias, D., Carvajal, C., Peyras, L., Breul, P., Jenck, O., & Guo, X. (2024). Pore Water Pressure Prediction Based on Machine Learning Methods—Application to an Earth Dam Case. Applied Sciences, 14(11), 4749. https://doi.org/10.3390/app14114749








