Vehicle Route Planning for Relief Item Distribution under Flood Uncertainty
Abstract
1. Introduction
2. Problem Formulation
2.1. Relief Items’ Distribution under Uncertainty
2.2. The Waiting Time
2.3. Mathematical Model
- n: Total number of victims.
- m: Total number of vehicles.
- : Set of victims.
- : Set of all nodes including the depot (depot indexed as 0).
- : Set of vehicles.
- : Travel time from victim i to victim j.
- : Capacity of vehicle k.
- : Demand of victim i.
- : Binary variable indicating whether vehicle k travels from victim i to victim j (1 = yes, 0 = no).
- : Continuous variable representing the waiting time for victim i to receive deliveries.
- Service Constraint. Each victim is visited exactly once by exactly one vehicle:
- Capacity Constraint. The demand of all victims served by a vehicle does not exceed its capacity:
- Flow Conservation. Ensuring vehicles leave a victim after arriving:
- Waiting Time Calculation. The waiting time for each victim takes into account the travel times from the previous victim:where M is a large number.
- Probability Constraint. Ensure that travel is only scheduled on paths with acceptable feasibility under uncertain conditions:where is the minimum acceptable probability for a path to be considered feasible. represents the probability that the road condition between nodes i and j is passable during the planning period.
- Non-Negativity and Integrality.
3. The Proposed Model
3.1. VRP-RIDFU Model
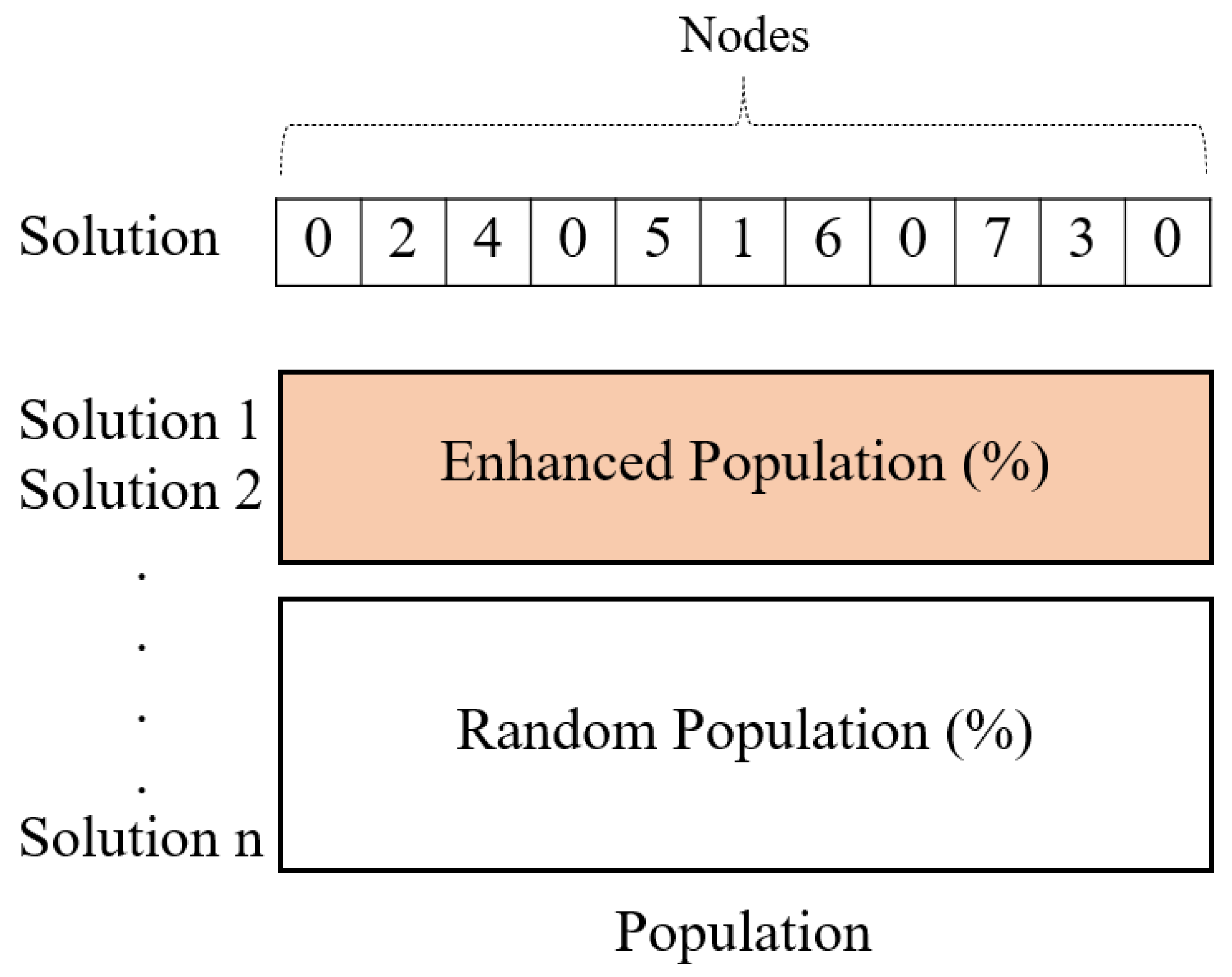
3.2. Enhanced Population
3.3. Population Sizing Module
| Algorithm 1 Generate Spatial Grid. |
| Input: List of nodes with their (x, y) coordinates |
| Output: A grid with each cell containing the count of nodes assigned to it |
| OptimizeGridDimensions(length of , , ) ▹ Call Algorithm 2 |
| Initialize an matrix with all values set to 0 |
| for each node in do |
| end for |
| Return grid |
| Algorithm 2 Optimize Grid Dimensions. |
| Input: Total number of nodes (nodes), area width (w), and height (h) |
| Output: Optimized grid dimensions (grid_w, grid_h) that best fit the area’s aspect ratio |
| while true do |
| if then |
| else |
| break |
| end if |
| end while |
| if then |
| return |
| else |
| return |
| end if |
| Algorithm 3 Analyze Distributions. |
| Input: Total number of nodes , area width , and height |
| Output: Statistical analysis of the node distribution within the grid |
| for each row in grid do |
| while do |
| Remove a zero from the row |
| Increment count by 1 |
| end while |
| end for |
3.4. EV Fitness Evaluation
3.5. CSOX
4. Experiment
4.1. Dataset and Parameter Settings
4.2. Simulation of Flood Uncertainty
5. Experimental Results
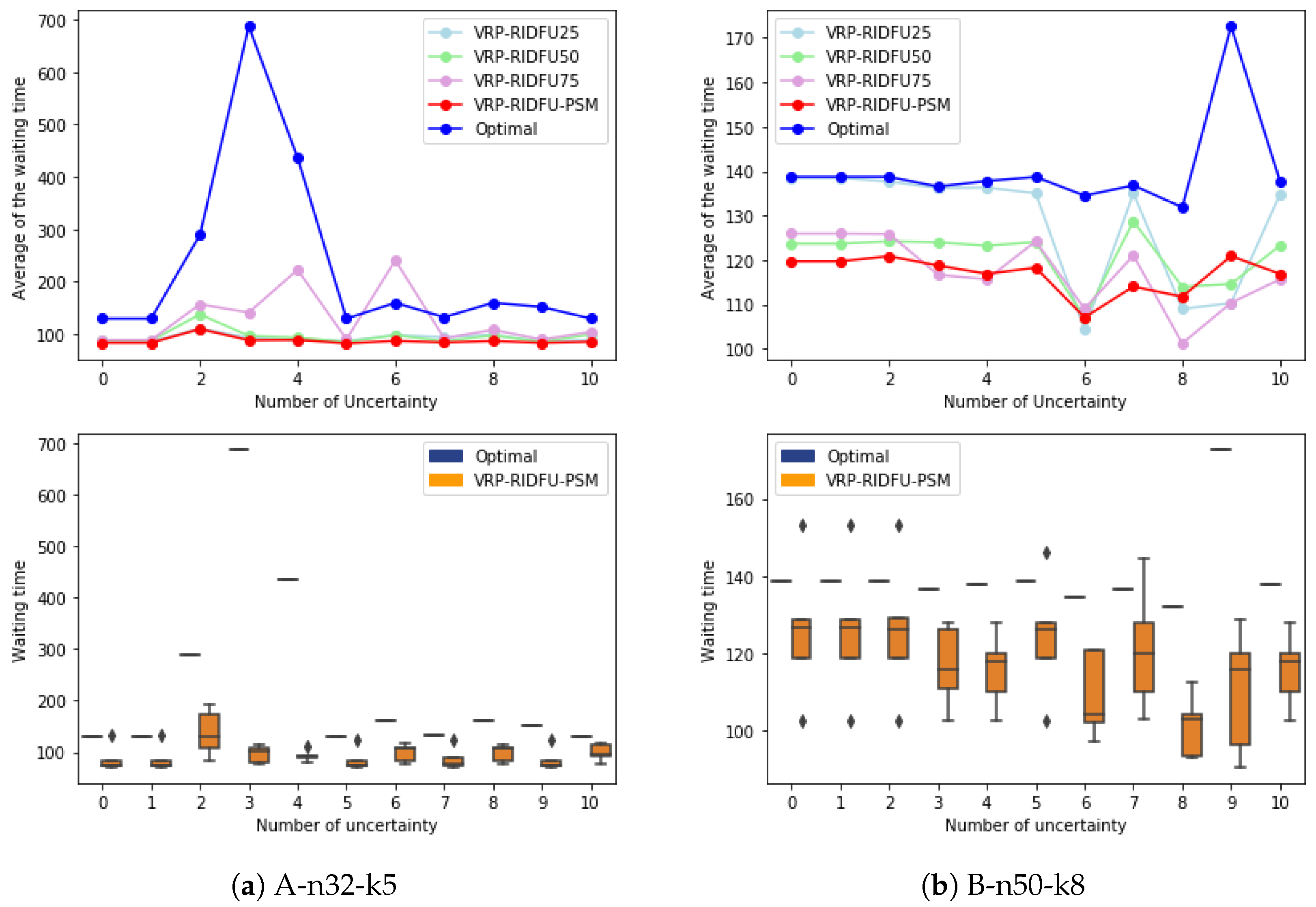
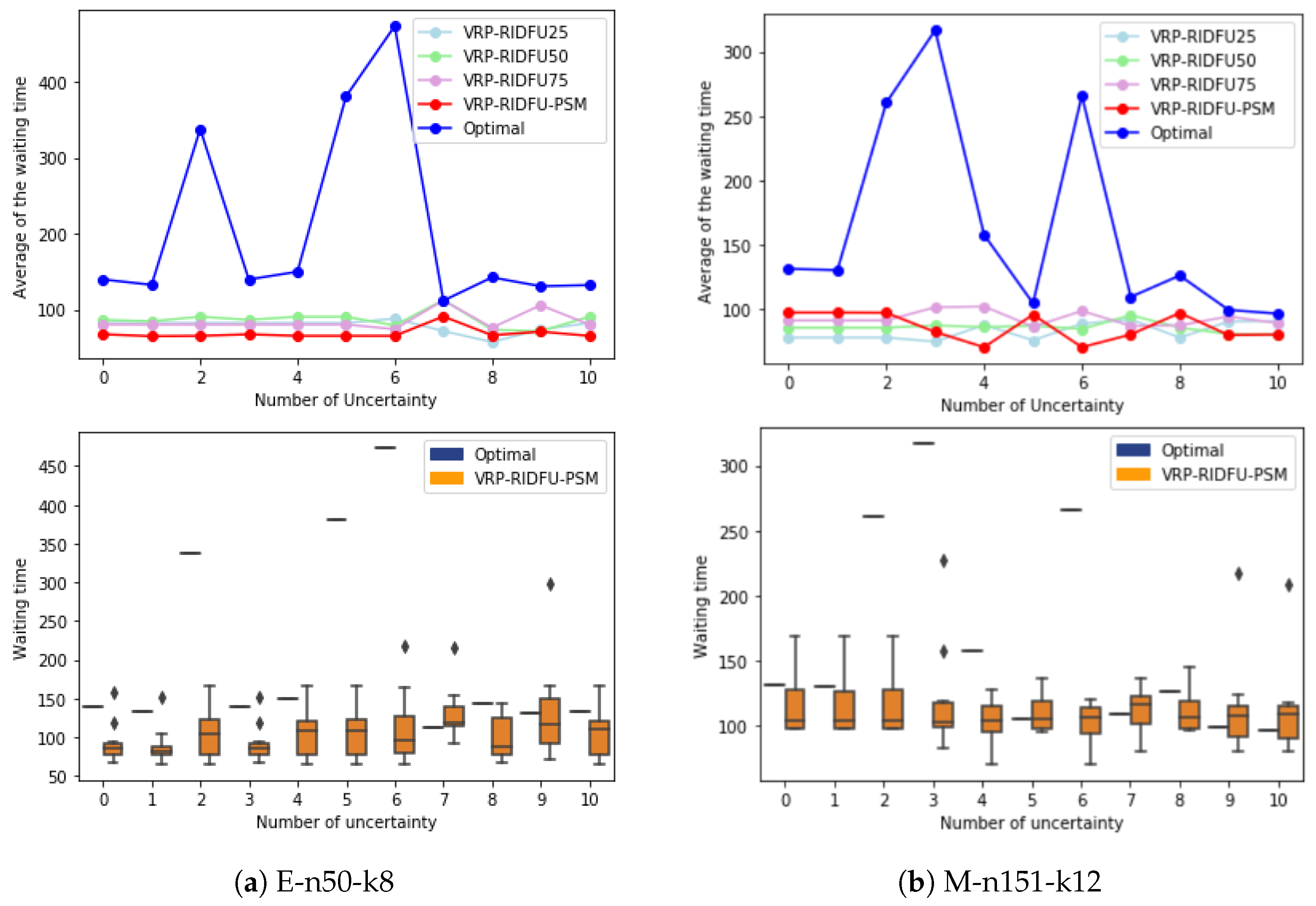
5.1. Efficiency Comparison Based on the Waiting Time
5.2. Efficiency Comparison Based on the Impact of Enhanced Population Size Variation
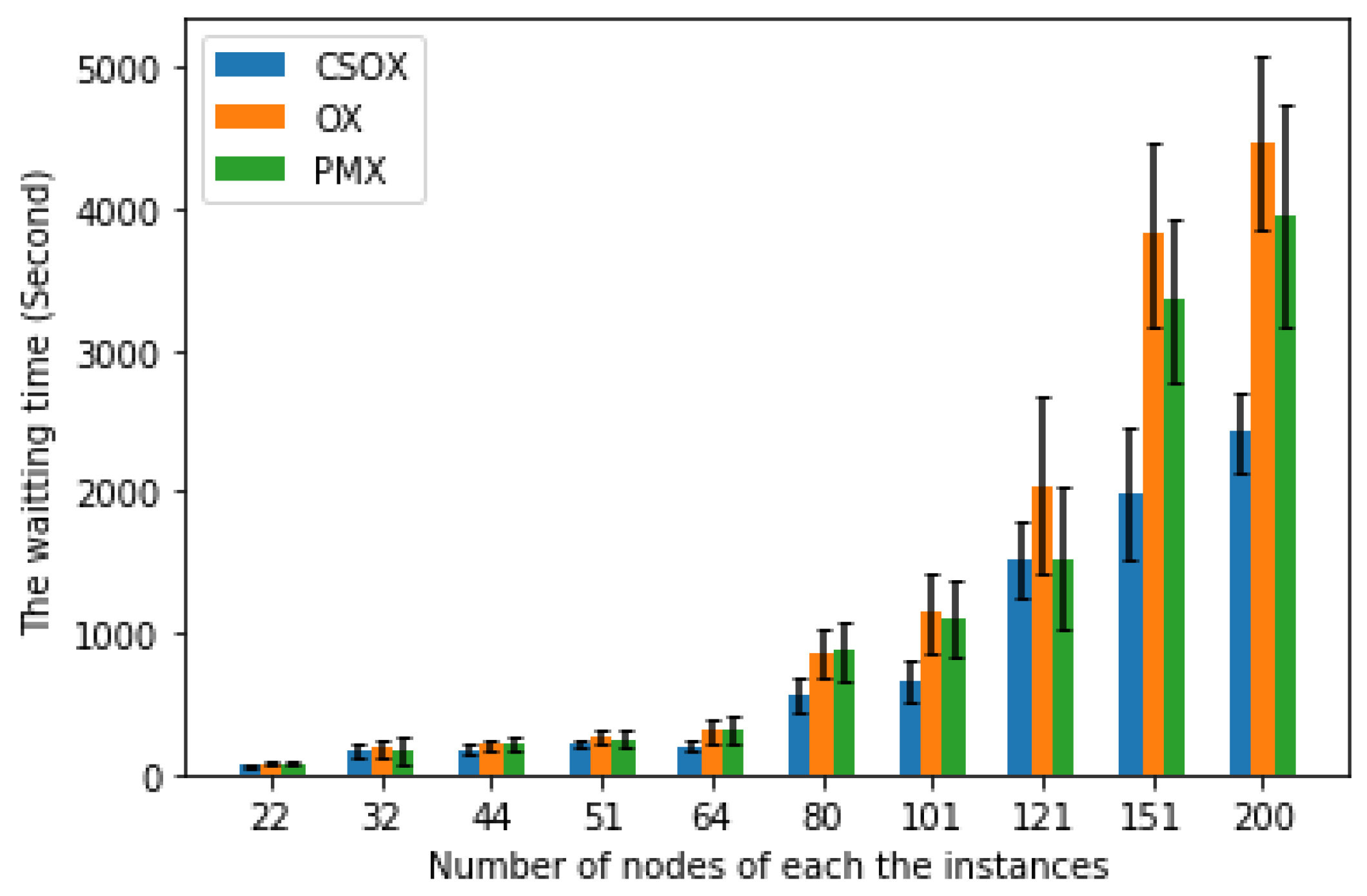
5.3. Efficiency Comparison Based on the Crossover Operator
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Wang, J. Global flood disaster research graph analysis based on literature mining. Appl. Sci. 2022, 12, 3066. [Google Scholar] [CrossRef]
- Watson, G.; Ahn, J.E. A systematic review: To increase transportation infrastructure resilience to flooding events. Appl. Sci. 2022, 12, 12331. [Google Scholar] [CrossRef]
- de Bruijn, K.M.; Maran, C.; Zygnerski, M.; Jurado, J.; Burzel, A.; Jeuken, C.; Obeysekera, J. Flood resilience of critical infrastructure: Approach and method applied to Fort Lauderdale, Florida. Water 2019, 11, 517. [Google Scholar] [CrossRef]
- Rebally, A.; Valeo, C.; He, J.; Saidi, S. Flood impact assessments on transportation networks: A review of methods and associated temporal and spatial scales. Front. Sustain. Cities 2021, 3, 732181. [Google Scholar] [CrossRef]
- Council, D.R. Emergency logistics and transport management, programme handbook, Chapter 8i, 1–9. Retrieved Dec. 2008, 7, 2011. [Google Scholar]
- Linet, O.; Ediz, E.; Beste, K. Emergency logistics planning in natural disasters. Ann. Oper. Res. 2004, 129, 217–245. [Google Scholar]
- Jiang, Y.; Yuan, Y. Emergency logistics in a large-scale disaster context: Achievements and challenges. Int. J. Environ. Res. Public Health 2019, 16, 779. [Google Scholar] [CrossRef] [PubMed]
- Haghani, A.; Tian, Q.; Hu, H. Simulation model for real-time emergency vehicle dispatching and routing. Transp. Res. Rec. 2004, 1882, 176–183. [Google Scholar] [CrossRef]
- Glock, K.; Meyer, A. Spatial coverage in routing and path planning problems. Eur. J. Oper. Res. 2023, 305, 1–20. [Google Scholar] [CrossRef]
- Wohlgemuth, S.; Oloruntoba, R.; Clausen, U. Dynamic vehicle routing with anticipation in disaster relief. Socio-Econ. Plan. Sci. 2012, 46, 261–271. [Google Scholar] [CrossRef]
- Hu, Z.H.; Sheng, Z.H. Integral transport scheduling in emergency relief based on an immune evolutionary algorithm. Int. J. Emerg. Manag. 2014, 10, 67–90. [Google Scholar] [CrossRef]
- Chang, F.S.; Wu, J.S.; Lee, C.N.; Shen, H.C. Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling. Expert Syst. Appl. 2014, 41, 2947–2956. [Google Scholar] [CrossRef]
- Gan, X.; Wang, Y.; Kuang, J.; Yu, Y.; Niu, B. Emergency Vehicle Scheduling Problem with Time Utility in Disasters. Math. Probl. Eng. 2015, 2015, 164194. [Google Scholar] [CrossRef]
- Lu, C.C.; Ying, K.C.; Chen, H.J. Real-time relief distribution in the aftermath of disasters—A rolling horizon approach. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 1–20. [Google Scholar] [CrossRef]
- Sabouhi, F.; Heydari, M.; Bozorgi-Amiri, A. Multi-objective routing and scheduling for relief distribution with split delivery in post-disaster response. J. Ind. Syst. Eng. 2016, 9, 17–27. [Google Scholar]
- Gan, X.; Liu, J.; Hao, X. Emergency logistics scheduling in disaster relief based on a multi-agent genetic algorithm. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 785–792. [Google Scholar]
- Zheng, Y.J.; Ling, H.F. Emergency transportation planning in disaster relief supply chain management: A cooperative fuzzy optimization approach. Soft Comput. 2013, 17, 1301–1314. [Google Scholar] [CrossRef]
- Ruan, J.; Wang, X.; Chan, F.T.; Shi, Y. Optimizing the intermodal transportation of emergency medical supplies using balanced fuzzy clustering. Int. J. Prod. Res. 2016, 54, 4368–4386. [Google Scholar] [CrossRef]
- Manopiniwes, W.; Irohara, T. Stochastic optimisation model for integrated decisions on relief supply chains: Preparedness for disaster response. Int. J. Prod. Res. 2017, 55, 979–996. [Google Scholar] [CrossRef]
- Sabouhi, F.; Bozorgi-Amiri, A.; Moshref-Javadi, M.; Heydari, M. An integrated routing and scheduling model for evacuation and commodity distribution in large-scale disaster relief operations: A case study. Ann. Oper. Res. 2019, 283, 643–677. [Google Scholar] [CrossRef]
- Sakiani, R.; Seifi, A.; Khorshiddoust, R.R. Inventory routing and dynamic redistribution of relief goods in post-disaster operations. Comput. Ind. Eng. 2020, 140, 106219. [Google Scholar] [CrossRef]
- Xu, P.; Liu, Q.; Wu, Y. Energy Saving-Oriented Multi-Depot Vehicle Routing Problem with Time Windows in Disaster Relief. Energies 2023, 16, 1992. [Google Scholar] [CrossRef]
- Huang, X.; Song, L. An emergency logistics distribution routing model for unexpected events. Ann. Oper. Res. 2018, 269, 223–239. [Google Scholar] [CrossRef]
- Pavai, G.; Geetha, T. A survey on crossover operators. ACM Comput. Surv. (CSUR) 2016, 49, 1–43. [Google Scholar] [CrossRef]
- Braekers, K.; Ramaekers, K.; Van Nieuwenhuyse, I. The vehicle routing problem: State of the art classification and review. Comput. Ind. Eng. 2016, 99, 300–313. [Google Scholar] [CrossRef]
- Feld, S.; Roch, C.; Gabor, T.; Seidel, C.; Neukart, F.; Galter, I.; Mauerer, W.; Linnhoff-Popien, C. A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer. Front. ICT 2019, 6, 13. [Google Scholar] [CrossRef]
- Meng, F.; Ding, Y.; Li, W.; Guo, R. Customer-oriented vehicle routing problem with environment consideration: Two-phase optimization approach and heuristic solution. Math. Probl. Eng. 2019, 2019, 1073609. [Google Scholar] [CrossRef]
- Toathom, T.; Champrasert, P. The Complete Subtour Order Crossover in Genetic Algorithms for Traveling Salesman Problem Solving. In Proceedings of the 2022 37th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), Phuket, Thailand, 5–8 July 2022; pp. 904–907. [Google Scholar]
- Mishra, B.K.; Dahal, K.; Pervez, Z. Dynamic relief items distribution model with sliding time window in the post-disaster environment. Appl. Sci. 2022, 12, 8358. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, F.; Li, S.; Chen, Z.; Dong, M. Peer-induced fairness capacitated vehicle routing scheduling using a hybrid optimization ACO–VNS algorithm. Soft Comput. 2020, 24, 2201–2213. [Google Scholar] [CrossRef]
- Toathom, T.; Promsuk, N.; Champrasert, P. Genetic Algorithm with Boosting based on Expected Value for Uncertain Routing. In Proceedings of the 2021 International Conference on Science & Contemporary Technologies (ICSCT), Dhaka, Bangladesh, 5–7 August 2021; pp. 1–6. [Google Scholar]
- Choo, K.S.; Kang, D.H.; Kim, B.S. Impact assessment of urban flood on traffic disruption using rainfall–depth–vehicle speed relationship. Water 2020, 12, 926. [Google Scholar] [CrossRef]





| GA Parameters | Environment Parameters | ||
|---|---|---|---|
| Population size: | 20–30 | Flooded probabilities: | 0.0–1.0 |
| Generation: | 100–2000 | Uncertainty situation: | 1–10 times |
| Crossover rate: | 0.7–1.0 | Vehicle speed: | 3–88 km/h [32] |
| Mutation rate: | 0.1–0.3 | ||
| Selection rate: | 0.5 | ||
| Number of runs: | 20 |
| Instance | SROS | VRP-RIDFU | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance | Flooded Roads | Travel Time | Waiting Time | Distance | Flooded Roads | Travel Time | Waiting Time | |||||
| Best | Avg. | Worst | SD | Runtime | ||||||||
| A-n32-k5 | 787.808 | 21/37 | 40.564 | 148.72 | 1307.367 | 14/37 | 42.144 | 74.165 | 111.956 | 163.941 | 28.488 | 0.952 |
| A-n45-k6 | 944.876 | 20/51 | 41.023 | 154.026 | 1745.027 | 10/51 | 52.277 | 106.621 | 151.285 | 181.846 | 25.852 | 1.34 |
| A-n54-k7 | 1171.784 | 34/61 | 62.181 | 247.615 | 2180.315 | 16/61 | 67.244 | 143.125 | 217.528 | 385.937 | 66.433 | 1.421 |
| A-n69-k9 | 1165.995 | 42/78 | 56.515 | 190.01 | 2256.247 | 24/78 | 75.391 | 151.121 | 181.329 | 209.124 | 20.387 | 13.371 |
| A-n80-k10 | 1766.5 | 43/90 | 79.954 | 338.92 | 2917.092 | 22/90 | 102.727 | 200.575 | 260.959 | 305.785 | 45.491 | 14.957 |
| B-n31-k5 | 1020.04 | 17/36 | 35.918 | 114.065 | 1199.534 | 9/36 | 39.714 | 44.801 | 71.096 | 90.342 | 14.999 | 0.871 |
| B-n44-k7 | 915.84 | 26/51 | 47.076 | 136.302 | 1504.949 | 20/51 | 60.758 | 91.352 | 132.654 | 289.601 | 60.521 | 1.228 |
| B-n50-k8 | 1322.562 | 35/58 | 66.325 | 194.469 | 2087.358 | 21/58 | 70.646 | 101.165 | 160.11 | 232.626 | 36.936 | 1.463 |
| B-n64-k9 | 869.316 | 39/73 | 42.451 | 125.108 | 1515.499 | 16/73 | 87.691 | 95.518 | 123.403 | 176.111 | 29.226 | 13.97 |
| B-n78-k10 | 1229.273 | 39/88 | 85.564 | 347.652 | 2344.841 | 25/88 | 150.854 | 207.544 | 451.637 | 981.318 | 168.77 | 14.761 |
| E-n22-k4 | 375.28 | 16/26 | 185.051 | 446.137 | 654.092 | 8/26 | 27.453 | 29.852 | 98.034 | 292.458 | 74.576 | 8.464 |
| E-n33-k4 | 838.721 | 16/37 | 78.219 | 315.045 | 1336.702 | 6/37 | 51.996 | 96.878 | 167.547 | 249.985 | 45.291 | 9.415 |
| E-n51-k5 | 524.944 | 28/56 | 47.921 | 214.457 | 1280.486 | 7/56 | 42.593 | 123.625 | 246.471 | 541.688 | 116.322 | 11.612 |
| E-n76-k7 | 687.603 | 43/83 | 63.001 | 368.738 | 1755.087 | 15/83 | 76.137 | 277.151 | 350.894 | 490.428 | 72.637 | 13.199 |
| E-n101-k8 | 826.908 | 56/108 | 79.466 | 537.964 | 2562.869 | 20/109 | 106.201 | 351.809 | 435.996 | 493.801 | 49.223 | 16.631 |
| M-n101-k10 | 819.811 | 56/111 | 1047.49 | 6972.741 | 2630.86 | 29/111 | 101.015 | 342.304 | 614.708 | 1167.073 | 279.548 | 17.296 |
| M-n121-k7 | 1045.16 | 54/128 | 1912.189 | 16205.98 | 3239.154 | 29/128 | 351.658 | 794.176 | 1741.898 | 3841.707 | 964.342 | 20.309 |
| M-n151-k12 | 1030.756 | 80/163 | 371.393 | 2819.523 | 3459.861 | 32/163 | 147.623 | 529.622 | 1355.167 | 5625.328 | 1556.315 | 24.946 |
| M-n200-k16 | 1294.666 | 82/216 | 2962.126 | 20472.488 | 4603.015 | 43/216 | 1815.141 | 2553.844 | 6115.756 | 14,210.947 | 4769.317 | 48.504 |
| M-n200-k17 | 1294.894 | 108/217 | 116.34 | 793.822 | 4716.01 | 43/217 | 193.205 | 554.435 | 1493.736 | 4676.866 | 1347.315 | 73.215 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toathom, T.; Champrasert, P. Vehicle Route Planning for Relief Item Distribution under Flood Uncertainty. Appl. Sci. 2024, 14, 4482. https://doi.org/10.3390/app14114482
Toathom T, Champrasert P. Vehicle Route Planning for Relief Item Distribution under Flood Uncertainty. Applied Sciences. 2024; 14(11):4482. https://doi.org/10.3390/app14114482
Chicago/Turabian StyleToathom, Thanan, and Paskorn Champrasert. 2024. "Vehicle Route Planning for Relief Item Distribution under Flood Uncertainty" Applied Sciences 14, no. 11: 4482. https://doi.org/10.3390/app14114482
APA StyleToathom, T., & Champrasert, P. (2024). Vehicle Route Planning for Relief Item Distribution under Flood Uncertainty. Applied Sciences, 14(11), 4482. https://doi.org/10.3390/app14114482








