Three-Dimensional Upper Bound Solution to Estimate Soil Thrust of a Track System on Saturated Clay Slopes under Undrained Conditions
Abstract
1. Introduction
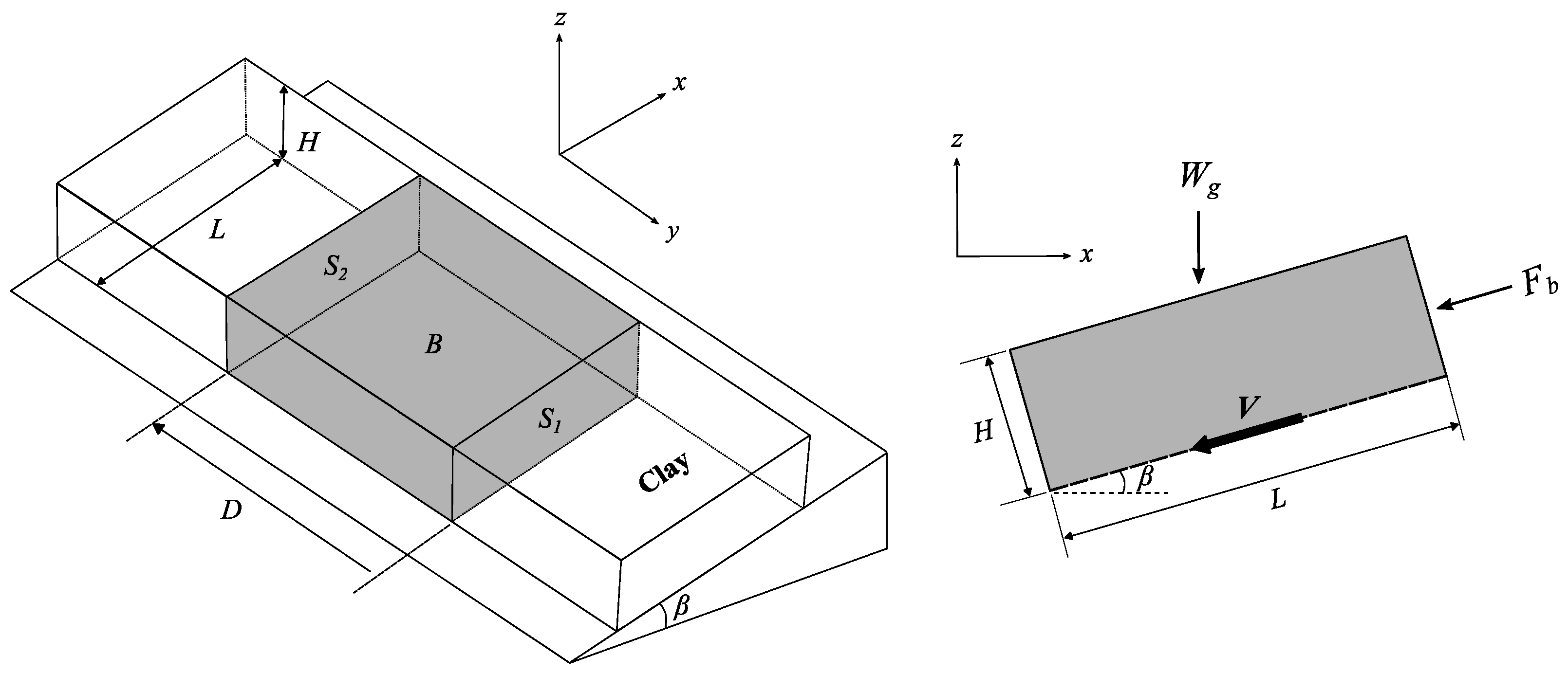
2. Upper Bound Solution
2.1. Assumption
2.2. Block Failure Mode
2.3. Triangular Wedge Failure Mode
2.4. Trapezoidal Wedge Failure Mode
2.5. Upper Bound Solution
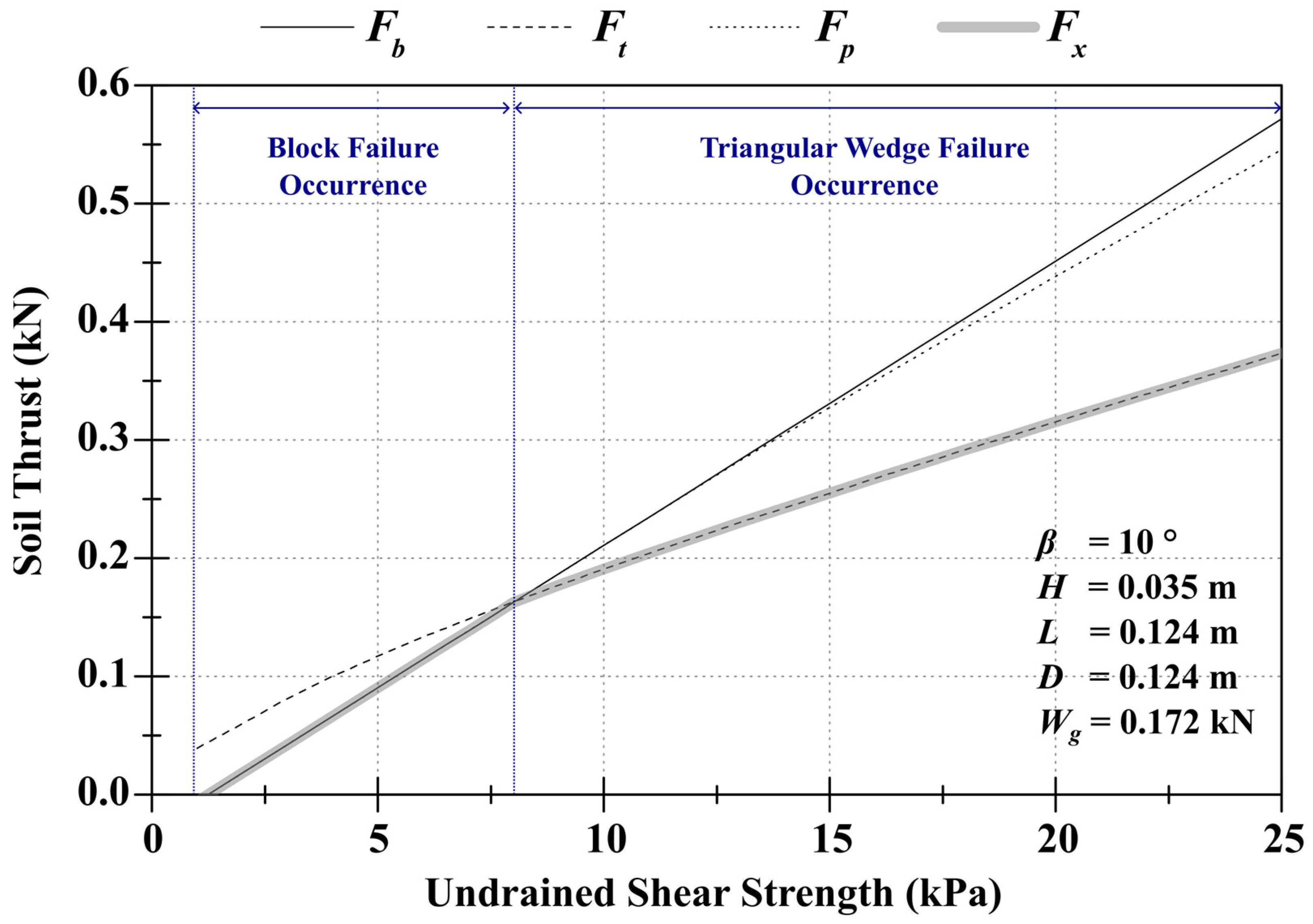
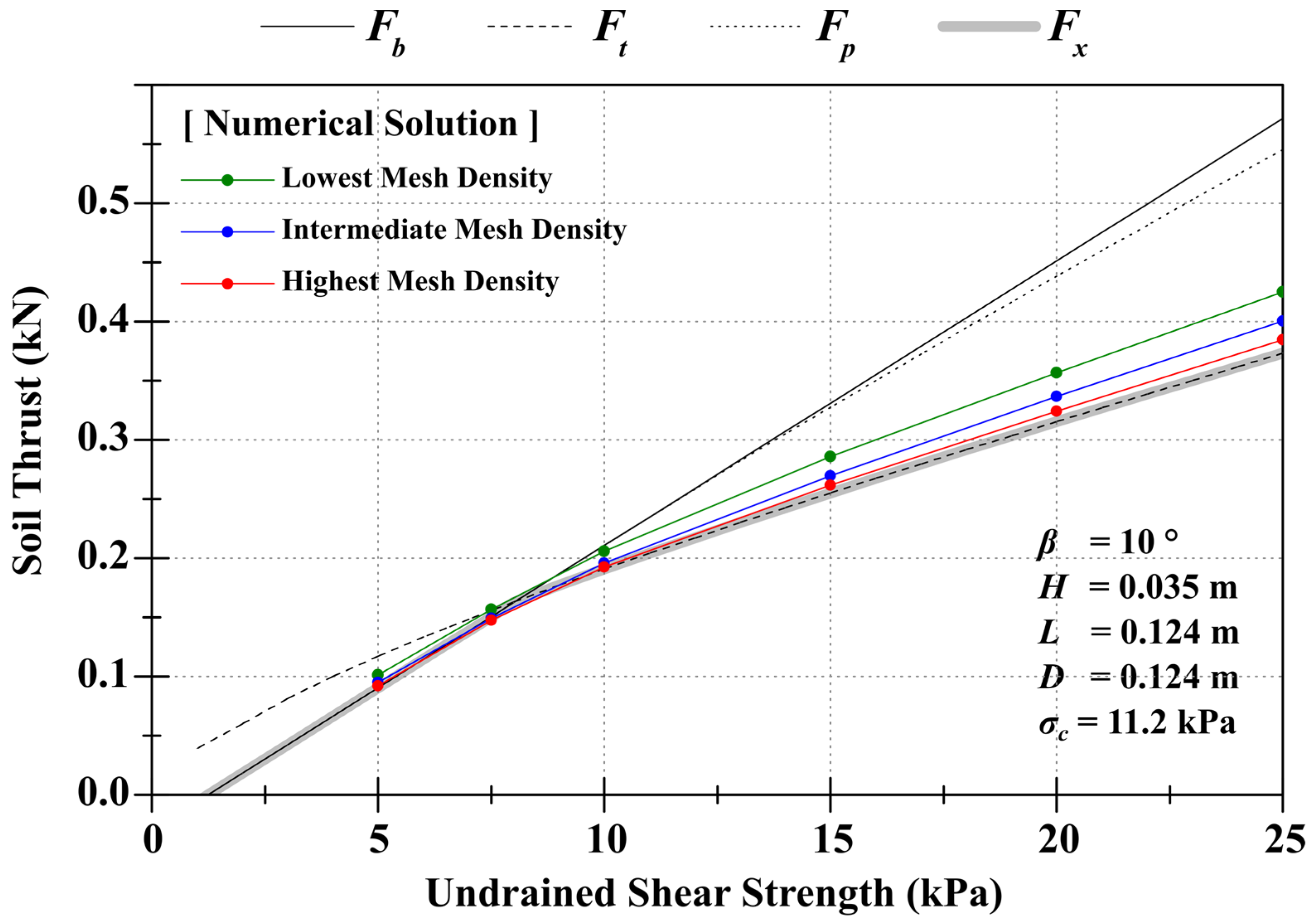
3. Verification with Numerical Solutions
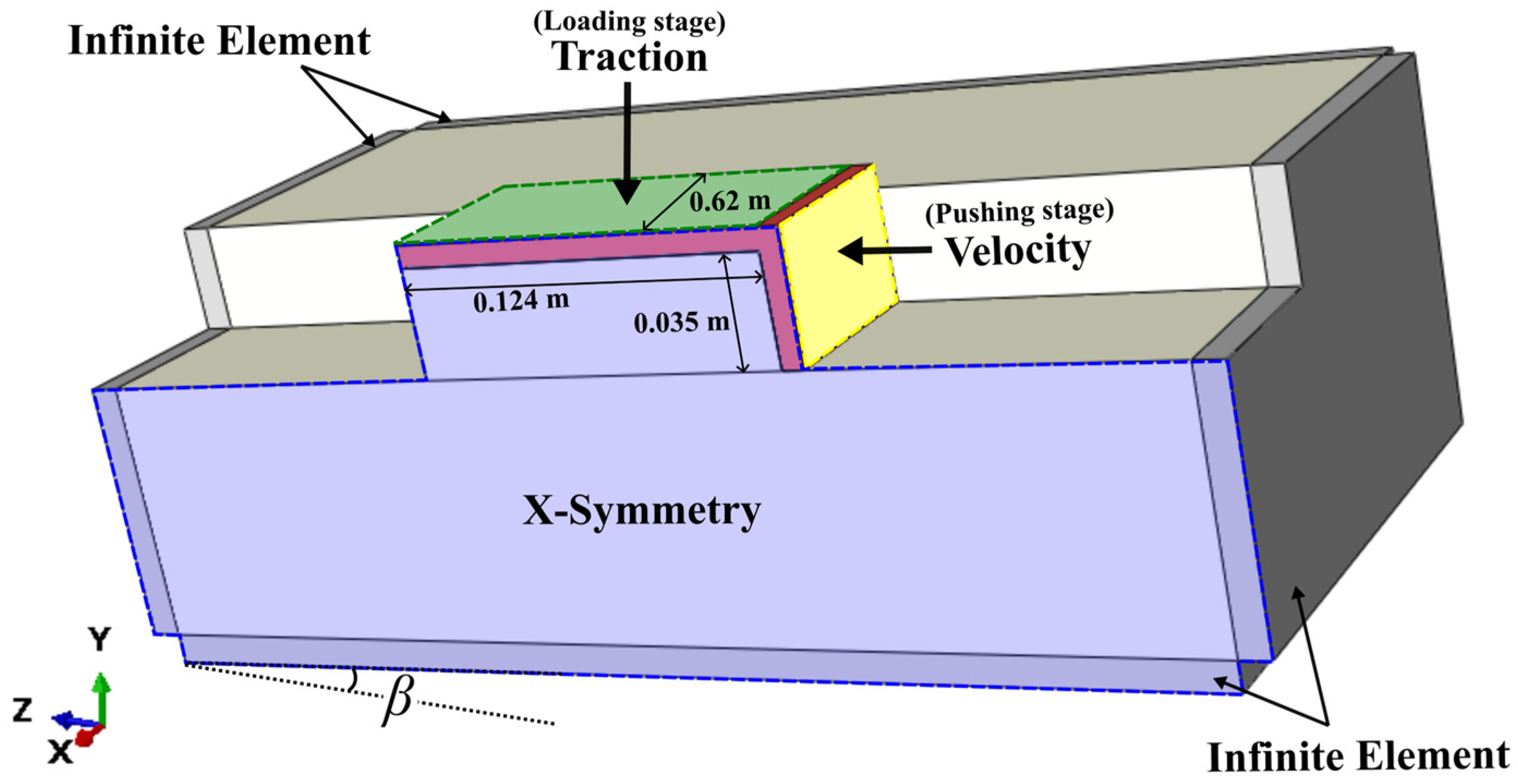
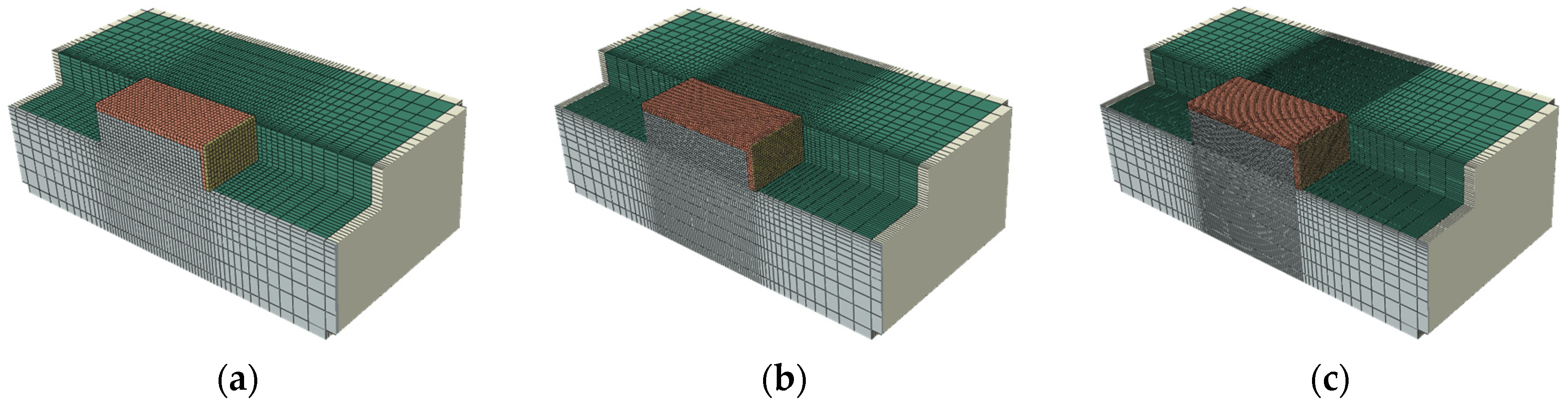
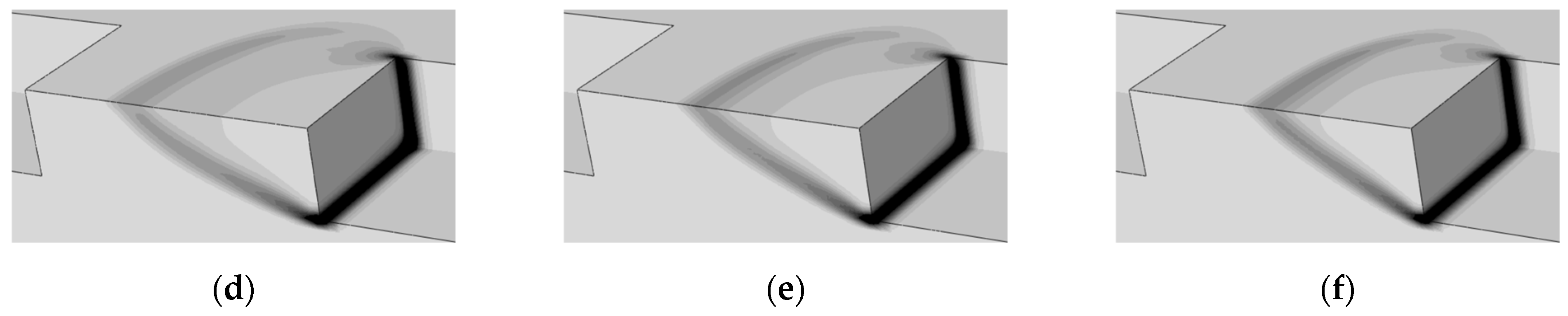
3.1. Numericla Modeling
3.2. Comparison of Upper Bound Solutions with Numerical Analysis Result
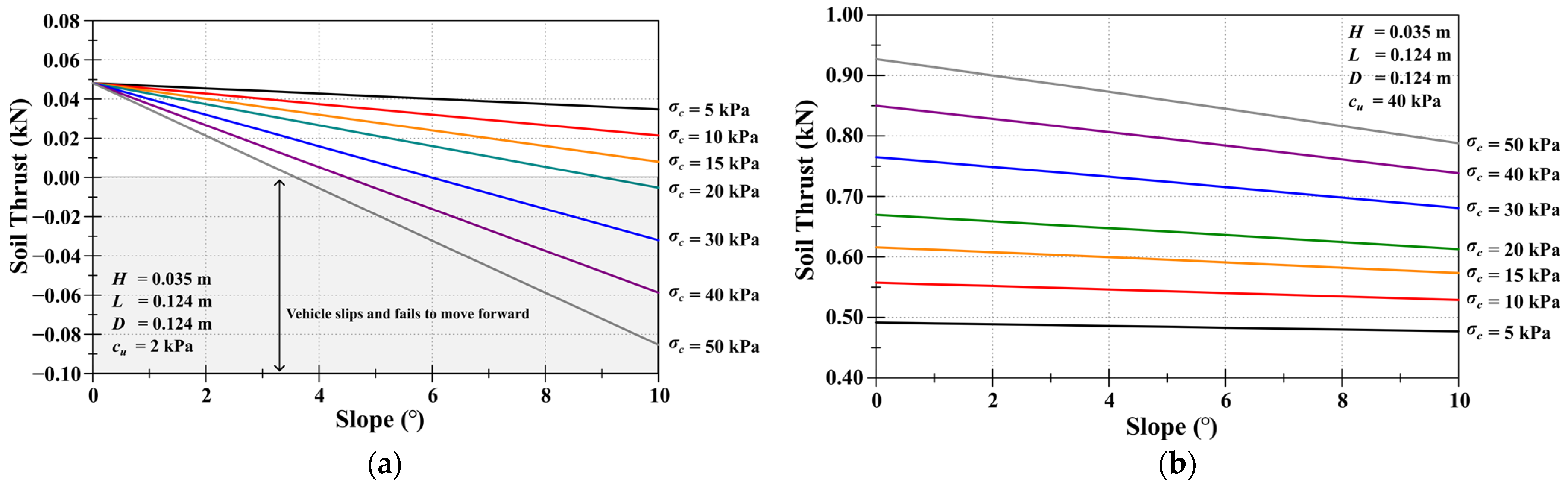
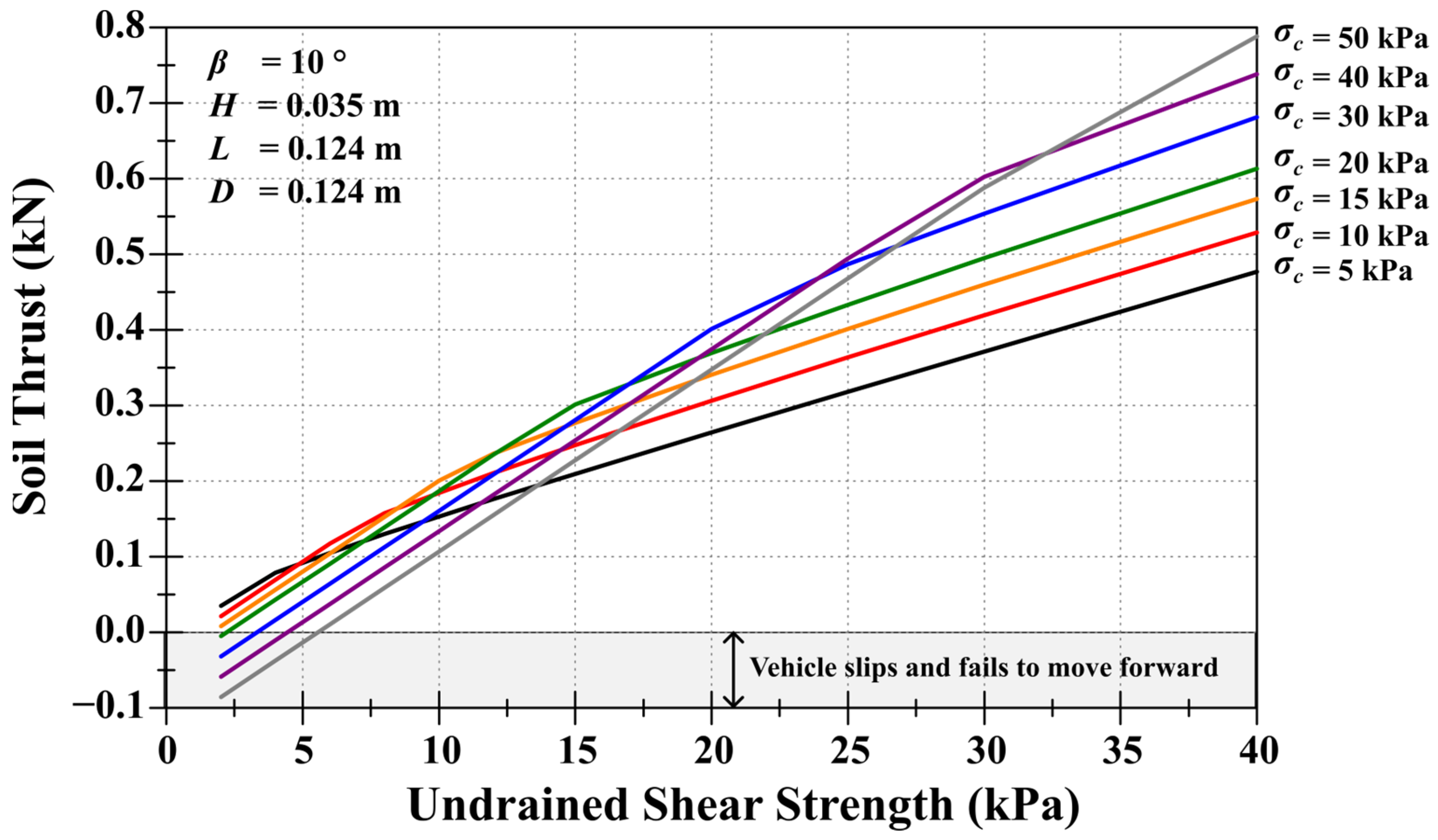
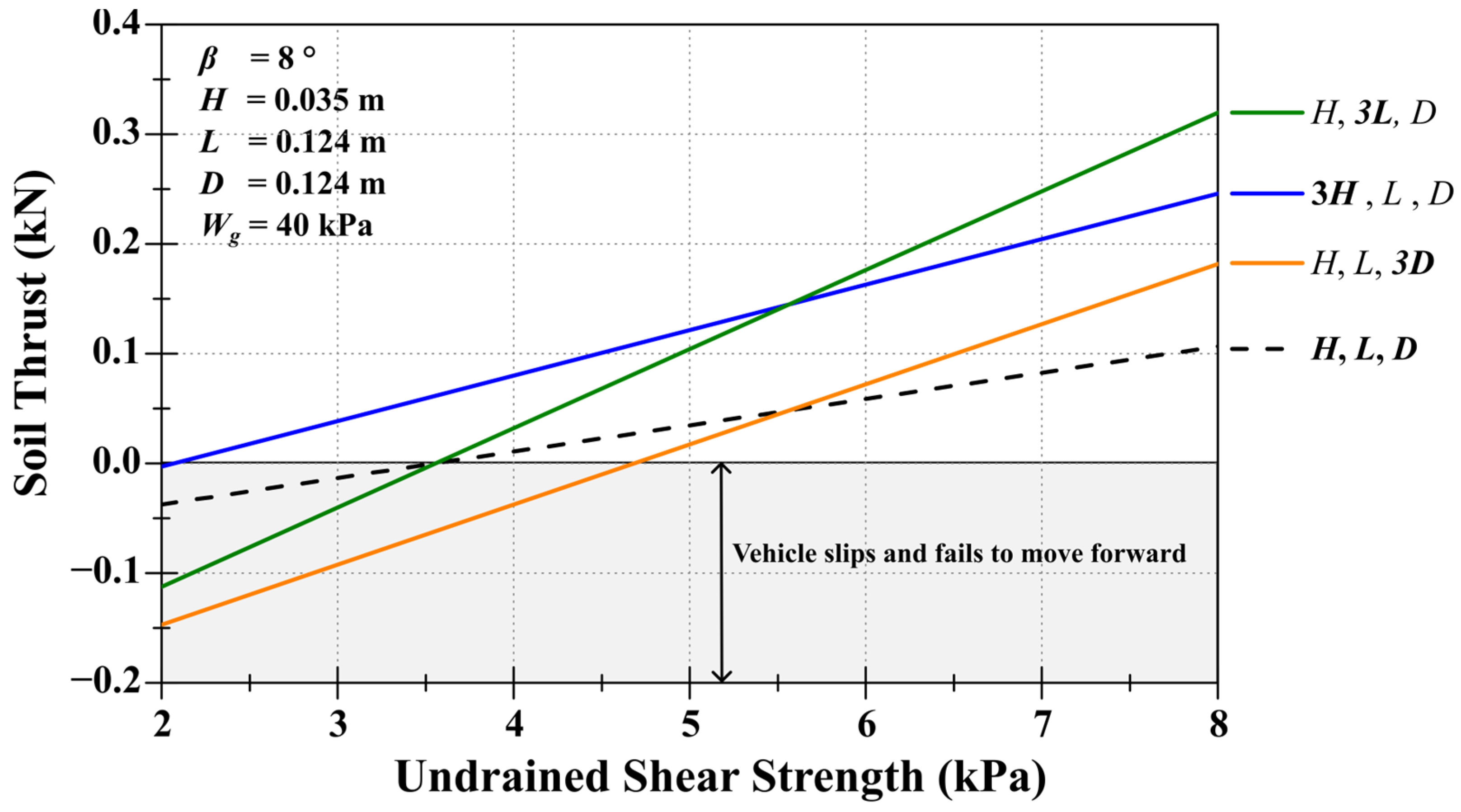
4. Parametric Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, X.; Fan, N.; Liu, Y.; Liu, X.; Wang, Z.; Xie, X.; Jia, Y. Deep seabed mining: Frontiers in engineering geology and environment. Int. J. Coal Sci. Technol. 2023, 10, 23. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, S. The Development History and Latest Progress of Deep-Sea Polymetallic Nodule Mining Technology. Minerals 2021, 11, 1132. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Zhai, X.; Zheng, H. Development of Hydraulic Lifting System of Deep-Sea Mineral Resources. Minerals 2022, 12, 1319. [Google Scholar] [CrossRef]
- Cho, S.-g.; Park, S.; Oh, J.; Min, C.; Kim, H.; Hong, S.; Jang, J.; Lee, T.H. Design optimization of deep-seabed pilot miner system with coupled relations between constraints. J. Terramech. 2019, 83, 25–34. [Google Scholar] [CrossRef]
- Leng, D.; Shao, S.; Xie, Y.; Wang, H.; Liu, G. A brief review of recent progress on deep sea mining vehicle. Ocean Eng. 2021, 228, 108565. [Google Scholar] [CrossRef]
- Chen, Q.; Yang, J.; Mao, J.; Liang, Z.; Lu, C.; Sun, P. A path following controller for deep-sea mining vehicles considering slip control and random resistance based on improved deep deterministic policy gradient. Ocean Eng. 2023, 278, 114069. [Google Scholar] [CrossRef]
- Vu, M.T.; Choi, H.-S.; Kim, J.-Y.; Tran, N.H. A study on an underwater tracked vehicle with a ladder trencher. Ocean Eng. 2016, 127, 90–102. [Google Scholar] [CrossRef]
- Wong, J.Y. Terramechanics and Off-Road Vehicle Engineering: Terrain Behaviour, Off-Road Vehicle Performance and Design; Butterworth-Heinemann: Oxford, UK, 2009. [Google Scholar]
- Bekker, M.G. Theory of Land Locomotion; University of Michigan Press: Ann Arbor, MI, USA, 1956. [Google Scholar]
- Grečenko, A. Re-examined principles of thrust generation by a track on soft ground. J. Terramech. 2007, 44, 123–131. [Google Scholar] [CrossRef]
- Grečenko, A. Compression–Sliding approach: Dependence of transitional displacement of a driving element on its size and load. J. Terramech. 2011, 48, 325–332. [Google Scholar] [CrossRef]
- Baek, S.-H.; Shin, G.-B.; Chung, C.-K. Assessment of the side thrust for off-road tracked vehicles based on the punching shear theory. J. Terramech. 2018, 79, 59–68. [Google Scholar] [CrossRef]
- Shin, G.-B.; Baek, S.-H.; Park, K.-H.; Chung, C.-K. Investigation of the soil thrust interference effect for tracked unmanned ground vehicles (UGVs) using model track tests. J. Terramech. 2020, 91, 117–127. [Google Scholar] [CrossRef]
- Yang, C.; Cai, L.; Liu, Z.; Tian, Y.; Zhang, C. A calculation method of track shoe thrust on soft ground for splayed grouser. J. Terramech. 2016, 65, 38–48. [Google Scholar] [CrossRef]
- Li, J.; Sun, S.; Sun, C.; Liu, C.; Tang, W.; Wang, H. Analysis of Effect of Grouser Height on Tractive Performance of Tracked Vehicle under Different Moisture Contents in Paddy Soil. Agriculture 2022, 12, 1581. [Google Scholar] [CrossRef]
- Wang, M.; Wang, X.; Sun, Y.; Gu, Z. Tractive performance evaluation of seafloor tracked trencher based on laboratory mechanical measurements. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 177–187. [Google Scholar] [CrossRef]
- Li, J.; Liu, S.; Dai, Y. Effect of grouser height on tractive performance of tracked mining vehicle. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2459–2466. [Google Scholar] [CrossRef]
- Li, Y.; He, D.; Si, Q.; Meng, X. Effect of track shoes structural parameters on traction performance of unmanned underwater tracked bulldozer. Ocean Eng. 2021, 237, 109655. [Google Scholar] [CrossRef]
- Sun, P.; Lu, H.; Yang, J.; Liu, M.; Li, S.; Zhang, B. Numerical study on shear interaction between the track plate of deep-sea mining vehicle and the seafloor sediment based on CEL method. Ocean Eng. 2022, 266, 112785. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Yang, G.; Xia, J.; Dou, Z.; Meng, Q.; Xu, X. Research on contact model of track-soft sediment and traction performance of four-tracked seabed mining vehicle. Ocean Eng. 2022, 259, 111902. [Google Scholar] [CrossRef]
- Xu, F.; Sun, Y.; Zhang, Y.; Li, Z.; Zhang, L. Discovery and verification of traction weakening effect between multi track shoe of deep-sea miner and sediment. Ocean Eng. 2023, 283, 115045. [Google Scholar] [CrossRef]
- Baek, S.-H.; Shin, G.-B.; Chung, C.-K. Experimental study on the soil thrust of underwater tracked vehicles moving on the clay seafloor. Appl. Ocean Res. 2019, 86, 117–127. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Wang, L.; Li, Z.; Yang, W. Mechanical properties and soil failure process of interface between grouser of tracked mining vehicle and deep-sea sediment. Ocean Eng. 2023, 285, 115336. [Google Scholar] [CrossRef]
- Woo, S.I.; Baek, S.-H. Upper-Bound Analysis for Soil Thrust of Single-Track System over Clay Ground. Int. J. Geomech. 2020, 20, 06019023. [Google Scholar] [CrossRef]
- Woo, S.I.; Beak, S.-H. Upper-bound solutions for the soil thrust of clay under a track system in 3D conditions. J. Terramech. 2023, 105, 41–51. [Google Scholar] [CrossRef]
- Na, S.H.; Woo, S.I. Theoretical Evaluation for Soil Thrust of Single-Track System over Clay Slope via Upper Bound Analysis. Appl. Sci. 2023, 13, 5222. [Google Scholar] [CrossRef]
- Spagnoli, G.; Freudenthal, T.; Strasser, M.; Weixler, L. Development and possible applications of Mebo200 for geotechnical investigations for the underwater mining. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- Grečenko, A. Thrust and slip of a track determined by the compression–sliding approach. J. Terramech. 2007, 44, 451–459. [Google Scholar] [CrossRef]
- Chen, W.-F. Limit Analysis in Soil Mechanics; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Costello, M.J.; Cheung, A.; De Hauwere, N. Surface area and the seabed area, volume, depth, slope, and topographic variation for the world’s seas, oceans, and countries. Environ. Sci. Technol. 2010, 44, 8821–8828. [Google Scholar] [CrossRef]



| Material | Clay Ground | Track System |
|---|---|---|
| Density ρ (t/m3) | 2.0 | 7.8 |
| Young’s modulus E (kPa) | 20,000 | 210 × 106 |
| Poisson’s ratio ν | 0.49 | 0.3 |
| Plasticity model | Tresca | - |
| Cohesion cu (kPa) | 5, 7.5, 10, 15, 20, 25 | - |
| Parameters | Values | ||
|---|---|---|---|
| Geometry | Slope angle | β (°) | 0~10 |
| Ground Strength | Undrained shear strength | cu (kPa) | 2~40 |
| Vehicle | Ground contact pressure | σc (kPa) | 5~50 |
| Height of the track | H (m) | 0.035, 0.105 | |
| Length of the track | L (m) | 0.124, 0.372 | |
| Width of the track | D (m) | 0.124, 0.372 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, S.; Woo, S.I. Three-Dimensional Upper Bound Solution to Estimate Soil Thrust of a Track System on Saturated Clay Slopes under Undrained Conditions. Appl. Sci. 2024, 14, 4335. https://doi.org/10.3390/app14104335
Shin S, Woo SI. Three-Dimensional Upper Bound Solution to Estimate Soil Thrust of a Track System on Saturated Clay Slopes under Undrained Conditions. Applied Sciences. 2024; 14(10):4335. https://doi.org/10.3390/app14104335
Chicago/Turabian StyleShin, Sehee, and Sang Inn Woo. 2024. "Three-Dimensional Upper Bound Solution to Estimate Soil Thrust of a Track System on Saturated Clay Slopes under Undrained Conditions" Applied Sciences 14, no. 10: 4335. https://doi.org/10.3390/app14104335
APA StyleShin, S., & Woo, S. I. (2024). Three-Dimensional Upper Bound Solution to Estimate Soil Thrust of a Track System on Saturated Clay Slopes under Undrained Conditions. Applied Sciences, 14(10), 4335. https://doi.org/10.3390/app14104335





