1. Introduction
Transmission lines inevitably pass through regions with complex topographies and harsh natural climates, and transmission lines are susceptible to extreme weather effects such as strong winds and icing [
1,
2]. Because of sunshine, temperature, airflow, load current and other factors, icing can be shed from overhead lines in large chunks, resulting in large oscillations in conductors, known as ice shedding. Ice shedding on overhead conductors is a low-frequency, large-amplitude vibration phenomenon that can cause transmission line destruction, conductor strand breakage, conductor interphase flashovers, damage to metal fixtures, pendant insulator clamp slippage, spacer bar fractures, transmission tower crossbar distortions, and loosening of tower bolts [
3,
4]. In serious cases, it can cause conductor fracture and tower collapse, resulting in wide-scale power supply interruptions, jeopardizing the stability and continuous operation of a power grid [
5,
6]. There are many factors affecting the ice shedding and jumping height of overhead lines, and the influencing factors are related to each other [
7]. Therefore, it is important to carry out in-depth studies on the ice shedding of overhead conductors and explore the influencing mechanism to guide the rational design of transmission line structures and improve anti-icing capabilities.
Under natural conditions, the operational conditions of transmission lines are highly complex. There are numerous factors influencing ice shedding bounce, including ice thickness, ice shedding amount, deicing method, span spacing, height differences, tension, insulators, spacer rods, and more. In order to explore the mechanisms of the bouncing process induced by ice shedding on overhead conductors, researchers around the world have carried out many numerical simulations and experimental studies. Jamaleddine used ADINA software (
https://www.bentley.com/software/adina/, 12 May 2024) to build a nonlinear finite element planar model to simulate the static and transient mechanical responses of a physical test model [
8]. Roshan Fekr used ADINA to build a two-stage conductor planar model, investigated the static and dynamic responses of the model under different combinations of ice cover thickness, stall spacing, suspension heights, stall frequency, unequal spans, and ice shedding conditions, and discussed the effects of each parameter [
9]. Kollar et al. simulated the dynamic response of a sub-conductor in a split conductor after ice shedding [
10]. Kalman studied the dynamic response of a conductor under different combinations of stall spacing and external impact loads, providing a basis for studying the damage criteria of icing [
11]. Barbieri proposed a nonlinear mathematical model to simulate the dynamic response of a conductor, and numerical models were established using the finite element method [
12]. The numerical simulation results were compared with the experimental values, and it was found that the deformation of the conductor depended on the excitation frequency, the quality of the conductor, and the excitation conditions. Justín Murín et al. used ANSYS software (
https://www.bentley.com/software/adina/, 12 May 2024) to build finite element models of a single conductor and a three-split conductor, simulated ice shedding at different locations, and investigated the similarities and differences between a single conductor and a three-split conductor in their dynamic responses to ice shedding with respect to the height of ice shedding jumps and the tension change [
13]. Yan B et al. used ABAQUS software (
https://www.ansys.com/, 12 May 2024) to investigate a seven span continuous transmission line numerical model, and analyzed the dynamic responses of multiple-span transmission lines with different structural parameters after different rates of ice shedding, and proposed a quantitative relationship and linear calculation formula between the sag difference and the maximum ice bouncing height according to the simulation results [
14]. In order to verify the validity of a numerical simulation of ice shedding bouncing, Meng X B et al. built a full-size transmission line test model, simulated the ice shedding response processes of single span, two span and three span conductors by remote control centralized load shedding, and investigated the changes in conductor displacement, tension, and swing angle of insulator strings [
15]. Xie Xianzhong et al. used a 220 kV transmission line as a prototype, and based on dynamic similarity theory, designed a 1:20 scale double-span transmission line model to realize the transient response under many conditions, such as zipper ice shedding, synchronous ice shedding, full ice shedding, and local ice shedding [
16]. Wen Y built a finite element model of a 500 kV overhead line and studied the effect of different spacer arrangement schemes on ice shedding suppression [
17].
In order to analyze the impact of strong winds on iced conductors, Zhang M et al. designed a 3D tower–line model to study the incremental relationship between the design wind speed and the amplification factor of the tower–line coupling effect based on measured data [
18]. Jiang Quancai et al. established a finite element model of a tower–line system and used the harmonic superposition method to simulate the time course of the pulsating wind speed at the height of the conductor to explore the effect of the pulsating wind speed on the bouncing process induced by ice shedding [
19]. Other studies have analyzed the effects of icing morphology and wind attack angle on icing protection, respectively [
20,
21]. Bian Rong et al. considered the sudden change in the wind load caused by changes in the aerodynamic shape and the aerodynamic parameters at the moment of ice shedding, and analyzed the functional relationship between the maximum ice shedding jump height of a conductor and the difference in the sag in the stationary state before and after ice shedding [
22]. The calculation formulas obtained from the above literature [
23] are mostly aimed at a specific working condition and are no longer applicable to the ice shedding situation under the coupling effect of ice and wind.
In addition to the factors mentioned above, iced conductors with different shapes experience even more complex forces under the action of wind angles. Significant wind deflection of iced conductors leads to lateral elastic potential energy, which has a clear impact on the dynamic response of ice shedding. Therefore, the ice shedding process of overhead lines under strong wind conditions constitutes a complex fluid–structure coupled vibration process. After ice shedding, the transmission line transitions from simple vertical motion to 3D motion, rendering traditional prediction methods inadequate. In this paper, a continuous overhead conductors model was established to analyze the influence of strong winds, ice shape, wind attack angle and other complex factors on the ice shedding jumping of transmission lines, and to explore the risks caused by the ice shedding jumping under complex working conditions. Moreover, the lateral displacement of conductors caused by ice shedding under strong winds was studied, and the possibility of discharge between horizontally arranged conductors was explored.
The structure of this paper is as follows. In
Section 1, the complex working conditions and forces of iced conductors under strong wind conditions are analyzed. In
Section 2, the fluid dynamics of iced conductors and numerical simulation models for ice shedding of transmission lines are established. In
Section 3, the lift and resistance for iced conductors with different icing shapes are calculated. In
Section 4 and
Section 5, the research results on the ice shedding response of overhead conductors under strong winds are analyzed and discussed.
3. Numerical Simulation Method for Ice Shedding
3.1. Analysis Method for Ice Shedding on Overhead Transmission Lines under Complex Conditions
Under natural icing and wind conditions, the longitudinal elastic potential energy and transverse elastic potential energy increased on iced conductors. Under suitable temperatures or external forces, the icing on the overhead conductor suddenly fell off; thus, the elastic energy on the conductor was transformed into kinetic energy and new potential energy, and the conductor underwent a complex swing. Due to air resistance, conductor self-damping, insulator string inertia force and other factors, the conductor vibration gradually weakened and eventually reached a new equilibrium position. The basic kinetic equation of the conductor ice shedding jump is:
where
u is the displacement vector;
is the velocity vector;
is the acceleration vector;
K is the stiffness matrix;
C is the damping matrix; and
M is the mass matrix.
3.2. Finite Element Calculation Procedure
The ice shedding problem is a complex nonlinear dynamics problem, and researchers have used a variety of methods to determine the ice shedding jump mechanical model for static loads, transient loads, simple harmonic loads, and any combination of time-varying stresses, strains, and displacements.
As shown in
Figure 3, the simulation of the bouncing process induced by ice shedding on overhead conductors under strong wind conditions contains the knowledge of nonlinear structural statics as well as structural dynamics, and the simulation process is generally divided into several load steps:
Step 1: Calculate the resistance and lift based on the hydrodynamic method for the bare and iced conductors.
Step 2: Static analysis of a conductor under its self-weight. It is determined by calculating whether the deformation of the conductor under its self-weight is equal to the known shape.
Step 3: On the basis of Step 1, apply the icing load and wind load and carry out static analysis without considering the ice shedding and the fluctuations of wind load.
Step 4: Simultaneously release the icing load and wind load, where the wind load is updated from the value before ice shedding to the bare conductor.
Step 5: Use the transient dynamics method to determine the final stabilization time.
Figure 3.
The flowchart of the simulation process for ice shedding on conductors.
Figure 3.
The flowchart of the simulation process for ice shedding on conductors.
During nonlinear finite element numerical simulation, pole elements were used to simulate the transmission conductors. The accuracy of the finite element simulation results is closely related to the number of elements used for discretization. Generally, higher numbers of elements lead to greater accuracy but also require longer computational time. To validate the convergence of the unit mesh, the 400 m transmission conductor span was discretized into 100, 200, 400, and 1000 elements, and the numerical values of sag and maximum bounce height were calculated under the same conditions. The results show that when the line is divided into 400 elements, the error between the sag and maximum bounce height values and those obtained with 1000 elements is less than 0.5%. Therefore, in this study, each meter of the conductor is divided into one element.
3.3. Calculation of Wind Loads Based on Aerodynamic Parameters
In this paper, the lift and drag of iced conductors were solved through aerodynamic methods, which mainly included the following steps:
Step 1: Elaborate modeling of the cross-section of the iced conductor is conducted. In this paper, it is assumed that ice formation is uniform, thus simplifying the two-dimensional airflow phenomenon on the plane.
Step 2: Establish boundary conditions. In actual scenarios, incoming winds typically flow horizontally. However, due to the potential occurrence of eccentric twisting in iced conductors, setting inputs, outputs, and airflow vectors is necessary during the modeling phase.
Step 3: Partition the domain into grids, and optimize grid construction. The quality of grid partitioning directly influences the calculation results of aerodynamic coefficients in numerical simulation.
Step 4: Solving the mathematical–physical equations of fluid mechanics, for a two-dimensional flow field, only requires considering the fundamental fluid mechanics control equations at the cross-section of the ice-covered conductor. The momentum conservation equation and mass conservation equation are as follows:
where
is the air fluid density, kg/m³;
and
represent the velocity components in the horizontal and vertical directions, respectively, m/s;
denotes the fluid pressure on the cross-section, Pa;
is the dynamic viscosity, Pa·s;
signifies divergence; grad indicates gradient;
is the velocity vector of the two-dimensional cross-section flow.
Step 5: Due to the change in the incoming wind direction caused by rotation, the output results in the software should be in terms of axial force coefficients and normal force coefficients. Therefore, it is necessary to convert lift and drag coefficients into angle form.
3.4. Finite Element Model (FEM) of Transmission Line
With reference to the actual parameters of a transmission line section, and ignoring the influence of the transmission tower, this paper established a three-span “conductor–insulator” finite element model including LGJ-630/45 conductor, FC7P/146 glass insulators, and a 400 m span distance. The self-weight of the LGJ-630/45 conductor was 20 N/m. The upper suspension point of the insulator string was fixed, and the connecting wire end could swing freely. To further analyze the risk of ice shedding response, it was assumed that the phase conductors on the transmission line were horizontally or vertically arranged, while the ground wire were arranged above the conductors.
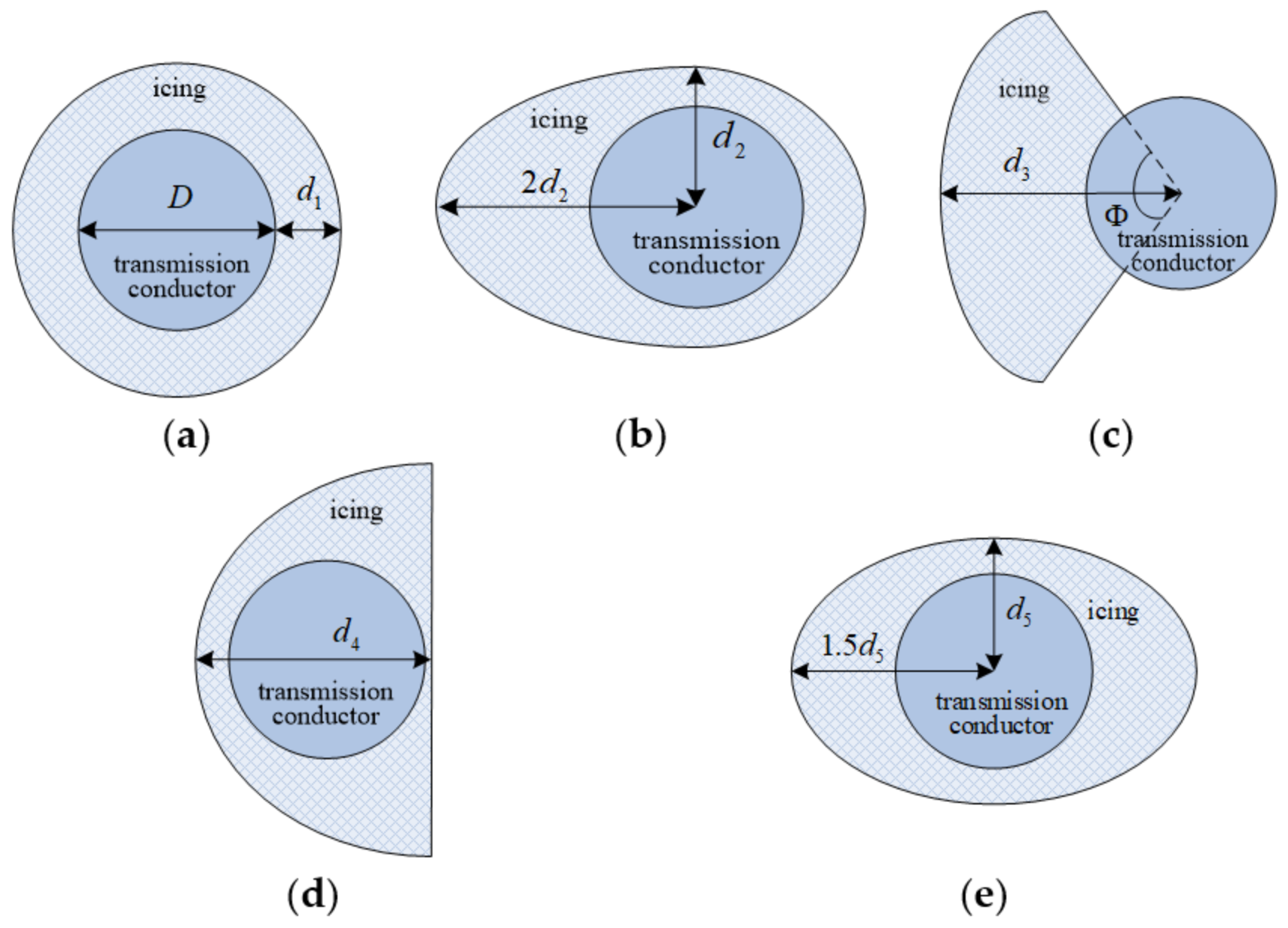
The finite element model of the designed transmission line had three spans. The spacing of each span was 400 m. The ice shedding position was the middle span, with a shedding rate of 100%. Icing is uniformly distributed at the same moment, without considering the height difference of the insulator suspension points. The shapes of the designed non-circular iced conductors include fan-shaped, D-shaped, elliptical, and crescent-shaped. The equivalent icing thickness was 15 mm, and according to Equation (1), the equivalent ice load was calculated as 20 N/m. The airflow velocity conditions were set to 10 m/s and 20 m/s, with wind angles of attack at 45°, 90°, and 180°.
Calculation of Lift and Resistance for Iced Conductors with Different Icing Shapes
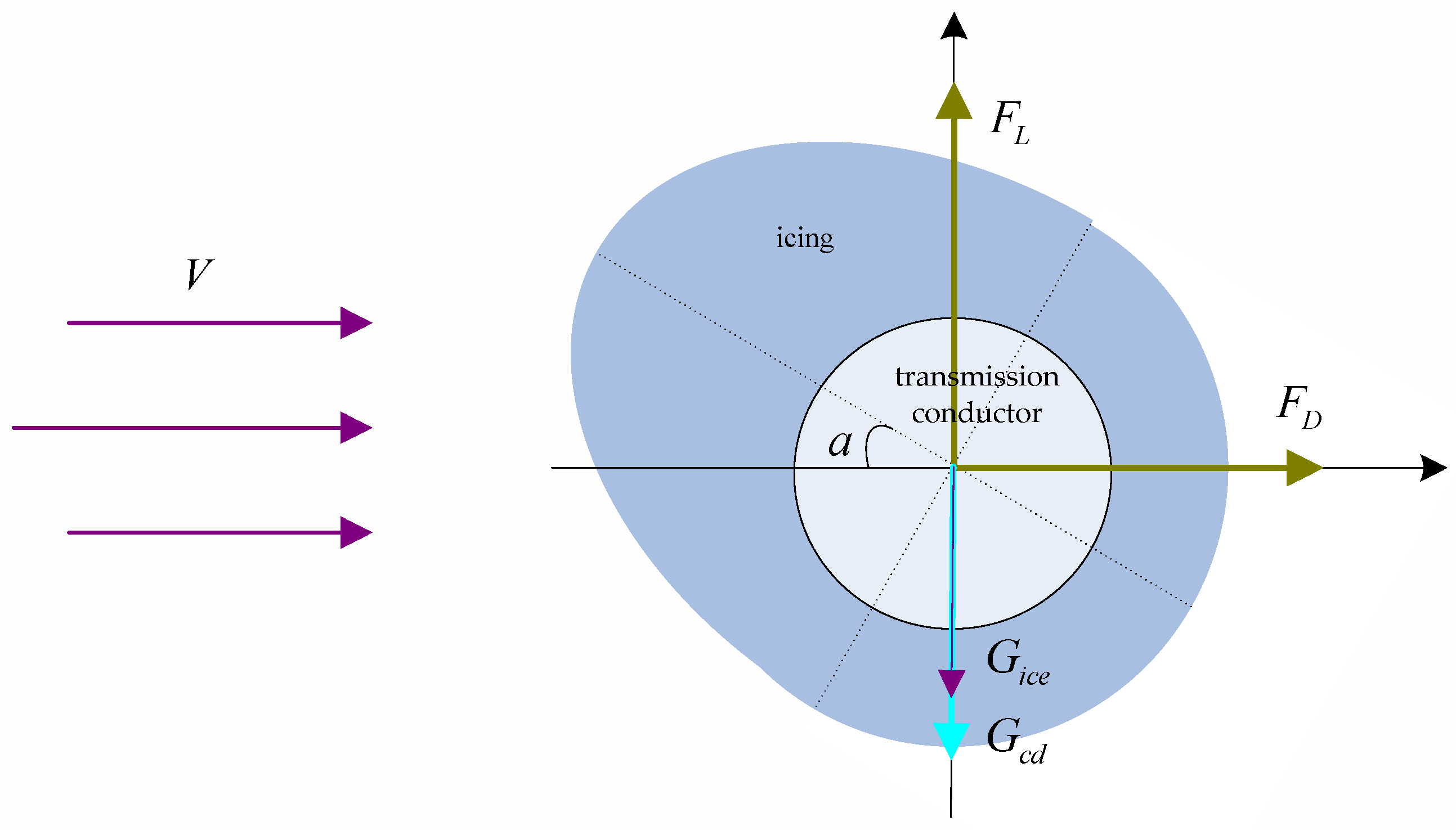
Before analyzing the dynamic response of ice shedding on overhead conductors under strong wind conditions, it is necessary to calculate the lift and resistance of the airflow received by the iced conductor before and after ice shedding. In order to simplify the calculation, in this paper, the definition in
Figure 1 shows the shape of the icing for a 0° wind attack angle (the wind direction is from left to right), and the shaped icing clockwise rotation angle was defined as the wind attack angle, as shown in
Figure 2.
Assuming that the equivalent ice thickness on the LGJ-630/45 wire was 15 mm and the equivalent icing load was 20 N/m, the resistance and lifting force of the crescent-shaped, fan-shaped, D-shaped and elliptical-shaped iced conductors at different wind attack angles are shown in
Figure 4 when the air velocity was 10 m/s. Among them, at a wind attack angle of 180°, the fan-shaped and D-shaped icing had a sharp curvature change and the maximum windward surface, so the obstruction to the airflow was the strongest. At this time, the resistance of the iced conductor was 13.5 N/m and 19.2 N/m, is more than 10 times that of the elliptic-shaped and crescent-shaped iced conductors. In addition, the crescent-shaped and elliptical-shaped icing at 90° and 270° angles of attack have relatively large wind attack areas, and the formation of two have obvious extreme maximum points.
Lifting force is the vertically upward force that air currents create on an iced conductor, which changes the elastic potential energy caused by the weight of the conductor and icing. The crescent-shaped and elliptical-shaped icing were more streamlined, and they generally experienced much less lift than the other two shapes. Due to the unique shape of the D-shaped icing, its lift was positive at 0–180° wind attack angles, and the maximum value reached 6.5 N/m at approximately 135°, reaching 1/3 of the icing load, while at 180–360° wind attack angles, the lift formed by the airflow was negative, and the lift curve formed a centrosymmetric shape at 180° wind attack angles.
Furthermore, the lift and drag acting on the iced conductor varied rapidly with wind speed, as shown in Equation (2). The lift and drag had a significant impact on the steady-state and ice shedding response process of iced conductors.
4. Analysis of Ice Shedding Response of Overhead Conductors under Strong Winds
Influenced by icing morphology, wind attack angle, wind speed and other factors, the airflow resistance and lifting force on the iced conductor were very different, resulting in completely different parameters such as conductor position and elastic potential energy before and after ice shedding. After ice shedding, the conductor quickly rebounded, and its rebound direction, displacement, and speed were significantly affected by the initial state, so the risk of ice shedding was also completely different.
4.1. Influence of Ice Morphology on the Ice Shedding Response of Transmission Lines
In order to analyze the ice shedding response of transmission lines with different ice shapes under strong winds, three consecutive transmission line spans were established, with a distance of each span of 400 m. The middle span was an ice shedding section, with a 100% ice shedding rate and the insulator height difference not being taken into account. The wind speed was taken to be 10 m/s, and the equivalent thickness of the ice cover was 15 mm (with the ice loading being 20 N). The displacement curves of the middle location of the ice shedding span with different icing shapes are shown in
Figure 5.
The curves of the elliptical, circular, and crescent shaped iced conductor were smooth, and the lateral deviation distance generated by wind force was less than 1 m. For circular, elliptical, and crescent shaped icing samples, the outer surface of the icing was approximately streamlined, with a smaller lateral displacement at the initial position at a 180° wind attack angle. After ice shedding, the lateral amplitude was 1 m, slightly larger than that of the circular case. The longitudinal amplitude of the ice shedding bounce for the three icing morphologies was about 10 m, which was much greater than the transverse amplitude. Therefore, it can be concluded that the risk of ice shedding condition still mainly lay in the vertical direction, including discharge faults and structural faults.
For fan-shaped and D-shaped iced conductors, the airflow resistance increased significantly at a 180° wind attack angle. The initial positions of the midpoint of the ice shedding span were 5.58 m and 8.82 m, respectively. The lateral amplitudes after ice shedding were 6.65 m and 11.71 m, while the longitudinal amplitudes were 9.35 m and 0.79 m, respectively. Therefore, in addition to the vertical direction, attention should also be paid to the lateral swing of the D-shaped iced conductor. Furthermore, the actual displacement of the fan-shaped iced conductor was greater than the other four types, and its risk is more complex.
4.2. Effect of Wind Attack Angle on the Ice Shedding Response of Transmission Lines
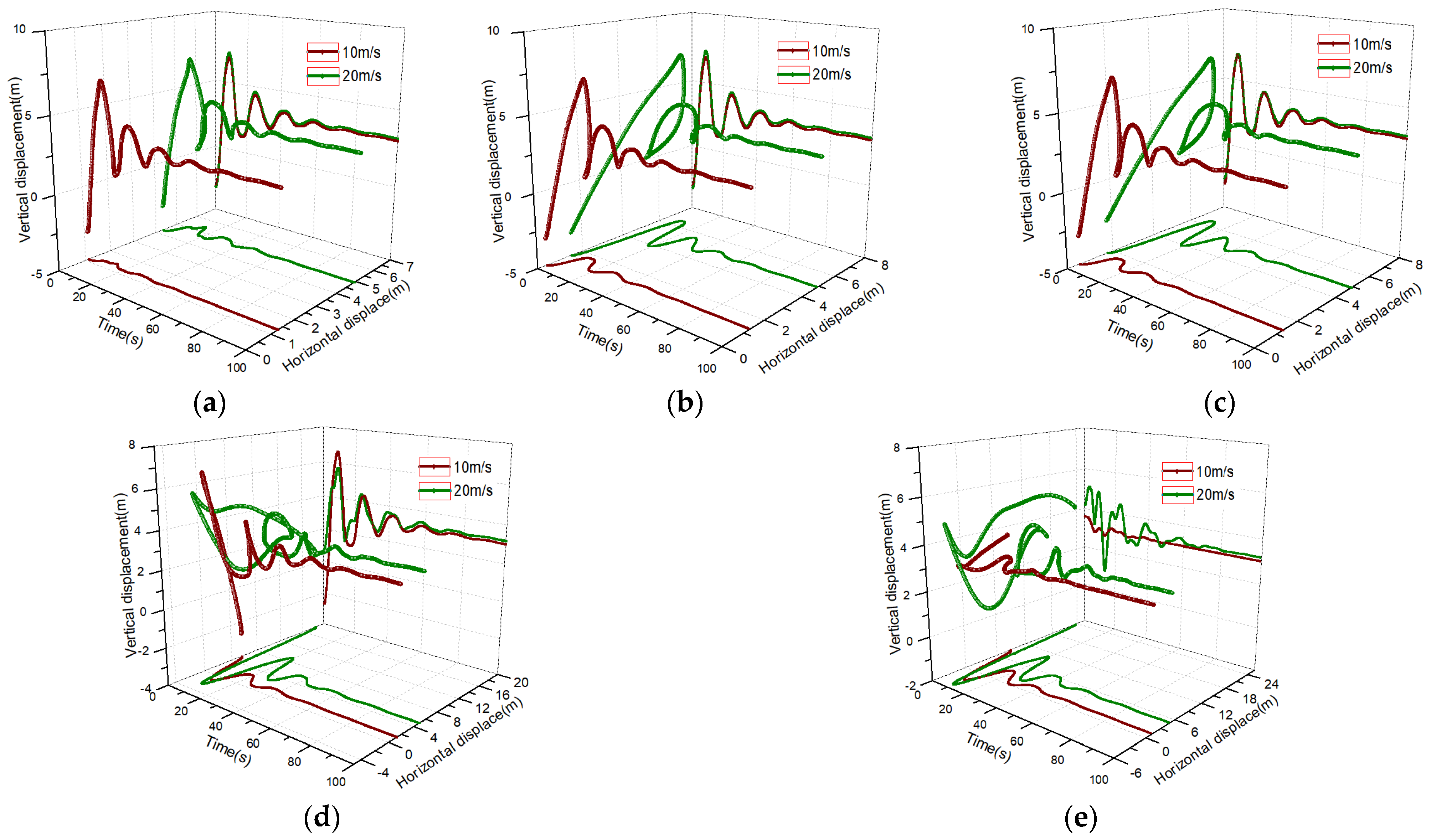
For a particular icing shape, the initial position of the iced conductor was completely different for different wind attack angles. At the moment of ice shedding, the direction of conductor displacement varied greatly. The displacement curves of the crescent-shaped and D-shaped ice-covered conductors under a 10 m/s wind speed and 45°, 90°, and 180° wind attack angles are shown in
Figure 6. For the crescent-shaped ice conductor, its initial position in the horizontal coordinate of a 45° wind attack angle was 1.3 m. And the static position difference of the conductor before and after the ice shedding was very small, so the lateral oscillation amplitude was less than 0.3 m. Due to the influence of the initial position, the lateral oscillation direction of the midpoint position of the ice shedding span was the opposite at 90° and 180° wind attack angles. Therefore, for horizontally arranged transmission lines, the risk of interphase discharges was different for ice shedding. The static longitudinal coordinates of the conductor before and after ice shedding were very small, and the difference in the longitudinal bounce height of the conductor ice shedding under the two angles of attack was less than 0.7 m.
As a hypothetical extreme icing morphology, D-shaped icing had a circular arc on the windward side and a plane on the leeward side. When the iced conductor twisted to form a specific wind attack angle, the wind resistance of the iced conductor changed significantly, and its trajectory after ice shedding became very complex, which is more significantly affected by the airflow. As shown in
Figure 6, the ice shedding bouncing trajectory of D-shaped icing at a 45° wind attack angle was very similar to the crescent case at a 90° wind attack angle. However, due to its larger lift, the longitudinal coordinate of the initial ice shedding position was only −1.6 m, which was less than the −3.5 m under the crescent case, and the longitudinal bounce amplitude of the conductor also decreased by 3.11 m. For the 90° and 180° wind attack angle conditions, under the action of airflow resistance and lifting force, the longitudinal coordinate of the initial ice shedding position of the conductor was not much different from that of the ice shedding steady state, so the difference in longitudinal bounce amplitudes was also very small. As shown in
Table 1, the difference in airflow resistance corresponding to the D-shaped iced conductor at 90° and 180° was very great, so the transverse coordinates of the initial ice shedding position of the conductor were 0.52 m and 8.22 m, respectively. After ice shedding, the transverse motion of the conductor corresponding to the two wind attack angles was completely opposite, and the amplitudes were 1.22 m and 11.71 m, respectively, which increased the discharge risk of horizontally arranging conductors caused by ice shedding bouncing.
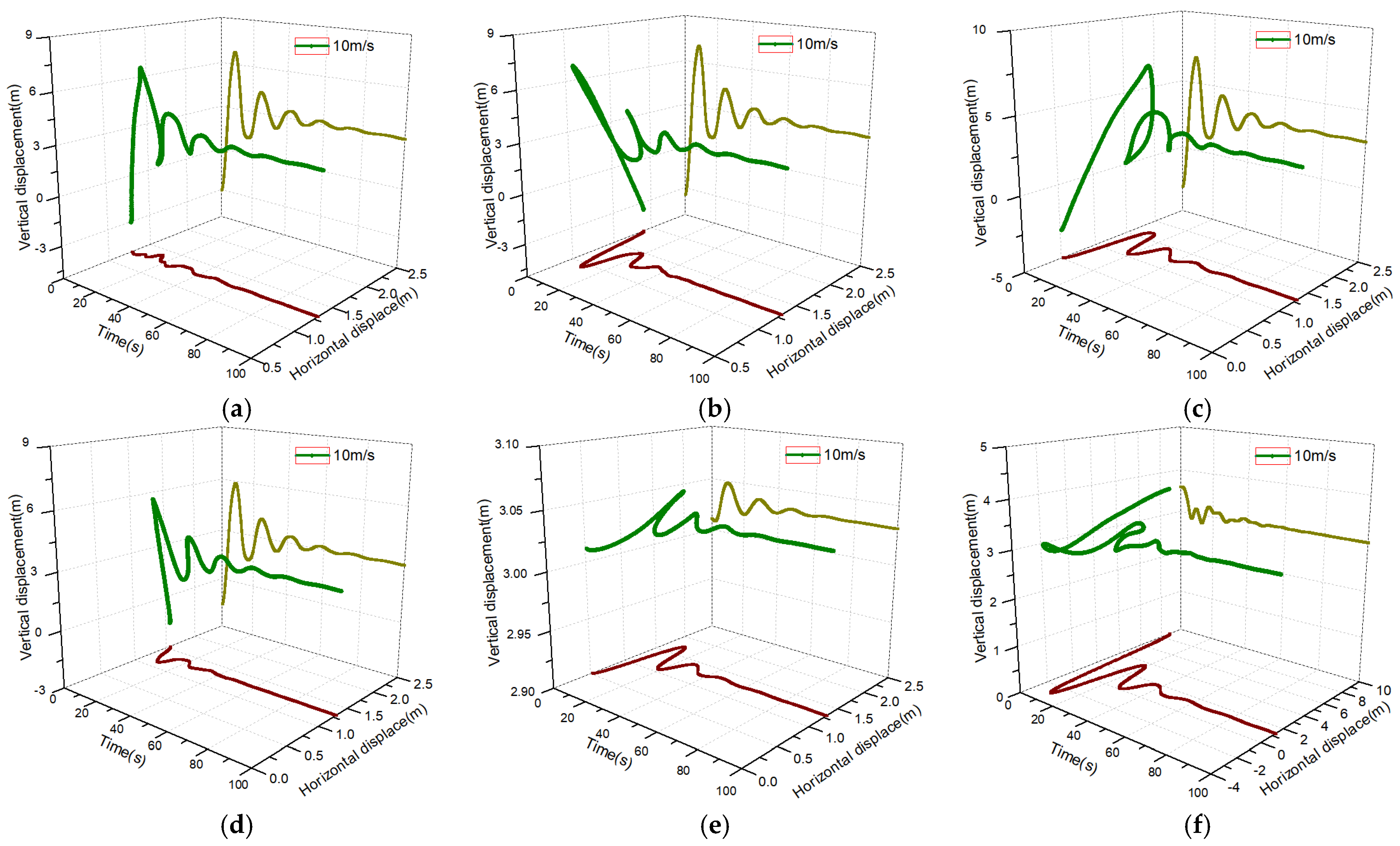
4.3. The Effect of Wind Speed on the Ice Shedding Response of Transmission Lines
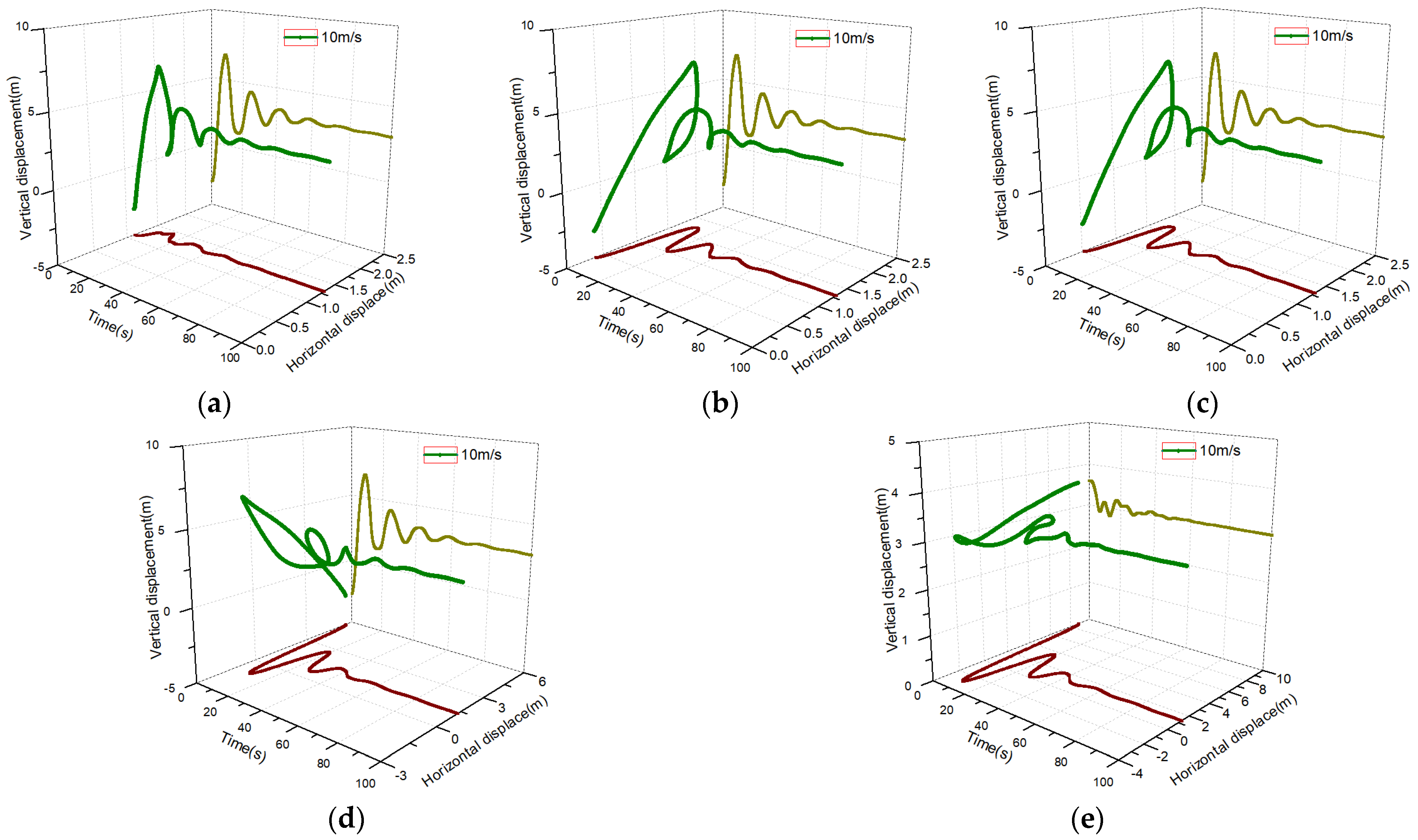
As the source of lift and drag force on the iced conductor, the wind speed will have a great influence on the oscillation process of ice shedding. For the wind speed conditions of 10 m/s and 20 m/s, the bouncing process of ice shedding at a 180° wind attack angle for different ice shapes is shown in
Figure 7. For the circular iced conductor, the longitudinal coordinates of the initial position were basically the same under the action of airflow, and the longitudinal bounce curve was almost the same. Because the airflow resistance under a 20 m/s wind speed was greater, the difference of transverse coordinates of the initial position was 3.21 m, while the difference of transverse bouncing amplitude was less than 1 m. The oscillation curves after ice shedding of elliptical-shaped and crescent-shaped iced conductors were approximate, and the transverse amplitude of the conductor increased significantly with the increasing wind speed, but the difference in longitudinal amplitude was not obvious. Therefore, it is important to pay attention to the distance between the ice shedding conductor and the overhead ground wire diagonally above it.
Compared with the round-shaped, elliptical-shaped, and crescent-shaped conditions, the airflow resistance of fan-shaped and D-shaped conditions increased significantly at a 180° wind attack angle and 20 m/s wind speed, and the direction of horizontal motion after ice shedding was also opposite to the above three cases. And the jumping amplitude increased significantly, with the horizontal coordinates jumping from the initial 18.36 m and 23.6 m to −2.48 m and −4.86 m, respectively. Therefore, it can be observed that the lateral amplitude exceeded 20 m, which represented a high possibility of causing phase-to-phase and phase-to-ground discharge. Under the condition of an airflow velocity of 20 m/s, the longitudinal coordinates of the initial position of the iced conductor were 0.71 m and 4.17 m, respectively. After ice shedding, the fan-shaped iced conductor bounced upwards to 5.75 m, while the D-shaped iced wire bounced downwards to 0.98 m. Compared to the other three shapes of iced conductors, the longitudinal bounce height under strong winds was very small.
Figure 7.
Effect of wind speed on ice shedding bouncing process. (a) round-shaped; (b) crescent-shaped; (c) elliptical-shaped; (d) fan-shaped; (e) D-shaped.
Figure 7.
Effect of wind speed on ice shedding bouncing process. (a) round-shaped; (b) crescent-shaped; (c) elliptical-shaped; (d) fan-shaped; (e) D-shaped.
5. Discussion
This paper established a continuous multi-span overhead transmission line model using finite element numerical simulation techniques to investigate the dynamic response of transmission lines during ice shedding under strong wind conditions. Furthermore, some complex factors were analyzed, such as high wind speeds, ice shapes, and wind angles on the bounce process of transmission lines, aiming to explore the risks posed by the ice shedding bounce of power lines under complex conditions.
- (1)
The calculation of lift and drag forces on the iced conductor is fundamental for understanding the dynamic response of conductors during ice shedding under strong wind conditions. Additionally, the stability of conductor galloping was assessed based on Den Hartog’s vertical vibration theory and Nigol’s torsional vibration theory, both of which rely on the concept of negative damping. In this study, finite element methods were utilized to compute the lift and drag forces on iced conductors under different conditions. It was found that fan-shaped and D-shaped ice covers exhibited sharp changes in curvature and planarity, with the strongest hindrance to airflow occurring at a 180° attack angle, resulting in the highest drag force on iced conductors. At this angle, the drag force on D-shaped ice covers could exceed ten times that of the elliptical and crescent-shaped samples. The unique shape of D-shaped icing resulted in positive lift between 0–180°, peaking around 135°. These results closely match those observed in wind tunnel experiments [
24]. At a wind angle of 225°, the airflow increased the directional additional load by one-third, leading to an increase in the conductor’s elastic potential energy.
- (2)
Due to variations in meteorological conditions and conductor characteristics, natural icing can exhibit significant differences in morphology, resulting in shapes such as circular, crescent, D-shaped, fan-shaped, and elliptical. Under the same icing mass (volume) and wind speed conditions, the dynamic response process of conductors after ice shedding becomes highly complex. Under the combined influence of airflow and icing, conductors possess both longitudinal and lateral elastic potential energy. Generally, iced conductors with circular, crescent, and elliptical shapes have smooth outer curves, resulting in minimal lateral displacement under wind forces. At a wind speed of 10 m/s, their maximum vertical bounce heights were 9.94 m, 10.6 m, and 10.07 m, respectively. The maximum lateral bounce heights were only 0.31 m, 1.16 m, and 1.36 m, indicating minimal differences from the no-wind condition. The maximum longitudinal displacement was approximately 1.62 times the difference in longitudinal positions before and after ice shedding, slightly smaller than the value of 1.8 reported in the literature [
14], but with minimal differences from the literature [
25]. Except for the crescent-shaped ice cover at a 45° wind angle, corresponding to the minimum bounce condition, the maximum lateral displacement was approximately 1.56 times the difference in lateral positions before and after ice shedding.
For fan-shaped and D-shaped icing, the airflow resistance significantly increased at a 180° attack angle. At a wind speed of 10 m/s, their maximum vertical bounce heights were 0.79 m and 9.32 m, respectively, while the maximum lateral bounce heights were 11.7 m and 6.65 m. At a wind speed of 20 m/s, the maximum lateral bounce heights reached 28.5 m and 20.85 m, respectively. The maximum lateral displacement was approximately 1.55 times the difference in lateral positions before and after ice shedding. The bounce distances exceeded the lateral spacing between transmission lines, greatly increasing the possibility of interphase discharge.