Abstract
This paper proposes a new spacecraft in-orbit launch design using a nonlinear configuration to utilize nonlinear dynamics for the enhancement of vibration isolation and launch performance. The in-orbit launch device has four springs, where the stroke directions of two springs are perpendicular to the launch direction so as to produce nonlinearity with negative stiffness for enhancing the launch velocity. The other two springs are designed to counterbalance the above negative stiffness when the launch outlet is shut down, leading to quasi-zero dynamic stiffness for vibration isolation enhancement. The dynamic equations of the in-orbit launch device for both the on- and off-launch are presented. Then the performance enhancement of both the vibration isolation and launch performance is thoroughly investigated via comparative study and parametric study. The resonance peak is reduced by 4.16 dB, the effective vibration isolation bandwidth is increased by 57%, and the launch speed is increased 1.64 times. This validates the performance improvement of the new launch device design and presents a useful guideline for application.
1. Introduction
With the rapid development of space technology, there is a growing demand for more efficient and reliable in-orbit launch systems [1,2]. In-orbit launch systems allow spacecraft to be launched directly in earth orbit or deep space, and they offer advantages over traditional ground-based launch methods, such as high cost effectiveness, low environmental impact, and short launch preparation time [3,4]. However, how to improve the launch speed while ensuring effective vibration isolation to protect sensitive payloads from damage remains a key challenge in the design of in-orbit launch systems.
Traditional vibration isolation systems are designed mostly based on linear dynamics design and face problems of low efficiency when dealing with large-amplitude vibrations and dynamic payload changes [5,6]. These systems often fail to provide ideal vibration isolation performance across a wide frequency range, especially in terms of low-frequency vibration. The limitations of this linear design approach have prompted researchers to explore the characteristics of nonlinear dynamics, especially the applications of nonlinear vibration isolation systems in the hope of achieving better vibration isolation performance.
Nonlinear vibration isolation technology in the form of quasi-zero stiffness (QZS) isolators has been proven to effectively reduce the system’s natural frequency and isolate vibrations across a wider frequency range [7,8]. This particularly applies to the low frequency vibrations commonly encountered in in-orbit launch systems. For example, Ye et al. [9] proposed an optimized QZS vibration isolation system with a multi-cam-roller mechanism, which demonstrated superior low-frequency vibration isolation performance. Zhao et al. [10] designed an advanced QZS isolator with three pairs of oblique springs, which offered enhanced design flexibility and superior performance over conventional one-pair and linear isolators. Wen et al. [11] presented a QZS system with an oblique linear spring structure, which showed enhanced low-frequency vibration isolation ability by expanding the zero stiffness range. Gatti et al. [12,13] designed an X-shaped-spring suspension nonlinear isolator, which could achieve QZS and a broader isolation frequency band through a quintic characteristic. Liu et al. [14] proposed a bi-directional horizontal QZS isolation system utilizing pre-compressed oblique spring mechanisms, showing superior low-frequency vibration isolation performance. Yu et al. [15] designed a five-spring QZS vibration isolator, in which four oblique springs provided negative stiffness and one vertical spring provided positive stiffness. The results show that the initial frequency of isolation could be reduced to 2.82 Hz. Yan et al. [16] proposed a new QZS vibration isolator composed of a link-oblique spring negative stiffness mechanism and a linear spring, which had a significantly better low-frequency isolation effect while maintaining high-frequency isolation ability compared with linear isolators. Chai et al. [17] designed a new “X” type QZS isolator using a spring arrangement method of tunable contact mechanism based on an X-shaped anti-vibration structure. This isolator was better than a linear isolator in the ultra-low frequency range with lower resonance frequency and wider isolation band. Han et al. [18] combined the Miura origami unit to propose a QZS vibration isolator composed of four rods and two springs. The structure could effectively reduce the formant and expand the effective vibration isolation band due to its nonlinear stiffness and nonlinear vertical damping. Zhou et al. [19] proposed a new type of passive asymmetric QZS isolator consisting of two linear springs in parallel with a negative stiffness element. Experimental results showed that the isolator had a smaller initial frequency and lower displacement transmissibility than the linear model. Yan et al. [20] proposed a lever-type QZS vibration isolator, using magnetic springs to achieve QZS characteristics. It was found that reasonable configuration of structural parameters could greatly improve vibration isolation performance.
The aforementioned studies indicate that the design of QZS isolators utilizes the nonlinear force-displacement relationship, which can significantly reduce the amplitude of vibrations transmitted to the payload, thereby protecting sensitive equipment from vibrational damage during the in-orbit and launch process. Furthermore, nonlinear characteristics can provide new ideas for in-orbit launch design.
Traditional linear launch system designs are often limited by their dynamic performance and cannot achieve significant launch speed improvement without sacrificing system stability and safety. In previous studies, nonlinear characteristics (especially the negative stiffness phenomenon) have been shown to significantly enhance the dynamic response of the system. The relationship of the enhancement mechanism of the negative stiffness mechanism, consisting of mechanical spring [21,22], buckled beam [23,24], magnetic structure [25,26] and bionic structure [27,28], to the dynamic response of nonlinear system has been widely studied. For example, Andrea et al. [29] replaced the traditional negative stiffness spring pair with super-elastic springs and found that the negative stiffness mechanism presented a dynamic amplification effect. Zhang et al. [30] constructed a negative stiffness mechanism based on magnetic springs, which was sensitive to micro-displacement and could amplify the response in the resonance region. Dai et al. [31] proposed a completely symmetrical cross-type structure with equal rod length to achieve negative stiffness characteristics. Results showed that the subharmonic response could be enhanced by adjusting the structural parameters of the cross-type structure. Therefore, compared with the traditional linear design, a nonlinear configuration can achieve higher system flexibility and adaptability under certain conditions, thereby improving the overall launch performance.
To address the evident limitations of traditional linear launch system designs in terms of vibration isolation and launch performance, this paper presents a novel aircraft in-orbit launch design utilizing nonlinear dynamic characteristics to enhance vibration isolation and launch performance. The design configures four springs, two of which are oriented perpendicularly to the launch direction to produce negative stiffness, thereby providing additional kinetic energy at critical moments to increase launch speed. The other two springs are designed to balance the aforementioned negative stiffness when the launch outlet is closed, achieving quasi-zero dynamic stiffness to enhance vibration isolation performance. By integrating quasi-zero stiffness isolation technology with nonlinear dynamics in the in-orbit launch system, this research not only overcomes the limitations of traditional linear design methods but also demonstrates how sophisticated nonlinear design can enhance launch speed and achieve efficient vibration isolation. These findings provide valuable insights for the further development of in-orbit launch technology and offer new ideas for future system design and optimization.
This paper is organized as follows. Section 2 presents the research model of the proposed aircraft in-orbit launch design. The governing equations for vibration isolation and in-orbit launch are derived in Section 3. Section 4 performs the performance comparison with linear design. Parametric study is conducted in Section 5. The influences on the vibration isolation and launch speed performance of the structure parameters are discussed in detail. All the findings are summarized in Section 6.
2. Design Concept
Figure 1a presents the spacecraft’s in-orbit launch design for in-orbit vibration isolation. The base frame is fixedly connected within the in-orbit launch system. When the launch outlet is closed, the spacecraft is supported by four springs. Two vertical springs, and , provide negative stiffness, and, together with the other two transverse springs, and , form quasi-zero stiffness characteristics. Therefore, these four springs constitute a quasi-zero stiffness (QZS) vibration isolation system to isolate the vibration generated by the base framework.
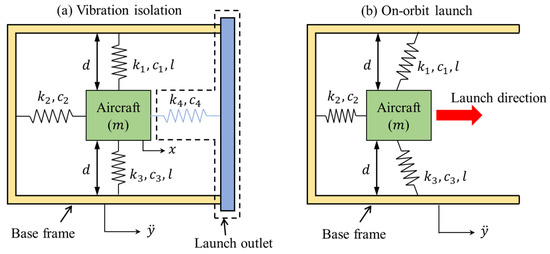
Figure 1.
Schematic of the spacecraft in-orbit launch design: (a) vibration isolation and (b) in-orbit launch.
Figure 1b shows the spacecraft’s in-orbit launch design for in-orbit launch. When the launch outlet is open, the spacecraft is supported by the two pre-stretched vertical springs and and the pre-compressed transverse spring . The vertical springs and produce negative stiffness to enhance launch speed. As shown in Figure 2, first, in the initial state (State 1), the spacecraft is prepared for release and then disconnects from these three springs when it moves to the position of State 2. Finally, the spacecraft leaves the base frame (the in-orbit launch system) with an initial velocity .
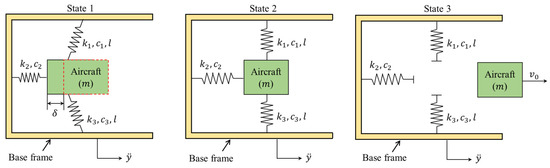
Figure 2.
Schematic of the in-orbit launch process.
3. Mathematical Modeling
In this section, to understand the dynamic insight of the spacecraft in-orbit launch design, the governing equations for vibration isolation and in-orbit launch subjected to fundamental harmonic excitation are formulated.
3.1. Dynamic Equations When the Launch Is Off
As shown in Figure 1a, in the vibration isolation design, the distances between the top and bottom of the base frame and the spacecraft are both , and the original lengths of the vertical springs and are both . When the spacecraft is in its initial position, the two transverse springs and are at their original lengths, and the two vertical springs are perpendicular to the direction of the transverse springs. The damping coefficients of the four springs are , respectively. is the distance by which the spacecraft deviates from its initial position. The kinetic energy , potential energy , and dissipation function of the system are expressed as follows:
The governing equation for vibration isolation obtained from the Lagrange equation is:
Based on the above equation, it can be seen that the two vertical springs and have the same effect on the vibration isolation system, and the two transverse springs and also have the same effect on the vibration isolation system. For the convenience of subsequent analysis, let:
Then, Equation (2) can be simplified as:
According to reference [32], the parameter condition for achieving quasi-zero stiffness is . Define the stiffness ratio , and length ratio ; then the condition for quasi-zero stiffness is:
For a general quasi-zero stiffness vibration isolation system,. Define the vibration transmissibility thusly:
Vibration isolation performance is evaluated by the vibration transmissibility : the smaller is, the better the vibration isolation performance. In the subsequent study of vibration isolation performance, it is assumed that the base excitation is a simple harmonic excitation , where is the excitation amplitude and is the excitation frequency.
3.2. Dynamic Equations When the Launch Is On
As shown in Figure 2, in the in-orbit launch design, the initial state (State 1) involves the transverse spring being pre-compressed by . Thus, the total elastic potential energy of the system at initial state is:
When Equation (5) is substituted with Equation (9), the following occurs:
The spacecraft is released when it moves to State 2. According to the law of energy conservation, the elastic potential energy is completely converted into kinetic energy at State 2:
Therefore, the launch velocity is:
It is noteworthy from the above equation that when the pre-compression length of the transverse spring is zero, since (), the two vertical springs have a pre-compression length. Hence the system still possesses unreleased elastic potential energy, which can also provide kinetic energy for launch. As increases, the pre-compression length of the vertical springs is actually reduced, and the reduced potential energy is not enough to balance the increased potential energy from the compression of the transverse spring, resulting in a decrease in the system’s total potential energy and launch velocity. During this process, there exists a minimum point . When , the launch velocity increases with . When the pre-compression length reaches the critical value (satisfying ), the system’s elastic potential energy is exactly equal to that when . Thereafter, the launch velocity increases approximately in direct proportion to . Moreover, it is obvious that the stiffness ratio determines the value and .
4. Performance Comparison
To further investigate the vibration isolation and launch velocity performance of the proposed spacecraft in-orbit launch design, this section will compare the proposed design with traditional linear design to demonstrate the advantages of the proposed design in enhancing performance. The mathematical model is validated through MSC Adams 2020 software in Appendix A. In the subsequent simulation calculations, the numerical solutions are solved through the 4th Runge–Kutta method subjected to the frequency-sweeping base excitations from 0.1 Hz to 5 Hz with a rate of 0.001 Hz/s.
4.1. Vibration Isolation Performance Comparison
Figure 3 shows the vibration transmissibility of linear design and the proposed design subjected to different fundamental excitations where amplitude . Table 1 lists the structure parameters. The selection of parameters considers the realization condition of quasi-zero stiffness (Equation (7)). It can be seen that the peak frequency of the proposed design increases with the increase of the base excitation amplitude, and the peak value of the vibration transmissibility corresponding to the peak frequency also gradually increases. However, the high-frequency low-orbit curves under these three excitations completely overlap and are much lower than those resulting from the linear design, exceeding 30 dB. With the linear design, once the structural parameters are determined, the vibration transmissibility is uniquely determined and unaffected by the base excitation. The peak frequency of the linear design is 2.25 Hz, with a corresponding peak amplitude of 36.43 dB. When the base excitation amplitude , the peak frequency of the proposed design is 0.96 Hz, with a peak amplitude of 32.27 dB. Compared to the linear design, the peak is reduced by 4.16 dB, and the effective vibration isolation bandwidth is increased by 57%. However, when the base excitation amplitude , the peak amplitude of the proposed design is slightly larger than that of the linear design, and the peak frequency is only slightly reduced compared to the linear design. This indicates that the vibration isolation performance of the proposed design under small amplitude excitation is significantly better than that of traditional linear vibration isolator. Therefore, in view of the common micro-vibration disturbance of spacecraft, the proposed design can effectively isolate the wide-band vibration to ensure the safety of spacecraft on orbit.
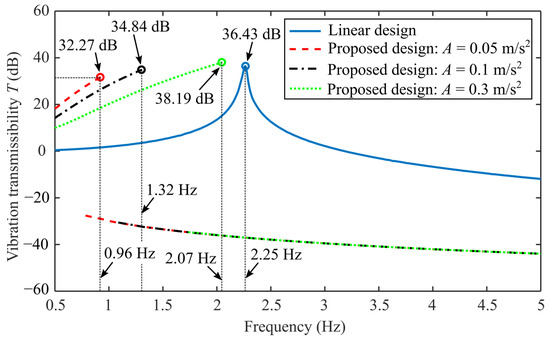
Figure 3.
The vibration transmissibility of the linear design and the proposed design with different excitation amplitudes .

Table 1.
The structure parameters for vibration isolation performance comparison.
4.2. Launch Velocity Comparison
Considering the realization condition of quasi-zero stiffness (Equation (7)), two sets of different parameter values shown in Table 2 are selected for comparative analysis of the launch velocity . Figure 4 shows the launch velocity curve versus pre-compression length under the two parameter sets. The comparison of parameter Set 1 shows that for linear design, the launch velocity is strictly proportional to the pre-compression length, with a slope of 10. Since the original length of the two vertical springs is greater than the vertical distance , there is pre-compression in the two vertical springs at the initial state. Thus, there is elastic potential energy at for the proposed design, which can be converted into launch kinetic energy. At the beginning (), the compression amount of the two vertical springs decreases with the increase of the transverse spring pre-compression length , and the reduced elastic potential energy is greater than that increased by the transverse spring compressing. Therefore, the total elastic potential energy of the system is lower than that of the initial state, and the launch velocity is also lower than the initial launch velocity. In this process, when , the launch velocity decreases with the increase of ; when , the launch velocity increases with the increase of . After , the launch velocity approximately shows a linear increasing relationship with , with a slope of 21.55, which means that the launch velocity of the proposed design is increased 1.16-fold compared to the linear design. Since the stiffness ratio of the two parameter sets is the same, the results of parameter Set 2 also show the same trend as the launch velocity curve of parameter Set 1. The slope of launch velocity relative to is approximately 26.38, which is 1.64 times higher than that of linear design.

Table 2.
The structure parameters for launch velocity comparison.
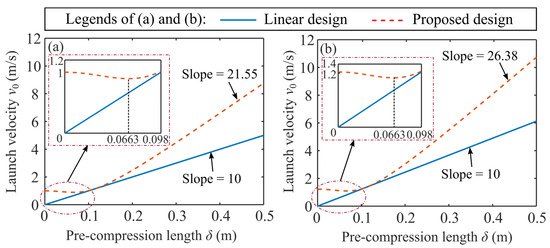
Figure 4.
The launch velocity curve versus pre-compression length of the linear design and the proposed design with (a) parameter set 1 and (b) parameter set 2.
5. Parametric Study
In this section, parametric study will be conducted to further investigate the impact of structural parameters on vibration isolation and launch velocity performance.
5.1. Comprehensive Study of Vibration Isolation
In the analysis of vibration isolation performance, the influence of vertical spring stiffness and damping on vibration isolation performance is mainly studied. Initially the conditions for achieving quasi-zero stiffness are disregarded, and only the vertical spring stiffness is changed, allowing for exploration of the variation of the vibration transmissibility in relation to . Figure 5a shows the vibration transmissibility curve under different , and the values of other parameters are the same as those shown in Table 1. The base excitation amplitude is . It can be seen that when changes from 1000 N/m to 2000 N/m, the peak of the vibration transmissibility curve gradually shifts to the left and the low orbit gradually decreases, indicating an improvement in vibration isolation performance. However, when continues to increase, the peak of the vibration transmissibility curve moves to the right and the low orbit increases, indicating a deterioration in vibration isolation performance.
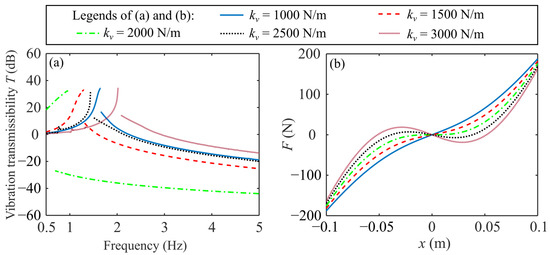
Figure 5.
(a) The vibration transmissibility and (b) the nonlinear restoring force with different of the proposed design.
To understand the essence of this changing pattern, the relation curve between nonlinear restoring force and displacement is drawn in Figure 5b. It can be seen that when , the negative stiffness provided by the two vertical springs is insufficient to offset the positive stiffness of the transverse springs, thus exhibiting positive stiffness characteristics near . The smaller is, the greater the positive stiffness, making the system tend towards a linear vibration isolation system. When , according to Equation (7), the condition for quasi-zero stiffness is exactly met, showing zero stiffness characteristics near . Figure 5a indicates that under this condition, the peak is the smallest, the low-frequency range is the lowest, and the vibration isolation performance is the best. When , the negative stiffness is too large, and the system exhibits negative stiffness near . The vibration transmissibility curve displays abnormal distortion, and the vibration isolation performance becomes worse. From the above analysis, it is clear that the best vibration isolation performance is achieved when the structural parameters satisfy the condition for quasi-zero stiffness.
When considering quasi-zero stiffness characteristics, the stiffness ratio and the length ratio have a definite relationship: ; thus, it can be said that the stiffness ratio and the length ratio have the same influence on the vibration isolation performance. Then, the influence of stiffness ratio on vibration isolation performance is studied by changing the parameter while keeping and unchanged. Based on the deterministic relation , the length ratio changes with the stiffness ratio , meaning that changes with . Figure 6 shows the vibration transmissibility curve under different stiffness ratio . The values of other parameters are the same as those shown in Table 1. The base excitation amplitude is . It can be seen that with the increase of stiffness ratio , the peak frequency gradually increases, and the peak amplitude also gradually increases. However, the stiffness ratio has no effect on the low-orbit region. This indicates that a smaller stiffness ratio provides better vibration isolation performance. However, as the transverse spring stiffness and vertical distance remain unchanged, a smaller stiffness ratio means a smaller vertical spring stiffness and a larger vertical spring original length , implying that the vertical springs are very soft, which does not meet the requirements of practical installation conditions. Therefore, it is necessary to consider the structural design requirements of vertical spring while reducing the stiffness ratio to obtain better vibration isolation performance.
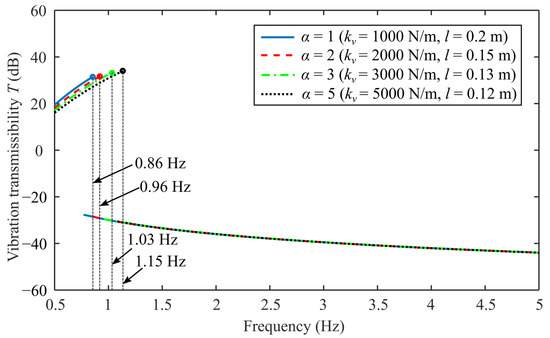
Figure 6.
The vibration transmissibility with different (configurations of and ) of the proposed design.
Finally, the effect of vertical spring damping on vibration isolation performance is discussed. Figure 7 shows the vibration transmissibility curve under a different , and the values of other parameters are the same as those shown in Table 1. The base excitation amplitude is . Results show that the damping coefficient has little influence on vibration isolation performance. With the increase of damping , the peak frequency only decreases slightly, and the peak amplitude also decreases slightly. Compared with the influence of stiffness , the influence of damping can be ignored.
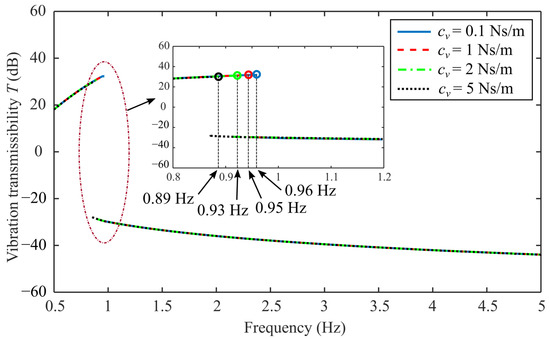
Figure 7.
The vibration transmissibility with different of the proposed design.
5.2. Comprehensive Study of Launch Velocity
In the previous section on vibration isolation performance parameter study, it was found that the vibration isolation performance is best when the structural parameters satisfy the quasi-zero stiffness condition. Based on the quasi-zero stiffness characteristics, this section will delve into the impact of structural parameters on launch velocity in detail. According to Equation (12), the structural parameters affecting the launch velocity include vertical spring stiffness , vertical spring original length , transverse spring stiffness , and vertical distance . Under the consideration of quasi-zero stiffness characteristics, the stiffness ratio and the length ratio satisfy a definite relationship . Thus, these four parameters are interdependently determined. Then, by keeping and unchanged, the effect of stiffness ratio on the launch velocity is studied by changing the parameter (with changing correspondingly with ). Figure 8 shows the launch velocity curve versus pre-compression length with a different . It is seen that when is less than 0.1 m, the launch velocity does not change much with the pre-compression length . In this range, the larger is, the smaller the launch velocity is. When is greater than 0.15, the slope of the second half of the launch velocity curve gradually increases with the increase of , which means that a small pre-compression can bring a higher launch velocity .
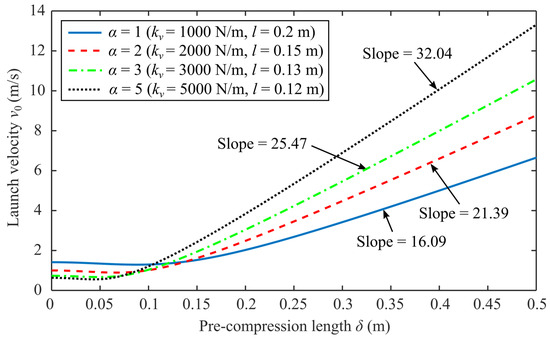
Figure 8.
The launch velocity curve versus pre-compression length with different (configurations of and ) of the proposed design.
Therefore, it can be concluded that when the pre-compression of the transverse spring is small, a smaller stiffness ratio can obtain a higher launch velocity . When the pre-compression of transverse spring is large, the higher stiffness ratio can produce the higher launch velocity . Moreover, the critical value of stiffness ratio should be determined according to different structural parameters.
6. Conclusions
This paper proposed a new in-orbit launch design utilizing nonlinear dynamics to enhance vibration isolation and in-orbit launch performance. The design consists of four springs, of which two vertical springs have a travel direction perpendicular to the launch direction to produce negative stiffness and increase launch speed. Two additional transverse springs are used to balance the negative stiffness when the launch outlet is closed, thus achieving quasi-zero stiffness to enhance vibration isolation performance. Based on the governing equation of vibration isolation and in-orbit launch validated by Adams, this paper comprehensively analyzes the enhancement effect of vibration isolation and launch performance by comparing with traditional linear design. The resonance peak is reduced by 4.16 dB, the effective vibration isolation bandwidth is increased by 57%, and the launch speed is increased 1.64-fold. The subsequent parametric study shows that reducing the stiffness ratio can obtain better vibration isolation performance while considering the structural design requirements of the vertical spring and quasi-zero stiffness conditions. In addition, when the pre-compression of the transverse spring is small, a smaller stiffness ratio can produce a higher launching speed. When the transverse spring pre-compression is large, the higher launch speed requires a larger stiffness ratio. These results validate the effect of the proposed in-orbit launch design on vibration isolation and launch speed performance, and provide useful guidance for subsequent applications.
Author Contributions
Conceptualization, B.W.; Methodology, X.Z. and W.T.; Software, W.T.; Validation, L.D.; Formal analysis, X.Z.; Data curation, W.T. and L.D.; Writing—original draft, X.Z.; Writing—review & editing, W.T. and B.W.; Supervision, B.W.; Funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Open Fund of the State Key Laboratory of Robotics and the Innovation Fund of the Maritime Defense Technology Innovation Center (Grant No. JJ2021-719-01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Xu Zhou was employed by the company Space Star Technology Co., Ltd. The remaining authors declare that the re-search was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. Model Validation Using the MSC Adams Software
The software program MSC Adams 2020 is used to validate the mathematical model of the spacecraft in-orbit launch design. Since the governing equation of launch velocity is a definite expression that can be calculated directly with parameter values, it does not require validation. Only the governing equation of vibration isolation is validated in this appendix. Figure A1 shows the dynamic model of the proposed spacecraft in-orbit launch design established in MSC Adams. The structure parameters are selected from Table 1. Figure A2 shows the displacement , velocity , and acceleration time-domain responses obtained by Adams and numerical results solved by the 4th Runge–Kutta method under forward swept harmonic base excitation from 0.1 Hz to 5 Hz with amplitude . The sweeping rate is 0.05 Hz/s. It can be seen that the numerical results are in good agreement with the Adams results for displacement , velocity , and acceleration .
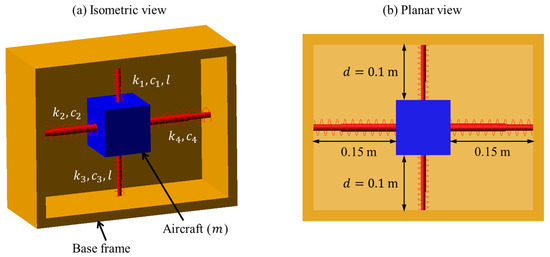
Figure A1.
The (a) isometric view and (b) planar view of the proposed spacecraft in-orbit launch design for vibration isolation in Adams software.
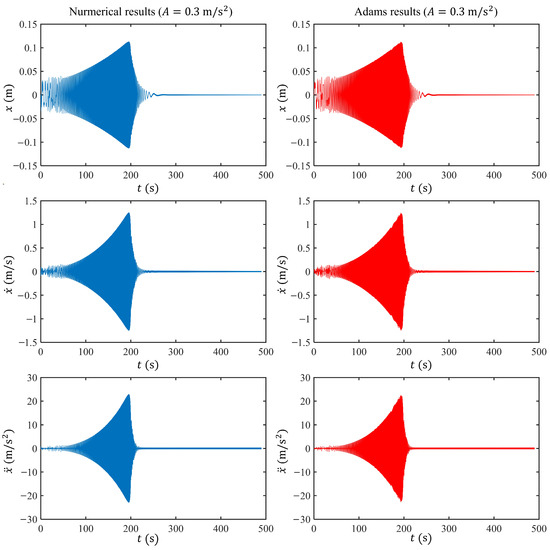
Figure A2.
The displacement , velocity , and acceleration time-domain responses obtained by Adams and numerical results solved by the 4th Runge–Kutta method under forward swept harmonic base excitation from 0.1 Hz to 5 Hz with the amplitude .
References
- Li, W.-J.; Cheng, D.-Y.; Liu, X.-G.; Wang, Y.-B.; Shi, W.-H.; Tang, Z.-X.; Gao, F.; Zeng, F.-M.; Chai, H.-Y.; Luo, W.-B.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Prog. Aerosp. Sci. 2019, 108, 32–120. [Google Scholar] [CrossRef]
- Chiarelli, M.R.; Borrometi, F.B.; Cipolla, V.; Binante, V.; Abu Salem, K.; Palaia, G. Design and Feasibility Study of Novel Flying Wing Carrier for Launching Small Satellites in Low Earth Orbit. Appl. Sci. 2023, 13, 4712. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, P.; Wu, C.; Chen, K.; Ren, W.; Liu, L.; Tang, Y.; Ji, C.; Sang, X. SIASAIL-I solar sail: From system design to on-orbit demonstration mission. Acta Astronaut. 2022, 192, 133–142. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, C.; Li, J.; Guan, Y.; Chen, S.; Zhang, L. Research on Design, Simulation, and Experiment of Separation Mechanism for Micro-Nano Satellites. Appl. Sci. 2022, 12, 5997. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wu, C. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms. Appl. Math. Mech. 2022, 43, 1045–1062. [Google Scholar] [CrossRef]
- Tong, W.; Wei, B.; Moshrefi-Torbati, M.; Zhou, X.; Yurchenko, D.; Yang, K. Investigation of a monostable nonlinear vibration isolator with the inertia-elastic boundary. Commun. Nonlinear Sci. Numer. Simul. 2024, 132, 107887. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Li, J. Negative stiffness devices for vibration isolation applications: A review. Adv. Struct. Eng. 2020, 23, 1739–1755. [Google Scholar] [CrossRef]
- Wang, S.; Xin, W.; Ning, Y.; Li, B.; Hu, Y. Design, experiment, and improvement of a quasi-zero-stiffness vibration isolation system. Appl. Sci. 2020, 10, 2273. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Wen, G.; He, J.; Liu, J.; Lin, Y. Design, analysis and semi-active control of a quasi-zero stiffness vibration isolation system with six oblique springs. Nonlinear Dyn. 2021, 106, 309–321. [Google Scholar] [CrossRef]
- Gatti, G. A nonlinear quasi-zero stiffness vibration isolator with quintic restoring force characteristic: A fundamental analytical insight. J. Vib. Control 2023, 1–14. [Google Scholar] [CrossRef]
- Gatti, G.; Svelto, C. Exploiting nonlinearity for the design of linear oscillators: Application to an inherently strong nonlinear X-shaped-spring suspension. Mech. Syst. Signal Process. 2023, 197, 110362. [Google Scholar] [CrossRef]
- Liu, T.; Li, A.; Zhang, H. Quasi-zero stiffness interval optimization design and dynamics analysis of a new bi-directional horizontal isolation system. Mech. Syst. Signal Process. 2024, 206, 110852. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K. Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs. Arch. Civ. Mech. Eng. 2020, 20, 67. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.-X.; Wang, S.; Zhao, L.-C.; Gao, Q.-H.; Tan, T.; Zhang, W.-M. Large stroke quasi-zero stiffness vibration isolator using three-link mechanism. J. Sound Vib. 2020, 478, 115344. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Chao, X. X-shaped mechanism based enhanced tunable QZS property for passive vibration isolation. Int. J. Mech. Sci. 2022, 218, 107077. [Google Scholar] [CrossRef]
- Han, H.; Sorokin, V.; Tang, L.; Cao, D. A nonlinear vibration isolator with quasi-zero-stiffness inspired by Miura-origami tube. Nonlinear Dyn. 2021, 105, 1313–1325. [Google Scholar] [CrossRef]
- Zhou, X.; Zhao, D.; Sun, X.; Yang, X.; Zhang, J.; Ni, T.; Tang, K. An asymmetric quasi-zero stiffness vibration isolator with long stroke and large bearing capacity. Nonlinear Dyn. 2022, 108, 1903–1930. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S.; Zhang, W. Lever-type quasi-zero stiffness vibration isolator with magnetic spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, W.; Gu, H.; Deng, E.; Wang, X.; Song, C. Force transmissibility of a 6-DOF passive quasi-zero stiffness vibration isolation platform. J. Mech. Sci. Technol. 2021, 35, 2313–2324. [Google Scholar] [CrossRef]
- Lan, C.-C.; Yang, S.-A.; Wu, Y.-S. Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. J. Sound Vib. 2014, 333, 4843–4858. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Seepersad, C.; Wilson, P.S. Analytical and Experimental Investigation of Buckled Beams as Negative Stiffness Elements for Passive Vibration and Shock Isolation Systems. J. Vib. Acoust. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Q.; Zhang, Z.; Zhou, X. An experiment investigation on the effect of Coulomb friction on the displacement transmissibility of a quasi-zero stiffness isolator. J. Mech. Sci. Technol. 2019, 33, 121–127. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech. Syst. Signal Process. 2018, 100, 135–151. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhao, C.; Wu, C.; Wang, K.; Wang, P. A vari-stiffness nonlinear isolator with magnetic effects: Theoretical modeling and experimental verification. Int. J. Mech. Sci. 2018, 148, 745–755. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X.; Dai, H.; Li, F.-M. Subharmonics and ultra-subharmonics of a bio-inspired nonlinear isolation system. Int. J. Mech. Sci. 2019, 152, 167–184. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X.; Guo, Y. Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints. Nonlinear Dyn. 2019, 95, 445–464. [Google Scholar] [CrossRef]
- Salvatore, A.; Carboni, B.; Lacarbonara, W. Nonlinear dynamic response of an isolation system with superelastic hysteresis and negative stiffness. Nonlinear Dyn. 2022, 107, 1765–1790. [Google Scholar] [CrossRef]
- Zhang, F.; Xu, M.; Shao, S.; Xie, S. A new high-static-low-dynamic stiffness vibration isolator based on magnetic negative stiffness mechanism employing variable reluctance stress. J. Sound Vib. 2020, 476, 115322. [Google Scholar] [CrossRef]
- Dai, H.; Cao, X.; Jing, X.; Wang, X.; Yue, X. Bio-inspired anti-impact manipulator for capturing non-cooperative spacecraft: Theory and experiment. Mech. Syst. Signal Process. 2020, 142, 106785. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).