Weighted Robust Tensor Principal Component Analysis for the Recovery of Complex Corrupted Data in a 5G-Enabled Internet of Things †
Abstract
1. Introduction
- This work presents an enhanced method for multivariate data reconstruction in 5G-operating IoTs. A TRPCA is combined with TC to enhance the method’s ability to handle missing data, noise, or missing values. This unique approach leverages correlations among multiple attributes to improve reconstruction performance.
- This study introduces a weighted approach to TC and the TRPCA, offering a means of handling singular values. In contrast to traditional methods, the proposed approach uses weighted tensor singular value thresholding (WTSVT) to shrink singular values based on their importance, potentially boosting reconstruction accuracy.
- The proposed approach effectively tackles complex types of corrupted data, such as mixture noise, outliers, and missing values, and stands out in comparison to other models.
2. Related Work
2.1. Data Reconstruction with Missing Values
2.2. Noise and Outlier Reduction Using Robust Principal Component Analysis
2.3. Primary Challenges in 5G-Enabled IoTs
3. Preliminaries
3.1. Introduction to Tensors
| Algorithm 1 Tensor singular value decomposition (t-SVD). |
|
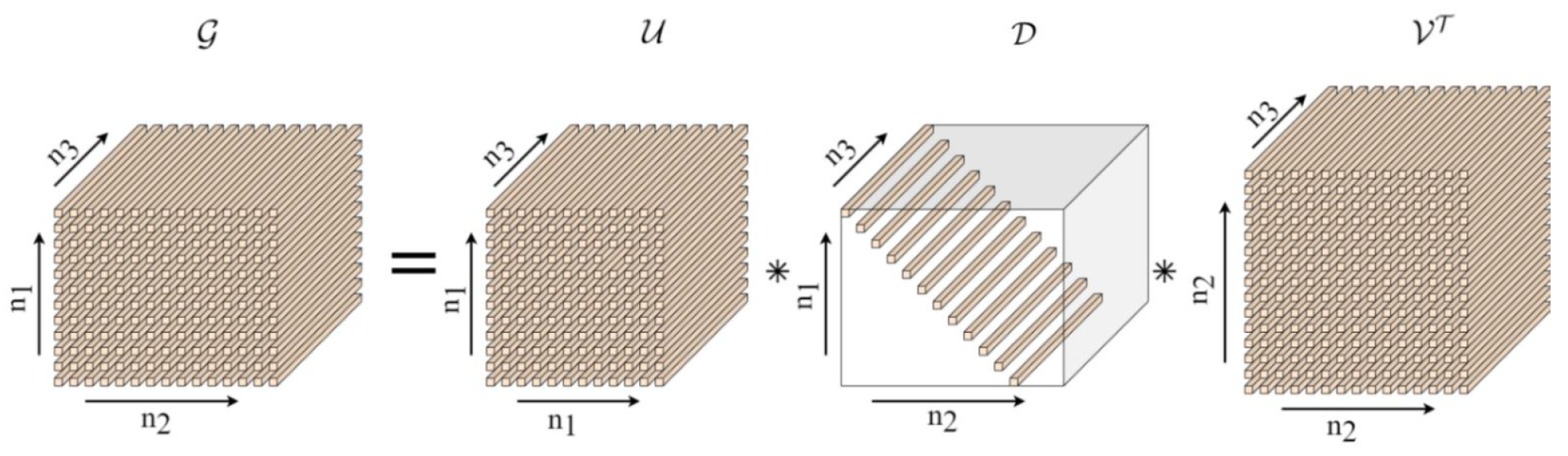
3.2. Tensor Robust Principal Component Analysis with Weighted Tensor Nuclear Norm Minimization
3.3. Tensor Completion with Weighted Tensor Nuclear Norm Minimization
4. The Proposed Model
| Algorithm 2 Weighted tensor singular value thresholding method (). |
|
| Algorithm 3 Weighted tensor completion. |
|
| Algorithm 4 Weighted robust tensor principal component analysis integrated with weighted tensor completion. |
|
5. Experiments and Results
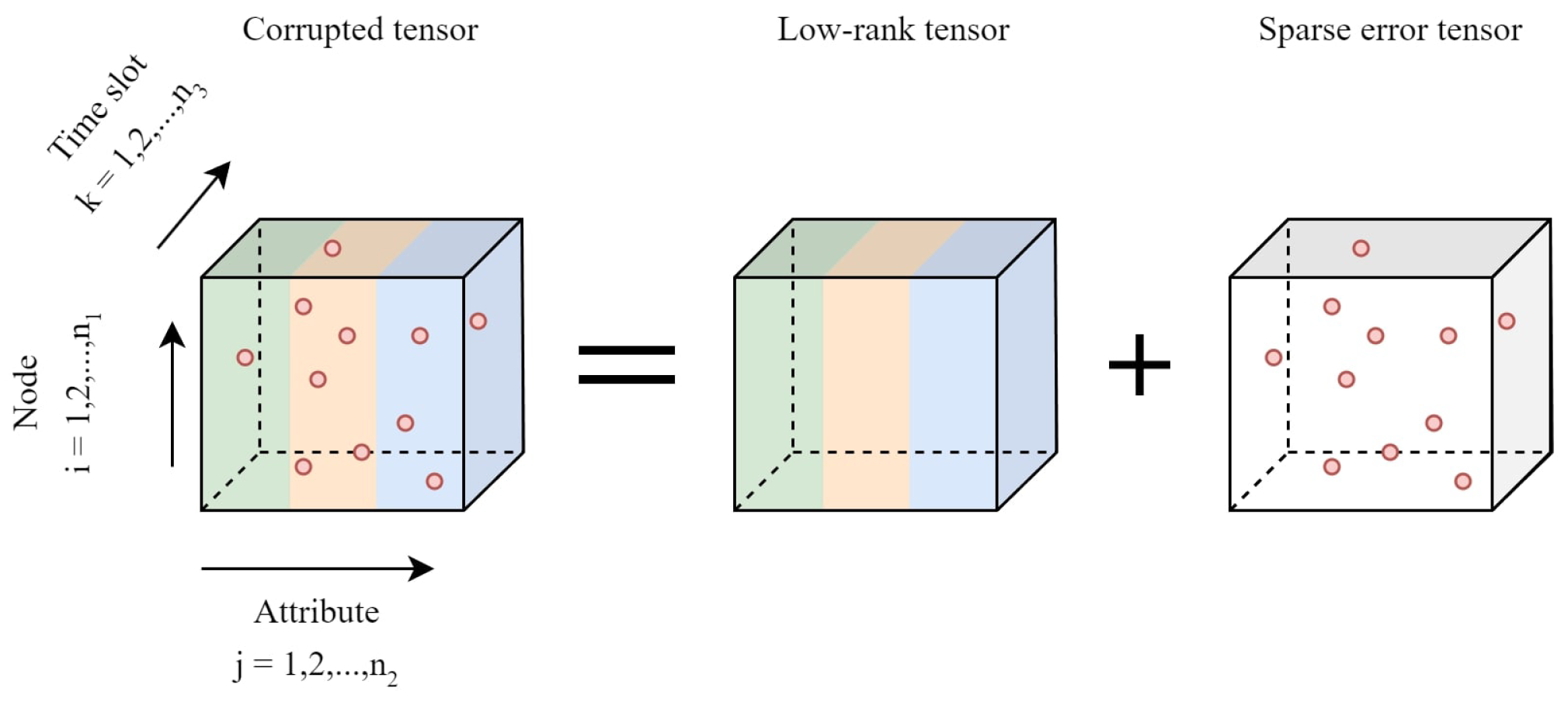
5.1. Dataset
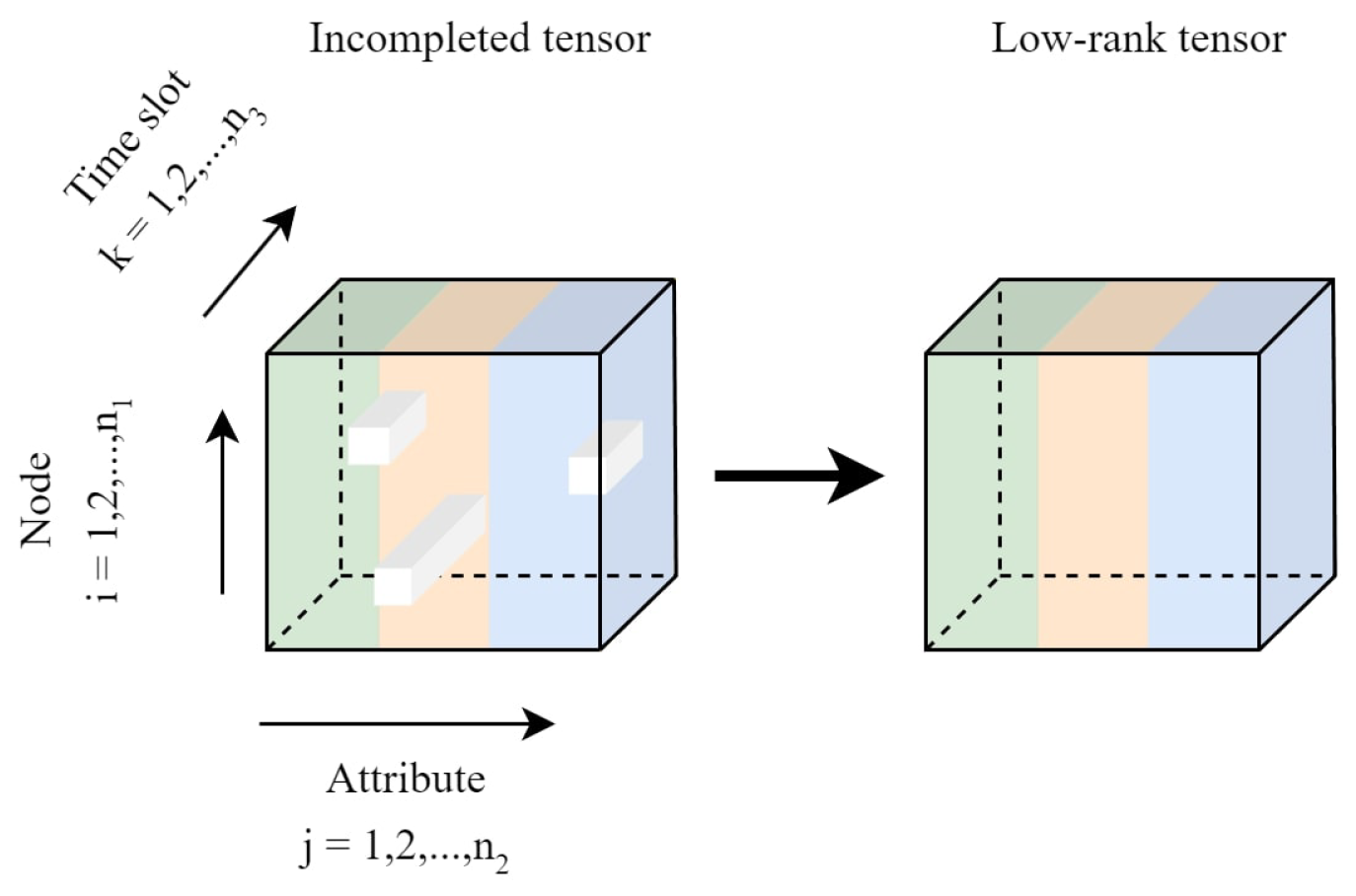
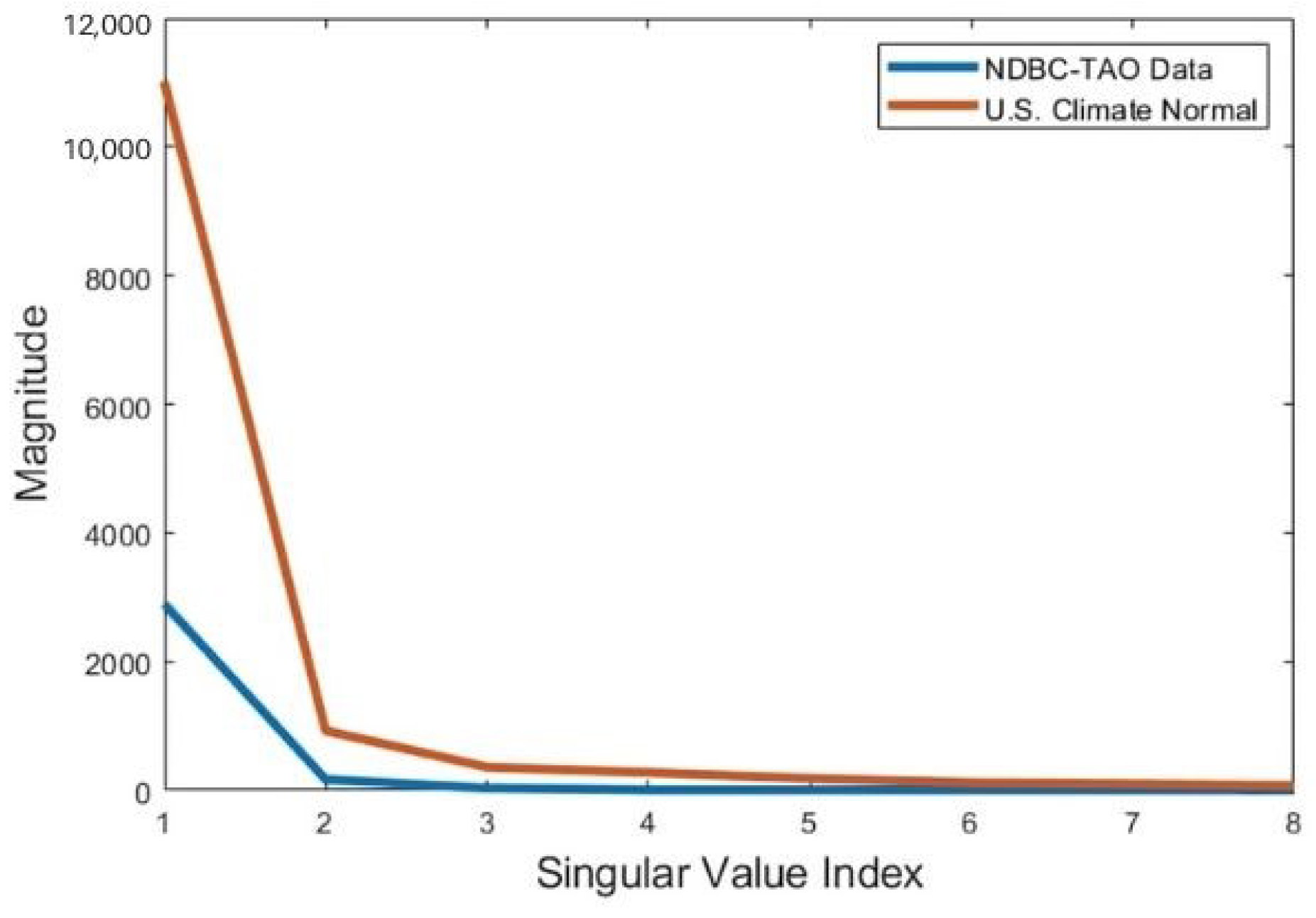
5.2. Low-Rank Structures and Correlation in Multi-Attribute Sensing Data
5.3. Experiment Setup
5.4. Metrics
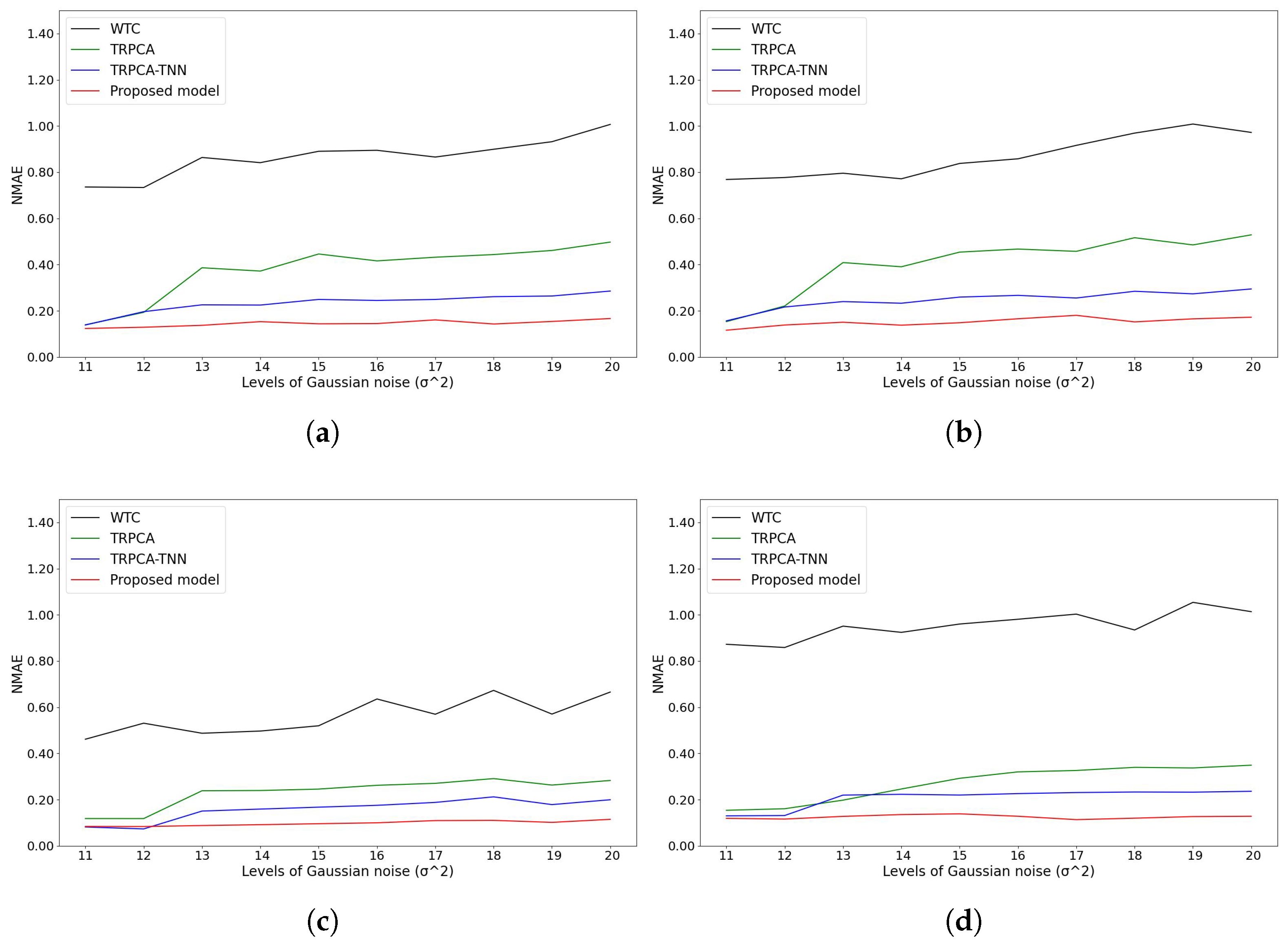
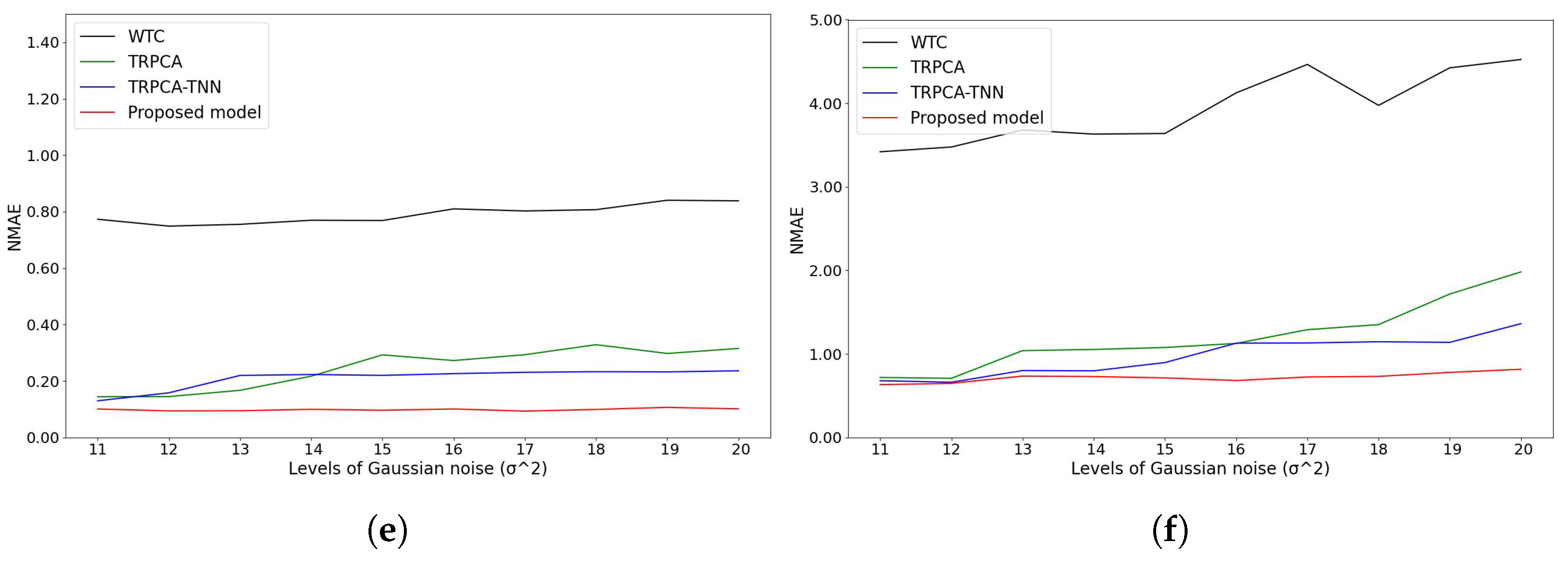
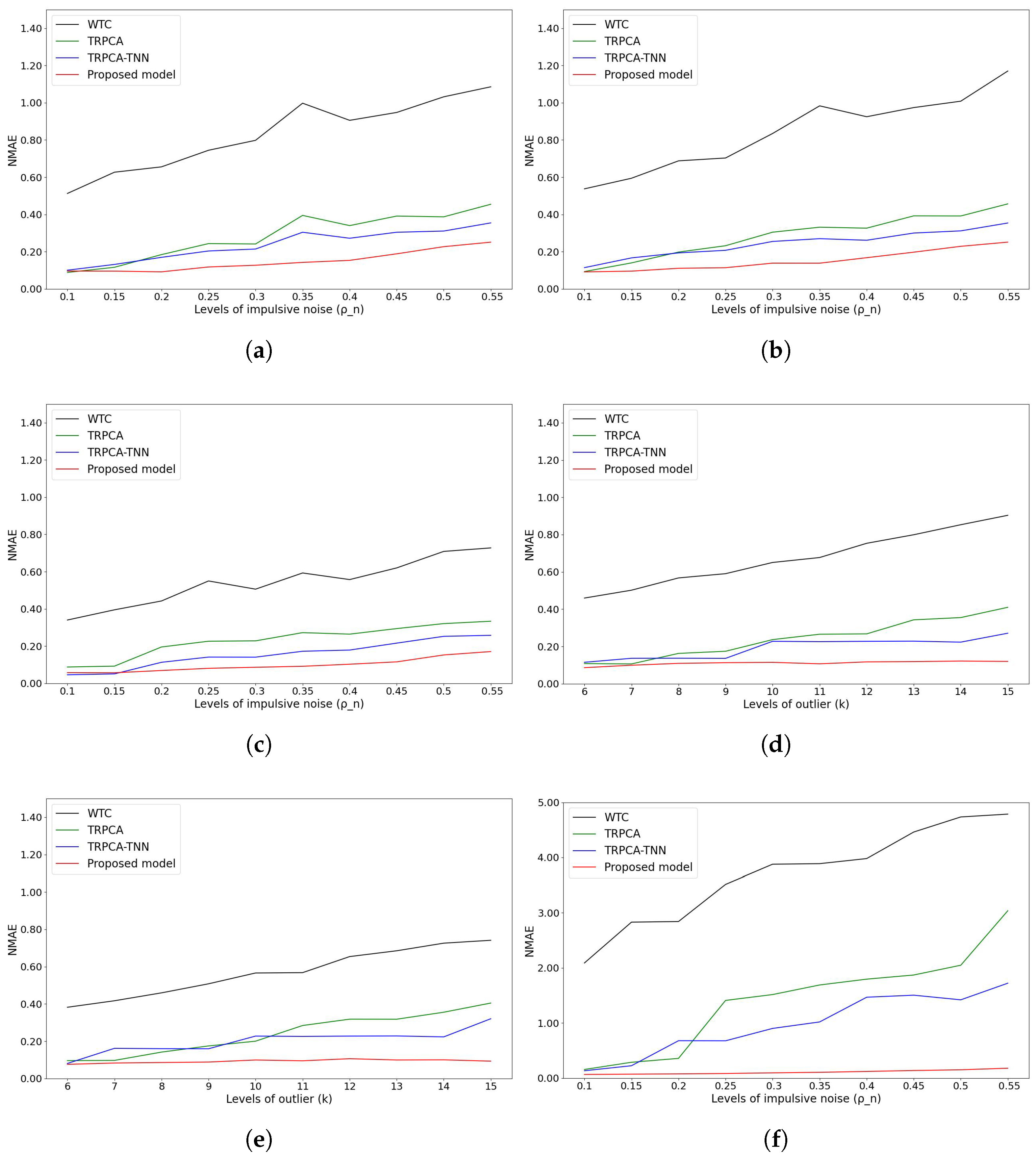
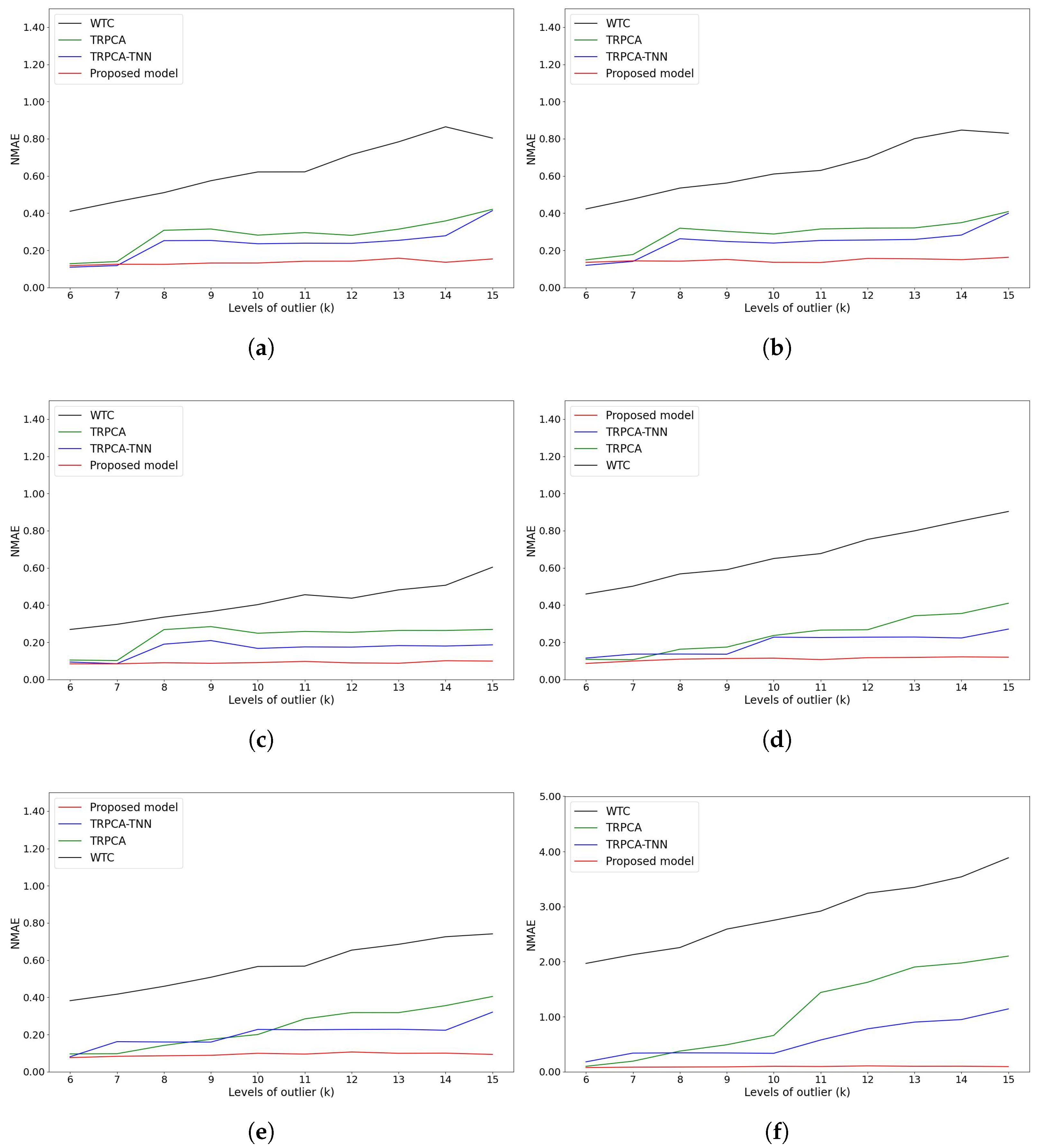
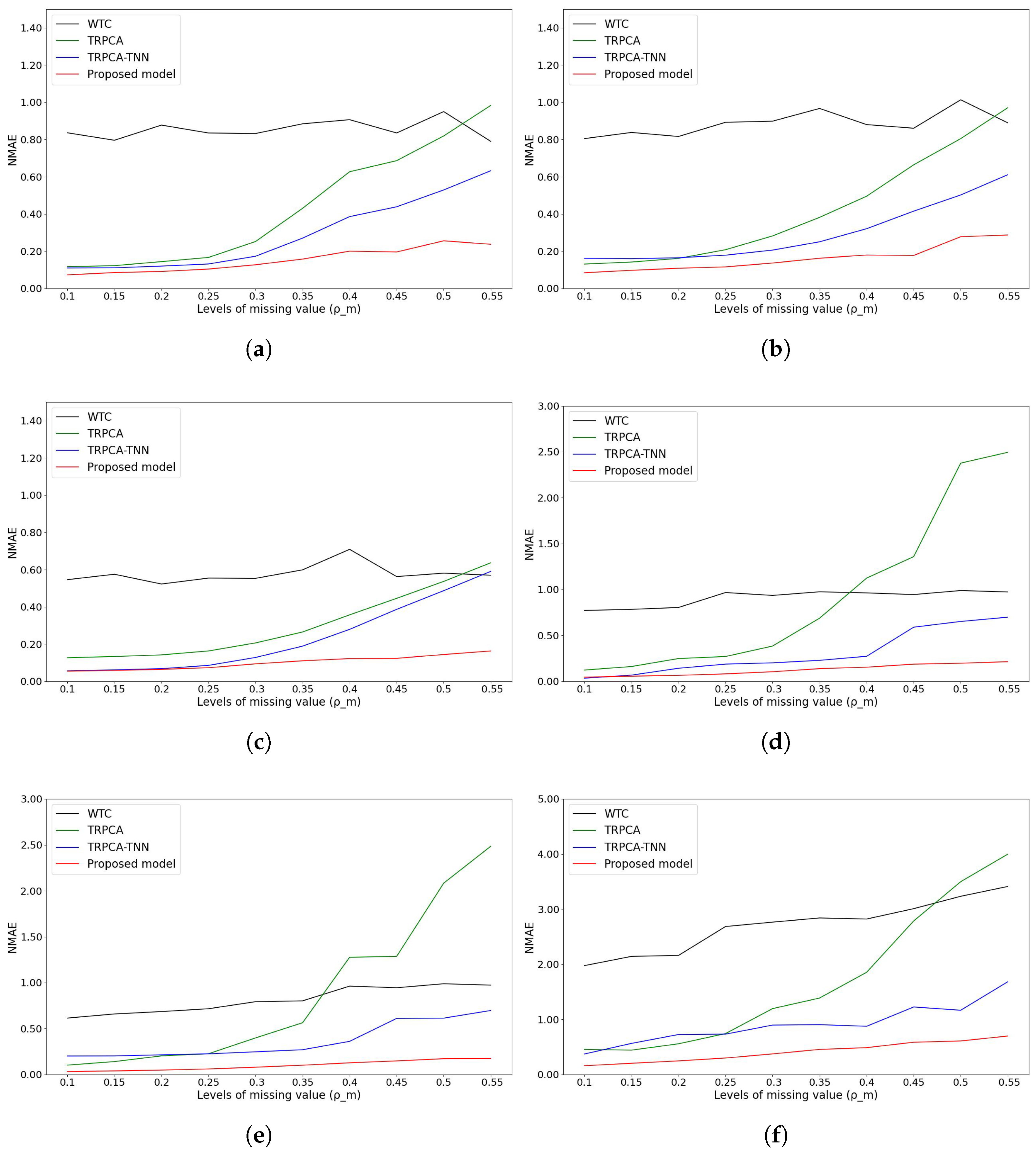
5.5. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elsheakh, D.; Shawkey, H. 5G wideband on-chip dipole antenna for WSN soil moisture monitoring. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22556. [Google Scholar] [CrossRef]
- Shawkey, H.; Elsheakh, D. Multiband dual-meander line antenna for body-centric networks’ biomedical applications by using UMC 180 nm. Electronics 2020, 9, 1350. [Google Scholar] [CrossRef]
- Alliance, N. 5G white paper. In Next Generation Mobile Networks, White Paper; 2015; Volume 1, Available online: https://pub.deadnet.se/Books%20and%20Docs%20on%20Hacking/Networking/Wireless%20LAN/NGMN%205G%20White%20Paper%20V1.0.pdf (accessed on 12 May 2024).
- Jaladi, A.R.; Khithani, K.; Pawar, P.; Malvi, K.; Sahoo, G. Environmental monitoring using wireless sensor networks (WSN) based on IOT. Int. Res. J. Eng. Technol. 2017, 4, 1371–1378. [Google Scholar]
- Corke, P.; Wark, T.; Jurdak, R.; Hu, W.; Valencia, P.; Moore, D. Environmental wireless sensor networks. Proc. IEEE 2010, 98, 1903–1917. [Google Scholar] [CrossRef]
- Alippi, C.; Camplani, R.; Galperti, C.; Roveri, M. A robust, adaptive, solar-powered WSN framework for aquatic environmental monitoring. IEEE Sens. J. 2010, 11, 45–55. [Google Scholar] [CrossRef]
- Ko, J.; Lu, C.; Srivastava, M.B.; Stankovic, J.A.; Terzis, A.; Welsh, M. Wireless sensor networks for healthcare. Proc. IEEE 2010, 98, 1947–1960. [Google Scholar] [CrossRef]
- Sharma, N.; Kaushik, I.; Bhushan, B.; Gautam, S.; Khamparia, A. Applicability of WSN and biometric models in the field of healthcare. In Deep Learning Strategies for Security Enhancement in Wireless Sensor Networks; IGI Global: Hershey, PA, USA, 2020; pp. 304–329. [Google Scholar]
- Xie, K.; Ning, X.; Wang, X.; Xie, D.; Cao, J.; Xie, G.; Wen, J. Recover corrupted data in sensor networks: A matrix completion solution. IEEE Trans. Mob. Comput. 2016, 16, 1434–1448. [Google Scholar] [CrossRef]
- Majumder, B.D.; Roy, J.K.; Padhee, S. Recent advances in multifunctional sensing technology on a perspective of multi-sensor system: A review. IEEE Sens. J. 2018, 19, 1204–1214. [Google Scholar] [CrossRef]
- Rajesh, G.; Chaturvedi, A. Data reconstruction in heterogeneous environmental wireless sensor networks using robust tensor principal component analysis. IEEE Trans. Signal Inf. Process. Netw. 2021, 7, 539–550. [Google Scholar] [CrossRef]
- Zhang, X.; He, J.; Li, Y.; Chi, Y.; Zhou, Y. Recovery of corrupted data in wireless sensor networks using tensor robust principal component analysis. IEEE Commun. Lett. 2021, 25, 3389–3393. [Google Scholar] [CrossRef]
- He, J.; Li, Y.; Zhang, X.; Li, J. Missing and Corrupted Data Recovery in Wireless Sensor Networks Based on Weighted Robust Principal Component Analysis. Sensors 2022, 22, 1992. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Liu, W.; Li, Z.; Chen, L.; Wang, R. Noise-tolerant wireless sensor networks localization via multinorms regularized matrix completion. IEEE Trans. Veh. Technol. 2017, 67, 2409–2419. [Google Scholar] [CrossRef]
- Madi, G.; Sacuto, F.; Vrigneau, B.; Agba, B.L.; Pousset, Y.; Vauzelle, R.; Gagnon, F. Impacts of impulsive noise from partial discharges on wireless systems performance: Application to MIMO precoders. EURASIP J. Wirel. Commun. Netw. 2011, 2011, 186. [Google Scholar] [CrossRef]
- Al Samara, M.; Bennis, I.; Abouaissa, A.; Lorenz, P. An efficient outlier detection and classification clustering-based approach for WSN. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Deng, Y.; Han, C.; Guo, J.; Sun, L. Temporal and spatial nearest neighbor values based missing data imputation in wireless sensor networks. Sensors 2021, 21, 1782. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Ye, Q.; Jiang, H.; Wang, D.; Wang, C. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks. IEEE Trans. Wirel. Commun. 2012, 12, 850–861. [Google Scholar] [CrossRef]
- Magán-Carrión, R.; Camacho, J.; García-Teodoro, P. Multivariate statistical approach for anomaly detection and lost data recovery in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2015, 11, 672124. [Google Scholar] [CrossRef]
- Srindhuna, M.; Baburaj, M. Estimation of missing data in remote sensing images using t-SVD based tensor completion. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–5. [Google Scholar]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Its Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef]
- He, J.; Zhou, Y.; Sun, G.; Geng, T. Multi-attribute data recovery in wireless sensor networks with joint sparsity and low-rank constraints based on tensor completion. IEEE Access 2019, 7, 135220–135230. [Google Scholar] [CrossRef]
- Li, T.; Ma, J. T-SVD based non-convex tensor completion and robust principal component analysis. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 6980–6987. [Google Scholar]
- Mu, Y.; Wang, P.; Lu, L.; Zhang, X.; Qi, L. Weighted tensor nuclear norm minimization for tensor completion using tensor-SVD. Pattern Recognit. Lett. 2020, 130, 4–11. [Google Scholar] [CrossRef]
- Ng, M.K.P.; Yuan, Q.; Yan, L.; Sun, J. An adaptive weighted tensor completion method for the recovery of remote sensing images with missing data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3367–3381. [Google Scholar] [CrossRef]
- Cheng, Q.; Yuan, Q.; Ng, M.K.P.; Shen, H.; Zhang, L. Missing data reconstruction for remote sensing images with weighted low-rank tensor model. IEEE Access 2019, 7, 142339–142352. [Google Scholar] [CrossRef]
- Geng, J.; Wang, L.; Xu, Y.; Wang, X. A weighted nuclear norm method for tensor completion. Int. J. Signal Process. Image Process. Pattern Recognit. 2014, 7, 1–12. [Google Scholar] [CrossRef][Green Version]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM (JACM) 2011, 58, 1–37. [Google Scholar] [CrossRef]
- Kang, J.; Wang, Y.; Schmitt, M.; Zhu, X.X. Object-based multipass InSAR via robust low-rank tensor decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3062–3077. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, F.; Du, R. Probability-weighted tensor robust PCA with CP decomposition for hyperspectral image restoration. Signal Process. 2023, 209, 109051. [Google Scholar] [CrossRef]
- Ruhan, A.; Mu, X.; He, J. Enhance tensor RPCA-based Mahalanobis distance method for hyperspectral anomaly detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6008305. [Google Scholar]
- Guyon, C.; Bouwmans, T.; Zahzah, E.H. Robust principal component analysis for background subtraction: Systematic evaluation and comparative analysis. Princ. Compon. Anal. 2012, 10, 223–238. [Google Scholar]
- Gao, Q.; Zhang, P.; Xia, W.; Xie, D.; Gao, X.; Tao, D. Enhanced tensor RPCA and its application. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 2133–2140. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tan, T.; Gong, Y.; Yang, W. Fingerprint database reconstruction based on robust PCA for indoor localization. Sensors 2019, 19, 2537. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Li, J.; Chen, Y. Nonlocal weighted robust principal component analysis for seismic noise attenuation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1745–1756. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Zhao, X.L.; Fang, H.; Zhang, Z.; Zhong, S. Weighted low-rank tensor recovery for hyperspectral image restoration. IEEE Trans. Cybern. 2020, 50, 4558–4572. [Google Scholar] [CrossRef]
- Mu, X.; He, J.; Zhang, J. Enhance tensor RPCA-LRX anomaly detection algorithm for hyperspectral image. Geocarto Int. 2022, 37, 11976–11997. [Google Scholar]
- Chander, B.; Kumaravelan, G. Outlier detection strategies for WSNs: A survey. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 5684–5707. [Google Scholar] [CrossRef]
- Tay, D.B. Sensor network data denoising via recursive graph median filters. Signal Process. 2021, 189, 108302. [Google Scholar] [CrossRef]
- Wilson, A.M.; Panigrahi, T.; Dubey, A. Robust distributed Lorentzian adaptive filter with diffusion strategy in impulsive noise environment. Digit. Signal Process. 2020, 96, 102589. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Gao, Q.; Xia, W.; Wan, Z.; Xie, D.; Zhang, P. Tensor-SVD based graph learning for multi-view subspace clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3930–3937. [Google Scholar]
- Candes, E.J.; Plan, Y. Matrix completion with noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]

| Paper | Year | Multivariate | Univariate | Corrupted Type | Weighted | Method | |||
|---|---|---|---|---|---|---|---|---|---|
| Missing Value | Noise | Outlier | |||||||
| Gaussian | Impulsive | ||||||||
| [11] | 2021 | X | X | X | TRPCA | ||||
| [12] | 2021 | X | X | X | TRPCA-TNN | ||||
| [13] | 2022 | X | X | X | X | WRPCA | |||
| Our | 2024 | X | X | X | X | X | X | WRTPCA-WTNN | |
| Notation | Definition |
|---|---|
| g, g, G, | scalar, vector, matrix, and tensor formats |
| ith singular value | |
| , , | ith horizontal slice, ith lateral slice, and ith frontal slice |
| , ith frontal slice | |
| Fourier transformation of , | |
| Frobenius norm | |
| nuclear norm | |
| weighted nuclear norm | |
| tensor Frobenius norm | |
| tensor nuclear norm | |
| weighted tensor nuclear norm | |
| rank of matrix G | |
| tubal rank of tensor | |
| t-SVD | tensor singular value decomposition |
| ADMM | alternative direction method of multipliers |
| WTNN | weighted tensor nuclear norm |
| position of missing elements in | |
| projection on |
| NDBC-TAO | U.S. Climate Normal | |
|---|---|---|
| No. of nodes | 8 | 89 |
| Period of observation | 1 October 2020 00:00:00 –3 October 2020 23:50:00 | 1 December 2022 00:00:00 –15 December 2022 23:00:00 |
| Measured attribute | Temperature, density, and salinity | Dew, temperature, and wind |
| Sampling period | 10 min | 1 h |
| Tensor dimension | 8 × 3 × 432 | 89 × 3 × 360 |
| Corruption Type | Parameter | Range | Step Size |
|---|---|---|---|
| Gaussian noise | 11 to 20 | 1 | |
| Impulsive noise | 0.1 to 0.55 | 0.05 | |
| Outlier | k | 6 to 15 | 1 |
| Missing value | 0.1 to 0.55 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, H.H.-P.; Nguyen, T.M.; Yoo, M. Weighted Robust Tensor Principal Component Analysis for the Recovery of Complex Corrupted Data in a 5G-Enabled Internet of Things. Appl. Sci. 2024, 14, 4239. https://doi.org/10.3390/app14104239
Vo HH-P, Nguyen TM, Yoo M. Weighted Robust Tensor Principal Component Analysis for the Recovery of Complex Corrupted Data in a 5G-Enabled Internet of Things. Applied Sciences. 2024; 14(10):4239. https://doi.org/10.3390/app14104239
Chicago/Turabian StyleVo, Hanh Hong-Phuc, Thuan Minh Nguyen, and Myungsik Yoo. 2024. "Weighted Robust Tensor Principal Component Analysis for the Recovery of Complex Corrupted Data in a 5G-Enabled Internet of Things" Applied Sciences 14, no. 10: 4239. https://doi.org/10.3390/app14104239
APA StyleVo, H. H.-P., Nguyen, T. M., & Yoo, M. (2024). Weighted Robust Tensor Principal Component Analysis for the Recovery of Complex Corrupted Data in a 5G-Enabled Internet of Things. Applied Sciences, 14(10), 4239. https://doi.org/10.3390/app14104239






