1. Introduction
Magnetic flux leakage (MFL), one of the nondestructive testing methods, is an effective and reliable technique that detects anomalies such as cracks, metal loss, and corrosion in the structure of magnetic materials [
1,
2]. Critical materials of industrial importance, such as oil and gas pipes [
3], tank floors [
4], steel ropes [
5], and railways [
6], are inspected by the MFL method. Safe material usage is ensured by conducting this inspection process periodically.
One of the essential steps in the MFL method is the defect characterization process [
7]. Defect characterization refers to estimating the physical properties of a defect, such as length, width, and depth, by evaluating the MFL signal. At this stage, depth information is a vital parameter that needs to be identified [
8]. The main challenge in determining the depth is that the relationship between the physical depth and the signal amplitude is not linear [
9]. This relationship involves varying complexity depending on factors such as the magnetic and physical properties of the MFL system components and the flux density level of the material under test. The inappropriate combination of these factors will make MFL signals difficult to interpret and make it challenging to estimate defect depth information. Therefore, a system design that considers the mentioned factors becomes crucial for an effective defect characterization.
The finite element analysis (FEA) method stands out as a tool that provides accurate and precise solutions in the design of electromagnetic systems [
10,
11,
12]. FEA can analyze complex designs incorporating magnetic materials by considering the nonlinear behavior of these materials [
13]. On the other hand, in studies such as design optimization and rapid prototyping, excessive time-consuming processes arise due to the high computational volume. This problem is escalated by large numbers of mesh assignments and leads to costly hardware requirements. Therefore, it seems impossible to overcome this problem using the FEA method.
Magnetic equivalent circuit (MEC) analysis based on Kirchhoff’s law offers a faster alternative solution. MEC is a permeance network in which the permeances corresponding to the primary flux paths of an electromagnetic system are modeled as a set of interconnected lumped elements [
14]. Although the MEC method has less accuracy than FEA, it has a lower computational cost due to reduced model complexity [
15,
16,
17]. These advantages make it an effective means of optimization for electromagnetic systems [
13,
16]. Additionally, the desired level of accuracy can be achieved by modeling the sufficient number of permeances corresponding to the flux paths.
There are few studies in the literature about the magnetic circuit of the MFL system. One of the studies [
18] is about optimizing the system parameters using the magnetic circuit method. Another study [
19] presents multi-objective optimization of the system’s magnetic circuit using the genetic algorithm. In the study of Wang et al. [
20], the effect of the eccentricity value of the magnets on the inspection is examined by using a simplified equivalent magnetic circuit of the system. However, in these studies, critical factors such as leakage flux and the material’s nonlinear behavior are not considered when designing the magnetic circuit. However, an efficient magnetic circuit design can only be achieved by taking into account the leakage flux and the nonlinear behavior of the magnetic material.
In this study, an efficient and reliable MEC model that can be used in the design of any MFL system is presented. In this context, our primary goal is to design an MEC model that not only models a specific MFL system but also adapts to systems with different dimensions and parameters. For this purpose, in addition to the main flux of the magnetic system, factors such as leakage flux and nonlinear behavior of the magnetic material are taken into consideration when designing the MEC model. Furthermore, the fringing effect caused by the air gap in the transition region of the main flux to the tested material is also considered. Finally, the performance of the MEC model is tested based on various MFL systems created in a 3D FEA environment.
The rest of this article is organized as follows.
Section 2 presents the general principles of the MFL testing, MFL system flux density distributions, and the flux types taken into account in the MEC design.
Section 3 presents the designed MEC model and dimensional parameters of the MFL system. Furthermore, the leakage flux permeances calculation is shown in
Section 3.
Section 4 explains the iterative algorithm used to calculate flux-dependent magnetic permeances.
Section 5 includes the performance evaluation of the MEC model based on results obtained from FEA studies. In addition, the calculation times of the MEC model and FEA studies are compared in
Section 5. Ultimately, in
Section 6, the evaluation of the findings achieved in this study is presented.
2. Principles of MFL Testing
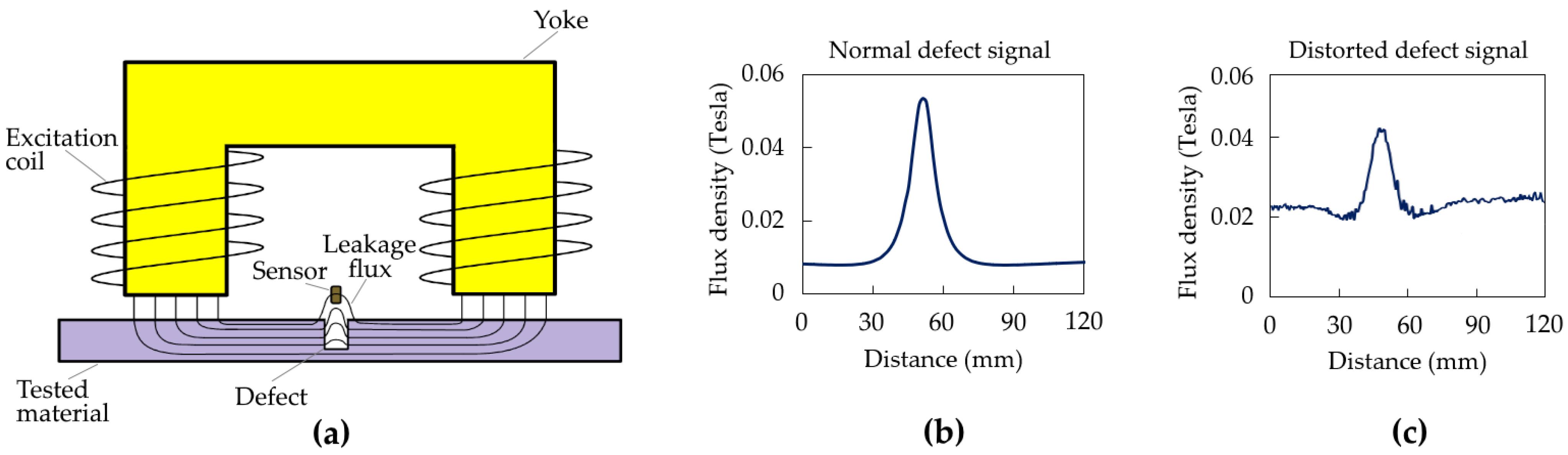
The MFL method is based on the principle of subjecting the material to be inspected to a closed magnetic flux loop. For this purpose, a U-shaped yoke made of high-permeability material is utilized. In the MFL system, magnetic flux sources are positioned on the poles of the yoke close to the material. The mechanical system created in this way is moved over the material to conduct the MFL inspection. Permanent magnets or coils can be used as magnetic flux sources. Using coils enables the adjustment of magnetic flux, providing flexible solutions in the system design [
21]. A magnetic neutral point occurs at the midpoint between the system’s poles, and magnetic sensors are placed at this point. The flux passing through the tested material exhibits a leaking effect from the defect region into the air. Finally, the sensors detect this effect, and MFL signals are obtained. The general representation of the MFL test and tangential (
x axis) component of sample defect signals are shown in
Figure 1.
In the MFL method, the flux density level formed in the test material is of critical importance. A flux density under saturation level produces weak and unstable signals, and minor defects cannot be detected. If the material is saturated, the leakage flux into the air is highly triggered. However, saturation conditions may lead to deformations in the defect signal. Therefore, it is necessary to form a flux density level defined as near saturation in the tested material [
9]. This preferred approach aims to generate effective and efficient MFL signals.
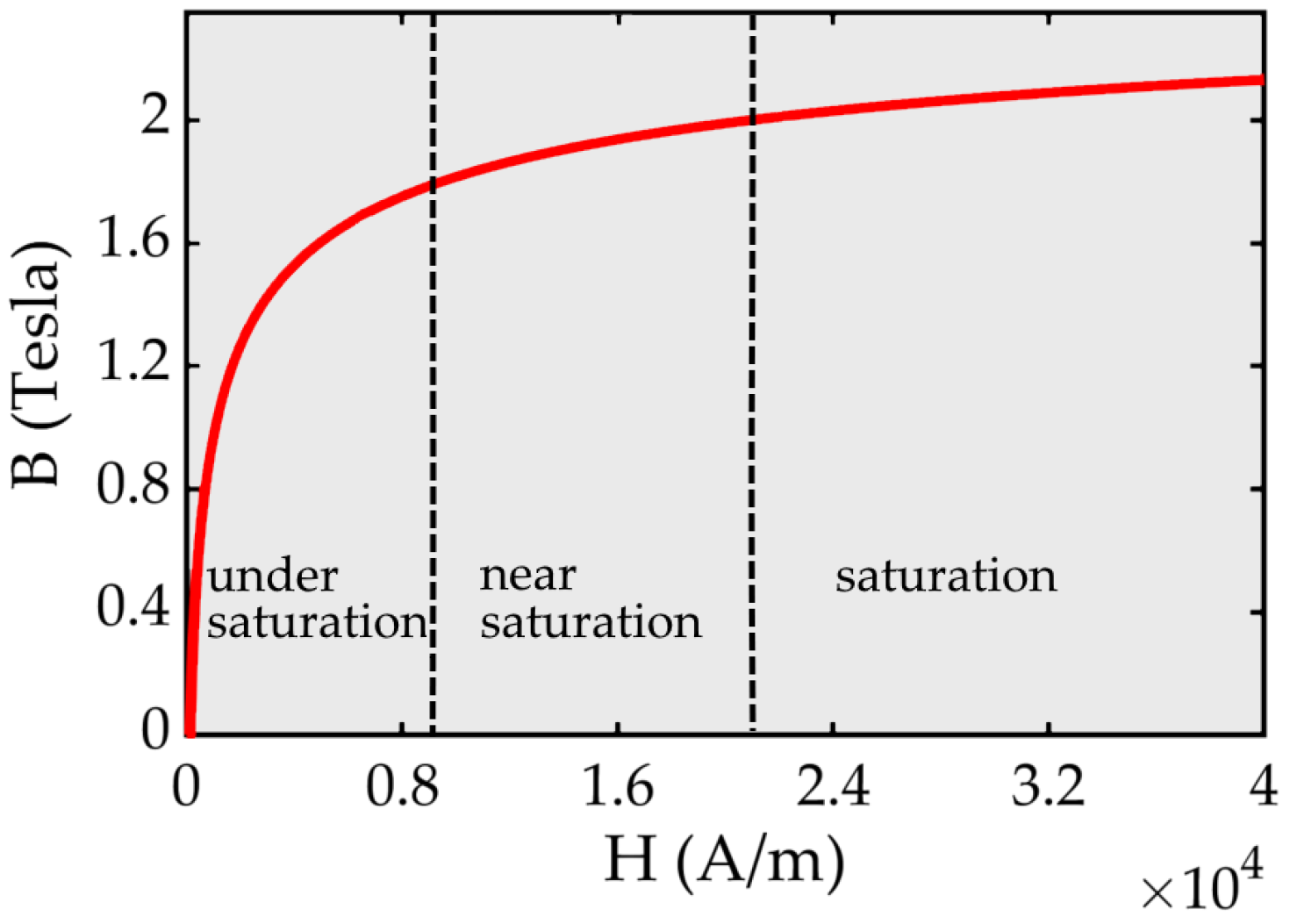
Figure 2 depicts an example of a
B-H curve and its flux density zones. While there are no exact limits, the zones, namely under saturation, near saturation, and saturation, can be approximately defined based on the behavior of the material’s
B-H curve.
Another interaction is that, with forming near saturation in the tested material, high flux densities and even saturation states can also occur in the pole regions of the MFL system. The first noticeable cost of these situations is the exponentially increasing energy consumption. This is because a much higher flux transition occurs from the system to the air in the high flux density or saturation states. However, what is more important is that the horizontal leakage flux and magnetic noise occurring at the inner-slot region increase significantly. This effect influences the sensor measurement area, resulting in distortions in the defect signal, increased signal noise, and a rise in the DC component. The defect signal in
Figure 1c illustrates an example of these distortions. Another noteworthy point is that shortening the distance between the poles positively contributes to increasing the flux density in the material. On the other hand, it also causes a significant increase in leakage flux occurring at the inner-slot region. This effect leads to erroneous and/or incomplete interpretations in defect characterization, negatively impacting test efficiency. Even small amplitude defect signals may be lost below the noise level.
Variation in the system dimensions has complex effects on the flux densities of the tested material and pole regions. Further, in real MFL applications, the flux densities of these regions cannot be directly measured. Therefore, an optimization process that will eliminate the aforementioned adverse effects becomes critical to achieving an efficient system design for actual application purposes. The requirement of such an MEC model that ensures sufficient accuracy becomes significant for such an optimization process, which can be carried out through multiple parameter changes.
Flux Density Distribution of MFL System
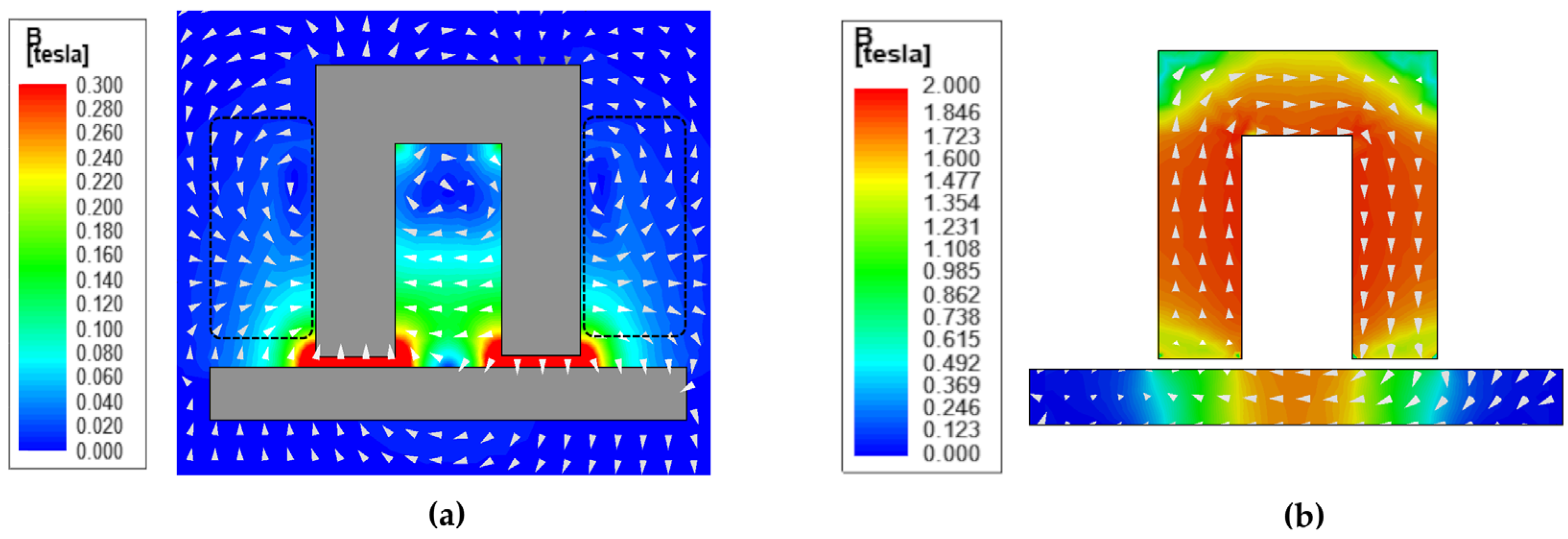
The flux types of the MFL system can be divided into two major groups: main flux and leakage flux. Φ
main represents the main flux, forming the necessary flux loop for the testing process.
Figure 3b shows that the main flux Φ
main completes its cycle by passing through the air gap and the test material over the yoke. This flux forms the desired flux density level within the material being tested.
During the transition of the main flux from the air gap to the test material, an additional fringing effect arises from the edges. Due to the significantly lower permeability of air compared to the magnetic material, the air gap exhibits high magnetic reluctance. The main flux Φmain is highly sensitive to these reluctance changes. In conjunction with this change, flux forms arcs in the air, entering the material and increasing the main flux. Therefore, neglecting the fringing effect in the MEC model calculations will reduce the degree of representation of the MFL system.
In the MFL system, the leakage flux completes its cycle through air. Although this flux typically forms at low levels, it reaches non-negligible high levels in saturation conditions. This is because saturated regions can no longer pass more flux and flux flows through the air medium. Moreover, the cross-sectional area of the air is much larger than the cross-sectional area of the system, leading to an exponential increase in this effect.
The leakage flux, which cannot be ignored in the MFL system, can be examined under two categories: inner-slot and outer-slot. Due to its orthogonal feature, the vectorial leakage flux generated at the inner-slot can be separated into horizontal and vertical components [
22]. However, due to the magnetic sources’ strong inter-pole interaction, the inner-slot region’s horizontal flux component is much more dominant. Therefore, the vertical component of the flux in this region can be neglected. The horizontal leakage flux component also tends to follow the main flux direction. This generally causes horizontal leakage flux to have a different directional distribution in the upper and lower inner-slot parts. Thus, it becomes crucial to represent the inner-slot leakage flux with at least two different flux types: the upper part horizontal leakage flux (Φ
hl1) and the lower part horizontal leakage flux (Φ
hl2). In the outer-slot region, winding leakage flux (Φ
eal) is dominant. This flux is shown with the black dashed line frame in
Figure 3a. Winding leakage flux symmetrically forms around the magnetic sources in both inner- and outer-slot regions. However, the effect within the inner-slot is generally neglected.
Considering the behaviors mentioned above, the flux types of the MFL system, namely main flux Φ
main, winding leakage flux Φ
eal, and horizontal leakage flux Φ
hl, are defined, as shown in
Figure 4. The horizontal leakage flux Φ
hl representation in two parts will be explained in detail later. Moreover, studies have been carried out under the assumption that the flux densities occurring in the magnetic regions are uniformly distributed.
3. Designing MEC Model for MFL System
In the MEC model, permeances are divided into two main types: air and magnetic. The designed MEC model, comprising both air and magnetic permeances, is illustrated in
Figure 5a. This model corresponds to the flux paths depicted in
Figure 4. It includes permeances for the yoke (
Pyoke), the pole region (
Pub,
Plb, and
Pmb), and the specimen (
Psp) as its magnetic elements. Air permeances account for both leakage flux types and flux passing through the air gap. Specifically, they include the winding leakage flux permeance (
Peal), upper and lower part permeances of the horizontal leakage flux (
Phl1 and
Phl2), and the air gap permeance (
Pgap).
Figure 5b shows the dimensional parameters of the MFL system. Also, descriptions of these parameters are given in
Table 1.
3.1. Calculation of the MEC Model Permeances
In the MEC solution, iterative methods are needed to calculate magnetic permeances [
23]. This is because the permeabilities of the magnetic permeances vary nonlinearly with flux density. The
B-H curve, which describes this variation, is used as a reference for calculating such permeances. The permeabilities of the air permeances, on the other hand, do not change with flux density and, therefore, remain fixed. Hence, these permeances can be calculated in a single step in the MEC solution. Additionally, both air and magnetic permeances vary depending on the system dimensions, directly affecting the model flux distributions. Therefore, reliable system design necessitates accurate calculation of all MEC model permeance elements.
3.1.1. Calculation of the Horizontal Leakage Flux Permeances
The permeance of the horizontal leakage flux Φ
hl is related to the total inner-slot magnetic energy and can be calculated by the Sudhoff method [
22]. The following equation is obtained by neglecting the MMF drops in the magnetic regions and applying Ampere’s law to the path of horizontal leakage flux.
where
Hx is the magnitude of the horizontal flux intensity in the winding slots, and
y is the vertical position of the
Hx.
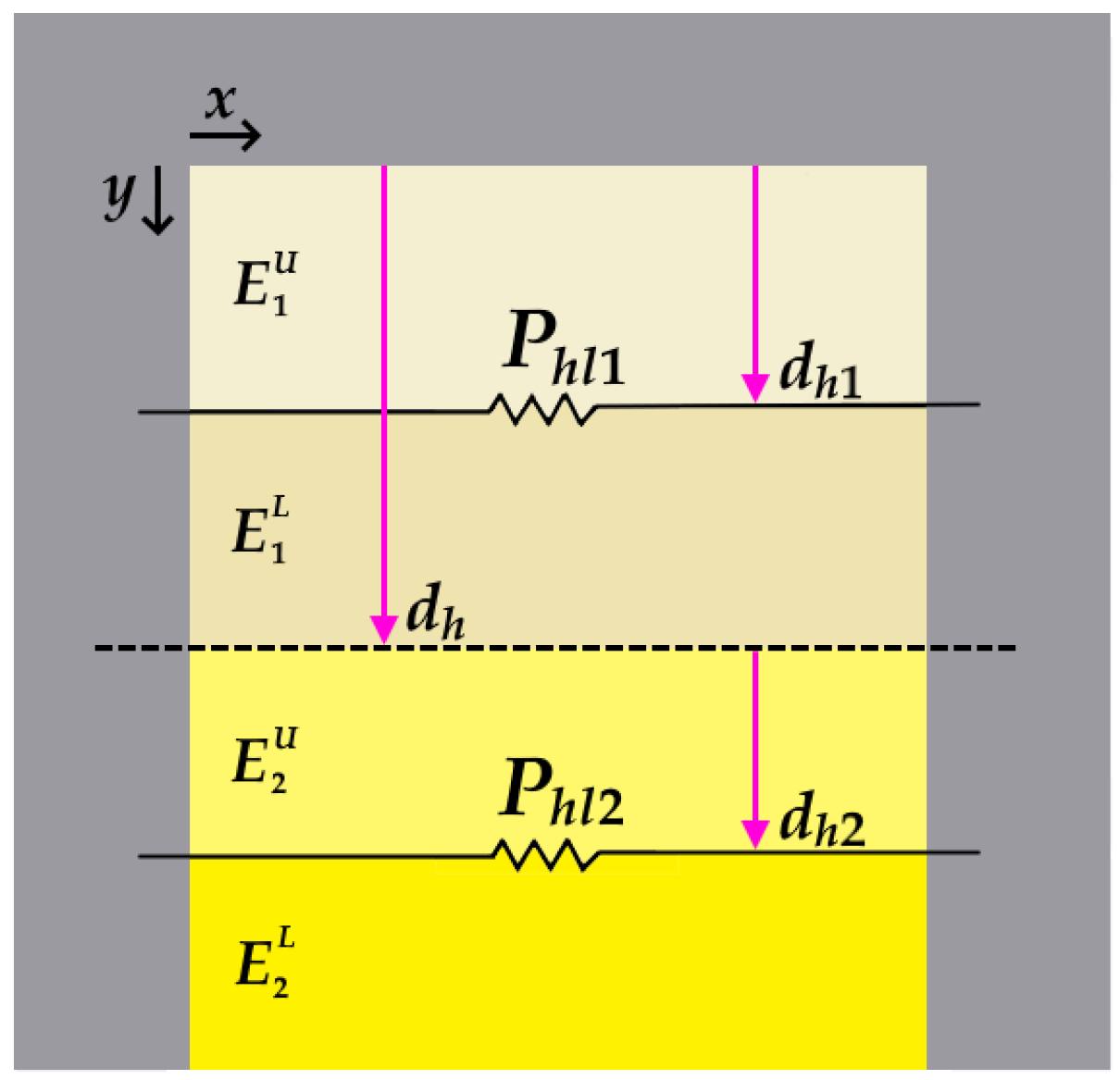
To represent horizontal leakage flux using two separate permeances, the inner-slot region needs to be divided into upper and lower parts, as shown in
Figure 6. The upper and lower parts will be represented by
Phl1 and
Phl2 permeances, respectively. The magnetic strength of these parts can be defined as follows:
where
dh is the depth of the upper part of the horizontal leakage flux Φ
hl1, ensuring that both regions’ energy is equal. The magnetic field energy can be calculated as follows:
where
µ is the permeability coefficient. Taking
µ =
µ0 and
dv =
wslcdy in Equation (5), the upper and lower part energies are defined by the following equations:
Determining the
dh parameter is the first step in calculating
Phl1 and
Phl2 permeances. By equating Equations (5) and (6), the
dh relation is obtained as follows:
By substituting the calculated
dh parameter in Equations (5) and (6), the
E1 and
E2 energies can now be solved. Additionally, magnetic energy can be calculated in terms of permeance as follows:
The obtained
E1 and
E2 equations are separately equated to Equation (8) and the
Phl1 and
Phl2 permeances are obtained as follows:
The permeance equations for
Phl1 and
Phl2 have been revealed in the operations performed so far. Additionally, in the MEC solution, the
dh1 and
dh2 distances that define the vertical positions of these permeances need to be determined. The
dh1 and
dh2 values are required to determine the lengths of the magnetic branches of the pole region. Using the energy approach described above at this stage would be appropriate. To determine the
dh1 and
dh2 values, we need to again divide each upper and lower part into two sections with equal energy. This solution, which enables the calculation of
dh1 for the upper part, is defined by the following equations:
where
E1U and
E1L show the energies of the upper and lower parts of the upper region, respectively. The parameter
dh1 can be shown as follows:
Similarly, the
dh2 parameter is calculated by applying the same method for the lower region. This process is carried out using the following Equations.
where
E2U and
E2L show the energies of the upper and lower parts of the lower region, respectively. The parameter
dh2 can be shown as follows:
3.1.2. Calculation of the Magnetic Branches Permeances
The general representation of a magnetic permeance can be expressed as follows:
where
lbr is the length of a branch,
Abr is the cross-sectional area of a branch, and
µB(.) refers to the variable permeability of a branch. The calculation method for the variable permeabilities will be explained in
Section 4 in detail. The permeance equations of the magnetic branches can be presented as follows:
3.1.3. Calculation of the Winding Leakage Flux Permeance
In this study, the calculation method used in ref. [
24] is selected to determine the permeance of the winding leakage flux Φ
eal. This flux consists of two parts: interior and exterior. The reluctance of the external part of the winding leakage flux can be calculated by Equation (22).
where
l =
lc + 2
we.
The permeance for the inner part of the winding leakage flux (
Peali) is shown in Equation (23).
where
Finally, the permeance of the winding leakage flux is calculated using Equation (25).
3.1.4. Calculation of the Permeances of the Air Gap and Fringing Effect
In the MFL system, fringing flux emerges from the inner and outer edges of the poles in the air gap region. A schematic illustration of the fringing flux is shown in
Figure 7. The calculation method used in ref. [
22] is selected to determine the fringing flux permeances.
The permeance of the inner edge fringing flux is as follows:
The permeance of the outer edge fringing flux is as follows:
Also, the permeance of the air gap can be calculated by Equation (28).
Because the fringing flux permeances are parallel with the air gap permeance, the total permeance of each air gap can be calculated as follows:
The fringing flux permeances are multiplied by two because MFL system poles have 2 outer and inner edges.
4. Nonlinear Solution of the MEC Model
The fundamental theory of the MEC model is Kirchhoff’s voltage law [
25]. The permeances of the MEC model are connected by nodes similar to the electric circuit. The relations among the magnetic potential of the nodes, permeances, and flux are represented as follows:
where [
F] is the magnetic potential matrix, [
P] is the permeance matrix, and [Φ] is the flux matrix.
Equation (30) can also be shown in detail as follows:
where
n is the total node number of the MEC model,
F(
i) is the magnetic potential of node
i,
P(
i,
j) is the permeance between node
i and node
j, and Φ(
i) is the flux of node
i. According to Kirchhoff’s voltage law, if node
i is connected to node
j, the permeance between these nodes is a negative number and is denoted as follows:
Moreover, the permeance located at the principal diagonal of the permeance matrix [
P] as follows:
After the precise calculation of the magnetic potential matrix is performed, new flux Φ
new and new flux density
Bnew between node
i and node
j can be calculated by the following Equations.
where
S represents the cross-sectional area through which Φ
new flows.
In the MEC model, permeabilities of magnetic permeances exhibit a nonlinear variation depending on the flux density. Therefore, iterative methods are employed to obtain the desired solution. In the iteration steps, the permeability values need to be updated according to the calculations. Discrete table data from the
B-H curve are used for the update process. Data from the
B-H curve shown in
Figure 2 are used for all the magnetic elements in this process. The
B-H table provides a fast and easy calculation method. Here, the portion of the
B-H curve between two sample points is defined as a straight line. In the iteration steps, the
Hnew value is calculated using the
B-H table data with the following equation:
In Equation (36), a derivative addition is defined to ensure rapid convergence of the algorithm. Thus, the new permeability of the magnetic permeances can be determined as follows:
The iterative process will end automatically when the iteration termination condition is met, which is as follows:
where
ε is the error limit,
μ(k) is the permeability of the
kth iterative process, and
μ(k−1) is the permeability of the (
k − 1)th iterative process. If the error condition is met, the result is considered convergent and saved for use.
Exceptional cases may occur during algorithm operation. The algorithm might not reach the error limit and could fail to achieve the desired convergence, leading to an infinite loop. Setting a maximum number of iterations alongside the error limit would be beneficial in such instances. It should also be noted that such issues are not expected to arise in a thoroughly structured algorithm. The encountered problems are usually due to programming errors, inappropriate MEC structure, and/or incorrect matrix solutions. If such problems occur, the obtained results are invalid and cannot be used for verification.
The iteration algorithm of the MEC model is given in
Figure 8. The algorithm is executed in the Matlab R2018b [
26] software environment. Additionally, the
ε error limit is set to 0.0001 to achieve high accuracy in the iteration process.
5. Testing the MEC Model with FEA
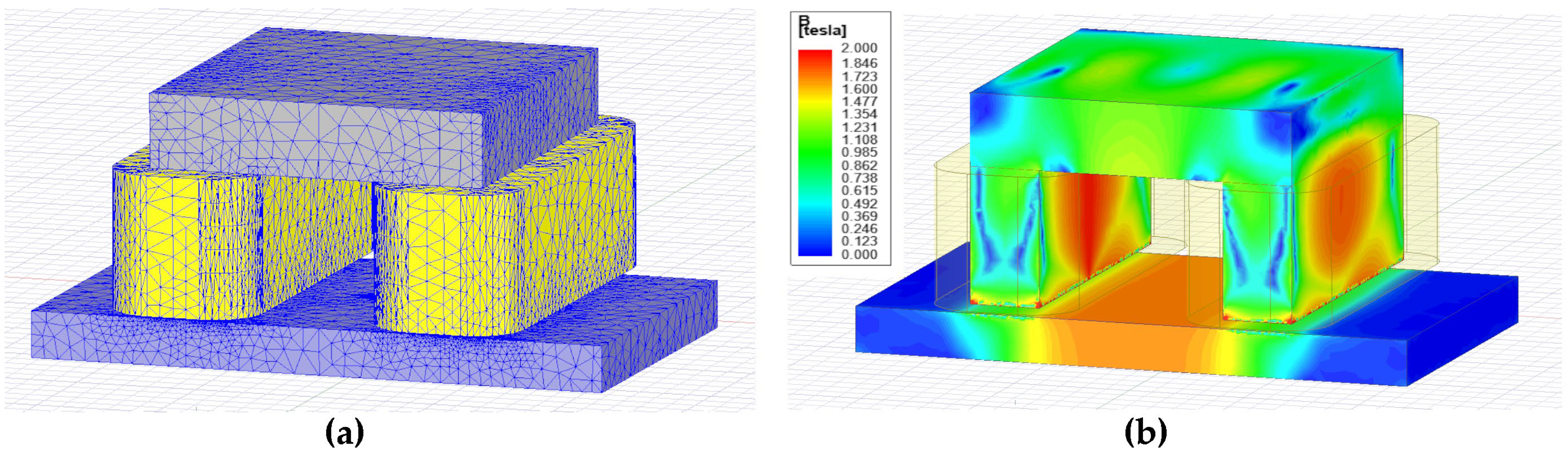
5.1. FEA Studies
The accuracy test of the designed MEC model was conducted with reference to FEA studies. For this purpose, a series of 3D MFL models with varying dimensions were established in the ANSYS Maxwell [
27] simulation environment.
Figure 9 illustrates the FEA solutions of the MFL system. Our fundamental approach in the FEA studies is to obtain results by forming a fixed flux density level in the tested material for different MFL models and to evaluate the MEC model using these results as a reference. Here, adjusting the MMF values is accomplished by forming a fixed flux density in the material. This enables a more effective evaluation of the proposed MEC model’s performance. This is because changes in the dimensions of different MFL models impact the overall system dynamics. This testing approach, combined with ensuring near saturation in the test material, offers valuable insights into achieving the most efficient system design. Moreover, the effects of cycle length brought by different system dimensions are also included in the problem solution.
The magnetostatic solver type was applied in FEA studies. The boundary parameter in the simulation model was set at a distance of 50 cm from the system to avoid boundary effects. Since our testing approach is not aimed at a specific test material or application, using different
B-H curves for yoke and test material will not affect the character of the observed results. Therefore, in FEA and MEC studies, the required
B-H data for the yoke and test material have been derived from the
B-H curve of the X-52 steel [
8] material shown in
Figure 2.
The variation in the
we and
ws parameters was taken as a basis for obtaining different MFL system models. Due to their nonlinear effect on the main and leakage flux,
we and
ws have a higher impact on the system operation than other parameters. The system height
ww parameter can be accepted within the effect caused by changes in
ws. Therefore, the
ww value was taken as fixed in the analyses. The
lg distance affects the horizontal leakage flux almost linearly. Therefore, this parameter was also fixed in the analyses. The
we and
ws values selected for analyses are given in
Table 2. The fixed parameters are defined as
wm = 5 mm,
ww = 40 mm,
lc = 60 mm,
dw = 8 mm, and
lg = 2 mm.
Twenty-five different MFL models were produced by combinational changes in the
we and
ws parameters, and corresponding FEA studies were conducted. In these studies, the necessary MMF values were adjusted for each model to form the flux density within the material at a level of 1.8T. The adjustment of MMF values, defined by the equation
F =
Ni, was performed by keeping the number of turns
N fixed and assigning different current values
i.
Figure 10 illustrates the variation in MMF values obtained from FEA studies for different combinations of
we and
ws. As seen from
Figure 10, the MMF values required to generate 1.8T within the tested material vary directly with
ws and inversely with
we.
The nonlinear change effect of the
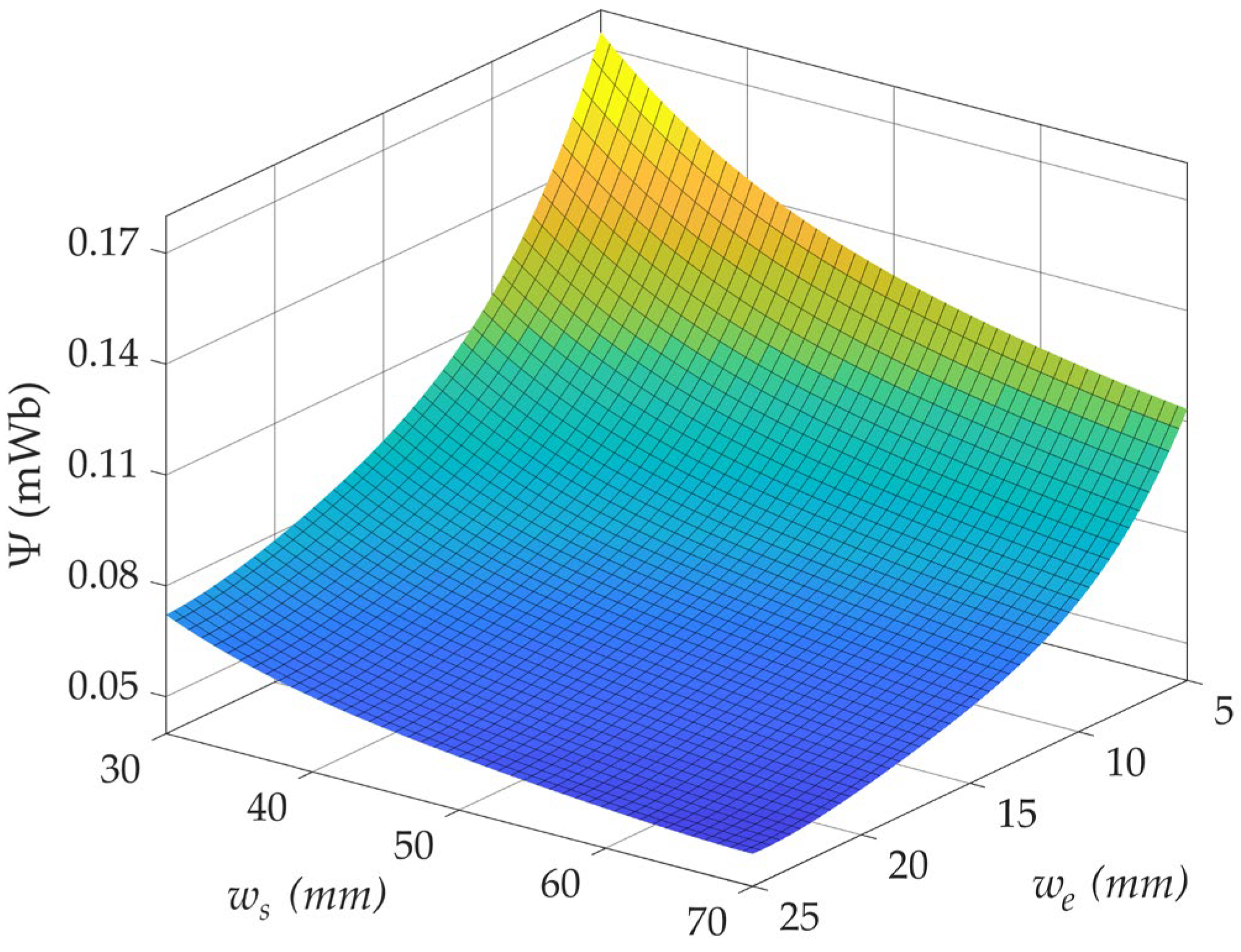
we and
ws parameters on the horizontal leakage flux is illustrated in
Figure 11. As observed, the variation in
we has a more dominant effect than
ws. This is because the
we dimension directly influences the main flux of the system. This effect becomes more pronounced when the
we value approaches the material’s thickness
wm. As a result, the flux densities in the pole regions increase, leading to an exponential increase in the horizontal leakage flux within the slot. A similar effect emerges with the variation in the
ws parameter. Since the
ws dimension determines the distance between the poles, it changes the air reluctance of the horizontal leakage flux. While a decrease in
ws contributes positively to the flux density in the test material, it also increases the horizontal leakage flux, depending on the pole flux densities. Forming near saturation flux density in the tested sample can be seen as the main reason for this dilemma. Ultimately, the variation in
we and
ws dimensions alters the character of the leakage flux within the slot, which is more critical for the system. An increase in horizontal leakage flux particularly affects the sensor measurement region directly, leading to adverse effects such as an increase in the DC level in the defect signal, shape distortions, and signal noise.
Figure 1c illustrates an example of these distortions.
5.2. MEC Model Verification
The main goal of the MFL system design is to achieve the appropriate flux density in the tested material. In addition, the fact that magnetic sources are located on the poles causes these regions to play a decisive role in the system’s main flux and leakage flux. Thus, the pole region flux densities, along with the flux density of the test material, were taken as a basis in the performance analysis of the designed MEC model. By its nature, the MEC calculates its measurements as the average of the branch cross-sectional area. Therefore, the flux densities of the FEA studies were also measured as volumetric average values. In addition, the pole region in the MEC model is represented by three separate permeances, Pub, Pmb, and Plb. Therefore, in the MEC model, the flux density of the pole region value was obtained by averaging the flux densities calculated for these three permeances.
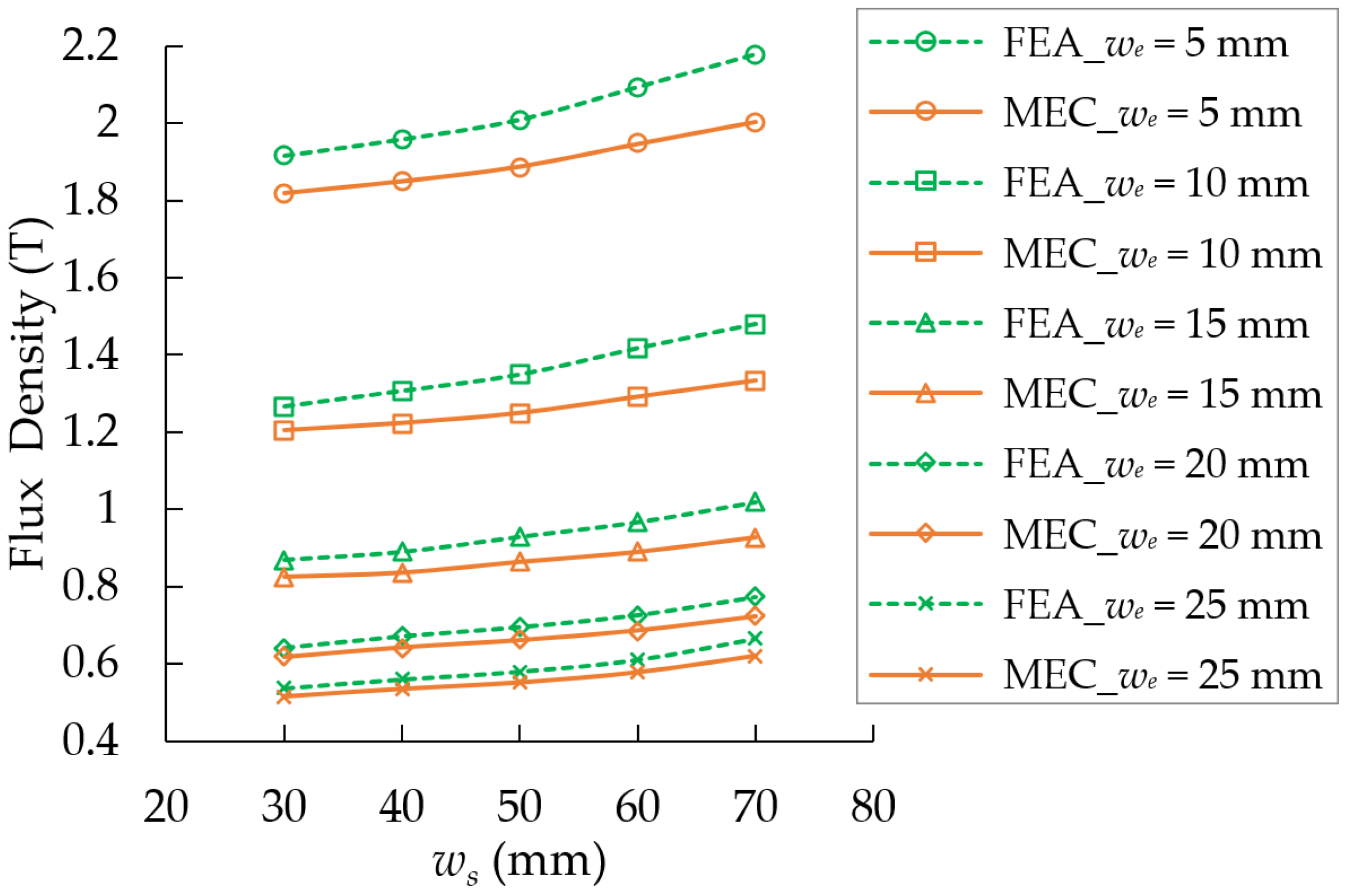
The MMF values derived from the FEA studies served as inputs for the MEC algorithm to perform analyses. The first performance criterion for verifying the MEC model is the consistency between the pole region flux densities calculated by the MEC and the FEA results.
Figure 12 shows the pole region flux densities obtained from both FEA and MEC studies comparatively for all tests. The graphs in
Figure 12 demonstrate that despite variations in
we and
ws, the MEC model tracks the FEA results. To observe the individual effects of changes based on
we and
ws on this result,
Table 3 is also generated.
Table 3 presents the mean absolute error (MAE) resulting from variations in one parameter while keeping the other fixed. Based on the findings from
Figure 12 and
Table 3, it is observed that as
we decreases and
ws increases, the discrepancies between MEC and FEA increase. Additionally, it is noted that
we has a more dominant effect, particularly as it approaches the value of
wm, compared to
ws.
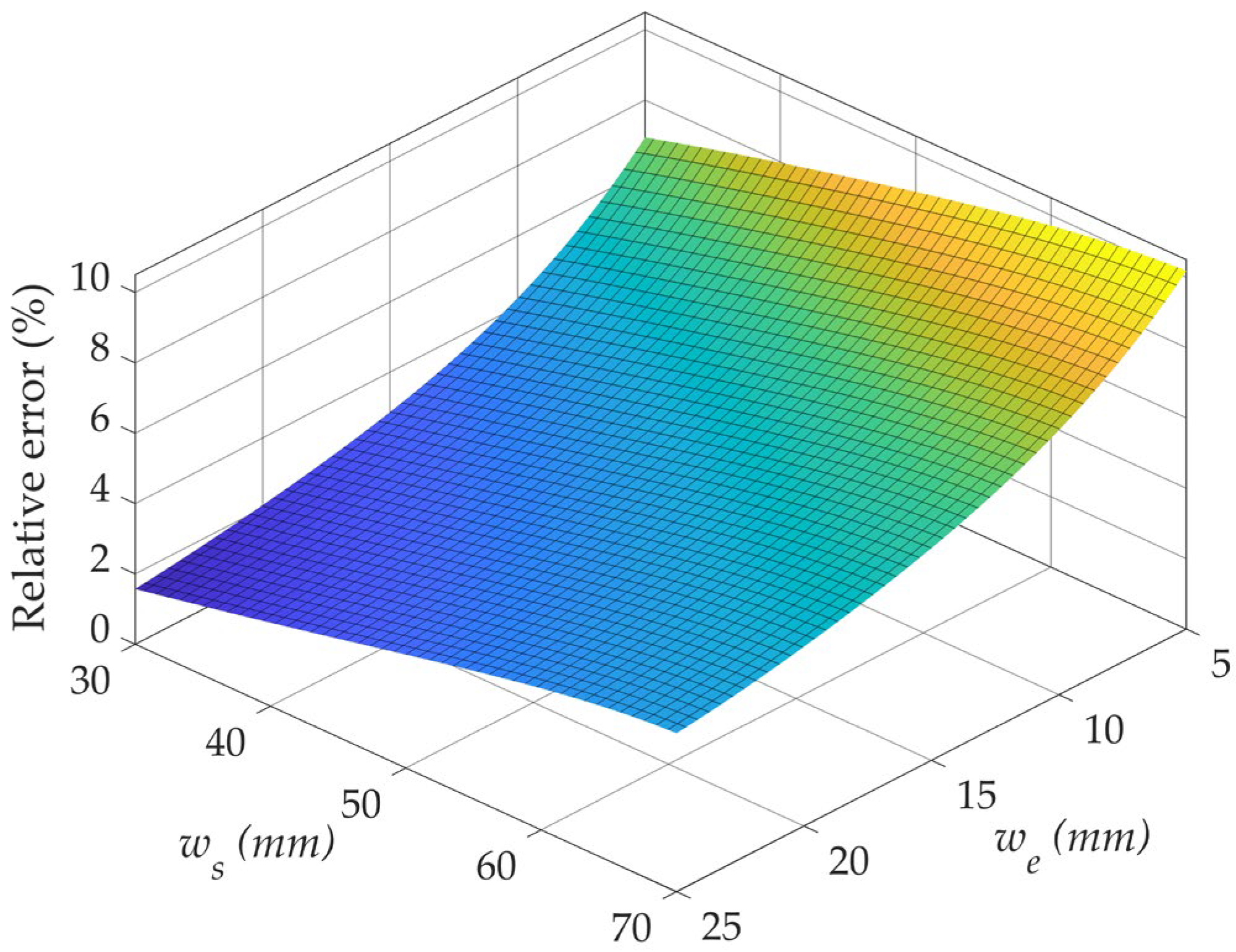
Another critical performance criterion in evaluating the MEC model is the accuracy of calculating the flux density level of the test material. At this stage, the relative error values of the test material’s flux densities obtained from MEC were calculated with respect to the 1.8T reference value used in FEA.
Figure 13 displays these relative error values.
Table 4 illustrates the individual effects of changes based on
we and
ws on the relative error values. It provides the average relative error (MRE) resulting from variations in one parameter while keeping the other parameter fixed.
According to the results shown in
Figure 13, the errors in flux density produced by the MEC model range from a maximum of 10.2% to a minimum of 1.6%, with an average of 5.2%. These results indicate the MEC model’s capability to represent the MFL system at a high level. From
Table 4, it is understood that the MRE values rise with increasing
ws and decreasing
we. Additionally, the variation in
we has a greater impact on the error rates than
ws.
In the flux density calculations, the primary factor contributing to differences between the FEA and MEC model results is that the flux density results must be measured as the average value in both methods. However, the flux densities throughout the system actually exhibit a non-uniform distribution. This is because the magnetic flux tends to flow predominantly through the inner parts of the system due to its preference for the shortest path. This effect results in high flux densities in the inner parts. In the results, the error values reaching their maximum, particularly as we approaches the material’s thickness wm, can be interpreted in this context. Because, in this case, the flux densities of the inner parts of the pole region dramatically increase, and the direction and magnitude of the leakage flux within the slot change. This primarily diminishes the adequacy of the MEC model permeances employed to represent the leakage flux within the slot. Additionally, the increasing impact of other neglected leakage fluxes also becomes a factor that escalates errors. A similar effect emerges due to the rising MMF values with the increase in ws. However, this effect remains at a lower level compared to we. The FEA method can model these effects perfectly because it analyzes the system by dividing it into tiny discrete elements using the mesh method. On the other hand, in the MEC model, the mentioned flux distributions are represented only by three permeances (Pub, Pmb, and Plb) along the vertical direction for the pole region and only by two permeances (Phl1, Phl2) for the inner-slot leakage flux.
5.3. Elapsed Times
MEC and FEA studies were conducted using a computer equipped with an Intel Core i9-12900H processor running at 2.9 GHz, 32 GB of RAM, and a 64-bit Windows 11 operating system. While the average time for FEA studies was 21.5 min, this duration was 5.2 s for MEC model analyses. Additionally, it was observed that consecutive FEA studies involve extra time-consuming processes such as geometry modifications, system reinstallations, and simulation restarts.
6. Conclusions
This study proposes a novel MEC model to achieve an efficient MFL system design. This model is designed considering the nonlinear behaviors of the magnetic elements, winding leakage flux, horizontal leakage flux within the slot, and the fringing effect. The proposed MEC model can comprehensively represent the system’s behavior with these features. The main requirement in the MFL system design is to form a level of flux density near saturation in the test material with the change in system dimensions. Additionally, it is also crucial to consider the undesired effects of slot leakage flux on the sensor for an efficient system design. In this study, a reverse engineering-like test approach is adopted to observe the mentioned effects, keeping the flux density of the test material fixed. This approach enables us to effectively and comparably observe other system parameters’ influence on common objectives.
The accuracy test of the proposed MEC model is carried out based on the FEA results, considering the variation in the we and ws parameters. In the flux density results of the pole region, as we decreases from 25 mm to 5 mm, the average absolute error MAE_we increases by 0.167T. The rise in the ws from 30 mm to 70 mm results in the MAE_ws value increasing by 0.05T. These results show the error variation in the MEC model in tracking the FEA. In terms of the flux density calculation of the test material, the maximum relative error is obtained as 10.2%, and the average relative error is 5.2%. Moreover, with the change in we from 25 mm to 5 mm, the average relative error MRE_we increases by 5.6%. With the increase in ws from 30 mm to 70 mm, the MRE_ws error value rises by 3.2%. These results show that the change in we significantly affects the errors compared to ws. This is because as we approaches the wm value, the increase in the flux density of the pole region is much greater than the increase associated with the change in ws. Ultimately, the results indicate that despite changes in critical system dimensions, the MEC model produces errors at a reasonable level and successfully tracks the FEA results.
The primary purpose of the designed MEC model is to generate fast solutions in the system design process. In this study, the average processing time is 5.2 s for the MEC model, whereas for FEA, this time is determined as 21.5 min. The proposed MEC model offers a significant time advantage compared to the FEA method while generating acceptable error levels. With this feature, the necessary MFL system design for rapid prototyping tasks requiring system optimization can be accomplished using the proposed MEC model.
The performance of the proposed MEC model can be enhanced through model refinement. In this regard, it is necessary to consider the naturally occurring inhomogeneous distribution effect in the flux densities of magnetic elements first. This process can be achieved by modeling the system’s magnetic yoke by dividing it into segments. Secondly, it is essential to define additional permeances in the MEC model to represent leakage fluxes more accurately. With these improvements, the MEC model can provide more accurate results.
Author Contributions
Conceptualization, O.K. and H.H.Ç.; methodology, O.K. and H.H.Ç.; formal analysis, O.K. and H.H.Ç.; software, O.K.; writing—original draft preparation, O.K.; validation H.H.Ç.; writing—review and editing, O.K. and H.H.Ç. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this study has been supported by the Marmara University Scientific Research Projects Coordination Unit, with financial support provided under Grant number FDK-2021-10373.
Data Availability Statement
The data presented in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Coughlin, C.R.; Clapham, L.; Atherton, D.L. Effects of Stress on MFL Responses from Elongated Corrosion Pits in Pipeline Steel. NDT & E Int. 2000, 33, 181–188. [Google Scholar] [CrossRef]
- Ravan, M.; Amineh, R.K.; Koziel, S.; Nikolova, N.K.; Reilly, J.P. Sizing of 3-D Arbitrary Defects Using Magnetic Flux Leakage Measurements. IEEE Trans. Magn. 2010, 46, 1024–1033. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, X.; Lu, S.; Yang, F. A Single-Stage Enhancement-Identification Framework for Pipeline MFL Inspection. IEEE Trans. Instrum. Meas. 2022, 71, 3513813. [Google Scholar] [CrossRef]
- Hosseingholizadeh, S.; Filleter, T.; Sinclair, A.N. Enhancement of Defect Characterization with AC Magnetic Flux Leakage: Far-Side Defect Shape Estimation and Sensor Lift-Off Compensation. IEEE Trans. Magn. 2022, 58, 6200811. [Google Scholar] [CrossRef]
- Liu, S.; Sun, Y.; Jiang, X.; Kang, Y. A New MFL Imaging and Quantitative Nondestructive Evaluation Method in Wire Rope Defect Detection. Mech. Syst. Signal Process 2022, 163, 108156. [Google Scholar] [CrossRef]
- Ji, K.; Wang, P.; Jia, Y.; Ye, Y.; Ding, S. Adaptive Filtering Method of MFL Signal on Rail Top Surface Defect Detection. IEEE Access 2021, 9, 87351–87359. [Google Scholar] [CrossRef]
- Suresh, V.; Abudhahir, A.; Daniel, J. Characterization of Defects on Ferromagnetic Tubes Using Magnetic Flux Leakage. IEEE Trans. Magn. 2019, 55, 6200510. [Google Scholar] [CrossRef]
- Azizzadeh, T.; Safizadeh, M.S. Estimation of the Diameters, Depths and Separation Distances of the Closely-Spaced Pitting Defects Using Combination of Three Axial MFL Components. Measurement 2019, 138, 341–349. [Google Scholar] [CrossRef]
- Pham, H.Q.; Trinh, Q.T.; Doan, D.T.; Tran, Q.H. Importance of Magnetizing Field on Magnetic Flux Leakage Signal of Defects. IEEE Trans. Magn. 2018, 54, 6201206. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Shi, M.; Douadji, L. A Novel Magnetic Equivalent Circuit Model for the Corner of Inductor Core. Appl. Sci. 2019, 9, 5341. [Google Scholar] [CrossRef]
- Jin, J.-M. Electromagnetic Radiation in Free Space. In Theory and Computation of Electromagnetic Fields; Wiley-IEEE Press: Hoboken, NJ, USA, 2015; pp. 54–55. [Google Scholar]
- Kano, Y.; Kosaka, T.; Matsui, N. Simple Nonlinear Magnetic Analysis for Permanent-Magnet Motors. IEEE Trans. Ind. Appl. 2005, 41, 1205–1214. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Y.; Chen, Q.; Xu, G.; Cao, D. Design and Analysis of a New Equivalent Magnetic Network Model for IPM Machines. IEEE Trans. Magn. 2020, 56, 8101112. [Google Scholar] [CrossRef]
- Asghari, B.; Dinavahi, V. Novel Transmission Line Modeling Method for Nonlinear Permeance Network Based Simulation of Induction Machines. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–9. [Google Scholar]
- Yilmaz, M.; Philip, T. Krein Capabilities of Finite Element Analysis and Magnetic Equivalent Circuits for Electrical Machine Analysis and Design. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; p. 4837. [Google Scholar]
- Sheikh-Ghalavand, B.; Vaez-Zadeh, S.; Hassanpour Isfahani, A. An Improved Magnetic Equivalent Circuit Model for Iron-Core Linear Permanent-Magnet Synchronous Motors. IEEE Trans. Magn. 2010, 46, 112–120. [Google Scholar] [CrossRef]
- Ned, M.; Tore, M.U.; William, P.R. Power Electronics, 2nd ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Song, X.C.; Huang, S.L.; Zhao, W. Optimization of the Magnetic Circuit in the MFL Inspection System for Storage-Tank Floors. Russ. J. Nondestruct. Test. 2007, 43, 326–331. [Google Scholar] [CrossRef]
- Parra-Raad, J.A.; Roa-Prada, S. Multi-Objective Optimization of a Magnetic Circuit for Magnetic Flux Leakage-Type Nondestructive Testing. J. Nondestr Eval. 2016, 35, 14. [Google Scholar] [CrossRef]
- Wang, X.; Wu, X.; Xu, J.; Ba, H. Study on the Lift-off Effect on MFL Signals with Magnetic Circuit Model and 3D FEM. Insight Nondestruct. Test. Cond. Monit. 2012, 54, 505–510. [Google Scholar] [CrossRef]
- Kara, O.; Çelik, H.H. The Homogeneity Effects of Magnetic Flux Density Distribution on the Detection of Railhead Surface Defects via the Magnetic Flux Leakage Method. Insight Nondestruct. Test. Cond. Monit. 2023, 65, 682–688. [Google Scholar] [CrossRef]
- Sudhoff, S.D. Magnetics and Magnetic Equivalent Circuits. In Power Magnetic Devices: A Multi-Objective Design Approach; Wiley: New York, NY, USA, 2014; pp. 70–81. [Google Scholar]
- Chen, J.; Hua, W.; Shao, L.; Wu, Z.; Yan, X.; Zhang, W. Modified Magnetic Equivalent Circuit of Double-Stator Single-Rotor Axial Flux Permanent Magnet Machine Considering Stator Radial-End Flux-Leakage. IET Electr. Power Appl. 2024, 18, 195–207. [Google Scholar] [CrossRef]
- Sudhoff, S.D.; Kuhn, B.T.; Corzine, K.A.; Branecky, B.T. Magnetic Equivalent Circuit Modeling of Induction Motors. IEEE Trans. Energy Convers. 2007, 22, 259–270. [Google Scholar] [CrossRef]
- Derbas, H.W.; Williams, J.M.; Koenig, A.C.; Pekarek, S.D. A Comparison of Nodal- and Mesh-Based Magnetic Equivalent Circuit Models. IEEE Trans. Energy Convers. 2009, 24, 388–396. [Google Scholar] [CrossRef]
- Math. Graphics. Programming. Available online: https://www.mathworks.com/products/matlab.html (accessed on 1 April 2024).
- Ansys Maxwell Low Frequency EM Field Simulation. Available online: https://www.ansys.com/products/electronics/ansys-maxwell (accessed on 17 December 2023).
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).