Determination of the Probabilistic Properties of the Critical Fracture Energy of Concrete Integrating Scale Effect Aspects
Abstract
1. Introduction
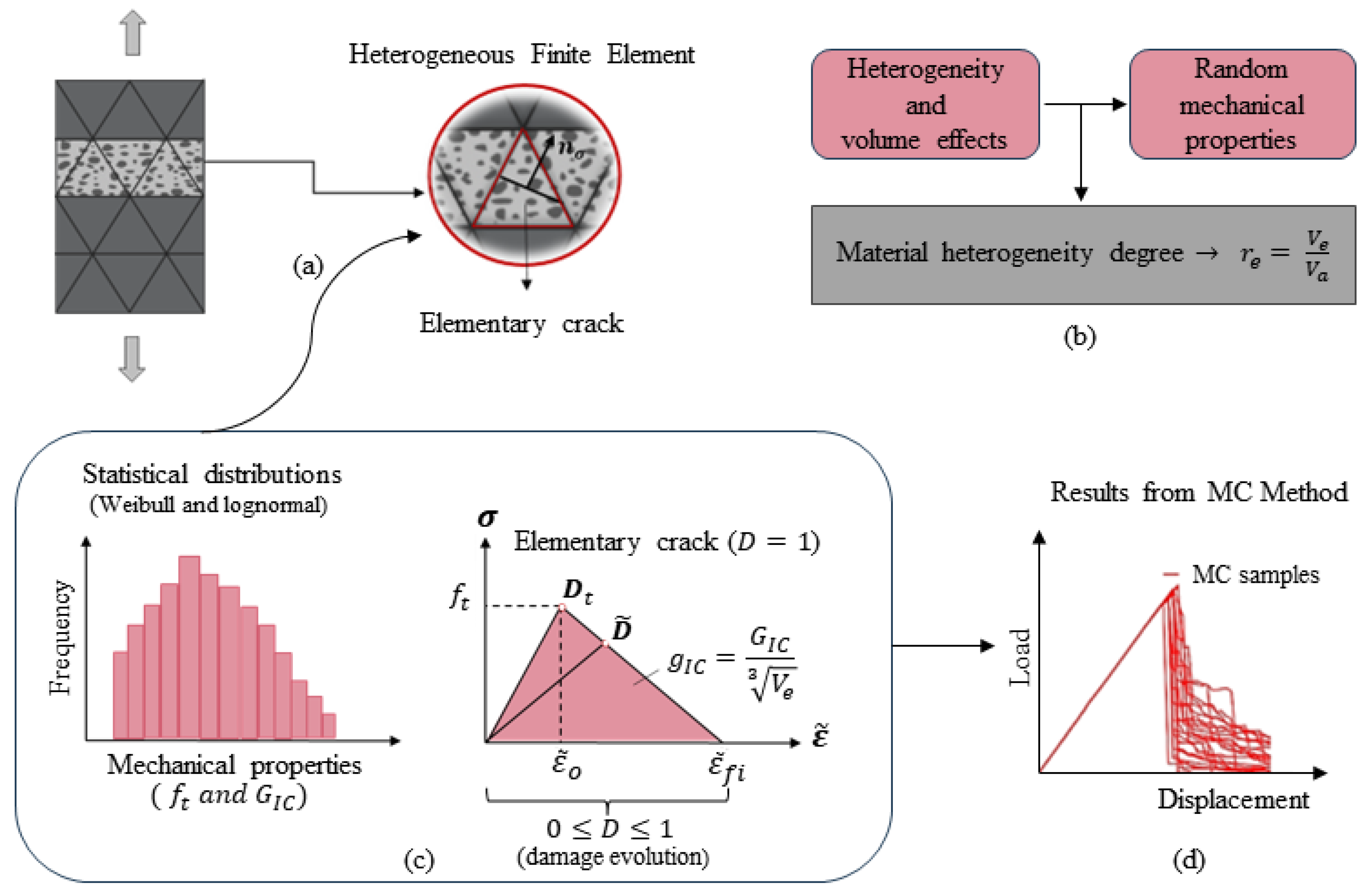
2. Determination of the Probabilistic Properties of
3. Validation
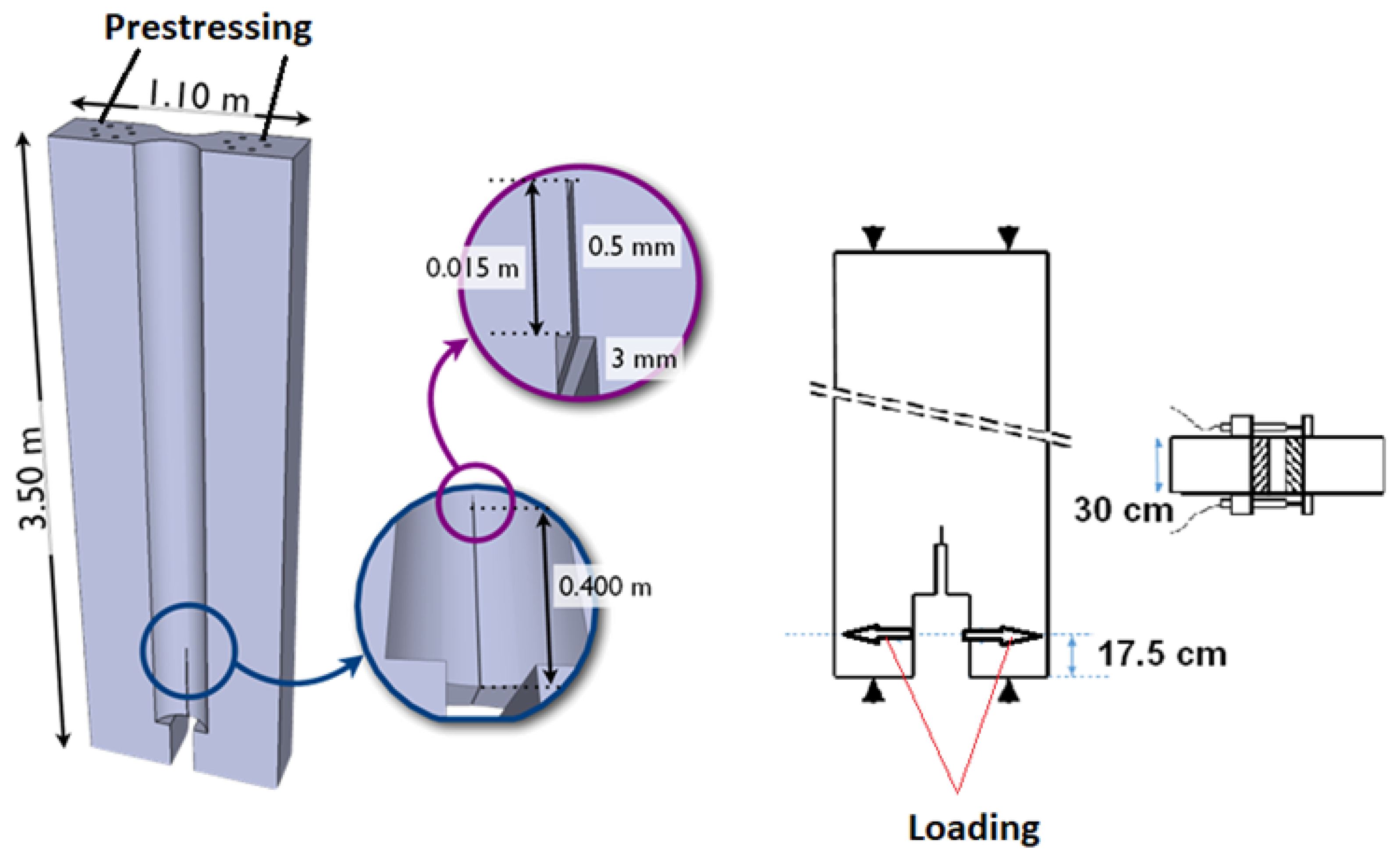
3.1. Experimental Test Chosen for the Validation
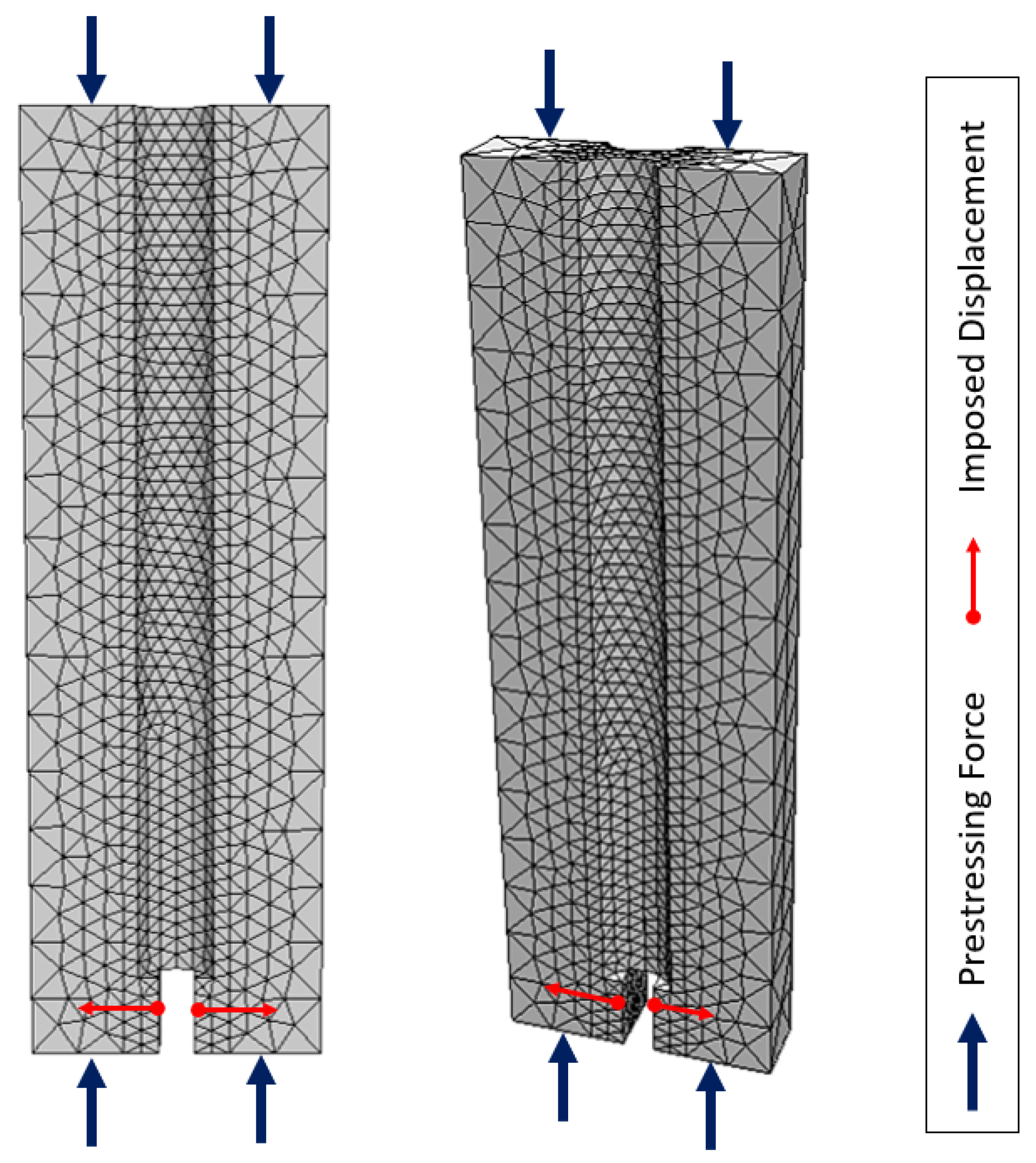
3.2. Probabilistic Numerical Model
| Algorithm 1: Basic steps of the FEM program |
|
3.2.1. Distribution of Random Material Properties
3.2.2. Estimation of the Model Parameters
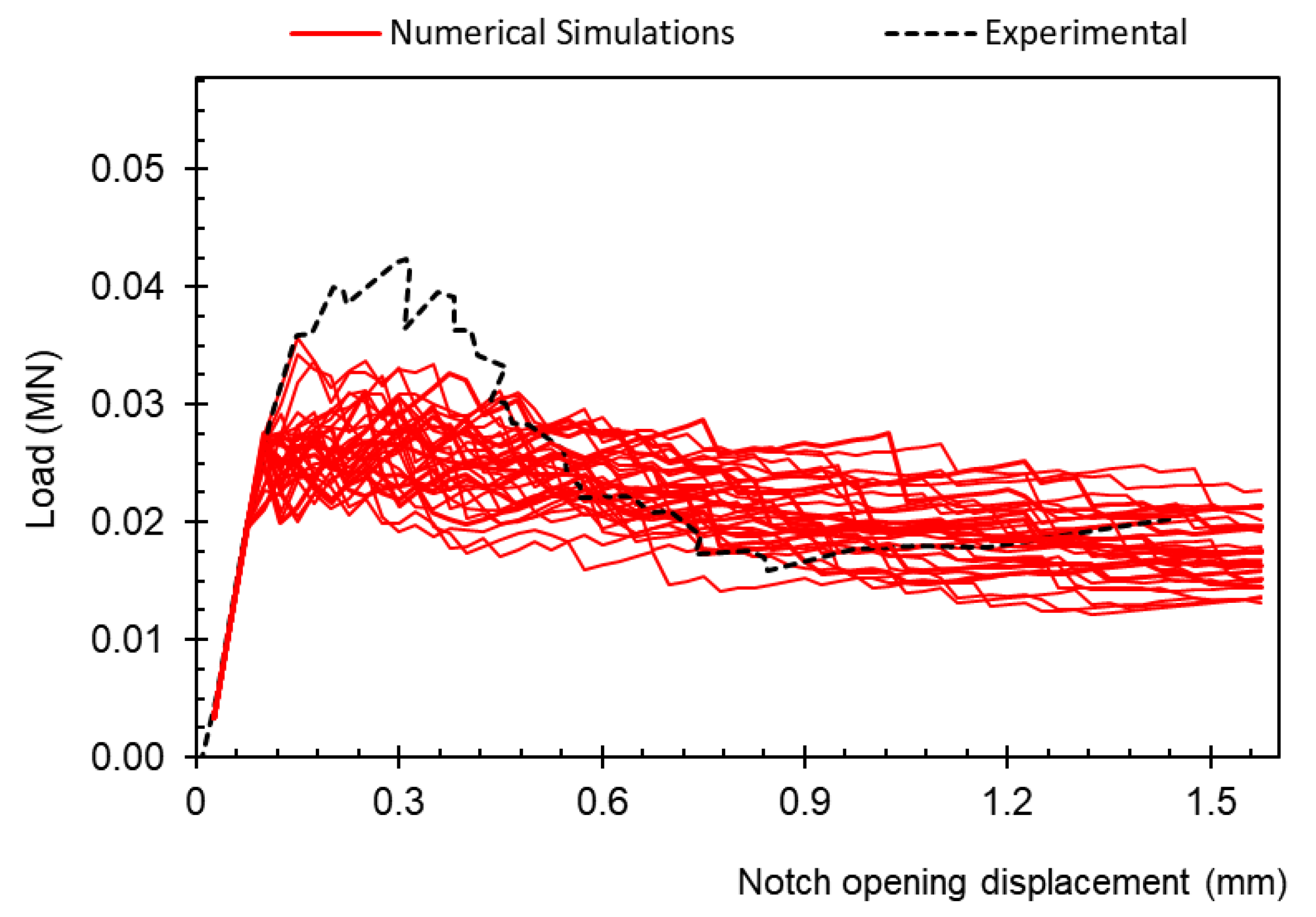
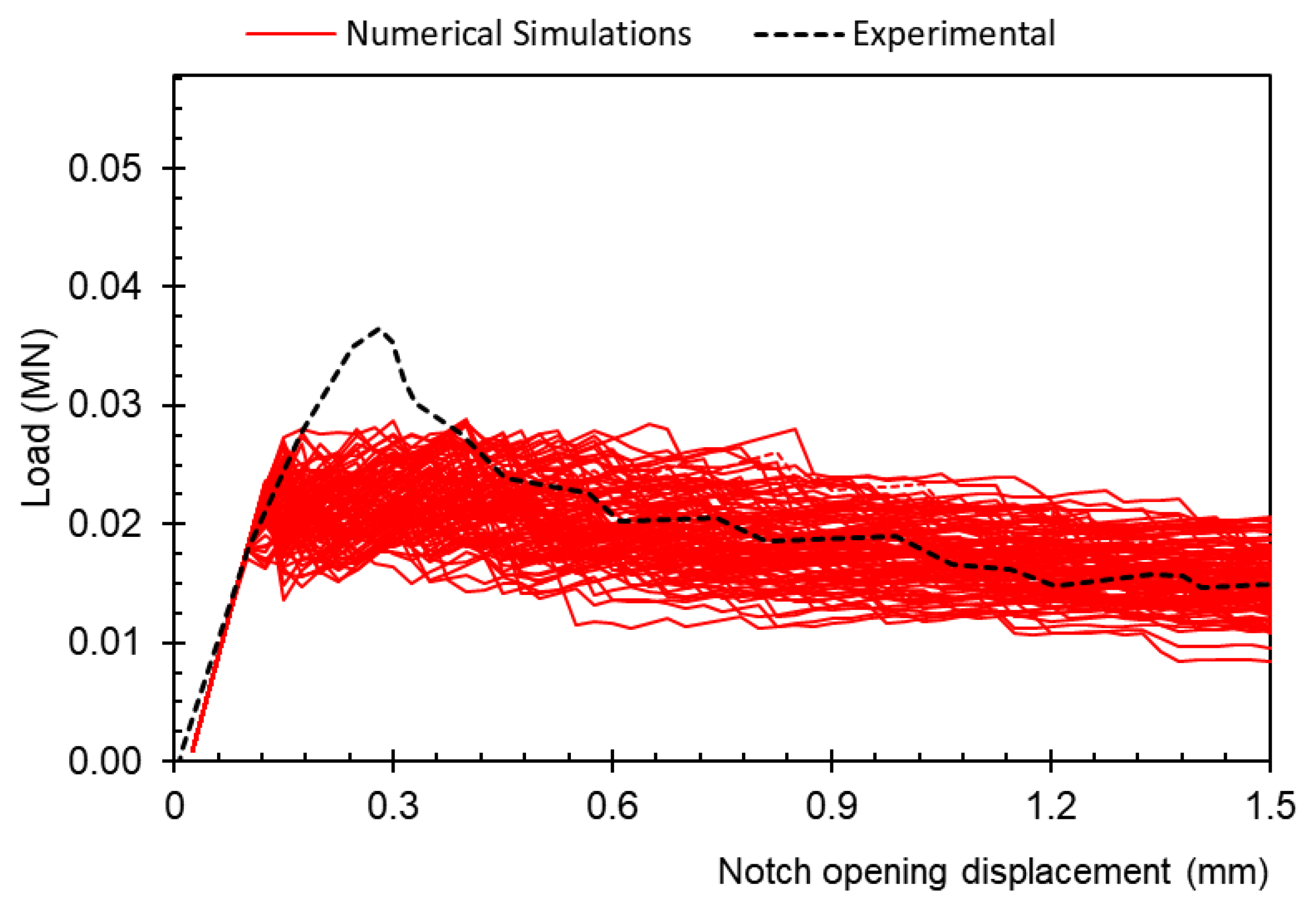
3.3. Numerical Simulations
4. Determination of the Mean Value of
5. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mazars, J. Application de la Mecanique de L’endommagement au Comportement non Lineaire et a la Rupture du Beton de Structure. Ph.D. Thesis, Ecole Normale Supériore de l’Enseignement Technique, Paris, France, 1984. [Google Scholar]
- Pijaudier-Cabot, G.; Bažant, Z. Nonlocal damage theory. J. Eng. Mech. 1987, 113, 1512–1533. [Google Scholar] [CrossRef]
- Rashid, Y.R. Ultimate Srength Analysis of Pre-stressed Concrete Pressure Vessels. Nucl. Eng. Des. 1968, 7, 334–344. [Google Scholar] [CrossRef]
- De Borst, R.; Nauta, P. Nonorthogonal cracks in a smeared finite element model. Eng. Comput. 1985, 2, 35–46. [Google Scholar] [CrossRef]
- Feenstra, P.H.; De Borst, R. A plasticity model and algorithm for mode-I cracking in concrete. Int. J. Numer. Methods Eng. 1995, 38, 2509–2529. [Google Scholar]
- Hillerborg, A.; Modeer, M.; Petersson, P. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement Concrete Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Hillerborg, A. Numerical methods to simulate softening and fracture of concrete. In Fracture Mechanics of Concrete: Structural Application and Numerical Calculation; Springer: Dordrecht, The Netherlands, 1985; pp. 141–170. [Google Scholar]
- Möes, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar]
- Armero, F.; Garikipati, K. An analysis of strong discontinuities in multiplicative nite strain plasticity and their relation with the numerical simulation of strain localization in solids. Int. J. Solids Struct. 1996, 33, 2863–2885. [Google Scholar] [CrossRef]
- Chang, Z.; Zhang, H.; Schlangen, E.; Šavija, B. Lattice Fracture Model for Concrete Fracture Revisited: Calibration and Validation. Appl. Sci. 2020, 10, 4822. [Google Scholar]
- Rastiello, G. Influence de la Fissuration sur le Transfert de Fluides Dans les Structures en Béton. Stratégies de Modélisation Probabiliste et Étude Expérimentale. Ph.D. Thesis, IFSTTAR, Paris, France, 2013. [Google Scholar]
- Rita, M.R. Implementation of a 3D Macroscopic Probabilistic Model for Semi-Explicit Concrete Cracking. Ph.D. Thesis, UFRJ, Rio de Janeiro, Brazil, 2022. [Google Scholar]
- Nadai, A. Theory of Flow and Fracture of Solids; McGraw-Hill: New York, NY, USA, 1950; Volume 1. [Google Scholar]
- Rots, J.G. Prediction of Dominant Cracks Using the Smeared Crack Concept; Technical Report; Institute TNO for Building Materials and Building Structures: Rijswijk, The Netherlands, 1983. [Google Scholar]
- Bazant, Z.P. Mechanics of distributed cracking. Appl. Mech. Rev 1986, 39, 675–705. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Pijaudier-Cabot, G. Measurement of Characteristic Length of Nonlocal Continuum. J. Eng. Mech. 1989, 115, 755–767. [Google Scholar] [CrossRef]
- Pijaudier-Cabot, G.; Mazars, J.; Pulikowski, J. Steel-Concrete Bond Analysis with Nonlocal Continuous Damage. J. Struct. Eng. 1991, 117, 862–882. [Google Scholar] [CrossRef]
- Fichant, S.; La Borderie, C.; Pijaudier-Cabot, G. Isotropic and anisotropic descriptions of damage in concrete structures. Mech. Cohesive-Frict. Mater. 1999, 4, 339–359. [Google Scholar] [CrossRef]
- Zhou, X.; Feng, B. A smeared-crack-based field-enriched finite element method for simulating cracking in quasi-brittle materials. Theor. Appl. Fract. Mech. 2023, 124, 103817. [Google Scholar] [CrossRef]
- Matos, L.M.P.; Barros, J.A.O.; Ventura-Gouveia, A.; Calçada, R.A.B. Two-dimensional integrated mixed-mode smeared crack model for simulating FRC structures. Eng. Fract. Mech. 2023, 289, 109401. [Google Scholar] [CrossRef]
- Rossi, P.; Wu, X.; Le Maou, F.; Belloc, A. Scale effect on concrete in tension. Mater. Struct. 1994, 27, 437–444. [Google Scholar] [CrossRef]
- Phan, T.S.; Tailhan, J.L.; Rossi, P. 3D numerical modelling of concrete structural element reinforced with ribbed flat steel rebars. Struct. Concr. 2013, 14, 378–388. [Google Scholar] [CrossRef]
- Rossi, P.; Tailhan, J.L.; Desnoyers, D. Numerical models for designing UHPRFC-fibre-reinforced concrete structures: Why and which ones? Special Publication FIB Bulletin 79-ACI SP 2017, 310, 289–300. [Google Scholar] [CrossRef]
- Nader, C.; Rossi, P.; Tailhan, J.L. Multi-scale strategy for modeling macrocracks propagation in reinforced concrete structures. Cem. Concr. Compos. 2019, 99, 262–274. [Google Scholar] [CrossRef]
- Xu, P.; Ma, J.; Zhang, M.; Ding, Y.; Meng, L. Fracture Energy Analysis of Concrete considering the Boundary Effect of Single-Edge Notched Beams. Adv. Civ. Eng. 2018, 2018, 3067236. [Google Scholar] [CrossRef]
- Ravindra, G.; Bažant, Z.P.; Karr, M.E. Fracture Properties and Brittleness of High-Strength Concrete. ACI Mater. J. 1990, 87, 608–618. [Google Scholar]
- Bažant, Z.P.; Kazemi, M.T. Determination of fracture energy, process zone length and brittleness number from size effect, with application to rock and concrete. Int. J. Fract. 1990, 44, 111–131. [Google Scholar] [CrossRef]
- Le, J.L.; Bažant, Z.P.; Bazant, M.Z. Unified nano-mechanics based probabilistic theory of quasibrittle and brittle structures: I. Strength, static crack growth, lifetime and scaling. J. Mech. Phys. Solids 2011, 59, 1291–1321. [Google Scholar] [CrossRef]
- Rossi, P.; Acker, P.; Francois, D. Measurements of the fracture toughness KIC of concrete. In Proceedings of the 6th International Conference on Fracture, New Delhi, India, 4–10 December 1984; pp. 2833–2839. [Google Scholar]
- Rossi, P. Fissuration du bÉton: Du Matériau à la Structure-Application de la mÉcanique Lineaire de la Rupture. Ph.D. Thesis, L’Ecole Nationale des Ponts et Chaussées, Paris, France, 1986. [Google Scholar]
- Ramamurty, U. Mechanical Testing Methods of Fibers and Composites. In Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; pp. 5271–5274. [Google Scholar]
- Broughton, W. Testing the Mechanical, Thermal and Chemical Properties of Adhesives for Marine Environments; Adhesives in Marine Engineering, Woodhead Publishing Series in Welding and Other Joining Technologies; Woodhead Publishing: Cambridge, UK, 2012. [Google Scholar]
- Entov, V.; Yagust, V. Experimental investigation of laws governing quasi static development of crack in concrete. Mech. Solids 1975, 10, 87–95. [Google Scholar]
- Watson, K. The estimation of fracture surface energy as a measure of the “toughness” of hardened cement paste. Cem. Concr. Res. 1978, 8, 651–656. [Google Scholar] [CrossRef]
- Wittman, F. Mechanisms and mechanics of fracture of concrete. In Proceedings of the 5th International Conference on Fracture (ICF5), Cannes, France, 29 March–3 April 1981; Invited lecture. Volume 4, pp. 1467–1487. [Google Scholar]
- Walsh, P. Fracture of plain concrete. Indian Concr. J. 1982, 89, 469–476. [Google Scholar]
- Carpinteri, A. Experimental determination of fracture toughness KIC for aggregative materials. Adv. Fract. Res. 1982, 4, 1491–1498. [Google Scholar]
- Shah, S.P. Application of Fracture Mechanics to Cementitious Composites. In Proceedings of the NATO Advanced Research Workshop, Evanston, IL, USA, 4–7 September 1984. [Google Scholar]
- Reinhardt, H.W. The role of fracture mechanics in rational rules for concrete design. IABSE Period. 1 1986, 10, 1–15. [Google Scholar]
- Rossi, P. Fracture properties of concrete determined by means of wedge splitting tests and tapered double cantilever beams tests. Fracture mechanics test methods for concrete. In Proceedings of the RILEM Report 5; Shah, S., Carpinteri, A., Eds.; CRC Press: New York, NY, USA, 1991. [Google Scholar]
- Bazant, Z.; Oh, B. Crack band theory for fracture of concrete. Mater. Struct. 1983, 3, 155–177. [Google Scholar]
- Rossi, P. Determination of Toughness Characteristics of Concretes. Curr. Trends Civ. Struct. Eng. 2023, 10, 1–7. [Google Scholar]

| Constituent | Concrete 1 | Concrete 2 |
|---|---|---|
| Quantity | ||
| Aggregate 1 (4–12 mm) | 1105 kg/m3 | - |
| Aggregate 2 (5–20 mm) | - | 1265 kg/m3 |
| Sand (0–5 mm) | 700 kg/m3 | 652 kg/m3 |
| Cement | 400 kg/m3 | 421 kg/m3 |
| Water | 190 L/m3 | 112 L/m3 |
| Silica fume | - | 42.1 kg/m3 |
| Superplasticizer (dry powder) | - | 7.6 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rita, M.R.; Rossi, P.; Fairbairn, E.d.M.R.; Ribeiro, F.L.B. Determination of the Probabilistic Properties of the Critical Fracture Energy of Concrete Integrating Scale Effect Aspects. Appl. Sci. 2024, 14, 462. https://doi.org/10.3390/app14010462
Rita MR, Rossi P, Fairbairn EdMR, Ribeiro FLB. Determination of the Probabilistic Properties of the Critical Fracture Energy of Concrete Integrating Scale Effect Aspects. Applied Sciences. 2024; 14(1):462. https://doi.org/10.3390/app14010462
Chicago/Turabian StyleRita, Mariane Rodrigues, Pierre Rossi, Eduardo de Moraes Rego Fairbairn, and Fernando Luiz Bastos Ribeiro. 2024. "Determination of the Probabilistic Properties of the Critical Fracture Energy of Concrete Integrating Scale Effect Aspects" Applied Sciences 14, no. 1: 462. https://doi.org/10.3390/app14010462
APA StyleRita, M. R., Rossi, P., Fairbairn, E. d. M. R., & Ribeiro, F. L. B. (2024). Determination of the Probabilistic Properties of the Critical Fracture Energy of Concrete Integrating Scale Effect Aspects. Applied Sciences, 14(1), 462. https://doi.org/10.3390/app14010462






