Water Heating and Circulating Heating System with Energy-Saving Optimization Control
Abstract
1. Introduction
2. Related Works
2.1. The History of Development—Water Heating and Circulating System
2.2. The Current Technical Features and Capabilities
- Vacuum-sealed foods;
- Precise and long-term temperature control;
- The control of water flow;
- The combination of heating and water temperature.
2.3. Temperature Control
2.4. The Water Flow Control
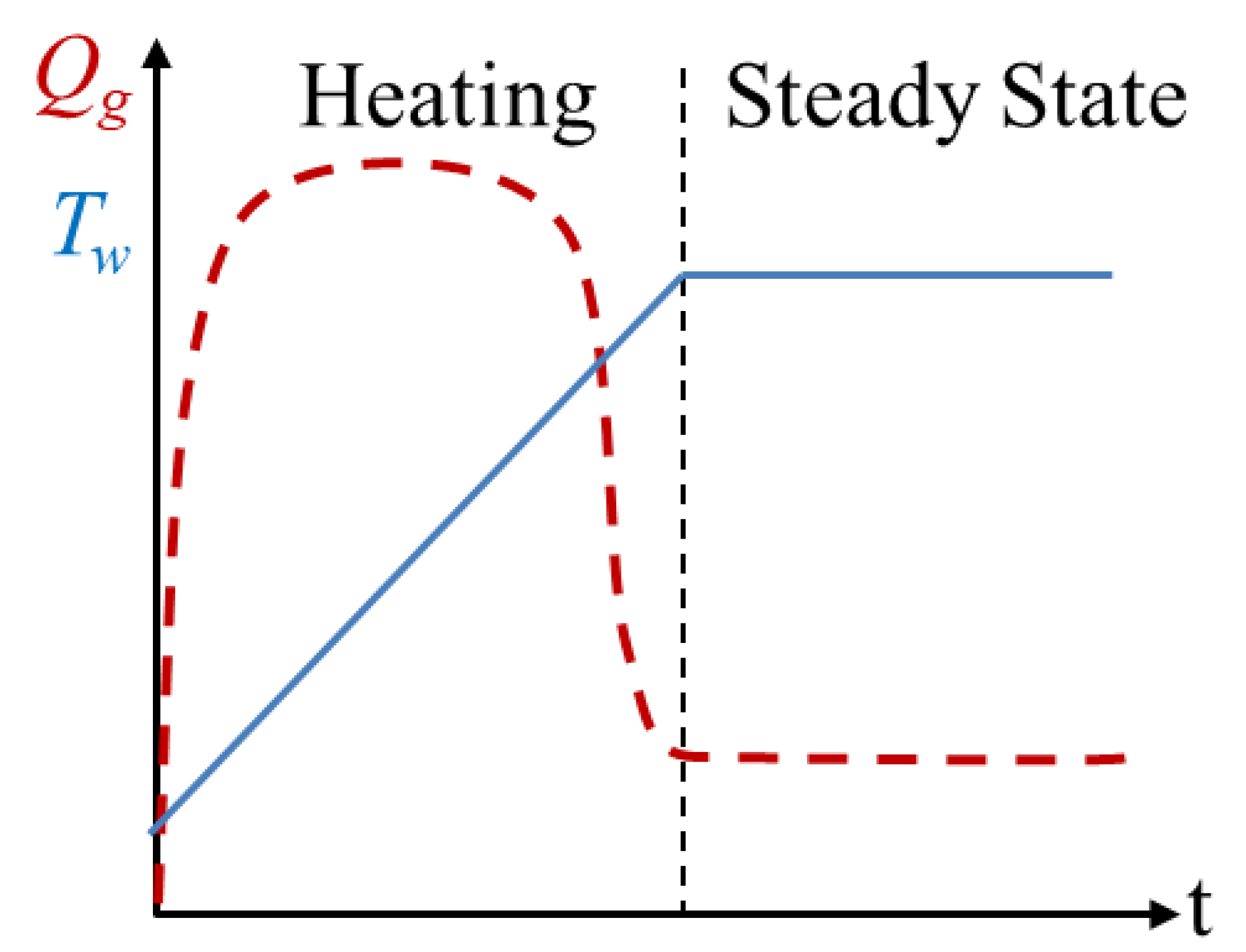
2.5. The Heating Efficiency of Water Heating and Circulating
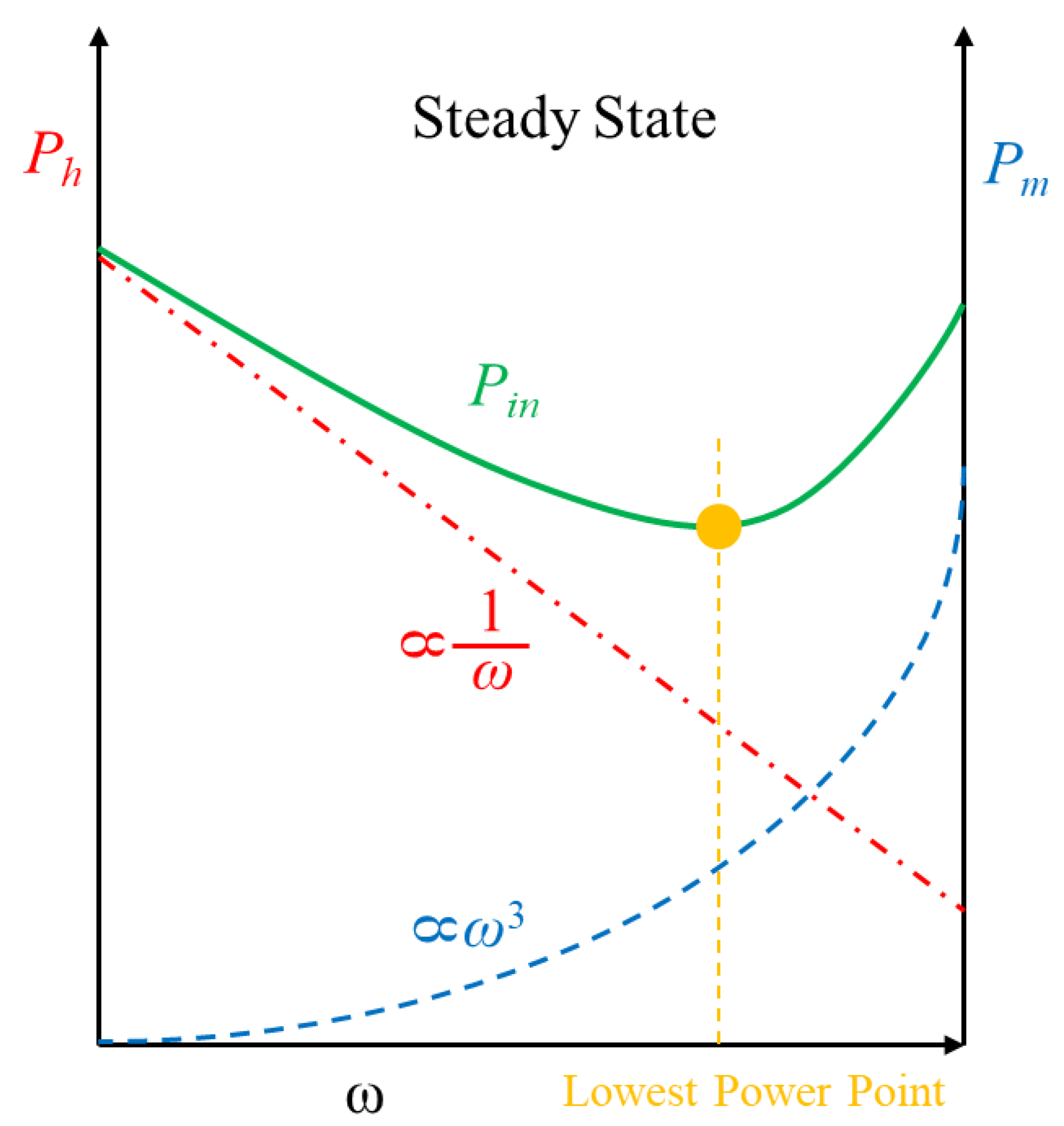
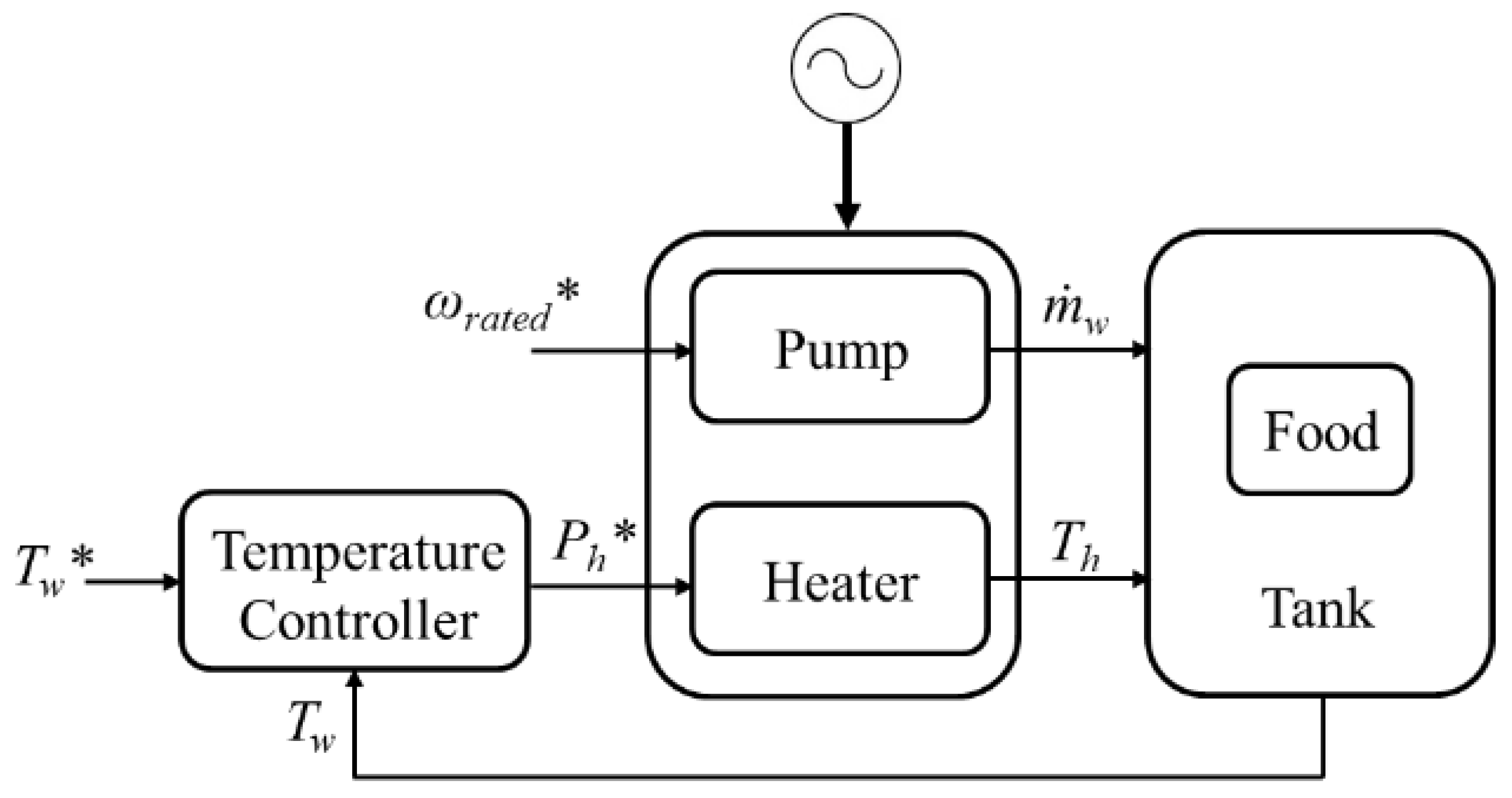
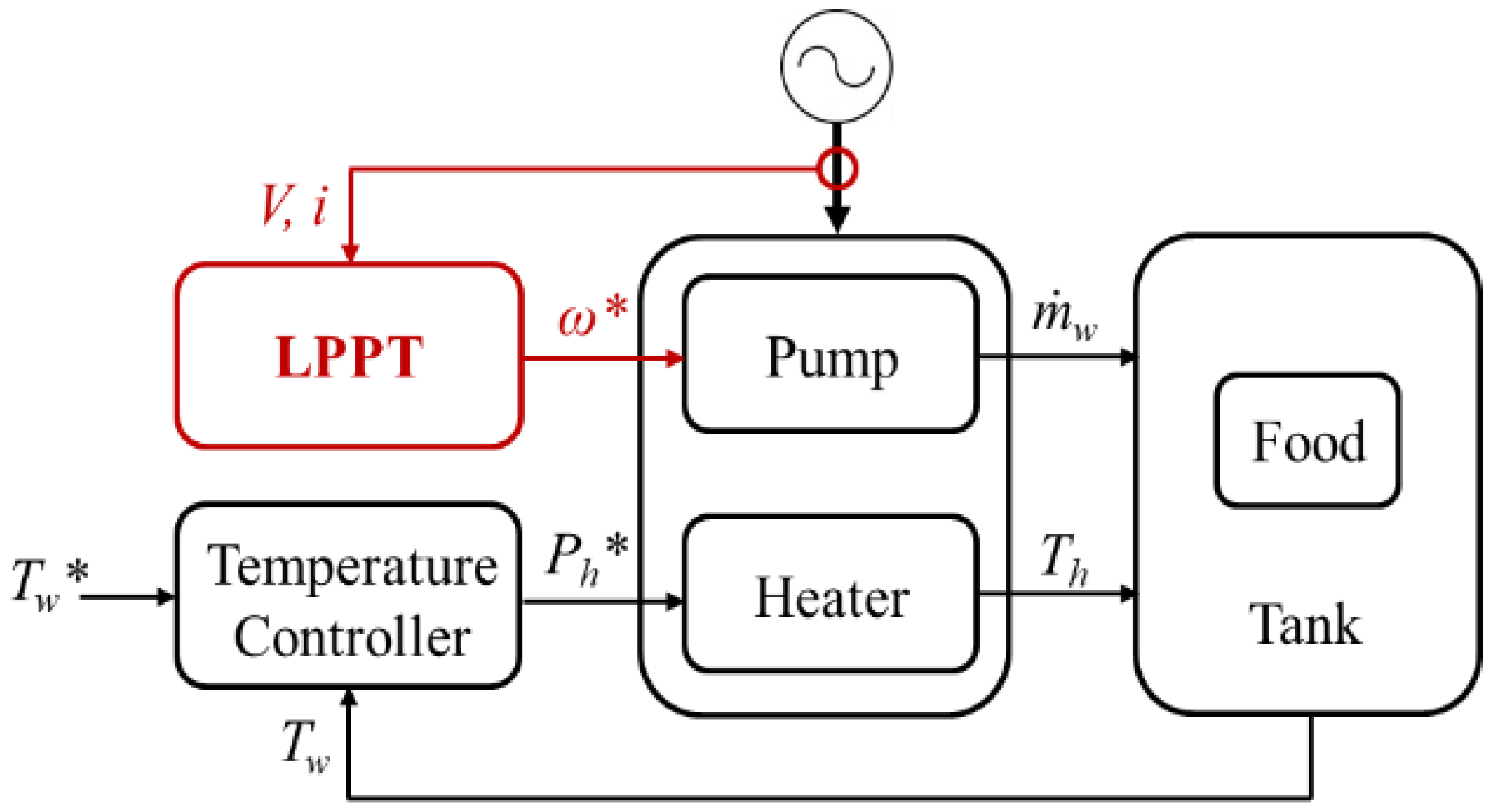
3. The LPPT Method
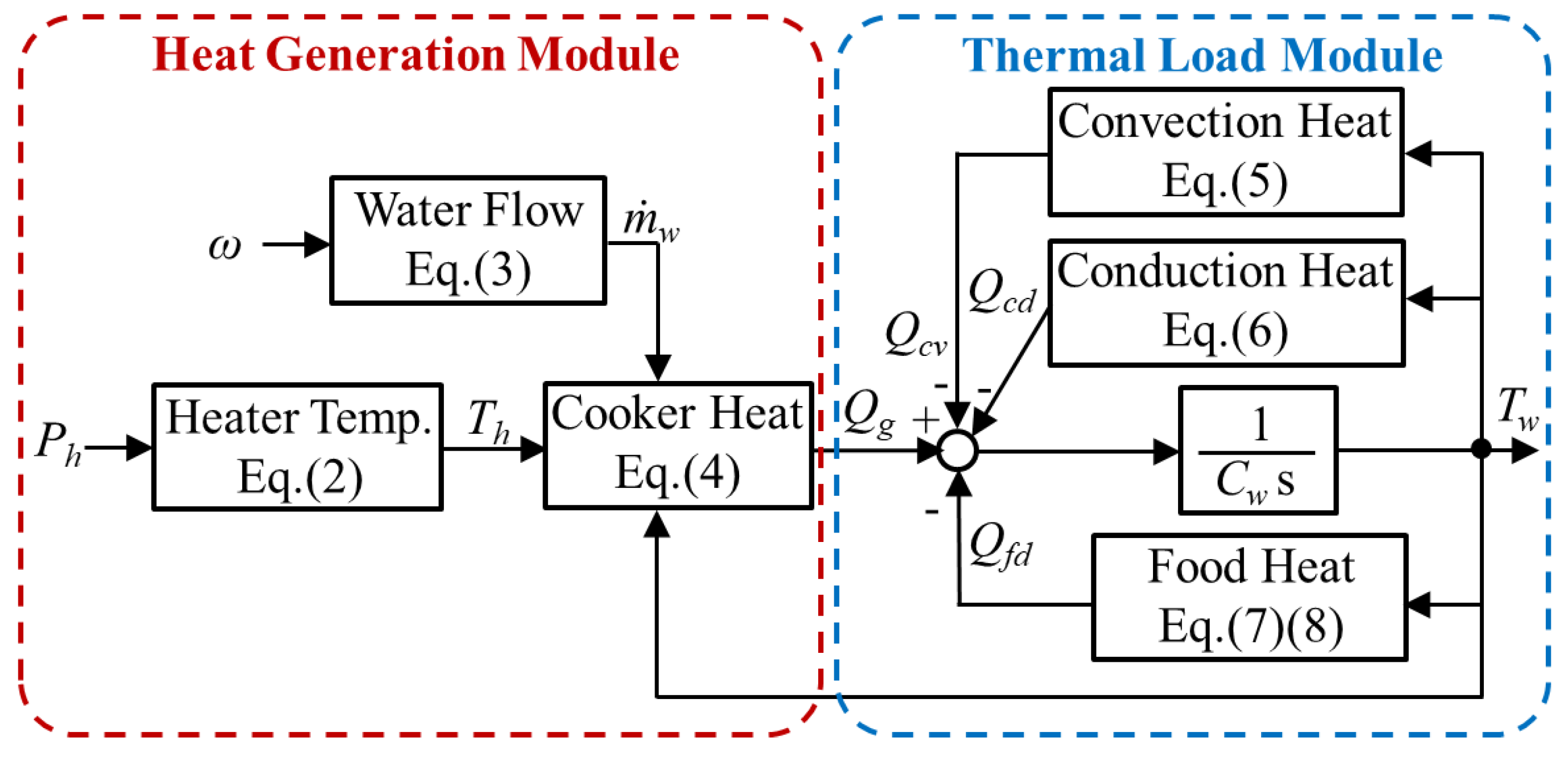
3.1. Water Heating and Circulating System and LPP
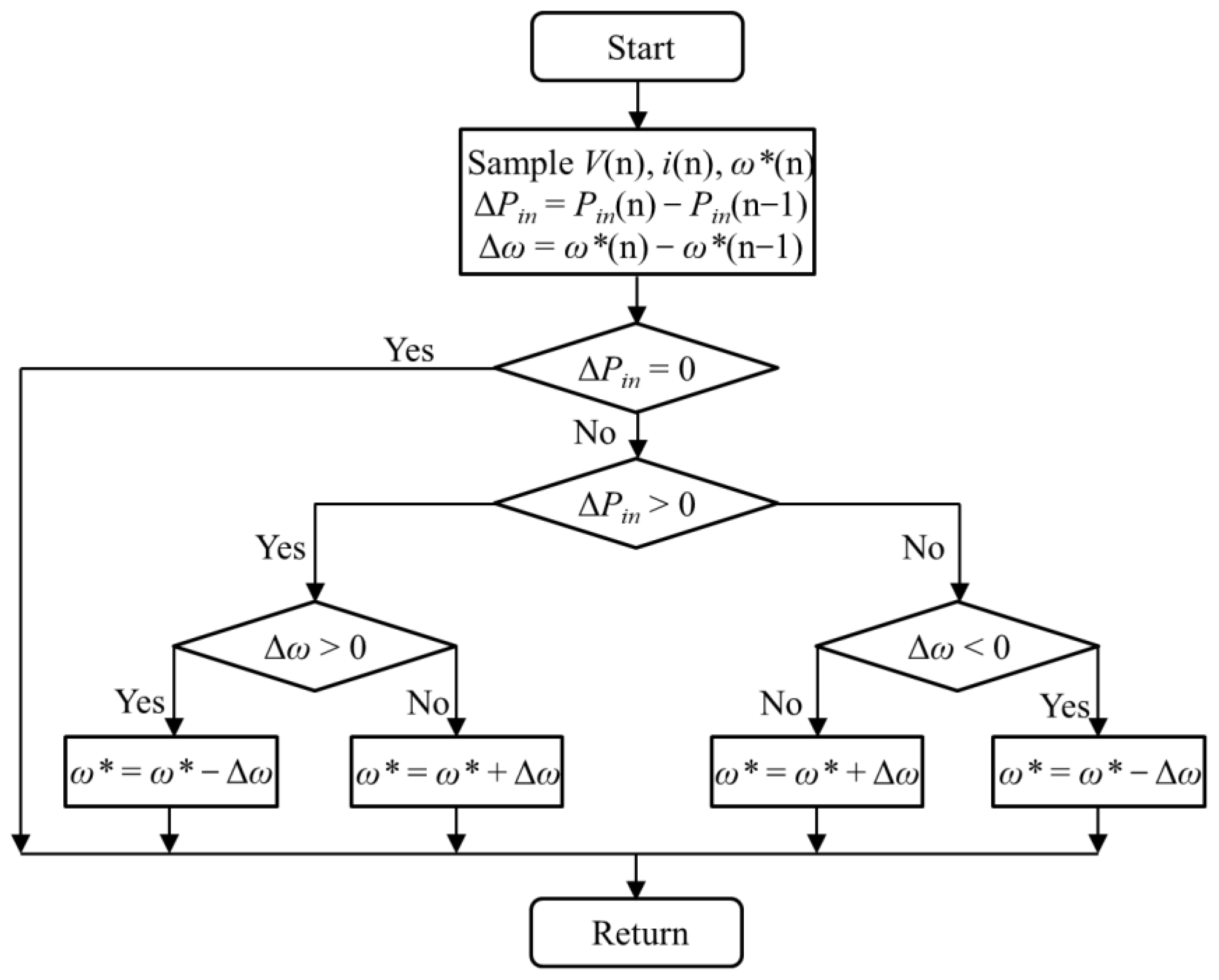
3.2. The Methodology of Control and Lowest Power Point Tracking
4. System Experiment Simulation
4.1. Simulation in Water Heating and Circulating System
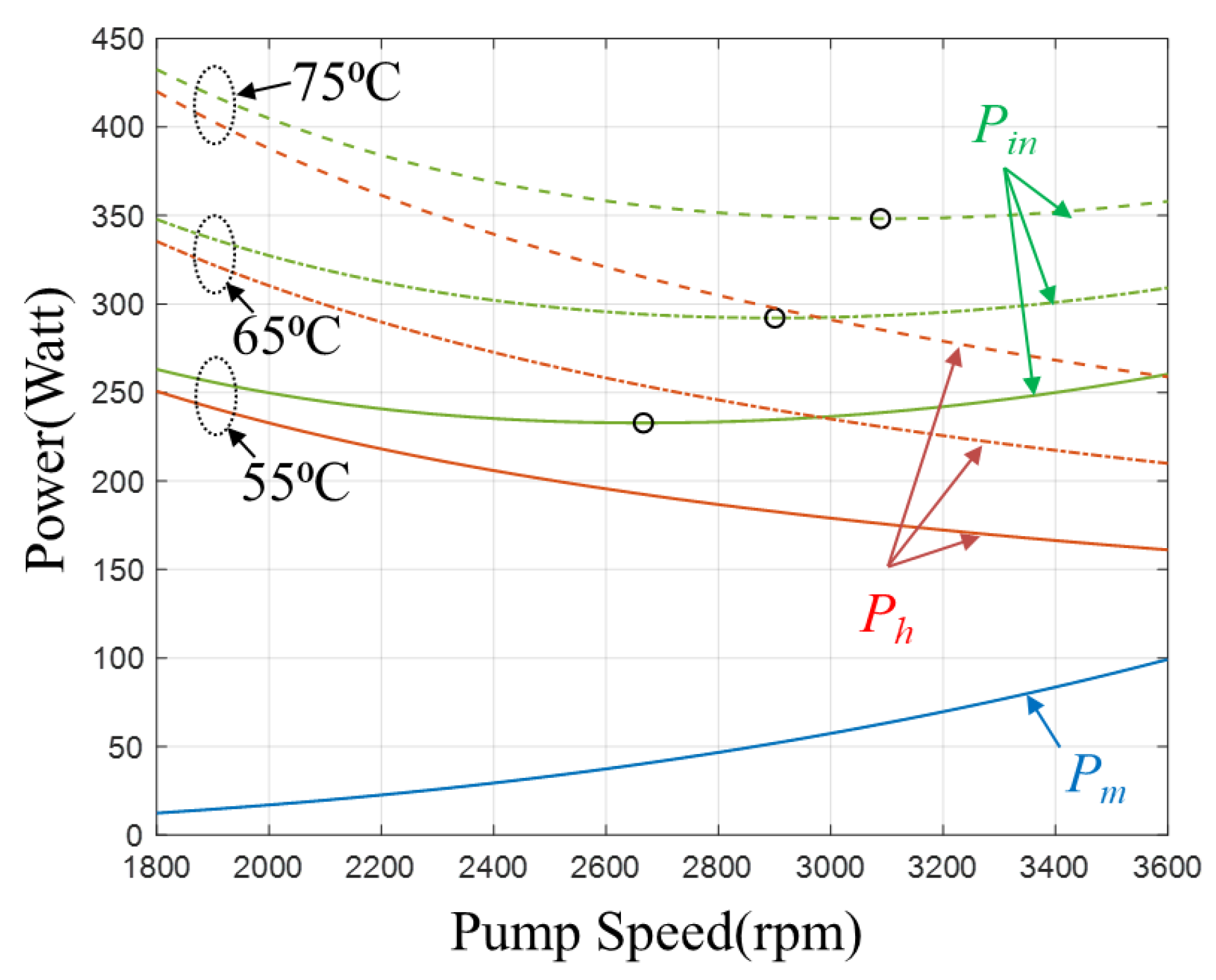
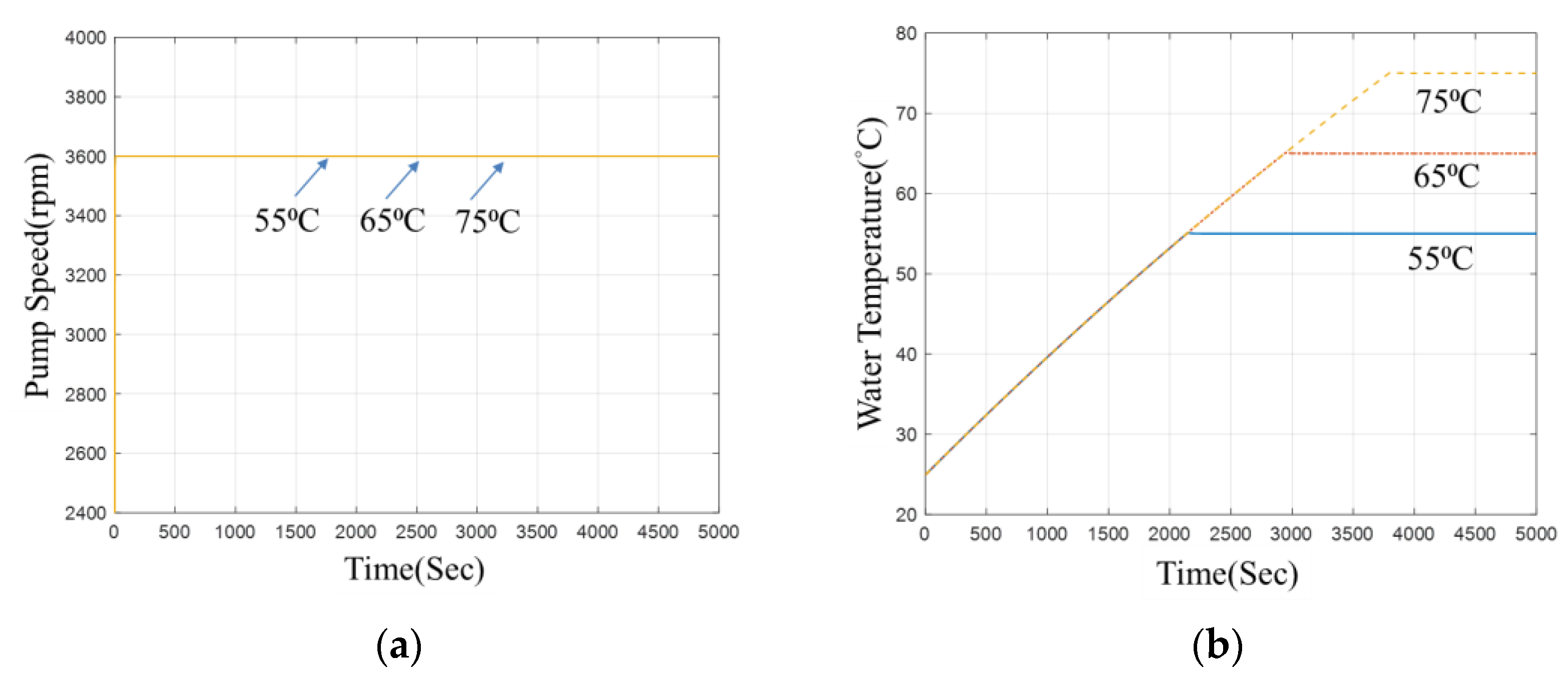
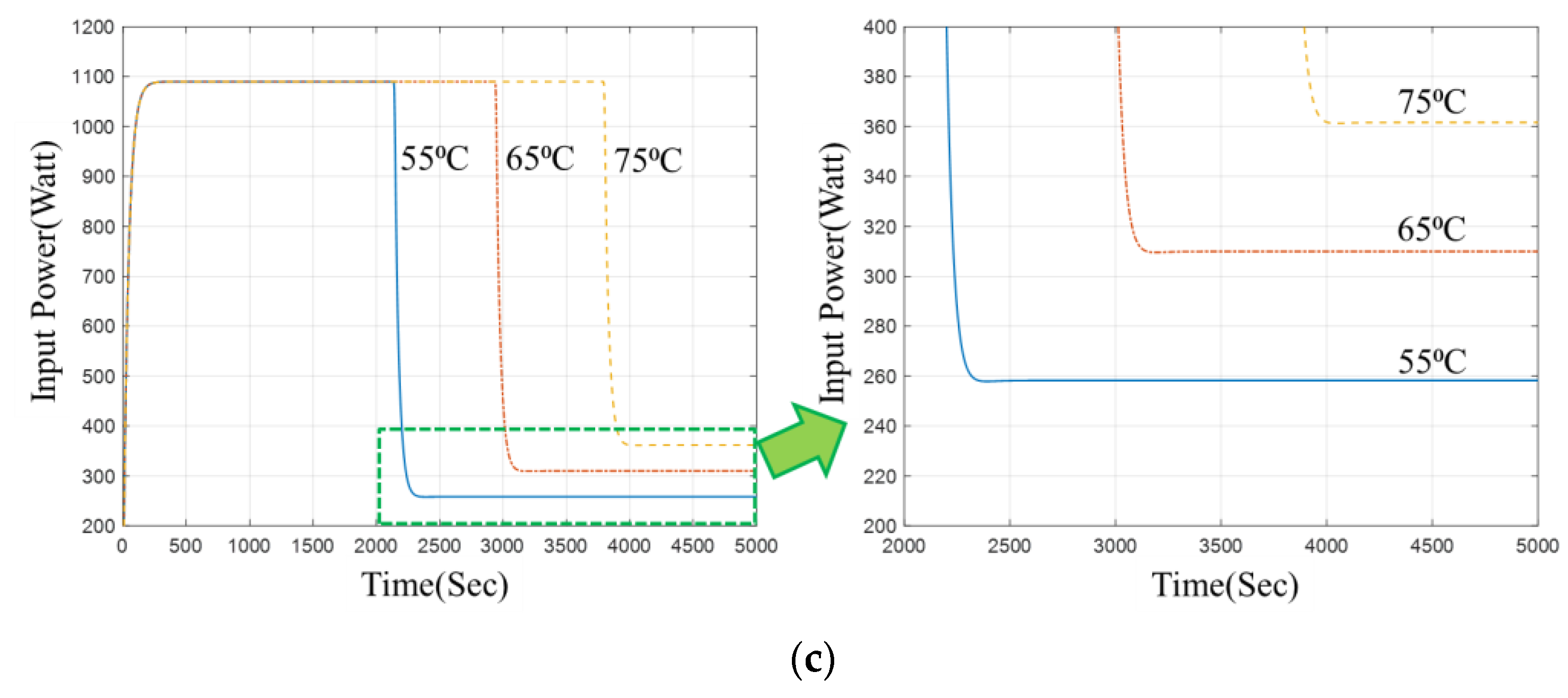
4.2. Same Pot Volume, Different Target Temperature
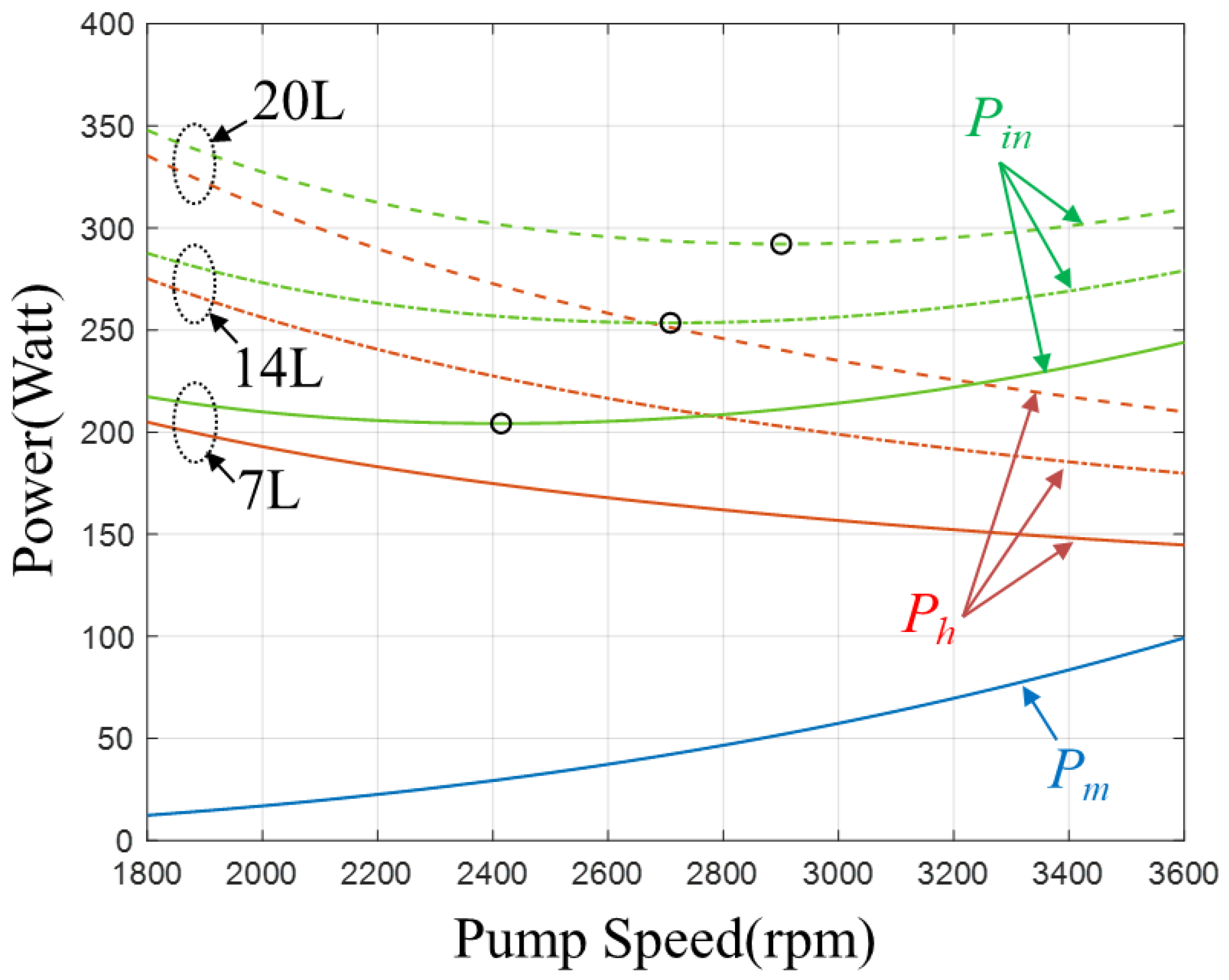
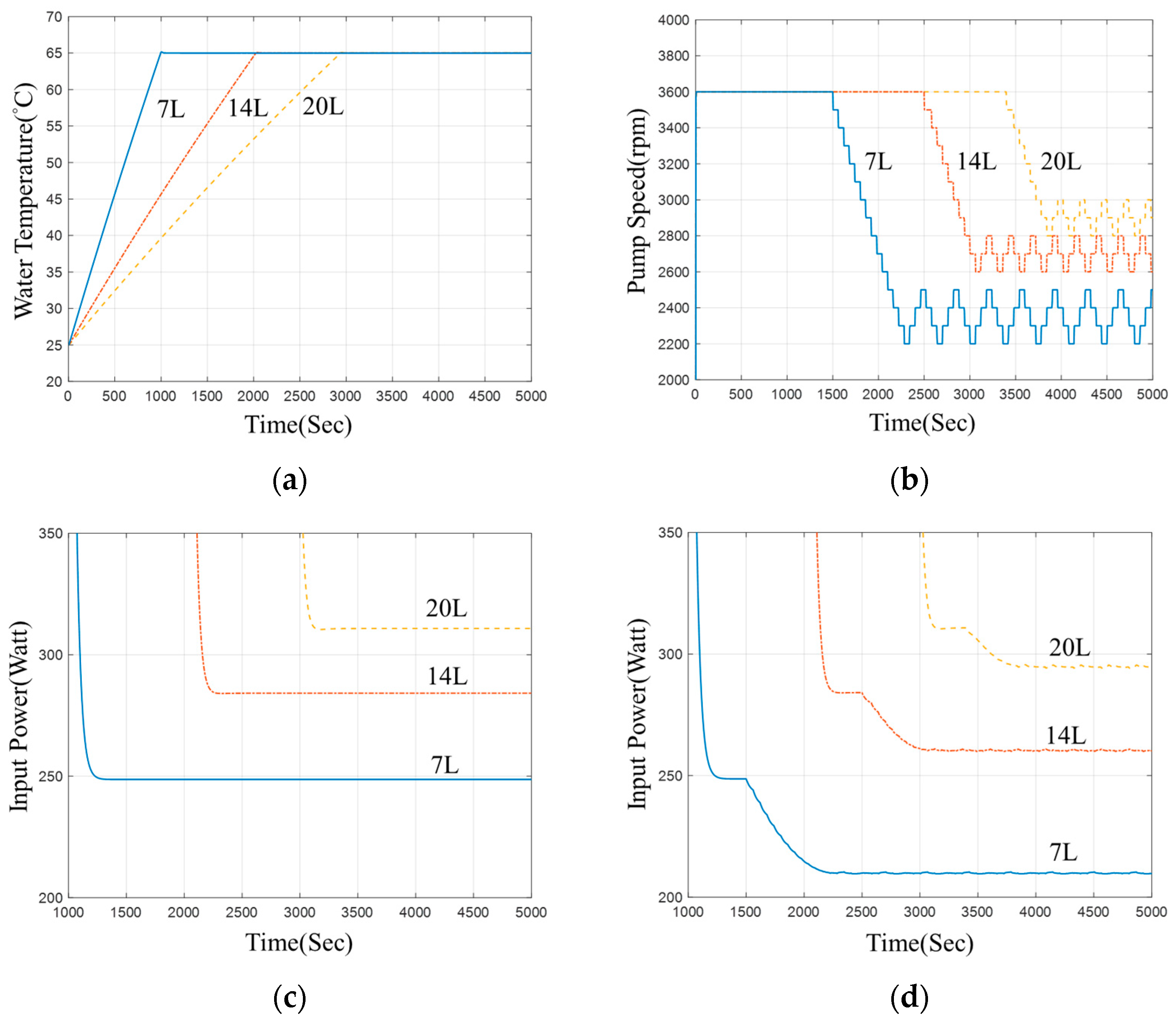
4.3. Same Target Temperature, Different Pot Volume
4.4. Simulation Result
5. Following the Experimental Study
5.1. Experimental System
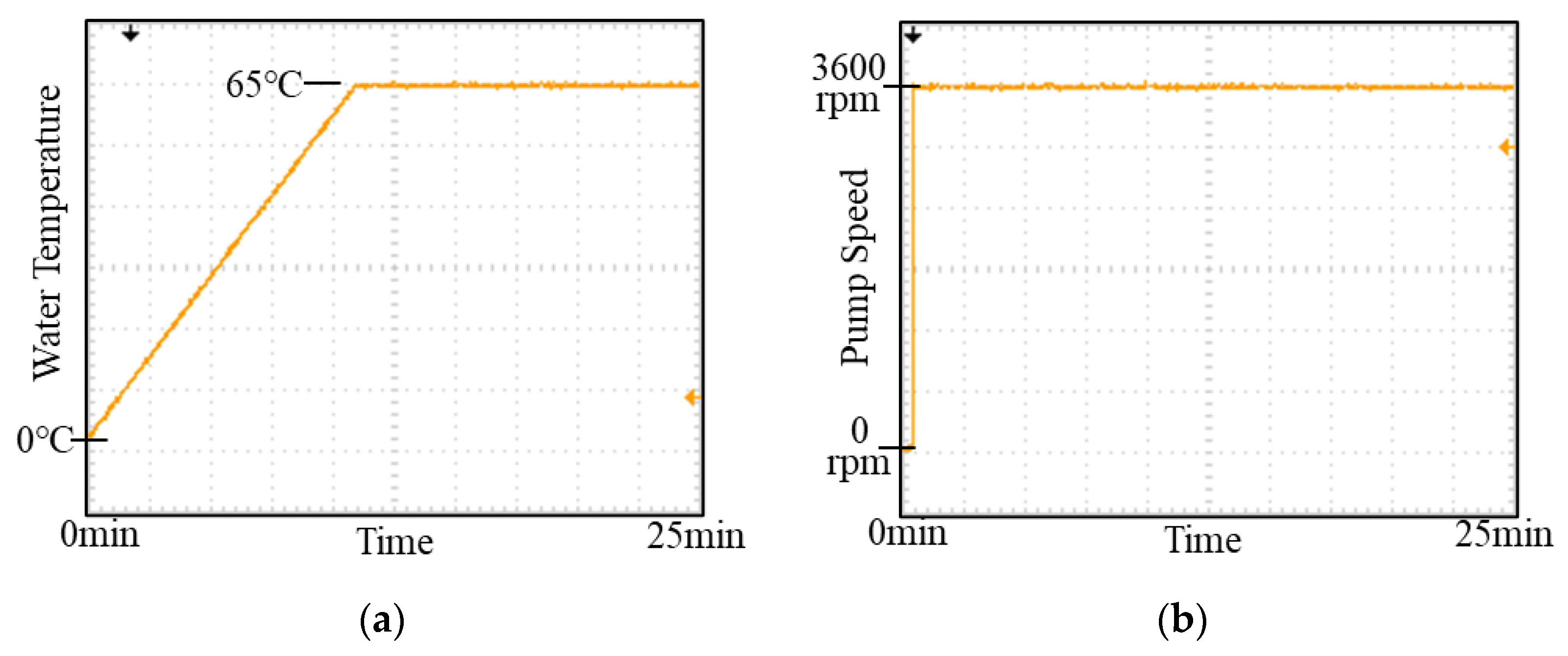
5.2. Experimental Results
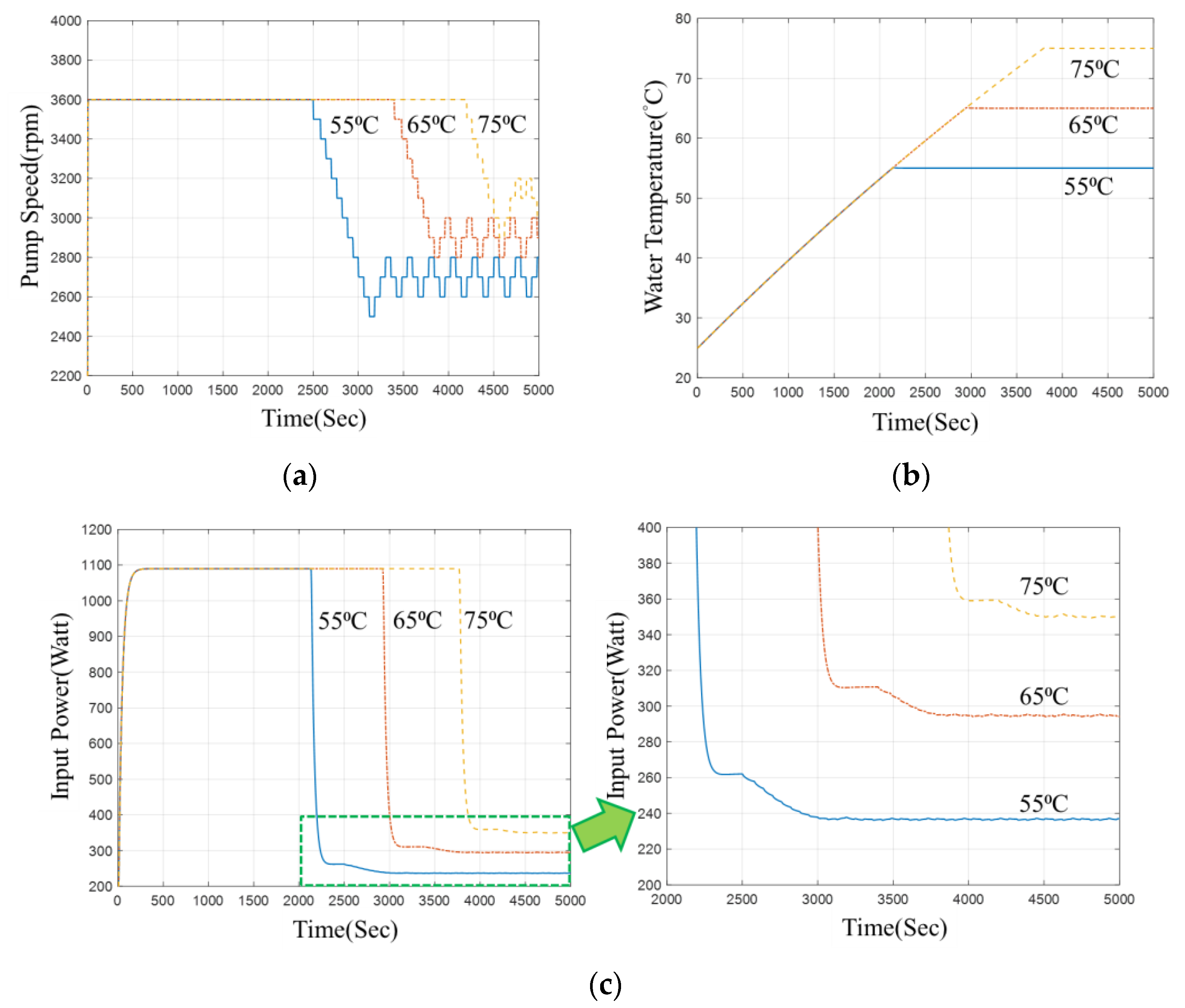
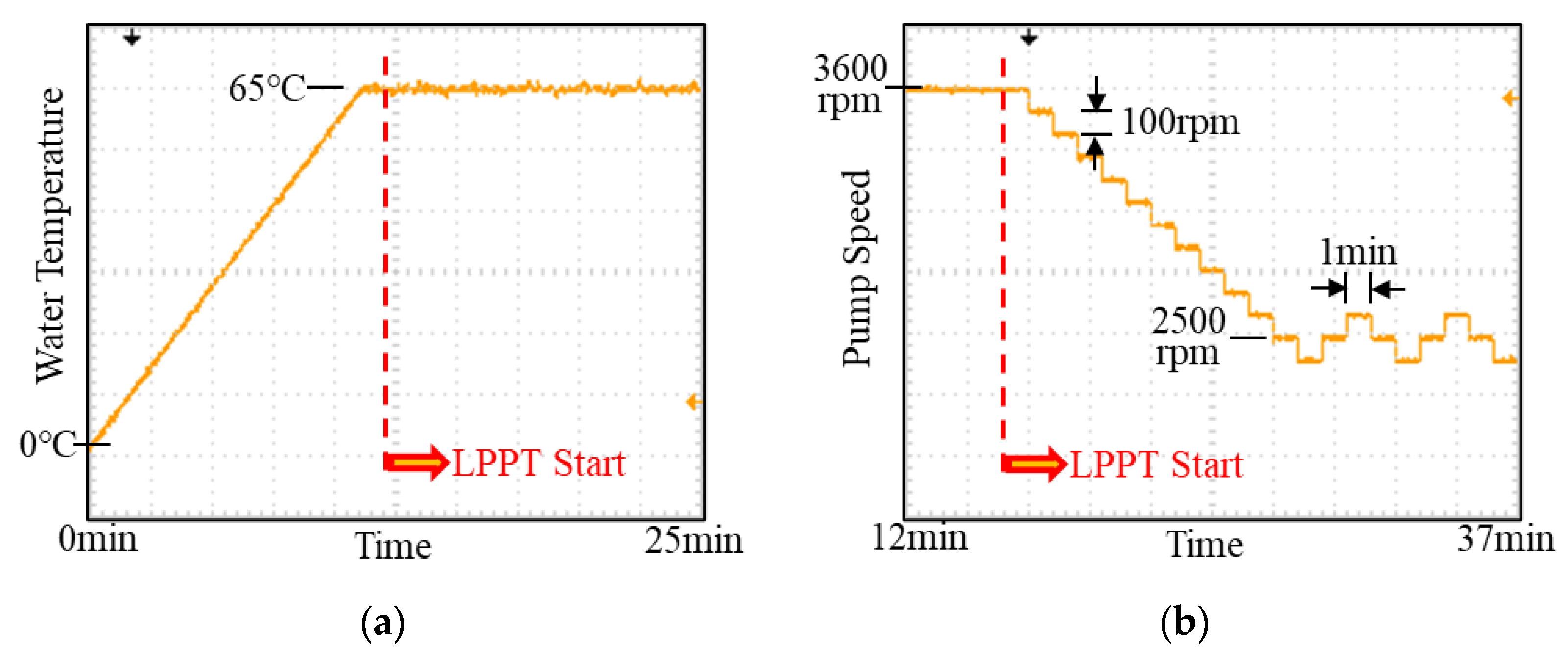
5.3. LPPT Control Results
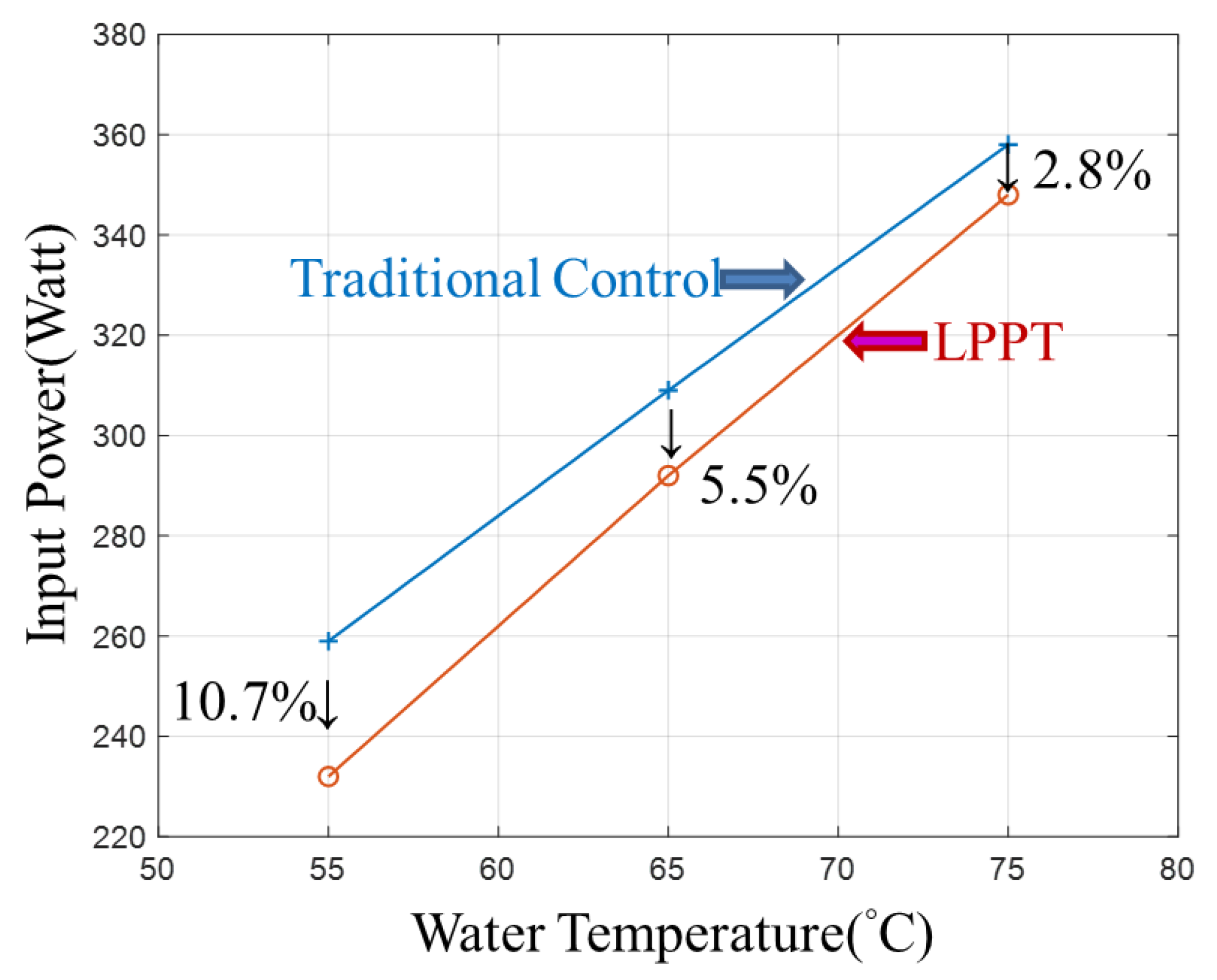
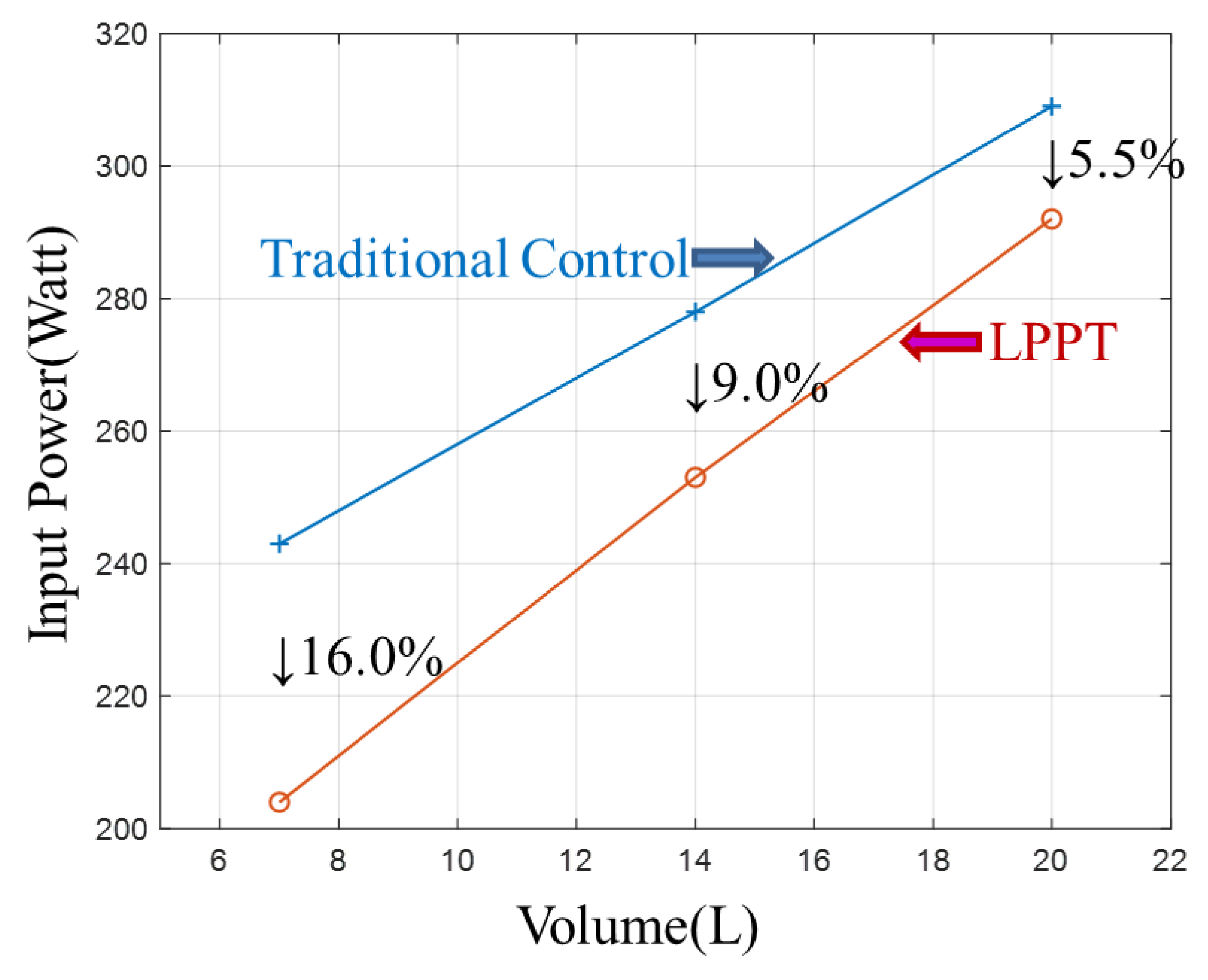
5.4. Experimental Data Comparison
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pérez-Lloréns, J.L. Cooking-Science-Communication (CSC): The ideal trident to enjoy the dining experience. Int. J. Gastron. Food Sci. 2019, 16, 100134. [Google Scholar] [CrossRef]
- Sörensen, P.M.; Mouritsen, O.G. Science education and public understanding of science via food, cooking, and flavour. Int. J. Gastron. Food Sci. 2019, 15, 36–47. [Google Scholar] [CrossRef]
- Ateş, E.; Unal, K. The effects of deep-frying, microwave, oven and sous vide cooking on the acrylamide formation of gluten-free chicken nuggets. Int. J. Gastron. Food Sci. 2023, 31, 100666. [Google Scholar] [CrossRef]
- Ilic, J.; Tomasevic, I.; Djekic, I. Purple eggplant and zucchini color, mechanical properties, mastication, and sensory perception influenced by steaming and Sous-vide. Int. J. Gastron. Food Sci. 2022, 28, 100549. [Google Scholar] [CrossRef]
- Myhrvold, N.; Young, C.; Bilet, M. Modernist Cuisine: The Art and Science of Cooking; The Cooking Lab: Port Washington, NY, USA, 2011. [Google Scholar]
- Baldwin, D.E. Sous Vide Cooking: A Review. Int. J. Gastron. Food Sci. 2012, 1, 15–30. [Google Scholar] [CrossRef]
- Schellekens, M. New Research Issues in Sous-Vide Cooking. Trends Food Sci. Technol. 1996, 7, 256–262. [Google Scholar] [CrossRef]
- Tornberg, E. Effect of Heat on Meat Proteins—Implications on Structure and Quality of Meat Products. Meat Sci. 2005, 70, 493–508. [Google Scholar] [CrossRef]
- Nel, P.J.C.; Booysen, M.J.; van der Merwe, B. A Computationally Inexpensive Energy Model for Horizontal Electric Water Heaters with Scheduling. IEEE Trans. Smart Grid 2018, 9, 48–56. [Google Scholar] [CrossRef]
- Wu, M.; Bao, Y.Q.; Zhang, J.; Ji, T. Multi-objective optimization for electric water heater using mixed integer linear programming. J. Mod. Power Syst. Clean Energy 2019, 7, 1256–1266. [Google Scholar] [CrossRef]
- Chakraborty, S.; Bera, S.K.; Bera, S.C.; Mandal, N. Design of a Simple Temperature Transmitter Circuit of an Electric Heater Operated Water Bath. IEEE Sens. J. 2018, 18, 3140–3151. [Google Scholar] [CrossRef]
- Badr, H.M.; Ahmed, W.H. Pumping Machinery Theory and Practice; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Fang, H.; Ma, J.; Zhang, W.; Yang, H.; Chen, F.; Li, X. Hydraulic Performance Optimization of Pump Impeller Based on a Joint of Particle Swarm Algorithm and Least-Squares Support Vector Regression. IEEE Access 2020, 8, 203645–203654. [Google Scholar] [CrossRef]
- Armintor, J.K.; Connors, D.P. Pumping Applications in the Petroleum and Chemical Industries. IEEE Trans. Ind. Appl. 1987, 23, 37–48. [Google Scholar] [CrossRef]
- Tarhan, Ü.; Selim, E.; Akın, Ö. Determination and Functional Implementation of Operating Point of a Centrifugal Pump With BLDC Motor. IEEE Can. J. Electr. Comput. Eng. 2022, 45, 105–113. [Google Scholar] [CrossRef]
- Li, W.T.; Thirugnanam, K.; Tushar, W.; Yuen, C.; Chew, K.T.; Tai, S. Improving the Operation of Solar Water Heating Systems in Green Buildings via Optimized Control Strategies. IEEE Trans. Ind. Inform. 2018, 14, 1646–1655. [Google Scholar] [CrossRef]
- Hepbasli, A.; Kalinci, Y. A review of heat pump water heating systems. Renew. Sustain. Energy Rev. 2009, 13, 1211–1229. [Google Scholar] [CrossRef]
- Ye, H.T.; Kang, X.; Joung, J.; Liang, Y.C. Optimization for Wireless-Powered IoT Networks Enabled by an Energy-Limited UAV Under Practical Energy Consumption Model. IEEE Wirel. Commun. Lett. 2021, 10, 567–571. [Google Scholar] [CrossRef]
- Kim, D.S.; So, J.Y.; Kim, D.K. Study on Heating Performance Improvement of Practical Induction Heating Rice Cooker With Magnetic Flux Concentrator. IEEE Trans. Appl. Supercond. 2016, 26, 0604304. [Google Scholar] [CrossRef]
- Monzó-Cabrera, J.; Pedreño-Molina, J.L.; Toledo, A. Feedback control procedure for energy efficiency optimization of microwave-heating ovens. Measurement 2009, 42, 1257–1262. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, X. Modeling and energy efficiency optimization of belt conveyors. Appl. Energy 2011, 88, 3061–3071. [Google Scholar] [CrossRef]
- Kioskeridis, I.; Margaris, N. Loss Minimization in Induction Motor Adjustable-Speed Drives. IEEE Trans. Ind. Electron. 1996, 43, 226–231. [Google Scholar] [CrossRef]
- Yang, S.M.; Lin, F.C. Loss-Minimization Control of Vector-Controlled Induction Motor Drives. J. Chin. Inst. Eng. 2003, 26, 37–45. [Google Scholar] [CrossRef]
- Bose, B.K.; Patel, N.R.; Rajashekara, K. A Neuro-Fuzzy-Based On-Line Efficiency Optimization Control of a Stator Flux-Oriented Direct Vector-Controlled Induction Motor Drive. IEEE Trans. Ind. Electron. 1997, 44, 270–273. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, Z.; Chen, C.; Zhuang, Y. Energy efficiency optimization of field-oriented control for PMSM in all electric system. Sustain. Energy Technol. Assess. 2021, 48, 101575. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Malinowski, M.; Al-Haddad, K. Photovoltaic Energy Conversion Systems; Wiley-IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Boztepe, M.; Guinjoan, F.; Velasco-Quesada, G.; Silvestre, S.; Chouder, A.; Karatepe, E. Global MPPT Scheme for Photovoltaic String Inverters Based on Restricted Voltage Window Search Algorithm. IEEE Trans. Ind. Electron. 2014, 61, 3302–3312. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Blaabjerg, F. Mitigation of Interharmonics in PV Systems With Maximum Power Point Tracking Modification. IEEE Trans. Power Electron. 2019, 34, 8279–8282. [Google Scholar] [CrossRef]
- Fathi, T.; Houda, J.; Abdelkader, M.; Khedher, N.B.; Aich, W.; Boudejemline, A.; Boujelbene, M. Comparative assessment between five control techniques to optimize the maximum power point tracking procedure for PV systems. Mathematics 2022, 10, 1080. [Google Scholar]
- Kashif, M.; Singh, B. Modified Active-Power MRAS Based Adaptive Control With Reduced Sensors for PMSM Operated Solar Water Pump. IEEE Trans. Energy Convers. 2023, 38, 38–52. [Google Scholar] [CrossRef]
- Balbino, A.J.; Nora, B.d.S.; Lazzarin, T.B. An Improved Mechanical Sensorless Maximum Power Point Tracking Method for Permanent-Magnet Synchronous Generator-Based Small Wind Turbines Systems. IEEE Trans. Ind. Electron. 2022, 69, 4765–4775. [Google Scholar] [CrossRef]
- Huynh, P.; Tungare, S.; Banerjee, A. Maximum Power Point Tracking for Wind Turbine Using Integrated Generator–Rectifier Systems. IEEE Trans. Power Electron. 2021, 36, 504–512. [Google Scholar] [CrossRef]
- Eronini, U.-E. System Dynamics and Control; PWS Publishers: Pacific Grove, CA, USA, 1998. [Google Scholar]
- Roffel, B.; Betlem, B. Process Dynamics and Control: Modeling for Control and Prediction; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]






| Symbol | Quantity | Value | Units |
|---|---|---|---|
| Sw | Water-Specific Heat | 4.184 | J/g⋅K |
| kh | Heater Heat Transfer Coefficient | 1.3 | W/m⋅K |
| kcd | Pot Heat Transfer Coefficient | 60 | W/m2.K |
| hcv | Air Heat Convection Coefficient | 5 | W/m2.K |
| ρ | Water Density | 1000 | kg/m3 |
| r | Pump Blade Radius | 0.021 | m |
| Ag | Pump Outlet Area | 0.0002 | m2 |
| Acd | Heat Transfer Area (20 L) | 0.292 | m2 |
| Acv | Heat Convection Area (20 L) | 0.146 | m2 |
| To | Ambient Temperature for Heat Conduction | 30 | °C |
| Tair | Ambient Temperature for Heat Convection | 30 | °C |
| 5 L | Traditional Control | LPPT Control | Improvement Percentage |
|---|---|---|---|
| 55 °C | 206 | 170 | 17.5% |
| 65 °C | 220 | 195 | 11.4% |
| 75 °C | 235 | 220 | 6.4% |
| 10 L | Traditional Control | LPPT Control | Improvement Percentage |
|---|---|---|---|
| 55 °C | 222 | 204 | 8.3% |
| 65 °C | 247 | 232 | 6.1% |
| 75 °C | 275 | 267 | 2.9% |
| 15 L | Traditional Control | LPPT Control | Improvement Percentage |
|---|---|---|---|
| 55 °C | 243 | 230 | 5.5% |
| 65 °C | 280 | 272 | 2.9% |
| 75 °C | 320 | 317 | 1.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.-C.; Chen, C.-S.; Lin, C.-J. Water Heating and Circulating Heating System with Energy-Saving Optimization Control. Appl. Sci. 2023, 13, 5542. https://doi.org/10.3390/app13095542
Lin F-C, Chen C-S, Lin C-J. Water Heating and Circulating Heating System with Energy-Saving Optimization Control. Applied Sciences. 2023; 13(9):5542. https://doi.org/10.3390/app13095542
Chicago/Turabian StyleLin, Feng-Chieh, Chin-Sheng Chen, and Chia-Jen Lin. 2023. "Water Heating and Circulating Heating System with Energy-Saving Optimization Control" Applied Sciences 13, no. 9: 5542. https://doi.org/10.3390/app13095542
APA StyleLin, F.-C., Chen, C.-S., & Lin, C.-J. (2023). Water Heating and Circulating Heating System with Energy-Saving Optimization Control. Applied Sciences, 13(9), 5542. https://doi.org/10.3390/app13095542









