Abstract
In this study, in order to achieve accurate detection of grain loss during the process of combine harvester harvesting, a piezoelectric-based grain loss sensor has been developed. The sensor utilizes a double-layer circular piezoelectric ceramic sheet as its sensitive element. When different grains come into contact with the sensitive element, the piezoelectric effect of the ceramic sheet generates corresponding charges. These charges are then converted into knock charge signals through a charge amplification signal processing circuit that has been specially designed for this purpose. The harsh operating conditions of the sensor, including the presence of significant vibration and noise interference, necessitate the incorporation of a double-layer vibration-damping structure in both the top and bottom layers of the sensor. This paper seeks to analyze the vibration-damping effect of various shock-absorbing materials and structures incorporated into the sensor. This is accomplished by creating a dynamic analysis model that accounts for vibration interference. Furthermore, an experimental bench is established for the purpose of verifying the vibration-damping test results. These tests demonstrate that the utilization of a properly selected vibration-damping structure and materials can effectively eliminate mechanical vibration and noise interference. This, in turn, leads to improved detection accuracy of charge signals after knocking and enhances the overall anti-interference ability of the sensor.
1. Introduction
With the ongoing progress in agricultural machinery technology in China, the dissemination of intelligent and automated agricultural machinery has reached a broad scale. Among these machines, grain combine harvesters have been proven essential in crop harvest season [1,2,3]. It has been reported that the mainstay of China’s agricultural sector consists of small-scale farmers, which comprise over 98% of the total population [4,5]. In addition, these farmers manage approximately 70% of the total cultivated land in China. In this type of farming system, an increased harvest loss can significantly impact the farmer’s crop yield. Therefore, it is crucial to accurately measure the harvest loss during harvester work and provide timely feedback to enhance the quality of the harvester’s performance and diminish losses incurred by farmers.
In the research process of loss detection sensors, according to different principles, the loss detection sensor can be divided into mechanical and electrical, acoustic, microwave, photoelectric, machine vision, piezoelectric, and so on. The loss detection sensor of the electromechanical principle detects the loss indirectly through flow detection. For example, Robert (1972) et al. [6] installed the flowmeter at the outlet of the conveying device of the harvester to calculate the number of grains. The principle of acoustoelectricity is to count the loss according to the sound signal. For example, the particle impact sensor designed by Strehoff (1977) et al. [7] and Batcheller (2016) et al. [8] distinguishes different materials by using the sound signal generated by the impact of materials on the sensor collected by microphones. Particle collision sensors based on the microwave principle, such as Kotyk (1989) et al. [9], can be used to detect whether the rice ear is clean by using different response signals triggered by substances of different qualities in the microwave field. The photoelectric method is to count the number of grains by taking advantage of the current interruption caused by cutting off the optical path of grains. For example, the grain loss sensor designed by Richard (1982) [10] first separated the grains from other materials in combination with a fan and other devices and then counted the grain loss by photoelectric pulse. With the development of new materials and new technologies, the above detection methods have gradually faded out of the particle impact sensor research field and market due to their limitations. At present, the main application and research direction is to use machine vision and piezoelectric principle for loss detection sensor research. With the development of machine vision, some researchers try to use machine vision technology to develop sensors to detect grain loss. For example, Zhang (2009) [11] from Jiangsu University designed the entrained loss sensor to calculate the number of grains after binarization, median filtering, and other processing of the pictures collected by the camera at the straw entrance. The application of the machine vision method can not only realize the detection of grain loss but also realize the detection of other operating quality parameters of combine harvesters, such as the degree of sprinkling, grain breakage rate, etc., which is also a research hotspot at present. For example, the grain quality detector designed by Deere Company [12] in 2017, At the same time complete grain loss detection and grain yield, moisture, and other online detection.
Because the problem of dust obscuring cameras can not be solved well at present, the application of machine vision has some difficulties. Therefore, the particle impact sensor based on the piezoelectric principle has been developed rapidly. The piezoelectric loss detection sensor generates piezoelectric signals with different frequencies and amplitudes when grains and other materials impact piezoelectric materials on the surface of the sensor, so as to identify materials. Piezoelectric materials do not need an additional power supply and can generate potential differences when subjected to impact pressure. Piezoelectric sensors have gradually become the mainstream of particle impact sensors due to their advantages such as wide response band, high sensitivity, high signal-to-noise ratio, simple structure, reliable operation, and light weight. Bischoff (2016) [13] of Deere Company designed a collision sensor for distinguishing grains from other stray particles. The structure of the sensor is divided into the upper conductive layer, the impact response layer, the lower conductive layer, and the base layer from top to bottom, in which the material of the impact response layer can be polar piezoelectric polymer. The upper layer can be divided into an array of isolated regions, which represent the transverse and longitudinal positions of the grain collision, while the lower layer is a continuous conductive layer. The upper regions and the lower layer respectively transmit signals to the signal processing circuit, through which the position of the grain collision sensor can be judged. Zhao (2016) [14] designed an eight-channel PVDF piezoelectric film sensor measurement system based on a single-chip microcomputer. The piezoelectric effect of the piezoelectric film was used to convert the sensor’s knock signal into a measurable voltage signal, so as to realize grain loss measurement.
By comparing the studies of various scholars, it is found that the loss sensor based on the acoustic principle is easy to be disturbed by acoustic noise in the working environment. The loss sensor based on machine vision is easy to be affected by light, occlusion, etc. Piezoresistive material loss sensor sensitivity is not high, and reaction lag; the PVDF piezoelectric film is easy to wear and has a low piezoelectric coefficient. In the practical application of piezoelectric materials, Shivashankar P and Gopalakrishnan S discovered that compared to piezoelectric polymer materials, piezoelectric ceramic components offer several advantages, including simple structure, easy wear, and high sensitivity to force [15]. As a result, researchers in the field of micro-vibration and acceleration detection prefer these components [16]. Most scholars have done more studies on loss detection sensors of different materials, but there are insufficient studies on the vibration and noise interference of sensors. Therefore, in order to improve the detection accuracy and sensitivity of loss detection sensors and reduce vibration and noise interference in the application process of sensors [17]. For this research, a double-layer piezoelectric ceramic disc has been selected as the sensing element for the sensor. Through dynamic analysis of vibration disturbance, a double-layer vibration-damping structure has been designed. Additionally, a verification test bench has been established to verify the vibration-damping effect, and the optimal approach for verifying the vibration absorption effect of the piezoelectric sensor has been proposed.
2. Working Principle
2.1. Sensor Structure
The sensitive constituents of the sensor under consideration have been meticulously selected from hard ceramic material with piezoelectric properties, namely PZT (lead zirconate titanate) disc, which has a low dielectric loss factor and high mechanical quality factor. The PZT coating thickness measures 0.1 mm. The comprehensive parameters of the ceramic disc are presented in Table 1, whereas the mechanical dimensions are illustrated in Figure 1.

Table 1.
Piezoelectric ceramic disc parameter table.
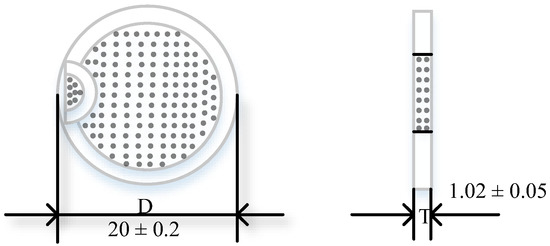
Figure 1.
Piezoelectric ceramic disc size structure diagram.
The loss detection sensor comprises a total of eight parts arranged from top to bottom. These components include (1) an impact plate, (2) a piezoelectric ceramic vibration plate, (3) a buffer connecting mechanism, (4) counter-weight metal connecting mechanism, (5) a two-stage buffer damping mechanism, (6) a data processing module, (7) dust protection shell, and (8) fixing bolts. The sensor configuration is graphically presented in Figure 2. The PZT ceramic disc is glued with GSE T-8000 adhesive in the central position below the impact plate. The first stage vibration reduction buffer mechanism is situated immediately below the impact plate. The counterweight metal is positioned under the first-stage buffer structure, while the second-stage buffer vibration reduction mechanism is located below the counterweight metal. Finally, the sensor’s dust protection shell is located at the bottom to ensure proper protection for the internal components of the sensor.
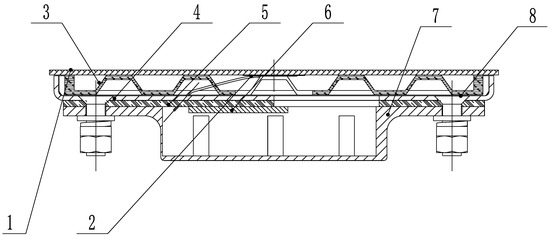
Figure 2.
Sensor structure diagram. 1. Impact plate; 2. Piezoelectric ceramic vibrox; 3. Primary buffer connection mechanism; 4. Counterweight metal connection mechanism; 5. Secondary buffer vibration reduction mechanism; 6. Data processing module; 7. Dustproof protective shell; 8. Fixed bolts.
When the impact plate is struck by moving grains, vibrations are transmitted to a piezoelectric ceramic-sensitive element situated below it. According to the positive piezoelectric effect principle, the piezoelectric sensitive element generates an electric charge, and the quantity of charge is dependent on both the impact force and inertial force of the impact plate. Due to the small amount of charge generated by piezoelectric sensing components, direct measurement is not possible. Consequently, a charge amplification circuit is devised to convert and amplify the charge signal into a voltage signal that can be measured. When different objects, (e.g., grain grains, straw, etc.) are affected by their mass, speed, and hardness. Additionally, the contact action time and force size between the grain and the impact plate varies. Loss detection can be achieved through either the action time or force size.
2.2. Vibration Damping Dynamics Model Analysis
In the practical application of the loss detection sensor, it is affixed to the rear of the wheat harvester, and the sensor is predominantly impacted by the mechanical operation vibrations operating at the same frequency. Excessive vibration interference could drown out the grain-knocking signal, resulting in the sensor detection accuracy being negatively affected. In an attempt to enhance the detection accuracy of the sensor, comprehensively analyze the factors influencing vibration interference, and determine the best method for vibration damping through the sensor damping structure, this paper establishes a vibration dynamics analysis model founded on the sensor structure.
The vibration interference of the sensor can be modeled as a two-degree-of-freedom vibration system, as depicted in Figure 3. In this model, m2 corresponds to the mass of the stressed plate and piezoelectric ceramic, while m1 represents the mass of the counterweight metal. k2 and k1 denote the stiffness of the primary and secondary buffer mechanism materials, respectively, while c2 and c1 indicate the viscous damping coefficients of the primary and secondary buffer mechanism materials. The system experiences simple harmonic excitation, represented by F(t).
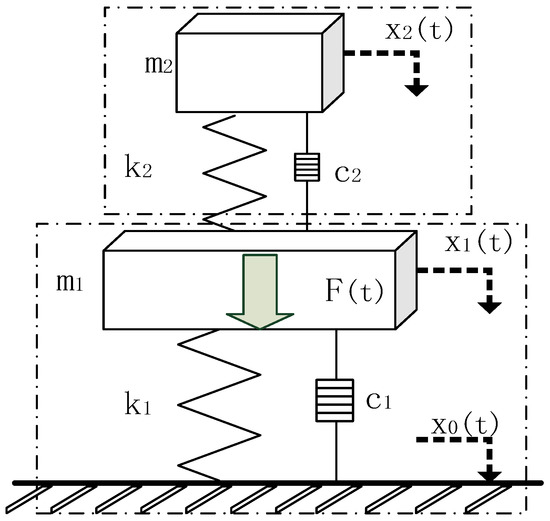
Figure 3.
Vibration damping structural dynamics analysis model.
Based on the kinetic analysis, it can be derived that the differential equation of motion of the two-degree-of-freedom vibration system model is expressed as Equation (1).
Formula
where x0 is the amplitude of the base, and its amplitude is determined by the vibration of the machine itself; x2 and x1 are the amplitude response of the stressed plate and the counterweight metal, respectively, whereas the amplitude response is related to the parameters of the primary and secondary damping materials, that is, it is determined by k1, k2 and c1, c2.
Incorporating Equation (2) into Equation (1), derived from the mechanical impedance equation, yields the system amplitude response Equation (3):
Excluding the damping of the main system, c1 = 0, Equation (4) for the amplitude response variable can be obtained by simplification.
There into
Premised on Equation (4), it can be observed that the amplitude response displacement x2 of the stressed plate is determined by the viscous damping coefficients c1, c2, and the stiffness k1 and k2 of the buffer mechanism material. According to the calculation formula of the damping ratio, the damping ratio of the damping material can be calculated. Amplitude responses under x0 excitation of different frequencies are drawn as shown in Figure 4. There are two resonance points in the figure, namely the resonant frequency Ω1 = 230.5 Hz and Ω2 = 409.6 Hz. Near the resonance point, the amplitude ratio B (B = X1/X2) gradually decreases with the increase of . When the frequency of the excitation vibration source Ω < Ω1, the amplitude ratio of m2 to m1 tends to be 1. When the frequency of excitation vibration source Ω > Ω2, the amplitude ratio of m2 to m1 tends to be 0. It shows that the designed structure has good vibration resistance to high-frequency vibration. According to dynamic analysis, the resonant frequencies of m1 and m2 are: . Therefore, by increasing the mass of m2 and m1, namely the mass of the stress plate of the sensor and the weight structure, and reducing the stiffness of vibration reduction materials k2 and k1, namely the first and second buffer mechanism materials of the sensor, and using flexible materials with low stiffness, the resonance frequency is finally reduced to the best advantage, so as to improve the vibration reduction effect.
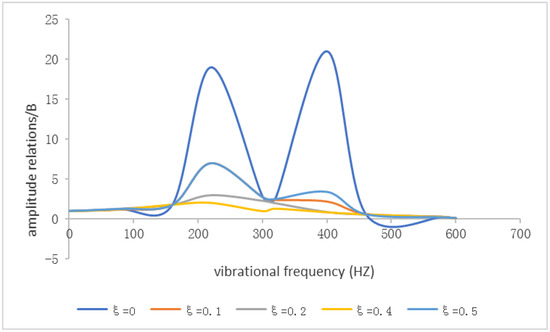
Figure 4.
The curve of amplitude ratio as a function of the excitation frequency.
3. Materials and Methods
3.1. Test Materials
To study the damping effect of the sensor devised in this paper, a vibration test is conducted with various damping materials. Considering that the practical application process entails minimal shape variability of vibration-damping materials, selecting commonly available materials with high-cost performance suffices, without considering the influence of material thickness. Hence, rubber and EVA sponge are selected as damping materials, each with dimensions of 140 mm × 75 mm × 7 mm, as illustrated in Figure 5. Meanwhile, the impact plate is composed of a knock-resistant single-sided glass fiber copper-clad laminate, which measures 150 mm × 85 mm × 1.5 mm, as depicted in Figure 6.

Figure 5.
Two vibration-damping materials. (a) Rubber materials; and (b) EVA sponge material.

Figure 6.
Single-side glass fiber-clad copper impact plate.
3.2. Test Device
A sensor vibration test bench was constructed in this study, as illustrated in Figure 7. The bench was designed primarily for sensor fixation, while an adjustable frequency vibration motor was installed beneath the test bench to simulate the input from a harvester vibration source. A vibration meter was positioned above the sensor to measure the vibration of the stressed plate. Additionally, a charge amplifier was employed to collect and record the charge–discharge voltage from the piezoelectric ceramic. The main instruments of the test bench are the charge amplifier instrument (VT CAMP-2G05) with ±0.5% charge accuracy and the vibration motor (HY30DC12V-G) with a vibration accuracy of ±1% Hz.
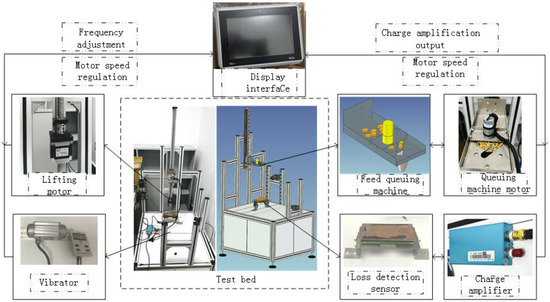
Figure 7.
Vibration test bench.
3.3. Experimental Design
To verify the effectiveness of various materials in damping vibrations, three vibration-damping strategies were selected for experimental verification. The vibration frequency of the vibration motor was set and multiple sets of vibration source frequencies were simulated, including the actual vibration frequency of the harvester. A vibration meter was used to record the amplitude and frequency of each test set. Additionally, a charge amplifier was employed to measure the voltage value of each piezoelectric ceramic after vibration, with a sampling frequency of 10 Hz and a sampling time of 30 s. Through this experimental design, the damping effect of vibration-damping materials on vibration sources with different frequencies can be accurately assessed, ultimately leading to the optimal selection of the ideal vibration-damping material.
The test procedures are described in detail below:
- (1)
- The impact plate of the loss detection sensor is fixed on the test bench without any damping material, and the charge amplifier is connected to the piezoelectric ceramic lead and can work normally.
- (2)
- Turn on the vibration motor, set the vibration frequency as 5 Hz, the charge amplifier collects vibration data at 30 s, and the sampling frequency as 10 Hz. A total of 300 groups of test data are collected, including voltage value and vibration amplitude value, which are recorded and saved.
- (3)
- Take the adhesive rubber material below the impact plate of the loss detection sensor as the vibration reduction material, and repeat step 2.
- (4)
- Take the EVA sponge material attached to the bottom of the impact plate of the loss detection sensor as the damping material, and repeat Step 2.
- (5)
- The three groups of test data are processed and saved, and used for vibration reduction effect analysis.
4. Evaluation and Calculation Methods
By analyzing the two-degree-of-freedom vibration system model, it was determined that the sensor system can be expressed as an undamped free vibration system, assuming that the damping coefficient is negligible. The differential equation of motion for the free vibration system can be expressed as Equation (6).
There into
So the differential equation of motion is expressed as Equation (8),
Assuming that the system undergoes simple harmonic vibration with the same frequency and phase Angle, the solution of vibration displacement of the system can be written as Equation (9).
where x1 and x2 are the maximum values of x1(t) and x2(t), m1 and m2 are the mass of the moving object, {X} is the amplitude column vector, is the natural frequency of free vibration of the system and is the initial phase of free vibration. Substitute Equation (9) into Equation (8) to obtain the algebraic system of amplitude column vector {X}, as shown in Equation (10),
By solving Equation (10), the natural frequency of the vibration system is Equation (11) and the amplitude response is Equation (12).
As proposed by Zhao et al. [18], the typical vibration frequency of the harvester vibrating screen ranges from 4 to 6 Hz. Moreover, the damping material rubber exhibits a stiffness of 30 KN/m, while the sponge has a stiffness of 80 N/m. To effectively showcase the vibration-damping effect, a vibration source frequency of 5 Hz was selected during the comparative test process. By combining the charge voltage collected by the charge amplifier and the vibration displacement data of the impact plate, the amplitude response results of x1 and x2 were derived from Equation (6). Subsequent analysis and comparison of these results demonstrate the vibration-damping effect.
5. Results and Analysis
5.1. No Vibration Damping Material Test Analysis
In this experiment, the loss detection sensor does not incorporate any vibration-damping materials. The impact plate is directly connected to the counterweight mechanism, and a vibration source frequency of 5 Hz was selected. During the experiment, the vibration of the impact plate was measured using a vibrating instrument. Additionally, the voltage conversion value was recorded using a charge amplifier. The data collected during the selected intermediate period are presented in Table 2.

Table 2.
Amplitude and voltage without damping material.
Finally, the collected vibration and voltage data were analyzed and processed, and the waveform is depicted in Figure 8. The analysis revealed that the vibration frequency of the stressed plate and the vibration source vibration frequency are closely aligned. The vibration amplitude is high, and the detection voltage amplitude of the charge amplifier is also high. In the absence of any vibration-damping material, the mechanical vibration interference was completely overwhelmed by the effective signal.
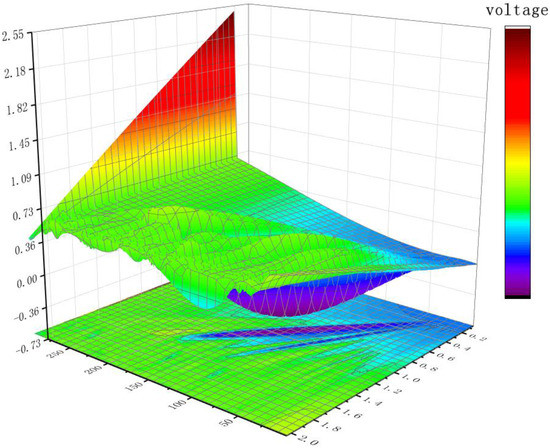
Figure 8.
Amplitude and voltage trend chart of non-vibration damping material.
5.2. Experimental Analysis Using Vibration-Damping Materials
Rubber was used as the damping material for the test, and the voltage and amplitude data were recorded and shown in Table 3.

Table 3.
Amplitude and voltage of rubber as damping material.
Figure 9 shows the amplitude and charge voltage diagram using rubber as the damping material, and Figure 10 shows the amplitude and charge voltage diagram using EVA sponge as the damping material. EVA sponge was adopted as the damping material for the test, and the voltage and amplitude data were recorded and shown in Table 4.
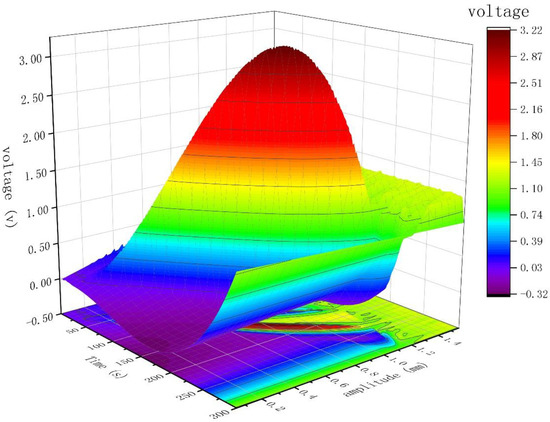
Figure 9.
Rubber as a vibration-damping material with amplitude and charge voltage.
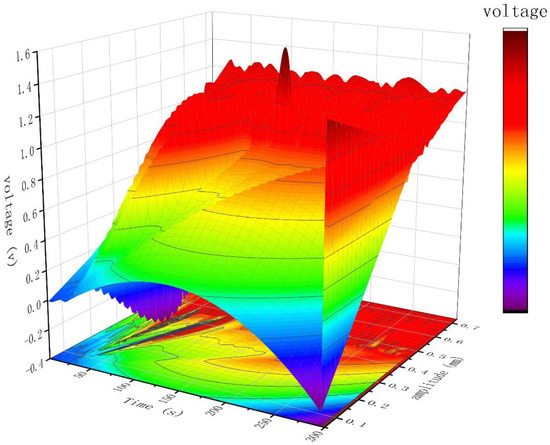
Figure 10.
Amplitude and charge voltage diagram of EVA sponge as vibration damping material.

Table 4.
Amplitude and voltage of EVA sponge as damping material.
A comparative analysis of Figure 8 and Figure 9 reveals a notable reduction in both amplitude and charge voltage when rubber is utilized as a damping material. Moreover, comparing Figure 10 with Figure 9 indicates that the employment of EVA sponge as a damping material yields superior damping performance. Specifically, the vibration interference-induced voltage signal is significantly suppressed, and the voltage signal arising from grain impact on the impact plate can be accurately distinguished.
To further verify the damping effect of vibration-damping materials at different vibration frequencies, a set of tests are added. Three vibration frequencies of 4 Hz, 5 Hz, and 6 Hz were set respectively when there was no vibration damping material, the vibration damping material was rubber and the vibration damping material was EVA sponge. The experimental procedure is as follows:
- (1)
- On the premise of the vibration test bench as shown in Figure 7, the impact plate of the loss detection sensor is fixed on the test bench without any vibration-damping material. The charge amplifier is connected to the piezoelectric ceramic lead and can work normally.
- (2)
- Start the vibrating motor, set the vibration frequency as 4 Hz, 5 Hz, and 6 Hz respectively, and collect 100 groups of data with a sampling frequency of 10 Hz using the charge amplifier. A total of 300 groups of test data are collected, including voltage value and vibration amplitude value, which are recorded and saved.
- (3)
- Take the adhesive rubber material below the impact plate of the loss detection sensor as the vibration reduction material, and repeat step 2.
- (4)
- Take the EVA sponge material attached to the bottom of the impact plate of the loss detection sensor as the damping material, and repeat Step 2.
- (5)
- Classify the data according to frequency and do mean processing. The mean value of the obtained data is taken as the effective data under the current frequency. The processed data is shown in Table 5.
 Table 5. Amplitude and charge voltage records at different source frequencies.
Table 5. Amplitude and charge voltage records at different source frequencies.
The data presented in Table 5 depicts the amplitude and charge voltage readings obtained at varying source frequencies. Through analysis, it has been determined that the resonance frequency is proximate to the resonance, resulting in a significant amplitude response of the impact plate and a corresponding increase in charge voltage. Accordingly, the optimal approach to achieve effective vibration damping is to adjust the resonance frequency during sensor design. Upon experimentation with vibration-damping materials, such as rubber and sponge, it was discovered that inherent parameters, including the rigidity constant, k, had a primary impact on the vibration-damping effect. As k decreases, there is an increase in the resonance frequency that triggers a larger amplitude response of high-frequency vibration sources. The implementation of vibration-damping materials is thereby effective in reducing the resonance effect and achieving the optimal treatment of vibration damping.
In the absence of vibration-damping materials and with the sensor rigidly connected to the test bench, K can be considered infinite. As a result, the vibration from the vibration source is entirely transmitted to the sensor, leading to voltage fluctuations within the range of 0~3 V. This situation results in the effective signal from the grain impacting the force plate being drowned out. When rubber is employed as the damping material, its stiffness constant, k, is approximately 30 kN/m, leading to high rigidity. Consequently, when the vibration source frequency is proximate to the sensor vibration frequency, a substantial amplitude response occurs, and the detected voltage value is around 2.6 V. This results in a direct submergence of a portion of the voltage signal produced by the grain hitting the stress plate. Upon implementing EVA foam as the damping material, the vibration-damping effect becomes more pronounced. The amplitude response of the interference source is effectively absorbed by the vibration-damping foam material. Additionally, the peak voltage output is regulated within 1.2 V, ensuring that the voltage signal generated by the grain impacting the stressed plate is not drowned out.
This study analyzed and verified the two-degree-of-freedom vibration system using kinetic knowledge. Through multiple sets of comparative tests, it was demonstrated that vibration-damping materials had a positive effect on weakening the vibration interference of the sensor, thereby enhancing the detection accuracy of the sensor.
6. Conclusions
A loss detection sensor with a double-layer vibration damping structure has been devised to decrease mechanical vibration interference and enhance sensor detection precision. To test and verify the vibration-damping efficacy of sensors using various damping materials, a dynamic analysis model of the sensor damping structure was formulated, and a simulation test bench was constructed. The results reveal that by selecting supple materials for vibration damping, properly augmenting the mass of the sensor impact plate and counterweight mechanism, and reducing the resonance frequency of the vibration damping structure, the impact of mechanical vibration on the sensor can be efficiently suppressed. This helps in elevating the sensor detection accuracy.
Author Contributions
In the research of this article. Conceptualization, J.W. and F.W.; methodology, Y.L.; software, W.Z.; validation, B.Z., X.F. and J.W.; formal analysis, W.Z.; investigation, Y.L.; resources, B.Z.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, F.W.; visualization, Y.L.; supervision, X.F.; project administration, J.W.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program Project of China (2021YFD2000601).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.P.; Shen, W.; Zhang, H.; Xu, C. Vibration Reduction Design and Vibration Performance Research of Shipborne Platform Equipment. Mech. Res. Appl. 2021, 34, 24–27. [Google Scholar] [CrossRef]
- Wang, Y.P.; Xu, C.; Tang, J.S.; Gao, C.J. The Effect of Suspending Method on Modal and Transfer Characteristics of Rolling Stock Equipment. Roll. Stock 2018, 56, 1–4+55. [Google Scholar] [CrossRef]
- Ji, F.; Zhang, H.D.; Li, G.N.; Wu, M. Tests for correlation between ship vibration isolator installation parameters and vibration isolation effect. J. Vib. Shock 2018, 37, 118–123. [Google Scholar] [CrossRef]
- Yang, T.J.; Shi, H.; Li, X.H.; Wu, L.; Zhu, M.G.; Wu, G.X.; Liu, Z.G. One active isolation system for marine machine based on smart isolators. J. Vib. Eng. 2017, 30, 167–176. [Google Scholar] [CrossRef]
- Tang, X.H.; Zhao, N.; Guo, Z.; Jin, C.Q.; Yu, M.Q.; Li, J.Q.; Xu, B. Design and Test of Multi Parameter Adjustable Cleaning Loss Distribution Detection Test Bench. J. Agric. Mech. Res. 2022, 44, 148–155. [Google Scholar] [CrossRef]
- Robert, R.L.; Klee, M. Gram Loss Monitorin.g Devace. U.S. Patent 3638659 A, 1 February 1972. [Google Scholar]
- Strelioff, W.P.; Elliott, W.S.; Johnson, D. Grain Loss Momtor. U.S. Patent 3598864 A, 16 September 1977. [Google Scholar]
- Batcheller, B.D.; Gelinske, J.N.; Ferrar, L. Systemand Method for Determining Material Yield or Loss from a Harvesting Machineusing Acoustic Sensors. EP Patent 4002983 A1, 16 October 2016. [Google Scholar]
- Kotyk, W.M.; Kirk, T.G.; Wilson, R.J. Unthreshed Head GRAM Loss Monitor. U.S. Patent 04825146 A, 4 May 1989. [Google Scholar]
- Richard, R.K. Absolute Grain Ioss Monitor. U.S. Patent 4896904 A, 25 May 1982. [Google Scholar]
- Zhang, T.; Zhao, D.A.; Zhou, T. Application of Image Processing on Combine Harvester Attachment Loss. J. Agric. Mech. Res. 2009, 31, 70–72. [Google Scholar] [CrossRef]
- Wellington, C.K.; Bruns, A.J.; Sierra, V.S.; Wilson, J.N. Grain Quality Momtormg. U.S. Patent 7168451 A, 28 September 2017. [Google Scholar]
- Bischoff, L.; Phelan, J.J. Pamculate Matter Impact Sensor. EP Patent 2977735B1, 14 February 2016. [Google Scholar]
- Zhao, W.B. Research on Planter Pressure Measurement System Based on PVDF Piezoelectric Film. Master’s Thesis, Harbin Engineering University, Harbin, China, 2016. [Google Scholar] [CrossRef]
- Shivashankar, P.; Gopalakrishnan, S. Review on the use of piezoelectric materials for active vibration, noise, and flow control. Smart Mater. Struct. 2020, 29, 053001. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Mokhtari, M.; Masoodi, A.R. Stability and free vibration analysis of tapered sandwich columns with functionally graded core and flexible connections. CEAS Aeronaut. J. 2018, 9, 629–648. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-Induced Vibration Mitigation in Tall Buildings Using the Tuned Mass-Damper-Inerter. J. Struct. Eng. 2017, 143, 04017127. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Y.; Chen, J.; Xu, J. Grain separation loss monitoring system in combine harvester. Comput. Electron. Agric. 2011, 76, 183–188. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).