Finite Element Simulation and Experimental Investigation of Nanostructuring Burnishing AISI 52100 Steel Using an Inclined Flat Cylindrical Tool
Abstract
1. Introduction
- Development of numerical and finite element simulations of the burnishing process with the application of a cylindrical indenter with an adjustable inclination angle to the treated surface;
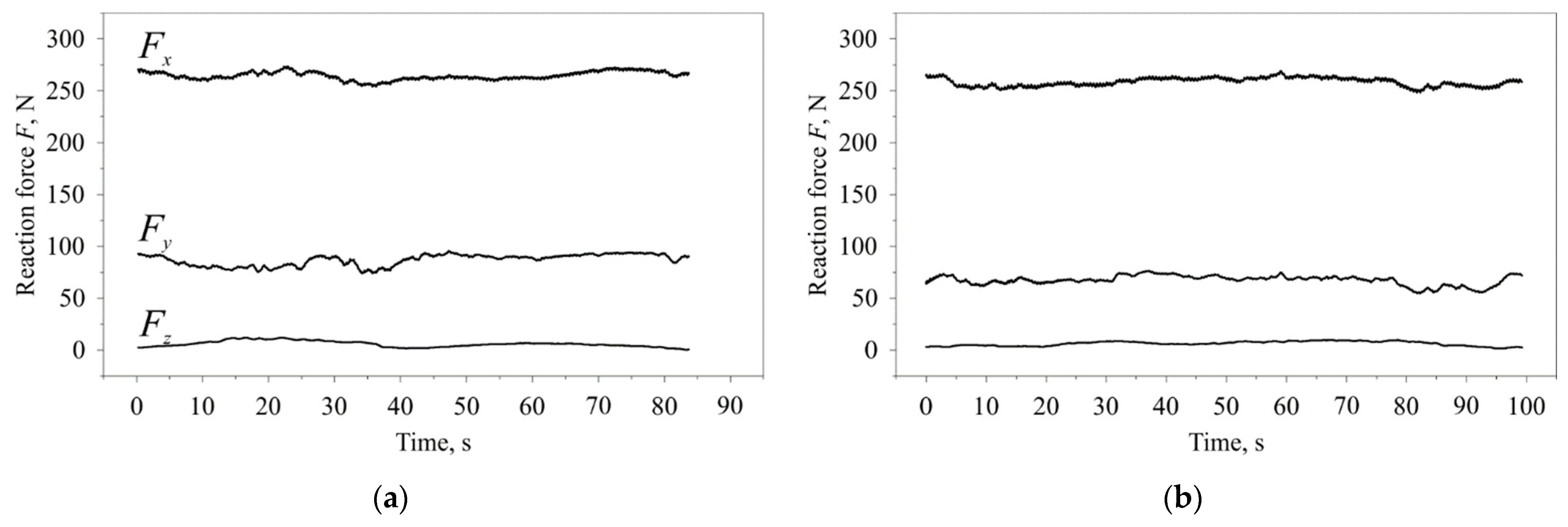
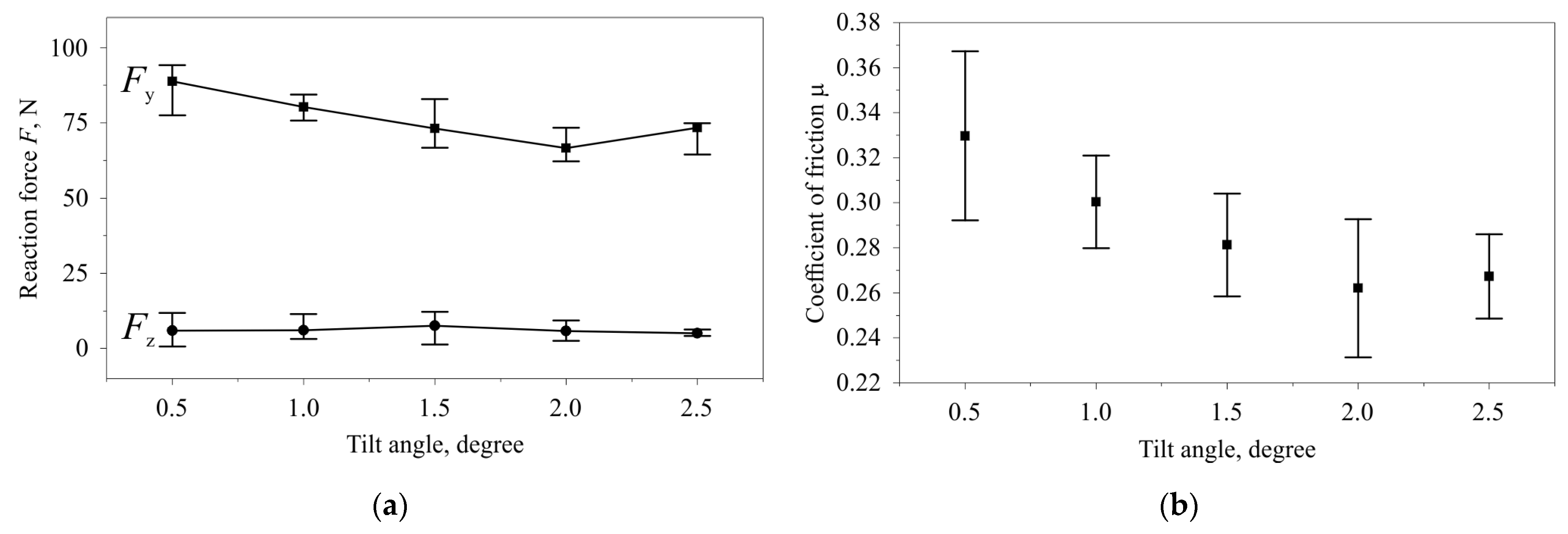
- Dynamometric studies of the process and establishment of the relationship of contact forces and the friction coefficient with the inclination angle of the indenter;
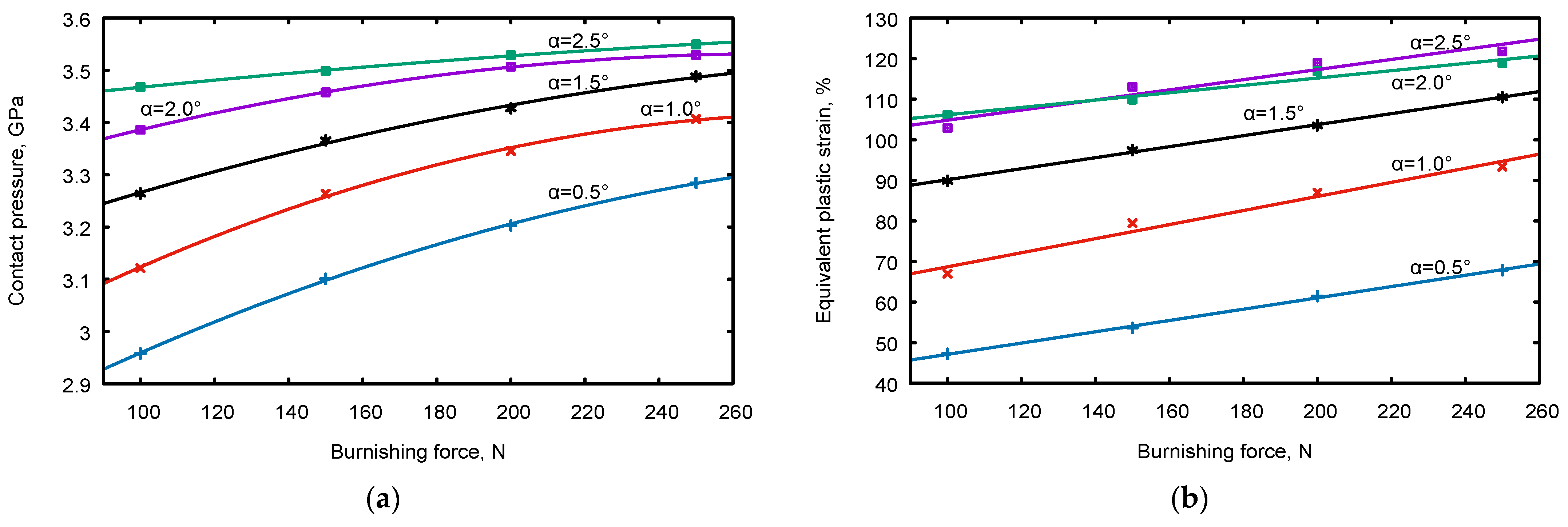
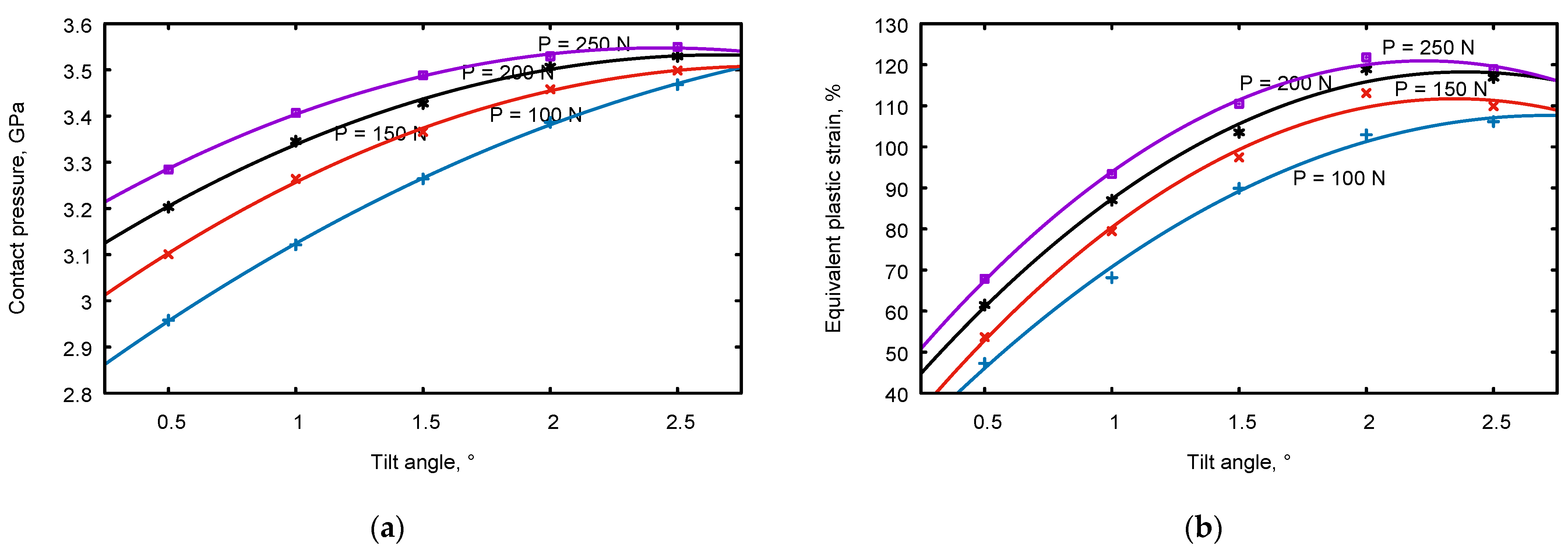
- Simulation and experimental study of the influence of the cylindrical indenter inclination angle and of burnishing force on the contact pressure and shear deformation;
- Establishment of microstructure change regularities, microhardness, and roughness depending on the inclination angle of the cylindrical indenter and its burnishing force.
2. Materials and Methods
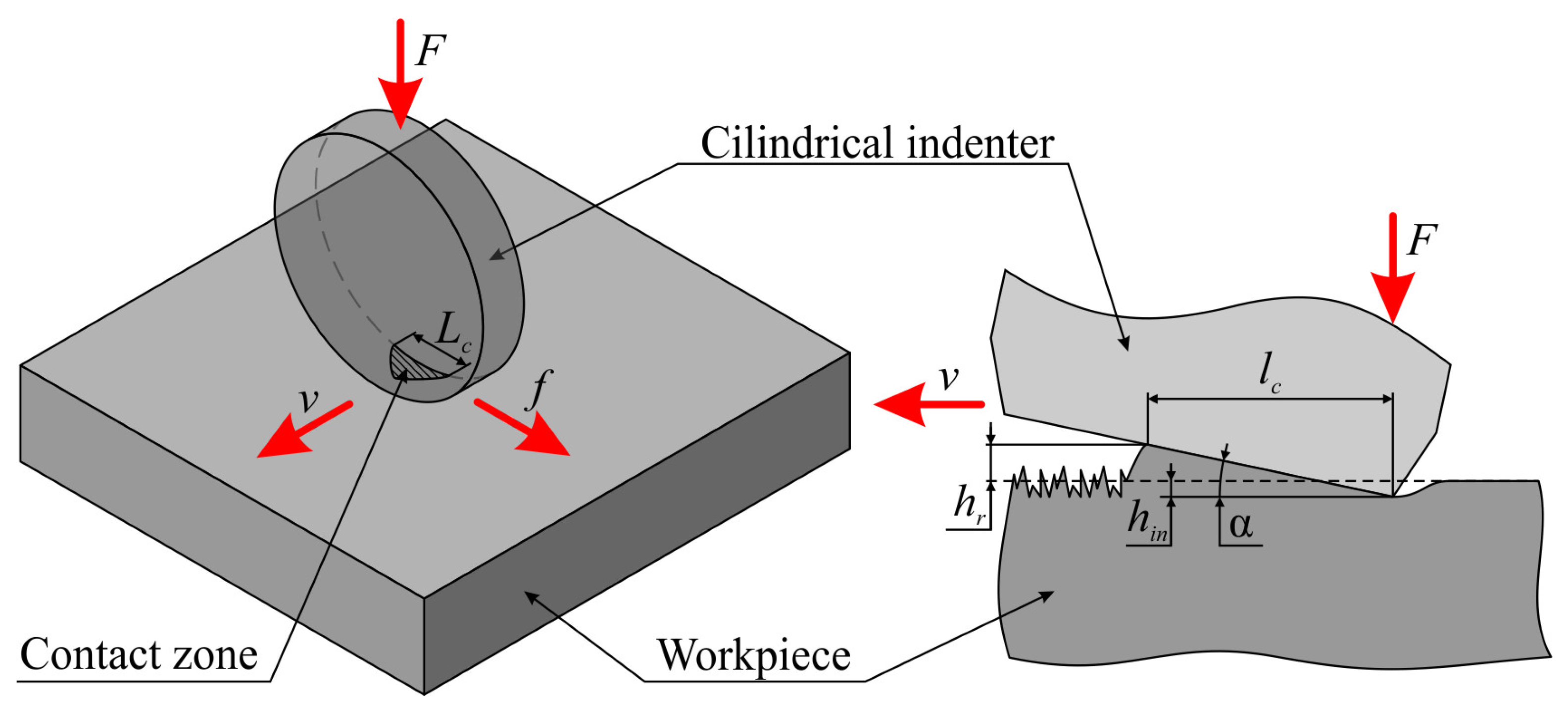
2.1. Material for Treatment and the Tool
2.2. Mathematical and Finite Element Models
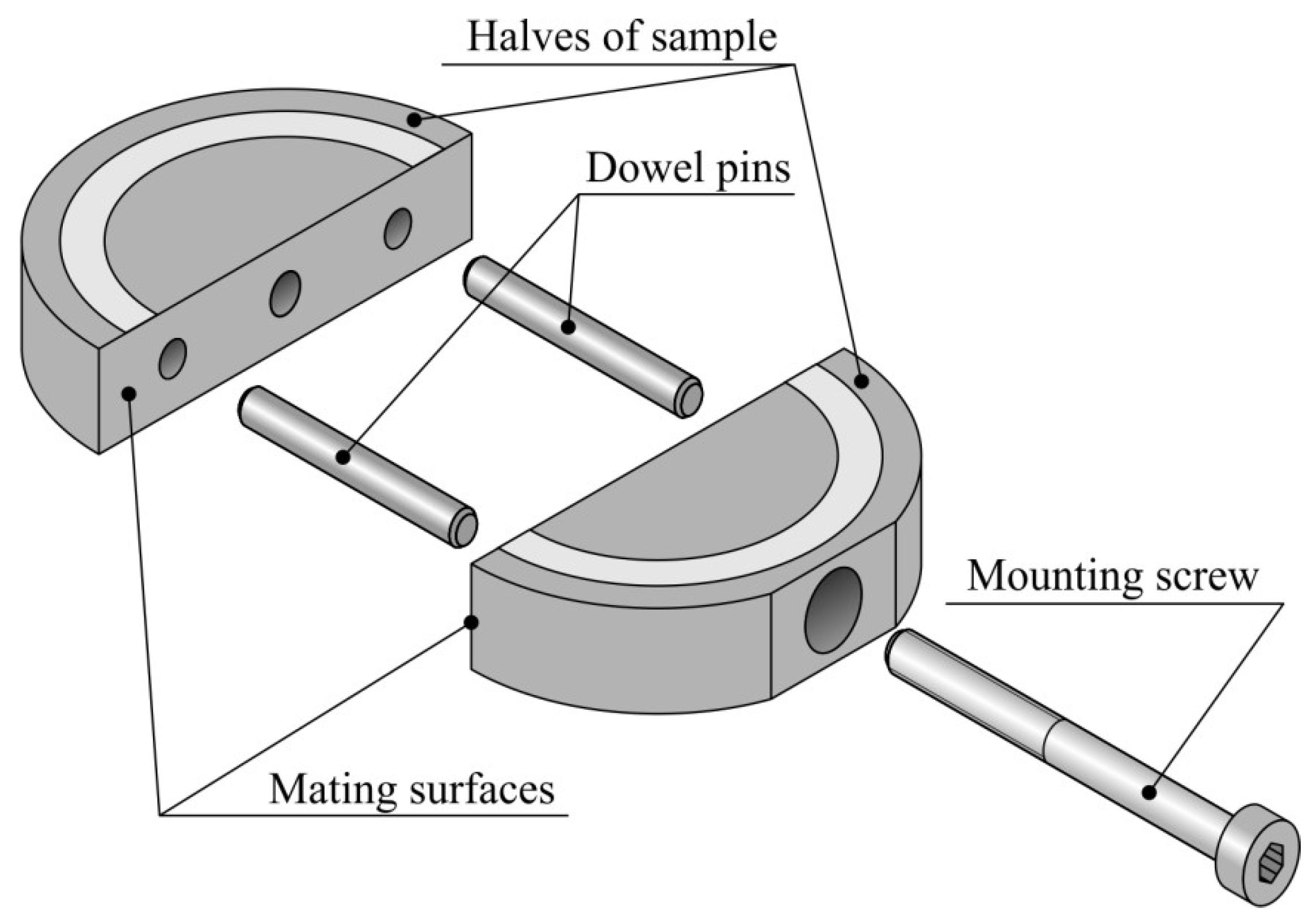
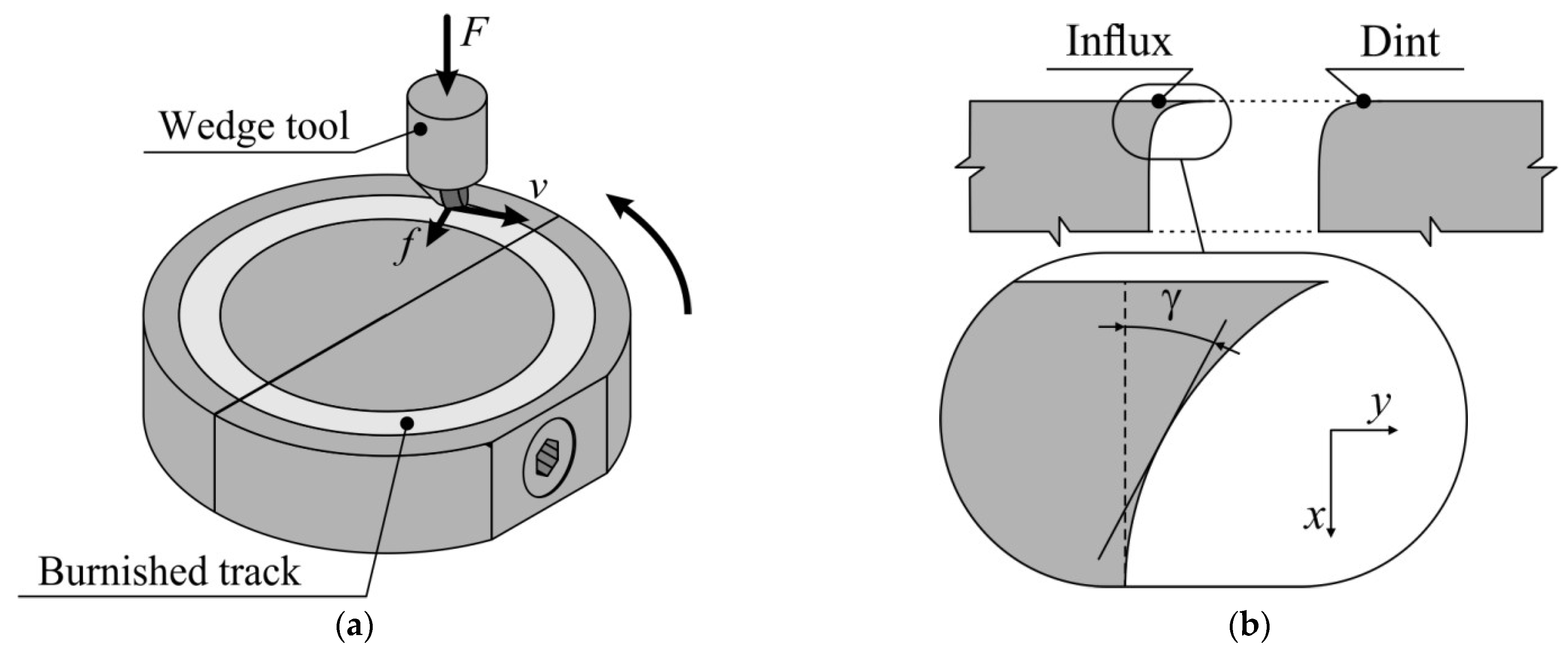
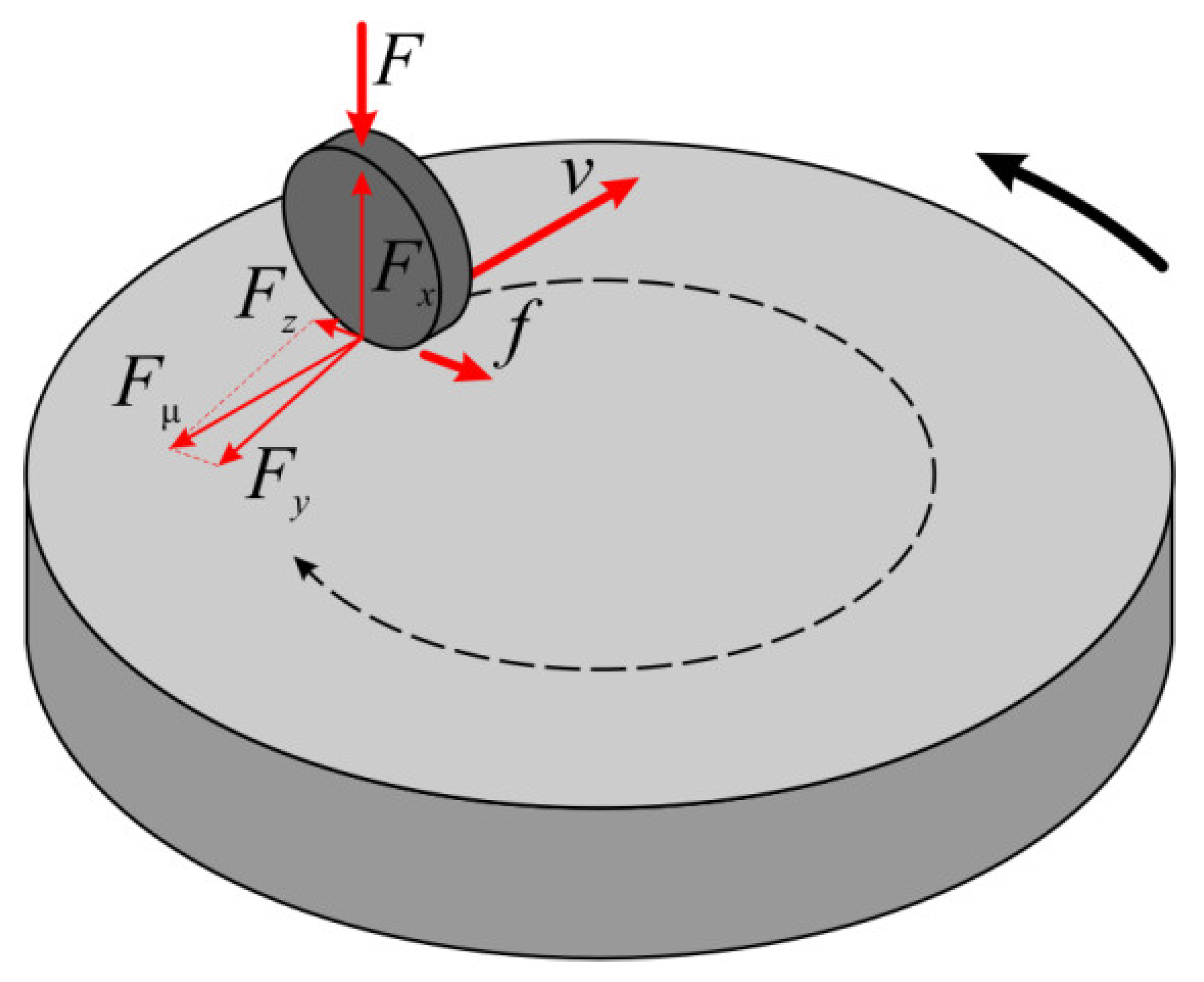
2.3. Methods of Experimental Research
3. Results
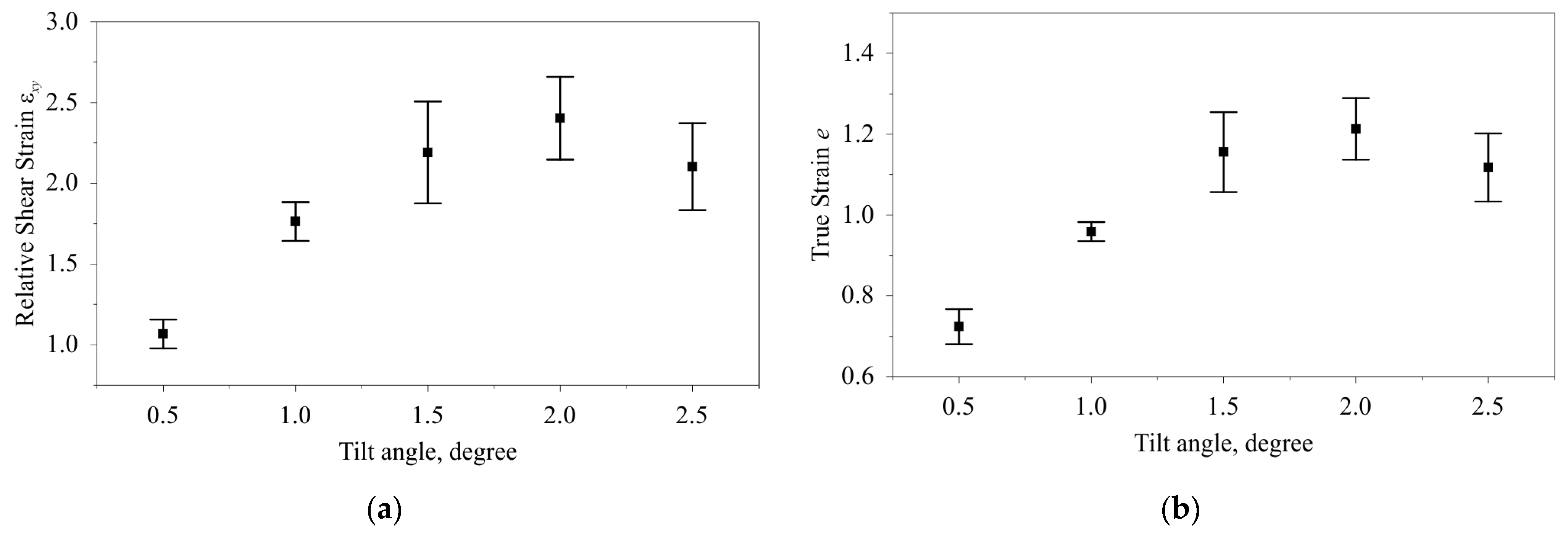
3.1. Experimental Study of the Friction Coefficient and Cumulative Shear Deformation
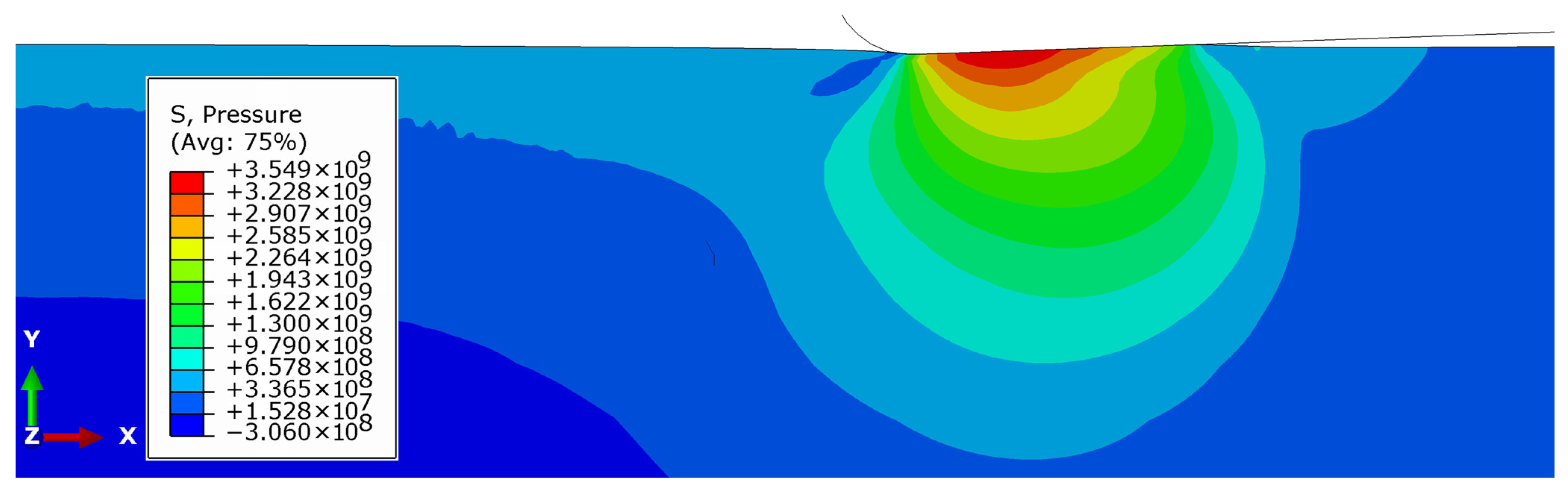
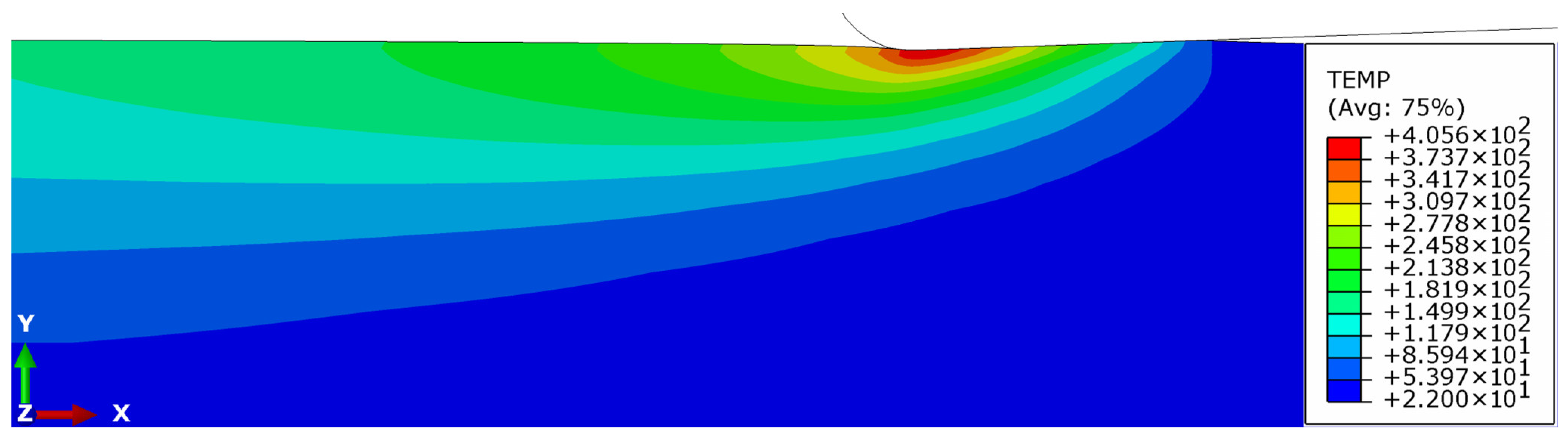
3.2. Numerical Results
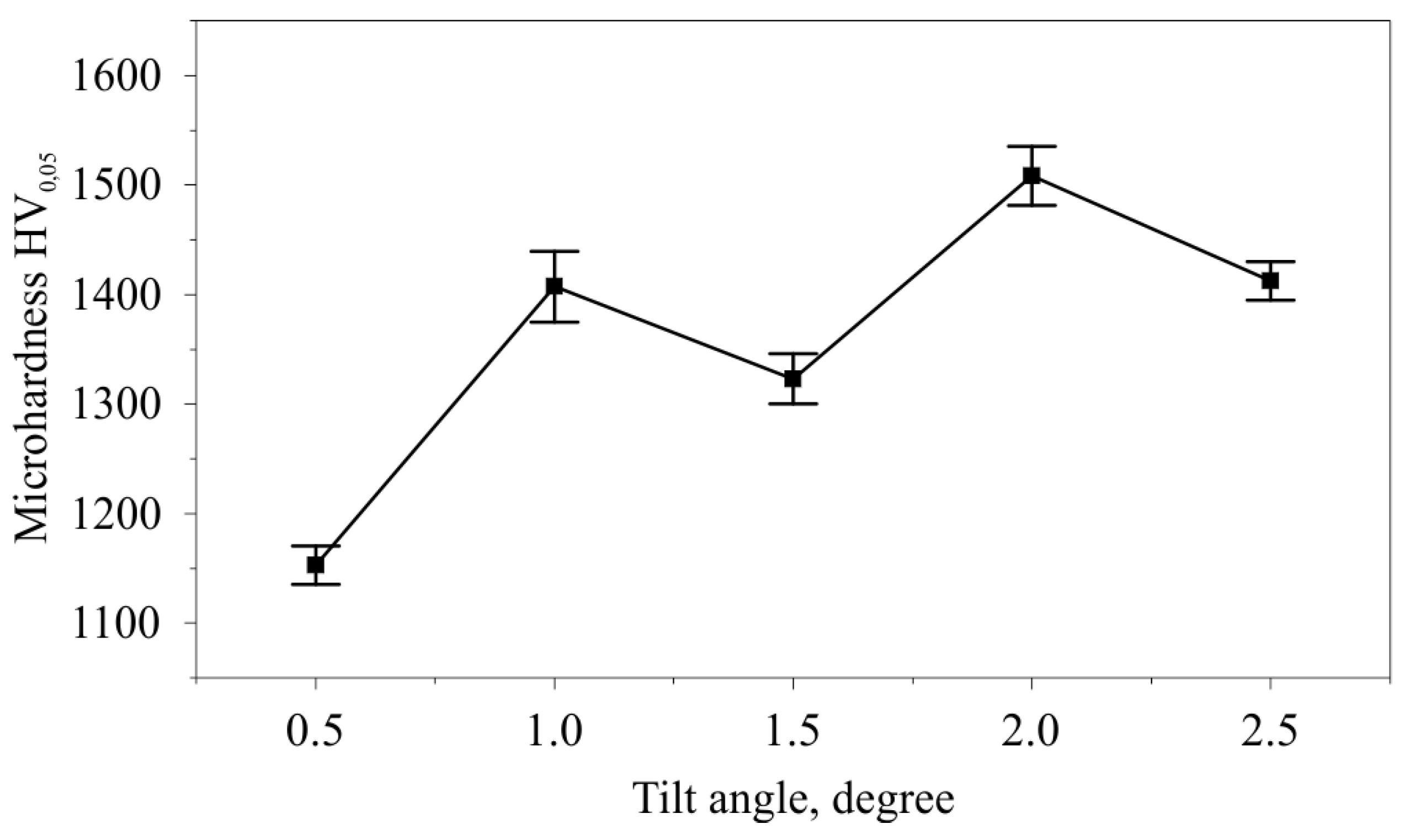
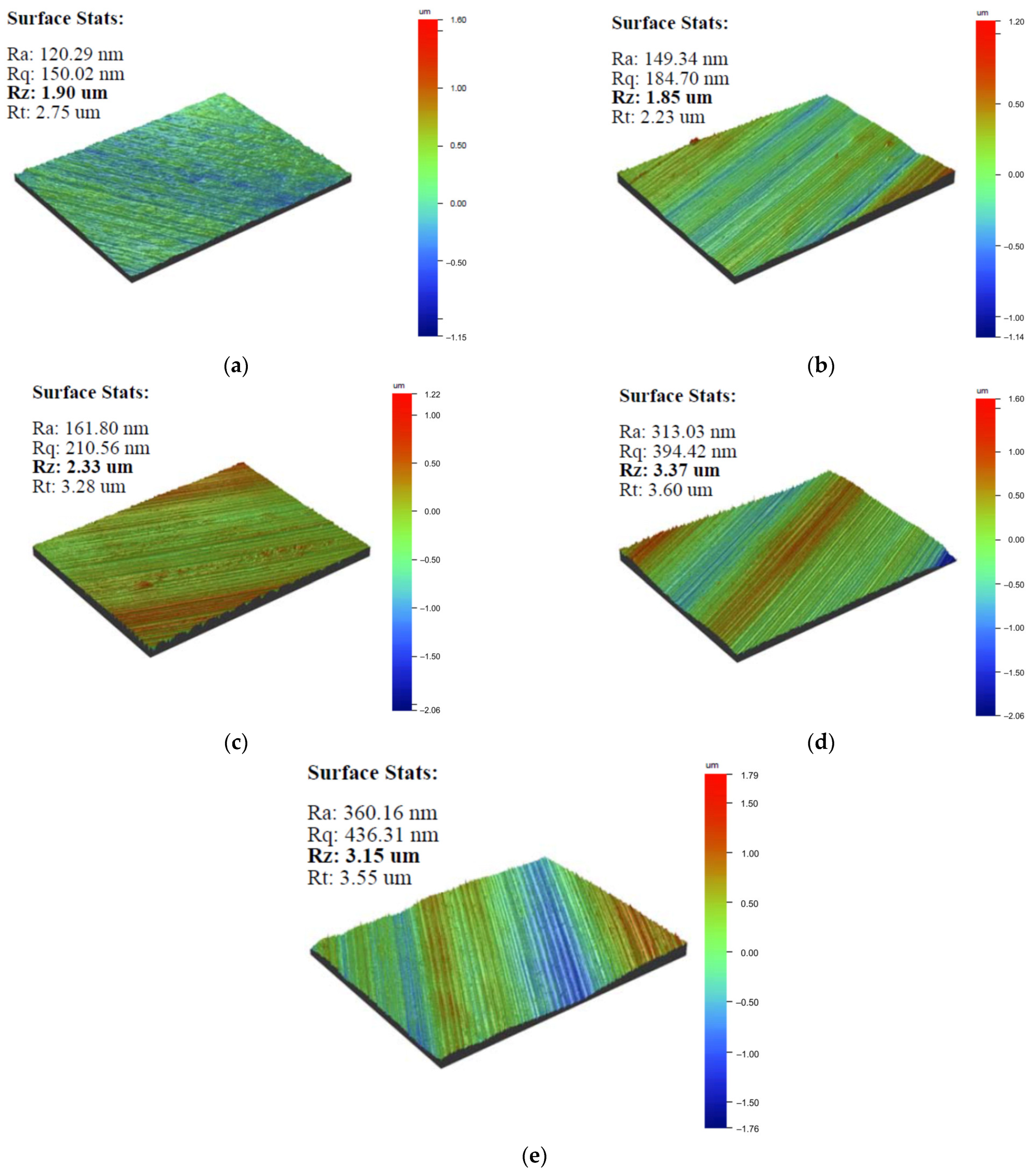
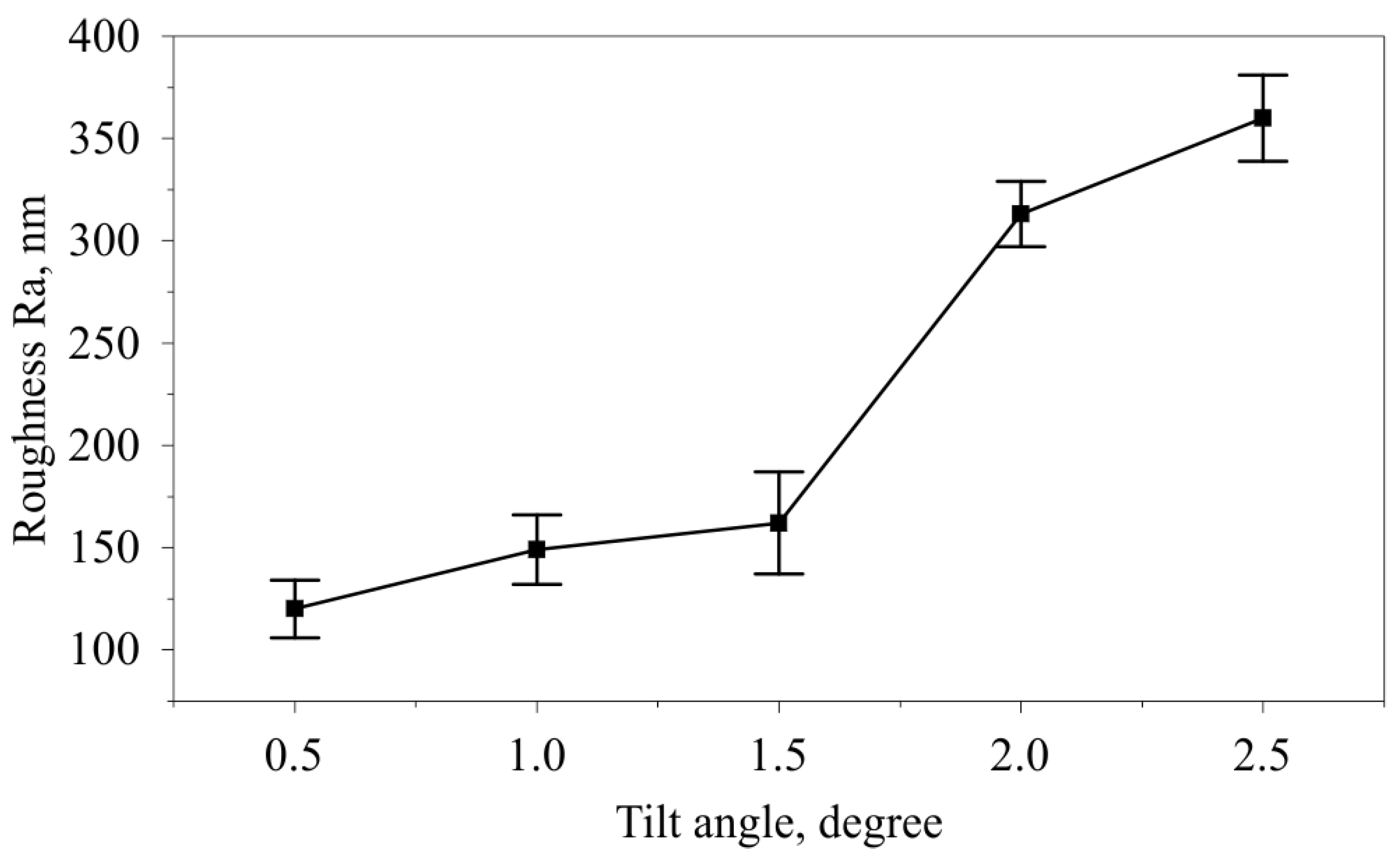
3.3. Investigation of the Influence of the Tilt Angle of the Cylindrical Indenter on the Microhardness, Microstructure, and Roughness of the Surface Layer
4. Discussion
5. Conclusions
- FEM analysis indicates that the maximum values of contact pressure and plastic strain occur when the tilt angle is 2°. At a burnishing force of 250 N, the pressure reaches 3.5 GPa, the plastic strain is more than 1.2, and the temperature is 405 °C, which fully corresponds to the conditions of steel nanostructuring;
- Burnishing the planes of the split disk with a tool installed in a Kistler 9257BA dynamometer made it possible to establish that the friction coefficient decreases linearly from 0.33 to 0.26 as the tilt angle varies from 0.5° to 2.0°;
- 3D profilometry of the mating surfaces of the split disk enabled the determination of shear strains. True strains increase from 1.05 to 2.4 within the same range of tilt angle;
- The studies at an optimal burnishing force of 250 N and a feed rate of 0.04 mm/rev reveal that the minimum value of microhardness 1,152.6 HV0.05 corresponds to an angle of 0.5°, while the maximum value of 1508.2 HV0.05 occurs at a tilt angle of 2°;
- Transmission microscopy fully explains the achieved level of microhardness since the minimum size of nanocrystallites in the range of 15–30 nm occurs at indenter tilt angles of 2–2.5°;
- The surface roughness changes in the opposite direction to hardness, ranging from 120.3 to 161.8 nm at small tilt angles to 360.16 nm at an angle of 2.5°.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Temperature, °C | Young’s Modulus E, GPa | Poison’s Ratio ν | Temperature, °C | TCLE α, 10−6 Degrees−1 |
|---|---|---|---|---|
| 22 | 201.33 | 0.277 | 22 | 11.5 |
| 200 | 178.58 | 0.269 | 204 | 12.6 |
| 400 | 162.72 | 0.255 | 398 | 13.7 |
| 600 | 103.42 | 0.342 | 704 | 14.9 |
| 800 | 86.87 | 0.396 | 804 | 15.3 |
| 1000 | 66.88 | 0.490 |
| Temperature, °C | Density ρ, kg/m3 | Temperature, °C | Thermal Conductivity k, W/(m × °C) | Temperature, °C | Specific Heat cp, J/(kg × °C) |
|---|---|---|---|---|---|
| 0 | 7834 | 0 | 37.5 | 0 | 486 |
| 100 | 7809 | 100 | 40.5 | 100 | 519 |
| 200 | 7781 | 200 | 40.0 | 200 | 544 |
| 300 | 7749 | 300 | 38.0 | 300 | 578 |
| 400 | 7713 | 400 | 36.5 | 400 | 615 |
| 500 | 7675 | 500 | 34.5 | 500 | 662 |
| 600 | 7634 | 550 | 33.0 | 600 | 745 |
| 700 | 7592 | 600 | 32.0 | 700 | 2089 |
| 800 | 7565 | 650 | 30.0 | 750 | 649 |
| 900 | 7489 | 700 | 28.5 | 800 | 657 |
| 1000 | 7438 | 750 | 25.5 | 900 | 619 |
| 1100 | 7388 | 800 | 24.5 | 1000 | 636 |
| 1200 | 7340 | 850 | 25.0 | 1100 | 649 |
| 1270 | 7302 | 900 | 25.5 | 1200 | 665 |
| 1450 | 7026 | 1270 | 29.0 | 1270 | 672 |
| 1500 | 6995 | 1450 | 39.3 | 1450 | 765 |
| 1600 | 6934 | 1538 | 40.3 | 1480 | 777 |
| 1627 | 41.5 | 1510 | 791 | ||
| 1540 | 804 | ||||
| 1600 | 804 |
References
- Luo, H.; Liu, J.; Wang, L.; Zhong, Q. Study of the mechanism of the burnishing process with cylindrical polycrystalline diamond tools. J. Mater. Process. Technol. 2006, 180, 9–16. [Google Scholar] [CrossRef]
- Korzynski, M.; Lubas, J.; Swirad, S.; Dudek, K. Surface layer characteristics due to slide diamond burnishing with a cylindrical-ended tool. J. Mater. Process. Technol. 2011, 211, 84–94. [Google Scholar] [CrossRef]
- Kuznetsov, V.; Smolin, I.; Dmitriev, A.; Tarasov, S.; Gorgots, V. Toward control of subsurface strain accumulation in nanostructuring burnishing on thermostrengthened steel. Surf. Coat. Technol. 2016, 285, 171–178. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zechetbauer, M.J.; Zhu, Y.T. Producing bulk ultrafine-grained materials by severe plastic deformation. JOM 2006, 58, 33–39. [Google Scholar] [CrossRef]
- Valiev, R.; Zhilyaev, A.; Langdon, T. Bulk Nanostructured Materials: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Kuznetsov, V.P.; Skorobogatov, A.S.; Gorgots, V.G. Impact of indentor sliding velocity and loading repetition factor on shear strain and structure dispersion in nanostructuring burnishing. Facta Univ. Ser. Mech. Eng. 2019, 17, 161. [Google Scholar] [CrossRef]
- Skorobogatov, A.S.; Kuznetcov, V.P.; Belorusets, A.M. Nanostructuring of surface layer of 1.3505 steel by wedge cylindrical tool. KnE Eng. 2019, 1, 145. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G. The Correlation between Surface Integrity and Operating Behaviour of Slide Burnished Components—A Review and Prospects. Appl. Sci. 2023, 13, 3313. [Google Scholar] [CrossRef]
- Becerra-Becerra, E.; Ojeda, C.A.; Saldaña-Robles, A.; Reveles-Arredondo, J.; Barco-Burgos, J.; Vidal-Lesso, A. A review of numerical simulation of ball burnishing process. Finite Elem. Anal. Des. 2023, 218, 103926. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Dunchev, V.P.; Anchev, A.P. Different strategies for finite element simulations of static mechanical surface treatment processes—A comparative analysis. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 371. [Google Scholar] [CrossRef]
- Maximov, J.T.; Duncheva, G.V.; Anchev, A.P.; Amudjev, I.M. New method and tool for increasing fatigue life of a large number of small fastener holes in 2024-T3 Al alloy. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 203. [Google Scholar] [CrossRef]
- Felhő, C.; Varga, G. 2D FEM Investigation of Residual Stress in Diamond Burnishing. J. Manuf. Mater. Process. 2022, 6, 123. [Google Scholar] [CrossRef]
- Kuznetsov, V.P.; Smolin, I.Y.; Dmitriev, A.I.; Konovalov, D.; Makarov, A.V.; Kiryakov, A.E.; Yurovskikh, A.S. Finite element simulation of nanostructuring burnishing. Phys. Mesomech. 2013, 16, 62–72. [Google Scholar] [CrossRef]
- Nowacki, W. Thermoelasticity, 2nd ed.; Pergamon Press: Oxford, UK, 1986; ISBN 9781483162485. [Google Scholar]
- Ziegler, H. An Introduction to Thermomechanics, 2nd ed.; North-Holland: Amsterdam, The Netherlands, 2012; ISBN 978-0444865038. [Google Scholar]
- Johnson, G.R.; Cook, W.N. A Constitutive Model and Data for Metals Subjected to Large Strains, High Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Yen, Y.; Sartkulvanich, P.; Altan, T. Finite Element Modeling of Roller Burnishing Process. CIRP Ann. 2005, 54, 237–240. [Google Scholar] [CrossRef]
- Poulachon, G.; Moisan, A.; Jawahir, I. On modelling the influence of thermo-mechanical behavior in chip formation during hard turning of 100Cr6 bearing steel. CIRP Ann. 2001, 50, 31–36. [Google Scholar] [CrossRef]
- Guo, Y.B.; Liu, C.R. Mechanical Properties of Hardened AISI 52100 Steel in Hard Machining Processes. J. Manuf. Sci. Eng. 2001, 124, 1–9. [Google Scholar] [CrossRef]
- Ramesh, A.; Melkote, S.N. Modeling of white layer formation under thermally dominant conditions in orthogonal machining of hardened AISI 52100 steel. Int. J. Mach. Tools Manuf. 2008, 48, 402–414. [Google Scholar] [CrossRef]
- Shrot, A.; Bäker, M. Determination of Johnson–Cook parameters from machining simulations. Comput. Mater. Sci. 2012, 52, 298–304. [Google Scholar] [CrossRef]
- Guo, Y.B.; Wen, Q.; Woodbury, K.A. Dynamic Material Behavior Modeling Using Internal State Variable Plasticity and Its Application in Hard Machining Simulations. J. Manuf. Sci. Eng. 2006, 128, 749–759. [Google Scholar] [CrossRef]
- Bapat, P.; Dhikale, P.; Shinde, S.; Kulkarni, A.; Chinchanikar, S. A Numerical Model to Obtain Temperature Distribution during Hard Turning of AISI 52100 Steel. Mater. Today Proc. 2015, 2, 1907–1914. [Google Scholar] [CrossRef]
- Shah, S.M.; Nélias, D.; Zain-Ul-Abdein, M.; Coret, M. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel. Finite Elem. Anal. Des. 2012, 61, 1–11. [Google Scholar] [CrossRef]
- Costes, F. Modélisation Thermomécanique Tridimensionnelle par Éléments Finis de la Coulée Continue d’Aciers. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 2004. Available online: https://pastel.archives-ouvertes.fr/pastel-00001334 (accessed on 18 March 2023).
- Simulia Abaqus 2019 Documentation. (n.d.). Available online: https://www.3ds.com/support/documentation/simulation-product/abacus (accessed on 18 March 2023).
- Speeding Up Quasi-Static Analysis in Abaqus/Explicit. Available online: https://caeassistant.com/blog/speed-up-quasi-static-in-explicit-1/ (accessed on 18 March 2023).
- ISO 6344-2:2021; Coated Abrasives—Determination and Designation of Grain Size Distribution—Part 2: Macrogrit Sizes P12 to P220. [s. n.]. ISO: Geneva, Switzerland, 2021.
- Wielki, N.; Heinz, N.; Meyer, D. Characterizing the Local Material Properties of Different Fe–C–Cr-steels by using Deep Rolled Single Tracks. Materials 2020, 13, 4987. [Google Scholar] [CrossRef] [PubMed]






| Authors, Paper | A, MPa | B, MPa | n | C | m | Tr, °C | Tm, °C |
|---|---|---|---|---|---|---|---|
| Poulachon et al. [18] | 11.032 | 4783 | 0.0946 | 0 | 1 | 0 | 775 |
| Guo et al. [19] and Ramesh et al. [20] | 688.17 | 150.82 | 0.3362 | 0.04279 | 2.7786 | 1370 | |
| Shrot et al. [21] | 635.926 | 101.703 | 0.649 | 2.259 | 635.926 | ||
| Guo et al. [22] and Bapat et al. [23] | 2482.24 | 1498.5 | 0.19 | 0.027 | 0.66 | ||
| This paper | 322 | 994 | 0.34 | 0.043 | 0.597 | 20 | 6510 |
| P3D, N | P2D, kN |
|---|---|
| 100 | 354 |
| 150 | 531 |
| 200 | 708 |
| 250 | 885 |
| No. | Tilt Angle | HV0.05 | Mean HV0.05 | SE of Mean | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 1152 | 1127 | 1177 | 1104 | 1203 | 1152.6 | 17.54024 |
| 2 | 1 | 1481 | 1463 | 1301 | 1379 | 1412 | 1407.2 | 32.13783 |
| 3 | 1.5 | 1362 | 1286 | 1379 | 1331 | 1257 | 1323 | 22.85388 |
| 4 | 2 | 1446 | 1463 | 1596 | 1499 | 1537 | 1508.2 | 26.95812 |
| 5 | 2.5 | 1463 | 1446 | 1379 | 1395 | 1379 | 1412.4 | 17.63973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, V.; Smolin, I.; Skorobogatov, A.; Akhmetov, A. Finite Element Simulation and Experimental Investigation of Nanostructuring Burnishing AISI 52100 Steel Using an Inclined Flat Cylindrical Tool. Appl. Sci. 2023, 13, 5324. https://doi.org/10.3390/app13095324
Kuznetsov V, Smolin I, Skorobogatov A, Akhmetov A. Finite Element Simulation and Experimental Investigation of Nanostructuring Burnishing AISI 52100 Steel Using an Inclined Flat Cylindrical Tool. Applied Sciences. 2023; 13(9):5324. https://doi.org/10.3390/app13095324
Chicago/Turabian StyleKuznetsov, Victor, Igor Smolin, Andrey Skorobogatov, and Ayan Akhmetov. 2023. "Finite Element Simulation and Experimental Investigation of Nanostructuring Burnishing AISI 52100 Steel Using an Inclined Flat Cylindrical Tool" Applied Sciences 13, no. 9: 5324. https://doi.org/10.3390/app13095324
APA StyleKuznetsov, V., Smolin, I., Skorobogatov, A., & Akhmetov, A. (2023). Finite Element Simulation and Experimental Investigation of Nanostructuring Burnishing AISI 52100 Steel Using an Inclined Flat Cylindrical Tool. Applied Sciences, 13(9), 5324. https://doi.org/10.3390/app13095324








