Automatic Interpretation of Potential Field Data Based on Euler Deconvolution with Linear Background
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology
3. Model Test
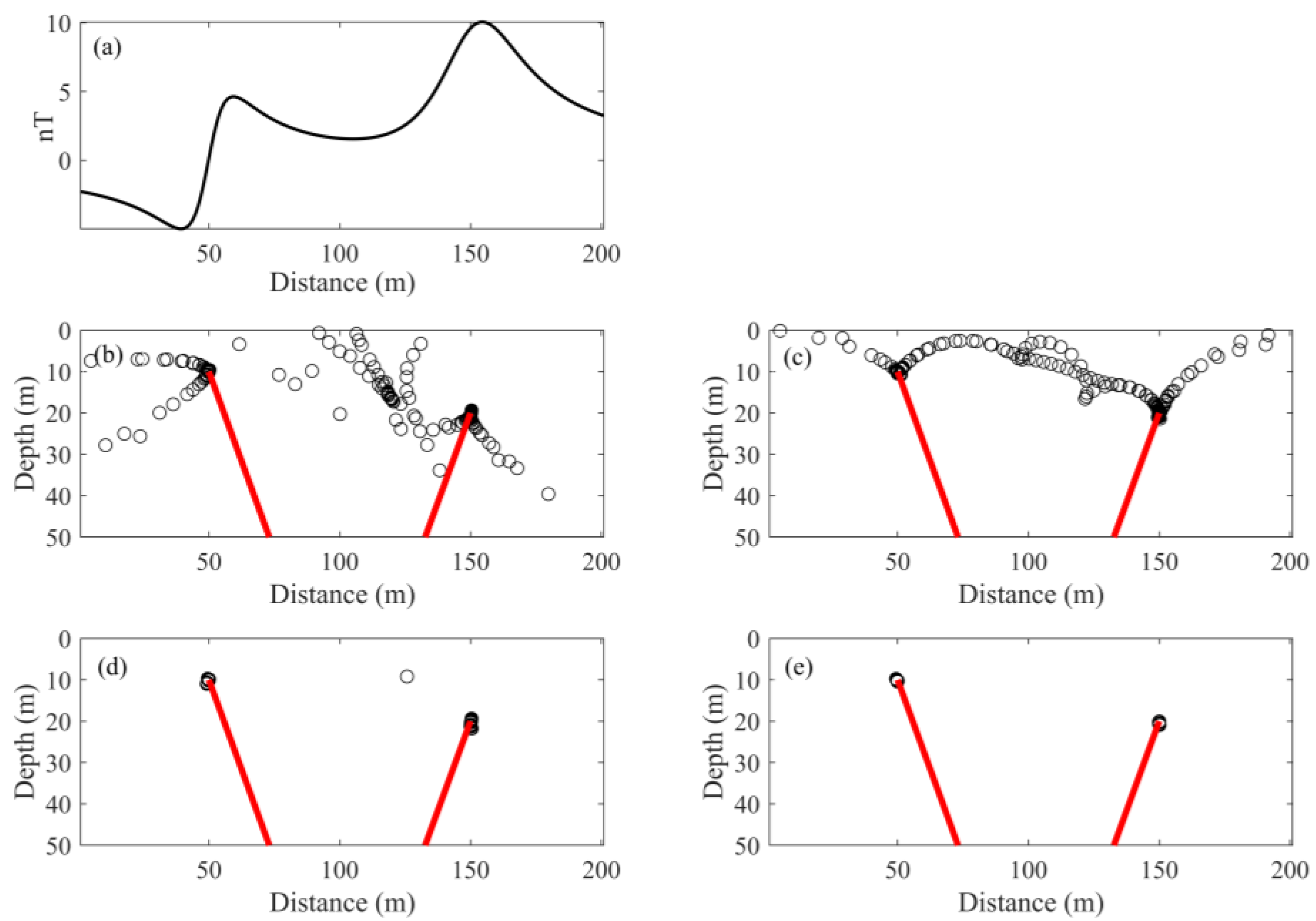
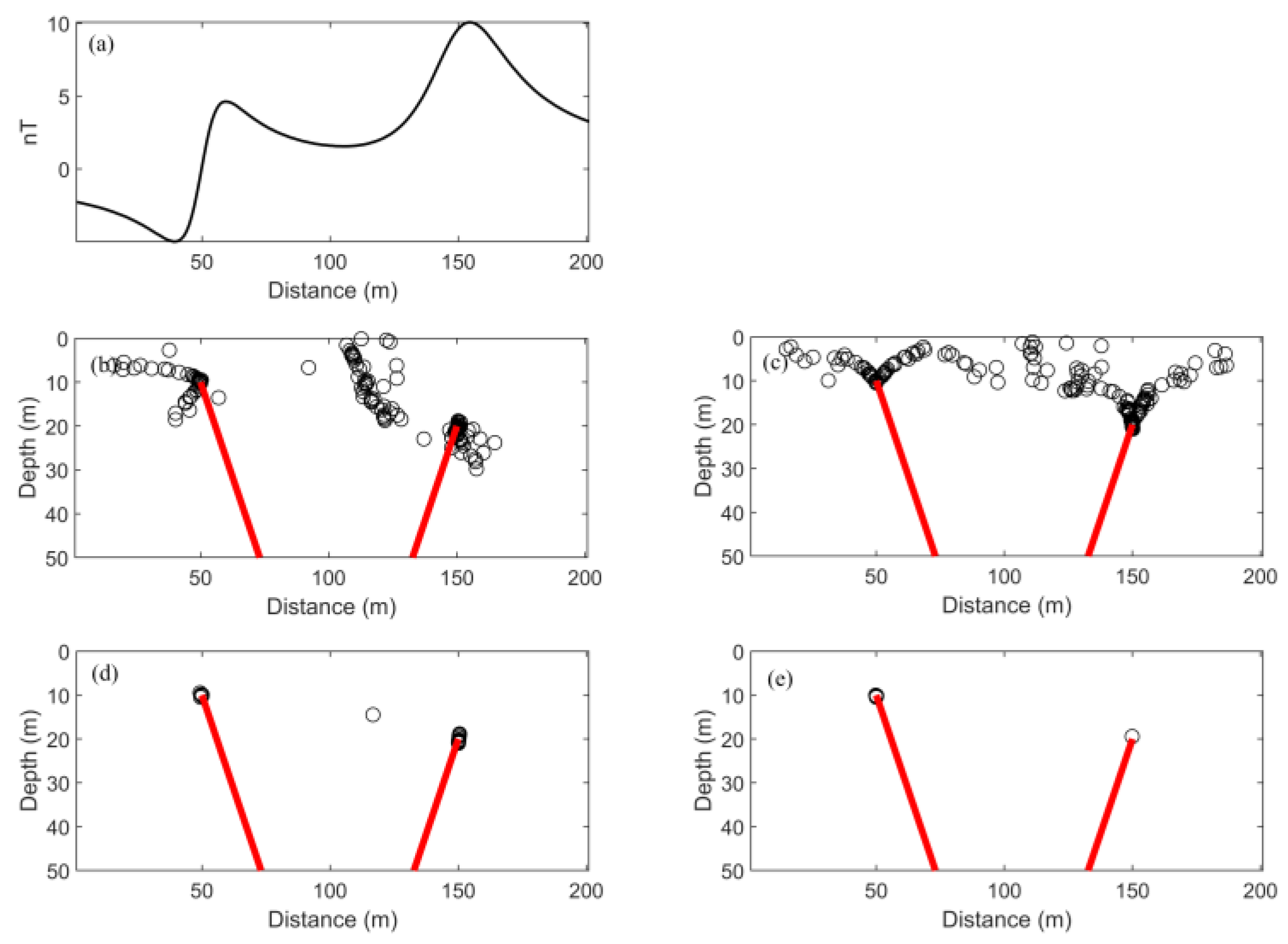
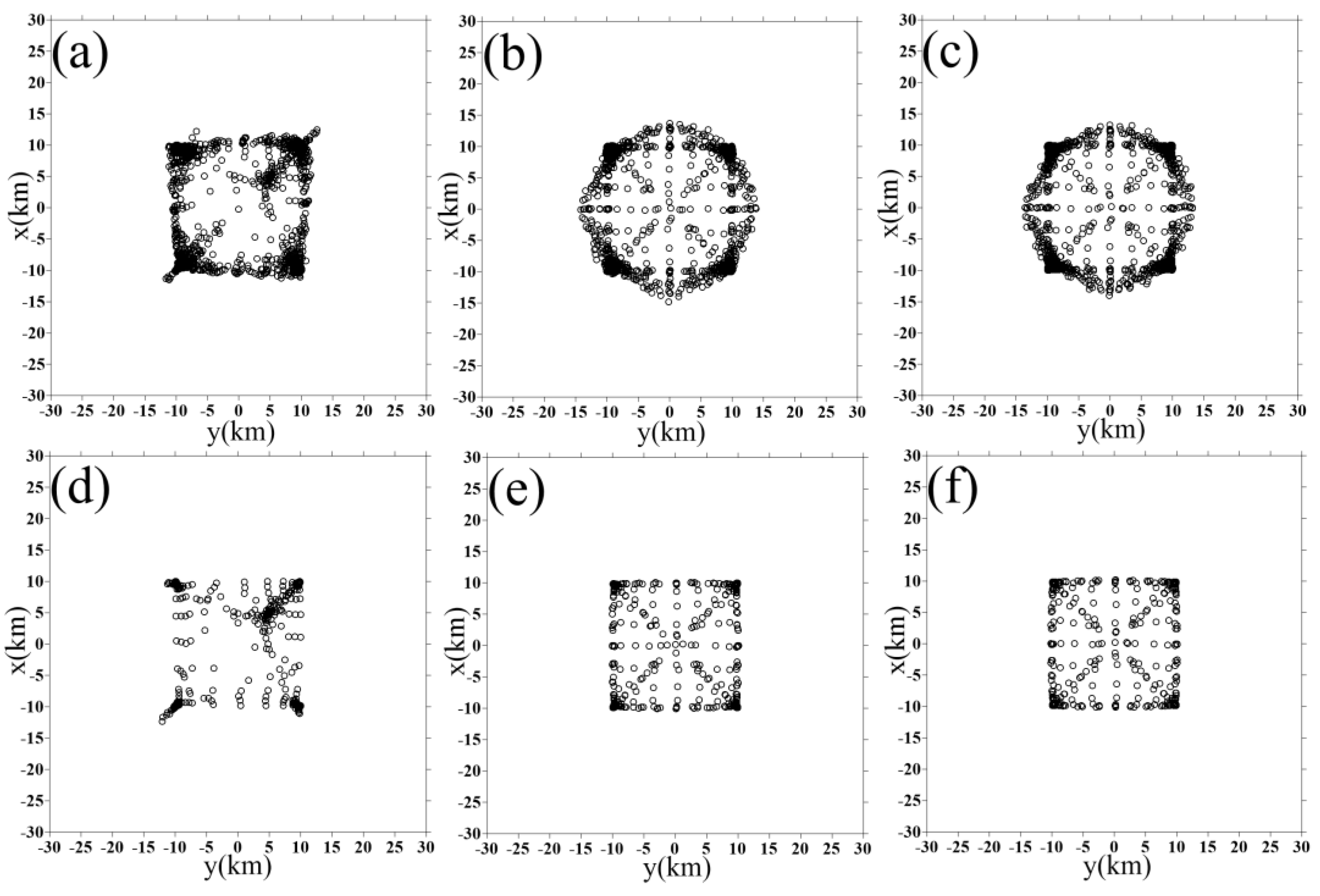
3.1. Test 1: Two Dykes Model Test
3.2. Test 2: Linear Background
Noisy Data
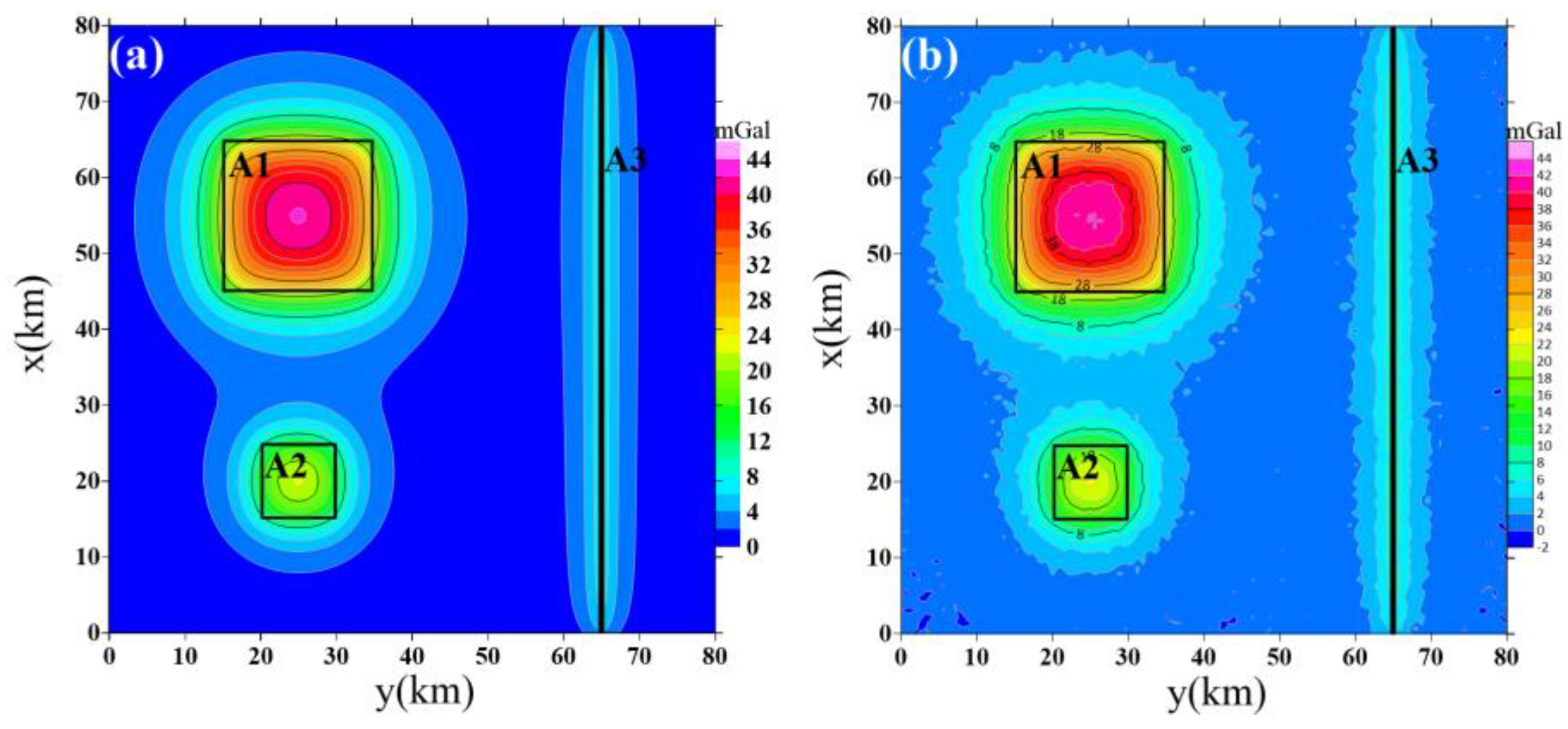
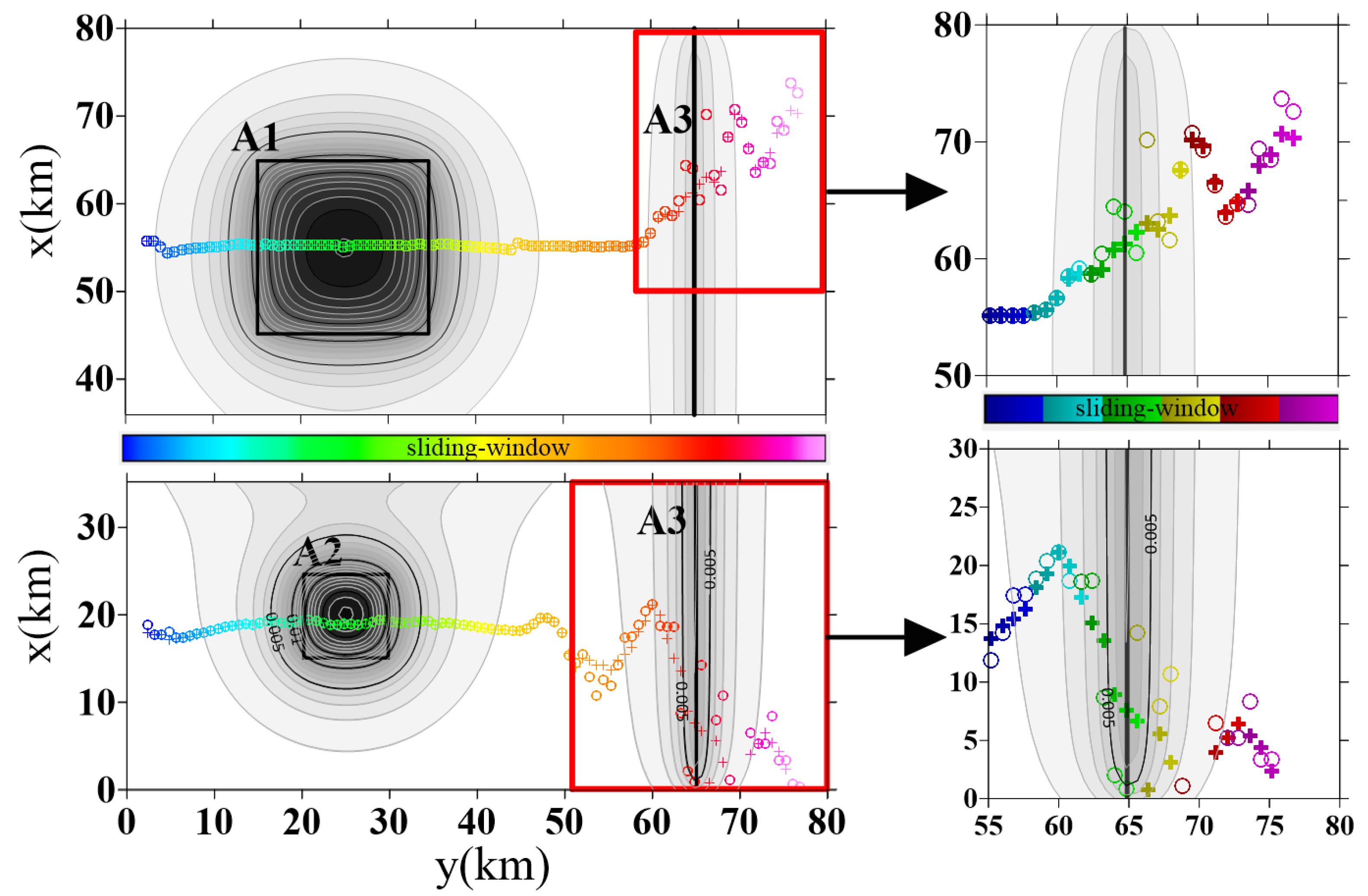
3.3. Test 3: Vertical Prisms Model Test
Noisy Data
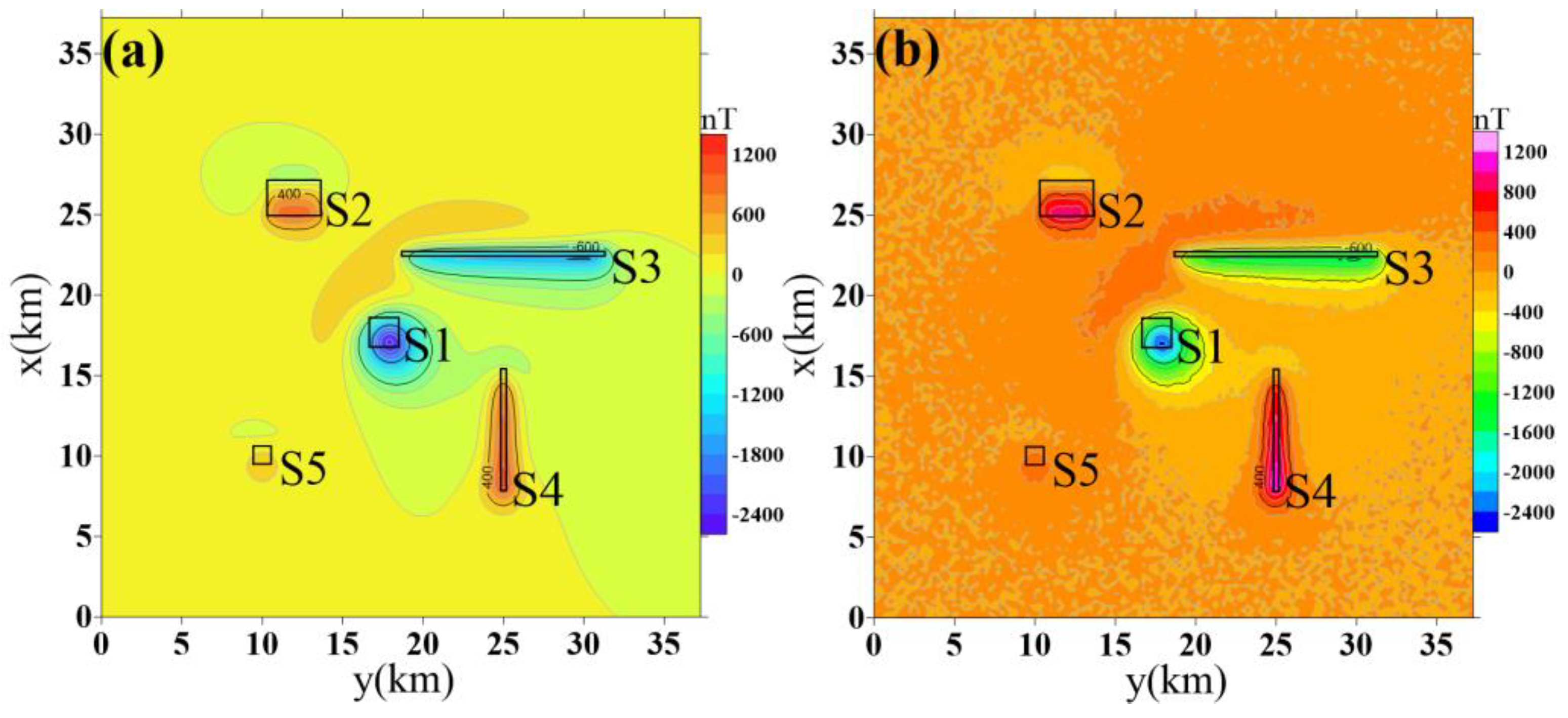
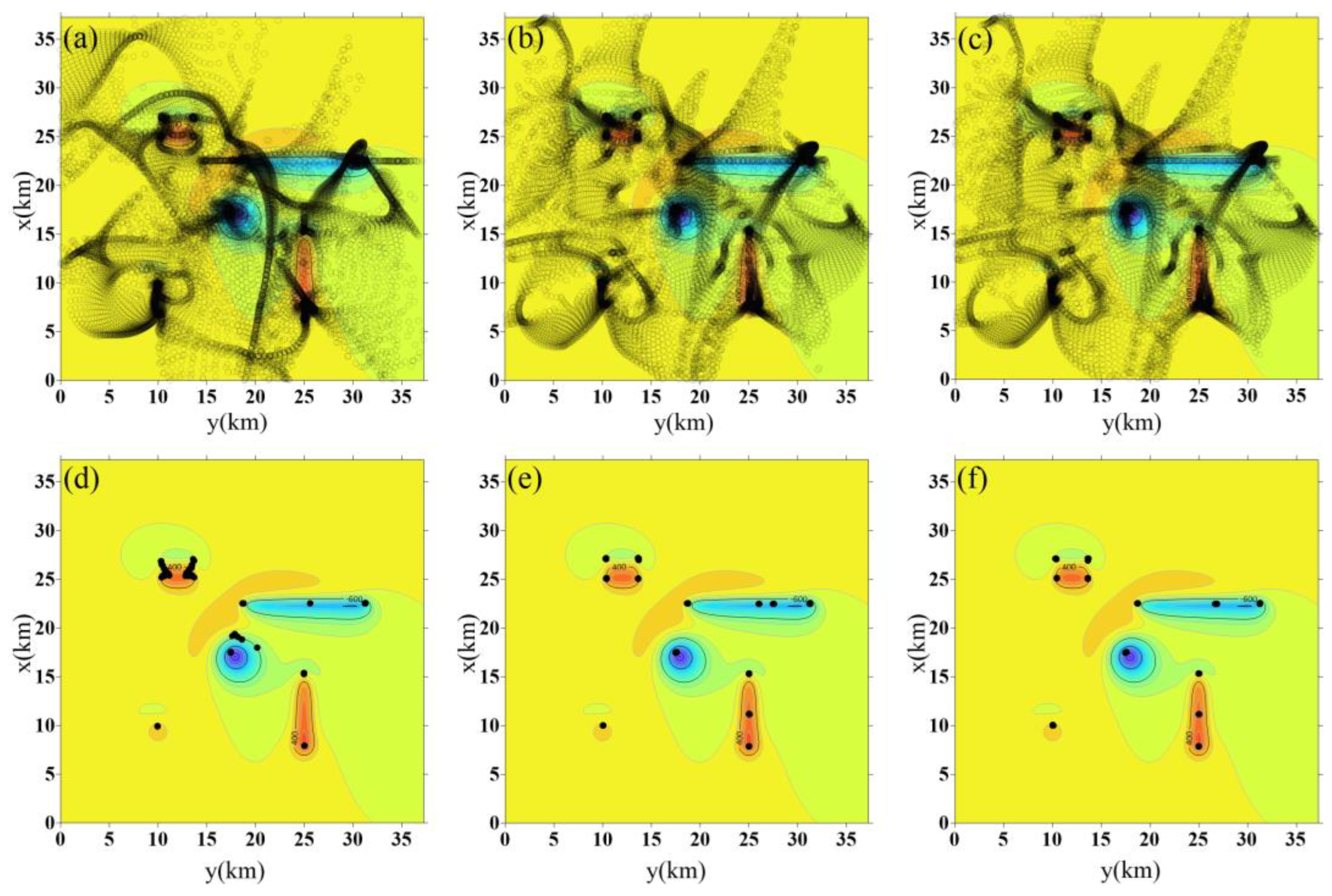
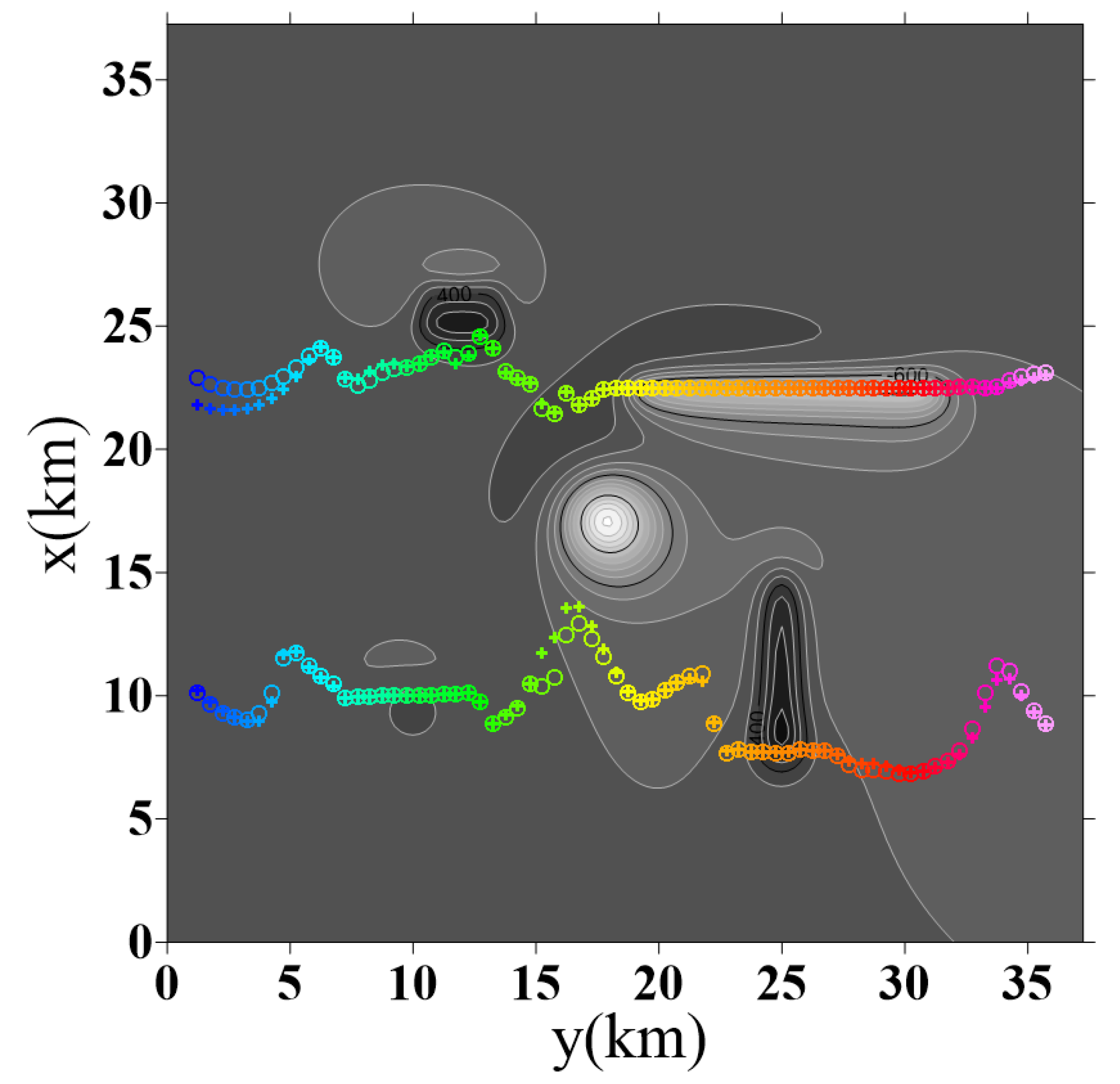
3.4. Test 4: Complex Model Test
Noisy Data
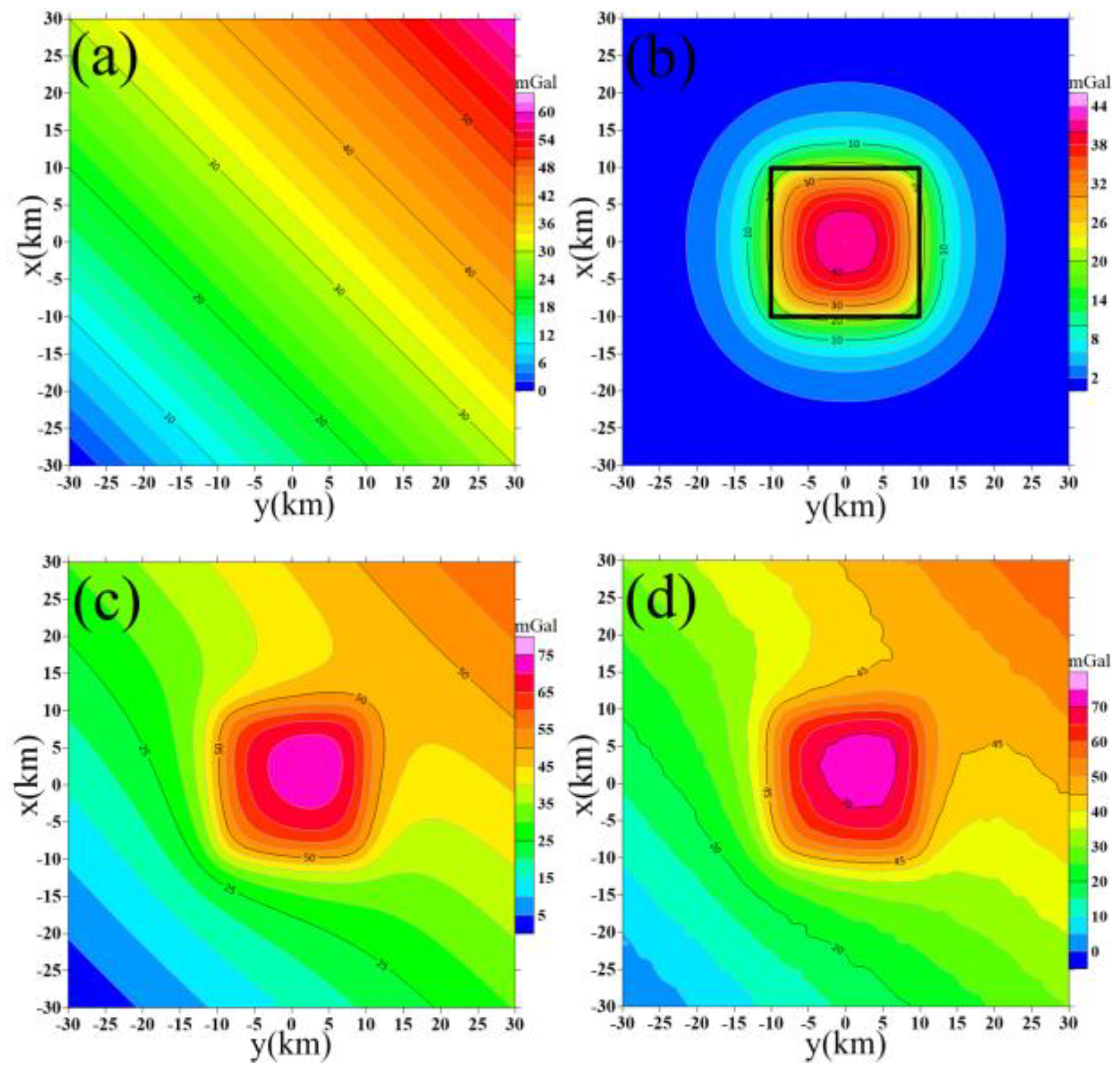
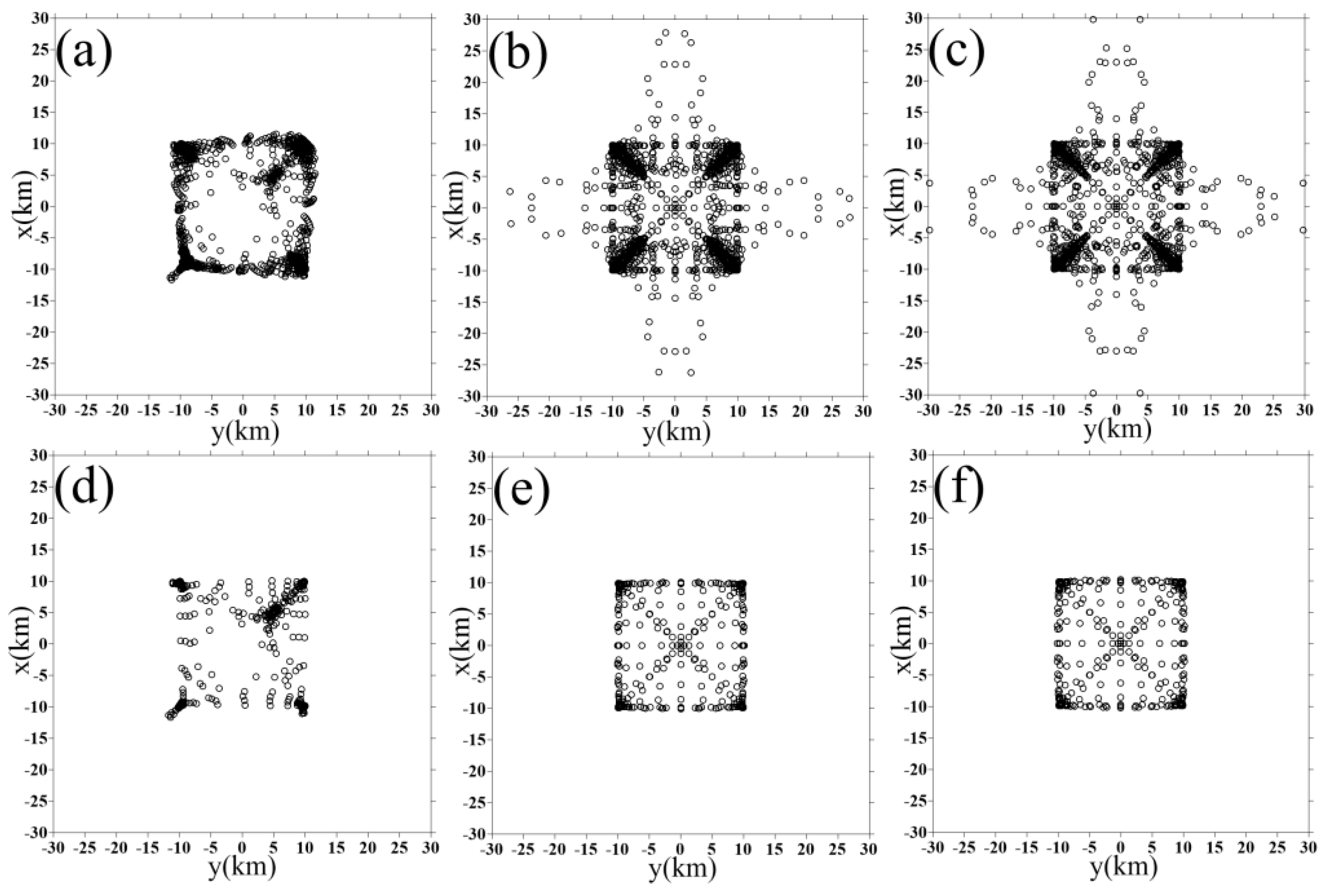
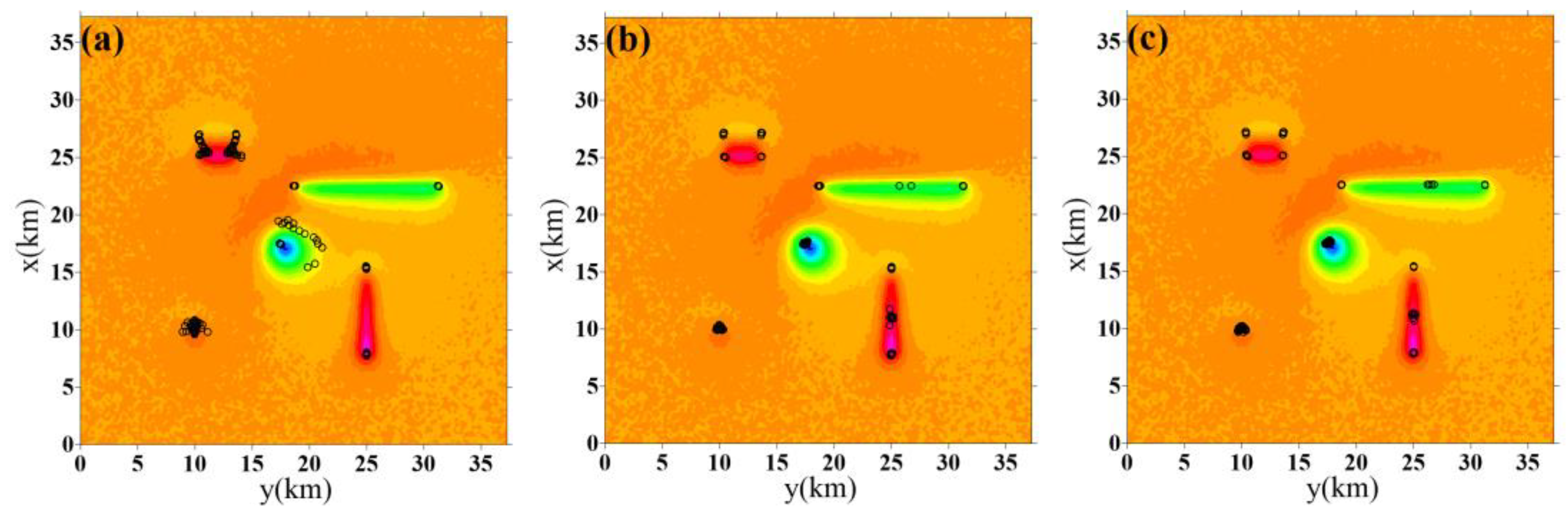
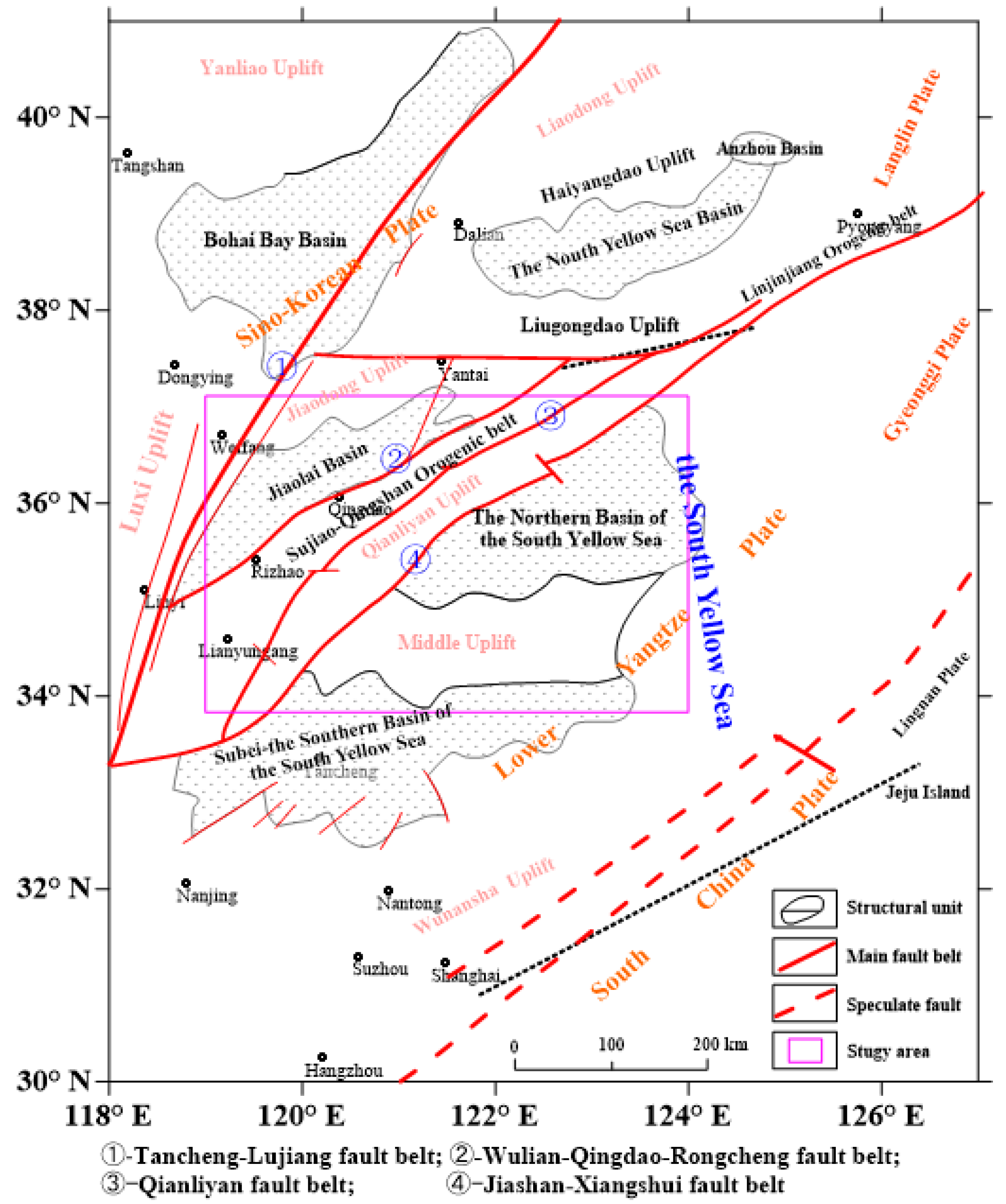
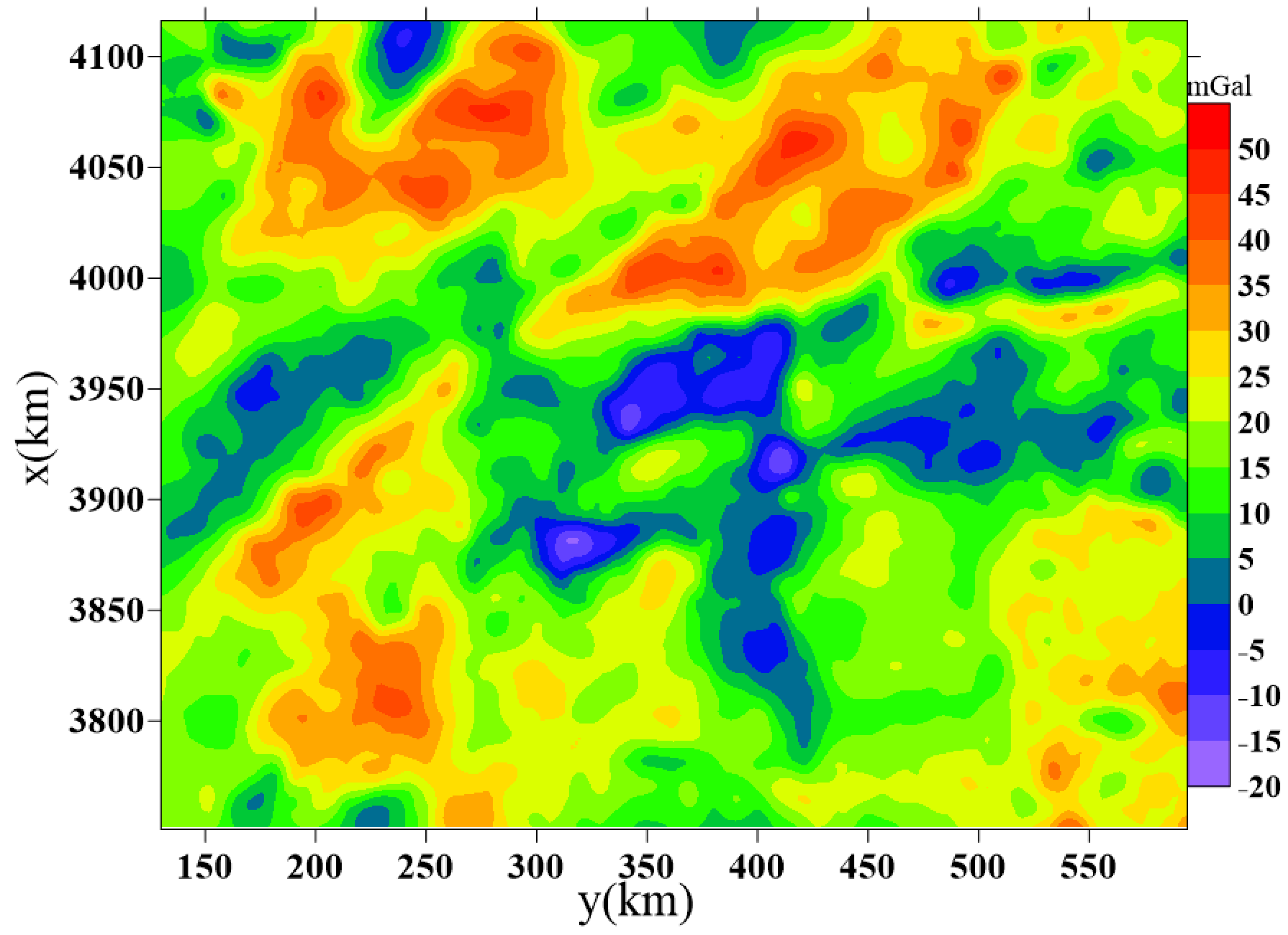
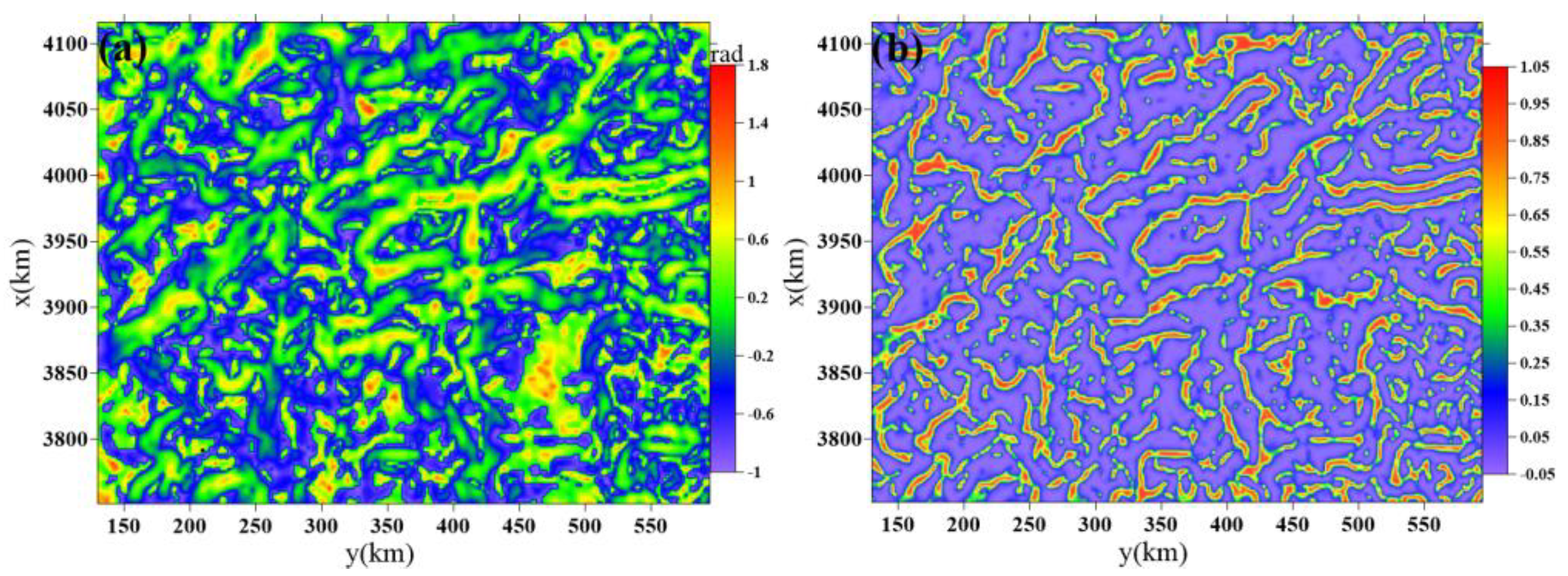
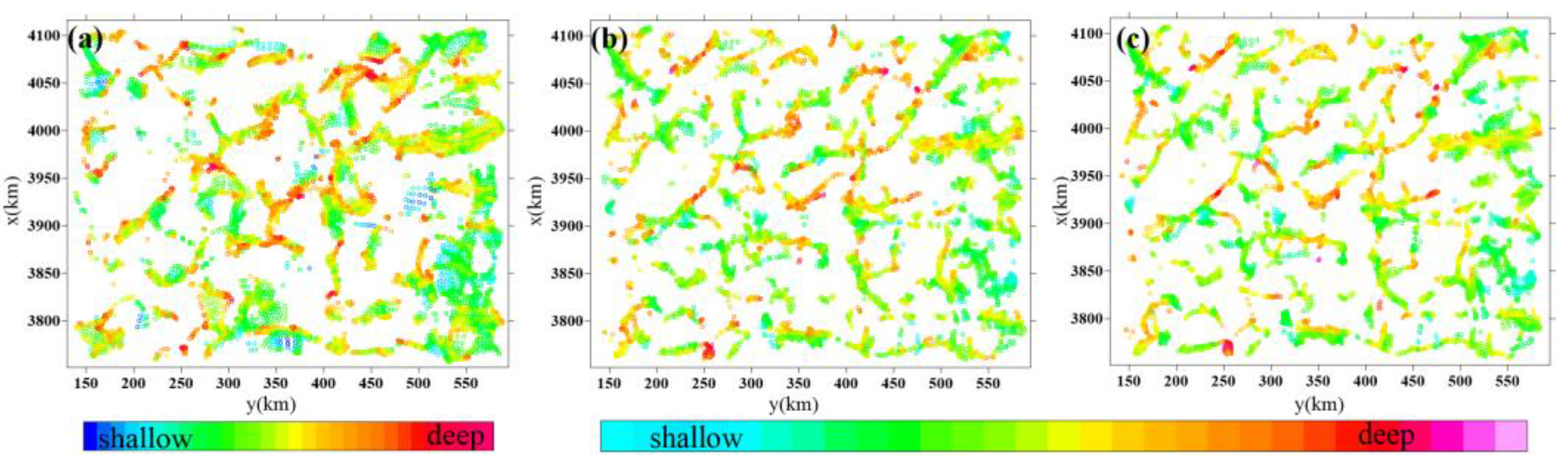
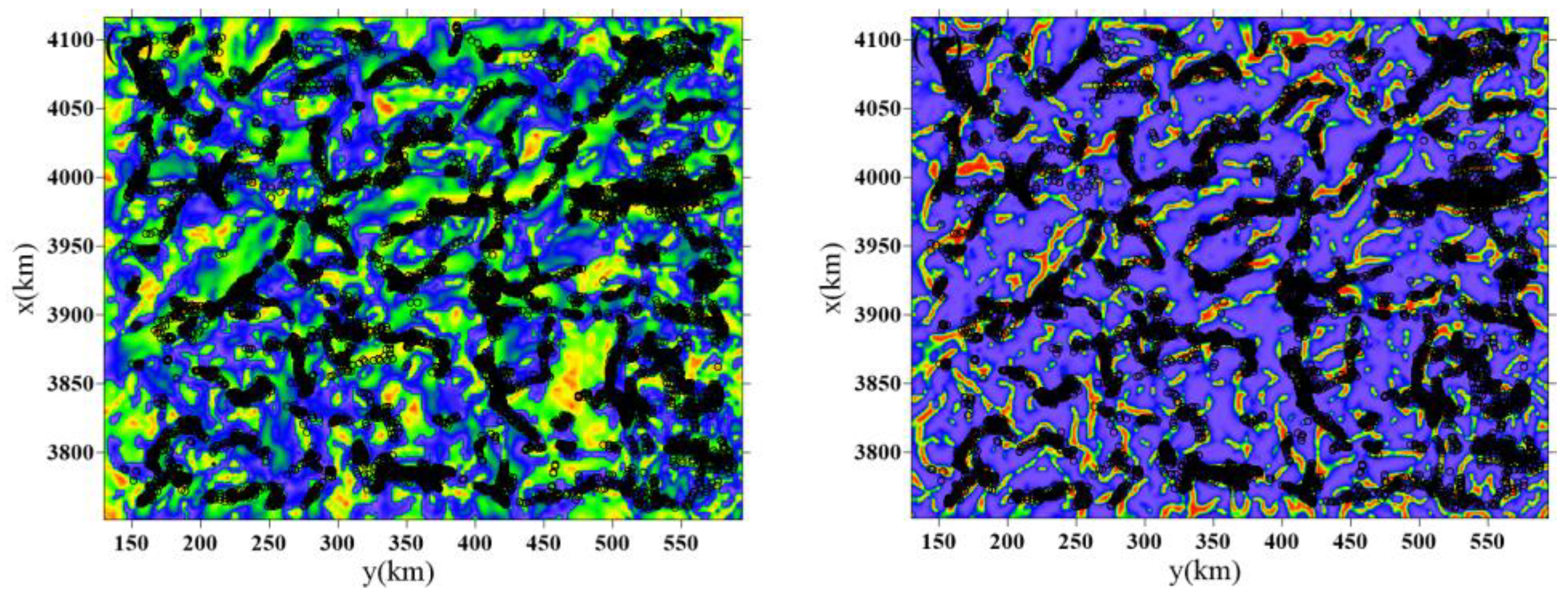
4. Application to Real Data
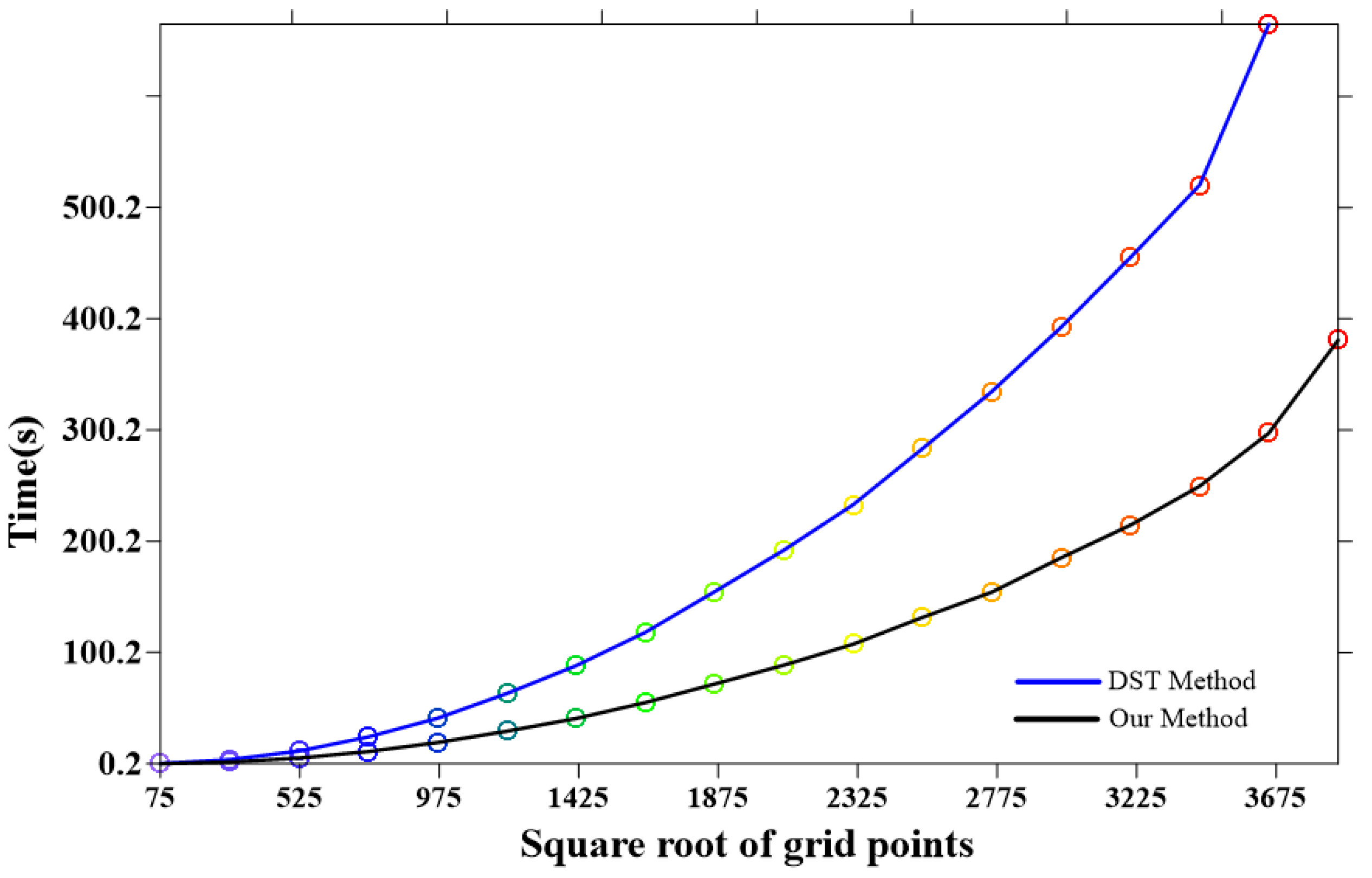
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Werner, R.T. Interpretation of Magnetic Anomalies at Sheet-Like Bodies. Sver. Geol. Unders. Ser. C Arsb. 1953, 6, 413–449. [Google Scholar]
- Hansen, R.O.; Simmonds, M. Multiple-source Werner deconvolution. Geophysics 1993, 58, 1792–1800. [Google Scholar] [CrossRef]
- Hansen, R.O. 3D multiple-source Werner deconvolution for magnetic data. Geophysics 2005, 70, L45–L51. [Google Scholar] [CrossRef]
- Thompson, D.T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data. Geophysics 1982, 47, 31–37. [Google Scholar] [CrossRef]
- Reid, A.B.; Allsop, J.M.; Granser, H.; Millett, A.T.; Somerton, I.W. Magnetic interpretation in three dimensions using Euler deconvolution. Geophysics 1990, 55, 80–91. [Google Scholar] [CrossRef]
- Barbosa, V.; Silva, J.B.C.; Medeiros, W.E. Stability analysis and improvement of structural index estimation in Euler deconvolution. Geophysics 1999, 64, 48–60. [Google Scholar] [CrossRef]
- Stavrev, P.; Reid, A. Degrees of homogeneity of potential fields and structural indices of Euler deconvolution. Geophysics 2007, 72, L1–L12. [Google Scholar] [CrossRef]
- Nabighian, M.N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section: Its properties and use for automated anomaly interpretation. Geophysics 1972, 37, 507–517. [Google Scholar] [CrossRef]
- Nabighian, M.N. Additional comments on the analytic signal of two-dimensional magnetic bodies with polygonal cross-section. Geophysics 1974, 39, 85–92. [Google Scholar] [CrossRef]
- Nabighian, M.N. Toward a three-dimensional automatic interpretation of potential field data via generalized Hilbert transforms: Fundamental relations. Geophysics 1984, 49, 780–786. [Google Scholar] [CrossRef]
- Bastani, M.; Pedersen, L.B. Automatic interpretation of magnetic dike parameters using the analytical signal technique. Geophysics 2001, 66, 551–561. [Google Scholar] [CrossRef]
- Fedi, M. DEXP: A fast method to determine the depth and the structural index of potential fields sources. Geophysics 2007, 72, I1–I11. [Google Scholar] [CrossRef]
- Abbas, M.A.; Fedi, M. Automatic DEXP imaging of potential fields independent of the structural index. Geophys. J. Int. 2014, 199, 1625–1632. [Google Scholar] [CrossRef]
- Hsu, S.-K. Imaging magnetic sources using Euler’s equation. Geophys. Prospect. 2002, 50, 15–25. [Google Scholar] [CrossRef]
- Nabighian, M.N.; Hansen, R.O. Unification of Euler and Werner deconvolution in three dimensions via the generalized Hilbert transform. Geophysics 2001, 66, 1805–1810. [Google Scholar] [CrossRef]
- Gerovska, D.; Stavrev, P.; Araúzo-Bravo, M. Finite-difference Euler Deconvolution Algorithm Applied to the Interpretation of Magnetic Data from Northern Bulgaria. Pure Appl. Geophys. 2005, 162, 591–608. [Google Scholar] [CrossRef]
- Stavrev, P.Y. Euler deconvolution using differential similarity transformations of gravity or magnetic anomalies. Geophys. Prospect. 1997, 45, 207–246. [Google Scholar] [CrossRef]
- Gerovska, D.; Araúzo-Bravo, M.J.; Stavrev, P.; Whaler, K. MaGSoundDST—3D automatic inversion of magnetic and gravity data based on the differential similarity transform. Geophysics 2010, 75, L25–L38. [Google Scholar] [CrossRef]
- Gerovska, D.; Araúzo-Bravo, M.J.; Whaler, K.; Stavrev, P.; Reid, A. Three-dimensional interpretation of magnetic and gravity anomalies using the finite-difference similarity transform. Geophysics 2010, 75, L79–L90. [Google Scholar] [CrossRef]
- Gerovska, D.; Arauzo-Bravo, M.J.; Whaler, K. A Comparison of Three Automatic Interpretation Techniques for Magnetic and Gravity Data. In Proceedings of the 72nd EAGE Conference and Exhibition Incorporating SPE EUROPEC 2010, Barcelona, Spain, 14–17 June 2010; p. 161-00120. [Google Scholar]
- Pasteka, R. The role of the interference polynomial in the Euler deconvolution algorithm. Boll. Geofis. Teor. Appl. 2006, 47, 171–180. [Google Scholar]
- Dewangan, P.; Ramprasad, T.; Ramana, M.V.; Desa, M.; Shailaja, B. Automatic Interpretation of Magnetic Data Using Euler Deconvolution with Nonlinear Background. Pure Appl. Geophys. 2007, 164, 2359–2372. [Google Scholar] [CrossRef]
- Reid, A.B.; Ebbing, J.; Webb, S.J. Avoidable Euler Errors-the use and abuse of Euler deconvolution applied to potential fields. Geophys. Prospect. 2014, 62, 1162–1168. [Google Scholar] [CrossRef]
- Cooper, G. Obtaining dip and susceptibility information from Euler deconvolution using the Hough transform. Comput. Geosci. 2006, 32, 1592–1599. [Google Scholar] [CrossRef]
- Liu, Q.; Yao, C.; Zheng, Y. Euler deconvolution of potential field based on damped least square method. Chin. J. Geophys. 2019, 62, 3710–3722. (In Chinese) [Google Scholar] [CrossRef]
- Qiang, L.; Changli, Y.; Yao, L.; Junjun, Y.; Zelin, L. Euler solution selecting method based on the damping factor. Acta Geophys. 2022, 70, 1551–1564. [Google Scholar] [CrossRef]
- Wang, J.; Meng, X.; Li, F. New improvements for lineaments study of gravity data with improved Euler inversion and phase congruency of the field data. J. Appl. Geophys. 2017, 136, 326–334. [Google Scholar] [CrossRef]
- Gerovska, D.; Araúzo-Bravo, M.J. Automatic interpretation of magnetic data based on Euler deconvolution with unprescribed structural index. Comput. Geosci. 2003, 29, 949–960. [Google Scholar] [CrossRef]
- Yao, C.L.; Guan, Z.N.; Wu, Q.B.; Zhang, Y.W.; Liu, H.J. An analysis of Euler deconvolution and its improvement. Geophys. Geochem. Explor. 2004, 28, 150–155. [Google Scholar]
- Wang, L.W. Basic characteristics of geology and prospects of oil andgas production in the Southern Huanghai Sea basin. Mar. Geol. Quat. Geol. 1989, 9, 41–50. [Google Scholar]
- Cai, Q.Z. Oil & Gas Geology in China Seas; Ocean Press: Beijing, China, 2005. [Google Scholar]
- Li, J.B. Regional Oceanography of China Seas Marine Geology; Ocean Press: Beijing, China, 2012. [Google Scholar]
- Xu, W.Q.; Yuan, B.Q.; Liu, B.L.; Yao, C.L. Multiple gravity and magnetic potential field edge detection methods and their application to the boundary of fault structures in northern South Yellow Sea. Geophys. Geochem. Explor. 2020, 44, 962–974. [Google Scholar] [CrossRef]
- Wanyin, W.; Jinlan, L.; Zhiyun, Q.; Yijian, H.; Dongsheng, C. A research on Mesozoic thickness using satellite gravity anomaly in the southern Yellow Sea. China Offshore Oil Gas 2004, 16, 151–156. [Google Scholar]
- Yao, C.L. Research of Gravity-Magnetic-Seismic Integrated Inversion Technology and Processing &Interpretation of Gravity and Magnetic Data in the Yellow Sea and Adjacent Regions; China University of Geosciences: Beijing, China, 2005. [Google Scholar]
- Pham, L.T.; Van Vu, T.; Le Thi, S.; Trinh, P.T. Enhancement of Potential Field Source Boundaries Using an Improved Logistic Filter. Pure Appl. Geophys. 2020, 177, 5237–5249. [Google Scholar] [CrossRef]


| Length along x (km) | Length along y (km) | Thickness along z (km) | Depth to Top (m) | Density (g/cm3) |
|---|---|---|---|---|
| 20 | 20 | 5 | 1.5 | 0.3 |
| Cuboid No. | Length along x (km) | Length along y (km) | Thickness along z (km) | Depth to Top (m) | Density (g/cm3) |
|---|---|---|---|---|---|
| A1 | 20 | 20 | 5 | 1.5 | 0.3 |
| A2 | 10 | 10 | 4 | 2 | 0.3 |
| A2 | 80 | 1 | 5 | 1 | 0.3 |
| Source | x0 | x1 | x2 | y0 | y1 | y2 | z0 | z1 | z2 | N0 | N1 | N2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 sphere | 17.5 | 17.50 | 17.50 | 17.5 | 17.52 | 17.53 | 3 | 3.06 | 3.04 | 3 | 3.11 | 3.07 |
| S2 sill | 25 | 25.09 | 25.11 | 10.5 | 10.39 | 10.42 | 1 | 0.80 | 0.85 | 1 | 0.69 | 0.77 |
| 25 | 25.07 | 25.09 | 13.5 | 13.62 | 13.60 | 1 | 0.82 | 0.86 | 1 | 0.68 | 0.75 | |
| 27 | 27.12 | 27.11 | 13.5 | 13.65 | 13.64 | 1 | 0.72 | 0.71 | 1 | 0.25 | 0.25 | |
| 27 | 27.12 | 27.11 | 10.5 | 10.33 | 10.34 | 1 | 0.73 | 0.72 | 1 | 0.25 | 0.25 | |
| S3 Dyke | 22.5 | 22.51 | 22.51 | 19 | 18.72 | 18.72 | 1 | 0.84 | 0.84 | 1 | 1.13 | 1.13 |
| 22.5 | 22.50 | 22.50 | 31 | 31.25 | 31.25 | 1 | 0.85 | 0.85 | 1 | 1.13 | 1.13 | |
| S4 Horioz. rod | 8 | 7.88 | 7.88 | 25 | 25.00 | 25.00 | 1.5 | 1.49 | 1.49 | 2 | 2.00 | 2.00 |
| 15.25 | 15.32 | 15.33 | 25 | 25.00 | 25.00 | 1.5 | 1.41 | 1.42 | 2 | 1.83 | 1.84 | |
| S5 sphere | 10 | 10.01 | 10.02 | 10 | 10.03 | 10.03 | 2 | 1.97 | 1.95 | 3 | 2.92 | 2.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Shu, Q.; Gao, W.; Luo, Y.; Li, Z.; Yang, J.; Xu, W. Automatic Interpretation of Potential Field Data Based on Euler Deconvolution with Linear Background. Appl. Sci. 2023, 13, 5323. https://doi.org/10.3390/app13095323
Liu Q, Shu Q, Gao W, Luo Y, Li Z, Yang J, Xu W. Automatic Interpretation of Potential Field Data Based on Euler Deconvolution with Linear Background. Applied Sciences. 2023; 13(9):5323. https://doi.org/10.3390/app13095323
Chicago/Turabian StyleLiu, Qiang, Qing Shu, Wei Gao, Yao Luo, Zelin Li, Junjun Yang, and Wenqiang Xu. 2023. "Automatic Interpretation of Potential Field Data Based on Euler Deconvolution with Linear Background" Applied Sciences 13, no. 9: 5323. https://doi.org/10.3390/app13095323
APA StyleLiu, Q., Shu, Q., Gao, W., Luo, Y., Li, Z., Yang, J., & Xu, W. (2023). Automatic Interpretation of Potential Field Data Based on Euler Deconvolution with Linear Background. Applied Sciences, 13(9), 5323. https://doi.org/10.3390/app13095323






