Machine Learning for Short-Term Prediction of Ship Motion Combined with Wave Input
Abstract
1. Introduction
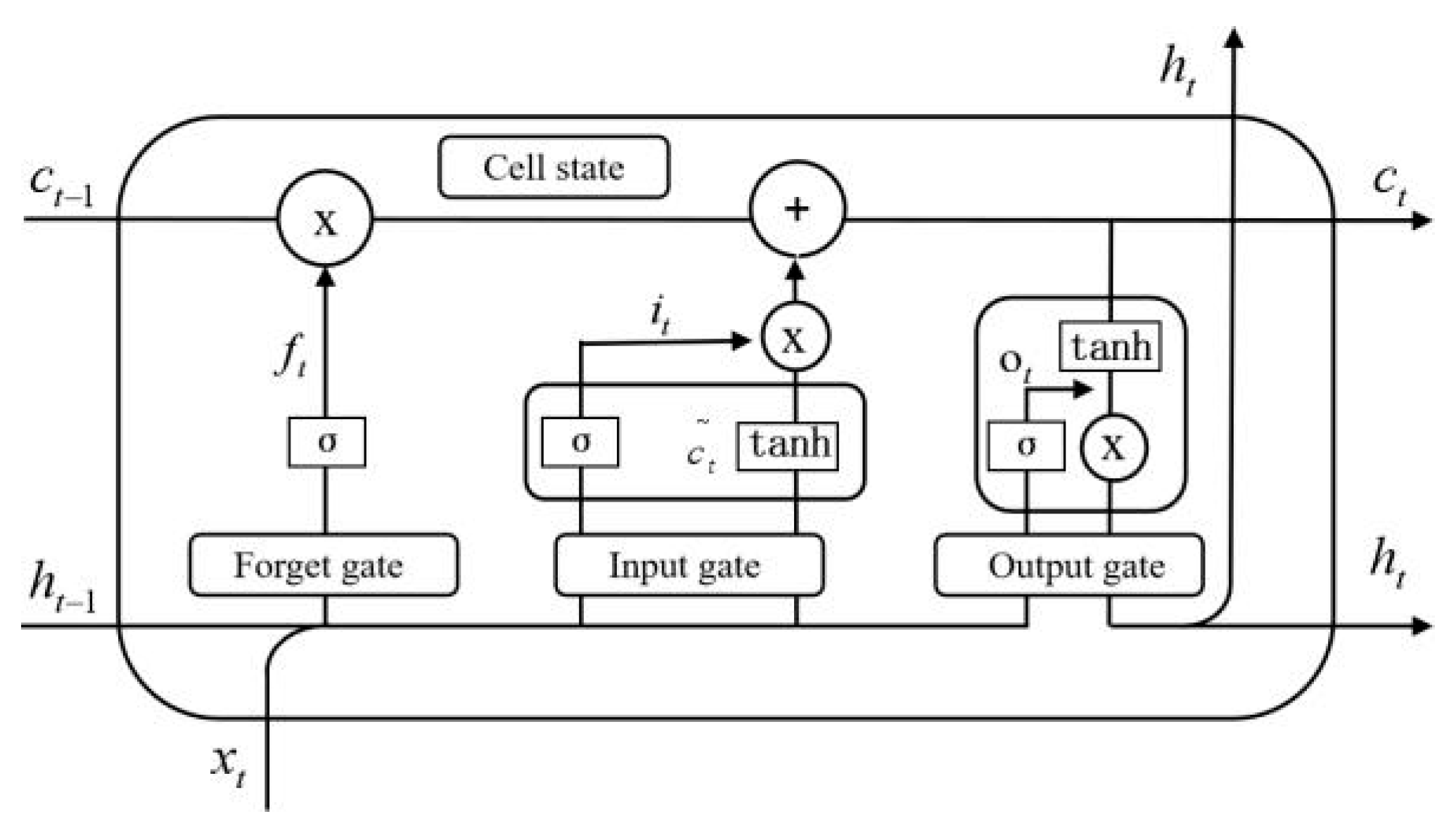
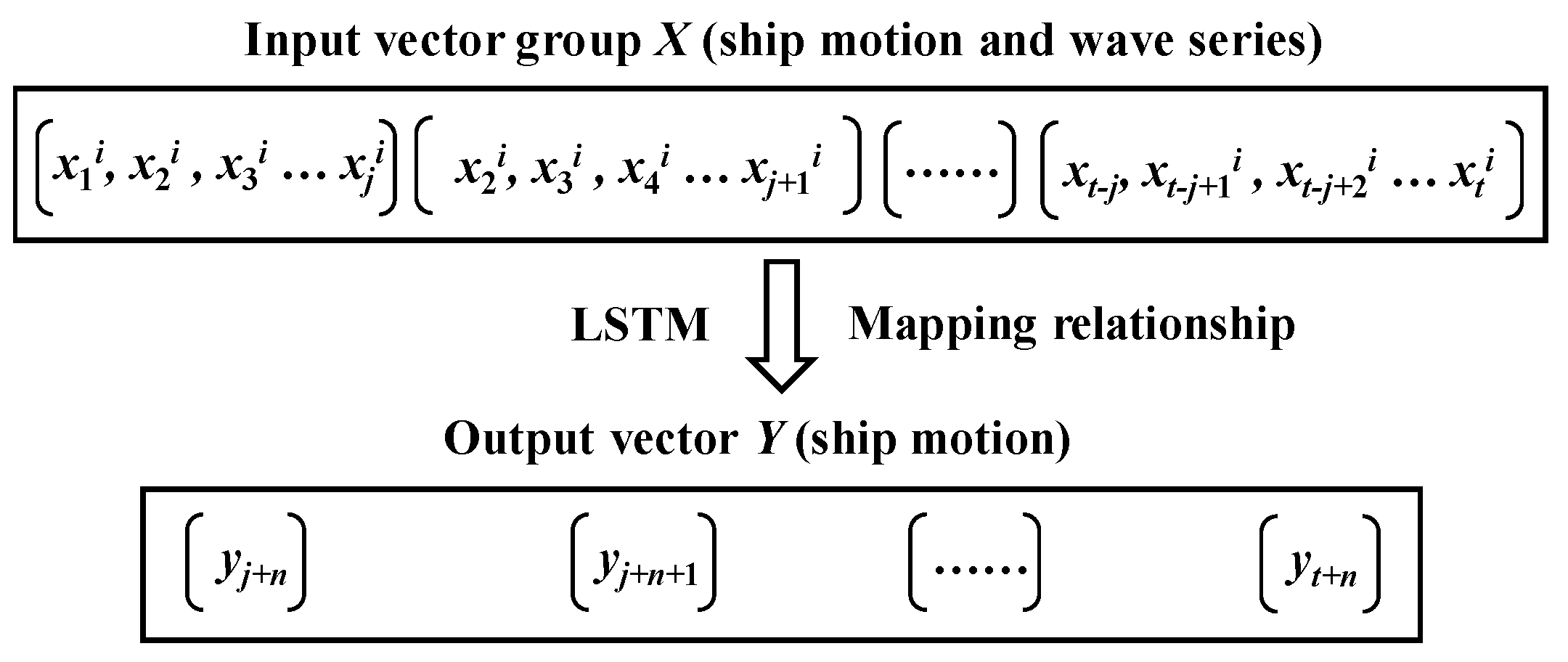
2. LSTM for Ship Motion Prediction
2.1. LSTM Theory
2.2. LSTM Theory
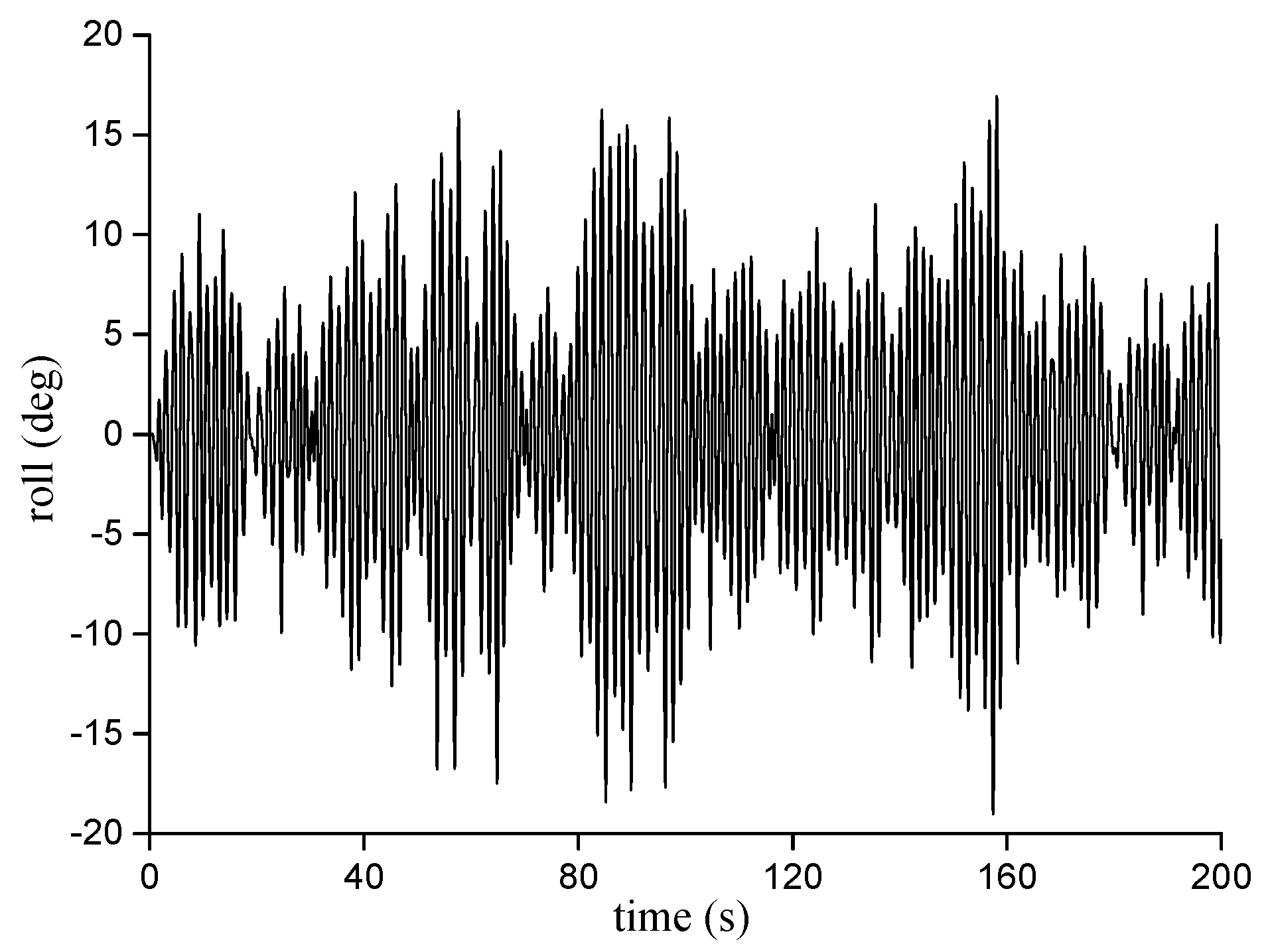
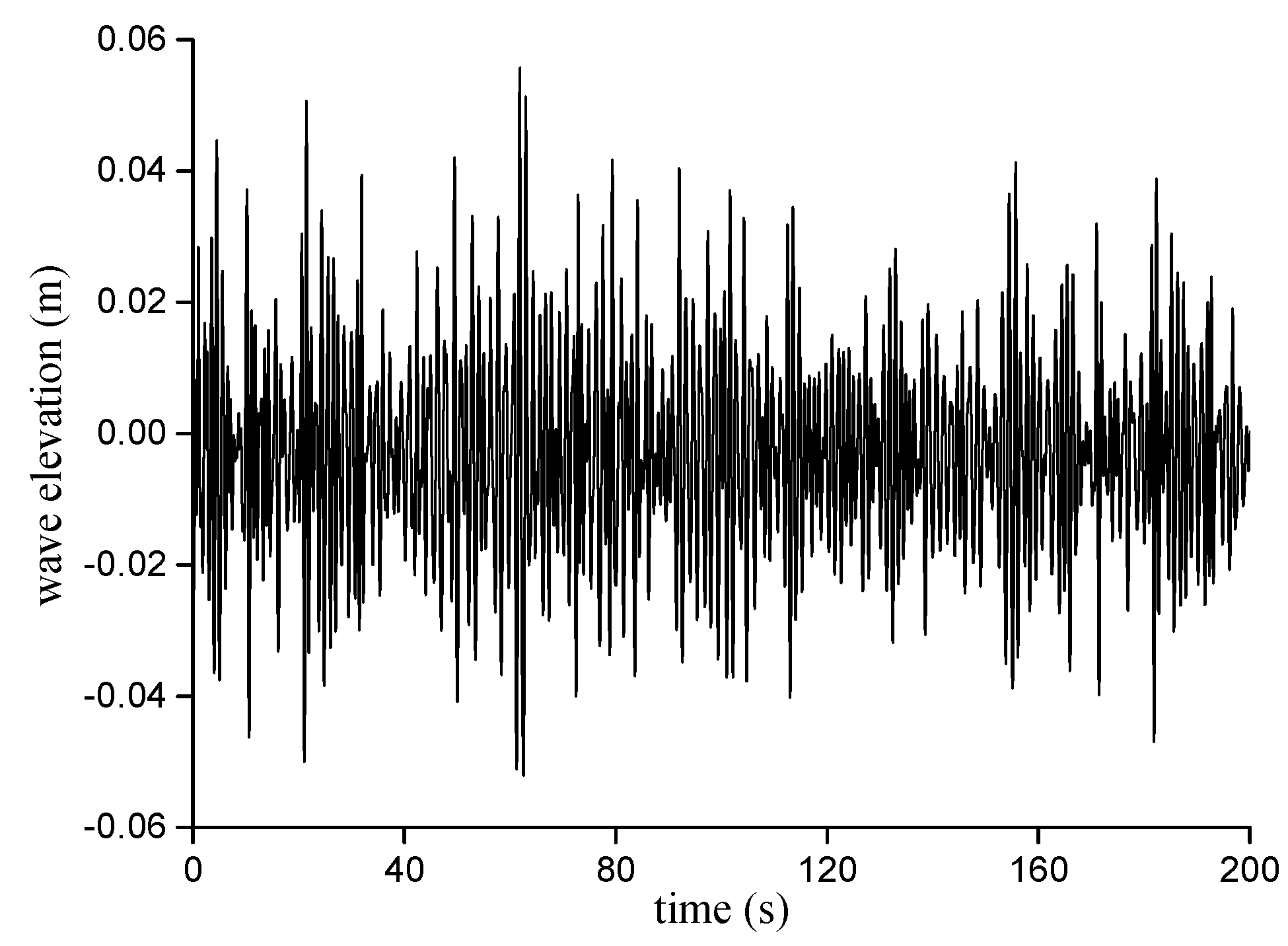
3. Ship Motion Data
4. Prediction based on LSTM
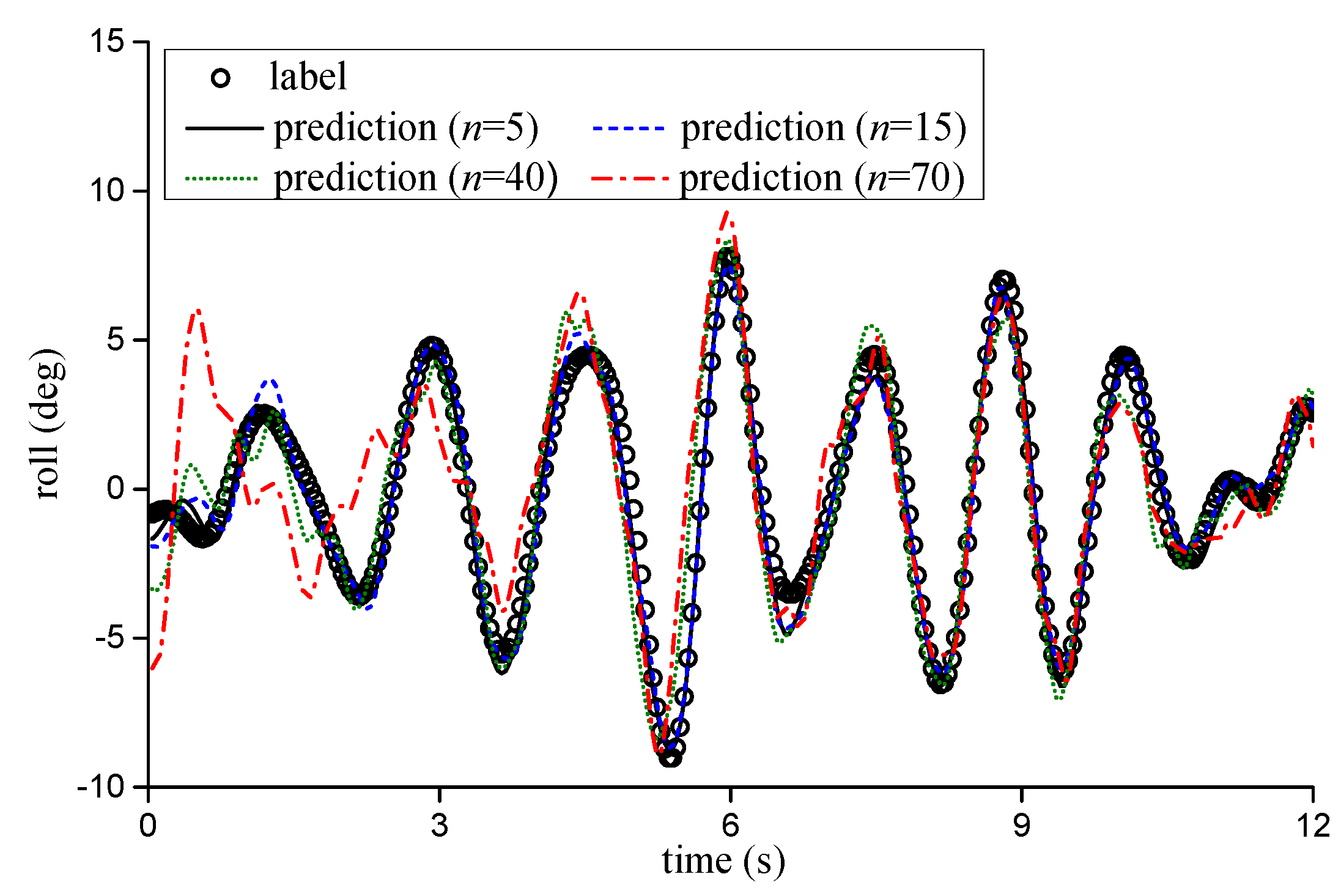
4.1. Prediction Solely Using Roll Data
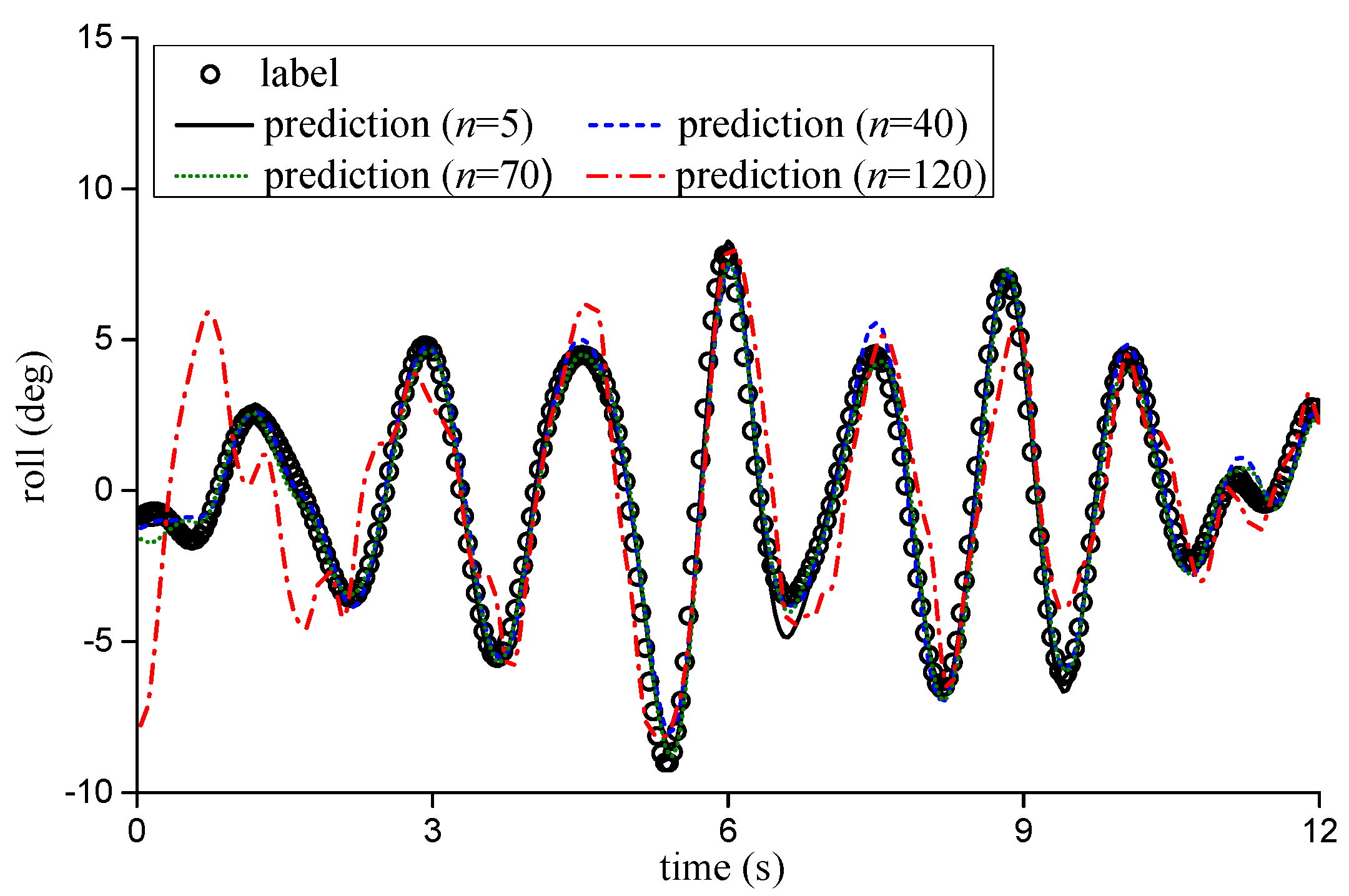
4.2. Prediction Combining with Single-Wave Data
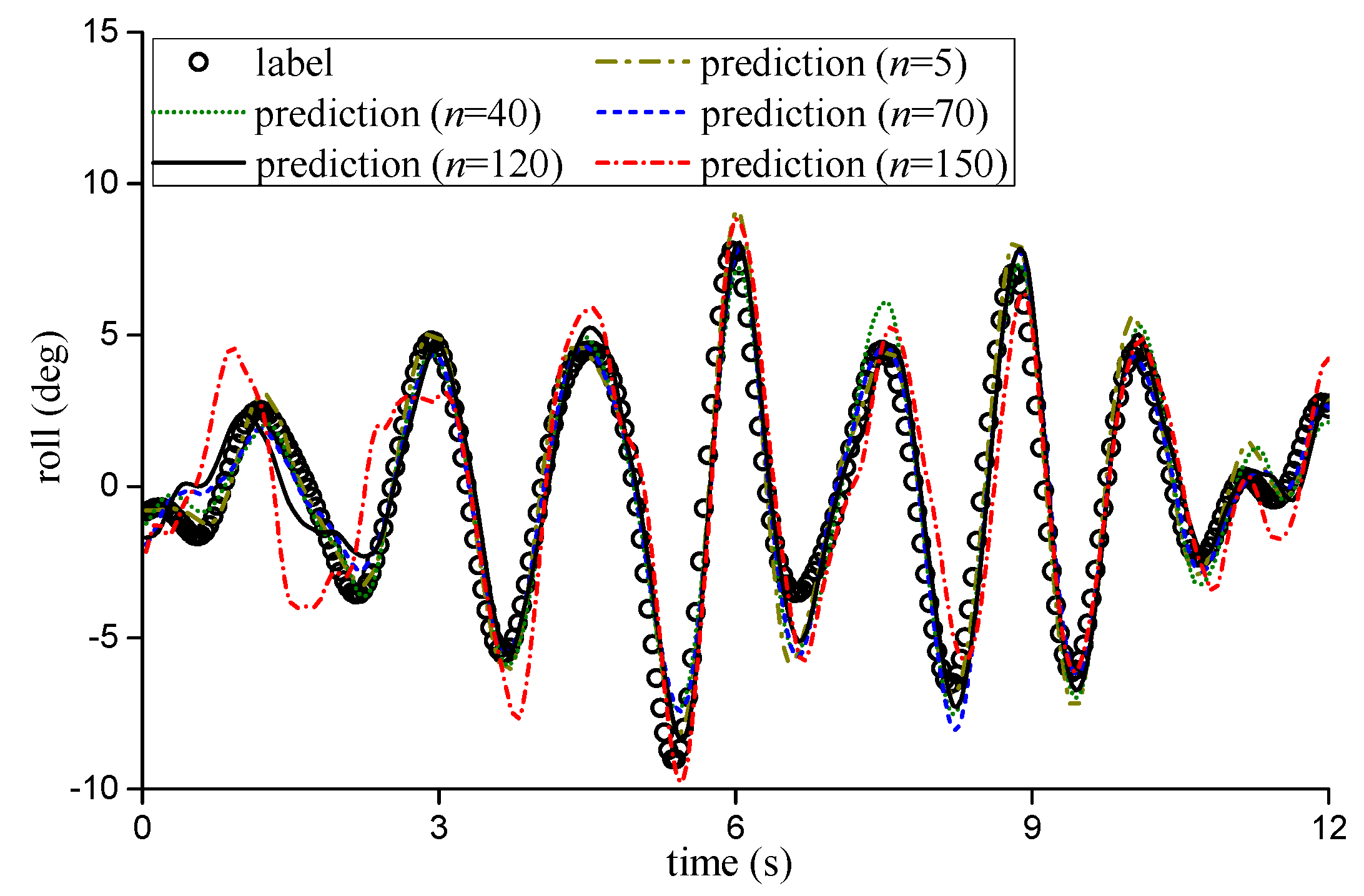
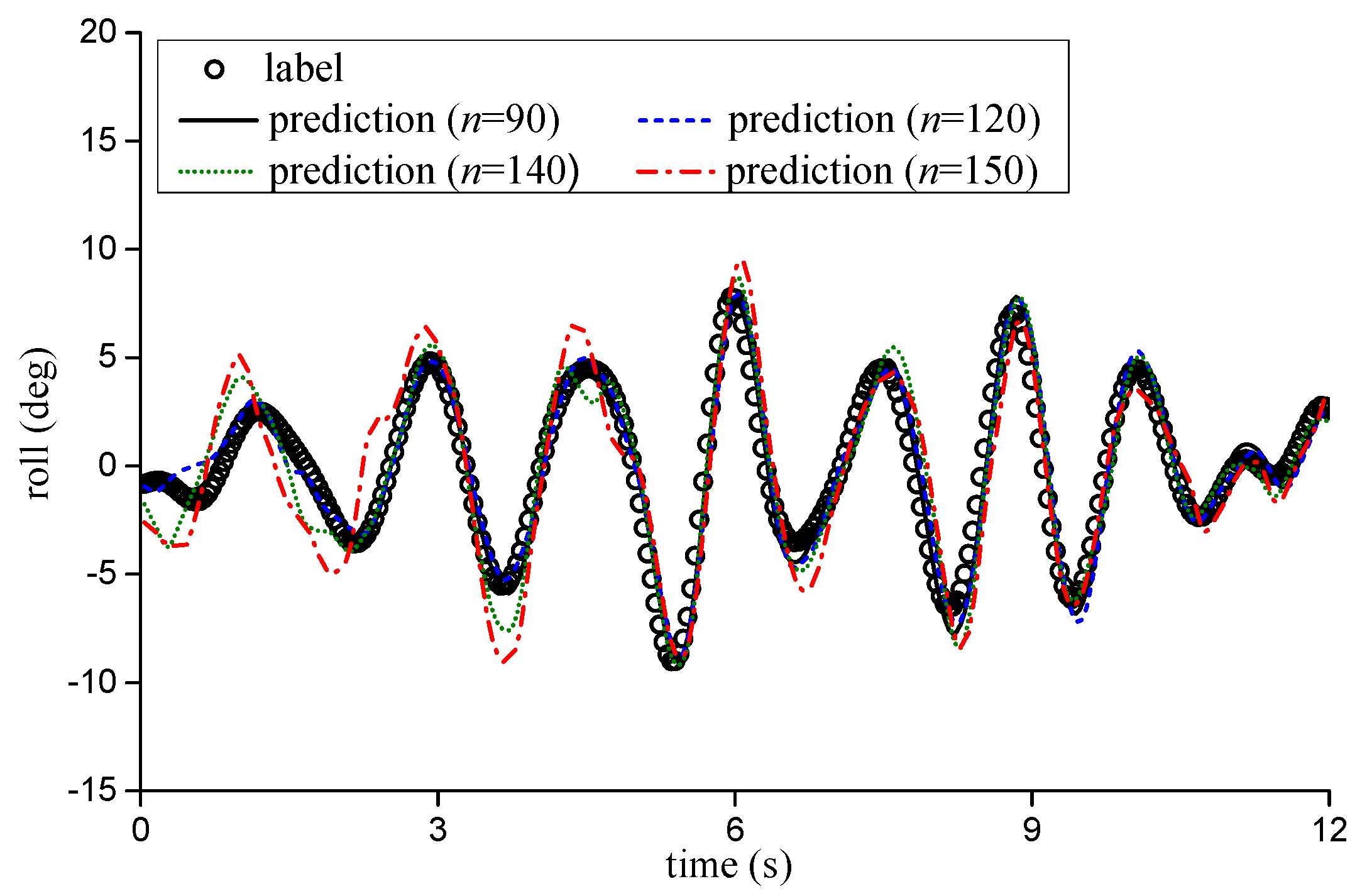
4.3. Prediction Combining with Multiple-Wave Data
5. Conclusions
- (1)
- Compared with the prediction results solely based on the roll data input, the roll motion prediction considering the wave elevation input greatly improves both the prediction accuracy and the advance prediction duration;
- (2)
- For single-wave data input, the LSTM model can mine the mapping relationship between the advance prediction duration and the distance of the wave height measurement points. The effective advance prediction time increases with the increase in the distance from the wave gauge to the ship;
- (3)
- Compared with the prediction results of the single-wave data input, the prediction of the multiple-wave data input has better stability for different advance times. As the amount of data increases, the overall advance prediction duration of the LSTM model improves, and the model also has better robustness for larger advance prediction durations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Triantafyllou, M.; Bodson, M.; Athans, M. Real time estimation of motions of a destroyer using Kalman filtering techniques. IEEE J. Ocean. Eng. 1983, 8, 9–20. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, R.; Kwan, C. Ship-motion prediction: Algorithms and simulation results. In Proceedings of the IEEE International Conference on Acoustics, Montreal, QC, Canada, 17–21 May 2004; IEEE: New York, NY, USA; Volume 5, pp. 125–128. [Google Scholar]
- Li, G.; Kawan, B.; Wang, H.; Zhang, H. Neural-network-based modelling and analysis for time series prediction of ship motion. Ship Technol. Res. 2017, 64, 30–39. [Google Scholar] [CrossRef]
- Suhermi, N.; Prastyo, D.D.; Ali, B. Roll motion prediction using a hybrid deep learning and ARIMA model. Procedia Comput. Sci. 2018, 144, 251–258. [Google Scholar] [CrossRef]
- Duan, W.Y.; Huang, L.; Yang, H.; Wang, R. IRF-AR model for short-term prediction of ship motion. In Proceedings of the Twenty-Fifth International Offshore and Polar Engineering Conference, Hawaii, HI, USA, 21–26 June 2015. ISOPE-I-15-584. [Google Scholar]
- Yin, J.C.; Perakis, A.N.; Wang, N. A real-time ship roll motion prediction using wavelet transform and variable RBF network. Ocean. Eng. 2018, 160, 10–19. [Google Scholar] [CrossRef]
- Li, M.; Geng, J.; Hong, W. Periodogram estimation based on LSSVR-CCPSO compensation for forecasting ship motion. Nonlinear Dyn. 2019, 97, 2579–2594. [Google Scholar] [CrossRef]
- Duan, W.; Huang, L.; Han, Y. A hybrid AR-EMD-SVR model for the short-term prediction of nonlinear and non-stationary ship motion. J. Zhejiang Univ. Sci. A 2015, 16, 562–576. [Google Scholar] [CrossRef]
- Shen, Y. On the Neural Network Theory and its Application in Ship Motion Prediction. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2005. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Han, B.; Sun, W. Short-term prediction of ship motion based on LSTM. Ship Sci. Technol. 2017, 39, 69–72. [Google Scholar]
- D’Agostino, D.; Serani, A.; Stern, F.; Diez, M. Recurrent-type neural networks for real-time short-term prediction of ship motions in high sea state. arXiv 2021, arXiv:2105.1310. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, P.; Peng, Y.; Liu, D. Roll motion prediction of unmanned surface vehicle based on coupled CNN and LSTM. Future Internet 2019, 11, 243. [Google Scholar] [CrossRef]
- Zhang, B.; Peng, X.; Gao, J. Ship motion attitude prediction based on ELM-EMD-LSTM integrated model. J. Ship Mech. 2020, 24, 1413–1421. [Google Scholar]
- Peng, X.; Zhang, B.; Zhou, H. An improved particle swarm optimization algorithm applied to long short-term memory neural network for ship motion attitude prediction. Trans. Inst. Meas. Control 2019, 41, 4462–4471. [Google Scholar] [CrossRef]
- Geng, X.; Li, Y.; Sun, Q. A Novel Short-Term Ship Motion Prediction Algorithm Based on EMD and Adaptive PSO–LSTM with the Sliding Window Approach. J. Mar. Sci. Eng. 2023, 11, 466. [Google Scholar] [CrossRef]
- Zhang, T.; Zheng, X.; Liu, M. Multiscale attention-based LSTM for ship motion prediction. Ocean. Eng. 2021, 230, 109066. [Google Scholar] [CrossRef]
- Sun, Q.; Tang, Z.; Gao, J.; Zhang, G. Short-term ship motion attitude prediction based on LSTM and GPR. Appl. Ocean. Res. 2022, 118, 102927. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Zou, D.; Fu, H. Ship roll prediction algorithm based on Bi-LSTM-TPA combined model. J. Mar. Sci. Eng. 2021, 9, 387. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Zhou, B.; Fu, H. Multi-dimensional prediction method based on Bi-LSTMC for ship roll. Ocean. Eng. 2021, 242, 110106. [Google Scholar] [CrossRef]
- Tang, G.; Lei, J.; Shao, C.; Hu, X.; Cao, W.; Men, S. Short-term prediction in vessel heave motion based on improved LSTM model. IEEE Access 2021, 9, 58067–58078. [Google Scholar] [CrossRef]



| Model | Input | Reference |
|---|---|---|
| KF | sway | Triantafyllou and Bodson (1982) [1] |
| MCA | 6-DoF motion | Zhao et al. (2004) [2] |
| NARX | state attribute | Li et al. (2017) [3] |
| DNN-AR | roll | Suhermi et al. (2018) [4] |
| IRF-AR | heave, pitch | Duan et al. (2015) [5] |
| DWT-RBF | roll | Yin et al. (2018) [6] |
| SVR-PSO | roll | Li and Hong (2019) [7] |
| AR-EMD-SVR | heave, pitch | Duan et al. (2015) [8] |
| RNN | 6-DoF motion | Shen (2005) [9] |
| LSTM | roll, pitch | Wang et al. (2017) [11] |
| GRU | state attribute | D’Agostino et al. (2021) [12] |
| CNN-LSTM | roll | Zhang et al. (2019) [13] |
| EMD-LSTM | motion | Zhang et al. (2020) [14] |
| PSO-EMD-LSTM | roll, pitch, heave | Peng et al. (2019) [15] |
| EMD-PSO-LSTM | roll, pitch | Geng et al. (2023) [16] |
| AM-LSTM | 6-DoF motion | Zhang et al. (2021) [17] |
| LSTM-GPR | roll, pitch | Sun et al. (2022) [18] |
| BLSTM-TPA | roll | Wang et al. (2021) [19] |
| MISO-BLSTM-TPA | roll | Wang et al. (2021) [20] |
| Parameter | Full Scale | Model Scale (1/51) |
|---|---|---|
| Water line (m) | 142.18 | 2.79 |
| Breadth (m) | 19.06 | 0.37 |
| Draft (m) | 6.15 | 0.12 |
| Displacement (m3) | 8424 | 0.0635 |
| Advance Prediction Step | Model Scale | Full Scale | Prediction Error (deg) | |
|---|---|---|---|---|
| RMSE | MAE | |||
| 5 | 0.2 s | 1.4 s | 0.43 | 1.41 |
| 10 | 0.4 s | 2.9 s | 0.54 | 1.53 |
| 15 | 0.6 s | 4.3 s | 0.57 | 1.58 |
| 20 | 0.8 s | 5.7 s | 0.81 | 3.12 |
| 30 | 1.2 s | 8.6 s | 1.31 | 3.48 |
| 40 | 1.6 s | 11.4 s | 1.36 | 4.29 |
| 50 | 2.0 s | 14.3 s | 1.51 | 4.35 |
| 60 | 2.4 s | 17.1 s | 1.57 | 4.48 |
| 70 | 2.8 s | 20.0 s | 2.22 | 7.60 |
| Advance Prediction Step | No Wave Data | 1 m from Ship | 3 m from Ship | 5 m from Ship | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| 5 | 0.43 | 1.41 | 0.28 | 0.98 | 0.44 | 1.39 | 0.79 | 2.48 |
| 10 | 0.54 | 1.53 | 0.25 | 0.98 | 0.51 | 1.58 | 0.84 | 2.84 |
| 15 | 0.57 | 1.58 | 0.26 | 0.90 | 0.50 | 1.58 | 0.86 | 2.94 |
| 20 | 0.81 | 3.12 | 0.27 | 0.77 | 0.56 | 1.64 | 1.04 | 3.10 |
| 30 | 1.31 | 3.48 | 0.35 | 1.01 | 0.53 | 1.92 | 0.87 | 2.55 |
| 40 | 1.36 | 4.29 | 0.50 | 1.29 | 0.53 | 1.63 | 0.90 | 2.20 |
| 50 | 1.51 | 4.35 | 1.02 | 3.20 | 0.55 | 1.80 | 0.85 | 2.22 |
| 60 | 1.57 | 4.48 | 1.24 | 3.69 | 0.56 | 1.67 | 0.94 | 2.71 |
| 70 | 2.22 | 7.60 | 1.85 | 3.90 | 0.57 | 1.72 | 0.91 | 2.25 |
| 80 | — | — | — | — | 0.66 | 1.91 | 0.96 | 2.59 |
| 90 | — | — | — | — | 0.94 | 2.43 | 0.92 | 2.47 |
| 100 | — | — | — | — | 1.13 | 3.27 | 0.98 | 2.70 |
| 110 | — | — | — | — | 1.69 | 5.67 | 1.00 | 2.47 |
| 120 | — | — | — | — | 2.19 | 7.02 | 1.06 | 2.24 |
| 130 | — | — | — | — | — | — | 1.23 | 3.13 |
| 140 | — | — | — | — | — | — | 1.40 | 3.58 |
| 150 | — | — | — | — | — | — | 1.94 | 5.03 |
| 160 | — | — | — | — | — | — | 2.58 | 7.30 |
| Advance Prediction Step | 1 m and 3 m from Ship | 3 m and 5 m from Ship | 1 m, 3 m and 5 m from Ship | |||
|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| 5 | 0.29 | 0.97 | 0.42 | 1.17 | 0.32 | 1.12 |
| 10 | 0.29 | 0.88 | 0.48 | 1.45 | 0.40 | 1.38 |
| 15 | 0.32 | 1.15 | 0.49 | 1.65 | 0.30 | 1.01 |
| 20 | 0.37 | 1.28 | 0.51 | 1.55 | 0.32 | 0.92 |
| 30 | 0.38 | 1.18 | 0.54 | 1.37 | 0.39 | 1.20 |
| 40 | 0.45 | 1.16 | 0.60 | 1.52 | 0.47 | 1.46 |
| 50 | 0.56 | 1.57 | 0.60 | 1.60 | 0.56 | 1.59 |
| 60 | 0.54 | 1.69 | 0.66 | 1.89 | 0.60 | 1.66 |
| 70 | 0.60 | 1.65 | 0.63 | 1.86 | 0.61 | 1.82 |
| 80 | 0.71 | 2.32 | 0.68 | 1.93 | 0.62 | 1.60 |
| 90 | 0.96 | 2.94 | 0.69 | 2.04 | 0.65 | 1.85 |
| 100 | 1.27 | 3.73 | 0.79 | 2.06 | 0.78 | 2.05 |
| 110 | 1.65 | 4.29 | 0.93 | 2.51 | 0.90 | 2.32 |
| 120 | 2.04 | 5.71 | 0.93 | 2.85 | 0.91 | 2.29 |
| 130 | — | — | 1.11 | 2.81 | 1.10 | 2.36 |
| 140 | — | — | 1.30 | 2.97 | 1.23 | 2.54 |
| 150 | — | — | 1.93 | 4.55 | 1.92 | 4.27 |
| 160 | — | — | 2.37 | 6.08 | 2.30 | 5.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Song, Y. Machine Learning for Short-Term Prediction of Ship Motion Combined with Wave Input. Appl. Sci. 2023, 13, 5298. https://doi.org/10.3390/app13095298
Tian X, Song Y. Machine Learning for Short-Term Prediction of Ship Motion Combined with Wave Input. Applied Sciences. 2023; 13(9):5298. https://doi.org/10.3390/app13095298
Chicago/Turabian StyleTian, Ximin, and Yang Song. 2023. "Machine Learning for Short-Term Prediction of Ship Motion Combined with Wave Input" Applied Sciences 13, no. 9: 5298. https://doi.org/10.3390/app13095298
APA StyleTian, X., & Song, Y. (2023). Machine Learning for Short-Term Prediction of Ship Motion Combined with Wave Input. Applied Sciences, 13(9), 5298. https://doi.org/10.3390/app13095298





