Featured Application
Different BIVA modalities create new opportunities to improve the study of body composition in athletes and their sport performance.
Abstract
Body composition (BC) determines strength, power, and agility in sports such as rugby. Not only is the study of morphology and BC essential to establish player positions, but it also allows the optimisation of competitive performance. The aim of this study was to analyse different BC models (anthropometry and bioelectrical impedance analysis (BIA)) in a female rugby team. Their somatotype was also compared with a bioelectrical impedance vector analysis (BIVA) graph. A cross-sectional study was carried out on 19 women (8 forwards and 11 backs). Anthropometric and BIA (50 kHz, tetrapolar electrode configuration) measurements were taken using standard protocols and BC was estimated. Somatotype was calculated using the Heath–Carter method. Classic and specific BIVA were applied. Student’s t, Mann–Whitney, or Chi-squared tests were used for variable comparisons. Agreement was determined via intraclass coefficient correlations. Forwards showed a higher BMI and fat mass, but there were no differences in skeletal muscle masses. Most of the players were of an endomorphic mesomorph somatotype. Specific BIVA, but not classic BIVA, detected BC differences according to player position. Moreover, an individual’s interpretation of BIVA was consistent with their somatotype. In a female rugby team, BC and morphology are different according to position. This was detected in both the somatotype and specific BIVA. The application of BIVA (classic and specific) may yet prove to be a very useful strategy for the study of BC in sports.
1. Introduction
Rugby is a field-based team sport that requires qualities such as endurance, speed, agility, power, and flexibility [1,2,3]. Similar to other team sports, some of a player’s abilities will predominate depending on their position in the field. Thus, in rugby players, it is essential to establish their positions as accurately as possible and design training strategies to optimise a player’s competitive performance. Currently, body composition (BC) is considered a determinant of athletic performance [4]. Therefore, a BC assessment, in addition to anthropometric characteristics and somatotype, helps to (1) select the athlete, (2) determine their playing position, and (3) optimise both the personal and team performance [1,2,3]. Over the last few years, the number of studies on athletes’ anthropometric characteristics, BC, and somatotype has increased. Moreover, specific profiles have been proposed as reference models for many sports [5]. However, there are few studies focused on rugby, especially female rugby.
Body composition can be determined at different levels and by applying various models and methods [6]. Firstly, an assessment settling a level and a model is recommended, and then one can estimate each body component by using the corresponding reference technique [7,8]. Reference techniques are expensive, require a qualified technician, present potential side effects, and are not suitable for use in “on-site work”. Thus, daily sport practice requires simple, fast, inexpensive, non-invasive, and accurate methods for the study of BC.
The most widely used method for BC assessment in sport is anthropometry [9]. Although this technique is commonly accepted in sports, it has low precision and requires a certain measurement time and a well-trained anthropometrist. Moreover, it does not detect changes in both BC and the hydration state on a short-term basis (before and after competition, during a sport season, etc.) [10]. It has been demonstrated that using specific predictive equations for athletes increases the accuracy of this method [11]. Additionally, this technique allows the identification of the athlete’s morphological conformation using the somatotype calculated by the Heath–Carter method [12].
Bioelectrical impedance analysis (BIA) is a fast, safe, accurate, and non-invasive indirect technique for estimating BC, and its use is increasing in both clinical and sport practice. This method determines the opposition of a tissue to an alternating current with very low intensity and a specific frequency [13]. Single-frequency BIA (SF-BIA) or conventional BIA at 50 kHz is the most used modality of BIA for BC assessment. It presupposes (1) a two-compartment model of BC; (2) non-hydration alterations [14,15,16]; and (3) as in anthropometry, the use of predictive equations is required to quantify body volumes (fat free mass (FFM) and total body water (TBW)). These predictive models should be developed in a similar population to the studied one (in terms of sex, age, race, physiological situation, pathology, etc.). Nowadays, the study of raw electrical values of BIA at 50 kHz, such as the bioelectrical impedance vector analysis (BIVA) [17] and phase angle (PA) (quantified as the arctangent of reactance (Xc)/resistance (R)), has been encouraged to avoid a dependency on mathematical models to quantify body volumes [15,18].
The BIVA (classic BIVA) is a semiquantitative analysis method that also allows the determination of changes in body fluids, hydration status, and body cell mass. It is based on the analysis of the impedance vectors, normalised to standing height (R/H and Xc/H). These vectors are represented in an RXc graph (in terms of age, race, and sex), which is made up of three concentric ellipses corresponding to the 50th, 75th, and 95th percentiles of the normal distribution of the values of the reference population (tolerance ellipses) [19]. Vector displacements parallel to the major axis of tolerance ellipses indicate changes in hydration status, dehydration with long vectors, and hyperhydration with short vectors, while vector displacements parallel to the short axis indicate changes in body cell mass and in the relationship between extracellular water (ECW)/intracellular water (ICW) [18,19]. The classic BIVA does not make assumptions about body compartments, body mass, geometry, or hydration, nor is it subject to the error sources of other modalities of BIA.
Recently, a new variation of BIVA has been developed that adjusts the individual values of R and Xc for cross-sectional areas to reduce the effect of body dimensions: the specific BIVA (BIVA-sp) [20]. In BIVA-sp, vector displacements parallel to the major axis of tolerance ellipses indicate changes in FM% (higher FM% with larger vectors); the interpretation of vector displacements parallel to the short axis (changes in PA) is the same as in the classic BIVA [21]. This method has demonstrated higher precision in FM% estimation and the ECW/ICW relationship than the classic BIVA in adults [20] and elderly adults [22].
Many studies on the application of different BIA modalities to monitor BC and hydration in sports have recently been published [23,24,25]. Given that the bioelectrical behaviour of athletes differs from the general population, specific models for BC estimation and reference tolerance ellipses have been created for them. Moreover, depending on the sport, differences in BIVA patterns between athletes have been found, which some authors suggest could be explained by the differences in their somatotype [26].
Considering that rugby players present important differences in BC according to player position [1], the BIVA (both classic and specific) could be useful for the monitoring of BC. Although BIA has proven to be a useful and fast technique, anthropometry is still the most used method for BC studies due to its affordability.
Therefore, the aim of this study was to analyse different models, based on both anthropometry and BIA, for the study of BC in a female semi-professional rugby team of the Spanish National Rugby League. Players´ somatotypes and positions in the BIVA graph were also compared.
2. Materials and Methods
A cross-sectional observational study was carried out on a sample of 19 women from a rugby team of the sub-elite Spanish National Rugby League. Athletes were studied as a total sample and classified by the player’s position: forwards (n = 8) and backs (n = 11). The study was conducted according to the guidelines of the Declaration of Helsinki. Written informed consent was obtained from all volunteers that participated in the study. Approval was acquired from the Clinical Research Ethics Committee (CEIC) of Valladolid-East Health Area (protocol code: PI 16-512).
Anthropometric measurements were taken according to standard procedures of the International Society for the Advancement of Kinanthropometry (ISAK) [27]. An electronic scale and a stadiometer SECA (Hamburg, Germany) were used for body mass (kg; precision: 100 g) and height measurements (m; precision: 0.1 cm). Body circumferences were determined with a flexible and non-extendible steel tape (to the nearest 1 cm). Skinfolds thicknesses (tricipital, bicipital, abdominal, suprailiac, subscapular, supraspinale, front thigh, and calf) were measured using a Holtain (Crymmych, UK) skinfold calliper (precision: 0.2 mm). Somatotype was calculated by the Heath–Carter method [12]. BMI was calculated and it was catalogued applying the cut-off points of the WHO [28]. Based on the Spanish Sports Medicine (Federación Española de Medicina del Deporte) guidelines [9], the equations applied to estimate BC components were (1) fat mass percentage (FM%) using the Yuhasz and Carter model [29], (2) bone mass (kg) using the Rocha model [30], (3) residual mass (kg) using the Würch model [31], and (4) skeletal muscle mass (SMM, kg) using the Lee model [32]. Reference values for national sport populations were used to analyse anthropometric and BC results [33].
Whole body BIA was conducted in the mono-frequency mode (at 50 kHz, 400 μARMS) using a tetrapolar electrode configuration, with a BIA 101 AKERN-Srl bioimpedance measuring device (Florence, Italy). Measurement errors of the system, determined with a precision resistor and capacitor, were <1% for R and <2% for capacitance. R and Xc were measured using a standard protocol [34] and specific procedures for athletes [24]. FFM (kg) was estimated using the BIA equation developed by Matias et al. for athletes [35]. Fat mass (FM, kg) was calculated as the difference between body mass and FFM. SMM (kg) was calculated by Janssen et al.’s formula [36].
For the classic BIVA, the components of the impedance vector (R and Xc) were standardised by the heights of the subjects (R/H (ohm/m) and Xc/H (ohm/m), respectively) and were represented on an R-Xc graph (abscissa axis: R/H; ordinate axis: Xc/H). The PA (degrees) was calculated as arc tangent (Xc/R). Individual impedance vectors were compared with the vector distribution from Campa et al.’s reference sports population (tolerance ellipses at 50%, 75%, and 95%) [37]. For the BIVA-sp approach, R and Xc were corrected by multiplying by A/L (Rsp and Xcsp), where A is the cross-sectional area (m2) estimated as 0.45 upper arm area + 0.10 waist area + 0.45 calf area, and L is the height multiplied by 1.1 (m). The segment areas were calculated as C2/4π, where C (m) is the circumference of the upper arm, waist, or calf. The length of the vector (Zsp) was calculated as (Rsp2 + Xcsp2)0.5. Specific values were rescaled by a factor of 100 [20]. Individual specific impedance vectors were compared with the vector distribution from the reference sports population (tolerance ellipses at 50%, 75%, and 95%) [38]. Finally, to compare the subgroups, the 95% confidence ellipses for mean vectors of the groups (classic and specific BIVA) were drawn.
Variables were described as means (SD) or medians (25th–75th percentiles). The normality of the distribution of the variables was checked by the Kolmogorov–Smirnov or the Shapiro–Wilk tests. Either Student t or Mann–Whitney U tests were used for pairwise comparisons. The categorical variables were compared using a Chi-squared test. Agreement was determined by the intraclass coefficient correlation (ICC) (95% CI). Vector analyses were performed with BIVA software developed and provided by A. Piccoli, BIVA Programs, 2002 release [39]. Statistically significant differences between the mean vectors were assessed with the Hotelling’s T2 test for vector analysis, and distance between groups was assessed with the Mahalanobis distance. Significance was reached at p < 0.05. The statistical analysis was performed using IBM SPSS Statistics 20.0 for Windows software.
3. Results
The sample was formed by 19 women with an average age of 24.7 years (SD: 5.9; range: 15.2 to 37.4). Considering the players positions in the field, eight subjects were forwards and eleven were backs. The mean BMI of the athletes was 26.03 kg/m2 (6.2) and was statistically significantly higher for the forwards (31.14 kg/m2 (6.1)) compared to the backs (22.32 kg/m2 (2.7)) (p = 0.004). The BMI cut-off points of the WHO show that one player (back) was underweight, ten were normal weight (one forward and nine backs), four were overweight (three forwards and one back), and four forwards presented obesity. There were statistically significant differences between forwards and backs (p = 0.007).
Table 1 shows the anthropometric characteristics and BC measurements. Forwards presented a statistically significant higher FM and residual mass versus the backs. No statistically significant differences in SMM nor in bone mass were found.

Table 1.
Anthropometric characteristics and BC measurements of rugby players (total sample and player’s position).
The FM% obtained by BIA was 26.5% (2.8): 28.7% (1.9) for forwards and 24.8% (2.1) for backs. This difference was statistically significant (p = 0.001). The SMM estimated for the total sample was 24.14 kg (9.5): 24.8 kg (3.9) for forwards and 23.7 kg (2.5) for backs. This difference was not statistically significant (p = 0.447).
The agreement between BC estimation models, BIA and anthropometry, was also analysed. The results showed a moderate ICC for BIA-FM% (Matias et al.’s equation) and anthropometry-FM% (Yuhasz and Carter’s equation) (ICC 0.626 (CI 95%: 0.028–0.856; p = 0.022)). Agreement between SMM estimation models was excellent, with an ICC of 0.899 (CI 95%: 0.737–0.961; p < 0.001) by using the Janssen (BIA) and Lee (anthropometry) models.
Somatotype components for the total sample and players´ position are presented in Table 2. There were statistically significant differences between forward and back players for the values of ectomorphy, mesomorphy, and endomorphy.

Table 2.
Somatotype characteristics of rugby players (total sample and player’s position).
Endomorphy and mesomophy values of forwards were much higher than the reference for Spanish rugby players [33]; however, the ectomorphy value was notably smaller. Endomorphy and ectomorphy values of backs were higher than the reference values, but the mesomorph component was lower.
Figure 1 represents somatochart of the players. Figure 1a displays the total sample and the player´s position subgroups (forwards: blue dot and backs: orange dot). The total sample somatotype was catalogued as mesomorph endomorph, although there were major differences between somatotype components values of forwards and backs. Figure 1b shows the somatochart for each individual player.
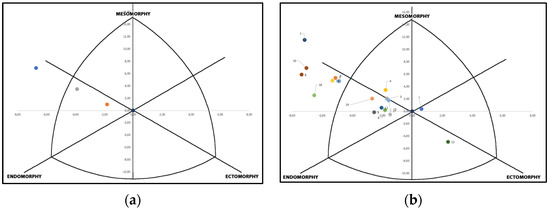
Figure 1.
Rugby players somatochart. (a) Total sample (grey dot), forwards (blue dot), and backs (orange dot); (b) Individual somatochart of the players.
Table 3 shows the raw electrical values from BIA. There were statistically significant differences between subgroups for the values of R, Z, PA, and the BIVA standardised variables for height and transverse areas (specific BIVA): Rsp, Xcsp, and Zsp.

Table 3.
Bioelectrical values of rugby players (total sample and player’s position).
The classic BIVA study showed an impedance individual vector distribution in the tolerance ellipses similar to the reference sports population (Figure 2).
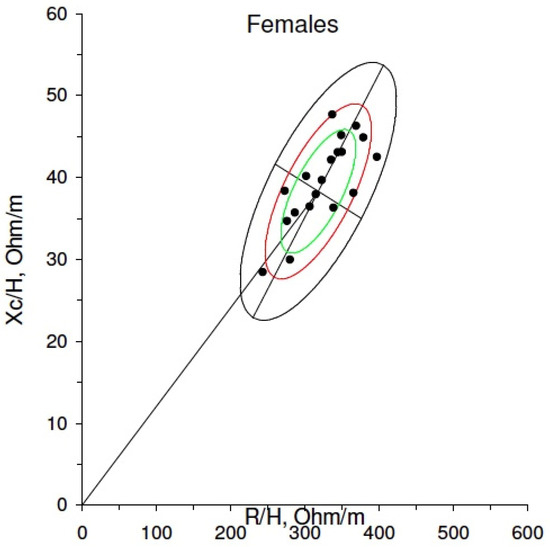
Figure 2.
Classic BIVA of studied rugby players vs. reference sports population. Green, red, and black ellipses are probability graphs showing the 50%, 75%, and 95% percentiles, respectively, of the bioelectrical values of the reference population.
Figure 3 shows the specific BIVA analysis. Some players are placed out of ellipses at 75% and even at 95% when the impedance individual vectors distribution in the tolerance ellipses for sports populations are performed.
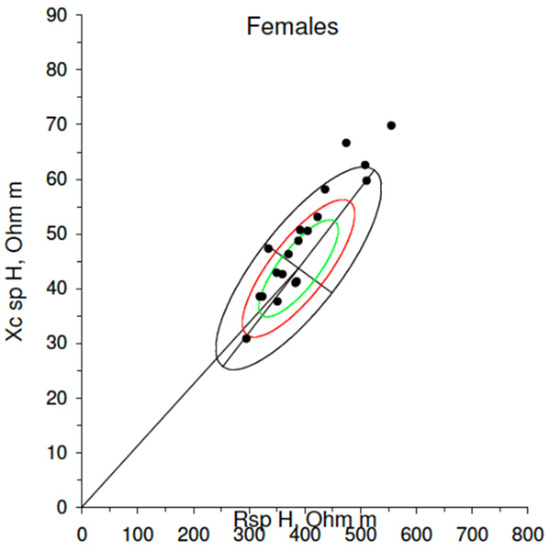
Figure 3.
Specific BIVA of studied rugby players vs. sports reference population. Green, red and black ellipses are probability graph showing the 50%, 75%, and 95% percentiles, respectively, of the bioelectrical values of the reference population.
Classic BIVA confidence ellipses did not show statistically significant differences in the mean impedance individual vector distribution between forwards and backs (p = 0.209) (Figure 4a). However, specific BIVA confidence ellipses showed statistically significant differences between both groups (p < 0.001) (Figure 4b).
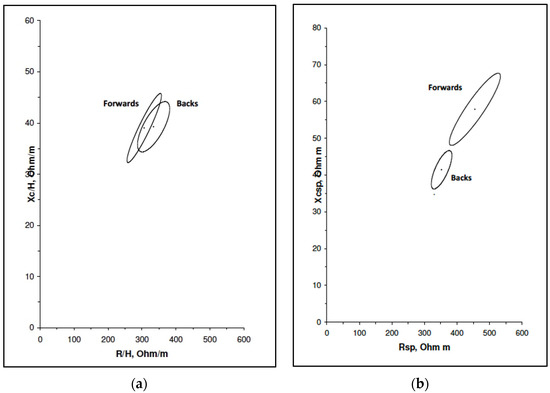
Figure 4.
(a) Classic BIVA confidence ellipses by player position; (b) Specific BIVA confidence ellipses by player position.
4. Discussion
The present study analysed the morphological characteristics and BC of a female sub-elite rugby team by two methods: anthropometry and BIA. Body mass and BC in rugby are directly related to the physical abilities of the players and their position in the field [2]. In this way, back players perform a greater amount of high speed running, involving a high heart rate, while forward players execute more medium speed running and moments with maximal demands of power and strength [40]. Given these physical demands, rugby players usually have a higher body mass and muscle mass than athletes of other sports such as soccer or hockey [2,41]. In the present study, statistically significant differences in body mass, BMI, and FM% were found depending on each player’s position; the forwards presented higher values of these variables than the backs (Table 1 and Table 2). These results are similar to other studies conducted on rugby players [1,42,43,44,45]. In forward players, a higher body mass and muscle mass give them more momentum and strength when making contact, more ability to soften the impacts, and more power in scrums or rucks [1,3]. Similarly, backs’ characteristics make them faster, more agile, and with greater relative strength than forwards, which allows them to better perform their functions on the field [46]. The BC characteristics of the Spanish sub-elite rugby players studied are very similar in BMI and FM% to other elite female rugby teams from South Africa [47] and England [46,48], despite the fact that the FM% of the Spaniards were lower.
In terms of somatotype, both backs and forwards were classified as mesomorph endomorph, with the endomorphy and mesomorphy components equally dominant for each position. Endomorphy represents relative adiposity, mesomorphy represents musculoskeletal robustness, and ectomorphy represents the relative linearity of the human body [12]. Although all the studied players were classified under the same terminology, statistically significant differences were found between positions, i.e., forwards vs. backs. These results agree with other studies conducted in Spanish rugby players; forwards were represented on the somatotype chart as endo-mesomorphic [45] or meso-endomorphs [49], and backs as mesomorphic–endomorphic [45] or balanced endomorphs [49].
In the present study, agreement between anthropometry and BIA for FM estimation by using predictive equations developed in athletes was moderate (ICC = 0.626; CI 95%: 0.028–0.856). The anthropometric Yuhasz equation is widely applied to athletes and several studies have proven its reliability [9]. However, rugby players present a very different BC than other athletes, having a higher FM% and a distribution of FM not exclusively or mostly at subcutaneous level, but widespread through other parts of the body [2]. Taking into account that the Yuhasz model is based on the summatory of six skinfolds, it could not estimate accurately the BC of ruby players. Considering the BIA, the need for further development of BIA equations for athletes from different sports has become apparent [24,35]; thus, we selected the equation of Matias et al. because it is the only one specific for sports populations [35]. This predictive model was developed and validated in an athlete sample of 142 subjects (105 males and 37 females) from various individual and team sports, including rugby. Ramos et al. recently analysed BC in a group of both male and female rugby players [45]. This study regarded anthropometry to be better than BIA for BC estimation. However, the authors used the BC values provided by the commercial BIA device, even though this is not recommended due to the lack of information offered about the equation applied [13,24,50,51]. This is possibly the reason why Ramos Álvarez et al. demonstrated a reduced agreement due to the use of an inadequate equation for their population rather than the inaccuracy of the method [45].
Conventional BIA requires mathematical models to estimate body compartments [15], which has promoted the development of the BIVA modality and the interpretation of raw electrical variables, such as PA, to avoid this dependency. This modality does not assume considerations about body compartments, mass, geometry, or hydration, nor it is subjected to the error derived from regression models vs. reference techniques [18,19,50]. In our results, the study of raw electrical variables demonstrated a higher PA of the forwards (7.26°) vs. the backs (6.73°). Recently, the reference percentiles of PA for sports populations have been published by Campa et al. [52]. Considering these reference values for team sports, our players were situated between P50 and P85. The research group of Campa documented that PA differs in each sport, according to the player’s position, which is related to BC and morphological characteristics, especially in team sports [52]. The same group underlined that in male athletes from team sports, PA is positively related to the mesomorphy component and negatively related to the ectomorphy component of somatotype [53]. Although there is no study that evaluates the association between impedance vectors and somatotype in female athletes, similar results could be expected. The high PA of our players compared to other sports could be explained by the high mesomorph component in their somatotype. Prior studies have suggested that PA is positively related to muscle mass and negatively related to the ECW/ICW relationship [50,54]. PA is also related to cellular health and hydration and muscular mass and quality. Moreover, it is suggested that PA could be a useful indicator for the study of athletes during sport season, especially if they present a low PA, in order to (1) identify changes in BC, (2) evaluate fatigue and sport performance, and (3) design specific nutritional strategies [52,55]. However, a number of authors have reported that the study of PA in isolation could lead to misinterpretations of BC [37,54]. It has been observed that athletes with similar PAs could differ in TBW or FM%. Since classic BIVA assesses the impedance vectors and not just PA (vector slope), it could be more useful because it also takes into account the length of the vector, which shows TBW (longer vectors are related to a lower TBW) [21,54]. In this modality of BIVA, considering the reference values of individual impedance vector distributions for sports populations, the majority of the studied rugby players presented a similar bioelectrical behaviour to other athletes (Figure 2), despite not belonging to an elite team. There were only two players out of the ellipses at 75% (although within ellipses at 95%); one was in the right upper quadrant and the other in the left lower quadrant. The first one (number 9) is a back player with a BMI of 21.4 kg/m2. They presented a greater endomorphy component than the rest of the players, so it is possible that their morphology explains their position in the BIVA graph. The second one (number 7) is a forward player with a high BMI (37.5 kg/m2), which explains their BIVA graph position. These results agree with Campa et al.’s research, which documented that athletes with a high body mass could be placed in the lower area of the BIVA graph, independently of their morphology [53].
Classic BIVA did not detect differences in BC according to the player’s position, which is shown by both the individual impedance vector distribution (Figure 3) and the mean impedance vector distribution of each subgroup (confidence ellipses, Figure 4a). This was an expected result, given that Marini et al. [54] proved that classic BIVA detects differences in TBW but not in FM%. The two studied subgroups of players differ in fat mass but not in TBW, as is shown by the mean impedance vectors (Figure 4a) and the Z/H values (Table 3).
Body geometry is a factor that affects bioimpedance measurements [35]. That is why in BIVA-sp, a correction in R and Xc values for cross-sectional areas is made in order to reduce the differences related to size and body shape. This modality is more sensitive to the bioelectrical properties of the tissues and evaluates BC in a more reliable way [20]. In fact, BIVA-sp showed, in a statistically significant way, the BC differences between forwards and backs (Figure 4b). In forward players, as other authors have documented, the length of mean impedance vectors is higher than in backs, which indicates a higher FM% [21,54,56]. Most of the players presented a similar specific individual impedance vector distribution in the tolerance ellipses of BIVA-sp (Figure 3) compared to the reference values in sports populations. The vectors of five players were allocated out of the ellipses at 75%, within the left upper quadrant (players number 7, 10, 13, 18, and 19). These players (all forwards) registered the highest values for BMI and FM%; therefore, their position in the BIVA-sp graph agrees with other studies [57]. However, player number 9, who is placed in the right upper quadrant in the BIVA graph, is in the centre of the ellipse in the BIVA-sp graph, which shows the normality of her BC. Additionally, there is a player out of the ellipse at 75% within the right lower quadrant, with a reduced length of the Zsp vector (subject 12). She is a back player with a BMI of 18.0 kg/m2 and a low FM. Finally, the back player (number 15) was situated out of ellipse at 75%, in the left at the limit of upper and lower quadrants. She presented a BMI of 21.5 kg/m2 with a moderate FM and a high SMM, as indicated by PA, and was the highest of the team (great body cell mass and lower ECW/ICW relationship, due to the higher ICW).
The somatotype analysis corroborates many of these BC characteristics. As an example, Figure 1b shows that player number 12 is the only one with an ectomorphic somatotype. Players with a high body mass and FM% are allocated in the mesomorph endomorph axis, but out of the somatochart (the values of players number 13 and 19 were so extreme for X and Y that they cannot be drawn on the somatochart). Little research has been conducted to analyse impedance vector distribution according to athlete somatotype [26,53,58,59]. Statistically significant correlations between impedance vector and PA and some components of somatotype have been found; however, the studied samples were reduced (only from sports such as soccer) and mainly in male athletes [26,53,58,59].
This study presents some limitations. On one hand, there was a reduced sample size; the subjects studied were only the players from a sub-elite rugby team who voluntarily wanted to participate, but it was a small team. Ideally, the sample size would be increased by including players from rugby and other sports, individual and team sports, and with sub-elite and elite athletes. Additionally, on the other hand, the obtained results can only be extrapolated to other research works that use similar BIA devices at 50 kHz with the same protocol and in similar populations.
In sports, where fast, accurate, and simple measurements are required, the application of BIVA, in both classic and specific modalities, can be a very helpful strategy for BC analysis [60]. Both conventional BIA and BIVA techniques do not present anthropometry limitations such as errors derived from predictive models, a high inter- and intra-observer variability, and a specific measurement time. Classic BIVA could be useful to evaluate hydration variations, while BIVA-sp could be employed to monitor changes in FM% during seasons or according to different training strategies in order to improve BC and competitive performance. Given the particularities of this sport and the physiological characteristics of women, this could be particularly important in rugby female players. Moreover, the use of BIVA to assess BC in semi-professional teams would assist in improving the physical condition and performance of the players.
In future research, it would be very interesting to study BIVAs applications in the long term to evaluate BC and hydration variations during the entire sport season and training sessions. It would also be relevant to study the association between impedance vectors and somatotype in a greater sample of both female and male athletes from different sports and levels of competition.
5. Conclusions
The BC and morphology of the players from a sub-elite female rugby team are different according to their playing position; forwards present a higher FM% than backs. These variations are shown in both somatotype and specific impedance vector distributions of BIVA. The application of BIVA in both modalities, i.e., classic and specific, can be a very useful strategy for BC study in sports.
Author Contributions
Conceptualisation, B.d.M.S., G.C.A. and P.R.d.R.; data curation, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R.; formal analysis, B.d.M.S. and P.R.d.R.; investigation, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R.; methodology, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R.; resources, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R.; software, B.d.M.S. and P.R.d.R.; supervision, B.d.M.S. and P.R.d.R.; validation, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R.; writing—original draft, B.d.M.S., G.C.A. and P.R.d.R.; writing—review and editing, B.d.M.S., G.C.A., S.d.l.C.M., L.C.E., E.Q.F. and P.R.d.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Clinical Research Ethics Committee (CEIC) of Valladolid-East Health Area on 17 January 2017 (protocol code: PI 16-512).
Informed Consent Statement
Written informed consent was obtained from all subjects that participated in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The research team thanks all volunteers who participated in the study for their collaboration.
Conflicts of Interest
The authors declare that there are no conflict of interest.
References
- Brazier, J.; Antrobus, M.; Stebbings, G.K.; Day, S.H.; Callus, P.; Erskine, R.M.; Mark, A. Anthropometric and physiological characteristics of elite male rugby athletes. J. Strength Cond. Res. 2020, 34, 1790–1801. [Google Scholar] [CrossRef] [PubMed]
- Duthie, G.; Pyne, D.; Hooper, S. Applied Physiology and Game Analysis of Rugby Union. Sports Med. 2003, 33, 973–991. [Google Scholar] [CrossRef] [PubMed]
- Quarrie, K.L.; Wilson, B.D. Force production in the rugby union scrum. J. Sports Sci. 2000, 18, 237–246. [Google Scholar] [CrossRef] [PubMed]
- Berral-Aguilar, A.J.; Schröder-Vilar, S.; Rojano-Ortega, D.; la Rosa, F.J.B.-D. Body Composition, Somatotype and Raw Bioelectrical Impedance Parameters of Adolescent Elite Tennis Players: Age and Sex Differences. Int. J. Environ. Res. Public Health 2022, 19, 17045. [Google Scholar] [CrossRef]
- Campa, F.; Gobbo, L.A.; Stagi, S.; Cyrino, L.T.; Toselli, S.; Marini, E.; Coratella, G. Bioelectrical impedance analysis versus reference methods in the assessment of body composition in athletes. Eur. J. Appl. Physiol. 2022, 122, 561–589. [Google Scholar] [CrossRef]
- Wang, Z.M.; Pierson, R.N.; Heymsfield, S.B. The five-level model: A new approach to organizing body-composition research. Am. J. Clin. Nutr. 1992, 56, 19–28. [Google Scholar] [CrossRef]
- Müller, M.J.; Braun, W.; Pourhassan, M.; Geisler, C.; Bosy-Westphal, A. Application of standards and models in body composition analysis. Proc. Nutr. Soc. 2016, 75, 181–187. [Google Scholar] [CrossRef]
- Heymsfield, S.B.; Ebbeling, C.B.; Zheng, J.; Pietrobelli, A.; Strauss, B.J.; Silva, A.M.; Ludwig, D.S. Multi-component molecular-level body composition reference methods: Evolving concepts and future directions. Obes. Rev. 2015, 16, 282–294. [Google Scholar] [CrossRef]
- Alvero Cruz, J.R.; Cabañas Armesilla, M.D.; Herrero de Lucas, A.; Martínez Riaza, L.; Moreno Pascual, C.; Porta Manzañido, J.; Sillero Quintana, M.; Sirvent Belando, J.E. Protocolo de valoración de la composición corporal para el reconocimiento médico-deportivo. Documento de consenso del Grupo Español de Cineantropometría de la Federación Española de Medicina del De-porte. Arch. Med. Deporte 2009, 26, 166–179. [Google Scholar]
- Ackland, T.; Lohman, T.G.; Sundgot-Borgen, J.; Maughan, R.J.; Meyer, N.L.; Stewart, A.; Müller, W. Current Status of Body Composition Assessment in Sport: Review and Position Statement on Behalf of the Ad Hoc Research Working Group on Body Composition Health and Performance, under the Auspices of the I.O.C. Medical Commission. Sports Med. 2012, 42, 227–249. [Google Scholar] [CrossRef]
- Campa, F.; Matias, C.N.; Moro, T.; Cerullo, G.; Casolo, A.; Teixeira, F.J.; Paoli, A. Methods over Materials: The Need for Sport-Specific Equations to Accurately Predict Fat Mass Using Bioimpedance Analysis or Anthropometry. Nutrients 2023, 15, 278. [Google Scholar] [CrossRef] [PubMed]
- Carter, J.E.L.; Heath, B. Somatotyping Development and Applications; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1990. [Google Scholar]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis, part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef] [PubMed]
- Lukaski, H.C. Evolution of bioimpedance: A circuitous journey from estimation of physiological function to assessment of body composition and a return to clinical research. Eur. J. Clin. Nutr. 2013, 67 (Suppl. S1), S2–S9. [Google Scholar] [CrossRef] [PubMed]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.-C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part II: Utilization in clinical practice. Clin. Nutr. 2004, 23, 1430–1453. [Google Scholar] [CrossRef] [PubMed]
- Norman, K.; Smoliner, C.; Valentini, L.; Lochs, K.; Pirlich, M. Is bioelectrical vector analysis of value in the elderly with malnutrition and impaired functionality? Nutrition 2007, 23, 564–569. [Google Scholar] [CrossRef] [PubMed]
- Piccoli, A.; Rossi, B.; Pillon, L.; Bucciante, G. A new method for monitoring body fluid variation by bioimpedance analysis: The RXc graph. Kidney Int. 1994, 46, 534–539. [Google Scholar] [CrossRef] [PubMed]
- Norman, K.; Stobäus, N.; Pirlich, M.; Bosy-Westphal, A. Bioelectrical phase angle and impedance vector analysis—Clinical relevance and applicability of impedance parameters. Clin. Nutr. 2012, 31, 854–861. [Google Scholar] [CrossRef]
- Piccoli, A.; Nescolarde, L.D.; Rosell, J. Análisis convencional y vectorial de impedancia en la práctica clínica. Nefrologia 2002, 23, 228–236. [Google Scholar]
- Buffa, R.; Saragat, B.; Cabras, S.; Rinaldi, A.C.; Marini, E. Accuracy of specific BIVA for the assessment of body composition in the United States population. PLoS ONE 2013, 8, e58533. [Google Scholar] [CrossRef]
- Mereu, E.; Buffa, R.; Lussu, P.; Marini, E. Phase angle, vector length, and body composition. Am. J. Clin. Nutr. 2016, 104, 845–847. [Google Scholar] [CrossRef]
- Marini, E.; Sergi, G.; Succa, V.; Saragat, B.; Sarti, S.; Coin, A.; Manzato, E.; Buffa, R. Efficacy of specific bioelectrical impedance vector analysis (BIVA) for assessing body composition in the elderly. J. Nutr. Health Aging 2013, 17, 515–521. [Google Scholar] [CrossRef] [PubMed]
- Castizo-Olier, J.; Irurtia, A.; Jemni, M.; Carrasco-Marginet, M.; Fernández-García, R.; Rodríguez, F.A. Bioelectrical impedance vector analysis (BIVA) in sport and exercise: Systematic review and future perspectives. PLoS ONE 2018, 13, e0197957. [Google Scholar] [CrossRef] [PubMed]
- Campa, F.; Toselli, S.; Mazzilli, M.; Gobbo, L.A.; Coratella, G. Assessment of Body Composition in Athletes: A Narrative Review of Available Methods with Special Reference to Quantitative and Qualitative Bioimpedance Analysis. Nutrients 2021, 13, 1620. [Google Scholar] [CrossRef]
- Di Vincenzo, O.; Marra, M.; Scalfo, L. Bioelectrical impedance phase angle in sport: A systematic review. J. Intern. Soc. Sports Nutr. 2019, 16, 49. [Google Scholar] [CrossRef]
- Campa, F.; Silva, A.M.; Talluri, J.; Matias, C.N.; Badicu, G.; Toselli, S. Somatotype and Bioimpedance Vector Analysis: A New Target Zone for Male Athletes. Sustainability 2020, 12, 4365. [Google Scholar] [CrossRef]
- Stewart, A.; Marfell-Jones, M.; Olds, T.; Riidder, H. International Standards for Anthropometric Assessment; ISAK: Lower Hutt, New Zealand, 2011. [Google Scholar]
- WHO. Clasificación Internacional Para Adultos de Bajo Peso, Sobrepeso y Obesidad en Relación al IMC: Criterios de la OMS. 2006. Available online: https://www.who.int/es/news-room/fact-sheets/detail/obesity-and-overweight (accessed on 1 March 2023).
- Carter, J.E.L. (Ed.) Body composition of Montreal Olympic athletes. In Physical Structure of the Olympic Athletes. Part I: The Montreal Olympic Games Anthropological Project; Karger: Basel, Switzerland, 1982; pp. 107–116. [Google Scholar]
- Rocha, M.L. Peso ósseo do brasileiro de ambos os sexos de 17 a 25 anos. Aeq. Anat. Antrop. 1975, 1, 445. [Google Scholar]
- Würch, A. La femme et le sport. Médecine Sport. Fr. 1974, 4, 441–445. [Google Scholar]
- Lee, R.C.; Wang, Z.; Heo, M.; Ross, R.; Janssen, I.; Heymsfield, S.B. Total-body skeletal muscle mass: Development and cross-validation of anthropometric prediction models. Am. J. Clin. Nutr. 2000, 72, 796–803. [Google Scholar] [CrossRef]
- Canda, A.S. Variables Antropométricas de la Población Deportista Española; Consejo Superior de Deportes de España: Madrid, Spain, 2012. [Google Scholar]
- Lukaski, H.C. Assessment of body composition using tetrapolar impedance analysis. In New Techniques in Nutritional Research; Whitehead, R.G., Prentice, A., Eds.; Academic Press: San Diego, CA, USA, 1991; pp. 303–315. [Google Scholar]
- Matias, C.N.; Campa, F.; Santos, D.A.; Lukaski, H.; Sardinha, L.B.; Silva, A.M. Fat-free Mass Bioelectrical Impedance Analysis Predictive Equation for Athletes using a 4-Compartment Model. Int. J. Sports Med. 2021, 42, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Janssen, I.; Heymsfield, S.B.; Baumgartner, R.N.; Ross, R. Estimation of skeletal muscle mass by bioelectrical impedance analysis. J. Appl. Physiol. 2000, 89, 465–471. [Google Scholar] [CrossRef]
- Campa, F.; Matias, C.; Gatterer, H.; Toselli, S.; Koury, J.C.; Andreoli, A.; Melchiorri, G.; Sardinha, L.B.; Silva, A.M. Classic Bioelectrical Impedance Vector Reference Values for Assessing Body Composition in Male and Female Athletes. Int. J. Environ. Res. Public Health 2019, 16, 5066. [Google Scholar] [CrossRef]
- Ibáñez, M.E.; Mereu, E.; Buffa, R.; Gualdi-Russo, E.; Zaccagni, L.; Cossu, S.; Rebato, E.; Marini, E. New specific bioelectrical impedance vector reference values for assessing body composition in the Italian-Spanish young adult population. Am. J. Hum. Biol. 2015, 27, 871–876. [Google Scholar] [CrossRef] [PubMed]
- Piccoli, A.; Pastori, G. BIVA Software; Department of Medical and Surgical Sciences, University of Padova: Padova, Italy, 2002. [Google Scholar]
- Dubois, R.; Paillard, T.; Lyons, M.; McGrath, D.; Maurelli, O.; Prioux, J. Running and Metabolic Demands of Elite Rugby Union Assessed Using Traditional, Metabolic Power, and Heart Rate Monitoring Methods. J. Sports Sci. Med. 2017, 16, 84–92. [Google Scholar]
- Rodríguez Rodríguez, F.J.; Berral de la Rosa, F.J.; Almagià Flores, A.A.; Iturriaga Zuleta, M.F.; Rodríguez Briceño, F. Comparación de la composición corporal y de la masa muscular por segmentos corporales, en estudiantes de educación física y deportistas de distintas disciplinas. Int. J. Morphol. 2012, 30, 7–14. [Google Scholar] [CrossRef]
- Harty, P.S.; Zabriskie, H.A.; Stecker, R.A.; Currier, B.S.; Moon, J.M.; Richmond, S.R.; Jagim, A.R.; Kerksick, C.M. Position-Specific Body Composition Values in Female Collegiate Rugby Union Athletes. J. Strength Cond. Res. 2021, 35, 3158–3163. [Google Scholar] [CrossRef] [PubMed]
- Suárez-Moreno Arrones, L.J.; Núñez, F.J. Physicological and antropometric characteristics of elite rugby players in Spain and relative power out as predictor of performance in sprint and RSA. J. Sport Health Res. 2011, 3, 191–202. [Google Scholar]
- Gabbett, T.J. Physiological and anthropometric characteristics of elite women rugby league players. J. Strength Cond. Res. 2007, 21, 875–881. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Álvarez, J.J.; Montoya, J.J.; Solís-Mencia, C.; Miguel-Tobal, F.; López-Tapia, P.; Sánchez-Oliver, A.J.; Domínguez, R.; Martínez-Sanz, J.M. Anthropometric Profile Assessed by Bioimpedance and Anthropometry Measures of Male and Female Rugby Players Competing in the Spanish National League. Appl. Sci. 2021, 11, 11759. [Google Scholar] [CrossRef]
- Jones, B.; Emmonds, S.; Hind, K.; Nicholson, G.; Rutherford, Z.; Till, K. Physical Qualities of International Female Rugby League Players by Playing Position. J. Strength Cond. Res. 2016, 30, 1333–1340. [Google Scholar] [CrossRef]
- Hene, N.M.; Bassett, S.H.; Andrews, B.S. Physical fitness profiles of elite women’s rugby union players. Afr. J. Phys. Health Educ. Recreat. Dance 2011, 17 (Suppl. S1), 1–8. [Google Scholar]
- Scantlebury, S.; McCormack, S.; Sawczuk, T.; Emmonds, S.; Collins, N.; Beech, J.; Ramirez, C.; Owen, C.; Jones, B. The anthropometric and physical qualities of women’s rugby league Super League and international players; identifying differences in playing position and level. PLoS ONE 2022, 17, e0249803. [Google Scholar] [CrossRef] [PubMed]
- Escrivá, D.; Caplliure-Llopis, J.; Benet, I.; Mariscal, G.; Mampel, J.V.; Barrios, C. Differences in Adiposity Profile and Body Fat Distribution between Forwards and Backs in Sub-Elite Spanish Female Rugby Union Players. J. Clin. Med. 2021, 10, 5713. [Google Scholar] [CrossRef] [PubMed]
- Lukaski, H.C.; Raymond-Pope, J.C. New frontiers of body composition in sport. Int. J. Sports Med. 2021, 42, 588–601. [Google Scholar] [CrossRef]
- Coratella, G.; Campa, F.; Matias, C.N.; Toselli, S.; Koury, J.C.; Andreoli, A.; Sardinha, L.B.; Silva, A.M. Generalized bioelectric impedance-based equations underestimate body fluids in athletes. Scand. J. Med. Sci. Sports 2021, 31, 2123–2132. [Google Scholar] [CrossRef]
- Campa, F.; Thomas, D.M.; Watts, K.; Clark, N.; Baller, D.; Morin, T.; Toselli, S.; Koury, J.C.; Melchiorri, G.; Andreoli, A.; et al. Reference Percentiles for Bioelectrical Phase Angle in Athletes. Biology 2022, 11, 264. [Google Scholar] [CrossRef]
- Campa, F.; Silva, A.M.; Matias, C.N.; Monteiro, C.P.; Paoli, A.; Nunes, J.P.; Talluri, J.; Lukaski, H.; Toselli, S. Body Water Content and Morphological Characteristics Modify Bioimpedance Vector Patterns in Volleyball, Soccer, and Rugby Players. Int. J. Environ. Res. Public Health 2020, 17, 6604. [Google Scholar] [CrossRef] [PubMed]
- Marini, E.; Campa, F.; Buffa, R.; Stagi, S.; Matias, C.N.; Toselli, S.; Sardinha, L.B.; Silva, A.M. Phase angle and bioelectrical impedance vector analysis in the evaluation of body composition in athletes. Clin. Nutr. 2020, 39, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Reis, J.F.; Matias, C.N.; Campa, F.; Morgado, J.P.; Franco, P.; Quaresma, P.; Almeida, N.; Curto, D.; Toselli, S.; Monteiro, C.P. Bioimpedance Vector Patterns Changes in Response to Swimming Training: An Ecological Approach. Int. J. Environ. Res. Public Health 2020, 17, 4851. [Google Scholar] [CrossRef]
- Campa, F.; Matias, C.N.; Nunes, C.L.; Monteiro, C.P.; Francisco, R.; Jesus, F.; Marini, E.; Sardinha, L.B.; Martins, P.; Minderico, C.; et al. Specific Bioelectrical Impedance Vector Analysis Identifies Body Fat Reduction after a Lifestyle Intervention in Former Elite Athletes. Biology 2021, 10, 524. [Google Scholar] [CrossRef]
- Buffa, R.; Mereu, E.; Succa, V.; Latini, V.; Marini, E. Specific BIVA recognizes variation of body mass and body composition: Two related but different facets of nutritional status. Nutrition 2017, 35, 1–5. [Google Scholar] [CrossRef]
- Kim, C.H.; Park, J.H.; Kim, H.; Chung, S.; Park, S.H. Modeling the human body shape in bioimpedance vector measurements. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 2010, 3872–3874. [Google Scholar] [PubMed]
- Campa, F.; Bongiovanni, T.; Matias, C.N.; Genovesi, F.; Trecroci, A.; Rossi, A.; Iaia, F.M.; Alberti, G.; Pasta, G.; Toselli, S. A New Strategy to Integrate Heath–Carter Somatotype Assessment with Bioelectrical Impedance Analysis in Elite Soccer Players. Sports 2020, 8, 142. [Google Scholar] [CrossRef] [PubMed]
- de la Cruz Marcos, S.; Redondo del Río, M.P.; de Mateo Silleras, B. Applications of bioelectrical impedance vector analysis (BIVA) in the study of body composition in athletes. Appl. Sci. 2021, 11, 9781. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).