Optimal Power Flow of Hybrid Wind/Solar/Thermal Energy Integrated Power Systems Considering Costs and Emissions via a Novel and Efficient Search Optimization Algorithm

Abstract

The OPF problem has significant importance in a power system’s operation, planning, economic scheduling, and security. Today’s electricity grid is rapidly evolving, with increased penetration of renewable power sources (RPSs). Conventional optimal power flow (OPF) has non-linear constraints that make it a highly non-linear, non-convex optimization problem. This complex problem escalates further with the integration of renewable energy resource (RES), which are generally intermittent in nature. This study suggests a new and effective improved optimizer via a TFWO algorithm (turbulent flow of water-based optimization), namely the ITFWO algorithm, to solve non-linear and non-convex OPF problems in energy networks with integrated solar photovoltaic (PV) and wind turbine (WT) units (being environmentally friendly and clean in nature). OPF in the energy networks is an optimization problem proposed to discover the optimal settings of an energy network. The OPF modeling contains the forecasted electric energy of WT and PV by considering the voltage value at PV and WT buses as decision parameters. Forecasting the active energy of PV and WT units has been founded on the real-time measurements of solar irradiance and wind speed. Eight scenarios are analyzed on the IEEE 30-bus test system in order to determine a cost-effective schedule for thermal power plants with different objectives that reflect fuel cost minimization, voltage profile improvement, emission gases, power loss reduction, and fuel cost minimization with consideration of the valve point effect of generation units. In addition, a carbon tax is considered in the goal function in the examined cases in order to investigate its effect on generator scheduling. A comparison of the simulation results with other recently published algorithms for solving OPF problems is made to illustrate the effectiveness and validity of the proposed ITFWO algorithm. Simulation results show that the improved turbulent flow of water-based optimization algorithm provides an effective and robust high-quality solution of the various optimal power-flow problems. Moreover, results obtained using the proposed ITFWO algorithm are either better than, or comparable to, those obtained using other techniques reported in the literature. The utility of solar and wind energy in scheduling problems has been proposed in this work.

1. Introduction

1.1. Motivation

The optimal power flow (OPF) is an optimization method to minimize a specific optimization benchmark while satisfying security, physical and feasibility limits. The various OPF problems have been broadly applied in recent studies, and have served as a multi-model, non-linear, and non-convex optimization problem [1,2]. In the last two decades, various OPF objective functions had a grandness due to the quick adoption of divided power resources in an energy network [3]. The accretion of divided and periodic renewable power sources (RPSs), as with wind energy (WE) and photovoltaic (PV) systems, into modern energy networks has generated novel types of problems for managing and operating the energy network [4,5]. Optimizing the various OPF problems has become more intricate with the enormous incorporation of RPSs that constrain volatile dynamics for the energy network due to their uncertainty [6,7].

Conventional search approaches, such as quadratic programming (QP) [8], and non-linear programming (NLP) [9,10,11] presented great convergence trends in optimizing the objective functions of the different OPF problems; however, these methods apply theoretical hypotheses not suitable for real-world problems, as they have non-smooth and non-differentiable objective functions [12,13,14]. In addition, the preceding methods sometimes fail to show the main trends of the objective function as a convex OPF function [12]. Therefore, metaheuristics have been applied to dominate the above-mentioned weaknesses [12,15].

1.2. Literature Review

The following algorithms have been successfully applied to optimize various OPF problems: manta ray foraging optimizer (MRFO) [3], grey wolf optimization (GWO) [16,17], a parallel genetic algorithm (GA) (EPGA) [18], multi-objective electromagnetism-like algorithm (MOELA) [19], a distributionally robust approach for OPF [20], a combination firefly-bat algorithm (HFBA-COFS) [21], social spider optimization (SSO) [22], solving OPF by GA and teaching-learning-based optimization (TLBO) (G-TLBO) [23], a bacterial foraging algorithm (BFA) [24], various differential evolution (DE) algorithms [25,26,27,28,29,30,31], Harris hawks optimization (HHO) [32], cuckoo search algorithm (ECSA) [33,34], chaotic invasive weed optimization algorithms (CIWOs) [35], multi-objective dynamic OPF (MODOPF) [36], salp swarm algorithm (SSA) [37], TLBO with Lévy mutation (LTLBO) [38], voltage stability constrained OPF (VSC-OPF) [39], considering effects of solar position [40], the hybridization of PSO with GWO, namely a PSO-GWO algorithm [41], symbiotic organisms search (SOS) [42], artificial bee colony (ABC) algorithms [43,44,45], group search optimization (GSO) [46,47], a new combine algorithm, SFLA-PSO [48], a colliding bodies optimization (CBO) [49], tunicate swarm algorithm (TSA) [50], a modified hybrid PSO [51] and GSA with chaotic maps (CPSOGSA) [52], sine-cosine algorithms (SCAs) [53,54], chaotic bonobo optimizer (CBO) [55], a honey bee mating optimization (HBMO) [56], a heap-based optimization (HBO) [57], slime mold algorithm (SMA) [58], mayfly algorithm (MA) [59], BAT search algorithm [60], moth swarm algorithms (MSA) [61,62], bird swarm algorithm (BSA) [63], a new evolutionary algorithm (EA) [64], etc.

1.3. Contribution and Paper Organization

In 2021, Ghasemi et al. [65] introduced the TFWO algorithm, which is inspired by the formula of turbulent fluctuations in water flow in nature. The recent research has demonstrated that TFWO can be effectively used to find optimal solutions to a variety of optimization problems. For example, TFWOs were used for optimal reactive power distribution (ORPD) in [66]. The chaotic TFWO (CTFWO) was introduced in [67] as a means of reducing voltage deviation (VD) and real power loss. The TFWO model has been successfully used to solve problems related to unit commitment model integration with electric vehicles in [68]. An estimation of the correlation parameter of the Kriging method, enhancing the accuracy of the Kriging surrogate modeling (KSM) used to approximate the complex and implicit performance functions in [69]. To solve short-term hydrothermal scheduling, the authors of [70,71] have proposed quasi-oppositional TFWO (QOTFWO). The cascading nature of hydro plants, valve-point loading (VPL), and multiple fuel sources have been assumed in their modeling. Through a comprehensive comparison of three robust performance and fast convergence algorithms, ref. [72] proved that the TFWO can optimize an isolated hybrid microgrid. The TFWO also have been applied for proportional integral derivative (PID) controller to ensure reliable operation of active foil bearings [73], and optimal allocation of shunt compensators in distribution systems [74]. Based on the results of [74], the TFWO algorithm was found to be effective in reducing power loss, enhancing the voltage profile, and determining the type, size, and location of the reactive power compensators (RPCs).

In different patterns of partial shading, TFWO was shown to be capable of maximizing duty cycle of DC/DC converters to achieve global optimal power [75]. In [76], the performance of the TFWO was compared and validated against seven well-known algorithms. As a result of optimizing photovoltaic models, the TFWO were able to provide the minimum fuel cost and significant robust solutions to the ELD problem over all networks tested in [77,78]. It was demonstrated in [77,78] that the estimated power-voltage (P-V) and current-voltage (I-V) curves achieved by the TFWO were very close to the experimental data.

It has been demonstrated in recent research that TFWO can be effective in solving real-world problems. It is worth noting that, due to its non-convex and non-linear nature, the OPF problems can be extremely challenging. The robustness and convergence speed of existing algorithms, such as turbulent water flow (TFWO), need to be improved in order to tackle such a complex problem. An innovative and successful improvement of the TFWO (ITFWO) approach is presented in this paper to address a variety of OPF problems encountered in hybrid power systems. To demonstrate the algorithm’s ability to solve OPF problems, this paper compares the developed algorithm with existing state-of-the-art methods.

This paper highlights the following points:

• Enhancing the TFWO algorithm’s convergence speed, exploration capabilities, and exploitation capabilities.
• The original TFWO algorithm has been improved by the addition of an enhanced operator to update the population, which increases the local search capability of the algorithm.
• The proposed improved algorithm is successfully applied to solve the non-convex and non-linear OPF problems considering different objective functions.
• The magnitude of the voltage at the WT and PV buses is considered a decision variable, while the forecasts of the WT and PV power generation are considered dependent variables.

The paper has been arranged as follows. The modeling of OPF is characterized in Section 2. The optimization process of TFWO and ITFWO is characterized in Section 3. Section 4 illustrates the obtained optimal results. Finally, the conclusions of this paper are supplied in Section 5.

2. Problem Formulation

OPF combining the uncertainties of PV and WT units has been formulated in this [79]:

$$\min \hspace{0.17em}F\left(y,x\right)$$

(1)

$$g\left(y,x\right)=0$$

(2)

$$h\left(y,x\right)\le 0$$

(3)

$$x\epsilon X$$

(4)

where: the objective function (F) to be solved; x indicates vector of decision parameters as Equation (5), output active power (P_Gi) excluding at the slack bus (i = 1: NG, the number of units), generator voltages including PV and WT (V_Gi; i = 1: NG), tap settings of transformer (T_i) (i = 1: NT, the number of regulating transformer), and (Q_Ci) (i = 1: NC, the number of VAR compensators) is the shunt VAR compensations [79]:

$$x=\left[\begin{array}{l}{P}_{G2},\dots ,P_{GNG},V_{G1},\dots ,V_{GNG},V_{WT},V_{PV},\\ T_1,\dots ,T_{NT},Q_{C1},\dots ,Q_{CNC}\end{array}\right]$$

(5)

$$y=\left[\begin{array}{l}{P}_{G1},,V_{L1},\dots ,V_{LNL},Q_{G1},\dots ,Q_{GNG},\\ Q_{WT},V_{PV},S_{l1},\dots ,S_{lNTL}\end{array}\right]$$

(6)

Here, y shows the resultant of dependent decision parameters including of voltages at load bus (V_Li; i = 1: NL, the size of load buses), slack bus power (P_G1), output reactive power of any generator (Q_Gi), and loads of transmission line (S_li) (i = 1: NTL, the size of transmission lines).

2.1. Constraints

The basic OPF Equation (2) indicates the equality constraints [79].

$$\begin{gathered} P_i-{\displaystyle \sum _{j=1}^{NB}{V}_i{V}_j\left[\hspace{0.17em} B_{ij}\times \sin ({\delta }_{ij})+G_{ij}\times \cos ({\delta }_{ij}) \right]} \\ \hspace{0.17em}i=1,\dots ,NB \end{gathered}$$

(7)

NB: the size of busses; P_i: active power; G_ij: the real section of bus admittance matrix; δ_ij: the voltage angle between i and j; B_ij: the imaginary section of bus admittance matrix.

$$Q_i-{\displaystyle \sum _{j=1}^{NB}{V}_i{V}_j\left[-B_{ij}\times \cos \hspace{0.17em}({\delta }_{ij})+G_{ij}\times \sin \hspace{0.17em}({\delta }_{ij})\right] }$$

(8)

Q_i: reactive power injected at bus i.

The inequality limits, i.e., Equation (3), includes the voltage magnitude limits, the generating units’ reactive power constraints, and power flow limits of the branches, which are expressed as follows [79]:

$$\begin{gathered} \mathrm{Voltage\; magnitudes:} \\ {V}_{Li}^{\min }\le V_{Li}\le V_{Li}^{\max } \end{gathered}$$

(9)

$$\begin{gathered} \mathrm{Generator’s\; reactive\; power:} \\ {Q}_{Gi}^{\min }\le Q_{Gi}\le Q_{Gi}^{\max } \end{gathered}$$

(10)

$$\begin{gathered} \mathrm{Branch\; flow\; limits:} \\ {S}_{li}\le S_{li}^{\max } \end{gathered}$$

(11)

Equation (4) shows the area of feasible search space for any OPF function including the following limits:

$$P_{Gi}^{\min }\le P_{Gi}\le P_{Gi}^{\max }$$

(12)

$$V_{Gi}^{\min }\le V_{Gi}\le V_{Gi}^{\max }$$

(13)

$$T_i^{\min }\le T_i\le T_i^{\max }$$

(14)

$$Q_{Ci}^{\min }\le Q_{Ci}\le Q_{Ci}^{\max }$$

(15)

2.2. Objective Functions

The principal optimization objective F has contemplated in the objective functions is the fuel cost of the energy units (Fcost). The cost of any generator is shown as a second-class optimization problem of the generation power of any unit (P_G):

$$\min Fcost\left(x,y\right)=\min {\displaystyle \sum _{i=1}^{NG}({\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2)}$$

(16)

where a_i, b_i and c_i show the cost factors of the ith generator.

To decrease active loss (Ploss) in the energy network OPF function for optimization has showed:

$$\min Ploss\left(x,y\right)=\min {\displaystyle \sum _{i=1}^{NTL}{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{NTL}\left(G_{ij}\hspace{0.17em}{V}_i^2\hspace{0.17em}+\hspace{0.17em}{B}_{ij}{V}_j^2\hspace{0.17em}-2V_i\hspace{0.17em}{V}_j\cos {\delta }_{ij}\right)}}$$

(17)

The OPF function to optimize the voltage deviations (VD) is as follows:

$$\min VD\left(x,y\right)=\min {\displaystyle \sum _{i=1}^{NL}\left|V_i-V_i^{ref}\right|}$$

(18)

where V_i indicates the voltage value of the ith bus, and V_i^ref has been contemplated as 1 p.u.

In this study, the emission level of the two significant pollutants, sulfur oxides (SOx) and nitrogen oxides (NOx), are considered to be minimized [80]:

$$\min Emission\left(x,y\right)=\min {\displaystyle \sum _{i=1}^{NG}\left({\alpha }_i+{\xi }_i\exp ({\theta }_i{P}_{Gi})+{\gamma }_i{P}_{Gi}^2+{\beta }_i{P}_{Gi}\right)}$$

(19)

where ξ_i (ton/h), γ_i (ton/h MW2), β_i (ton/h MW), α_i (ton/h), and θ_i (1/MW) are pollution factors of ith unit.

So, the main function is considered as follows:

$$\begin{array}{l}J\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{F}_i\hspace{0.17em}(\hspace{0.17em}{P}_{Gi})}\hspace{0.17em}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\hspace{0.17em}+\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}\\ +\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}\end{array}$$

(20)

where λ_Q, λ_V, λ_P, and λ_S show the penalty coefficients; and x^lim shows a variable as an auxiliary variable:

$$x^{\lim }\hspace{0.17em}=\left\{\begin{array}{l}{x}^{\min };\hspace{0.17em}x<x^{\min }\\ x^{\max };x>x^{\max }\\ x\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} x^{\min } \le x \le \hspace{0.17em}{x}^{\max }\end{array}\right.$$

(21)

2.3. Modelling of RPSs

2.3.1. Modelling of WT Units

The generation power of a WT unit at wind speed v, is modeled as follows [79]:

$$P_{WT}\left(v\right)=\left\{\begin{array}{l}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}v\le v_{ci}\\ \frac{v-v_{ci}}{v_n-v_{ci}}{P}_{wtn}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_{ci}\le v\le v_n\\ P_{wtn}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_n\le v\le v_{co}\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}v\ge v_{co}\end{array}\right.$$

(22)

where v_co is cut-out wind speed, v_ci is cut-in wind speed; v_n is nominal wind speed; and P_wtn, is the nominal generation active energy of the wind turbine.

The non-linear characteristics of wind speed in a predefined process at a special locality have been shown via Weibull PDF:

$$f_v\left(v\right)=\frac{K}{C}{\left(\frac{v}{C}\right)}^{K-1}{e}^{-{\left(\frac{v}{C}\right)}^k},\hspace{0.17em}\hspace{0.17em}v>0$$

(23)

The CDF (cumulative distribution function) for the Weibull dispersion (WD) is:

$$F_v\left(v\right)=1-e^{-{\left(\frac{v}{C}\right)}^k}$$

(24)

$$v=C{\left(-\ln \left(r\right)\right)}^{\frac{1}{k}}$$

(25)

where f_v(v) describes Weibull PDF of v; k and C are the shape and scale parameters of WD; r is a haphazard value uniformly generated on 0 and 1.

The active power of the WT unit has been modeled via the probability of any feasible state for that time interval [79]:

$$P_{WT}=\frac{{\displaystyle \sum _{g=1}^{N_v}{P}_{WTg}.f_v\left(v_g^t\right)}}{{\displaystyle \sum _{g=1}^{N_v}{f}_v\left(v_g^t\right)}}$$

(26)

where f_ν(ν_g^t) is the probability of v for state g during the special space t; P_WTg is the out active power of WT computed by (22) for v = $v_g^t$; $v_g^t$ is the gth state of v at the tth time space.

2.3.2. Modelling of PV Units

The active energy provided of a PV generator is associate on the solar irradiancy [79]:

$$P_{PV}\left(S\right)=\left\{\begin{array}{l}{P}_{pvn}\left(\frac{S^2}{R_C{S}_{stc}}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\le R_C\\ P_{pvn}\left(\frac{S}{S_{stc}}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}S\hspace{0.17em}\ge R_C\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}\right.$$

(27)

where R_c is a particular irradiancy point; S_stc is the solar irradiancy at test states; S is the solar irradiancy on the PV surface (W/m²); P_pvn is the nominal active power of the PV generator.

Beta PDF role of S (f_s(S)) has been proposed to formulate the dynamic nature of solar irradiancy [79,81]:

$$f_s\left(S\right)=\left\{\begin{array}{l}\frac{\Gamma \left(\alpha +\beta \right)}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{S}^{\alpha +1}{\left(1-S\right)}^{\left(\beta -1\right)}\hspace{0.17em}for\hspace{0.17em}0\le S\le 1,\hspace{0.17em}\alpha \ge 0,\beta \ge 0\\ 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{otherwise}\hspace{0.17em}\end{array}\right.$$

(28)

where $\Gamma$ represents Gamma role; α, β indicates its shape variables.

The forecasted active power of PV (P_PVg) at the tth time interval and the gth state of solar irradiancy (S_g^t) has been calculated as follows [79]:

$$P_{PV}=\frac{{\displaystyle \sum _{g=1}^{N_s}{P}_{PVg}.f_s\left(S_g^t\right)}}{{\displaystyle \sum _{g=1}^{N_s}{f}_s\left(S_g^t\right)}}$$

(29)

3. The Proposed Improved Optimizer

3.1. The Basic TFWO

3.1.1. Formation of Whirlpools

Firstly, the particle (X) of TFWO (N_p: the size of swarm) is distributed similarly between N_Wh swarms, and then the best population of the any swarm or whirlpool (Wh) has been defined as the center of the swarm and its cavity that pulls the particles based on their spaces to the whirlpool.

3.1.2. Pulling the Objects

In a whirlpool the objects are whirling with their angle (δ) circa their whirlpool’s center, the novel location (X_i^new) of the ith object is gone as same as Wh_j −∆X_i, and method to it. In addition, ${\delta }_i$ at any generation is modifying: ${\delta }_i^{\mathrm{new}}={\delta }_i+{\left(rand\right)}^2\times \pi$:

$${\Delta }_t=\frac{f\left(W{h}_t\right)}{{\left|sum\left(X_i\right)-sum\left(W{h}_t\right)\right|}^{-0.5}}$$

(30)

where $W{h}_w$ is Wh with an up cost of ${\mathsf{\Delta }}_t$ and Wh_f is Wh with a minimum cost of ${\mathsf{\Delta }}_t$, respectively.

$$\Delta X_i=\left(\left|-\sin \left({\delta }_i^{\mathrm{new}}\right)+\cos \left({\delta }_i^{\mathrm{new}}\right)\right|+1\right)\times \left(-\sin \left({\delta }_i^{\mathrm{new}}\right)\times \left(W{h}_w-X_i\right)+\cos \left({\delta }_i^{\mathrm{new}}\right)\times \left(W{h}_f-X_i\right)\right)$$

(31)

$$X_i^{\mathrm{new}}=W{h}_j-\Delta X_i$$

(32)

3.1.3. Centrifugal Force (FE_i)

FE_i is formulated according to ${\delta }_i^{\mathrm{new}}$, and if FE_i is more than the random number r, FE_i is executed for the elected kth dimension randomly as Equation (34):

$$F{E}_i={\left({\left(\sin \left({\delta }_i^{\mathrm{new}}\right)\right)}^2\times {\left(\cos \left({\delta }_i^{\mathrm{new}}\right)\right)}^2\right)}^2$$

(33)

$$x_{i,k}=-x_{i,k}+\left(x_k^{\min }+x_k^{\max }\right)$$

(34)

3.1.4. Interplay between the Swarms

Whirlpools (swarms) displace and interact together. To the determined ∆Wh_j, the nearest swarm is determined according to its cost and the minimum value of Equation (35) and based on the Equations (36) and (37) and according to the amount of δ_j, change of the whirlpool’s location is determined as follows.

$${\Delta }_t=\frac{f\left(W{h}_t\right)}{{\left|sum\left(W{h}_t\right)-sum\left(W{h}_j\right)\right|}^{-1}}$$

(35)

$$\Delta W{h}_j=\left|\sin \left({\delta }_j^{\mathrm{new}}\right)+\cos \left({\delta }_j^{\mathrm{new}}\right)+\right|\times rand\left(1,D\right)\times \left(W{h}_f-W{h}_j\right)$$

(36)

$$W{h}_j^{\mathrm{new}}=W{h}_f-\Delta W{h}_j$$

(37)

Optimization process of TFWO has been given in Figure 1.

Figure 1. Optimization process of TFWO.

3.2. Improved TFWO (ITFWO)

In this paper is proposed a novel ITFWO in optimizing very complex real-world problems. Equation (38) shows the new learning and effective search in the proposed ITFWO optimizer. In Equation (38), local and global searches are integrated, similar to the original algorithm, and also separated from each other, which makes the population move towards the global optimum with different equations of motion and with different accelerations, and the search range of the population effectively increases. This new equation makes the proposed algorithm much better at searching both locally and globally. As a result, the proposed algorithm can solve more problems.

$$\left\{\begin{array}{l}\left\{\begin{array}{l}\Delta X_i=\left|\cos \left({\delta }_i^{\mathrm{new}}\right)\right|\times \left(W{h}_f-X_i\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}f\left(W{h}_f\right)\le f\left(W{h}_w\right)\hspace{0.17em}\hspace{0.17em}\\ \Delta X_i=\left|\sin \left({\delta }_i^{\mathrm{new}}\right)\right|\times \left(W{h}_w-X_i\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}f\left(W{h}_f\right)>f\left(W{h}_w\right)\end{array}\right.if\hspace{0.17em}rand\le 0.5\\ \Delta X_i=\cos \left({\delta }_i^{\mathrm{new}}\right)\times \left(W{h}_f-X_i\right)-\sin \left({\delta }_i^{\mathrm{new}}\right)\times \left(W{h}_w-X_i\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}rand>0.5\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}\right.$$

(38)

$$X_i^{\mathrm{new}}=W{h}_j-\Delta X_i$$

(39)

4. ITFWO for Various OPF Problems

The TFWO and ITFWO are used on the IEEE 30 bus test system to optimize eight various types of OPF problem, the generation size is 400 for two algorithms TFWO (with N_Wh = 3 and Npop = 45) and ITFWO (with N_Wh = 3 and Npop = 45). Test network information shown in [80], as shown in Figure 2 and also in Table 1.

Figure 2. The IEEE 30-bus system.

Table 1. ITFWO’s simulation optimal results.

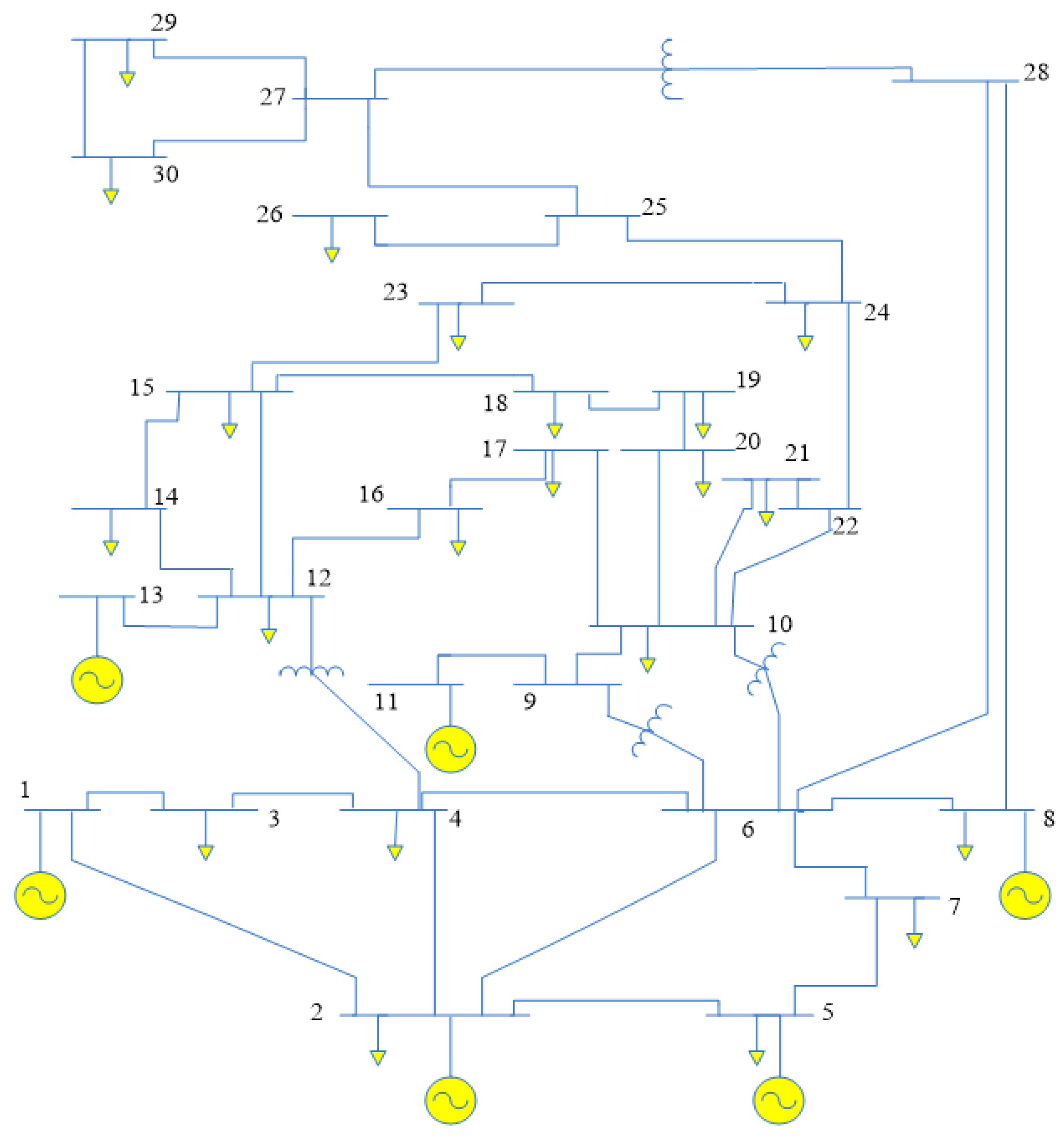
Optimal Values	Case:
	1	2	3	4	5	6
PG1	177.1347	102.6206	176.3672	139.9997	198.7625	122.3638
PG2	48.7297	55.5463	48.7697	55.0000	44.8823	52.4055
PG5	21.3767	38.1105	21.6725	24.0139	18.4464	31.4755
PG8	21.2495	35.0000	22.2509	34.9996	10.0000	35.0000
PG11	11.9308	30.0000	12.2195	18.4412	10.0001	26.7264
PG13	12.0000	26.6523	12.0006	17.6877	12.0000	21.0223
VG1	1.0838	1.0698	1.0420	1.0744	1.0813	1.0728
VG2	1.0606	1.0576	1.0227	1.0572	1.0579	1.0572
VG5	1.0337	1.0359	1.0156	1.0313	1.0306	1.0327
VG8	1.0382	1.0438	1.0076	1.0392	1.0371	1.0409
VG11	1.0996	1.0831	1.0480	1.0876	1.0998	1.0380
VG13	1.0514	1.0573	0.9874	1.0674	1.0642	1.0252
T6–9	1.0708	1.0862	1.0694	1.0247	1.0445	1.0972
T6–10	0.9185	0.9000	0.9000	0.9580	0.9700	0.9499
T4–12	0.9768	0.9900	0.9415	1.0015	0.9959	1.0349
T28–27	0.9739	0.9750	0.9710	0.9725	0.9780	1.0048
QC10	2.6779	4.7116	4.9366	4.8400	4.7709	2.9093
QC12	1.2768	0.1325	1.5448	0.0025	1.1157	0.2184
QC15	4.2837	4.4642	4.9993	3.0309	4.3867	3.8418
QC17	5.0000	5.0000	0.0019	4.9531	5.0000	5.0000
QC20	4.3330	4.2529	4.9985	4.8425	4.2343	4.9969
QC21	4.9993	5.0000	4.9996	5.0000	5.0000	4.9998
QC23	3.3775	3.2605	4.9995	2.1931	3.2950	4.3332
QC24	4.9997	5.0000	4.9998	4.9996	4.9999	5.0000
QC29	2.6234	2.5530	2.6538	2.5168	2.5933	2.6286
Cost ($/h)	800.4787	859.0009	803.8167	646.4799	832.1611	830.1598
Emission (t/h)	0.3663	0.2289	0.3639	0.2835	0.4379	0.2531
Power losses (MW)	9.0214	4.5297	9.8804	6.7421	10.6913	5.5935
V.D. (p.u.)	0.9087	0.9275	0.0941	0.9199	0.8625	0.2969

4.1. Basic OPF Solutions

Table 1 shows ITFWO’s simulation optimal results for six types of basic OPF without RPSs.

4.1.1. Type 1: Total Fuel Cost

This type of OPF has been given in Equation (40):

$$\begin{array}{l}J\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}({\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2)}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}\\ +\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\hspace{0.17em}\end{array}$$

(40)

Optimization results has been given in Table 1, the illustrate that the objective function by ITFWO is 800.4787 ($/h) that is better in comparison to the recent methods in the papers in Table 2 such as MICA-TLA [82], MGBICA [83], SFLA-SA [84], HFAJAYA [85], TS [86], MSA [80], IEP [87], SKH [88], MRFO [89], GWO [56], ARCBBO [90], MHBMO [29], PSOGSA [91], ABC [92], MFO [80], AGSO [51], FA [85], DE [93], JAYA [94], EP [95], PPSOGSA [96], AO [97], MPSO-SFLA [48], FPA [90] and TFWO. The convergence trends of the algorithms for this type have been given in Figure 3.

Table 2. The optimal results for Type 1.

Method	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)
SFLA-SA [84]	801.79	-	-	-
HFAJAYA [85]	800.4800	0.3659	9.0134	0.9047
TS [86]	802.29	-	-	-
MSA [80]	800.5099	0.36645	9.0345	0.90357
IEP [87]	802.46	-	-	-
SKH [88]	800.5141	0.3662	9.0282	-
MRFO [89]	800.7680	-	9.1150	-
GWO [56]	801.41	-	9.30	-
ARCBBO [90]	800.5159	0.3663	9.0255	0.8867
MHBMO [29]	801.985	-	9.49	-
PSOGSA [91]	800.49859	-	9.0339	0.12674
ABC [92]	800.660	0.365141	9.0328	0.9209
MFO [80]	800.6863	0.36849	9.1492	0.75768
AGSO [51]	801.75	0.3703	-	-
MGBICA [83]	801.1409	0.3296	-	-
FA [85]	800.7502	0.36532	9.0219	0.9205
DE [93]	802.39	-	9.466	-
JAYA [94]	800.4794	-	9.06481	0.1273
EP [95]	803.57	-	-	-
MICA-TLA [82]	801.0488	-	9.1895	-
PPSOGSA [96]	800.528	-	9.02665	0.91136
AO [97]	801.83	-	-	-
MPSO-SFLA [48]	801.75	-	9.54	-
FPA [80]	802.7983	0.35959	9.5406	0.36788
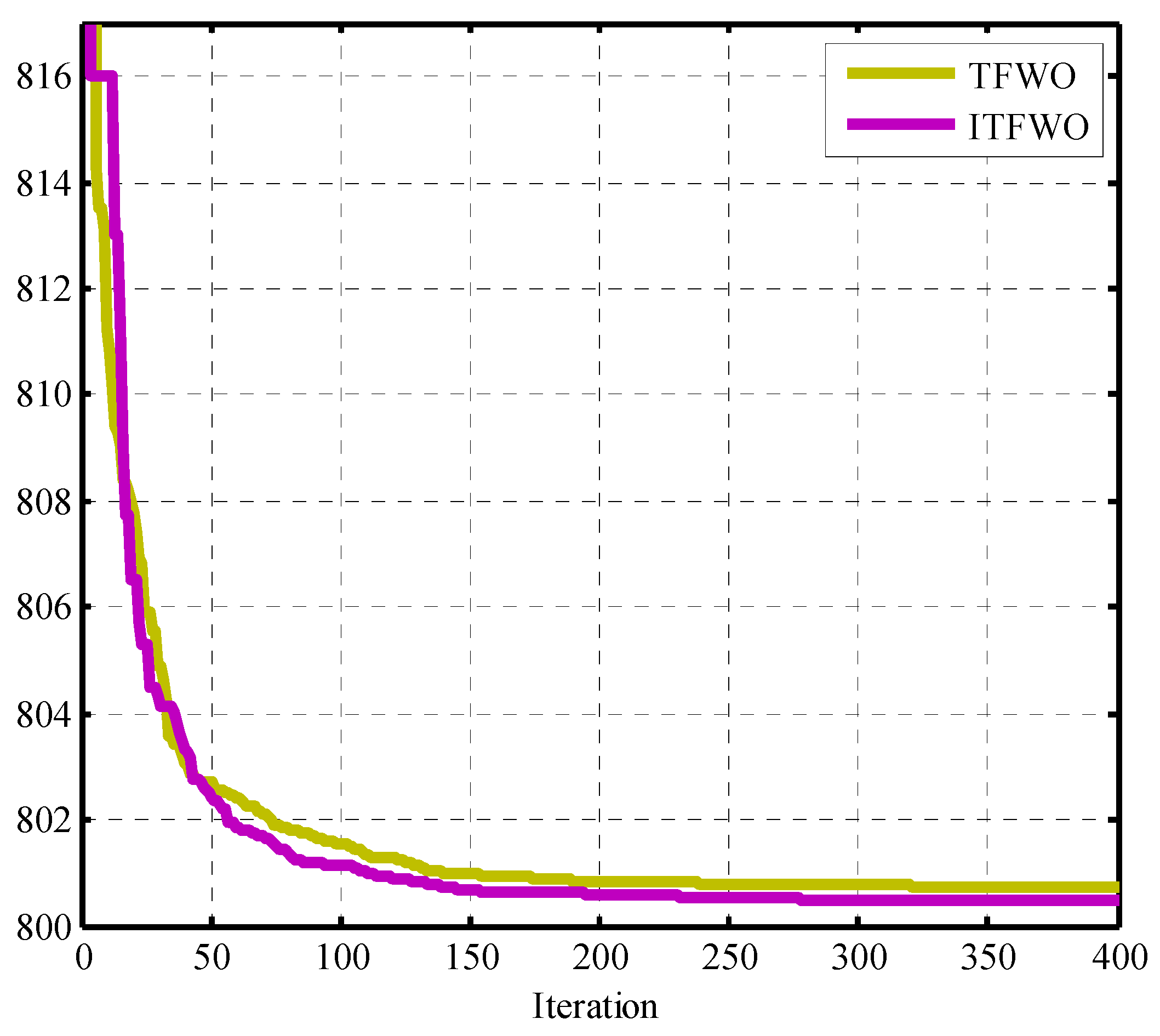
TFWO	800.7494	0.3702	9.2996	0.9015
ITFWO	800.4787	0.3663	9.0214	0.9087

Figure 3. Optimization process for Type 1.

4.1.2. Type 2: Including the Power Loss and the Fuel Cost

For this type of OPF problem, the network losses and the fuel cost are considered as the objective function, Equations (16) and (17), as given in Equation (44):

$$\begin{array}{l}{J}_4\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2}+{\varphi }_p{\displaystyle \sum _{i=1}^{NTL}{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{NTL}{G}_{ij}\hspace{0.17em}{V}_i^2\hspace{0.17em}+\hspace{0.17em}{B}_{ij}{V}_j^2\hspace{0.17em}-2V_i\hspace{0.17em}{V}_j\cos {\delta }_{ij}}}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\hspace{0.17em}\\ +\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}\end{array}$$

(41)

where, the amount of ${\varphi }_p$ has been choosen 40 [80].

The achieved optimal variables by ITFWO has been given in Table 1. In addition, the optimization processes of the problem have been given in Figure 4. The achieved best objective functions by ITFWO are 859.0009 ($/h) and 4.5297 (MW). By testing the simulation optimal results in Table 3, the amount of the optimization function that has been achieved via ITFWO is better in comparison to the other methods.

Figure 4. Optimization process for Type 2.

Table 3. The optimization results for Type 2.

Method	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)	${\mathit{J}}_4$
MSA [80]	859.1915	0.2289	4.5404	0.92852	1040.8075
QOMJaya [98]	826.9651	-	5.7596	-	1402.9251
SpDEA [99]	837.8510	-	5.6093	0.8106	1062.223
MOALO [100]	826.4556	0.2642	5.7727	1.2560	1057.3636
MJaya [98]	827.9124	-	5.7960	-	1059.7524
EMSA [101]	859.9514	0.2278	4.6071	0.7758	1044.2354
TFWO	859.2999	0.2292	4.5600	0.9207	1041.6999
ITFWO	859.0009	0.2289	4.5297	0.9275	1040.1889

4.1.3. Type 3: Including the Voltage Deviation (V.D.) and Fuel Cost

In this type of OPF problems has been considered $Fcost$ and V.D. in order to increase service and security indexes at buses as follows:

$$\begin{array}{l}{J}_5\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2}+{\varphi }_v{\displaystyle \sum _{i=1}^{NL}\left|\hspace{0.17em}V{L}_i-1.0\hspace{0.17em}\right|}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\hspace{0.17em}\\ +\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}\end{array}$$

(42)

where, the amount of ${\varphi }_v$ has been choosen 100 [80].

The best setting for control parameters has been achieved by ITFWO has been given in Table 1. Moreover, the simulation solutions of the methods have been given in Table 4, ITFWO has significantly decreased this multiobjective OPF. In addition, the optimization processes of the problem with the studied methods have been in Figure 5.

Table 4. The optimization results for Type 3.

Method	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)	${\mathit{J}}_5$
SSO [102]	803.73	0.365	9.841	0.1044	814.1700
SpDEA [99]	803.0290	-	9.0949	0.2799	831.0190
MFO [80]	803.7911	0.36355	9.8685	0.10563	814.3541
MPSO [80]	803.9787	0.3636	9.9242	0.1202	815.9987
DA-APSO [103]	802.63	-	-	0.1164	814.2700
MNSGA-II [104]	805.0076	-	-	0.0989	814.8976
MOMICA [104]	804.9611	0.3552	9.8212	0.0952	814.4811
PSO-SSO [102]	803.9899	0.367	9.961	0.0940	813.3899
TFWO [1]	803.416	0.365	9.795	0.101	813.5160
EMSA [101]	803.4286	0.3643	9.7894	0.1073	814.1586
PSO [102]	804.477	0.368	10.129	0.126	817.0770
BB-MOPSO [104]	804.9639	-	-	0.1021	815.1739
TFWO	804.1210	0.3640	10.0753	0.0979	813.9110
ITFWO	803.8167	0.3639	9.8804	0.0941	813.2267

Figure 5. Optimization process for Type 3.

4.1.4. Type 4: Piecewise OPF Problem

The fuel cost features for the network generators linked at first and second buses are modeled via a piecewise OPF problem because of various fuel types shown by:

$$f_i(P_{Gi})={\displaystyle \sum _{k=1}^{n_f}{\alpha }_{i,k}+b_{i,k}{P}_{Gi}+c_{i,k}{P}_{Gi}^2}$$

(43)

where a_i,k, c_i,k, b_i,k, are factors for the objective function of ith unit for kth fuel type; n_f is the number of fuel types for ith generator.

The OPF problem for this type is modeled via Equation (44).

$$\begin{array}{l}{J}_2\hspace{0.17em}={\displaystyle \sum _{k=1}^{NG}{\alpha }_{i,k}+b_{i,k}{P}_{Gi}+c_{i,k}{P}_{Gi}^2}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}\\ +\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\end{array}$$

(44)

Optimization results are in Table 1, which indicate that the objective function via the ITFWO is 646.4799 ($/h). The best objective function achieved by ITFWO is compared to the optimal solutions achieved via optimization methods in Table 5 such as IEP [87], LTLBO [38], FPA [80], MFO [80], SSA [105], SSO [22], MSA [80], MDE [93], GABC [106] and TFWO, and shows that ITFWO has the lowest objective function in comparison to the other methods. The convergence trends of the problem are given in Figure 6.

Table 5. The optimization results for Type 4.

Optimizer	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)
IEP [87]	649.312	-	-	-
LTLBO [38]	647.4315	0.2835	6.9347	0.8896
FPA [80]	651.3768	0.28083	7.2355	0.31259
MDE [93]	647.846	-	7.095	-
GABC [106]	647.03	-	6.8160	0.8010
MFO [80]	649.2727	0.28336	7.2293	0.47024
SSA [105]	646.7796	0.2836	6.5599	0.5320
SSO [22]	663.3518	-	-	-
MSA [80]	646.8364	0.28352	6.8001	0.84479
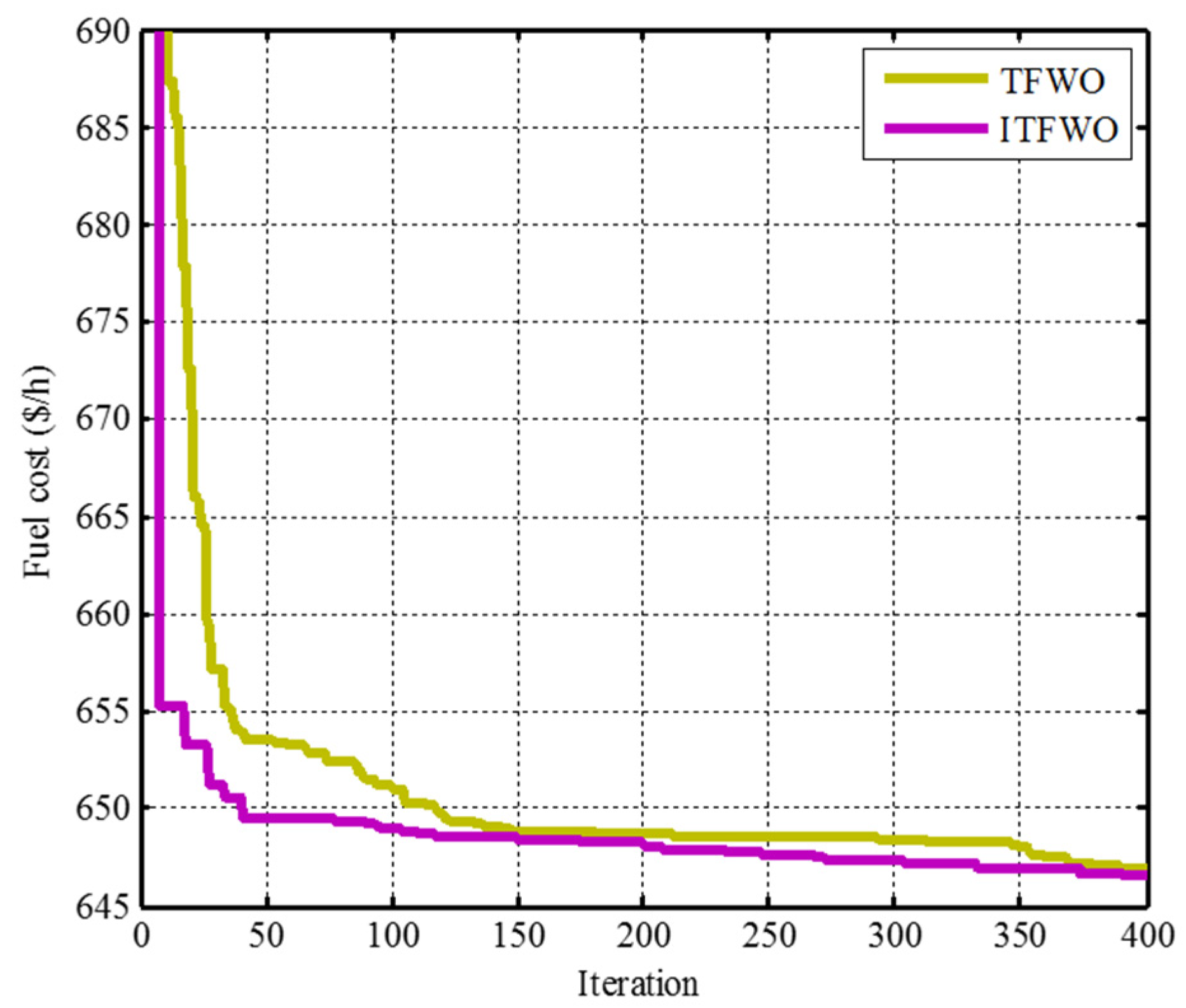
TFWO	646.9958	0.2839	6.7999	0.9135
ITFWO	646.4799	0.2835	6.7421	0.9199

Figure 6. Optimization process for Type 4.

4.1.5. Type 5: OPF Considering VPEs

In this situation, we included valve point loading effects (VPEs) on the generator’s cost function by adding a sine part to the objective function of the units:

$$\begin{array}{l}{J}_3\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2+\left|e_i\sin \left(f_i\left(P_{Gi}^{\min }-P_{Gi}\right)\right)\right|}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2\hspace{0.17em}\\ +\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}\end{array}$$

(45)

where e_i and f_i are VPEs cost factors of ith unit.

The achieved optimal variables by ITFWO has been given in Table 1. Table 6 shows the comparison of the ITFWO with recent modern methods. Based on Table 6, the optimum objective function has been achieved by ITFWO is 832.1611 ($/h) which is better compared to solutions of existing methods. The convergence trends of the objective function are shown in Figure 7.

Table 6. The simulation solutions for Type 5.

Method	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)
PSO [49]	832.6871	-	-	-
HFAJAYA [85]	832.1798	0.4378	10.6897	0.8578
FA [85]	832.5596	0.4372	10.6823	0.8539
SP-DE [107]	832.4813	0.43651	10.6762	0.75042
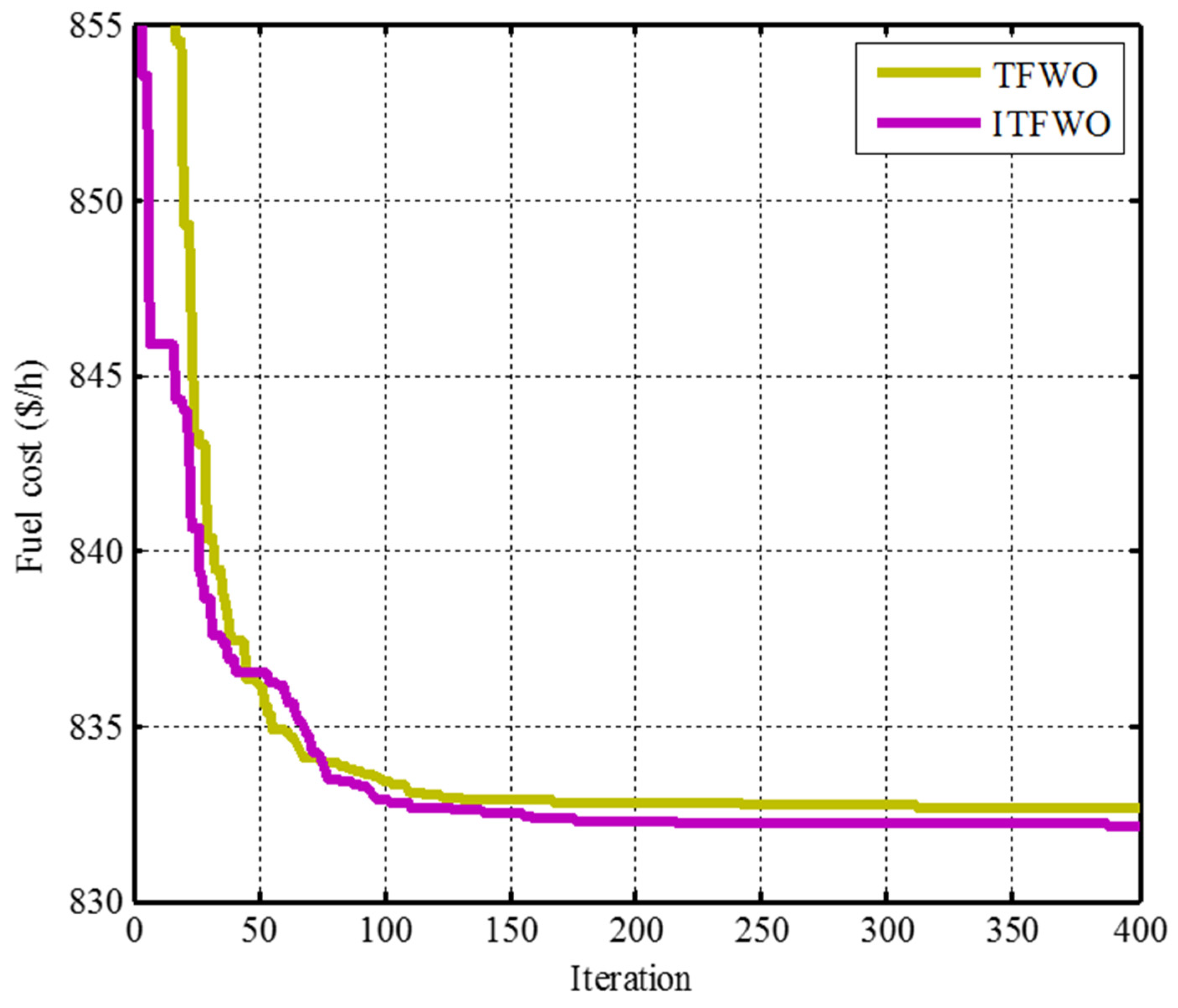
TFWO	832.6795	0.4381	10.9230	0.8288
ITFWO	832.1611	0.4379	10.6913	0.8625

Figure 7. Optimization process for Type 5.

4.1.6. Type 6: Considering the Losses, Voltage Deviation, Emissions and Fuel Cost

In this type, two main kinds of emission gases, SOX and NOX, have been considered, and the OPF function is determined via Equation (46) to optimize $Fcost$ and V.D., emission, and $Ploss$.

$$\begin{array}{l}{J}_6\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2}+{\varphi }_p{\displaystyle \sum _{i=1}^{NTL}{\displaystyle \sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^{NTL}{G}_{ij}\hspace{0.17em}{V}_i^2\hspace{0.17em}+\hspace{0.17em}{B}_{ij}{V}_j^2\hspace{0.17em}-2V_i\hspace{0.17em}{V}_j\cos {\delta }_{ij}}}+{\varphi }_v{\displaystyle \sum _{i=1}^{NL}\left|\hspace{0.17em}V{L}_i-1.0\hspace{0.17em}\right|}\\ +{\varphi }_e\min {\displaystyle \sum _{i=1}^{NG}\left({\alpha }_i+{\beta }_i{P}_{Gi}+{\gamma }_i{P}_{Gi}^2+{\xi }_i\exp ({\theta }_i{P}_{Gi})\right)}\hspace{0.17em}+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}\\ +\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2+\hspace{0.17em}{\lambda }_P{(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em})}^2}\end{array}$$

(46)

The amount of weights have been chosen as in [80] with ${\varphi }_p$ = 22, ${\varphi }_v$ = 21, and ${\varphi }_e$ = 19.

The best setting for control parameters that has been achieved by ITFWO has been given in Table 1. Moreover, the minimal objective function has been achieved by ITFWO compared to the optimal solutions achieved by optimization methods in Table 7; it can be seen that the optimum solution is 964.2606, which is suitable and better in comparison than the achieved optimal solutions in the recent papers. Furthermore, the convergence trends of the problem via the studied methods are given in Figure 8.

Table 7. The optimization results for Type 6.

Method	Fuel Cost ($/h)	Emission (t/h)	Power Losses (MW)	V.D. (p.u.)	${\mathit{J}}_6$
MODA [108]	828.49	0.265	5.912	0.585	975.8740
MOALO [100]	826.2676	0.2730	7.2073	0.7160	1005.0512
J-PPS2 [108]	830.8672	0.2357	5.6175	0.2948	965.1201
MNSGA-II [104]	834.5616	0.2527	5.6606	0.4308	972.9429
SSO [102]	829.978	0.25	5.426	0.516	964.9360
MSA [80]	830.639	0.25258	5.6219	0.29385	965.2907
J-PPS3 [108]	830.3088	0.2363	5.6377	0.2949	965.0228
PSO [102]	828.2904	0.261	5.644	0.55	968.9674
MFO [80]	830.9135	0.25231	5.5971	0.33164	965.8080
J-PPS1 [108]	830.9938	0.2355	5.6120	0.2990	965.2159
BB-MOPSO [104]	833.0345	0.2479	5.6504	0.3945	970.3379
TFWO	830.9726	0.2539	5.6305	0.2994	965.9551
ITFWO	830.1598	0.2531	5.5935	0.2969	964.2606

Figure 8. Optimization process for Type 6.

4.2. OPF with PV and WT Units

4.2.1. Type 7: Considering the Total Cost

The optimization function is to optimize the total generation cost determined by Equation (47) as follows:

$$\begin{array}{l}{J}_7\hspace{0.17em}={\displaystyle \sum _{i=1}^{NG}{\alpha }_i+b_i{P}_{Gi}+c_i{P}_{Gi}^2}+\left({\displaystyle \sum _{i=1}^{NV}F\cos t\left(P{V}_i\right)}\right)+\left({\displaystyle \sum _{i=1}^{NW}F\cos t\left(W{T}_i\right)}\right)\\ \hspace{0.17em}{\lambda }_P(\hspace{0.17em}{P}_{G1}-P_{G1}^{\lim }\hspace{0.17em}{)}^2+\hspace{0.17em}{\lambda }_S{\displaystyle \sum _{i=1}^{NTL}{(\hspace{0.17em}{S}_i-S_i^{\lim })}^2}+\hspace{0.17em}\hspace{0.17em}{\lambda }_V\hspace{0.17em}{\displaystyle \sum _{i=1}^{NL}{(\hspace{0.17em}V{L}_i-V{L}_i^{\lim })}^2}+\hspace{0.17em}{\lambda }_Q{\displaystyle \sum _{i=1}^{NG}{(\hspace{0.17em}{Q}_{Gi}-Q_{Gi}^{\lim })}^2}\hspace{0.17em}\end{array}$$

(47)

The best setting for control parameters that achieved by ITFWO are given in Table 8, with the highly minimized power generation cost in Type 7 compared to the basic TFWO. Furthermore, the convergence trends of the problem via the studied methods are shown in Figure 9.

Table 8. The optimization results for Type 7.

Variables	TFWO	ITFWO
PG1 (MW)	134.90791	134.90791
PG2	28.6365	27.873
Pws1	43.8208	43.3921
PG3	10	10
Pws2	36.991	36.6362
Pss	34.9256	36.3708
VG1 (p.u.)	1.0722	1.0722
VG2	0.954	1.0572
VG5	1.0996	1.0351
VG8	1.04	1.0397
VG11	1.1	1.0999
VG13	1.0815	1.055
QG1 (MVAR)	13.2357	−1.94508
QG2	−20	13.2188
Qws1	35	23.1987
QG3	34.7168	35.0261
Qws2	29.5148	30
Qss	25	17.5088
Fuelvlvcost ($/h)	441.0225	438.4895
Wind cost ($/h)	246.6480	243.9527
Solar cost ($/h)	94.6478	99.5521
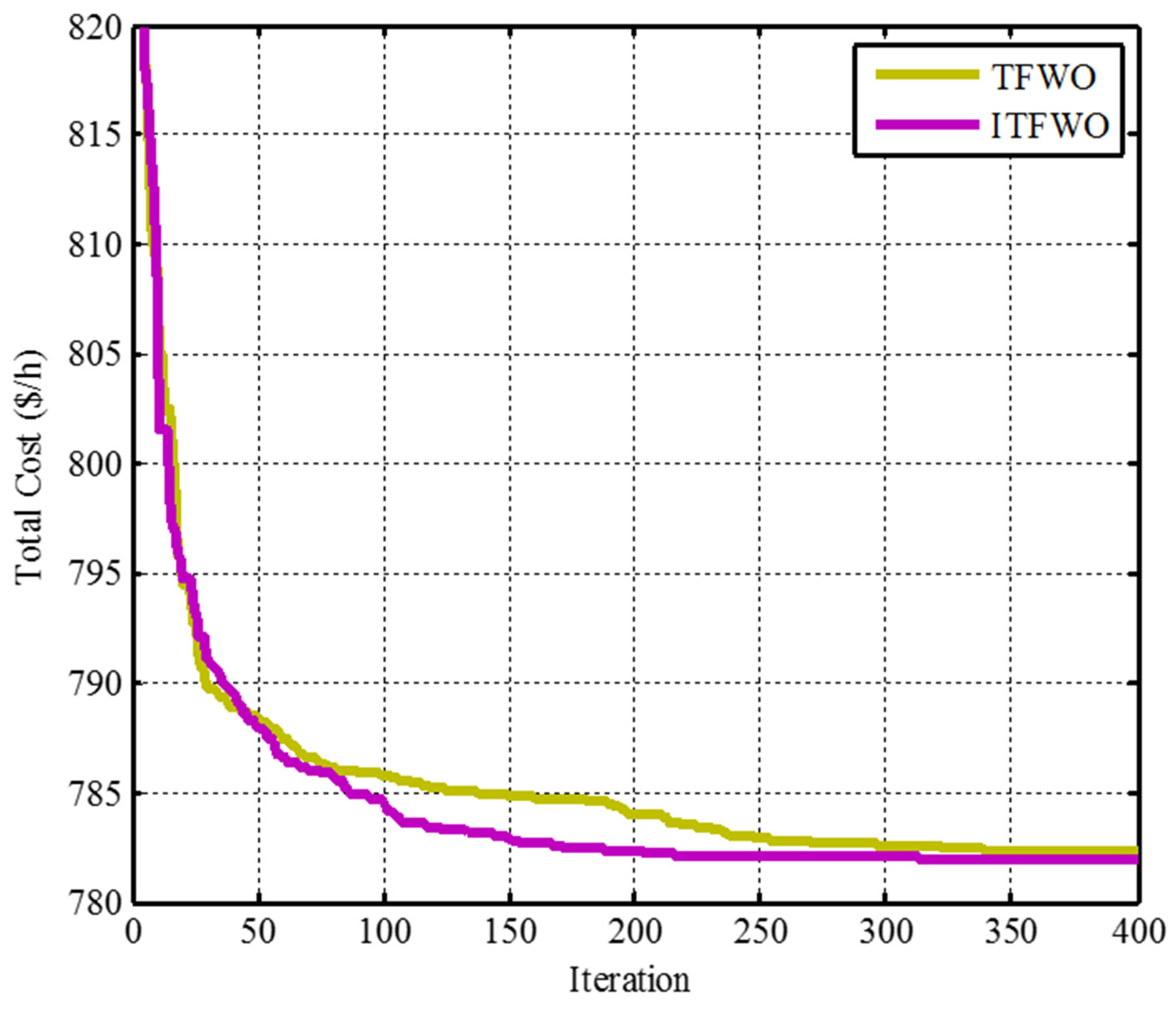
Total Cost ($/h)	782.3182	781.9943
Emission (t/h)	1.76205	1.76224
Power losses (MW)	5.8819	5.7801
V.D. (p.u.)	0.53921	0.46395

Figure 9. Optimization process for Type 7.

4.2.2. Type 8: Considering the Total Cost with Carbon Tax

Carbon tax (C_tax) has been imposed on any unit amount of liberated greenhouse gases for modelling investment in greener kinds of power such as solar and wind. The evolutionary function of emissions has been modeled in [27]:

$$C_E=C_{tax}E$$

(48)

$$J_8=J_7+C_{tax}E$$

(49)

C_tax had been considered to be $20 per tonne in [27].

According to the optimal results shown in Table 9, it is clear that the ITFWO achieves highly stable and quality optimal results in comparison with TFWO.

Table 9. The optimization results for Type 8.

Variables	TFWO	ITFWO
PG1 (MW)	123.73211	123.23758
PG2	33.6227	32.2873
Pws1	46.3179	45.6242
PG3	10	10
Pws2	38.9983	38.4356
Pss	36.01	39.0957
VG1 (p.u.)	1.0701	1.0697
VG2	1.0567	1.0562
VG5	1.0356	1.0352
VG8	1.0615	1.0997
VG11	1.0982	1.0983
VG13	1.0503	1.0511
QG1 (MVAR)	−3.04844	−3.18412
QG2	10.9594	10.7783
Qws1	22.2316	22.2315
QG3	40	40
Qws2	30	30
Qss	15.5342	15.8684
Fuelvlvcost ($/h)	431.9829	426.2436
Wind cost ($/h)	262.4784	258.0072
Solar cost ($/h)	98.3979	108.3925
Total Cost ($/h)	792.8592	792.6434
Emission (t/h)	0.90197	0.87689
J8	810.8986	810.1812
Power losses (MW)	5.2811	5.2804
V.D. (p.u.)	0.45991	0.46169
Carbon tax ($/h)	18.0394	17.5378

Furthermore, the convergence trends of the problem via the studied methods are shown in Figure 10.

Figure 10. Optimization process for Type 8.

4.3. Discussions

This part illustrates the optimal results of the studied methods achieved for various OPF problems to indicate ITFWO’s effectiveness, such as indexes Time (simulation time) Max (maximum), Mean (average), Min (minimum), and standard deviation (Std.) of the various problems shown in Table 10 for the eight types. According to Table 10, the optimal solutions of ITFWO are more suitable than the optimal solutions of the basic TFWO. These comparisons show the optimization power of ITFWO to optimize the various complex OPF problems; ITFWO is also able to discover a near-optimum solution in an adequate running time. The effectiveness and importance of any algorithm should decide on three terms: solution quality, computational efficiency, and robustness. The obtained values of the objective function for each case are shown in the summarized result. The best values of the objective functions are achieved for the majority of test cases and compared to existing techniques. The obtained values of the objective function are superior to the recent technique as well as previous techniques, and even obtained cost is better than for hybrid and developed based techniques; the comparisons are shown in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. The results of the proposed approach are very competitive compared with notable results from previous research. So, from the comparisons, ITFWO is superior in terms of solution quality. In comparison with TFWO, a convergence characteristic of ITFWO that it is smoother and achieved convergence in fewer generations. The Std. results of Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 show the enhanced ability of ITFWO to achieve superior quality solutions, in a computationally efficient and robust way. Furthermore, the proposed ITFWO provided a suitable balance between exploration and exploitation in the search space, which has led to finding the global optima in the presence of a large number of local optimum solutions. In summary, the improved mechanism of the proposed ITFWO has many advantages over the other methods—such as faster convergence characteristics, a lower standard deviation and simpler implementation.

Table 10. The optimal solutions to show the optimization power of the TFWO and ITFWO algorithms.

Type	Method	Min	Mean	Max	Std.	Time (s)
1	TFWO	800.7494	800.9724	801.3421	0.47	24
	ITFWO	800.4787	800.5890	800.6625	0.15	27
2	TFWO	646.9958	647.3823	647.5492	0.61	26
	ITFWO	646.4799	646.5597	646.6483	0.19	22
3	TFWO	832.6795	832.9914	833.4756	0.52	27
	ITFWO	832.1611	832.2704	832.37921	0.12	25
4	TFWO	1041.6999	1041.9880	1042.3729	0.35	25
	ITFWO	1040.1889	1040.2974	1040.3582	0.18	28
5	TFWO	813.9110	814.3185	814.7001	0.44	28
	ITFWO	813.2267	813.4023	813.5199	0.21	23
6	TFWO	965.9551	966.4769	966.9814	0.52	24
	ITFWO	964.2606	964.4160	964.5976	0.23	24
7	TFWO	782.3182	782.5711	782.8745	0.43	29
	ITFWO	781.9943	782.1624	782.3004	0.25	33
8	TFWO	810.8986	811.1852	811.5639	0.39	31
	ITFWO	810.1812	810.3045	810.4496	0.16	27

5. Conclusions

This study suggested a novel modified ITFWO algorithm for optimizing various complex OPF problems such as piecewise quadratic and quadratic objective functions, total cost while considering emissions, and losses and valve point effects in the IEEE 30-bus network with PV and WT units while satisfying security, physical and feasibility limits. Firstly, the various complex OPF problems have been illustrated as real-world optimization problems with different limits in a typical network. OPF with the various complex cost functions has been efficiently solved through the proposed ITFWO method whose computational efficiency, robustness and applicability have been also evidenced. ITFWO has efficiently fulfilled the objective to discover near-global optimal or optimum solutions of the non-linear test functions of the typical power network more effectively than previous optimal solutions and confirms the optimization power of the ITFWO method in comparison with the other optimization techniques based on the result quality for the various complex OPF problems. An equation of this nature cannot be solved using conventional methods, such as the equal consumed energy increase ratio law, when the constraint is complex and the cost function is not convex. In terms of solving such problems, the proposed ITFWO provides a feasible and effective reference scheme. It is found that the proposed ITFWO provides the lowest minimum of total cost among all the heuristic optimization techniques and confirms its capability in yielding a suitable balance between exploitation and exploration with better performance in terms of efficiency and robustness.

It has been found that the proposed ITFWO algorithm performs better than the other algorithms. This algorithm beats the original TFWO and a lot of other optimization algorithms in recent papers. In light of the ITFWO’s success in solving various OPF problems, it should also be applicable to other optimization problems. As part of our future studies, we will use the proposed algorithm to solve problems related to micro-grid power dispatch, global optimization of overcurrent relays, and dust control systems. Furthermore, ITFWO can solve complex hydrothermal scheduling, dynamic OPF, and optimal reactive power dispatch (ORPD). The author is particularly interested in the field of intelligent control of industrial dust in environmental protection, which is one of the areas of future research he plans to pursue.