Dynamic Responses of Semi-Flexible Pavements Used for the Autonomous Rail Rapid Transit
Abstract
1. Introduction
2. Materials and Methods
2.1. SFP and AC Materials
2.2. Test Section Implementation and In Situ Test
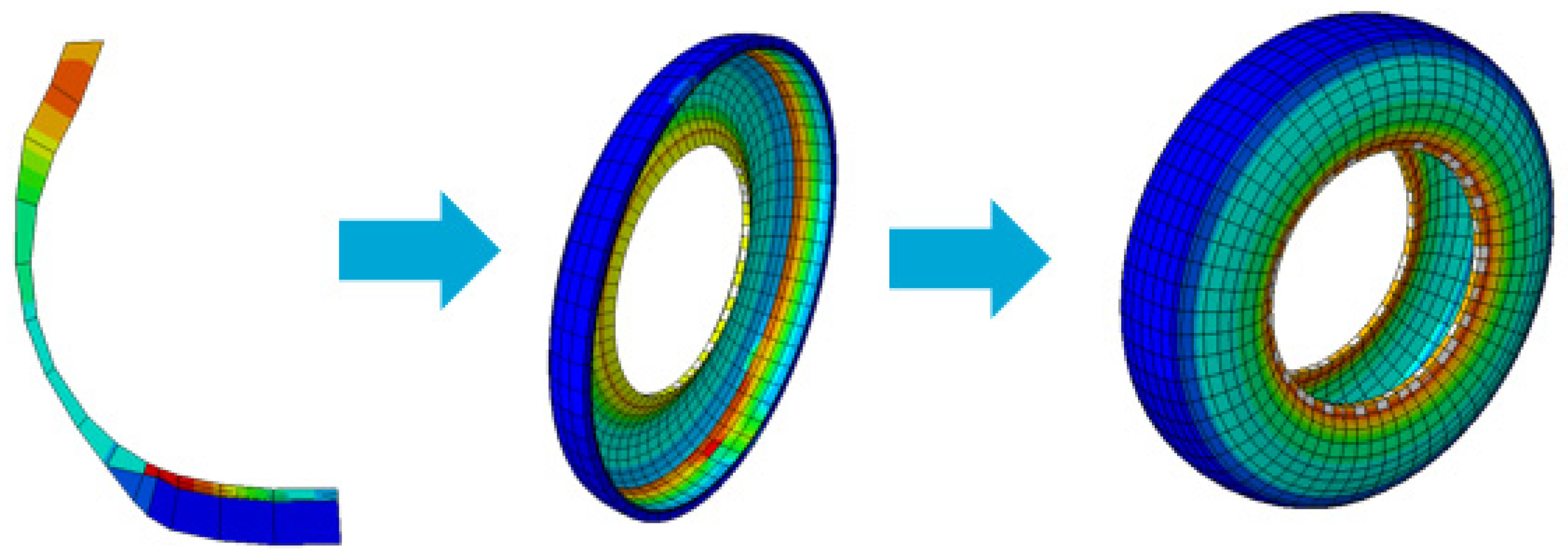
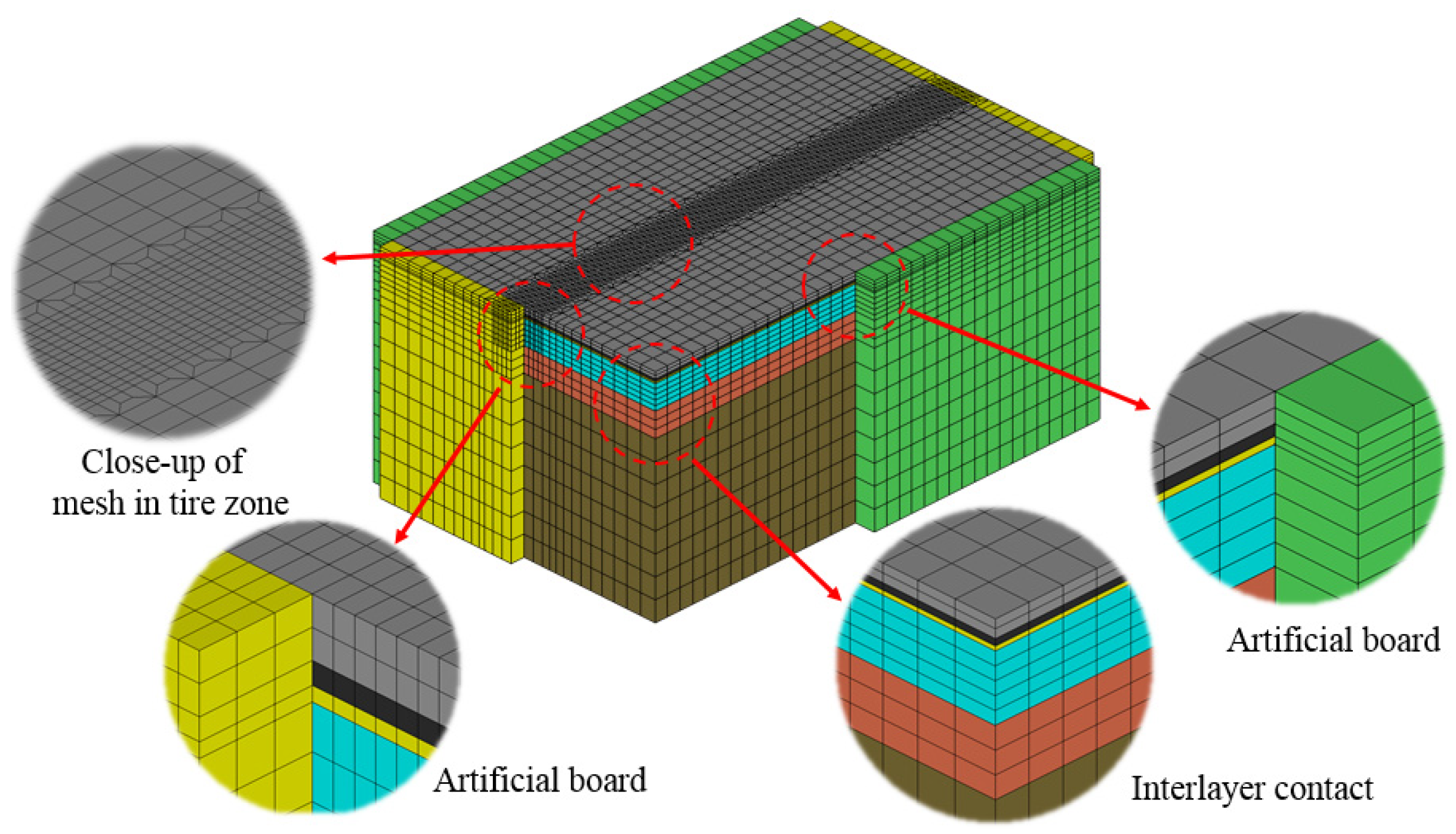
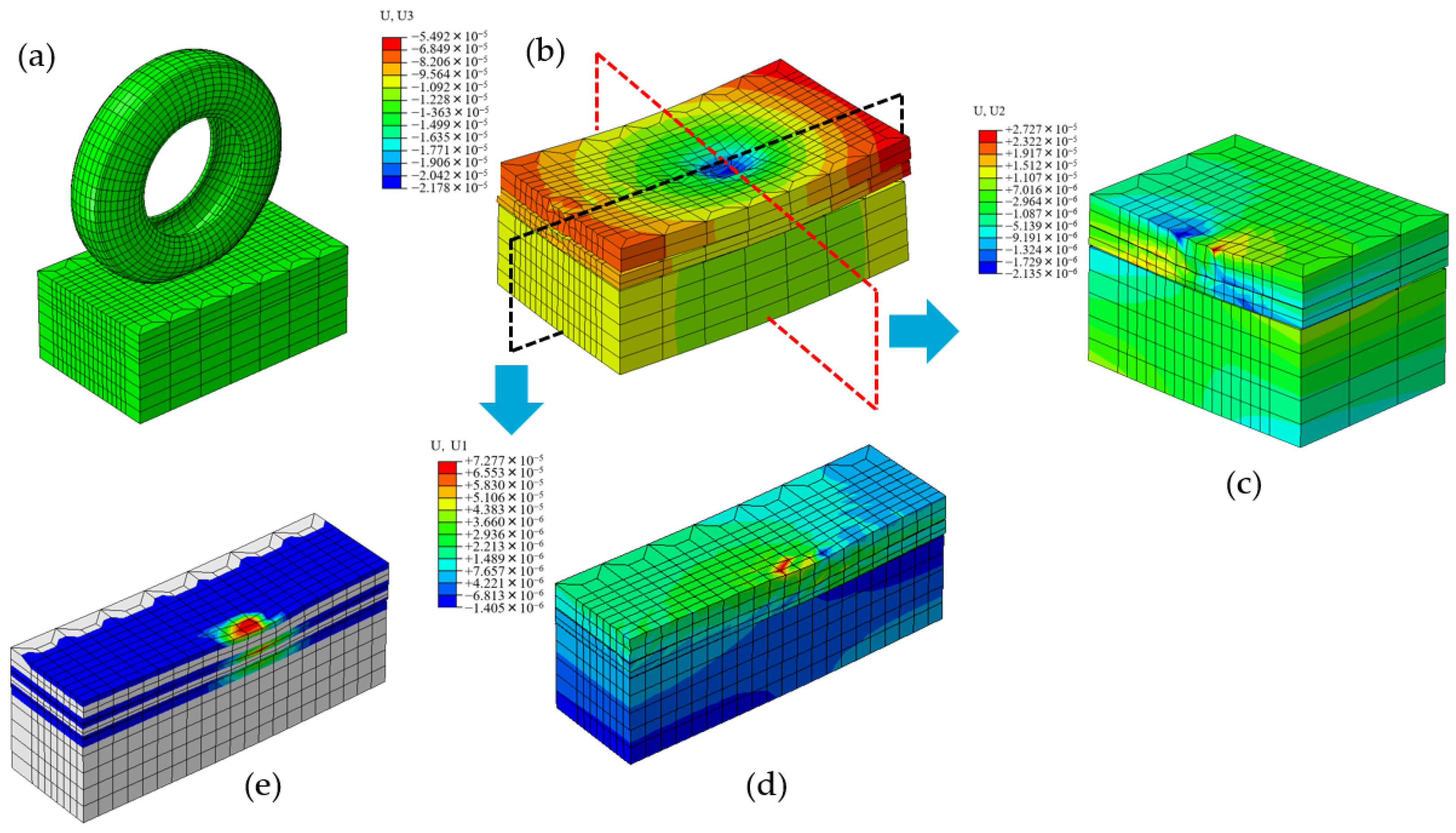
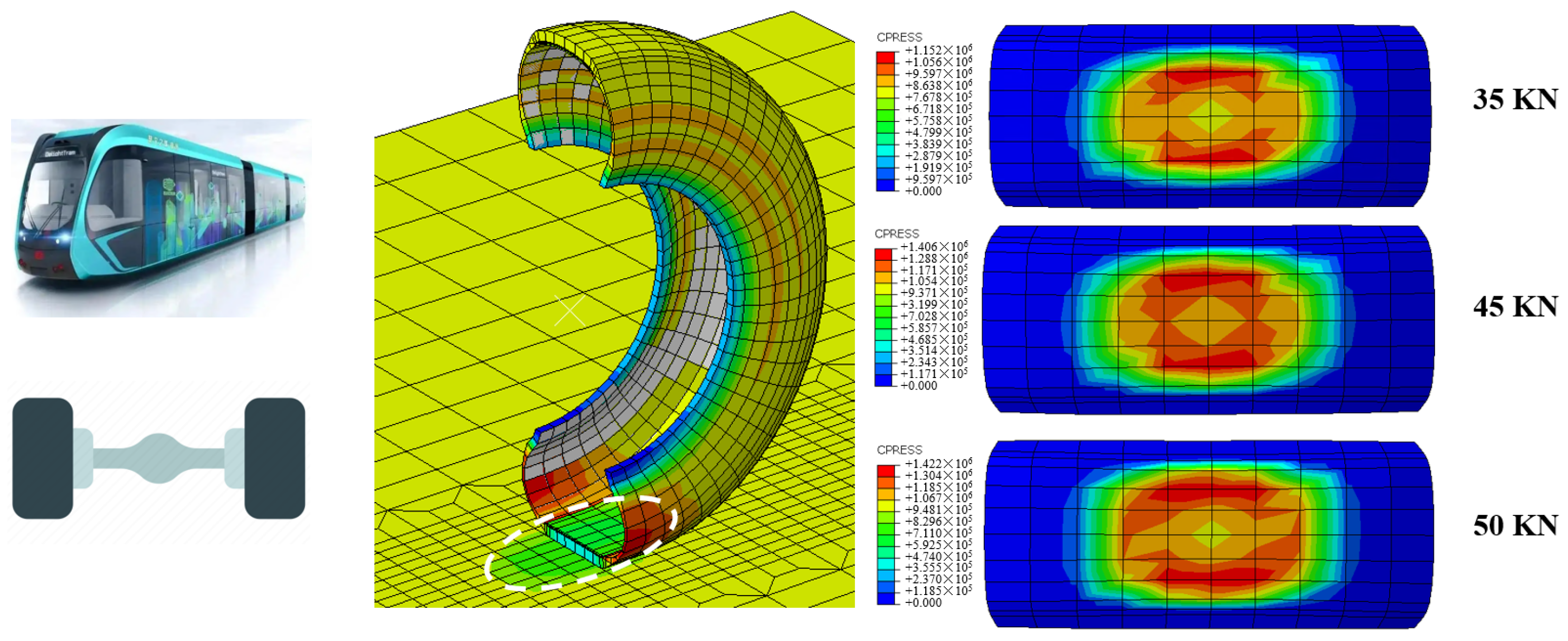
2.3. Setup of FE Model
2.4. Parameter Analysis
3. Results and Discussions
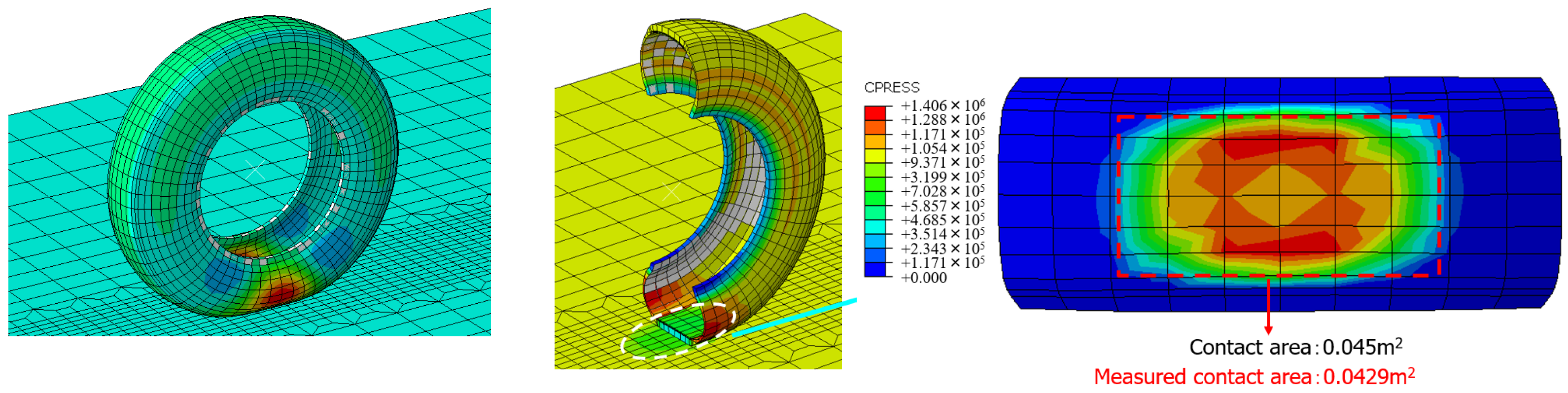
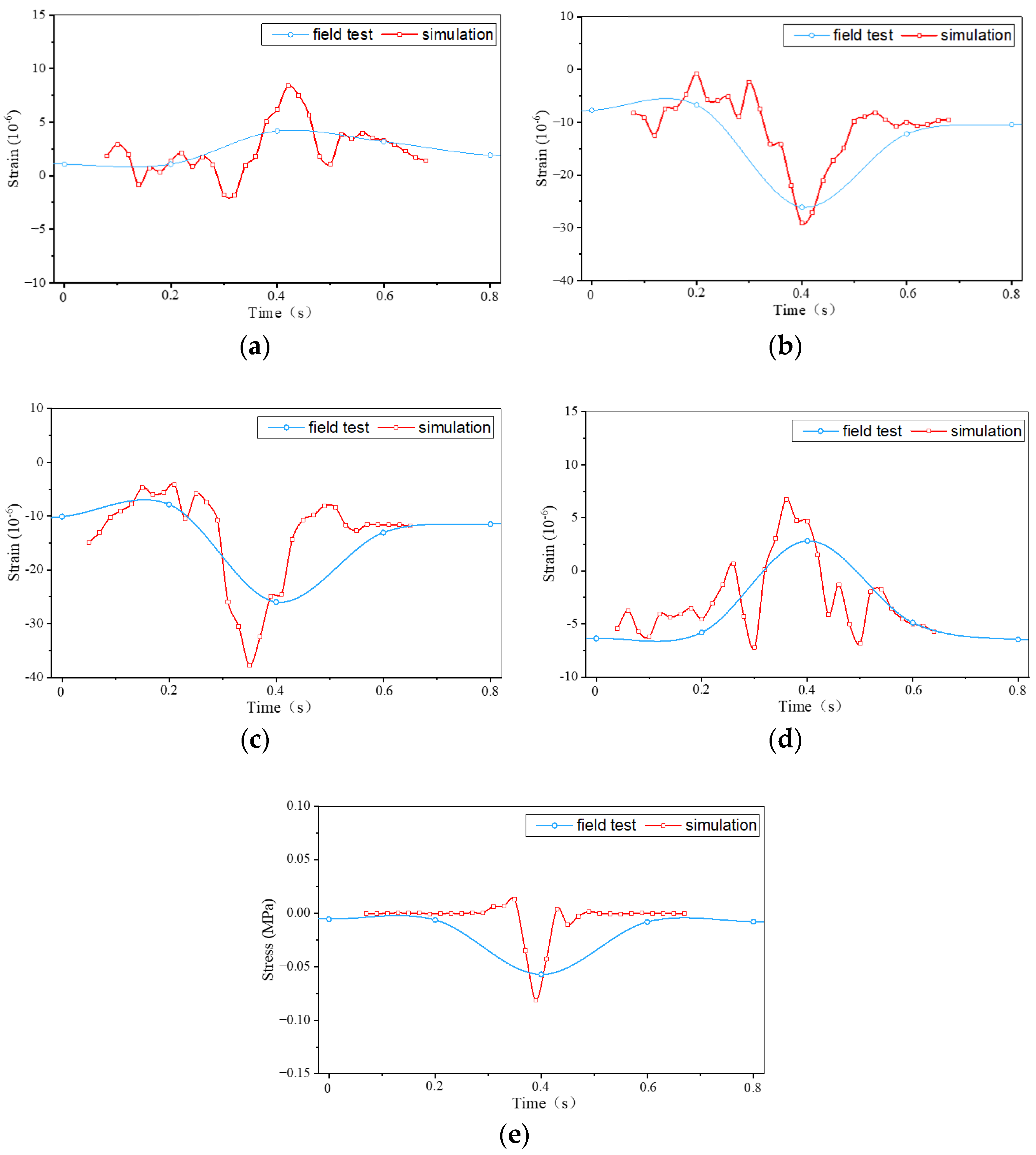
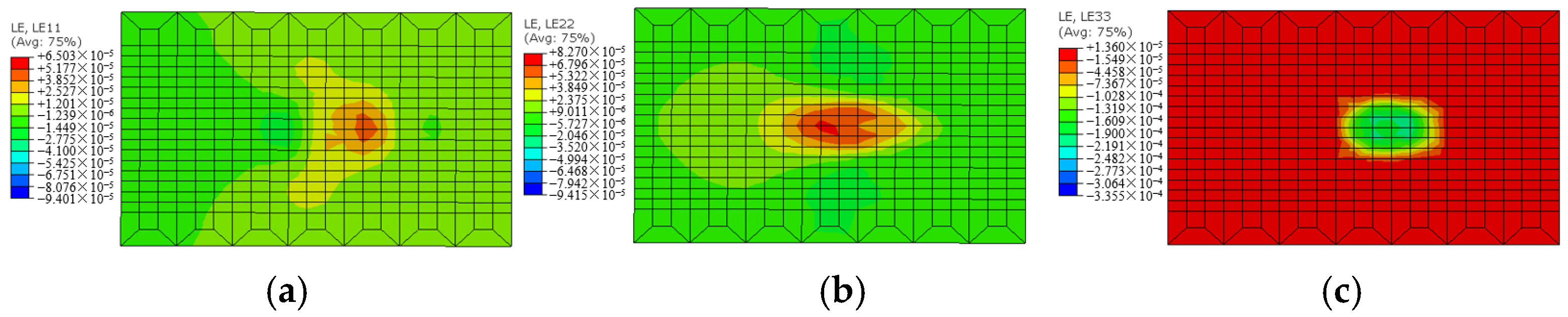
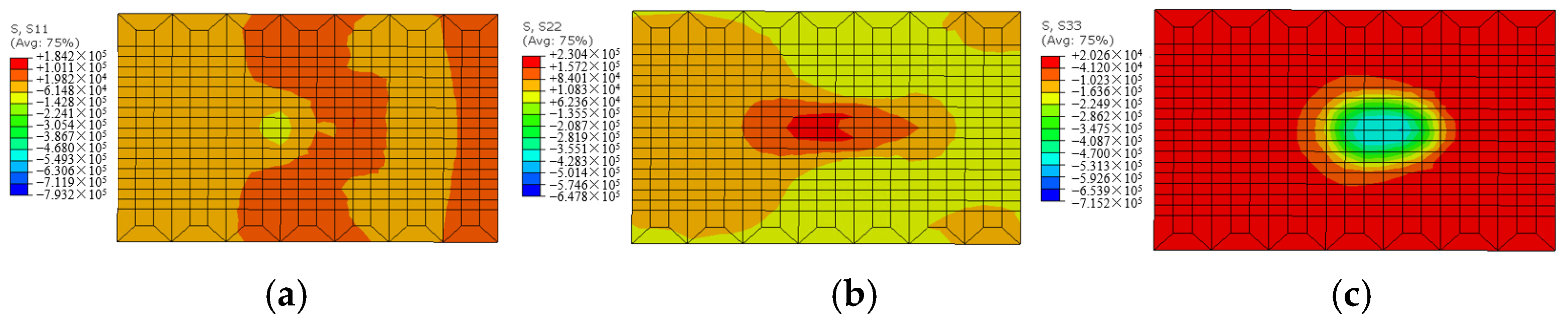
3.1. In Situ Test Results and FE Model Verification
- (1)
- Static analysis
- (2)
- Dynamic analysis
3.2. Distribution Features of Dynamic Responses under ART Train Load
3.3. The Effects of ART Train Operating Conditions
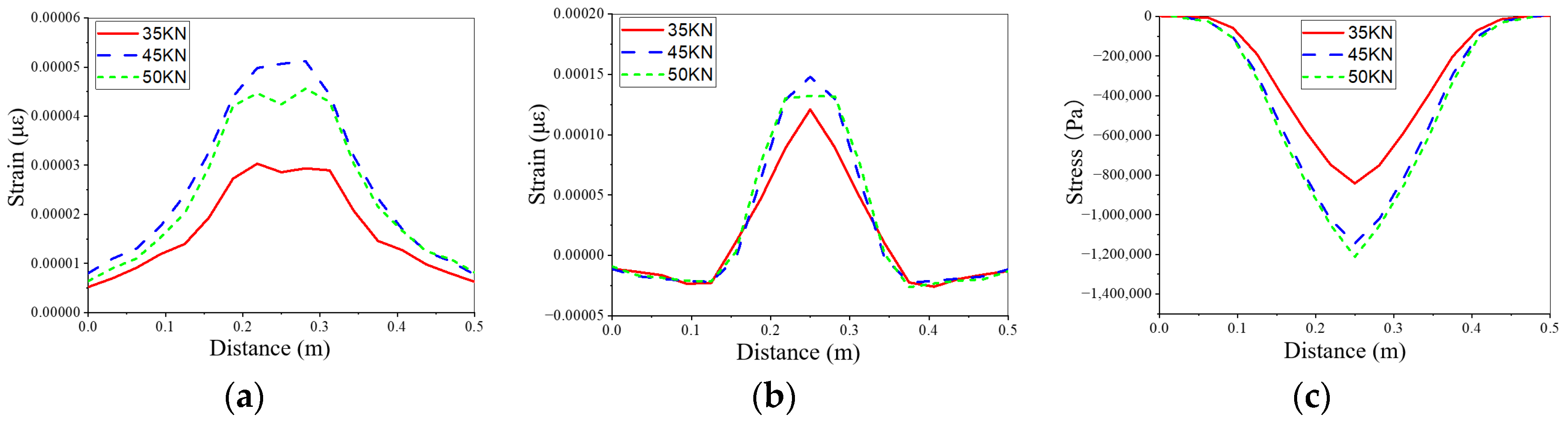
3.3.1. The Impact of Axle Load
3.3.2. The Impact of Tire Pressure
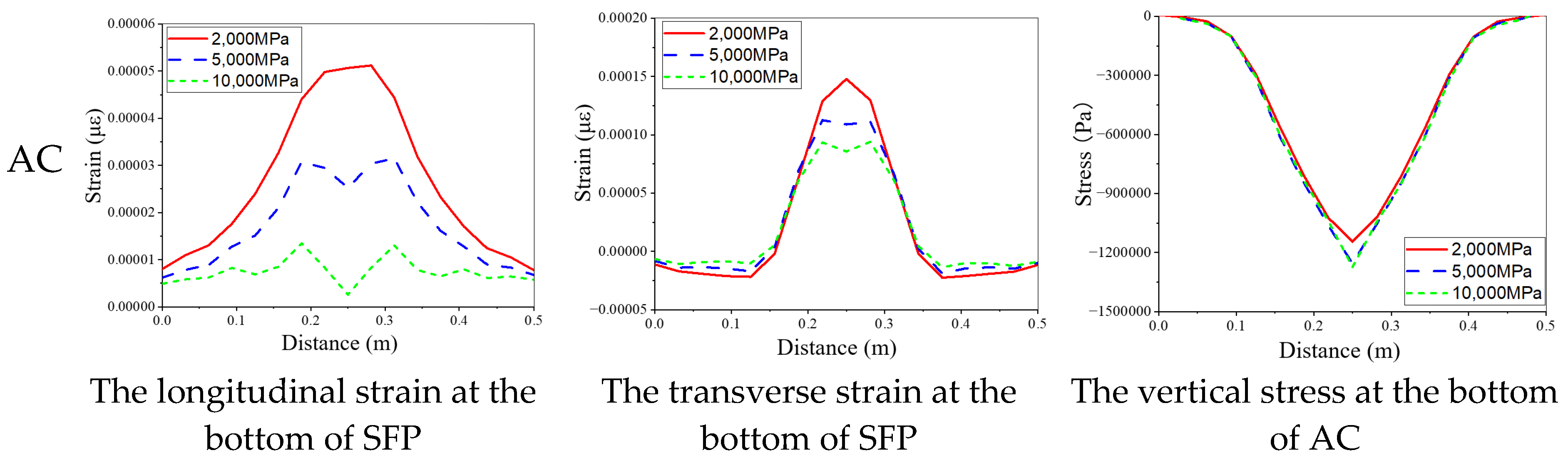
3.4. The Effects of Pavement Material Propeties
3.5. The Effects of Pavement Structural Composite
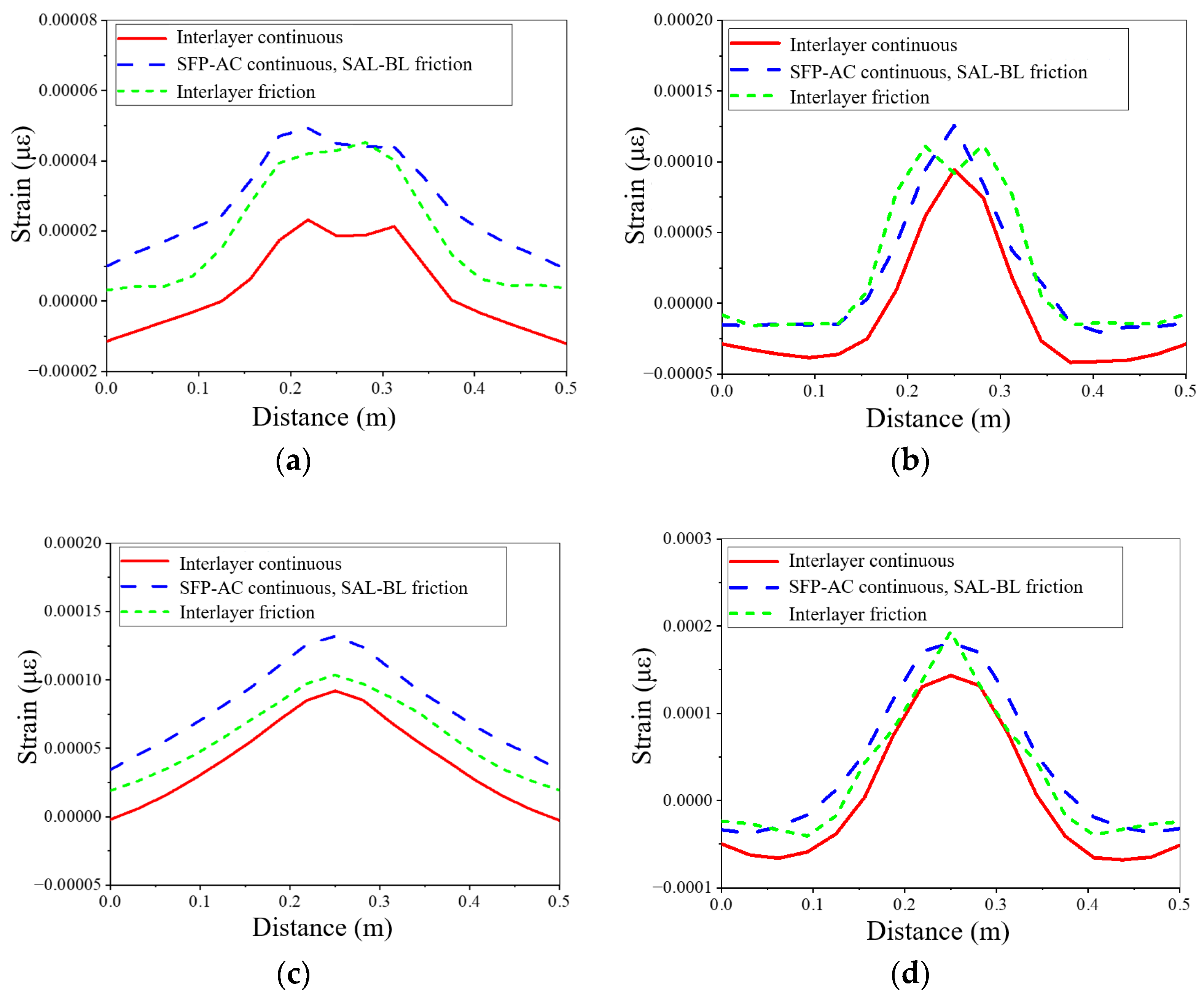
3.5.1. The Impact of Interlayer Conditions
3.5.2. The Impact of SFP Layer Thickness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Liu, W.; Zhang, C.; Wang, F.; Zhang, J.; Wang, L. Study on the Selection of Middle Urban Mass Rapid Transit System and Adaptability Analysis. J. Internet Technol. 2021, 22, 605–613. [Google Scholar]
- Newman, P.; Hargroves, C.; Davies-Slate, S.; Conley, D.; Verschuer, M.; Mouritz, M.; Yangka, D. The trackless tram: Is it the transit and city shaping catalyst we have been waiting for? J. Transp. Technol. 2019, 9, 31–55. [Google Scholar] [CrossRef]
- Li, T.; Zhang, S.; Xiao, G.; Wang, M.; Zhong, H.; Feng, J. Brake Instability Dynamic Model and Active Control Strategy for a Multiunit Articulated Rubber-Wheel Autonomous Rail Rapid Transit System. Sustainability 2022, 14, 14531. [Google Scholar] [CrossRef]
- Bachtiar, R.R.; Septione, A.D.; Larasati, N.A.; Perwira, D.A.; Pribadi, F.S.; Nurtanto, M.; Subramaniam, T.S. Autonomous Rail Rapid Transit (ART) Prototype Concept Using Wireless Charging System with Electromagnetic Induction Coupling. J. Railw. Transp. Technol. 2022, 1, 1–12. [Google Scholar]
- Wang, C.; Zhang, J.; Zhou, H.; Lu, H. Analysis of the running quality and road friendliness of the virtual track train in multiple running stages between stations. J. Mech. Sci. Technol. 2022, 36, 593–605. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Zhou, H. Analysis of Tire-Pavement Contact Morphology Characteristics during the Virtual Track Train Maneuvering. Adv. Civ. Eng. 2022, 2022, 1285552. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Zhou, H.; Lu, H. Dynamic Response and Permanent Deformation Analysis of Asphalt Pavement under the Virtual Rail Train. Tongji Daxue Xuebao/J. Tongji Univ. 2021, 49, 60–66. [Google Scholar]
- Cai, X.; Huang, W.; Wu, K. Study of the Self-Healing Performance of Semi-Flexible Pavement Materials Grouted with Engineered Cementitious Composites Mortar based on a Non-Standard Test. Materials 2019, 12, 3488. [Google Scholar] [CrossRef]
- Hassani, A.; Taghipoor, M.; Karimi, M.M. A state of the art of semi-flexible pavements: Introduction, design, and performance. Constr. Build. Mater. 2020, 253, 119196. [Google Scholar] [CrossRef]
- Pratelli, C.; Betti, G.; Giuffre, T.; Marradi, A. Preliminary In-Situ Evaluation of an Innovative, Semi-Flexible Pavement Wearing Course Mixture Using Fast Falling Weight Deflectometer. Materials 2018, 11, 611. [Google Scholar] [CrossRef]
- Cai, X.; Zhang, H.; Zhang, J.Y.; Chen, X.H.; Yang, J.; Hong, J.X. Investigation on reinforcing mechanisms of semi-flexible pavement material through micromechanical model. Constr. Build. Mater. 2019, 198, 732–741. [Google Scholar] [CrossRef]
- Ling, S.L.; Chen, Z.B.; Sun, D.Q.; Ni, H.T.; Deng, Y.; Sun, Y. Optimal Design of Pouring Semi-Flexible Pavement via Laboratory Test, Numerical Research, and Field Validation. Transp. Res. Rec. 2022, 2676, 479–495. [Google Scholar] [CrossRef]
- Zarei, S.; Ouyang, J.; Yang, W.T.; Zhao, Y.Q. Experimental analysis of semi-flexible pavement by using an appropriate cement asphalt emulsion paste. Constr. Build. Mater. 2020, 230, 116994. [Google Scholar] [CrossRef]
- Alae, M.; Zarei, S.; Ouyang, J.; Xiao, F.P. Prediction of top-down crack resistance in semi-flexible pavements under coupling effect of rutted surface and temperature gradient. Int. J. Pavement Eng. 2022. [Google Scholar] [CrossRef]
- Guo, X.G.; Hao, P.W. Influential Factors and Evaluation Methods of the Performance of Grouted Semi-Flexible Pavement (GSP)-A Review. Appl. Sci. 2021, 11, 6700. [Google Scholar] [CrossRef]
- Gong, M.H.; Xiong, Z.J.; Deng, C.; Peng, G.; Jiang, L.; Hong, J.X. Investigation on the impacts of gradation type and compaction level on the pavement performance of semi-flexible pavement mixture. Constr. Build. Mater. 2022, 324, 126562. [Google Scholar] [CrossRef]
- Xiong, Z.J.; Gong, M.H.; Hong, J.X.; Deng, C. The Influential Factors of Semi-Flexible Pavement Cracking Performance. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2022, 37, 953–962. [Google Scholar] [CrossRef]
- Hu, C.; Zhou, Z.G.; Chen, G.H. Effects of different types of acid rain on water stability of asphalt pavement. Constr. Build. Mater. 2022, 322, 126308. [Google Scholar] [CrossRef]
- Bharath, G.; Shukla, M.; Nagabushana, M.N.; Chandra, S.; Shaw, A. Laboratory and field evaluation of cement grouted bituminous mixes. Road Mater. Pavement Des. 2020, 21, 1694–1712. [Google Scholar] [CrossRef]
- Cai, J.; Pei, J.; Luo, Q.; Zhang, J.; Li, R.; Chen, X. Comprehensive service properties evaluation of composite grouting materials with high-performance cement paste for semi-flexible pavement. Constr. Build. Mater. 2017, 153, 544–556. [Google Scholar] [CrossRef]
- Hong, J.; Wang, K.; Xiong, Z.; Gong, M.; Deng, C.; Peng, G.; Zhu, H. Investigation into the freeze–thaw durability of semi-flexible pavement mixtures. Road Mater. Pavement Des. 2020, 21, 2198–2214. [Google Scholar] [CrossRef]
- Ma, X.; Jiang, J.; Zhao, Y.; Wang, H. Characterization of the interconnected pore and its relationship to the directional permeability of porous asphalt mixture. Constr. Build. Mater. 2021, 269, 121233. [Google Scholar] [CrossRef]
- Zarei, S.; Ouyang, J.; Zhao, Y.A. Evaluation of fatigue life of semi-flexible pavement with cement asphalt emulsion pastes. Constr. Build. Mater. 2022, 349, 128797. [Google Scholar] [CrossRef]
- Li, S.; Ni, F.; Dong, Q.; Zhao, Z.; Ma, X. Effect of filler in asphalt mastic on rheological behaviour and susceptibility to rutting. Int. J. Pavement Eng. 2021, 22, 87–96. [Google Scholar] [CrossRef]
- Dong, Q.; Zhao, X.; Chen, X.; Ma, X.; Cui, X. Long-term mechanical properties of in situ semi-rigid base materials. Road Mater. Pavement Des. 2021, 22, 1692–1707. [Google Scholar] [CrossRef]
- Xiong, H.; Han, J.F.; Wang, J.; Ren, Q.; Wu, L.B. Application of high viscosity-high modulus modified asphalt concrete in bus rapid transit station pavement-A case study in Chengdu, China. Case Stud. Constr. Mater. 2022, 17, e01337. [Google Scholar] [CrossRef]
- Li, G.S.; Xiong, H.; Ren, Q.; Zheng, X.G.; Wu, L.B. Experimental Study and Performance Characterization of Semi-Flexible Pavements. Coatings 2022, 12, 241. [Google Scholar] [CrossRef]
- Du, Y.F.; Chen, J.Q.; Han, Z.; Liu, W.Z. A review on solutions for improving rutting resistance of asphalt pavement and test methods. Constr. Build. Mater. 2018, 168, 893–905. [Google Scholar] [CrossRef]
- Xu, J.; Kong, C.; Xu, T. Displacemental and mesomechanical responses of semi-flexible pavement based on discrete element method. Int. J. Pavement Res. Technol. 2021, 15, 1484–1497. [Google Scholar] [CrossRef]
- Zarei, S.; Alae, M.; Ouyang, J.; Zhao, Y. Rutting and surface-initiated cracking mechanisms of semi-flexible pavements with cement asphalt emulsion pastes. Int. J. Pavement Eng. 2022. [Google Scholar] [CrossRef]
- Dong, Z.; Ma, X. Analytical solutions of asphalt pavement responses under moving loads with arbitrary non-uniform tire contact pressure and irregular tire imprint. Road Mater. Pavement Des. 2018, 19, 1887–1903. [Google Scholar] [CrossRef]
- Machemehl, R.B.; Wang, F.; Prozzi, J.A. Analytical study of effects of truck tire pressure on pavements with measured tire–pavement contact stress data. Transp. Res. Rec. 2005, 1919, 111–120. [Google Scholar] [CrossRef]
- Liu, S.; Chen, X.; Ma, Y.; Yang, J.; Cai, D.; Yang, G. Modelling and in-situ measurement of dynamic behavior of asphalt supporting layer in slab track system. Constr. Build. Mater. 2019, 228, 116776. [Google Scholar] [CrossRef]
- Jingbo, L.; Yin, G.; Yixin, D. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements. Chin. J. Geotech. Eng. 2006, 28, 1070–1075. [Google Scholar]
- Yin, G.U.; Jingbo, L.I.U.; Yixin, D.U. 3D Consistent Viscous-spring Artificial Boundary and Viscous-spring Boundary Element. Eng. Mech. 2007, 24, 31–37. [Google Scholar]








| Tenperature (°C) | Modulus (MPa) | |
|---|---|---|
| SFP-13 | AC-13 | |
| 20 | 8545 | 8654 |
| 30 | 4756 | 5104 |
| 40 | 2346 | 3270 |
| 50 | 1091 | 2278 |
| 60 | 207 | 1703 |
| Material | Modulus (MPa) | Possion Ratio | Density (kg/m3) | Damping Ratio |
|---|---|---|---|---|
| SFP-13 (33 °C) | 4346 | 0.25 | 2500 | 0.06 |
| AC-13 (35 °C) | 4690 | 0.25 | 2500 | 0.1 |
| SAL | 400 | 0.3 | 2200 | 0.3 |
| Base | 8500 | 0.3 | 2000 | 0.08 |
| Subbase | 700 | 0.3 | 1900 | 0.1 |
| Subgrade | 50 | 0.35 | 1900 | 0.2 |
| Correction Coefficient | Ranges of Values | Recommended Value |
|---|---|---|
| αT | 1~2.0 | 1.33 |
| αN | 0.5~1 | 0.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, B.; Zhang, H.; Liu, S.; Gong, M.; Yang, J. Dynamic Responses of Semi-Flexible Pavements Used for the Autonomous Rail Rapid Transit. Appl. Sci. 2023, 13, 3673. https://doi.org/10.3390/app13063673
Pan B, Zhang H, Liu S, Gong M, Yang J. Dynamic Responses of Semi-Flexible Pavements Used for the Autonomous Rail Rapid Transit. Applied Sciences. 2023; 13(6):3673. https://doi.org/10.3390/app13063673
Chicago/Turabian StylePan, Biao, Hongjian Zhang, Song Liu, Minghui Gong, and Jun Yang. 2023. "Dynamic Responses of Semi-Flexible Pavements Used for the Autonomous Rail Rapid Transit" Applied Sciences 13, no. 6: 3673. https://doi.org/10.3390/app13063673
APA StylePan, B., Zhang, H., Liu, S., Gong, M., & Yang, J. (2023). Dynamic Responses of Semi-Flexible Pavements Used for the Autonomous Rail Rapid Transit. Applied Sciences, 13(6), 3673. https://doi.org/10.3390/app13063673








