Metro Track Geometry Defect Identification Model Based on Car-Body Vibration Data and Differentiable Architecture Search
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Train Vibration Data Analysis Methods
2.2. ML-Based Train Vibration Data Analysis Method
2.3. Network Architecture Search in the Field of ML
2.4. Discussion of Existing Research
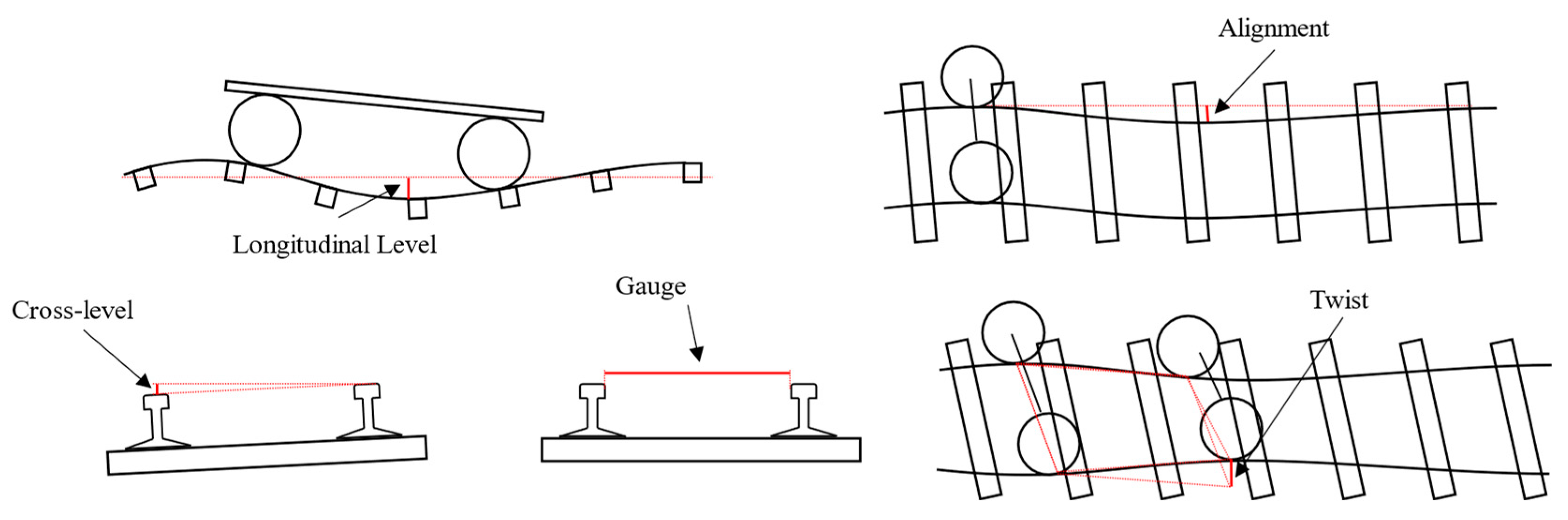
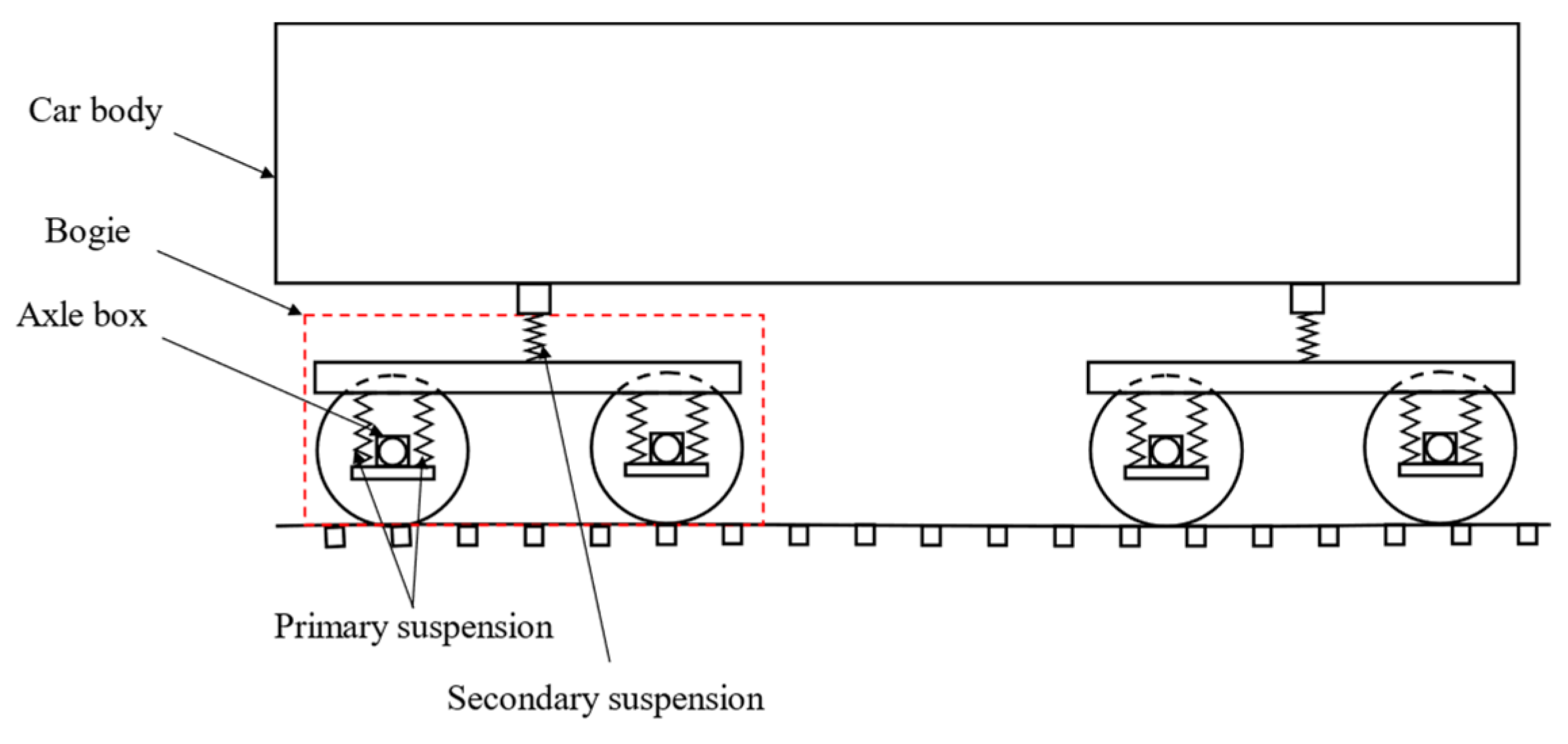
3. Problem Description
3.1. Basic Problem
3.2. Transformed Problem
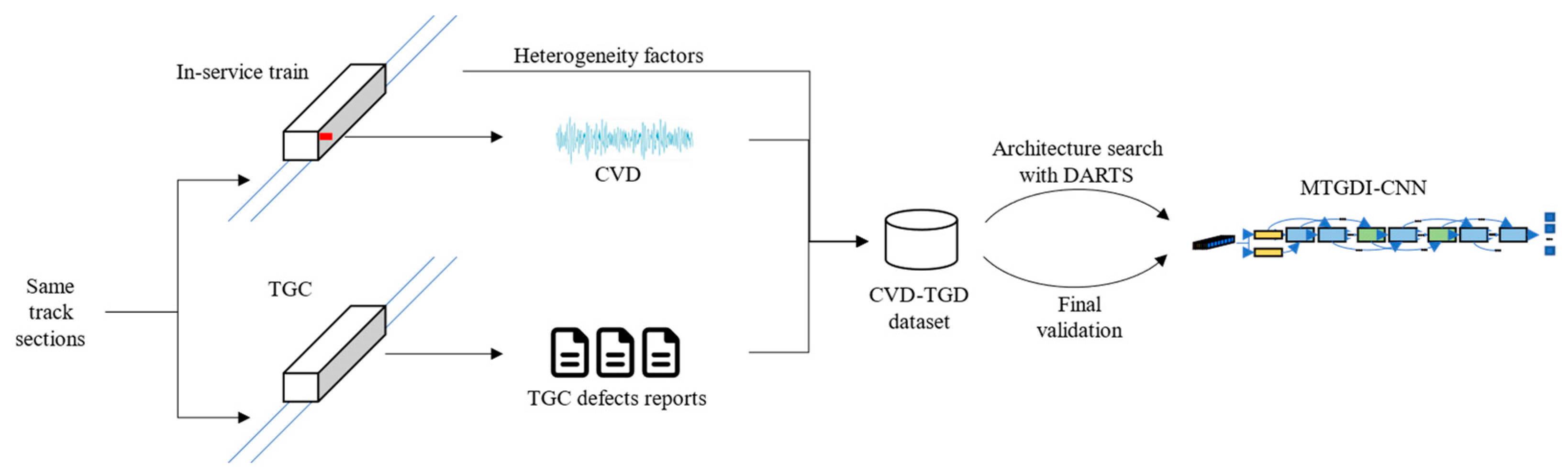
4. Metro Track Geometry Defect Identification Model and Its Optimization Method
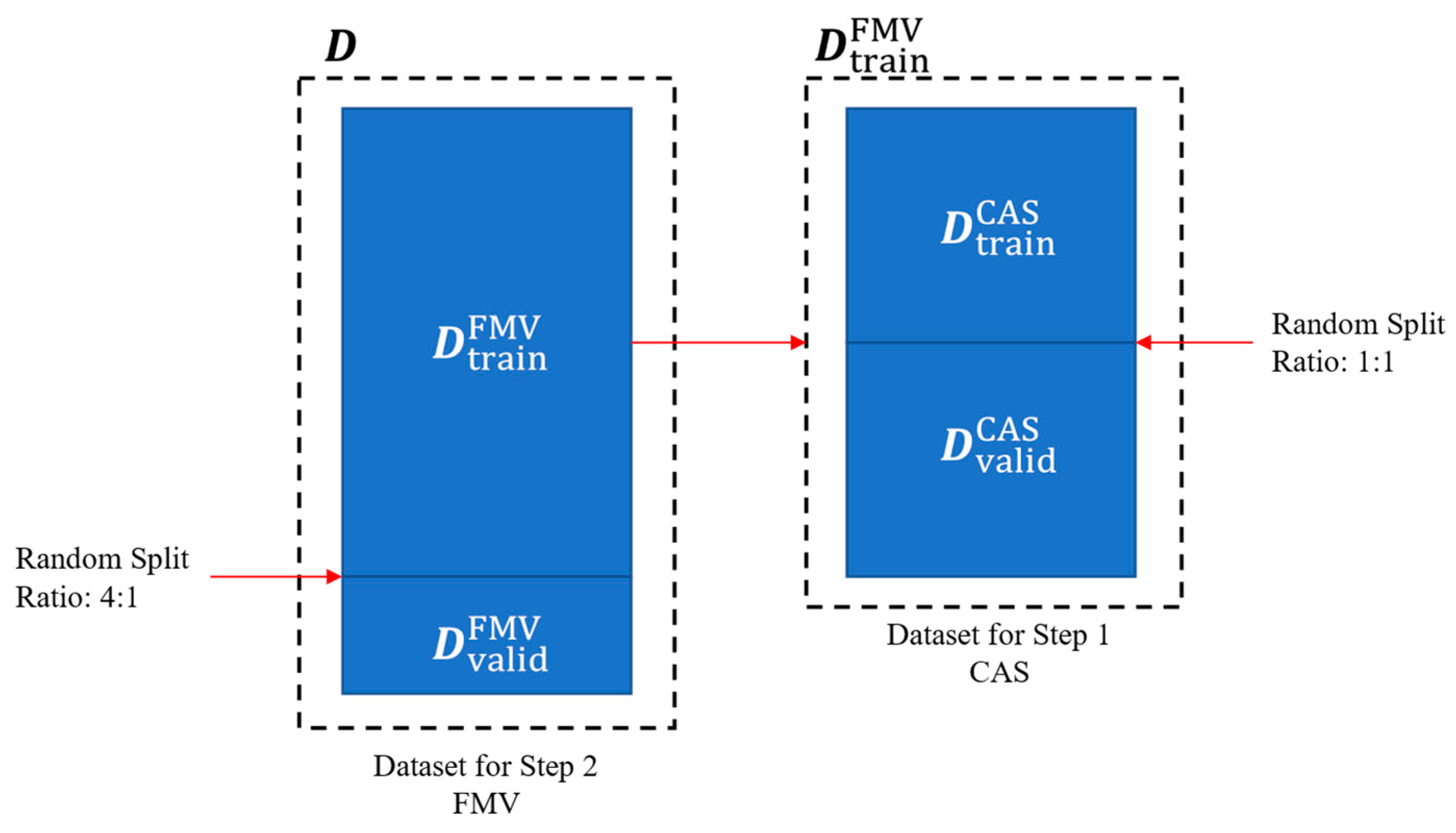
4.1. Example Dataset Design
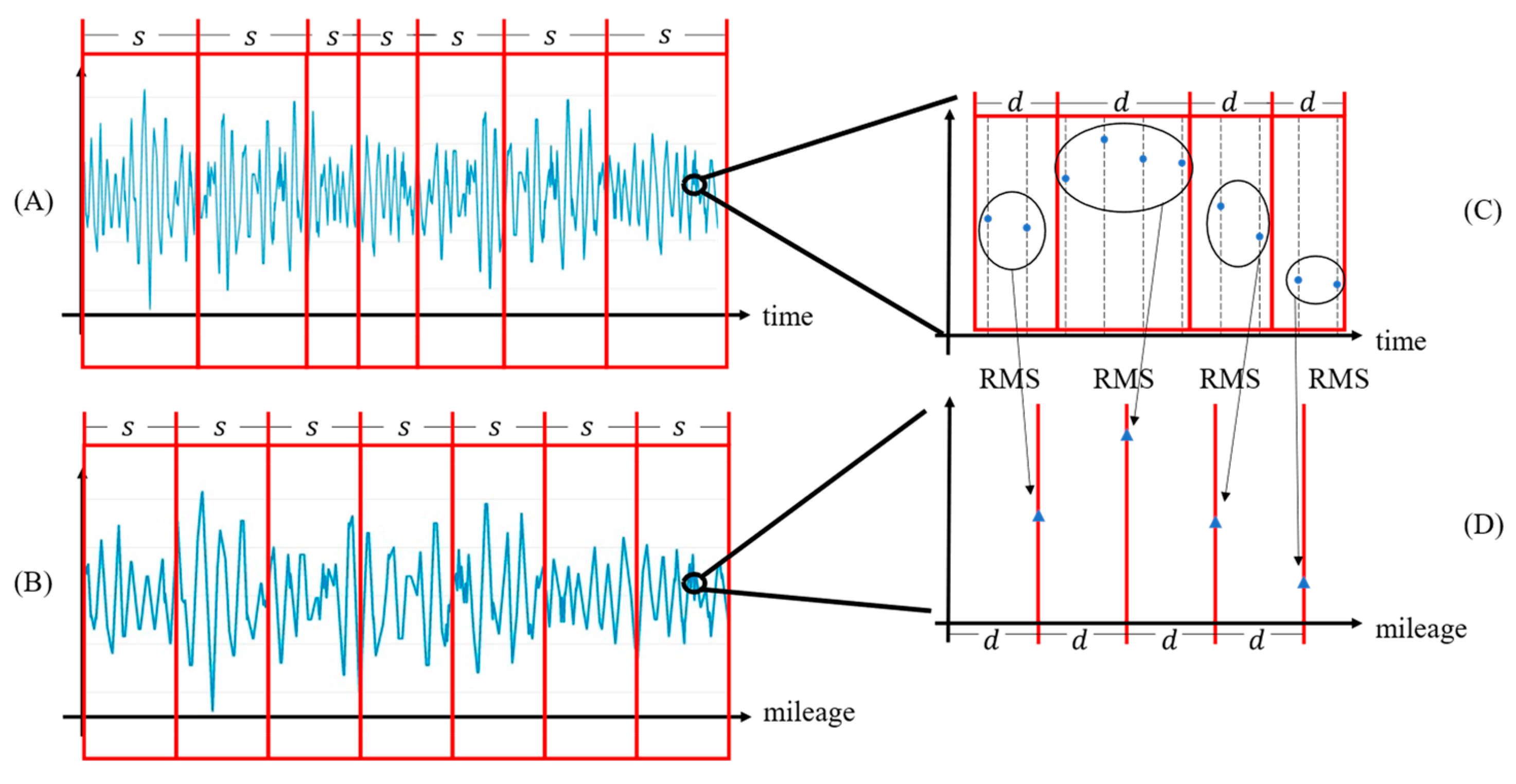
4.1.1. Sample Generation Rules
4.1.2. Sample Labeling Rules
4.2. MTGDI-CNN Based on DARTS
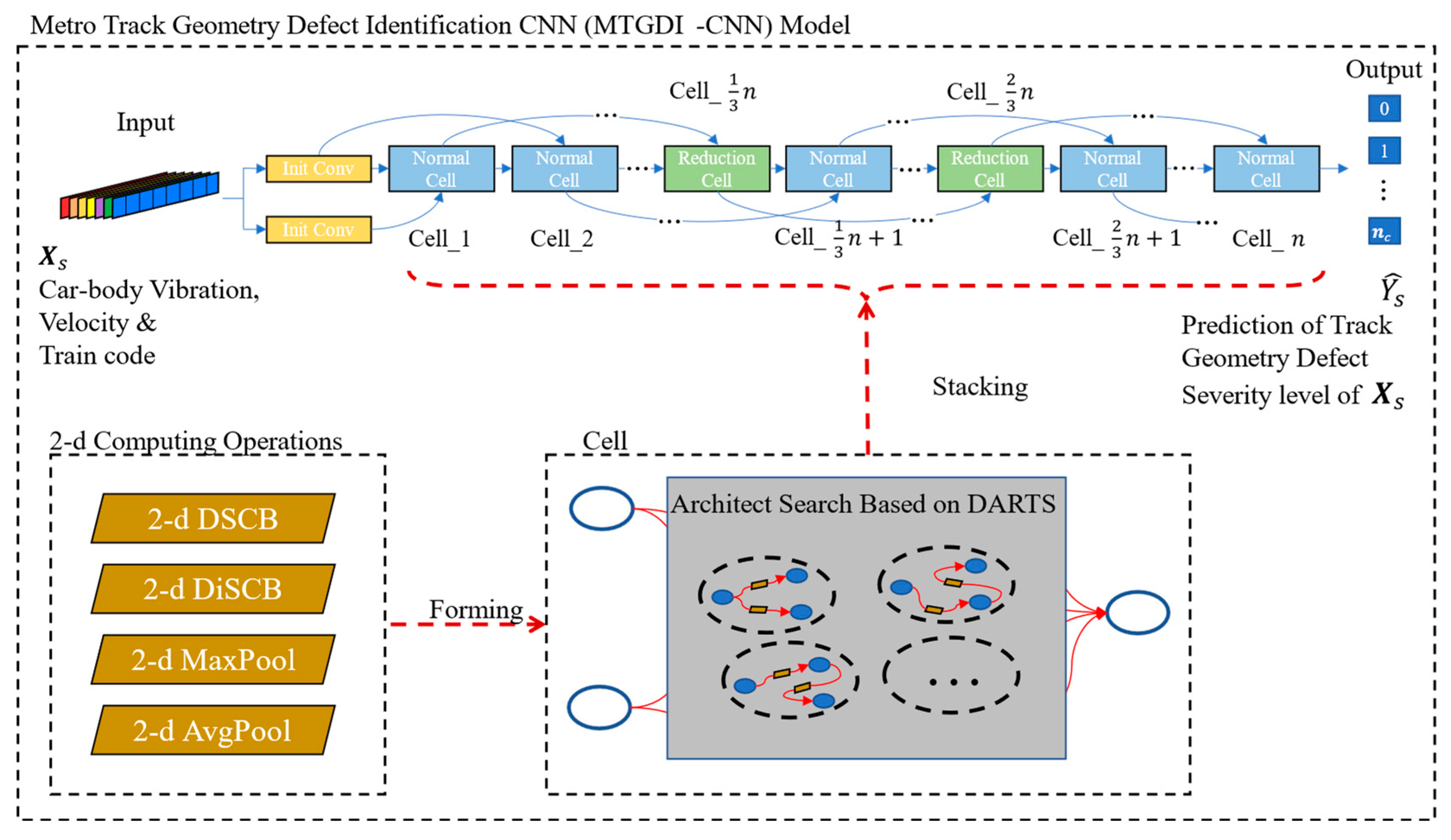
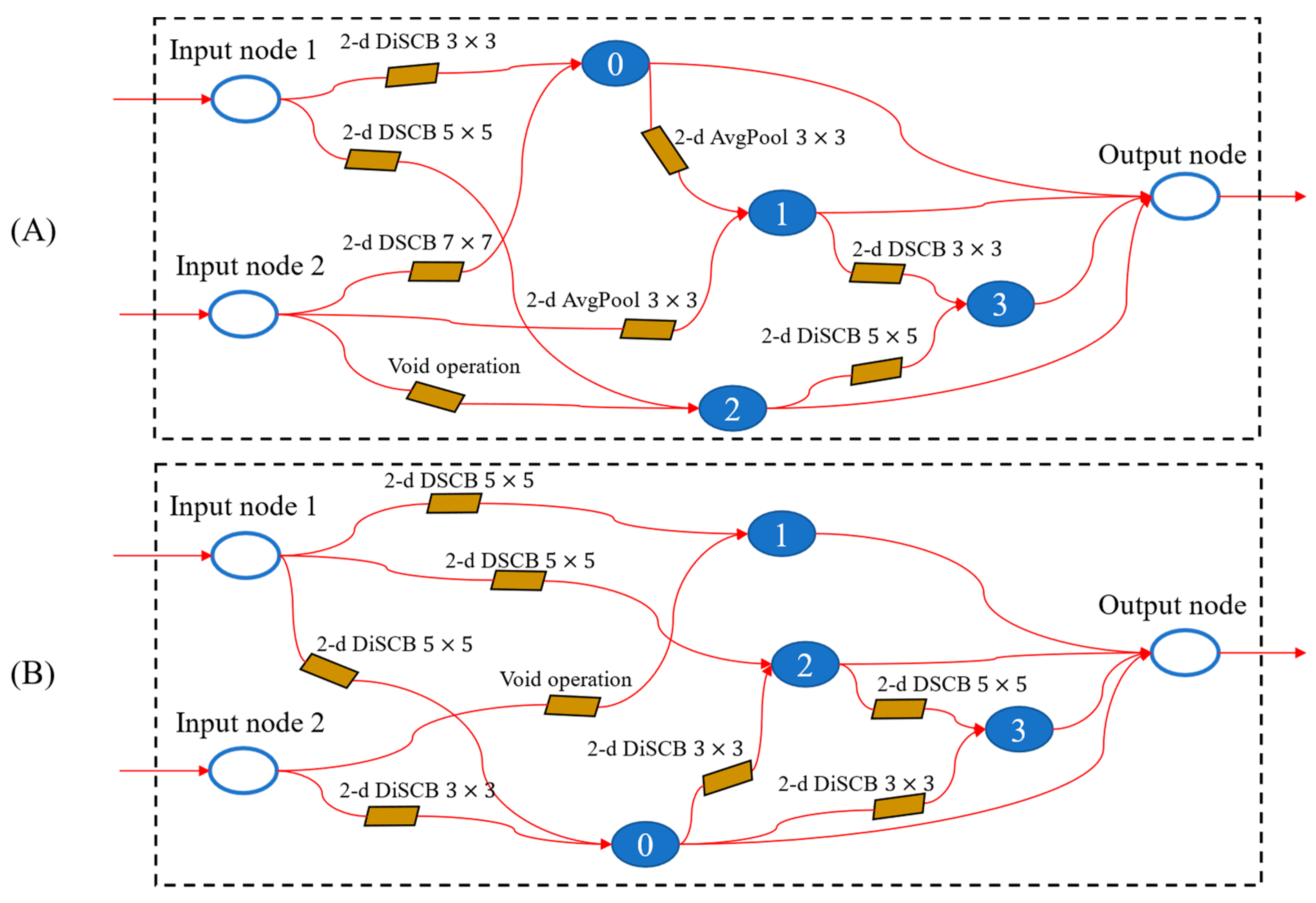
4.2.1. Model Architecture
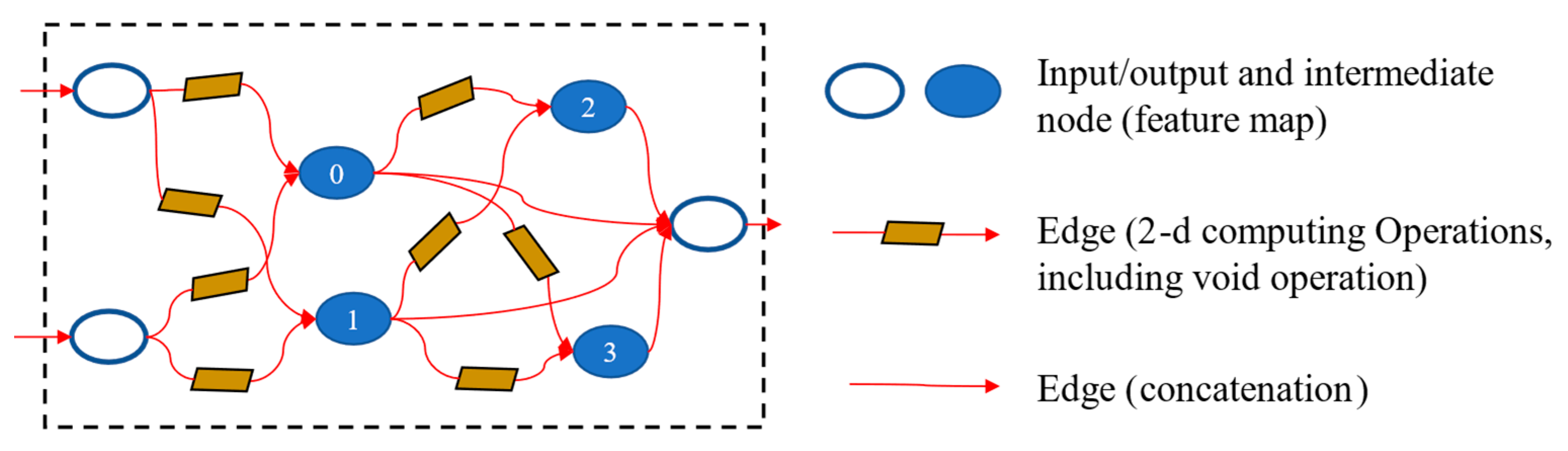
4.2.2. Cell Architecture
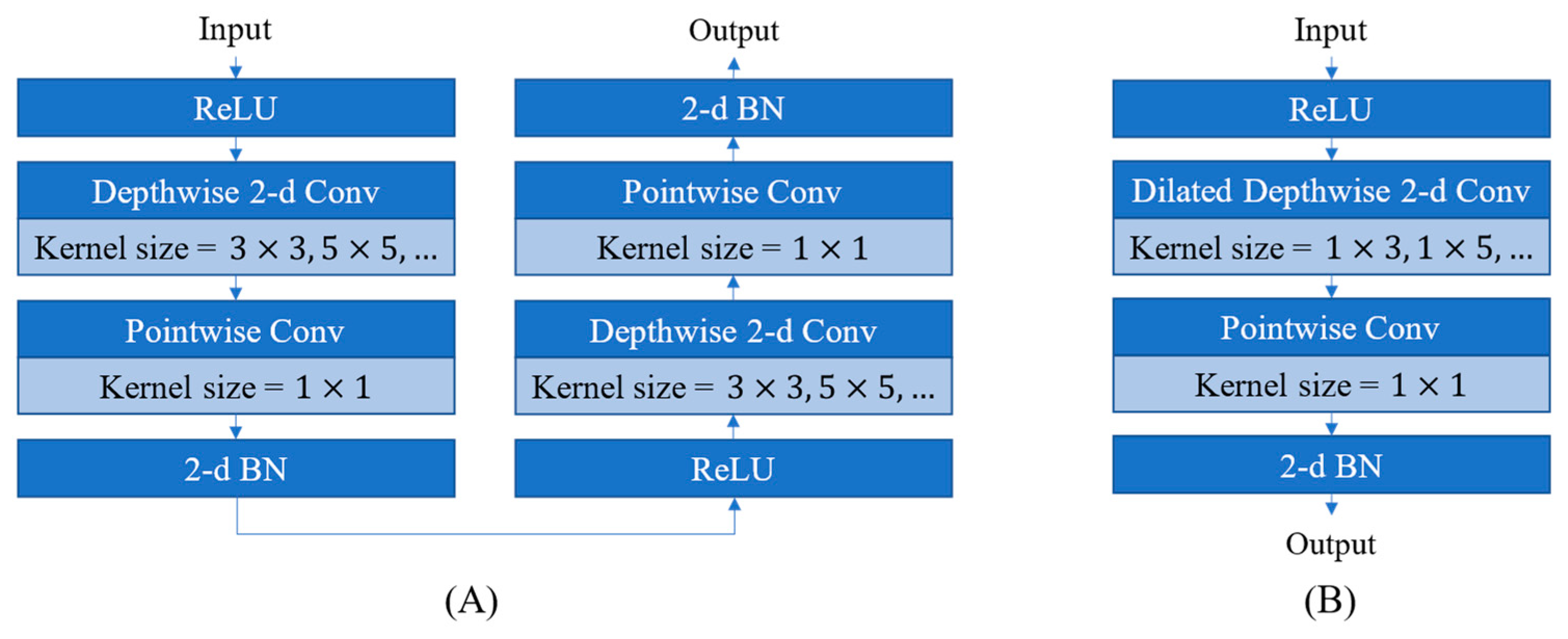
4.2.3. Computing Operation Architecture
4.2.4. Cell Architecture Search Based on DARTS
4.2.5. Coping with Dataset Class-Imbalance Problem
4.3. Model-Performance Evaluation Metric
4.3.1. Selection Principles of Model-Performance Evaluation Metrics
4.3.2. TGD-Identification Performance-Evaluation Metric
5. Case Study
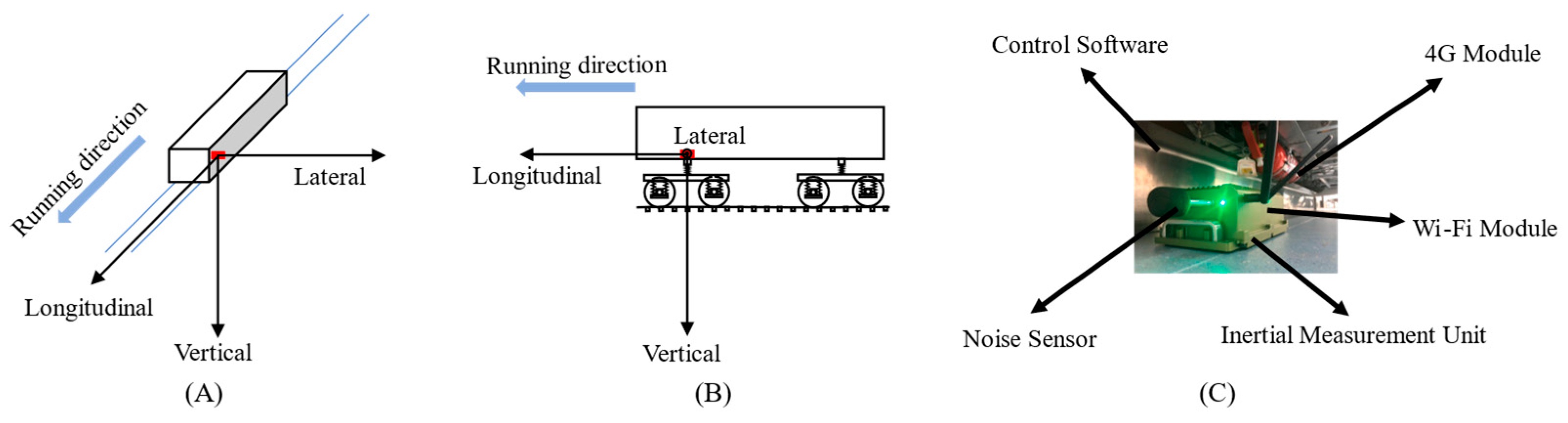
5.1. Case Data Description
5.2. Analysis of Identification Effect
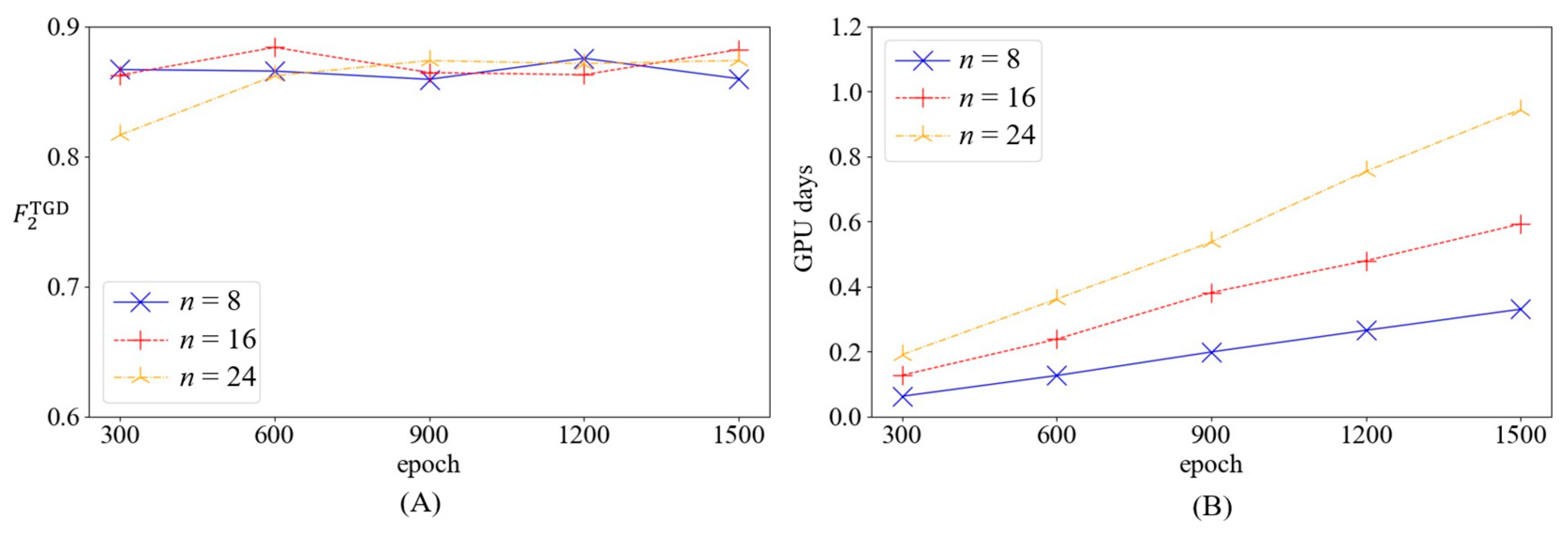
5.2.1. Setting of Model Parameters
5.2.2. Model Identification Results
5.3. Validation of the Effectiveness of Coping Strategies for Class-Imbalance Problem
5.3.1. Setting of Validation
5.3.2. Results of Validation
5.4. Comparison with Other Models
5.4.1. Comparison with the Model Constructed by 1D Convolution
- (1)
- Setting of 1D model parameters
- (2)
- Model validation results of 1D model
5.4.2. Comparison with the Model Obtained by a Black Box Trial Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soleimanmeigouni, I.; Ahmadi, A.; Kumar, U. Track geometry degradation and maintenance modelling: A review. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 232, 73–102. [Google Scholar] [CrossRef]
- Bai, L.; Liu, R.; Sun, Q.; Wang, F.; Wang, F. Classification-learning-based framework for predicting railway track irregularities. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 598–610. [Google Scholar] [CrossRef]
- EN 13848-5:2017; Railway Applications—Track—Track Geometry Quality—Part 5: Geometry Quality Levels—Plain Line, Switches and Crossings. CEN (European Committee for Standardization): Brussels, Belgium, 2017.
- FRA (Federal Railroad Administration). Track and Rail and Infrastructure Integrity Compliance Manual: Volume II Track Safety Standards. 2018. Available online: https://railroads.dot.gov/elibrary/track-and-rail-and-infrastructure-integrity-compliance-manual-volume-ii-chapter-2-track-0 (accessed on 30 March 2022).
- GB/T 39559.4-2020; Specifications of Operational Monitoring of Urban Rail Transit Facilities—Part 4: Track and Earthworks. SAC (Standardization Administration of the P.R.C.): Beijing, China, 2020.
- Andrade, A.R.; Teixeira, P.F. Hierarchical Bayesian modelling of rail track geometry degradation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2013, 227, 364–375. [Google Scholar] [CrossRef]
- Xu, P.; Sun, Q.; Liu, R.; Souleyrette, R.R.; Wang, F. Optimizing the Alignment of Inspection Data from Track Geometry Cars. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 19–35. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Rusk, K.; Clouse, A.L. Decades of automated track inspection success and strategy for tomorrow. In Proceedings of the 2012 AREMA Annual Conference, Chicago, IL, USA, 16–19 September 2012. [Google Scholar]
- Sadeghi, J.M.; Askarinejad, H. Development of track condition assessment model based on visual inspection. Struct. Infrastruct. Eng. 2011, 7, 895–905. [Google Scholar] [CrossRef]
- Sadeghi, J.; Fathali, M.; Boloukian, N. Development of a new track geometry assessment technique incorporating rail cant factor. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2008, 223, 255–263. [Google Scholar] [CrossRef]
- Jamieson, D.; Bloom, J.; Kelshaw, R. T-2000: A railroad track geometry inspection vehicle for the 21st century. In Proceedings of the 2001 AREMA Annual Conference, Chicago, IL, USA, 9–12 September 2001. [Google Scholar]
- Weston, P.; Roberts, C.; Yeo, G.; Stewart, E. Perspectives on railway track geometry condition monitoring from in-service railway vehicles. Veh. Syst. Dyn. 2015, 53, 1063–1091. [Google Scholar] [CrossRef]
- Balouchi, F.; Bevan, A.; Formston, R. Development of railway track condition monitoring from multi-train in-service vehicles. Veh. Syst. Dyn. 2021, 59, 1397–1417. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, R.; Wang, F.; Tang, Y. Development of metro track geometry fault diagnosis convolutional neural network model based on car-body vibration data. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 1135–1144. [Google Scholar] [CrossRef]
- Tsunashima, H. Condition Monitoring of Railway Tracks from Car-Body Vibration Using a Machine Learning Technique. Appl. Sci. 2019, 9, 2734. [Google Scholar] [CrossRef]
- Li, C.; Luo, S.; Cole, C.; Spiryagin, M. An overview: Modern techniques for railway vehicle on-board health monitoring systems. Veh. Syst. Dyn. 2017, 55, 1045–1070. [Google Scholar] [CrossRef]
- Scott, G.; Chillingworth, E.; Dick, M. Development of an Unattended Track Geometry Measurement System. In Proceedings of the 2010 Joint Rail Conference, Urbana, IL, USA, 27–29 April 2010. [Google Scholar]
- Weston, P.F.; Ling, C.S.; Goodman, C.J.; Roberts, C.; Li, P.; Goodall, R.M. Monitoring lateral track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 89–100. [Google Scholar] [CrossRef]
- Weston, P.F.; Ling, C.S.; Roberts, C.; Goodman, C.J.; Li, P.; Goodall, R.M. Monitoring vertical track irregularity from in-service railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2007, 221, 75–88. [Google Scholar] [CrossRef]
- Wei, X.; Liu, F.; Jia, L. Urban rail track condition monitoring based on in-service vehicle acceleration measurements. Measurement 2016, 80, 217–228. [Google Scholar] [CrossRef]
- Li, C.; He, Q.; Wang, P. Estimation of railway track longitudinal irregularity using vehicle response with information compression and Bayesian deep learning. Comput.-Aided Civ. Infrastruct. Eng. 2020, 37, 1260–1276. [Google Scholar] [CrossRef]
- Kawasaki, J.; Youcef-Toumi, K. Estimation of rail irregularities. In Proceedings of the 2002 American Control Conference (IEEE Cat. No.CH37301), Anchorage, AK, USA, 8–10 May 2002. [Google Scholar]
- Lee, J.S.; Choi, S.; Kim, S.; Park, C.; Kim, Y.G. A Mixed Filtering Approach for Track Condition Monitoring Using Accelerometers on the Axle Box and Bogie. IEEE Trans. Instrum. Meas. 2012, 61, 749–758. [Google Scholar] [CrossRef]
- Tsunashima, H.; Naganuma, Y.; Kobayashi, T. Track geometry estimation from car-body vibration. Veh. Syst. Dyn. 2014, 52, 207–219. [Google Scholar] [CrossRef]
- De Rosa, A.; Alfi, S.; Bruni, S. Estimation of lateral and cross alignment in a railway track based on vehicle dynamics measurements. Mech. Syst. Signal Proc. 2019, 116, 606–623. [Google Scholar] [CrossRef]
- Ma, S.; Gao, L.; Liu, X.; Lin, J. Deep Learning for Track Quality Evaluation of High-Speed Railway Based on Vehicle-Body Vibration Prediction. IEEE Access 2019, 7, 185099–185107. [Google Scholar] [CrossRef]
- Tsunashima, H.; Hirose, R. Condition monitoring of railway track from car-body vibration using time-frequency analysis. Veh. Syst. Dyn. 2022, 60, 1170–1187. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W. A novel model for determining the amplitude-wavelength limits of track irregularities accompanied by a reliability assessment in railway vehicle-track dynamics. Mech. Syst. Signal Proc. 2017, 86, 260–277. [Google Scholar] [CrossRef]
- Paixão, A.; Fortunato, E.; Calçada, R. Smartphone’s Sensing Capabilities for On-Board Railway Track Monitoring: Structural Performance and Geometrical Degradation Assessment. Adv. Civ. Eng. 2019, 2019, 1729153. [Google Scholar] [CrossRef]
- Liu, R.; Wang, F.; Wang, Z.; Wu, C.; He, H. Identification of Subway Track Irregularities Based on Detection Data of Portable Detector. Transp. Res. Rec. J. Transp. Res. Board 2022, 2676, 703–713. [Google Scholar] [CrossRef]
- Wang, R.; Jiang, H.; Li, X.; Liu, S. A reinforcement neural architecture search method for rolling bearing fault diagnosis. Measurement 2020, 154, 107417. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. A comprehensive review on convolutional neural network in machine fault diagnosis. Neurocomputing 2020, 417, 36–63. [Google Scholar] [CrossRef]
- Li, X.; Zheng, J.; Li, M.; Ma, W.; Hu, Y. One-shot neural architecture search for fault diagnosis using vibration signals. Expert Syst. Appl. 2022, 190, 116027. [Google Scholar] [CrossRef]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.; Li, Z.; Chen, X.; Wang, X. A Comprehensive Survey of Neural Architecture Search. ACM Comput. Surv. 2022, 54, 1–34. [Google Scholar] [CrossRef]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural Architecture Search: A Survey. J. Mach. Learn. Res. 2019, 20, 1–21. [Google Scholar]
- Zoph, B.; Le, Q.V. Neural architecture search with reinforcement learning. arXiv 2017. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Naik, N.; Raskar, R. Designing Neural Network Architectures using Reinforcement Learning. arXiv 2017. [Google Scholar] [CrossRef]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable Architecture Search. In Proceedings of the Seventh International Conference on Learning Representations (ICLR 2019), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. SMASH: One-Shot Model Architecture Search through HyperNetworks. arXiv 2017. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef]
- Bai, L.; Liu, R.; Li, Q. Data-Driven Bias Correction and Defect Diagnosis Model for In-Service Vehicle Acceleration Measurements. Sensors 2020, 20, 872. [Google Scholar] [CrossRef] [PubMed]
- Vinberg, E.M.; Martin, M.; Firdaus, A.H.; Tang, Y.; Qazizadeh, A. Railway Applications of Condition Monitoring; Technical Report; KTH Royal Institute of Technology: Stockholm, Sweden, 2018. [Google Scholar]
- Abdeljaber, O.; Avci, O.; Kiranyaz, M.S.; Boashash, B.; Sodano, H.; Inman, D.J. 1-D CNNs for structural damage detection: Verification on a structural health monitoring benchmark data. Neurocomputing 2018, 275, 1308–1317. [Google Scholar] [CrossRef]
- Sony, S.; Gamage, S.; Sadhu, A.; Samarabandu, J. Multiclass Damage Identification in a Full-Scale Bridge Using Optimally Tuned One-Dimensional Convolutional Neural Network. J. Comput. Civil. Eng. 2022, 36, 4021035. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Li, H.; Zhou, B.; Wang, Q.; Shahrour, I. Subway tunnel damage detection based on in-service train dynamic response, variational mode decomposition, convolutional neural networks and long short-term memory. Autom. Constr. 2022, 139, 104293. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zoph, B.; Vasudevan, V.; Shlens, J.; Le, Q.V. Learning Transferable Architectures for Scalable Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 30TH IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Honolulu, HI, USA, 21–26 July 2016; pp. 1800–1807. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. arXiv 2016. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of Machine Learning Research, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines Vinod Nair. In Proceedings of the International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Liu, C.; Zoph, B.; Neumann, M.; Shlens, J.; Hua, W.; Li, L.J.; Fei-Fei, L.; Yuille, A.; Huang, J.; Murphy, K. Progressive Neural Architecture Search. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- Bowyer, K.W.; Chawla, N.V.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. arXiv 2011. [Google Scholar] [CrossRef]
- Chinchor, N.; Sundheim, B.M. MUC-5 evaluation metrics. In Proceedings of the Fifth Message Understanding Conference (MUC-5), Baltimore, MA, USA, 25–27 August 1993. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2017. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Devries, T.; Taylor, G.W. Improved Regularization of Convolutional Neural Networks with Cutout. arXiv 2017. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., Buc, F.D.T.A., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
| Metric | No LLs | Level-I LL | Level-II LL |
|---|---|---|---|
| 0.9971 | 0.9392 | 0.6444 | |
| 0.9984 | 0.8528 | 0.8529 |
| Mode | CAS Train | CAS Test | FMV Train | FMV Test |
|---|---|---|---|---|
| M-1 | ROS | ROS | ROS | ORI |
| M-2 | ROS | ORI | ROS | ORI |
| M-3 | ORI | ORI | ROS | ORI |
| BASE | ORI | ORI | ORI | ORI |
| Mode | Avg. Training Time (GPU Days) | |||
|---|---|---|---|---|
| M-1 | 0.8561 | 0.8346 | 0.8141 | 0.0669 |
| M-2 | 0.8538 | 0.8367 | 0.8202 | 0.0755 |
| M-3 | 0.8684 | 0.8428 | 0.8187 | 0.0655 |
| BASE | 0.8043 | 0.8035 | 0.8029 | 0.0250 |
| Mode | CAS Train | CAS Test | FMV Train | FMV Test |
|---|---|---|---|---|
| M-3-1D | ORI | ORI | ROS | ORI |
| BASE-1D | ORI | ORI | ORI | ORI |
| Mode | Avg. Training Time (GPU Days) | |||
|---|---|---|---|---|
| M-3 | 0.8684 | 0.8428 | 0.8187 | 0.0655 |
| M-3-1D | 0.6516 | 0.6482 | 0.6456 | 0.0648 |
| BASE-1D | 0.5286 | 0.5613 | 0.5997 | 0.0238 |
| Metrics | |||
|---|---|---|---|
| MTGDI-CNN Avg. metrics | 0.8684 | 0.8428 | 0.8187 |
| 0.8142 | 0.7821 | 0.7681 | |
| 0.7924 | 0.8205 | 0.8144 | |
| 0.7900 | 0.8038 | 0.8180 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, R.; Gao, Y.; Tang, Y. Metro Track Geometry Defect Identification Model Based on Car-Body Vibration Data and Differentiable Architecture Search. Appl. Sci. 2023, 13, 3457. https://doi.org/10.3390/app13063457
Wang Z, Liu R, Gao Y, Tang Y. Metro Track Geometry Defect Identification Model Based on Car-Body Vibration Data and Differentiable Architecture Search. Applied Sciences. 2023; 13(6):3457. https://doi.org/10.3390/app13063457
Chicago/Turabian StyleWang, Zhipeng, Rengkui Liu, Yi Gao, and Yuanjie Tang. 2023. "Metro Track Geometry Defect Identification Model Based on Car-Body Vibration Data and Differentiable Architecture Search" Applied Sciences 13, no. 6: 3457. https://doi.org/10.3390/app13063457
APA StyleWang, Z., Liu, R., Gao, Y., & Tang, Y. (2023). Metro Track Geometry Defect Identification Model Based on Car-Body Vibration Data and Differentiable Architecture Search. Applied Sciences, 13(6), 3457. https://doi.org/10.3390/app13063457





