Abstract
The distributed dynamic load is difficult to obtain due to the complexity of loads in practical engineering, such as the aerodynamic loads of aircraft and the distributed dynamic loads of sea-crossing bridges. Thus, distributed dynamic load identification is important to deal with these difficulties, which is generally an ill-posed problem considering the inversion of the infinite dynamic loads. The traditional Tikhonov regularization technique is limited on the optimal regularization parameters selection. Consequently, in this paper, we develop a novel distributed dynamic load identification algorithm in combination with the orthogonal polynomials and the Bayesian framework. Thus, the orthogonal polynomial coefficients in the load identification model are regarded as the prior probability distribution of unknown variables in the Bayesian inference. Simultaneously, the posterior probability distribution of the orthogonal polynomial coefficients is derived based on the Bayesian formula and the likelihood function. The regularization parameters and the standard deviation of the response error are also treated as random variables to obtain the corresponding prior distribution in the multi-level Bayesian model. Moreover, the maximum posterior estimate is applied aiming at determining the regularization parameters, as well as the orthogonal polynomial coefficients to reconstruct the distributed dynamic loads. Compared with the Tikhonov regularization, a series of numerical simulations are studied to verify the effectiveness and high accuracy, as well as the noise resistance, and the results illustrate that this approach is effective to reconstruct the distributed dynamic loads.
1. Introduction
Dynamic load identification is a typical class of inverse problems aiming at determining the unknown loads acting on the mechanical structures from the measured responses and dynamical models. It is of great significance to measure the force for a large number of industrial applications, e.g., the dynamic model design and optimization [1,2,3,4,5,6,7,8,9], vibration control [10], and structural health monitoring [11].
In the past decades, numerous load identification studies have been developed, involving concentrated dynamic load identification and distributed dynamic load identification. In terms of concentrated load identification, the time history of the load, that is, the one-dimensional function of time, is obtained assuming that the excitation location of the load is known. On the contrary, the distributed dynamic load involves two-dimensional variables of space and time. Due to the continuous distribution characteristic in space and the dynamicity in time, the distributed loads are more complex compared with the concentrated load, hence, limited research is available in the area of distributed dynamic load identification. For example, line distributed dynamic load identification [12] acting on the composite structures was discussed via separating the time–space domain based on an iterative algorithm, and the identified loads are well in agreement with the real distributed loads considering the spatial distribution and the magnitude with the small cost of iteration operation. In order to reconstruct the external excitation and improve the efficiency, the spatial variable of the unknown force [13], as well as the system response, were decomposed and denoted as the local basis functions, and the feasibility was also proved by introducing the regularization to decrease the effect of the noise on load identification and improve the accuracy. Moreover, the finite-difference schemes were developed by Djamaa to carry out the local distributed load identification research acting on a cylindrical thin shell structure; however, this method can lead to a higher sensitivity of the noise when the displacements are given through integrating the velocities [14]. Then, the difference procedure can be converted to the integral form based on the virtual field method, and the robustness of distributed dynamic load identification, as well as the local dynamic lateral force of the thin plate surface, were verified by numerical simulation and experiment, which indicated the better behavior on the problem of the smooth pressure distributions through measuring the plane deflections at some definite grids [15]. The problem of identifying one-dimensional distributed dynamic loads applied on the cutting instrument point by point was also discussed in space from the displacement response based on the conjugate gradient method, and the results were evaluated with the various loads, the sensors, and the noise levels [16]. Meanwhile, considering the sensitivity of the noise to the identification of distributed dynamic loads, the correction coefficient was used in the load analysis approach, which improved the accuracy without the regularization [17]. Other distributed load identification methods were investigated by Kumar [18], Coates [19], Hwang [20], and Nakamura [21] to reconstruct the distributed loads of the engineering structures with different approaches, e.g., the equivalent nodal force method and the Kalman filter method. More recently, the identification of distributed loads were studied in the context of uncertain structures. For instance, when dealing with uncertainty systems, an interval analysis utilized the Taylor expansion and the polynomial coefficients was developed to obtain the envelope interval of unknown distributed loads for the interval analysis of multiple uncertainties structures with the cost of lower computation, including the load identification model, the achievement of the interval analysis method based on Taylor expansion (IAMBTE), and the estimation of the unknown load [22]. Subsequently, this approach was employed in the aircraft via the Taylor expansion and the particle swarm optimization algorithm, which balanced the sensor cost and the performance of load identification in the system framework. However, only the polynomial distributed load can be identified, and it is critical to discuss the intricate load identification [23]. In another work, a comprehensive method based on the Latin hypercube sampling genetic algorithm (LHS-GA) and the improved L-curve method was proposed to determine the upper and lower bounds of the distributed force on uncertain structures, which improved the ill-posedness and the anti-noise compared with the traditional regularization method [24].
Unfortunately, distributed dynamic load identification is often an ill-posed problem. A common method to bypass the problem is to apply the regularization technique to stabilize the solution. The most widely adopted regularization is the Tikhonov regularization [25,26,27]. For example, based on the truncated singular value decomposition (TSVD) and the L-curve, the regularization method was presented to evaluate the internal excitations and the regularization efficiency, which encouraged obtaining knowledge of the defects on the drive train models [28]. Although widely used, it should be noted that there is a significant limitation on the selection of the optimal regularization parameters. For this particular reason, extensive research efforts have been focused on the Bayesian method in recent years. For example, a sparse convex optimization model of the load identification was established with different basis functions by minimizing the components of the non-zero status in the coefficients of the sparse regularization, and the effectiveness and applicability of the cantilever thin plate structure were verified through the simulation and the experiment [29]. Furthermore, B. Jin proposed the augmented Tikhonov regularization method, namely, the Bayesian regularization method, which provided a novel idea for the selection of the regularization parameters in load identification [30,31]. In the same vein, the superiority of the Bayesian method, using the Gaussian kernel functions to obtain the time history of unknown impact load, was presented for the impact load identification of the composite structures by organizing the simulations and the test [32,33]. Apparently, the enormous advance was observed by making the most of the Bayesian inference and the generalized iterative weighted least squares algorithm to identify the external excitation [34,35,36]. In general, the aforementioned application of the Bayesian method mainly focused on the concentrated load identification, however, there was no relevant research on distributed dynamic load identification. Therefore, it is essential to develop the Bayesian framework to reconstruct the distributed dynamic load. In this paper, a novel distributed dynamic load identification based on the Bayesian method is proposed. The key of the proposed method is that the orthogonal polynomial coefficients are regarded as random variables to obtain the prior probability distribution. Then, the estimate of the posterior probability distribution is carried out by using the statistical inference.
This paper is arranged as follows. In Section 2, the load identification algorithm of the proposed method is introduced, including the load identification model and the application of the Bayesian method in load identification for a simply supported beam; in Section 3, the effectiveness and the accuracy under various noise levels are discussed and compared with the Tikhonov regularization. Some conclusions are generalized in Section 4.
2. The Bayesian Formulation of the Distributed Dynamic Load Identification
2.1. Identification Model for Simply Supported Beams in the Frequency Domain
For the simply supported beam shown in Figure 1, the connection between the distributed dynamic load and the response in the frequency domain is given by:
Figure 1.
Simply supported beam model under distributed forces.
Here, denotes the frequency response function (FRF), is the response position, and is the frequency response. , which is rewritten as Equation (2) in the complex field, is the fast Fourier transform (FFT) of . Substituting Equation (2) into Equation (1), Equation (1) is rewritten as Equation (3).
where is the normalized one-dimensional Legendre polynomials, and are the polynomial coefficients. are the real and imaginary parts of FRF, while denote the system responses. Therefore, Equation (3) is converted as Equation (4) in the case of a multipoint response and then abbreviated as Equation (5).
In Equation (4), are the representations of the symbols , while in Equation (5) are given as:
where is the dynamic calibration matrix [3]. Therefore, we have the coefficient vectors as Equation (8):
Consequently, the distributed dynamic load is identified by
2.2. Bayesian Basis Framework
The core of the Bayesian framework is the Bayesian formula. Based on the conditional probability and the prior probability of the assumed unknown variable, the posterior probability is obtained and estimated through the Bayesian formula. Therefore, the Bayesian framework is written as:
Notice that can be regarded as a constant. Additionally, , which means the prior knowledge, represents the prior probability distribution of the unknown variable; represents the likelihood function, i.e., the conditional probability that the measurement is with the unknown variables . Similarly, is the posterior probability of the unknown variables, representing the probability that the unknown variables are when the measured response is . Based on Equation (10) and the maximum a posteriori (MAP) estimation, the estimated value is obtained as Equation (11).
We assume the measurement is contaminated by a noise , which is written as in Equation (12). The noise is considered to be independent identically distributed Gaussian noise with the mean value 0 and the standard deviation . Consequently, the likelihood function is given by Equation (13).
where is the Euclidean norm, is the positive proportion symbol and is the dimension of the discrete signal .
2.3. The Prior Probability Distribution and the Bayesian Model
The prior model , which is a measure of the prior knowledge of the experimenter reflecting the no-determinacy relevant to the unknown knowledge , plays an important role in dealing with the inverse problems. In fact, the appropriate prior model, containing almost all the knowledge of the unknown parameters, can accurately solve the statistical inversion problem in the Bayesian framework. Here, the Markov random field is employed as the prior model, while the prior probability distribution is written as Equation (14):
where are the amplification coefficient and the non-negative function, respectively. is a non-negative weight. Assuming , Equation (14) is rewritten as Equation (15):
where are the vector of and the symmetric matrix of , respectively. The parameter is the scaling parameter. Substituting Equations (13) and (15) into Equation (10), the posterior probability is transformed into Equation (16) and the maximum a posteriori probability estimation of is obtained as Equation (17).
Compared with the Tikhonov regularization, the MAP is equivalent to the Tikhonov minimization functional:
where . Therefore, the scaling parameter and the standard deviation assume the crucial role of the regularization parameters, which affect substantially posterior probability density function and the posterior point estimates.
2.4. Distributed Dynamic Load Identification Algorithm Based on the Bayesian Method
The identification model of the distributed dynamic load is given by:
where represent the measurement response, dynamic calibration matrix, and the orthogonal polynomial coefficients, respectively. We assume the noise is the Gaussian noise and the prior distribution is the Markov random field, thus, the posterior probability density of the orthogonal polynomial coefficients is derived as Equation (20) based on the Bayesian inference:
To determine the parameters , the hierarchical Bayesian model is adopted via treating the parameters as random variables with its own prior distribution to obtain the prior probability distribution. The Gamma distribution is used as the prior distribution of and , that is,
where denote the Gamma distribution parameters. Consequently, the hierarchical model for the joint posteriori probability density of the orthogonal polynomial coefficients and the parameter is derived using:
where is the likelihood function and is the prior probability density of the orthogonal polynomial coefficients. Based on Equations (13) and (15), the expressions are defined as:
Combining Equations (21), (22), (24), and (25) with Equation (23), the posteriori probability density is rewritten as Equation (26).
In this paper, the maximum a posteriori estimation given by Equation (27), as proposed in Equation (11), is performed to determine the values of the unknown variables. However, it should be noted that there are some limitations to solving various estimators of parameters through the posterior probability distribution with the common methods. Therefore, the maximum of the posterior density function can be converted to the minimizer of the functional, and then derived with the iterative methods. By the logarithm and the negative of Equation (26), we have Equation (28):
Taking the partial derivative of and setting as 0, we have
That is,
Thus, the orthogonal polynomial coefficient vectors and the unknown parameters are given by:
Therefore, the unknown distributed load is identified based on the coefficient vectors and the orthogonal polynomials. Moreover, the common difficulty to solve the maximum posterior estimator of the hierarchical model is to obtain the minimum value of the function. Some approaches have been developed, such as the gradient iterative, the simulated annealing method, and the genetic algorithm. In this paper, we mainly employ the alternating direction iterative algorithm to solve the optimization problem. The following steps present the numerical iteration of the unknown parameters, and the schematic diagram of the distributed dynamic load identification is shown in Figure 2:
(1) Select the appropriate initial value , and set .
(2) Determine the regularization parameters .
(3) Determine the orthogonal polynomial coefficient vectors .
(4) Update the regularization parameters by:
(5) Set and repeat from Step (2) until the iteration stopping criterion is supplied:
Considering the iteration accuracy and the computing time, the value of is .
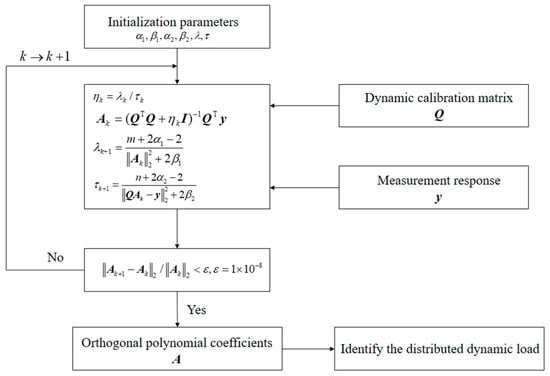
Figure 2.
Schematic diagram of the distributed dynamic load identification.
In conclusion, the distributed dynamic load identification approach based on the Bayesian estimation is constructed according to the above deduction. Obviously, it is critical to select the appropriate prior model to reconstruct the unknown loads. Meanwhile, contrasted with the Tikhonov regularization, the prior model selection of the parameters in the Bayesian model is also important to determine the optimal parameters. Therefore, the hierarchical Bayesian model of the load identification is derived by combining the prior distribution and the posterior probability distribution to solve the MAP estimation, as well as the corresponding parameters. Next, the simulations are performed to investigate the feasibility and effectiveness.
3. Numerical Simulation
In the previous section, it can be seen that the identification method established in this paper based on the Bayesian method can identify the distributed loads using a recognition system different from the traditional Tikhonov regularization.
In this section, the numerical examples are presented to verify the proposed method in the frequency domain. The simply supported beam is selected as the simulation model. The simple and complicated distributed loads are all considered in order to verify the feasibility. Simultaneously, the simulation examples with low-level noise and high-level noise are presented, respectively. We employ various error descriptions to evaluate the identification results, e.g., relative error (RE), peak relative error (PRE), and average relative error (ARE), as shown in Equation (37). The identification errors are listed in the tables, including the proposed method, the Tikhonov regularization with L_curve method, and the Tikhonov regularization with generalized cross-validation (GCV) method. This proves the superiority of the method proposed in this paper.
The distributed dynamic load acting on the simply supported beam shown in Figure 1 is given by Equation (38), and the beam parameters are given in Table 1.
where and are the amplitude and phase of the distributed load, respectively, while is the excitation frequency. We define , . Here, are fitted by Legendre orthogonal polynomials.

Table 1.
The beam parameters.
3.1. Test Example 1
To test the accuracy of this numerical simulation in the case of low-level noise, the load acting on a simply supported beam is given by: with the excitation frequency . Meanwhile, the measuring points, , are uniformly distributed and the orders of polynomials are 8 to accurately identify the load. Moreover, this method is compared with the Tikhonov regularization to evaluate the superiority. To analyze the resistance to the various noise levels, Gaussian noise was added with RMS amplitudes of 1% and 5% of the response amplitudes. All the computations are run on a Windows PC with an Intel Core(TM) i5 1.6 GHz CPU and 8 GB of RAM. The identification results are shown in Figure 3 and Figure 4 and the error analysis is shown in Table 2. Furthermore, to investigate the operation efficiency of the proposed method, the CPU time of the algorithm and the Tikhonov regularization [37] are compared in Table 3.
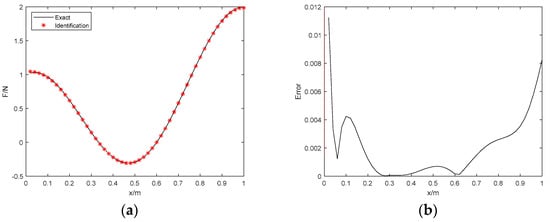
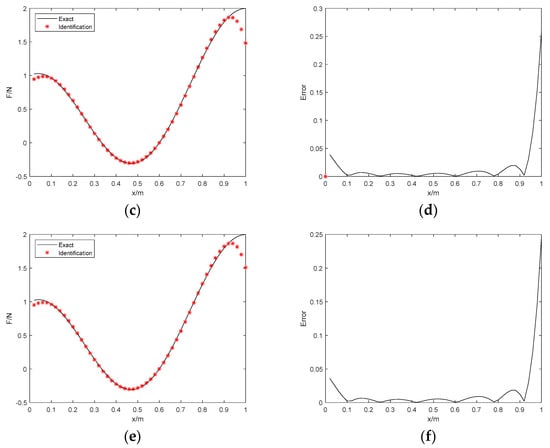
Figure 3.
The identification results with 1% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.
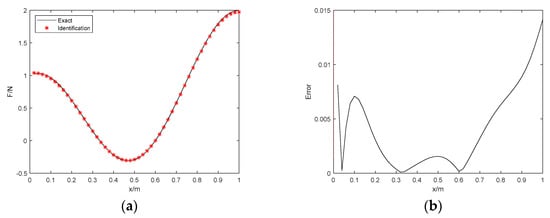
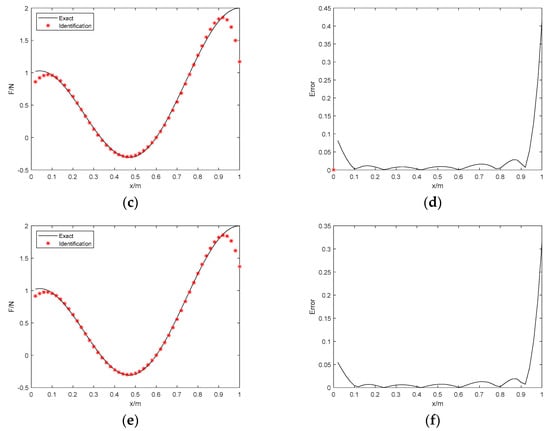
Figure 4.
The identification results with 5% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.

Table 2.
Identification error in Example 1.

Table 3.
Calculation time in Example 1.
Figure 3 and Figure 4 show the identification results of the 3 methods in the case of 1% and 5% Gaussian noise, respectively. Figure 3a and Figure 4a show the best approximation of the proposed method. In addition, compared with the Bayesian method, some fluctuations are observed based on the Tikhonov regularization at both ends of the simply supported beam. This suggests the improved algorithm in this paper is accurate even while the responses are contaminated. Table 2 shows the various errors, e.g., RE, PRE, and ARE. The RE and PRE of the proposed method with 1% noise are 0.64% and 1.12%, respectively, while the RE and PRE of the proposed method with 5% noise are 1.13% and 1.41%, respectively. Although these 3 methods are all in low noise conditions, the 2 errors of the Tikhonov method with GCV regularization with 5% noise are 11.4% and 31.5%, which indicates that the errors are more greatly magnified than the proposed method at the identical noise level. Table 3 indicates that the operation time of the Tikhonov regularization is nearly three times that of the Bayesian method, which regards the unknown variable as a prior probability distribution; hence, it is superior in increasing the operational efficiency.
3.2. Test Example 2
In this example, a more complicated distributed load is considered compared with the test example 1. The load is now defined as with the excitation frequency of . This helps to investigate the reconstruction effect in case of high noise levels and irregular loads. Other parameters of the problem remain unchanged as in Example 1. Moreover, this method is compared with the Tikhonov regularization to evaluate the superiority. We applied 10% and 15% Gaussian noise to the measurement vectors to investigate the anti-noise performance of the proposed approach and the identification results are demonstrated in Figure 5 and Figure 6. Moreover, the identification errors are shown in Table 4 and the calculation time is compared in Table 5.
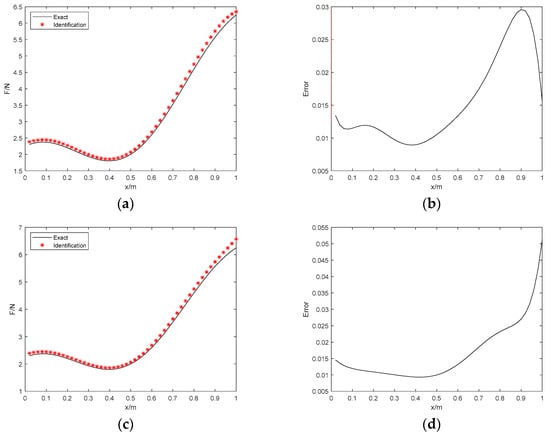
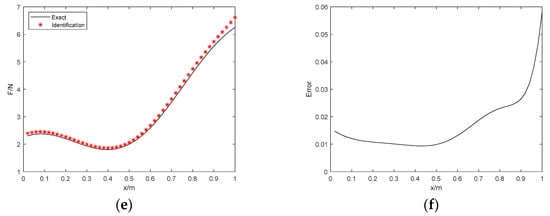
Figure 5.
The identification results with 10% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.
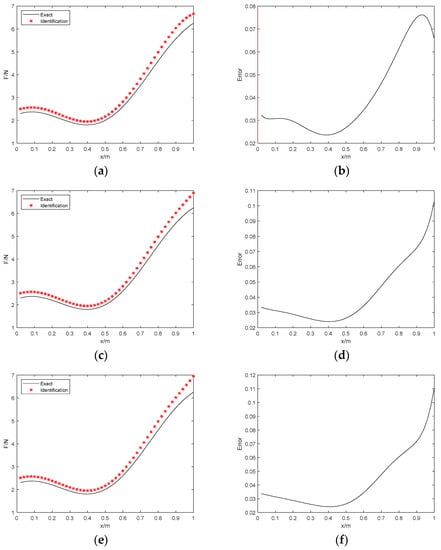
Figure 6.
The identification results with 15% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.

Table 4.
Identification error in Example 2.

Table 5.
Calculation time in Example 2.
Figure 5 and Figure 6 show the results with the high-level noise. Although the errors still exist in identified load and the exact load, the results suggest that the identified load obtained by the proposed method is well in agreement with the exact load of the simply supported beam. Table 4 also illustrates the corresponding errors in the two considered cases. Through the error analysis of the results, we find that the RE errors of the 2 noise conditions are 3.05% and 8.11%, respectively, the PRE errors are 2.96% and 7.61%, respectively, and the ARE errors are 1.54% and 4.08%, respectively. In addition, the RE, PRE, and ARE errors are lower compared with the Tikhonov regularization method. Therefore, despite the error increasing significantly with the improvement of noise level when identifying the distributed load, the PRE errors remain reasonably small, which demonstrates the obvious suppression effect on the PRE error of the proposed method. Furthermore, the larger error is focused on both ends of the distributed load. The accuracy of the proposed distributed load identification algorithm in this paper is validated considering the perspective. Table 5 indicates that this algorithm is superior to the Tikhonov regularization method in efficiency.
3.3. Test Example 3
In this subsection, we aim to investigate the identification accuracy, while the real and imaginary parts are both considered. The distributed load is now rewritten as with an excitation frequency of . Other parameters of the problem remain unchanged. Moreover, this method is compared with the Tikhonov regularization to evaluate the superiority. Again, the 3 different cases of noise level are all considered, e.g., 5% noise, 10% noise, and 15% noise to investigate the anti-noise performance of the proposed approach. Figure 7, Figure 8 and Figure 9 show the identified results using the proposed algorithm and the Tikhonov method. The RE, PRE, and ARE errors are shown in Table 6. Table 7 lists the calculation time required for the proposed approach and Tikhonov to compare their operation efficiency.
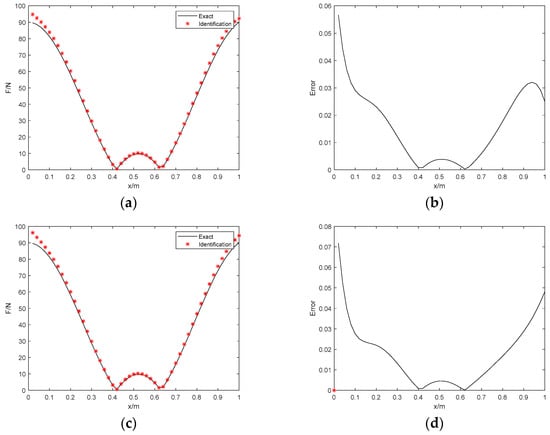
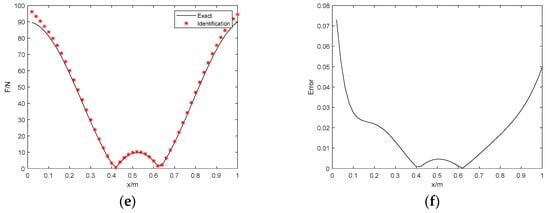
Figure 7.
The identification results with 5% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.
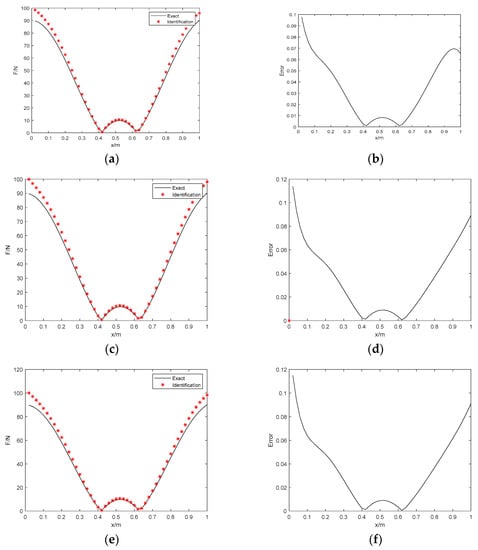
Figure 8.
The identification results with 10% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.
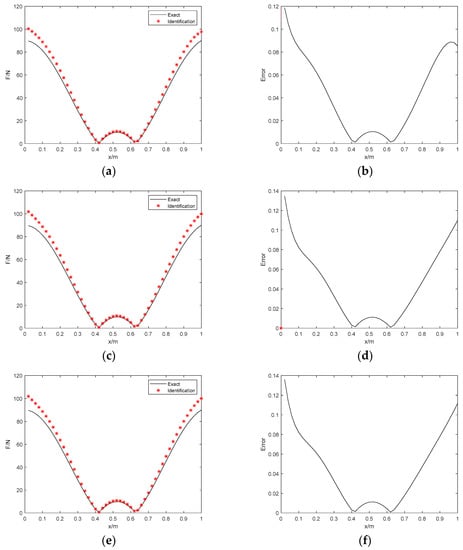
Figure 9.
The identification results with 15% noise. (a) Proposed method; (b) identification error; (c) Tikhonov with L−curve regularization; (d) identification error; (e) Tikhonov with GCV regularization; (f) identification error.

Table 6.
Identification error in Example 3.

Table 7.
Calculation time in Example 3.
Figure 7, Figure 8 and Figure 9 show the identification results with the real and imaginary parts. It can be shown that the feasibility of this algorithm for the simulation model is tested. As we can see, considering the proposed method, the RE errors of the three noise conditions are 3.67%, 7.7%, and 9.74%, respectively, the PRE errors are 5.67%, 9.79%, and 11.86%, respectively, and the ARE errors are 1.63%, 3.48%, and 4.4%, respectively. The identifications under 15% noise conditions have some slight fluctuations in spatial distribution. However, the error is still within the acceptable range, which proves that the proposed approach can realize satisfactory identification effects under high levels of noise. On the contrary, these errors of the Tikhonov regularization with 5%, 10%, and 15% noise are higher than the algorithm proposed in this paper. Thus, the proposed distributed dynamic load identification combining Bayesian inference and numerical iteration can perform perfectly for the beam structure. Table 7 shows that the Bayesian method spends much less time and is more efficient than the Tikhonov regularization method for distributed dynamic load identification. In general, the main advantages of the proposed method are verified in terms of the identification accuracy and efficiency.
4. Conclusions
In this paper, we proposed distributed dynamic load identification using a Bayesian method based on the Bayesian inference to identify the distributed dynamic load. This method is discussed with the various noise levels and the irregular loads in the frequency domain. Firstly, the identification model of the simply supported beam is given by using the generalized Fourier series expansion, while the dynamic calibration matrix is also determined to obtain the orthogonal polynomial coefficient vectors. Secondly, based on the Bayesian inference, the Markov random field is employed as the prior model and the Gaussian noise is used to obtain the likelihood function. Therefore, the hierarchical Bayesian model of the load identification is derived to better determine the parameters. Finally, we select the Gamma distribution to derive the joint posteriori probability density function of the orthogonal polynomial coefficients through combining the likelihood function and the prior probability distribution, and the coefficients, as well as the unknown parameters, are solved via the numerical iteration.
The algorithm performance is tested through a series of numerical simulations with various spatial distributions. Meanwhile, the comparison between the Tikhonov regularization and the proposed method is performed to show the advantage of the proposed method. In example 1, the results show the RE error of the proposed method is 0.64% when the 1% noise is added; on the contrary, the RE are 9.3% and 8.86% using the Tikhonov regularization, which is a higher error level compared with the proposed method at the identical noise level. This suggests that the prior information fully used in the distributed dynamic load identification achieves the better accuracy. Test example 2 indicates the suppression effect on the PRE error of the proposed method is obvious in the case of more complicated distributed load and high noise levels. In example 3, the proposed approach resilience to noise is investigated with different levels of noise, considering both the real part and imaginary parts. In these circumstances, identified distributed loads remain robust and accurate, which reflect a strong anti-noise performance. In addition, the operation accuracy based on the Bayesian method is superior contrasted with the Tikhonov regularization in the three different cases of simulation examples. This work presents a first attempt to obtain the distributed loads using the Bayesian inference and has broad application prospects.
Author Contributions
Conceptualization, S.L. and J.J.; methodology, J.J.; software, S.L.; validation, S.L.; formal analysis, F.Z.; investigation, F.Z.; resources, F.Z.; data curation, S.L.; writing—original draft preparation, S.L. and J.J.; writing—review and editing, M.S.M.; visualization, S.L.; supervision, M.S.M.; project administration, S.L.; funding acquisition, J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Foundation of National Key Laboratory of Science and Technology on Rotorcraft Aeromechanics (No. 61422202105), Qing Lan Project.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Shepard, W.S., Jr. Dynamic force identification based on enhanced least squares and total least-squares schemes in the frequency domain. J. Sound Vib. 2005, 282, 37–60. [Google Scholar] [CrossRef]
- Xue, S.; Shen, R. Real time cable force identification by short time sparse time domain algorithm with half wave. Measurement 2020, 152, 107355. [Google Scholar] [CrossRef]
- Jiang, J.; Luo, S.; Zhang, F. One novel dynamical calibration method to identify two-dimensional distributed load. J. Sound Vib. 2021, 515, 116465. [Google Scholar] [CrossRef]
- Jiang, J.; Ding, M.; Li, J. A novel time-domain dynamic load identification numerical algorithm for continuous systems. Mech. Syst. Signal Process. 2021, 160, 107881. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, J.; Chen, G.; Zhao, J. Dynamic load identification based on deep convolution neural network. Mech. Syst. Signal Process. 2023, 185, 109757. [Google Scholar] [CrossRef]
- He, W.Y.; Wang, Y.; Ren, W.X. Dynamic force identification based on composite trigonometric wavelet shape function. Mech. Syst. Signal Process. 2020, 141, 106493. [Google Scholar] [CrossRef]
- Sanchez, J.; Benaroya, H. Asymptotic approximation method of force reconstruction: Proof of concept. Mech. Syst. Signal Process. 2017, 92, 39–63. [Google Scholar] [CrossRef]
- Kroworz, A.; Katunin, A. Non-destructive testing of structures using optical and other methods: A review. Struct. Durab. Health Monit. 2018, 12, 1–18. [Google Scholar]
- Jia, Y.; Yang, Z. Prediction of random dynamic loads using second-order blind source identification algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1720–1732. [Google Scholar] [CrossRef]
- Qiao, B.; Zhao, T.; Chen, X.; Liu, J. The assessment of active vibration isolation performance of rotating machinery using power flow and vibrational energy: Experimental investigation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 159–173. [Google Scholar] [CrossRef]
- Van der Seijs, M.V.; de Klerk, D. General framework for transfer path analysis: History, theory and classification of techniques. Mech. Syst. Signal Process. 2016, 68, 217–244. [Google Scholar] [CrossRef]
- Liu, G.R.; Ma, W.B.; Han, X. An inverse procedure for identification of loads on composite laminates. Compos. Part B Eng. 2002, 33, 425–432. [Google Scholar] [CrossRef]
- Liu, Y.; Shepard, W.S., Jr. An improved method for the reconstruction of a distributed force acting on a vibrating structure. J. Sound Vib. 2006, 291, 369–387. [Google Scholar] [CrossRef]
- Djamaa, M.C.; Ouelaa, N.; Pezerat, C. Reconstruction of a distributed force applied on a thin cylindrical shell by an inverse method and spatial filtering. J. Sound Vib. 2007, 301, 560–575. [Google Scholar] [CrossRef]
- Berry, A.; Robin, O.; Pierron, F. Identification of dynamic loading on a bending plate using the virtual fields method. J. Sound Vib. 2014, 333, 7151–7164. [Google Scholar] [CrossRef]
- Huang, C.H.; Shih, C.C.; Kim, S. An inverse vibration problem in estimating the spatial and temporal-dependent external forces for cutting tools. Appl. Math. Model. 2009, 33, 2683–2698. [Google Scholar] [CrossRef]
- Leclere, Q.; Pézerat, C. Vibration source identification using corrected finite difference schemes. J. Sound Vib. 2012, 331, 1366–1377. [Google Scholar] [CrossRef]
- Padmanabhan, S.; Kumar, A.V. Inverse Problem for Estimation of Loads and Support Constraints from Structural Response Data. AIAA J. 2007, 45, 1199–1207. [Google Scholar] [CrossRef]
- Coates, C.W.; Thamburaj, P. Inverse method using finite strain measurements to determine flight load distribution functions. J. Aircr. 2008, 45, 366–370. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kareem, A.; Kim, H. Wind load identification using wind tunnel test data by inverse analysis. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 18–26. [Google Scholar] [CrossRef]
- Nakamura, T.; Igawa, H.; Kanda, A. Inverse identification of continuously distributed loads using strain data. Aerosp. Sci. Technol. 2012, 23, 75–84. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Liu, Y. An inverse method for distributed dynamic load identification of structures with interval uncertainties. Adv. Eng. Softw. 2019, 131, 77–89. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y. A novel method of distributed dynamic load identification for aircraft structure considering multi-source uncertainties. Struct. Multidiscip. Optim. 2020, 61, 1929–1952. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Chen, J. Distributed load identification for uncertain structure based on LHS-GA and improved L-curve method. Int. J. Comput. Methods 2021, 18, 2050022. [Google Scholar] [CrossRef]
- Yi, L.; Shepard, W.S. Reducing the Impact of Measurement Errors When Reconstructing Spatial Dynamic Forces. J. Vib. Acoust. 2006, 128, 586–593. [Google Scholar]
- Mao, Y.M.; Guo, X.L.; Zhao, Y. Experimental study of hammer impact identification on a steel cantilever beam. Exp. Tech. 2010, 34, 82–85. [Google Scholar] [CrossRef]
- Turco, E. Tools for the numerical solution of inverse problems in structural mechanics: Review and research perspectives. Eur. J. Environ. Civ. Eng. 2017, 21, 509–554. [Google Scholar] [CrossRef]
- Leclere, Q.; Pezerat, C.; Laulagnet, B. Indirect measurement of main bearing loads in an operating diesel engine. J. Sound Vib. 2005, 286, 341–361. [Google Scholar] [CrossRef]
- Qiao, B.; Zhang, X.; Wang, C.; Zhang, H.; Chen, X. Sparse regularization for force identification using dictionaries. J. Sound Vib. 2016, 368, 71–86. [Google Scholar] [CrossRef]
- Jin, B.; Zou, J. Augmented Tikhonov regularization. Inverse Probl. 2008, 25, 025001. [Google Scholar] [CrossRef]
- Jin, B.; Zou, J. A Bayesian inference approach to the ill-posed Cauchy problem of steady-state heat conduction. Int. J. Numer. Methods Eng. 2008, 76, 521–544. [Google Scholar] [CrossRef]
- Lei, B.; Zheng, H. Dynamic Load Identification Approach Based on Bayesian Estimation. Noise Vib. Control 2018, 38, 215–219. [Google Scholar]
- Yan, G.; Sun, H. Identification of impact force for composite structure using Bayesian compressive sensing. J. Vib. Eng. 2018, 31, 483–489. [Google Scholar]
- Aucejo, M.; De Smet, O. On a full Bayesian inference for force reconstruction problems. Mech. Syst. Signal Process. 2018, 104, 36–59. [Google Scholar] [CrossRef]
- Aucejo, M.; De Smet, O. An optimal Bayesian regularization for force reconstruction problems. Mech. Syst. Signal Process. 2019, 126, 98–115. [Google Scholar] [CrossRef]
- Tang, H.; Jiang, J.; Mohamed, M.S. Dynamic Load Identification for Structures with Unknown Parameters. Symmetry 2022, 14, 2449. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, S.; Fei, Q. Distributed dynamic load identification on irregular planar structures using sub region Interpolation. J. Aircr. 2021, 58, 288–299. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).