Abstract
There is a growing trend towards the development of high resolution and multiplexing metasurface holograms. In this paper, we propose the reconstruction of polarization multiplexing terahertz (THz) holographic images based on transmissive metasurface. The metasurface composed of all-dielectric meta-atoms is designed as a multi-foci metalens and the focal points of the metalens are utilized as the pixels of a reconstructed image. We analyze the effects of focal length and phase pixel number of the metalens on focal point to achieve high-resolution holographic images. In addition, by switching the polarization of incident lights, holographic images with different patterns are reconstructed on its focal plane. Such high-resolution and polarization multiplexing metasurface holograms is promising for applications in THz communications, information engineering, and encryption.
1. Introduction
Holography, an optical technique that can record and reconstruct wavefronts with amplitude and phase information, has attracted tremendous interest [1]. A complicated system for interference and recording is indispensable for conventional optical holography. The development of spatial light modulator (SLM) and computer technology makes holography easier by replacing the recording and reconstruction processes with numerical calculation. However, conventional SLMs, suffering from low resolution, narrow bandwidth, and small field of view, degrade the quality of reconstructed images and restrict their practical applications [1,2,3].
Metasurfaces enable the manipulation of amplitude, phase, and polarization of light fields in a subwavelength-scale planar configuration. Through elaborate design and spatial arrangement of meta-atoms, various metasurface devices have been studied with novel functionalities, such as beam splitter [4,5,6], metalens [7,8,9], optical vortex generator [10,11,12], holography [13,14,15], and so on. Especially, terahertz (THz) holograms with transmissive metasurfaces have great perspectives for applications in communications, information storage, compared with the reflective metasurface holograms [16,17,18]. Many studies of THz metasurface holograms have been reported based on metallic or dielectric metasurfaces [16,17,18,19,20]. For example, Wang et al. [16] demonstrated a multiplexed THz hologram with simultaneous binary amplitude and binary phase modulation in every pixel by utilizing C-shape bar resonators as the basic unit cells. Different holographic images can be realized at different polarizations and different frequencies. However, the metallic plasmonic metasurfaces suffer from relatively low efficiency resulting from their material nature and weak coupling in the polarization conversion process [21], indicating that ultrathin, compact, and efficient all-dielectric metasurfaces have great prospects.
Among the dielectric materials, silicon (Si) is selected as the most constituent material of metasurfaces in the THz range for its merits of low loss, high refractive index, and ease of fabrication [22,23]. It has been reported that Si meta-atoms can be implemented for versatile applications, such as polarization-independent metalenses [24,25], polarization-dependent THz wavefront manipulation [26], polarization-sensitive modulated optical vortices generation [27,28], achromatic metalenses [29,30], and reconfigurable THz metasurface pure phase holograms [31]. In addition, traditional metasurface holograms were achieved based on iterative optimization algorithms (the most commonly used being the Gerchberg–Saxton (GS) algorithms) [31,32,33,34]. For example, Zhao et al. demonstrated a high-efficiency transmissive hologram based on GS algorithms and discussed the wave propagation from hologram plane to image plane using the Fresnel diffraction method and Rayleigh–Sommerfeld diffraction method [33]. Sufficient iterations and appropriate modifications are needed to get a convergent map, which makes the design process more complex. Besides, this phase-only modulation method for metasurface holograms brings noise and flaws in image quality stemming from the absence of amplitude information [16,35,36,37]. The simultaneous control of phase and amplitude can achieve better image quality, yet the resolution of the reconstructed holographic images is not at the subwavelength scale [38,39,40,41].
The metalenses utilized to generate holographic images [41,42,43] provide inspiration for our work. The focal plane of a metalens can be regarded as a reconstructed image with only a single bright spot, which can be further designed to reconstruct patterned holographic images with subwavelength resolution by optimizing the focal point. Notably, the interleaved meta-atoms for the multiplexing metasurface hologram are well-known concepts in the visible range metasurface. In the reference [13], four TiO2 nanopillars arranged on 2 × 2 square grids were used to define one metasurface superpixel. Based on the design, the authors demonstrated synchronous generation of four-channel nanoprinting-hologram images at the wavelength of 530 nm. In the reference [42], three hybrid all-dielectric meta-atoms were arranged interleaved to generate multi-channel polarization wavelength multiplexing metasurface holograms in the visible region. Furthermore, studies on the metasurface holograms with a single functionality are now mature, and there is a growing trend towards the development of subwavelength resolution and multiplexing metasurface holograms in the THz range.
In this paper, we realize the reconstruction of high-resolution and polarization multiplexing THz holographic images by designing a multi-foci metalens, which is different from traditional metasurface holograms that were achieved based on iterative optimization algorithms. The metalens is composed of all-dielectric meta-atoms and the focal points of the metalens are utilized as the pixels of a holographic image. The effects of focal length and phase pixel number of the metalens on image quality are discussed to achieve high-resolution holographic images. Furthermore, by switching the polarization of incident lights, holographic images with different patterns are reconstructed on the focal plane. Our work achieves holographic images with both subwavelength resolution and polarization multiplexing holograms with advantages of miniaturization, integration, multiplicity, and high storage capacity, which has potential for applications in THz communications, information engineering, and encryption.
2. Theoretical Analysis
The design of the metalens is of great significance for reconstructing holographic images. The phase profile for a typical metalens that leads to a distinct focal point following the Fermat’s principle can be described by Formula (1) [41,42]:
where f0 is the operating frequency, are the coordinates of the focal point on its focal plane, f is the focal length, is the distance between the center of the focal point and the center of the metalens, and c is the speed of light in vacuum. When a beam passes through the metalens with the phase profile in Formula (1), one focal point is produced on the focal plane of the metalens, which means a single bright spot can be reconstructed on the holographic image. To further generate a patterned holographic image, the consecutive foci are arranged in an m × n array, and the phase profile of metalens can be written as Formula (2):
where . Each pixel in the designed holographic image corresponds to the ith column and the jth row focal point with coordinates on the focal plane, where , , and d0 is the distance between two adjacent foci. The evaluation and optimization for the quality of the focal point is vital to achieve high-resolution and multiplexing holographic images. Huygens principle qualitatively points out that each point of the wavefront can serve as the secondary point source of the emitted waves [33]. When the incident light propagates from wave surface S1 to S2, according to Huygens principle, the complex amplitude of the wave emitted by point P0 in surface S1 at the point Q in surface S2 is: , where is the complex amplitude of the wave located at the z = 0 plane with surface area S, r0 is the distance between points P0 and Q, is the phase factor, and k = 2π/λ is the wavevector. It is worth noting that the magnitude of the amplitude is inversely proportional to the moving distance, and the phase change is k0 times the moving distance. By using Huygens principle and the principle of electromagnetic wave superposition, the complex amplitude at another point P can be obtained. According to the Huygens–Fresnel principle, the complex amplitude can be written as: , where r is the distance between points Q and P, and K(θ) is an additional tilt factor reflecting the relationship between amplitude and direction. Based on the above Fresnel’s mathematical expression, the Fresnel hypothesis and Huygens–Fresnel principle can be approximately simplified according to Kirchhoff diffraction theory, and the undetermined tilt factor K(θ) in Fresnel theory can be given as: , where normal direction , is the vector between the source point and a point in the S1 plane, and is the vector between the point in the S1 plane and a point in the propagation distance z = f. Thus, the intensity distributions on the focal plane can be calculated by using the Fresnel–Kirchhoff diffraction integral method [44,45]:
In other words, the quality of the focal point is evaluated and optimized by using the Fresnel–Kirchhoff diffraction integral [45] according to the intensity distributions on the focal plane.
When a THz beam with specific polarization propagates through the metalens, a target image is reconstructed on its focal plane. The schematic representation of the transmissive all-dielectric metasurface for the polarization multiplexing holograms is shown in Figure 1. The incident THz beam can be focused by the metalens at each focal point with the nominated location on the focal plane to form the target holograms. Particularly, different holographic images are generated under different incident polarizations. When left-handed circularly polarized (LCP) light illuminates the metalens, the reconstructed image in the upper panel of Figure 1 is letters “EL”. Alternatively, when the incident lights are with right-handed circularly polarized (RCP), pattern of numbers “17” is presented in the lower panel of Figure 1. Consequently, by controlling the polarization of incident lights, independent images can be reconstructed on the focal plane of the metalens. Moreover, the retrieved partial phase profiles are also given in Figure 1, where the required phase profiles are imposed by rotating the meta-atoms with angle , where “+” and “−” correspond to the incident LCP and RCP lights, respectively.
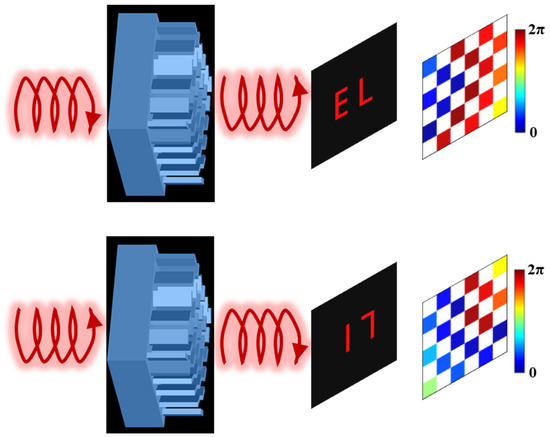
Figure 1.
Schematic of the transmissive all-dielectric metasurface for the polarization multiplexing THz holograms. The hologram patterns with “EL” and “17” are reconstructed under the incident LCP and RCP light, respectively. The retrieved partial phase profiles φL and φR are also shown.
3. Structure Design
As shown in Figure 2a, the meta-atom is composed of a Si micro-pillar on a Si substrate, and the permittivity of Si is 11.9 [28]. P, H, L, and W represent the period, height, length, and width of the meta-atom, respectively. The meta-atom is optimized to behave as a half-wave plate (HWP), which can convert the incident LCP(RCP) light into the RCP(LCP) light with an additional phase that is twice the rotation angle θ. Based on geometric phase or the Pancharatnam–Berry (PB) phase, the desired phase of the cross-polarized light can be achieved by varying the rotation angle θ (0~180 degree). The mechanism of geometric phase can be easily revealed by the Jones matrix [12]. The incident LCP(RCP) light can be expressed with Jones’ vector , where “+” and “−” correspond to the incident LCP and RCP lights, respectively. For the designed Si meta-atom with a rotation angle of θ, the transmitted light under the illumination of LCP(RCP) light with can be written as Formula (4):
where txx and tyy represent the transmission coefficients under x-linearly polarized (XLP) and y-linearly polarized (YLP) lights illumination, and φxx and φyy represent the corresponding phases. Moreover, the second term indicates the cross-polarized component with the additional phase of ±2θ. In order to make the meta-atom work as an HWP, the transmission is near unity, and the phase difference between the x- and y-directions should be π. The geometric optimization is carried out by using a commercial simulation software from FDTD Solutions based on the finite-difference time-domain (FDTD) method. Periodic boundary conditions are adopted in the x-y plane and a perfectly matched layer boundary condition is utilized in the z-direction. To ensure the convergence and accuracy of the results, the mesh cell size is set to 5 μm in the x- and y-directions, and 10 μm in the z-directions, which are smaller than λ/10. Normal-incident circularly polarized light is established by two polarized lights along the x- and y-directions with the same amplitudes, and phase difference of π/2. One 2D “frequency-domain field and power” monitor is placed in the transmitted field to collect the transmission data. By fixing P = 80 μm, H = 500 μm, and varying L and W of the meta-atom, the transmission coefficient and phase profile for the illumination of the XLP light at the frequency of 0.85 THz are shown in Figure 2b. Based on the mirror symmetry of the meta-atom corresponding to L = W, the transmission coefficient and the phase profile under the YLP light illumination can be extracted from the results of txx and φxx [12]. At the geometric parameters of L = 65 μm and W = 15 μm, the transmission is near unity, and the phase difference in the two orthogonal directions is π, consistent with the HWP-like operation. Therefore, the optimized structural parameters are L = 65 μm, W = 15 μm, H = 500 μm, and P = 80 μm, respectively. Meanwhile, we calculate the cross-polarized and co-polarized transmission spectra, which are plotted in Figure 2c. Here, the cross-polarized and co-polarized transmissions are defined as the ratio of transmitted light power of the cross-polarized component and the co-polarized component to the total incident light power, respectively. At the frequency of 0.85 THz (corresponding to the wavelength of 282.55 μm), the cross-polarized transmission reaches up to 98.9%, while the co-polarized transmittance is less than 0.1%, satisfying the condition of an HWP. Therefore, with the LCP light illuminating the metalens at the frequency of 0.85 THz, the transmitted light is converted into the RCP light carrying an additional phase φL and focused on its focal plane to reconstruct a patterned hologram. Similarly, with the RCP light illuminating the metalens at the frequency of 0.85 THz, the transmitted light is converted into the LCP light carrying an additional phase φR and focused on its focal plane to reconstruct another patterned hologram. Thus, we choose 0.85 THz as the working frequency in the following metalens design.
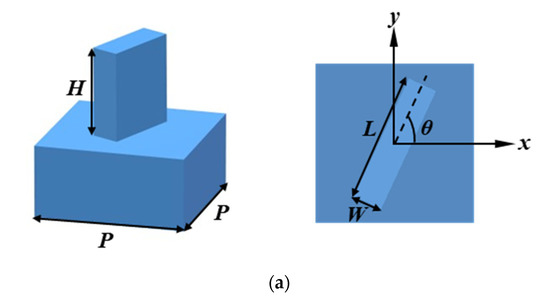
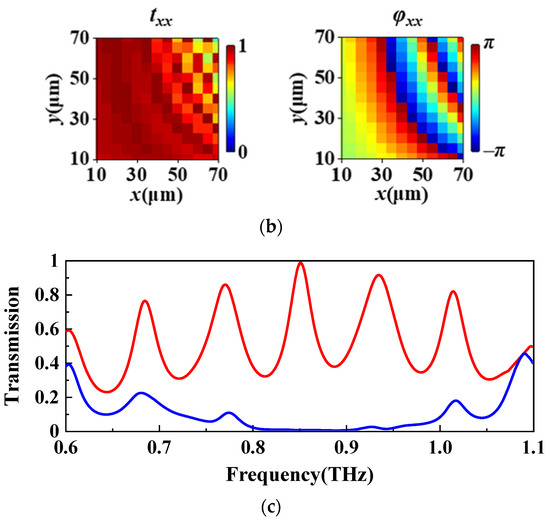
Figure 2.
(a) The schematic illustration of the Si meta-atom with rotation angle θ. L, W, H, and P are the length, width, height, and period of the meta-atom, respectively; (b) the transmission coefficient and phase profile under XLP light illumination; (c) the cross-polarized transmittance (red line) and co-polarized transmittance (blue line) with the frequency ranging from 0.6 to 1.1 THz under the LCP light incidence.
4. Results and Discussion
We fully explore the intensity distributions of the focal point to obtain a high-resolution holographic image since the focal point produced by a metalens is utilized as the pixel of the image. In general, the clear aperture and focal length of the metalens have an effect on the focal point. The clear aperture of the metalens is D = PN, in which N represents the phase pixel number along the diameter of the metalens [41,42]. In Figure 3a, the intensity distributions of one focal point with various phase pixel number N and focal length f are displayed. For a fixed phase pixel number, the size of the focal point grows as the focal length increases. Conversely, when the focal length remains the same, the size of the focal point decreases with the increase of the phase pixel number, indicating the increase of the clear aperture. The relationship between the phase pixel number (clear aperture) and focal length produces results in agreement with the classical formula for the focal point diameter of a lens [41,42]. Here, the focal point diameter d is defined as twice the width at which the intensity drops to 1/e2 (13.5%). Figure 3b presents the corresponding horizontal cross-sections of the intensity distribution at y = 0 mm with different focal lengths, where the phase pixel number is 100, 200, 300, and 400 (from left to right), respectively. It can be seen that d decreases with the increase of N. Thus, we can obtain a smaller equivalent pixel size (higher resolution) at a larger phase pixel number because the holographic image is reconstructed by the metalens. Unfortunately, the diffraction becomes more severe at a smaller focal point size due to more concentric ring fringes on its focal plane. It should be considered to obtain a balance between quality and resolution of the reconstructed image during the design. Thus, we utilize two crucial parameters, i.e., the focal length f = 10 mm and the phase pixel number N = 300, to produce the focal point at the subwavelength scale without excessive diffraction. Meanwhile, the focal point diameter d is 268 μm, and the dimension of the metalens is 24 mm along both the x- and y-directions. As the metalens width of 24 mm is larger than the focal length of 10 mm, it does not satisfy the Fresnel approximation in diffractive optics [17], namely, . Therefore, we use the Fresnel–Kirchhoff diffraction integral method.
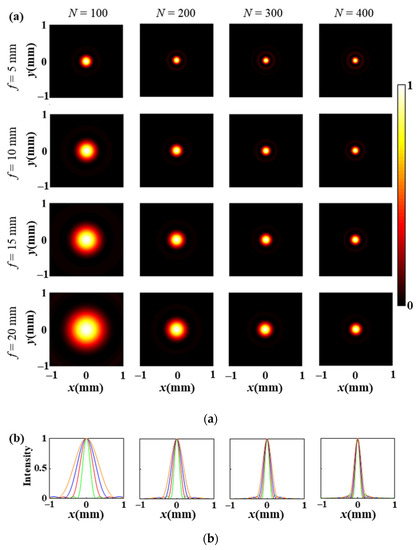
Figure 3.
(a) Normalized intensity distributions of a single focal point at the focal plane for various combinations of phase pixel numbers N and focal lengths f; (b) the corresponding horizontal cross-section of the intensity at y = 0 mm with different focal lengths (colorful solid lines), where the phase pixel number is 100, 200, 300, and 400 (from left to right), respectively.
The intensity distribution of two pixels exhibiting continuous, non-overlap, and uniform characteristic is a prerequisite for a better quality of the holographic image. Thus, the distance d0 between the center of two adjacent foci is significant in the formation of holograms with better quality. In general, the continuity of focal points depends on the distance d, which can emerge from the concept of a diffraction limit [41]. The results of two focal points produced on the x-axis with x1 = 134 μm and different distances d0 () are investigated. The intensity distributions and the corresponding horizontal cross-sections of the intensity distribution at y = 0 mm with different d0 are shown in Figure 4a,b, respectively. It can be seen from Figure 4 that when , the two adjacent foci are indistinguishable resulting from the serious overlap. When the distance d is equal to 268 μm, the distribution between two pixels with continuous, non-overlap, and uniform intensity is satisfied. The two focal points are clearly distinguished as the distance d continues to increase. However, there is obvious cutoff between two focal points, indicating that the intensity is not uniform. Thus, to achieve a better quality of the holographic image, the distance d between the center of two adjacent foci is chosen to be 268 μm. Notably, the holographic images can be reconstructed on the focal plane of the metalens with the optimized parameters f0 = 0.85 THz, f = 10 mm, N = 300, and d = 268 μm.
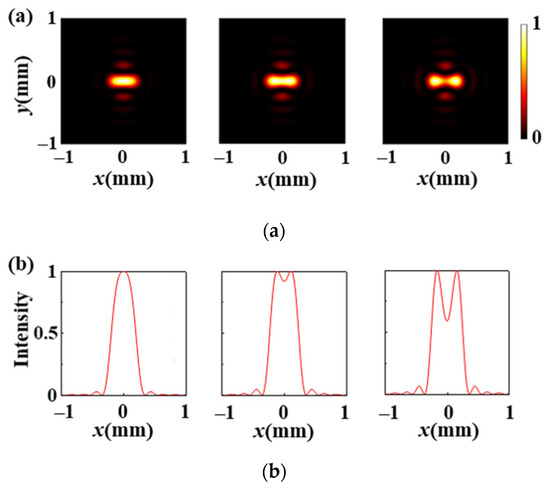
Figure 4.
(a) Normalized intensity profiles of the two adjacent foci generated on the x-axis with different distances d0 between the center of two adjacent foci; (b) the corresponding horizontal cross-section of the intensity at y = 0 mm with different distance d0.
For verification, we design a metalens for generating polarization multiplexing holograms. The phase profiles of the hologram for the incident LCP and RCP lights are accomplished by interleaved meta-atoms with the rotation angles θL and θR, respectively, as shown in Figure 5a. The merged phase profile can be expressed as Formula (5):
where and represent the phase profile under LCP and RCP lights incidence, respectively. The patterns of letter and number form the target holograms corresponding to two polarizations (i.e., LCP and RCP input lights, respectively), indicating that these images include polarization information. According to Formula (3), we encoded the phase profiles onto the metalens to achieve the polarization multiplexing holographic images. Figure 5b presents the retrieved phase profile for the holographic image. The reconstructed images with letters “EL” and numbers “17” on the focal plane under LCP and RCP illumination are clearly shown in Figure 5c,d, respectively. Notably, with the help of extra spatial freedom (meta-atoms with different rotation angles arranged interleaved), the cross-talk among different polarizations of incident light (i.e., LCP and RCP) can be suppressed. As we know, a linearly polarized (LP) light can be written as a combination of the two orthogonal components (LCP and RCP lights). Hence, in the situation that a LP light illuminates the metasurface, the combination of designed letters “EL” and numbers “17” are displayed in the reconstructed holographic image in Figure 5e, which forms a new pattern with numbers “80”. From Figure 5, we can obtain that by utilizing focal points as the pixels of holographic image and switching the incident polarizations, the metalens can reconstruct different holographic images accordingly on its focal plane.
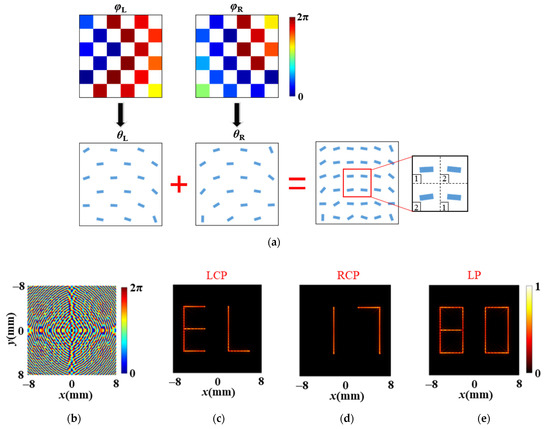
Figure 5.
(a) The designed metasurface with merged phase profiles to reconstruct polariza-tion-multiplexing holographic images. (b) Retrieved phase profile for the hologram patterns with LP light illumination. The reconstructed images on the focal plane to present the polarization multiplexing holograms with the incident (c) LCP, (d) RCP, and (e) LP lights for working fre-quency of 0.85 THz.
To clearly show distributions of the focal points at each location, we demonstrate the holographic images formed by half of the foci, i.e., the distance between two adjacent foci becomes 536 μm. It means that a fixed interval, rather than the continuous profile, can be observed in the reconstructed holographic images. As shown in Figure 6, the patterns “EL” and “17” with a fixed focal-point interval can be reconstructed on the focal plane, respectively, by switching the incident polarization from LCP to RCP. A new pattern, numbers “80” with a fixed focal-point interval, is also produced under the incidence of LP light. These results verify that the reconstructed images are formed by focal-point pixels.
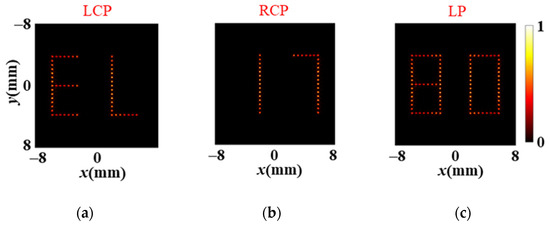
Figure 6.
The corresponding reconstructed images with half of focal points when illuminated by (a) LCP, (b) RCP, and (c) LP lights for working frequency of 0.85 THz.
It is noted that the design is feasible because the proposed metalens could be fabricated on silicon wafer by standard electron beam lithography and etching process [19], which can follow the following steps: (a) clean the Si wafer in ultrasonic bath; (b) the photoresist is spin-coated onto the cleaned Si wafer; (c) the resist film is exposed by using a mask aligner and developed; (d) the resist film is etched; (e) the photoresist is removed, and the Si meta-atom is finally obtained. On the other hand, the successful demonstration of the terahertz multifocal polarization-controlled metalens shows that it is feasible to use the near-field scanning terahertz microscope system to perform the characterization of the designed metalens samples in this paper. A femtosecond fiber laser is used to generate a laser beam with a pulse width of 50 fs and a central wavelength of 1550 nm, and the laser beam is divided into two parts by a beam splitter. A part of the light is transmitted to the emitter of the commercial photoconductive antenna, which can generate 0.2~1.5 THz broadband terahertz radiation and irradiate the metalens sample. Another part of the light will be converted in free space, and then the second harmonic will be generated in periodically poled lithium niobate (PPLN). When it is irradiated on the terahertz probe used to detect the electric field distribution, the terahertz beam can be detected with high-resolution pixels. In front of the metalens sample, a group of terahertz polarizers are placed to ensure that the incident terahertz beam has the needed polarization (i.e., LCP, RCP, and LP). After passing through the metalens sample, the hologram pattern can be observed with an objective lens in the confocal plane with the metalens sample, and the polarization profile of the hologram pattern can be detected with an analyzer and collected by a terahertz probe. The terahertz probe is installed on the three-dimensional translation platform, which can realize the three-dimensional electric field scanning. The terahertz probe scans the electric field distribution of the terahertz beam in the imaging area to collect the target focal points at the focal plane of the metalens.
5. Conclusions
In conclusion, polarization multiplexing THz holograms are realized by utilizing multi-foci metalens composed of all-dielectric meta-atoms with specific orientation angles, which is different from traditional metasurface holograms that were achieved based on iterative optimization algorithms. The focal points of the metalens are regarded as the pixel of a holographic image in our design. We analyze the effects of focal length and phase pixel number of metalens on the focal point, which shows that the holographic images with subwavelength resolution could be obtained at the optimized parameters. Moreover, by switching the polarization of incident lights, holographic images with different patterns are reconstructed on the focal plane. Such high-resolution and polarization multiplexing metasurface holograms have potential applications in THz communications, information engineering, and encryption.
Author Contributions
Conceptualization, X.W.; methodology, X.W. and R.W.; software, X.W.; validation, X.W.; formal analysis, X.W.; investigation, X.W., J.W., R.W., L.L. and Y.J.; resources, X.W.; data curation, X.W.; writing—original draft preparation, X.W. and J.W.; writing—review and editing, X.W. and J.W.; supervision, L.L. and Y.J.; funding acquisition, Y.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 62075048, 62205106), and the Natural Science Foundation of Shandong Province (Grant No. ZR2020MF129).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, Q.; Jin, G.; Cao, L. When metasurface meets hologram:principle and advances. Adv. Opt. Photon. 2019, 11, 518–576. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Zhao, R.; Huang, L.; Wang, Y. Recent advances in multi-dimensional metasurfaces holographic technologies. Photonix 2020, 1, 20. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Zhu, W.; Crozier, K.B. Efficient polarization beam splitter pixels based on a dielectric metasurface. Optica 2015, 2, 376–382. [Google Scholar] [CrossRef]
- Ozer, A.; Yilmaz, N.; Kocer, H.; Kurt, H. Polarization-insensitive beam splitters using all-dielectric phase gradient metasurfaces at visible wavelengths. Opt. Lett. 2018, 43, 4350–4353. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef]
- Kang, M.; Ra’Di, Y.; Farfan, D.; Alù, A. Efficient focusing with large numerical aperture using a hybrid metalens. Phys. Rev. Appl. 2020, 13, 044016. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-insensitive metalenses at visible wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef]
- Huang, L.; Xu, S.; Reineke, B.; Li, T.; Zentgraf, T. Volumetric generation of optical vortices with metasurfaces. ACS Photonics 2017, 4, 338–346. [Google Scholar] [CrossRef]
- Bai, Y.; Lv, H.; Fu, X.; Yang, Y. Vortex beam: Generation and detection of orbital angular momentum [Invited]. Chin. Opt. Lett. 2022, 20, 012601. [Google Scholar] [CrossRef]
- Wang, X.; Liu, B.; Yao, J.; Song, J.; Jiang, Y. High-efficiency optical vortex generation with hybrid all-dielectric geometric-metasurface in visible frequency. Appl. Phys. Express 2021, 14, 012008. [Google Scholar] [CrossRef]
- Liu, M.; Zhu, W.; Huo, P.; Feng, L.; Song, M.; Zhang, C.; Chen, L.; Lezec, H.J.; Lu, Y.; Agrawal, A.; et al. Multifunctional metasurfaces enabled by simultaneous and independent control of phase and amplitude for orthogonal polarization states. Light Sci. Appl. 2021, 10, 107. [Google Scholar] [CrossRef] [PubMed]
- Georgi, P.; Wei, Q.; Sain, B.; Schlickriede, C.; Wang, Y.; Huang, L.; Zentgraf, T. Optical secret sharing with cascaded metasurface holography. Sci. Adv. 2021, 7, eabf9718. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhong, J.; Li, B.; Qi, S.; Li, Y.; Li, P.; Wen, D.; Liu, S.; Wei, B.; Zhao, J. Full-color holographic display and encryption with full-polarization degree of freedom. Adv. Mater. 2022, 34, 2103192. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, X.; Plum, E.; Xu, Q.; Wei, M.; Xu, Y.; Zhang, H.; Liao, Y.; Gu, J.; Han, J.; et al. Polarization and frequency multiplexed terahertz meta-holography. Adv. Opt. Mater. 2017, 5, 1700277. [Google Scholar] [CrossRef]
- Wang, Q.; Plum, E.; Yang, Q.; Zhang, X.; Xu, Q.; Xu, Y.; Han, J.; Zhang, W. Reflective chiral meta-holography: Multiplexing holograms for circularly polarized waves. Light Sci. Appl. 2018, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Su, D.; Wang, X.; Shang, G.; Ding, X.; Burokur, S.N.; Liu, J.; Li, H. Amplitude-phase modulation metasurface hologram with inverse angular spectrum diffraction theory. J. Phys. D Appl. Phys. 2022, 55, 235102. [Google Scholar] [CrossRef]
- Zang, X.; Ding, H.; Intaravanne, Y.; Chen, L.; Peng, Y.; Xie, J.; Ke, Q.; Balakin, A.V.; Shkurinov, A.P.; Chen, X.; et al. A multi-foci metalens with polarization-rotated focal points. Laser Photonics Rev. 2019, 13, 1900182. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Y.; Li, X.; Wang, Q.; Huang, L. Switchable active phase modulation and holography encryption based on hybrid metasurfaces. Nanophotonics 2020, 9, 905–912. [Google Scholar] [CrossRef]
- Jia, D.; Tian, Y.; Ma, W.; Gong, X.; Yu, J.; Zhao, G.; Yu, X. Transmissive terahertz metalens with full phase control based on a dielectric metasurface. Opt. Lett. 2017, 42, 4494–4497. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Du, J.; Liu, Y.; Zang, X. Helicity multiplexed terahertz multi-foci metalens. Opt. Lett. 2020, 45, 463–466. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Zhang, X.; Wei, M.; Zhang, W. Spin-decoupled multifunctional metasurface for asymmetric polarization generation. ACS Photonics 2019, 6, 2933–2941. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Quan, X.; Wang, Q.; Zhang, W. Polarization-independent all-silicon dielectric metasurfaces in the terahertz regime. Photonics Res. 2018, 6, 24–29. [Google Scholar] [CrossRef]
- Hui, Y.; Guanhai, L.; Guangtao, C.; Zengyua, Z.; Feilong, Y.; Xiaoshuang, C.; Wei, L. Polarization-independent metalens constructed of antennas without rotational invariance. Opt. Lett. 2017, 42, 3996–3999. [Google Scholar]
- Zhang, H.; Zhang, X.; Xu, Q.; Tian, C.; Wang, Q.; Xu, Y.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C. High-efficiency dielectric metasurfaces for polarization-dependent terahertz wavefront manipulation. Adv. Opt. Mater. 2018, 6, 1700773. [Google Scholar] [CrossRef]
- Yan, C.; Li, X.; Pu, M.; Ma, X.; Luo, X. Generation of polarization-sensitive modulated optical vortices with all-dielectric metasurfaces. ACS Photonics 2019, 6, 628–633. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Q.; Xu, Q.; Jiang, X.; Wu, T.; Wang, K.; Gu, J.; Han, J.; Zhang, W. Multifunctional all-dielectric metasurfaces for terahertz multiplexing. Adv. Opt. Mater. 2021, 9, 2100506. [Google Scholar] [CrossRef]
- Cheng, Q.; Ma, M.; Yu, D.; Shen, Z.; Xie, J.; Wang, J.; Xu, N.; Guo, H.; Hu, W.; Wang, S. Broadband achromatic metalens in terahertz regime. Sci. Bull. 2019, 64, 1525–1531. [Google Scholar] [CrossRef]
- Heiden, J.T.; Min, S.J. Design framework for polarization-insensitive multifunctional achromatic metalenses. Nanophotonics 2022, 11, 583–591. [Google Scholar] [CrossRef]
- Guo, J.; Wang, T.; Zhao, H.; Wang, X.; Feng, S.; Han, P.; Sun, W.; Ye, J.; Situ, G.; Chen, H.-T.; et al. Reconfigurable terahertz metasurface pure phase holograms. Adv. Opt. Mater. 2019, 7, 1801696. [Google Scholar] [CrossRef]
- Gerchberg, R.W. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972, 35, 237–250. [Google Scholar]
- Zhao, W.; Jiang, H.; Liu, B.; Song, J.; Jiang, Y.; Tang, C.; Li, J. Dielectric Huygens’ metasurface for high-efficiency hologram operating in transmission mode. Sci. Rep. 2016, 6, 30613. [Google Scholar] [CrossRef] [PubMed]
- Shang, G.; Li, H.; Wang, Z.; Zhang, K.; Ding, X. Coding metasurface holography with polarization-multiplexed functionality. J. Appl. Phys. 2021, 129, 035304. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Hao, Z.; Chen, S.; Bai, B.; Tan, Q.; Jin, G.; Cheah, K.W.; Qiu, C.W. Three-dimensional optical holography using a plasmonic metasurface. Nat. Commun. 2013, 4, 2808. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, J.; Wang, Y.; Pu, M.; Li, X.; Zhao, Z.; Gao, P.; Wang, C.; Luo, X. Metasurface-based broadband hologram with high tolerance to fabrication errors. Sci. Rep. 2016, 6, 19856. [Google Scholar] [CrossRef]
- Montelongo, Y.; Tenorio-Pearl, J.O.; Williams, C.; Zhang, S.; Milne, W.I.; Wilkinson, T.D. Plasmonic nanoparticle scattering for color holograms. Proc. Natl. Acad. Sci. USA 2014, 111, 12679–12683. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Q.; Zhang, X.; Tian, C.; Xu, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Zhang, X.; Han, J. All-dielectric meta-holograms with holographic images transforming longitudinally. ACS Photonics 2018, 5, 599–606. [Google Scholar] [CrossRef]
- Overvig, A.C.; Shrestha, S.; Malek, S.C.; Ming, L.; Yu, N. Dielectric metasurfaces for complete and independent control of the optical amplitude and phase. Light Sci. Appl. 2019, 8, 92. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Xu, Y.; Gu, J.; Li, Y.; Tian, Z.; Singh, R.; Zhang, S.; Han, J.; Zhang, W. Broadband metasurface holograms: Toward complete phase and amplitude engineering. Sci. Rep. 2016, 6, 32867. [Google Scholar] [CrossRef]
- Wang, R.; Ren, G.; Ren, Z.; Liu, J.; Li, S.; Chen, X.; Li, L. Reconstructing subwavelength resolution terahertz holographic images. Opt. Express 2022, 30, 7137–7146. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cui, Y.; Ren, B.; Tang, S.; Wu, J.; Jiang, Y. Metalens for generating multi-channel polarization-wavelength multiplexing metasurface holograms. Opt. Express 2022, 30, 47856–47866. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Huang, L.; Li, X.; Li, X.; Wang, Y. All-dielectric bifocal isotropic metalens for single-shot hologram generation device. Opt. Express 2020, 28, 21549–21559. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics. In Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Zhang, Y.; Liu, W.; Gao, J.; Yang, X. Generating focused 3D perfect vortex beams by plasmonic metasurfaces. Adv. Opt. Mater. 2018, 6, 1701228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).