An AMR-Based Liquid Film Simulation with Surfactant Transport Using PLIC-HF Method
Abstract
1. Introduction
2. Governing Equations
2.1. Fluid Dynamic Equations
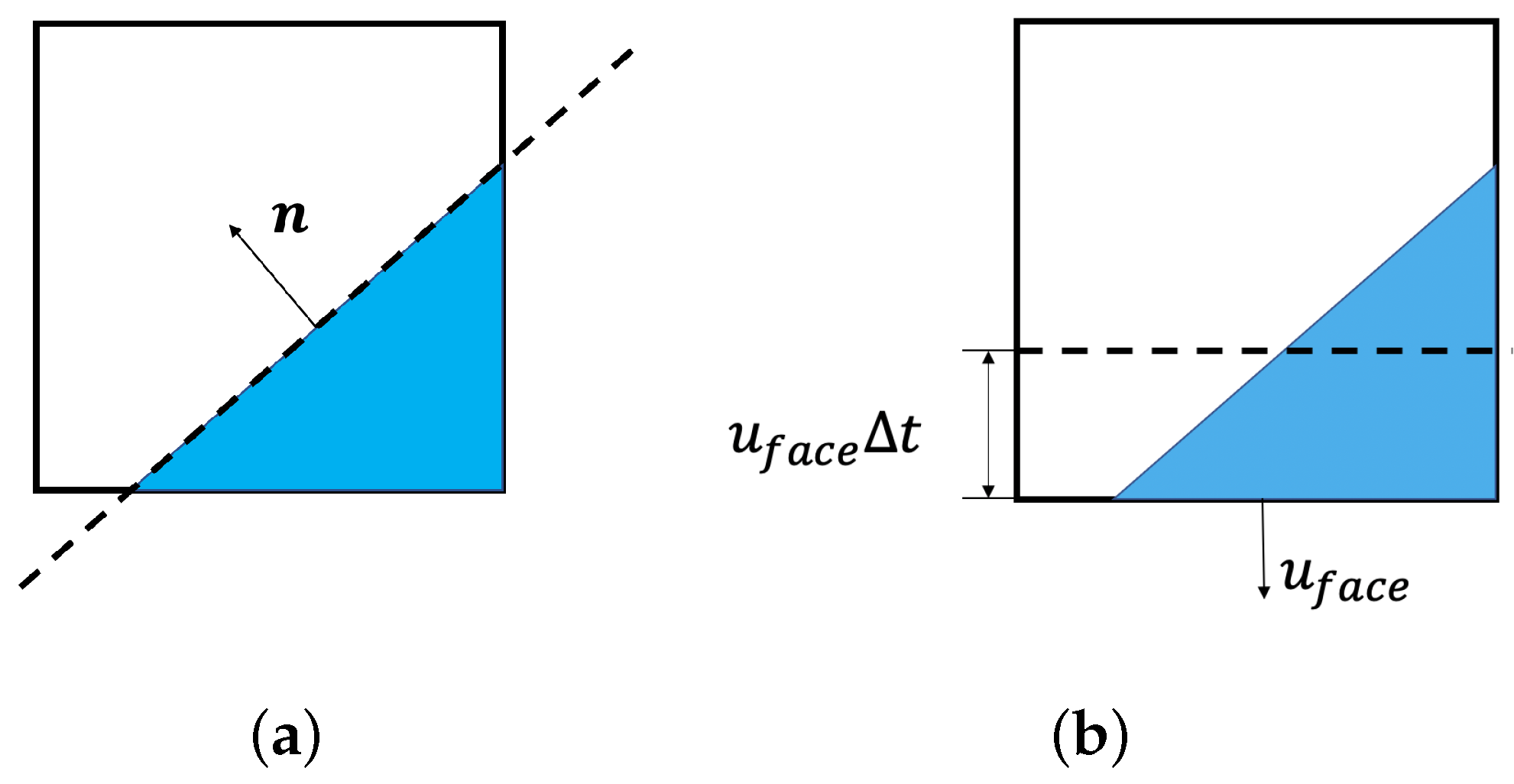
2.2. Conservative PLIC-VOF Method
2.3. Level Set Advection and Re-Initialization
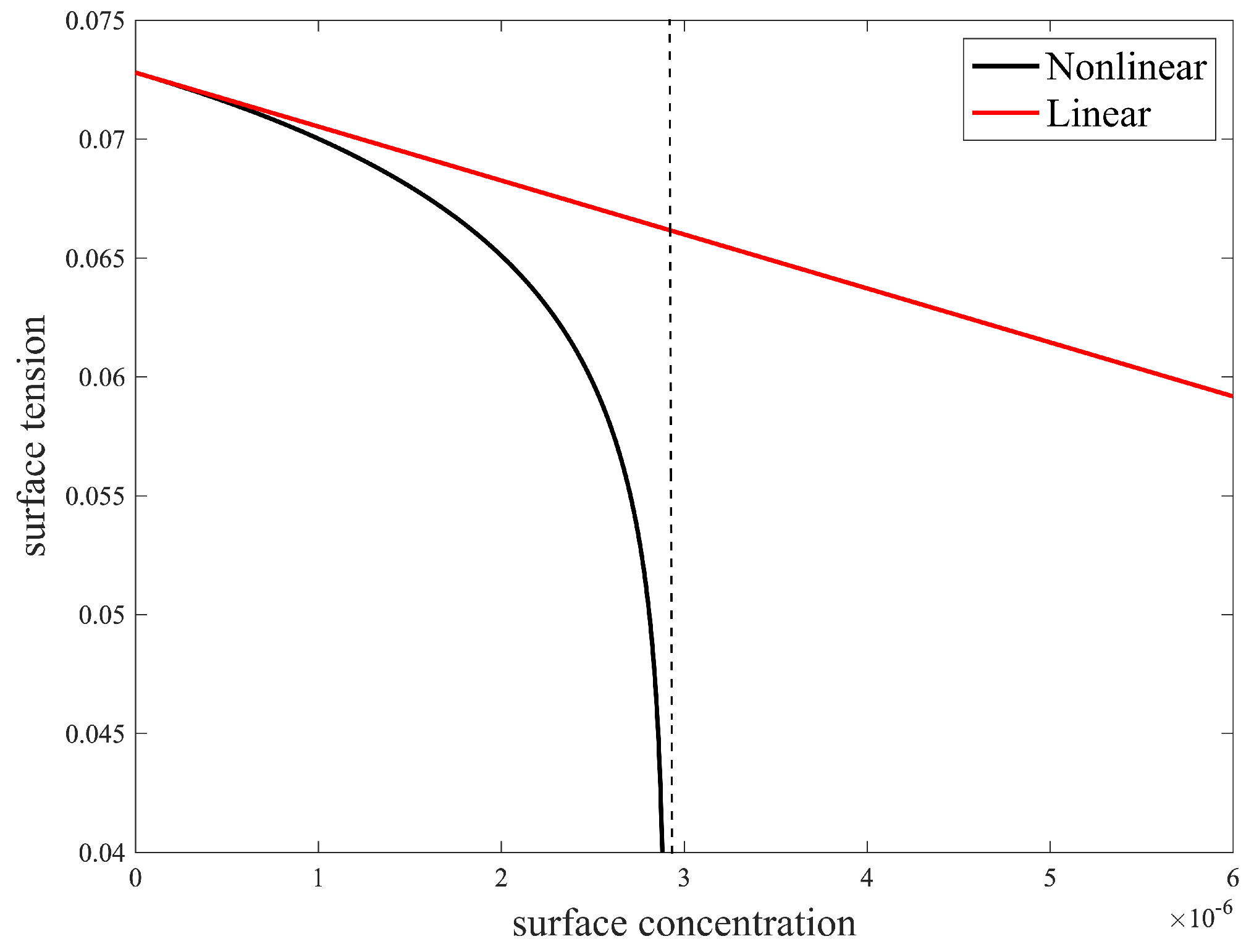
2.4. Surfactant Transport Equations and the Marangoni Effect
3. Numerical Methods
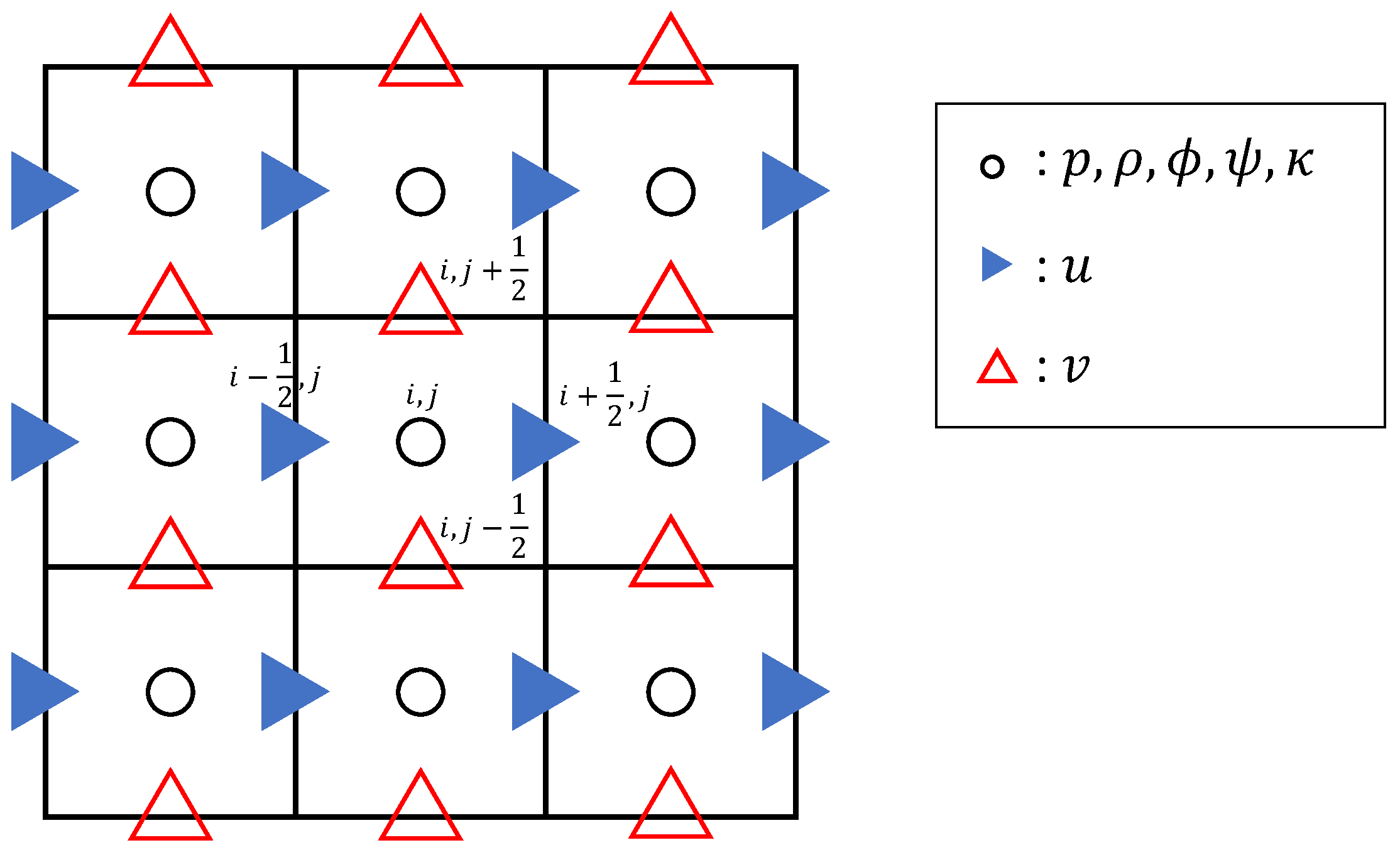
3.1. Spatial Discretization on Staggered Grid
3.2. Finite Difference Method to Solve Fluid Calculations
3.3. Dimension Split Method to the Solve Transport Equation of the Volume Fraction
3.4. Time Integration
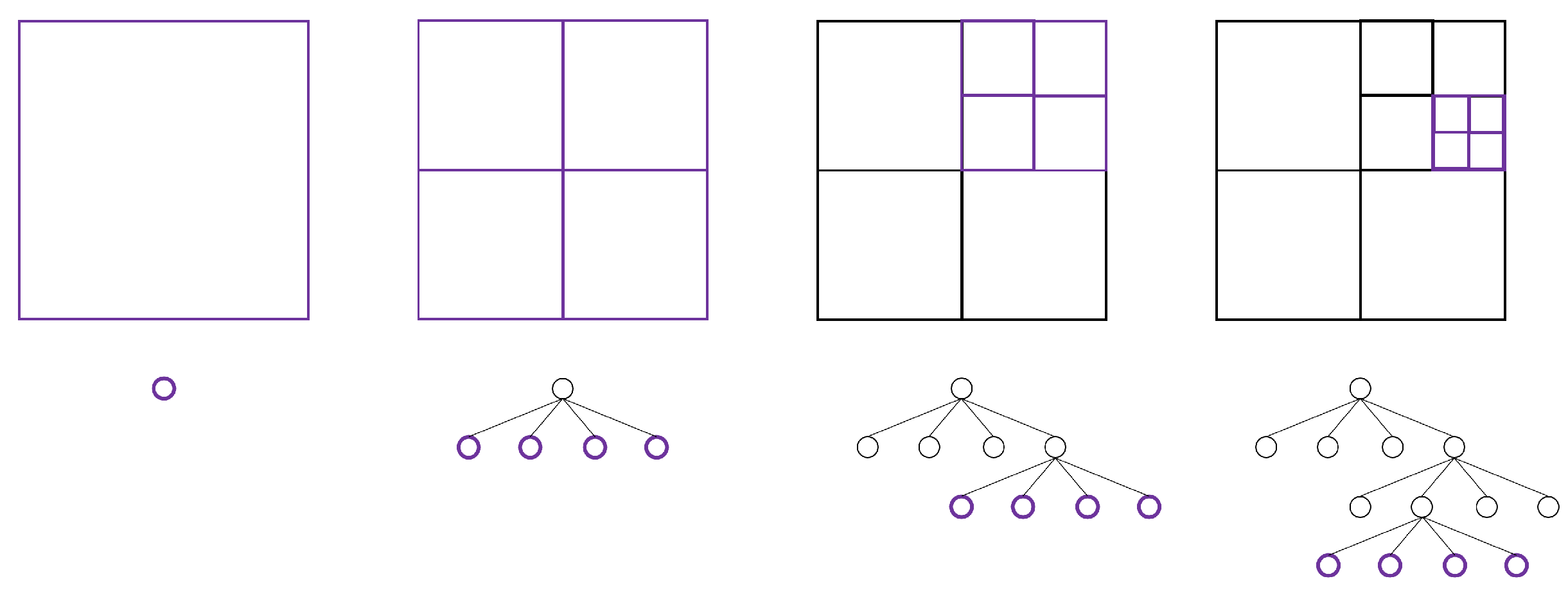
4. AMR Implementation by Using GPU Parallel Computing
5. Numerical Results
5.1. Two-Dimensional Time-Reversed VOF Advection in a Single Vortex
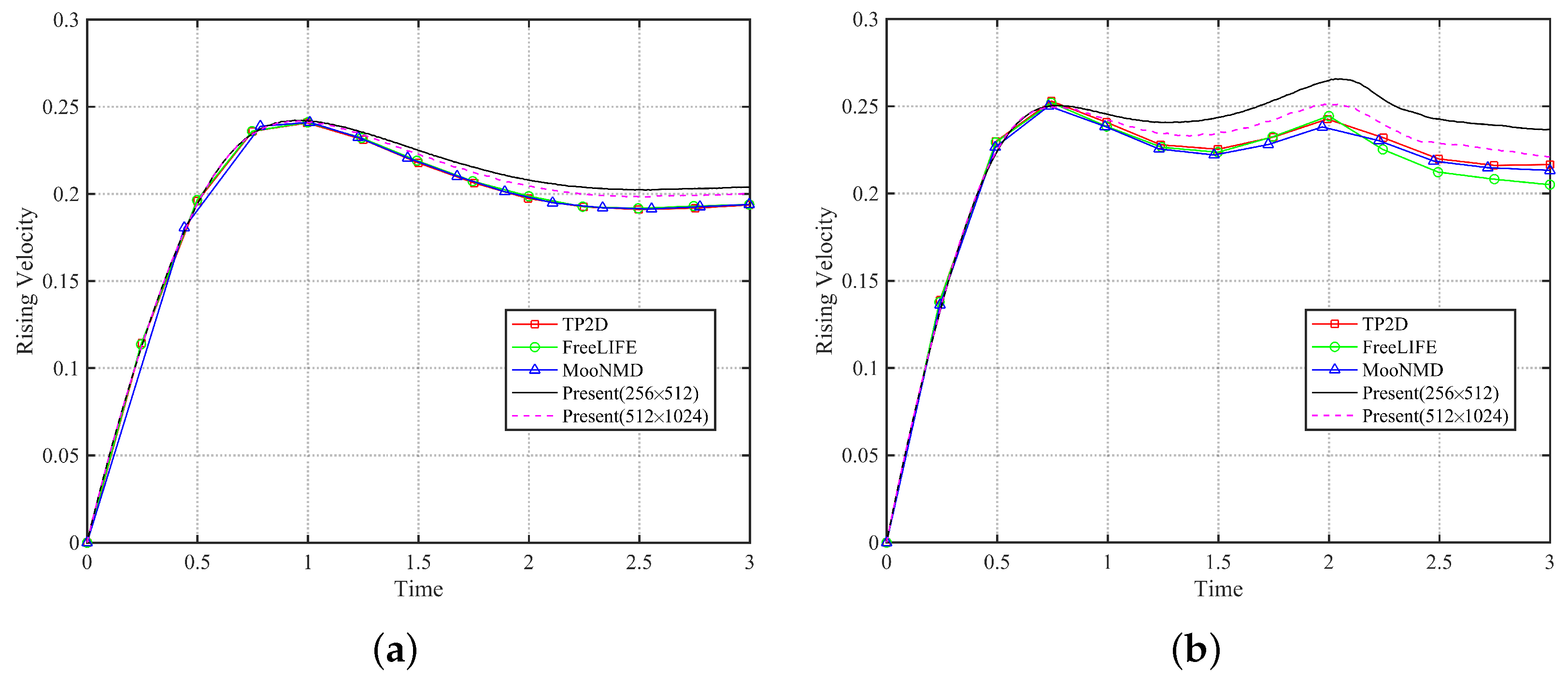
5.2. Two-Dimensional Single Rising Bubble
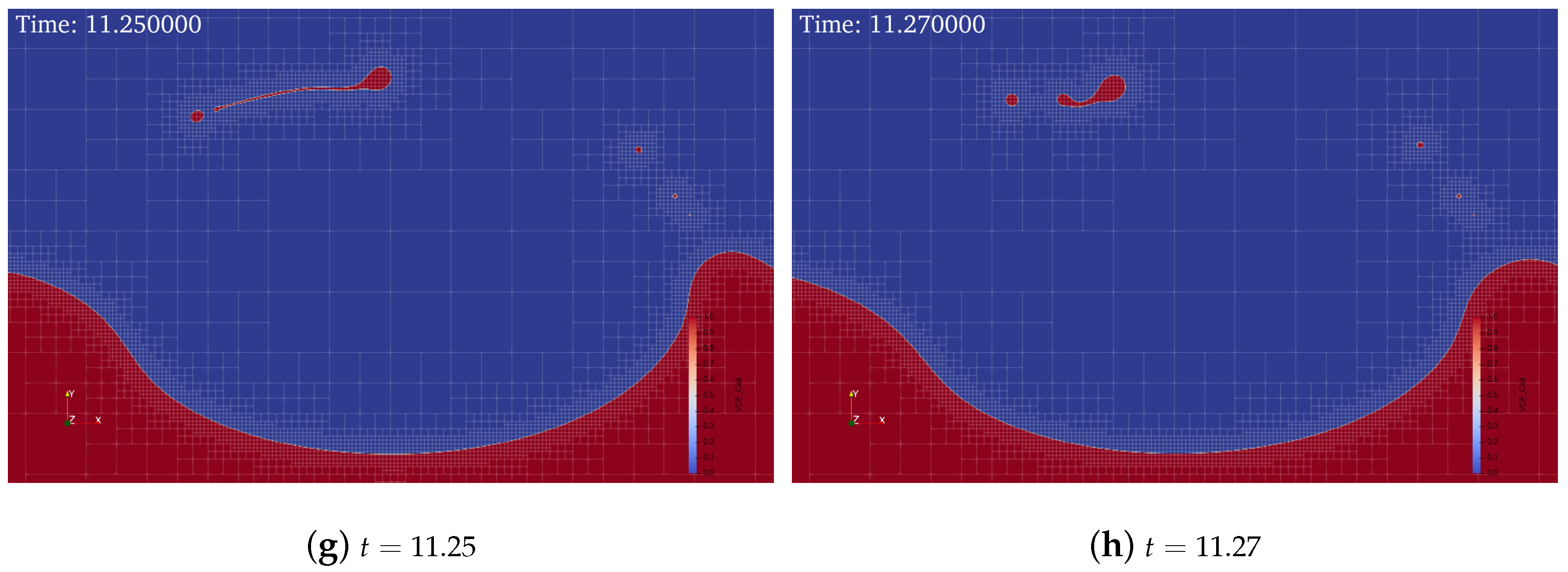
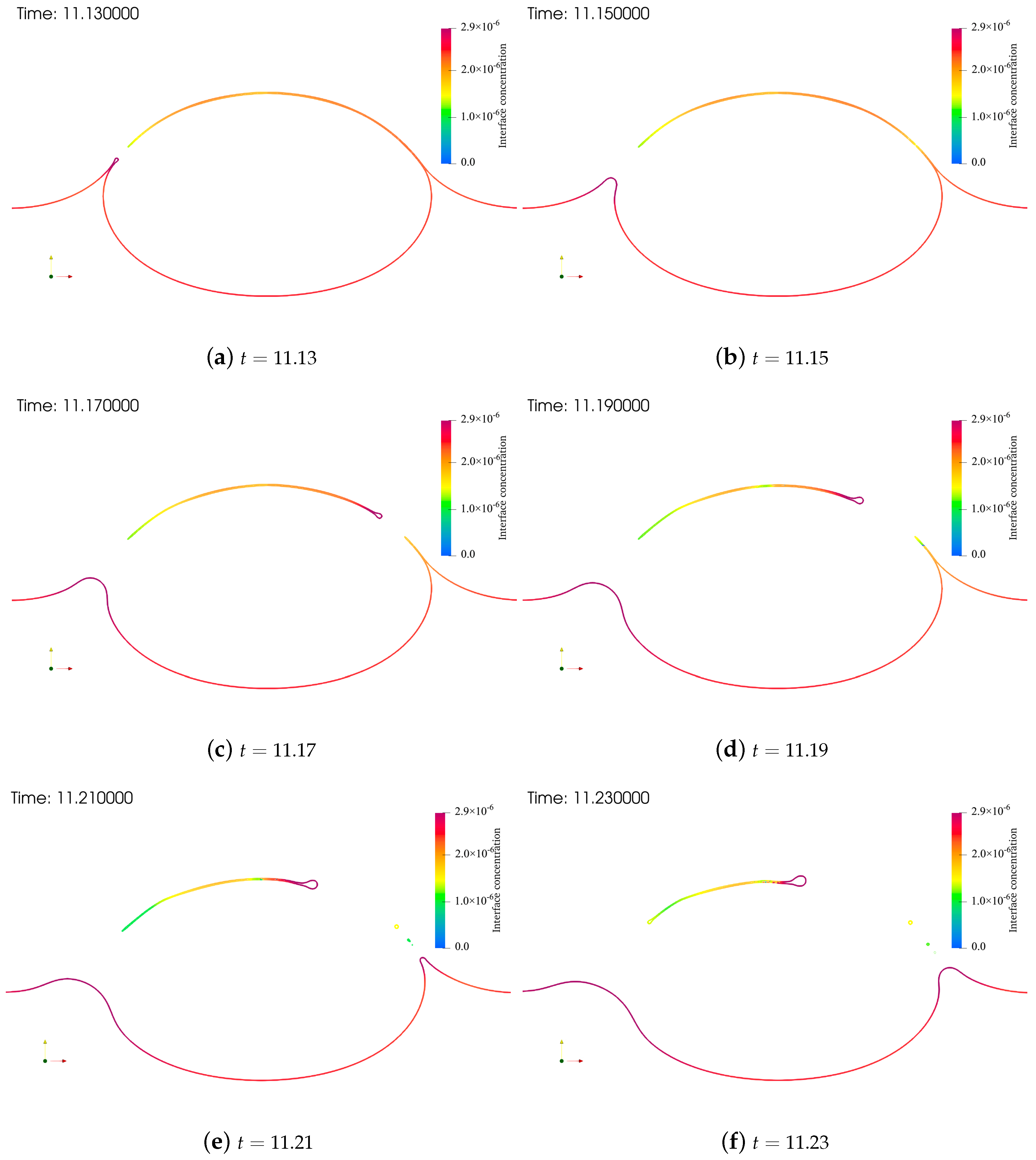
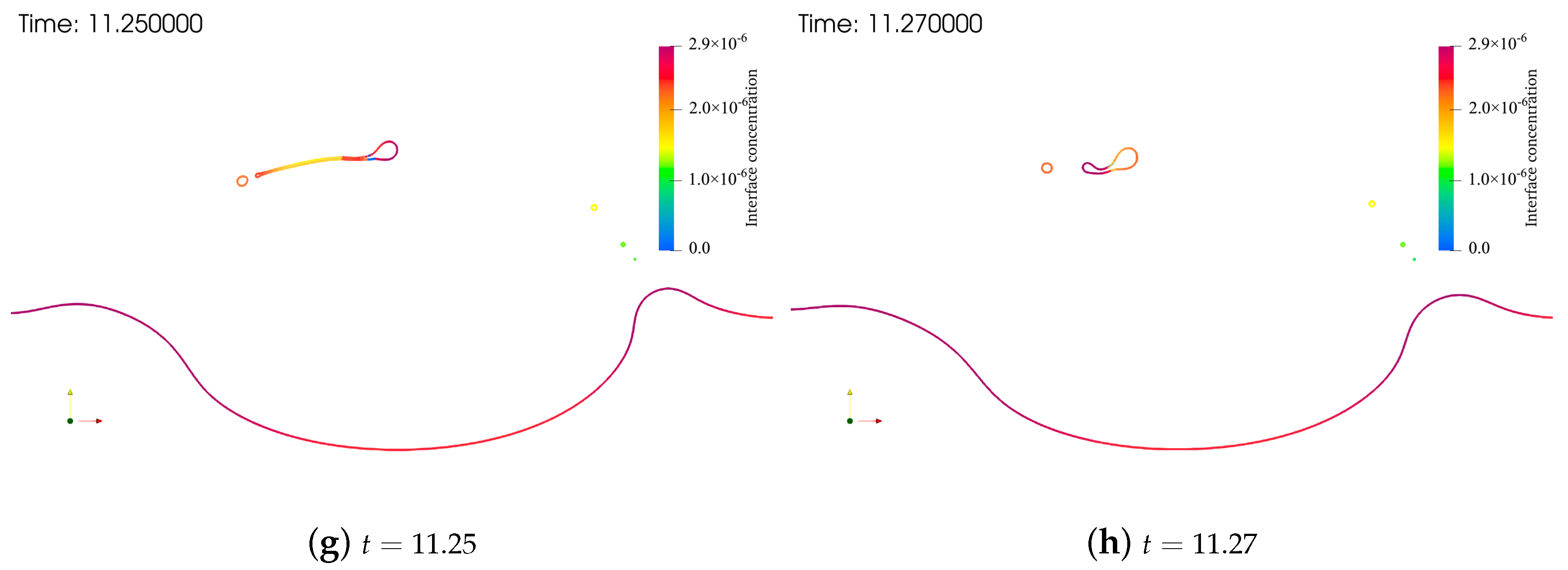
5.3. Liquid Film Generation and Rupture by a Single Bubble Rising to the Interface
6. Discussion
- The results shown in Section 5.1 verify the accuracy and efficiency of the presented PLIC-VOF method on AMR mesh. The conservation in the results is satisfactory, which indicates that the implementation of the AMR mesh is valid. The number of cells and the required memory are reduced with the AMR method, which decreases the execution time and the computer cost;
- The results shown in Section 5.2 verify the accuracy and ability of the two-phase solver. The accuracy of the weakly compressible solver is shown by its good agreement with references for the center of mass and the rising velocity of the bubble;
- Section 5.3 describes a simulation of the generation of liquid film by a single bubble rising to a horizontal interface and the rupture process of that liquid film with surfactant transport and the Marangoni effect. The motion of the liquid rim after the rupture of the liquid film observed in the present study’s simulation showed good agreement with the results of previous experiments, which indicates the accuracy of this method and its potential for use in further simulations of multi-scale problems.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimension |
| AMR | Adaptive Mesh Refinement |
| CPU | Central Processing Unit |
| FreeLIFE | Free-surface LIbrary of Finite Element |
| GPU | Graphics Processing Unit |
| HF | Height Function |
| HJ | Hamilton-Jacobi |
| IBM | Immersed Boundary method |
| LS | Level Set |
| MooNMD | Mathematics and object-oriented Numerics in MagDeburg |
| MPI | Message Passing Interface |
| MYC | Mixed Youngs-Centered |
| NS | Navier–Stokes |
| PF | Phase Field |
| PLIC | Piece-wise Linear Interface Calculation |
| SOR | Successive Over-Relaxation |
| SSP-RK | Strong Stability-Preserving Runge–Kutta |
| TP2D | Transport Phenomena in 2D |
| VOF | Volume of Fluid |
| WCS | Weakly Compressible Scheme |
| WENO | weighted essentially non-oscillatory |
| Nomenclature | |
| color function on cell center | |
| sound speed | |
| color function | |
| interface diffusive coefficient | |
| bulk diffusive coefficient | |
| f | interface concentration |
| saturation interface concentration | |
| F | bulk concentration |
| external force | |
| surface tension | |
| gravity force | |
| volume flux across cell faces | |
| H | height function |
| i | index on X-direction |
| j | surfactant source term, index on Y-direction |
| adsorption rate coefficient | |
| desorption rate coefficient | |
| Langmuir number | |
| Mach number | |
| normal vector | |
| p | pressure |
| R | gas constant |
| t | time |
| T | temperature, period of single vortex flow |
| u | x-direction velocity component |
| U | typical velocity |
| velocity | |
| v | y-direction velocity component |
| V | total volume fraction inside circle of single vortex flow |
| coordinate | |
| Greek Symbols | |
| PLIC constant | |
| delta function | |
| relative error function of total volume of single vortex flow | |
| density | |
| density of heavy fluid | |
| density of light fluid | |
| viscosity | |
| viscosity of heavy fluid | |
| viscosity of light fluid | |
| virtual time step | |
| viscous stress tensor | |
| volume fraction | |
| level set | |
| stream function of single vortex flow | |
| surface tension coefficient | |
| curvature | |
| computational volume | |
| the ratio of a circle’s circumference to its diameter | |
| gradient on the interface | |
| length of cell |
References
- Qiao, C.; Yang, D.; Mao, X.; Xie, L.; Gong, L.; Peng, X.; Peng, Q.; Wang, T.; Zhang, H.; Zeng, H. Recent Advances in Bubble-based Technologies: Underlying Interaction Mechanisms and Applications. Appl. Phys. Rev. 2021, 8, 011315. [Google Scholar] [CrossRef]
- Abid, S.; Chesters, A. The Drainage and Rupture of Partially-Mobile Films Between Colliding Drops at Constant Approach Velocity. Int. J. Multiph. Flow 1994, 20, 613–629. [Google Scholar] [CrossRef]
- Mileva, E.; Exerowa, D. Foam Films as Instrumentation in the Study of Amphiphile Self-assembly. Adv. Colloid Interface Sci. 2003, 100–102, 547–562. [Google Scholar] [CrossRef]
- Chan, D.Y.C.; Klaseboer, E.; Manica, R. Film drainage and coalescence between deformable drops and bubbles. Soft Matter 2011, 7, 2235–2264. [Google Scholar] [CrossRef]
- Karakashev, S.I.; Manev, E.D. Hydrodynamics of Thin Liquid Films: Retrospective and Perspectives. Adv. Colloid Interface Sci. 2015, 222, 398–412. [Google Scholar] [CrossRef]
- Liu, B.; Manica, R.; Xu, Z.; Liu, Q. The Boundary Condition at the Air–liquid Interface and Its Effect on Film Drainage Between Colliding Bubbles. Curr. Opin. Colloid Interface Sci. 2020, 50, 101374. [Google Scholar] [CrossRef]
- Vakarelski, I.U.; Langley, K.R.; Yang, F.; Thoroddsen, S.T. Interferometry and Simulation of the Thin Liquid Film between a Free-Rising Bubble and a Glass Substrate. Langmuir 2022, 38, 2363–2371. [Google Scholar] [CrossRef]
- Aoki, T.; Hasegawa, Y. A Large-scale Aerodynamics Study on Bicycle Racing. JSAE J. 2020, 74, 18–23. [Google Scholar]
- Berger, M.J.; Oliger, J. Adaptive Mesh Refinement for Hyperbolic Partial Differential Equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Matsushita, S.; Aoki, T. A Computation with Tree-based Amr Method Using Multi-moment Scheme for Conservative Phase-field Equation with a Flux Term. Trans. Jpn. Soc. Comput. Eng. Sci. 2018, 2018, 20180005. [Google Scholar] [CrossRef]
- Matsushita, S.; Aoki, T. A gas-liquid two-phase flow simulation with interface-adapted amr method. Jpn. J. Multiph. Flow 2019, 33, 96–102. [Google Scholar] [CrossRef]
- Hirt, C.; Nichols, B. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Chiu, P.H.; Lin, Y.T. A Conservative Phase Field Method for Solving Incompressible Two-phase Flows. J. Comput. Phys. 2011, 230, 185–204. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A Coupled Level Set and Volume-of-Fluid Method for Computing 3D and Axisymmetric Incompressible Two-Phase Flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Matsushita, S.; Aoki, T. A Weakly Compressible Scheme with a Diffuse-interface Method for Low Mach Number Wwo-phase Flows. J. Comput. Phys. 2019, 376, 838–862. [Google Scholar] [CrossRef]
- Sato, K.; Koshimura, S. Fundamental Verification for Tsunami Numerical Simulation Using Lattice Boltzmann Method and PLIC-VOF method. J. JSCE B2 2017, 73, I7–I12. [Google Scholar]
- Sato, K.; Koshimura, S. Development of Three-dimensional Free Surface Flow Simulation Method by Lattice Boltzmann Method and PLIC-VOF Method. J. JSCE B1 2018, 74, I427–I432. [Google Scholar] [CrossRef]
- Nahed, J.; Dgheim, J. Estimation Curvature in PLIC-VOF Method for Interface Advection. Heat Mass Transf. 2020, 56, 773–787. [Google Scholar] [CrossRef]
- Matsushita, S.; Aoki, T. Gas-liquid Wwo-phase Flows Simulation Based on Weakly Compressible Scheme with Interface-adapted AMR Method. J. Comput. Phys. 2021, 445, 110605. [Google Scholar] [CrossRef]
- Afkhami, S.; Bussmann, M. Height Functions for Applying Contact Angles to 2D VOF Simulations. Int. J. Numer. Methods Fluids 2008, 57, 453–472. [Google Scholar] [CrossRef]
- López, J.; Zanzi, C.; Gómez, P.; Zamora, R.; Faura, F.; Hernández, J. An Improved Height Function Technique for Computing Interface Curvature from Volume Fractions. Comput. Methods Appl. Mech. Eng. 2009, 198, 2555–2564. [Google Scholar] [CrossRef]
- Evrard, F.; Denner, F.; van Wachem, B. Height-function Curvature Estimation with Arbitrary Order on Non-uniform Cartesian Grids. J. Comput. Phys. X 2020, 7, 100060. [Google Scholar] [CrossRef]
- Connington, K.; Lee, T. A review of spurious currents in the lattice Boltzmann method for multiphase flows. J. Mech. Sci. Technol. 2012, 26, 3857–3863. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Clausen, J.R. Entropically Damped Form of Artificial Compressibility for Explicit Simulation of Incompressible Flow. Phys. Rev. E 2013, 87, 013309. [Google Scholar] [CrossRef]
- Toutant, A. General and exact pressure evolution equation. Phys. Lett. A 2017, 381, 3739–3742. [Google Scholar] [CrossRef]
- Kajzer, A.; Pozorski, J. Application of the Entropically Damped Artificial Compressibility model to direct numerical simulation of turbulent channel flow. Comput. Math. Appl. 2018, 76, 997–1013. [Google Scholar] [CrossRef]
- Yang, K.; Aoki, T. Weakly Compressible Navier-Stokes Solver Based on Evolving Pressure Projection Method for Two-phase Flow Simulations. J. Comput. Phys. 2021, 431, 110113. [Google Scholar] [CrossRef]
- Aslam, T.D. A Partial Differential Equation Approach to Multidimensional Extrapolation. J. Comput. Phys. 2004, 193, 349–355. [Google Scholar] [CrossRef]
- Xu, J.J.; Li, Z.; Lowengrub, J.; Zhao, H. A Level-set Method for Interfacial Flows with Surfactant. J. Comput. Phys. 2006, 212, 590–616. [Google Scholar] [CrossRef]
- Erik Teigen, K.; Song, P.; Lowengrub, J.; Voigt, A. A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 2011, 230, 375–393. [Google Scholar] [CrossRef]
- Hayashi, K.; Tomiyama, A. Effects of Surfactant on Terminal Velocity of a Taylor Bubble in a Vertical Pipe. Int. J. Multiph. Flow 2012, 39, 78–87. [Google Scholar] [CrossRef]
- Weymouth, G.; Yue, D.K.P. Conservative Volume-of-Fluid Method for Free-surface Simulations on Cartesian-grids. J. Comput. Phys. 2010, 229, 2853–2865. [Google Scholar] [CrossRef]
- Yang, K.; Aoki, T. Scaling of a Conservative Weakly Compressible Solver for Large-scale Two-phase Flow Simulation. In Proceedings of the Parallel and Distributed Computing, Applications and Technologies: 23rd International Conference, PDCAT 2022, Sendai, Japan, 7–9 December 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Scardovelli, R.; Zaleski, S. Analytical Relations Connecting Linear Interfaces and Volume Fractions in Rectangular Grids. J. Comput. Phys. 2000, 164, 228–237. [Google Scholar] [CrossRef]
- Aulisa, E.; Manservisi, S.; Scardovelli, R.; Zaleski, S. Interface Reconstruction with Least-squares Fit and Split Advection in Three-dimensional Cartesian Geometry. J. Comput. Phys. 2007, 225, 2301–2319. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts Propagating with Curvature-dependent Speed: Algorithms Based on Hamilton-Jacobi Formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Yokoi, K. A Density-Scaled Continuum Surface Force Model within a Balanced Force Formulation. J. Comput. Phys. 2014, 278, 221–228. [Google Scholar] [CrossRef]
- Jiang, G.S.; Peng, D. Weighted ENO Schemes for Hamilton–Jacobi Equations. SIAM J. Sci. Comput. 2000, 21, 2126–2143. [Google Scholar] [CrossRef]
- Harten, A. High Resolution Schemes for Hyperbolic Conservation Laws. J. Comput. Phys. 1997, 135, 260–278. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Cotronis, Y. Graphics Processing Unit Acceleration of the Red/Black SOR Method. Concurr. Comput. Pract. Exp. 2012, 25, 1107–1120. [Google Scholar] [CrossRef]
- Fuster, D.; Popinet, S. An All-Mach Method for the Simulation of Bubble Dynamics Problems in the Presence of Surface Tension. J. Comput. Phys. 2018, 374, 752–768. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Fakhari, A.; Geier, M.; Lee, T. A Mass-conserving Lattice Boltzmann Method with Dynamic Grid Refinement for Immiscible Two-phase Flows. J. Comput. Phys. 2016, 315, 434–457. [Google Scholar] [CrossRef]
- Yerry, M.A.; Shephard, M.S. Automatic Three-dimensional Mesh Generation by the Modified-octree Technique. Int. J. Numer. Methods Eng. 1984, 20, 1965–1990. [Google Scholar] [CrossRef]
- Rider, W.J.; Kothe, D.B. Reconstructing Volume Tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef]
- Hysing, S.; Turek, S.; Kuzmin, D.; Parolini, N.; Burman, E.; Ganesan, S.; Tobiska, L. Quantitative Benchmark Computations of Two-dimensional Bubble Dynamics. Int. J. Numer. Methods Fluids 2009, 60, 1259–1288. [Google Scholar] [CrossRef]
- Aland, S.; Voigt, A. Benchmark Computations of Diffuse Interface Models for Two-dimensional Bubble Dynamics. Int. J. Numer. Methods Fluids 2012, 69, 747–761. [Google Scholar] [CrossRef]
- Klostermann, J.; Schaake, K.; Schwarze, R. Numerical Simulation of a Single Rising Bubble by VOF with Surface Compression. Int. J. Numer. Methods Fluids 2013, 71, 960–982. [Google Scholar] [CrossRef]
- Turek, S. Efficient Solvers for Incompressible Flow Problems: An Algorithmic and Computational Approache; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; Volume 6. [Google Scholar]
- Parolini, N.; Burman, E. A Finite Element Level Set Method For Viscous Free-surface Flows. In Applied and Industrial Mathematics in Italy; World Scientific Publishing Co. Pte., Ltd.: Chennai, India, 2005; pp. 416–427. [Google Scholar] [CrossRef]
- John, V.; Matthies, G. MooNMD—A Program Package Based on Mapped Finite Element Methods. Comput. Vis. Sci. 2004, 6, 163–170. [Google Scholar] [CrossRef]
- Lin, S.Y.; Chang, H.C.; Chen, E.M. The Effect of Bulk Concentration on Surfactant Adsorption Processes: The Shift from Diffusion-Control to Mixed Kinetic-Diffusion Control with Bulk Concentration. J. Chem. Eng. Japan 1996, 29, 634–641. [Google Scholar] [CrossRef]
- Matsushita, S. Incompressible Gas-Liquid Two-Phase Flow Simulation Based on Weakly Compressible Scheme. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2020. [Google Scholar]
- Pandit, A.B.; Davidson, J.F. Hydrodynamics of the rupture of thin liquid films. J. Fluid Mech. 1990, 212, 11–24. [Google Scholar] [CrossRef]
- Takagi, S. The Effect of Surfactant on the Motion of Rising Bubbles. Nagare J. JSFM 2004, 23, 17–26. [Google Scholar] [CrossRef]

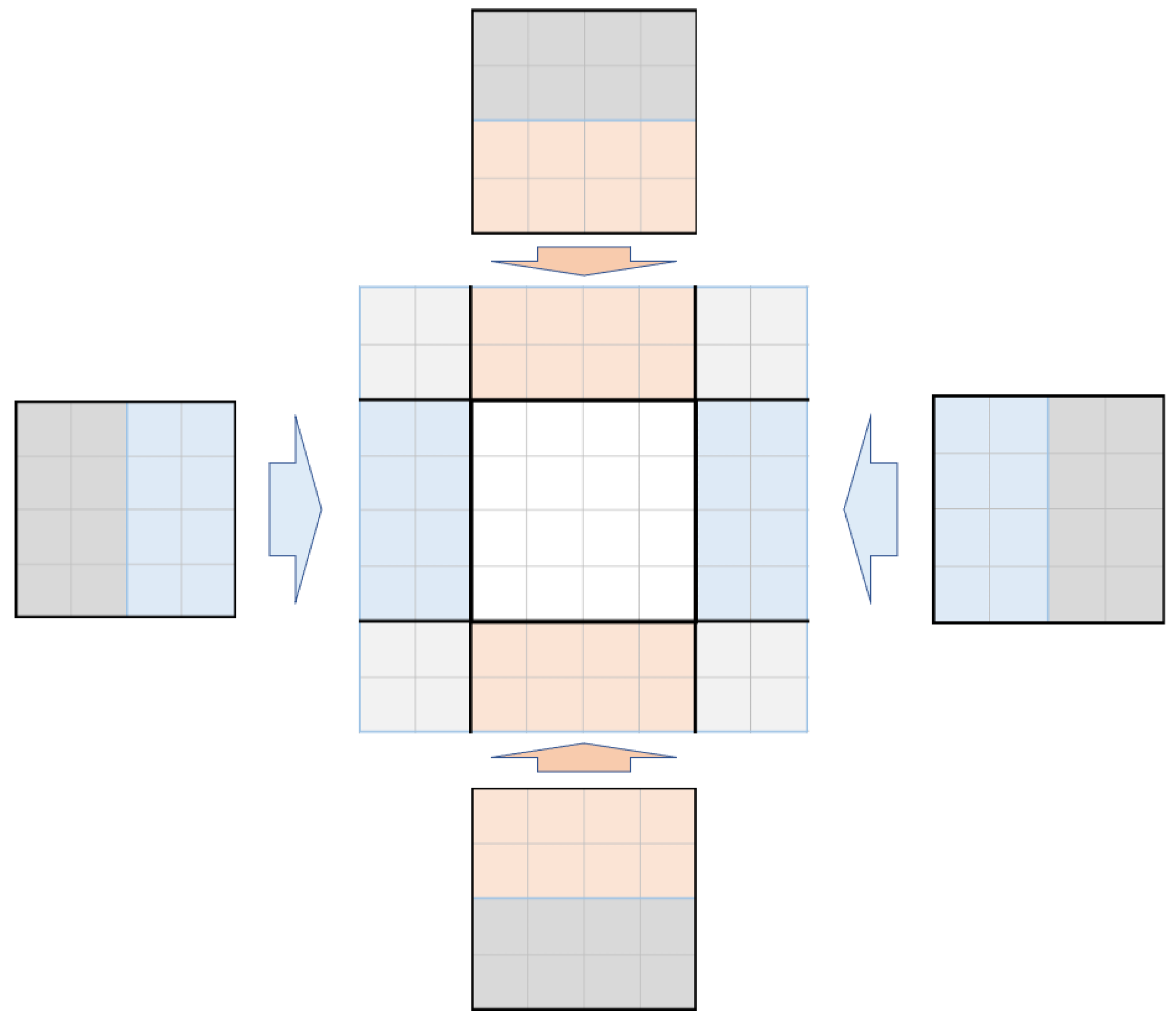
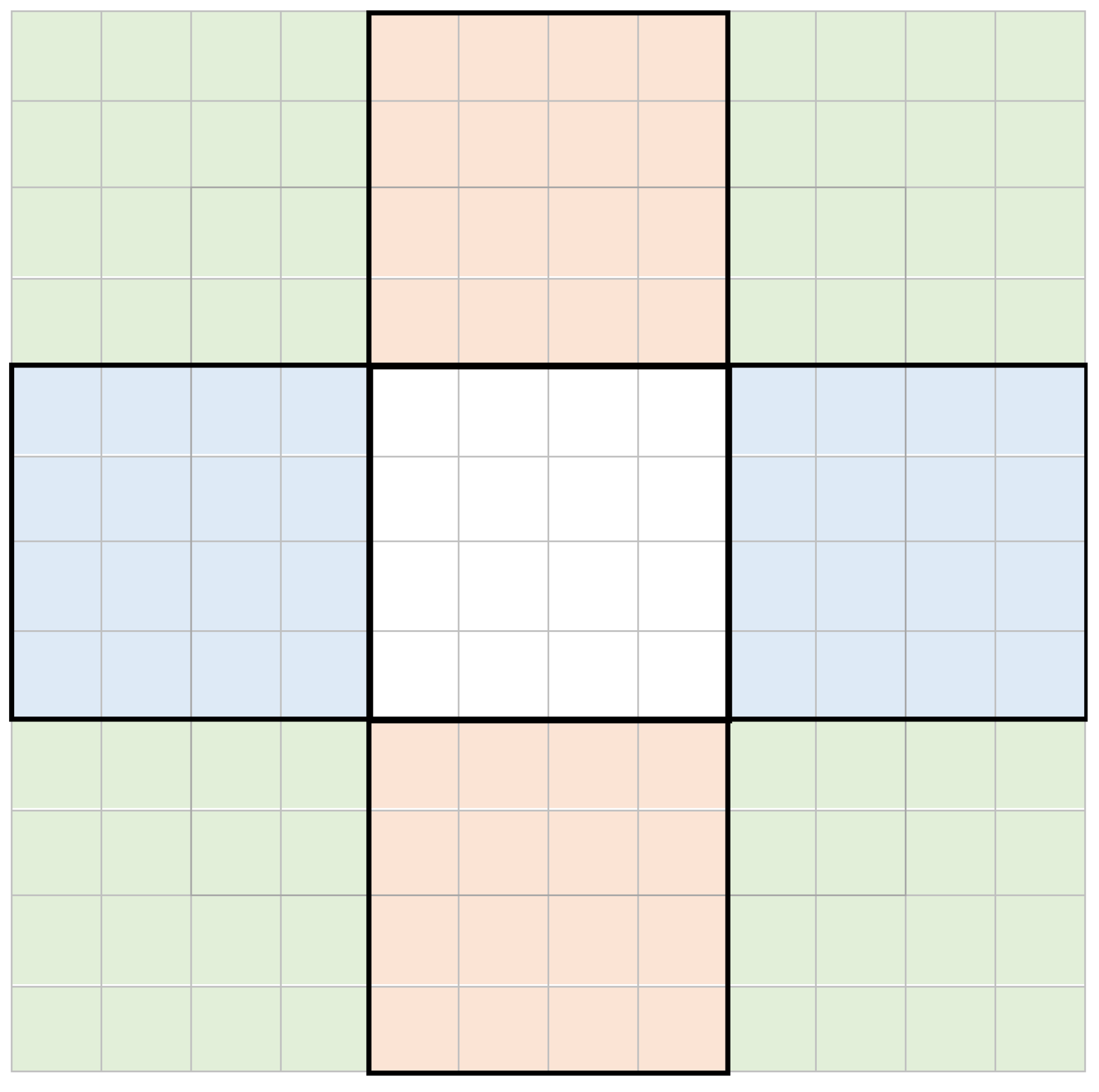









| Case | g | |||||
|---|---|---|---|---|---|---|
| Case A | ||||||
| Case B |
| Case | Number of Cells on Uniform Mesh | Maximum Number of Cells on Finest 256 × 512 AMR Grid | Maximum Number of Cells on Finest AMR Grid |
|---|---|---|---|
| Case A | 131,072 | 21,728 | 43,328 |
| Case B | 524,288 | 29,696 | 62,432 |
| Surfactant | ||||
|---|---|---|---|---|
| Triton X100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, T.; Matsushita, S.; Aoki, T. An AMR-Based Liquid Film Simulation with Surfactant Transport Using PLIC-HF Method. Appl. Sci. 2023, 13, 1955. https://doi.org/10.3390/app13031955
Lian T, Matsushita S, Aoki T. An AMR-Based Liquid Film Simulation with Surfactant Transport Using PLIC-HF Method. Applied Sciences. 2023; 13(3):1955. https://doi.org/10.3390/app13031955
Chicago/Turabian StyleLian, Tongda, Shintaro Matsushita, and Takayuki Aoki. 2023. "An AMR-Based Liquid Film Simulation with Surfactant Transport Using PLIC-HF Method" Applied Sciences 13, no. 3: 1955. https://doi.org/10.3390/app13031955
APA StyleLian, T., Matsushita, S., & Aoki, T. (2023). An AMR-Based Liquid Film Simulation with Surfactant Transport Using PLIC-HF Method. Applied Sciences, 13(3), 1955. https://doi.org/10.3390/app13031955





