Is It Worth It? Comparing Six Deep and Classical Methods for Unsupervised Anomaly Detection in Time Series
Abstract
1. Introduction
- “Is it worthwhile to sacrifice the interpretability of classical methods for potentially superior performance of deep learning methods?”
- “What different types of anomalies are the methods capable of detecting?”
- We conduct a comprehensive comparison of six state-of-the-art anomaly detection methods for time series data using the UCR Anomaly Archive benchmark dataset. Our comparison is carried out in a well-defined and fair benchmark environment.
- We enhance the UCR Anomaly Archive by annotating it with 16 distinct anomaly types, providing a more nuanced and informative benchmark.
- We address two crucial questions in the field of anomaly detection: (1) whether the superior performance of deep-learning methods justifies the loss of interpretability of traditional methods and (2) the similarities and differences between the analyzed methods in terms of detecting different anomaly types.
- We examine the impact of subsequence length on the performance of the MDI and MERLIN methods, and compare point-wise to subsequence-wise features for the RRCF method.
1.1. Time Series Data
1.2. Anomalies
1.3. Related Work
2. Materials and Methods
2.1. Analyzed Methods
2.1.1. Robust Random Cut Forest (RRCF)
2.1.2. Maximally Divergent Intervals (MDI)
2.1.3. MERLIN
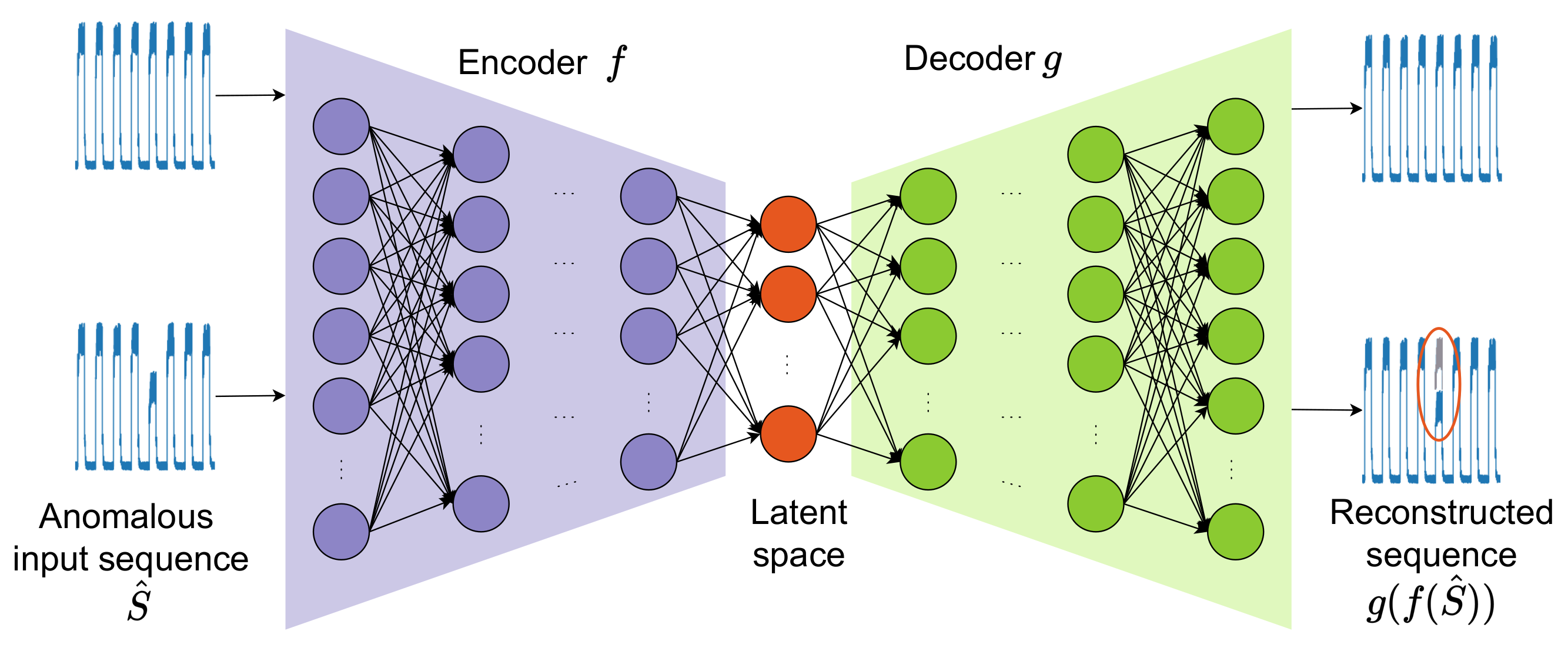
2.1.4. Autoencoder (AE)
2.1.5. Graph Augmented Normalizing Flows (GANF)
2.1.6. Transformer Network for Anomaly Detection (TranAD)
2.2. Benchmark Dataset: UCR Anomaly Archive
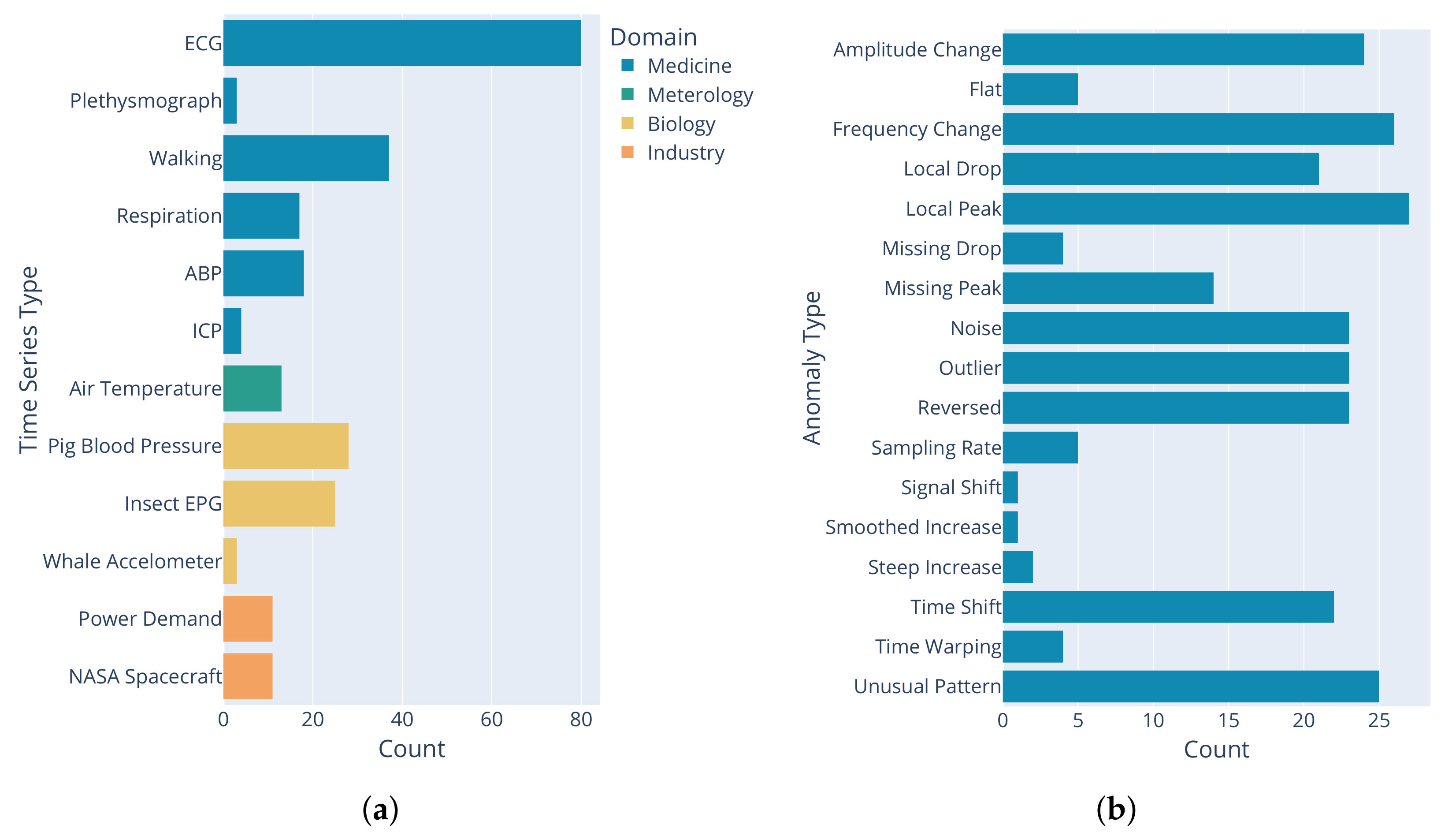
2.2.1. Included Time Series
2.2.2. Anomaly Types
2.3. Experimental Setup
2.3.1. Benchmark Pipeline
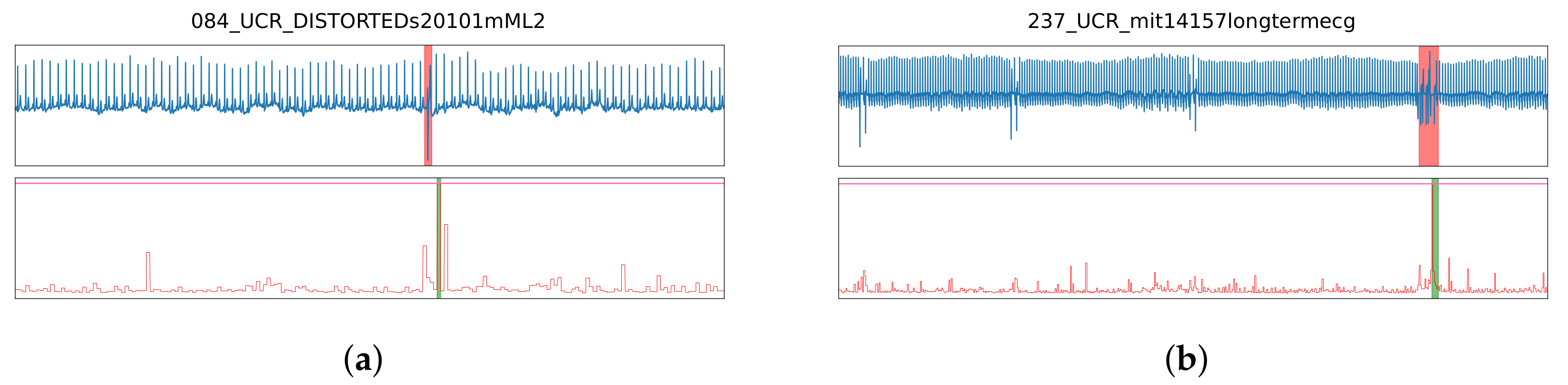
2.3.2. Anomaly Score Classification
2.3.3. Quality Measures
AUC ROC
F1 Score
UCR Score
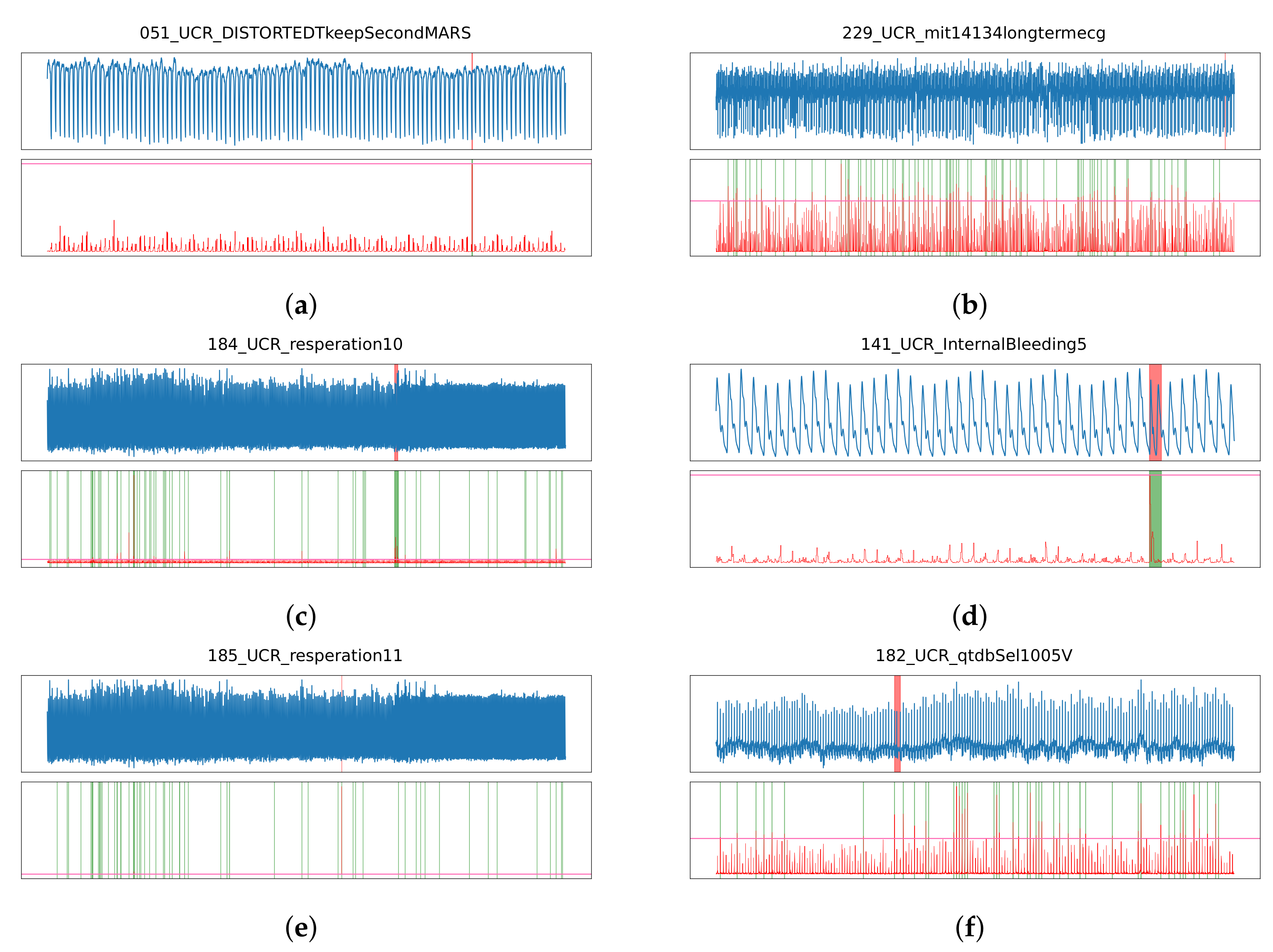
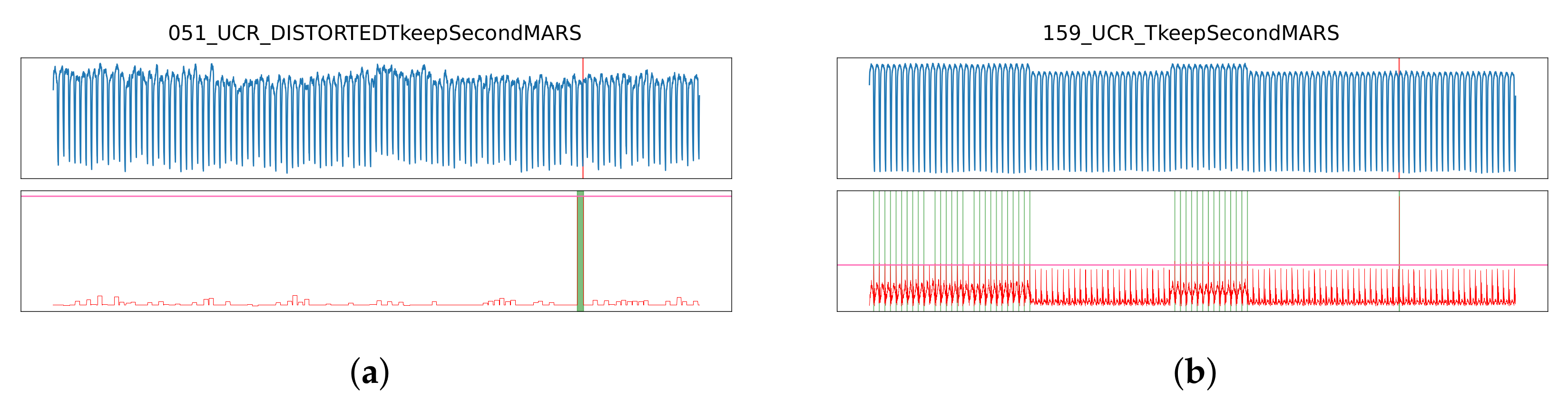
3. Results
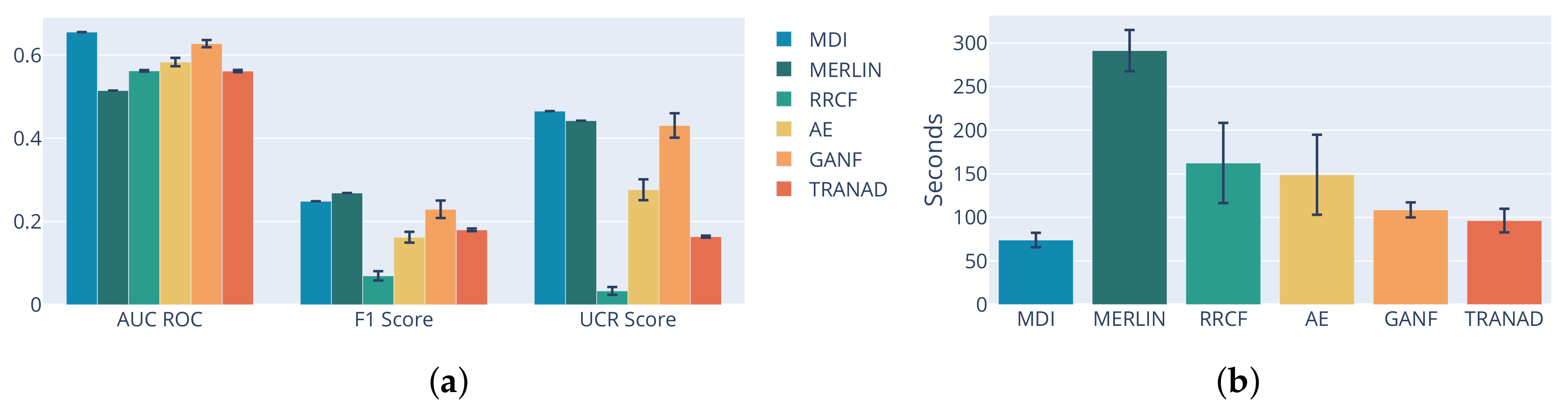
3.1. Performance Analysis by Method
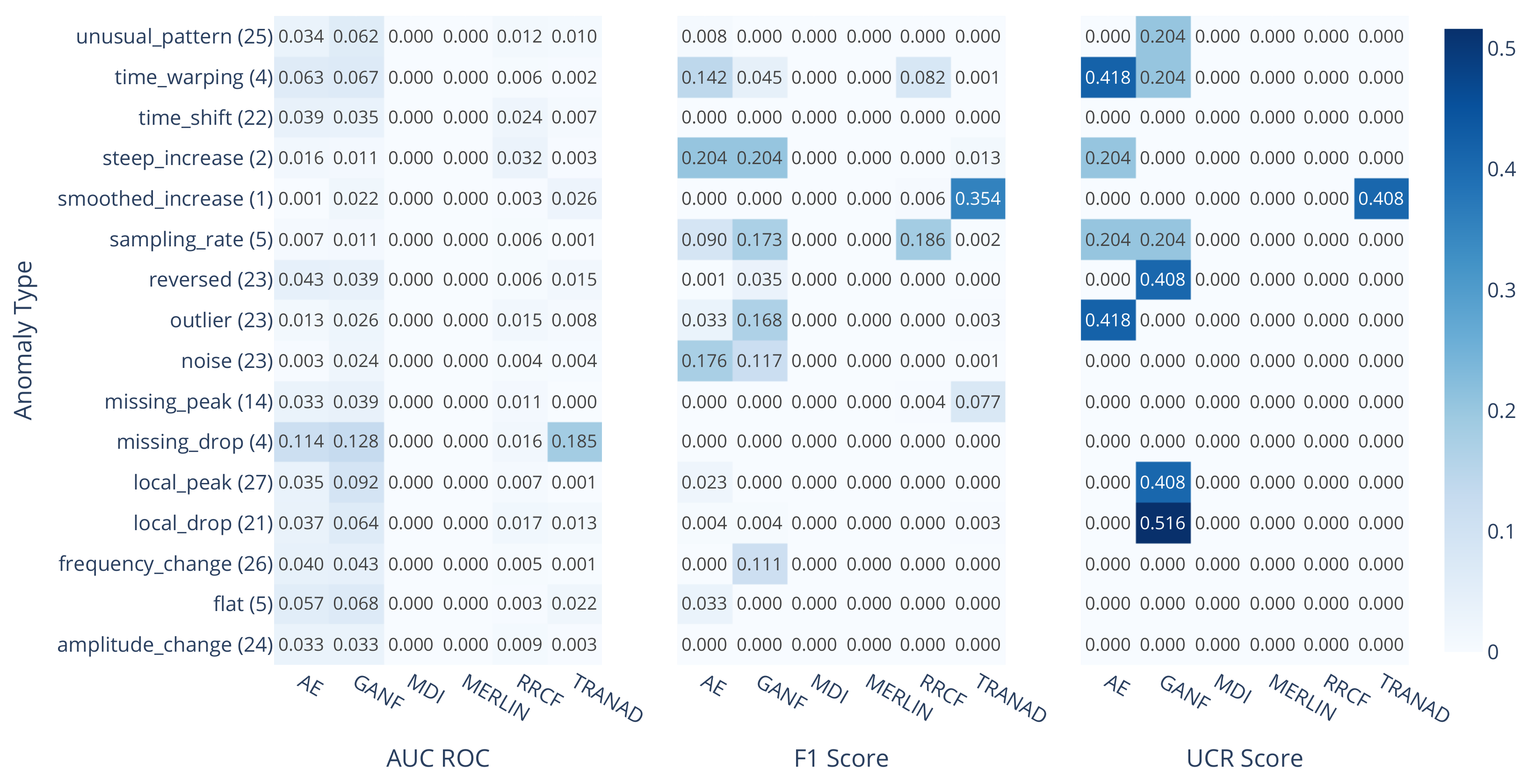
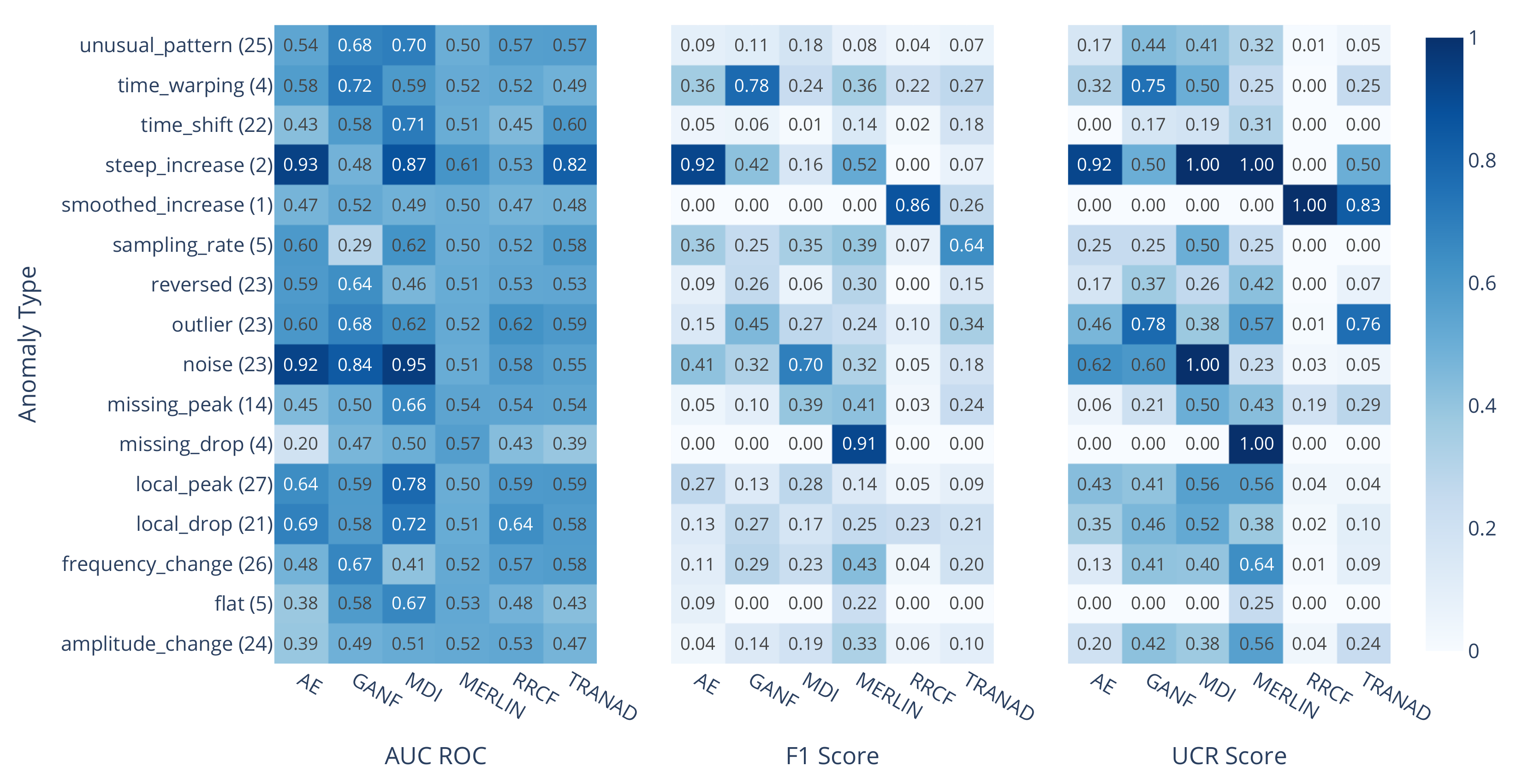
3.2. Performance Analysis by Anomaly Type
3.3. The Influence of Subsequence Length on MDI and MERLIN
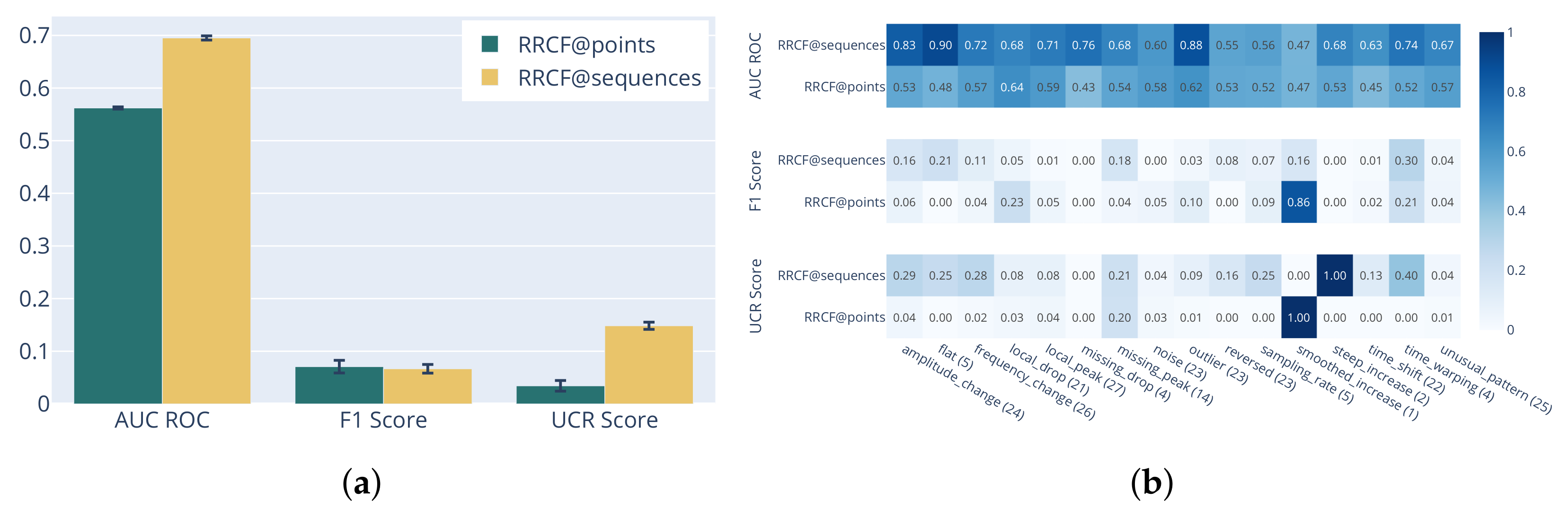
3.4. RRCF on Sliding Window Statistics
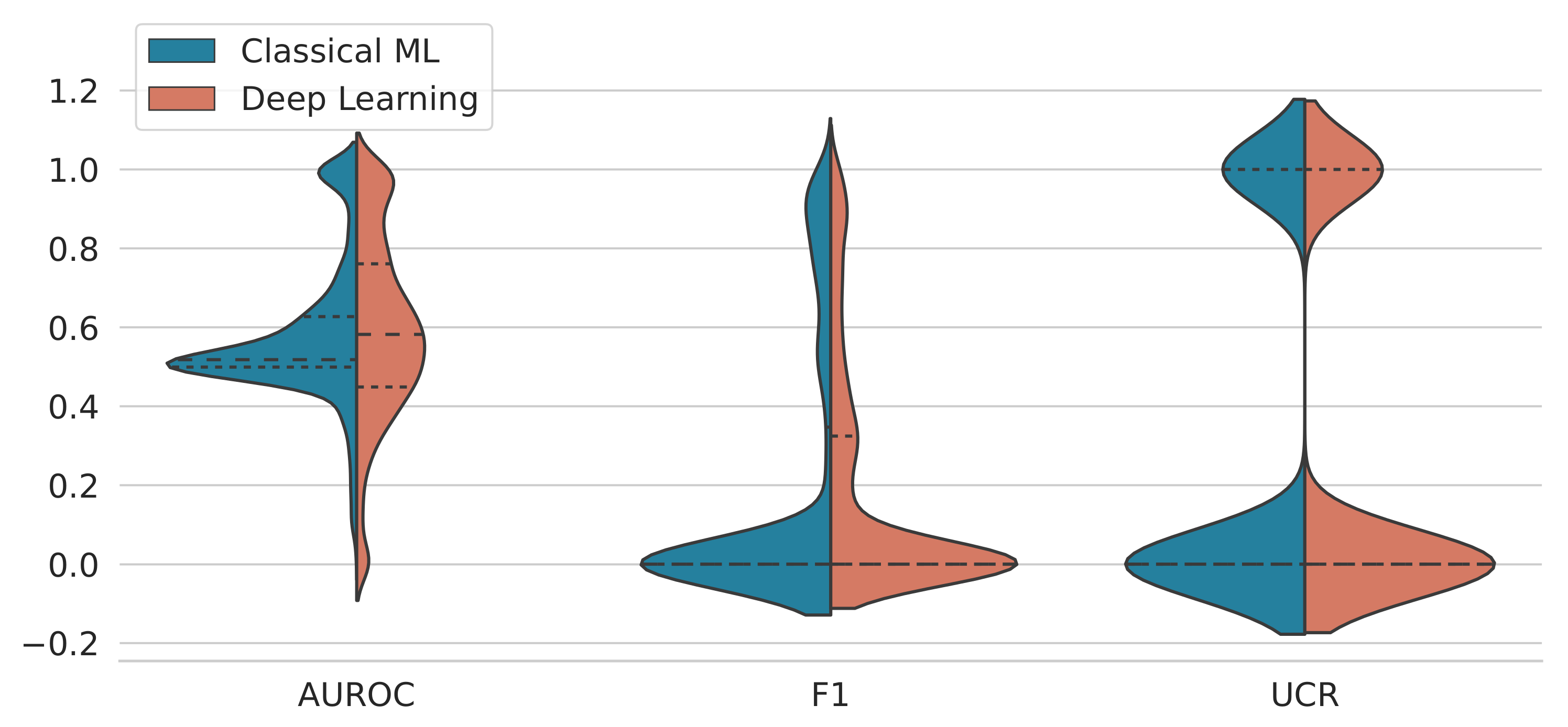
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABP | Arterial Blood Pressure |
| AE | Autoencoder |
| ECG | Electrocardiogram |
| EPG | Electrical Penetration Graph |
| EVT | Extreme Value Theory |
| GANF | Graph Augmented Normalizing Flows |
| GPD | Generalized Pareto Distribution |
| ICP | Intracranial Pressure |
| MDI | Maximally Divergent Intervals |
| POT | Peaks Over Threshold |
| RRCF | Robust Random Cut Forest |
| TranAD | Transformer Network for Anomaly Detection |
Appendix A
Appendix A.1
| Anomaly Type | Description | Example |
|---|---|---|
| Amplitude Change | Amplitude of the signal increased or decreased within a section. |  |
| Flat | Flat section was added. | 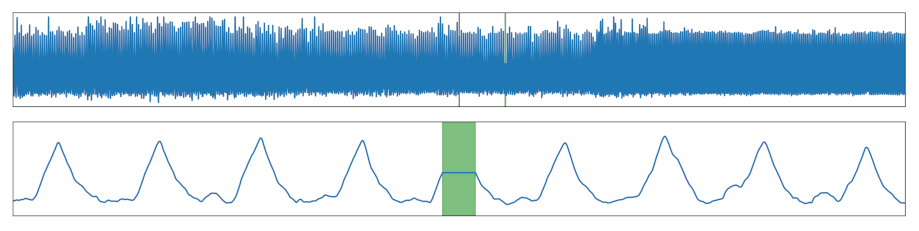 |
| Frequency Change | The cycle length was modified within a section. | 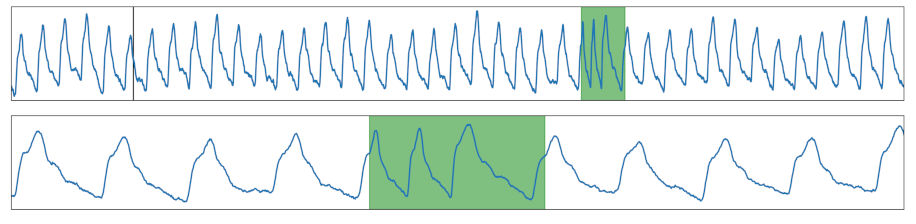 |
| Local Drop | A drop was added, which is shallower than the minimal value of the time series. | 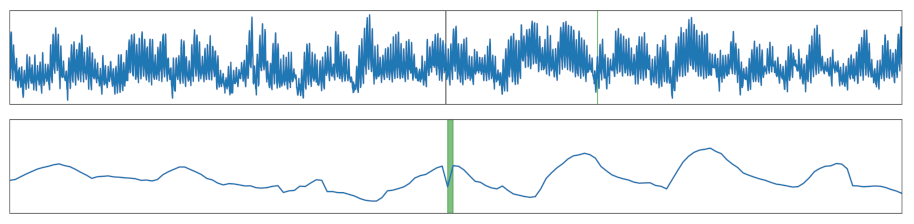 |
| Local Peak | A peak was added, which is lower than the maximal value of the time series. | 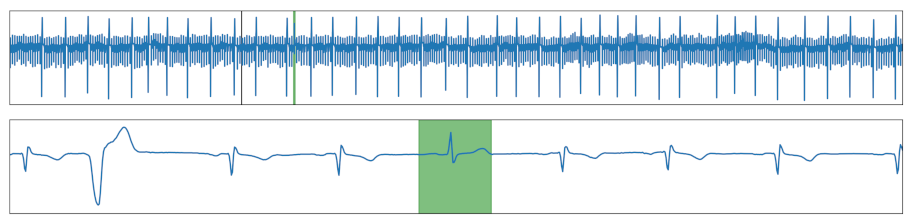 |
| Missing Drop | A drop was removed. | 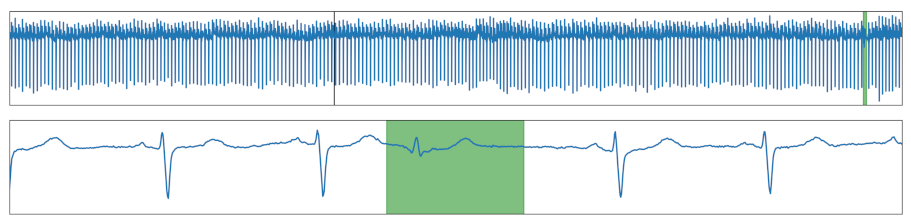 |
| Missing Peak | A peak was removed. | 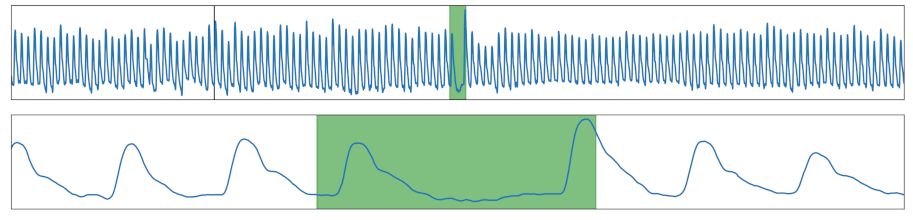 |
| Noise | Noise was added to a section. | 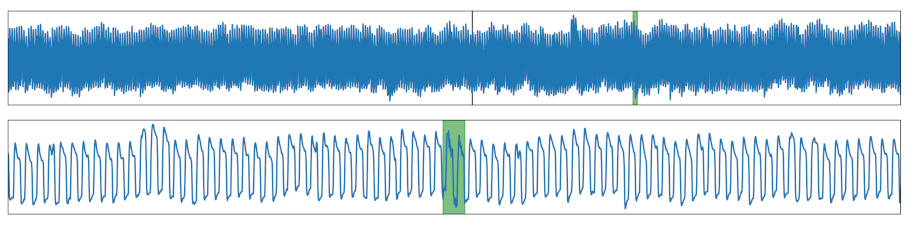 |
| Outlier | A global outlier. | 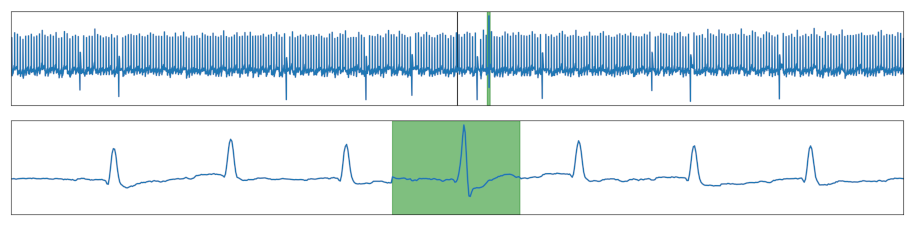 |
| Reversed | Cycle(s) got reversed. | 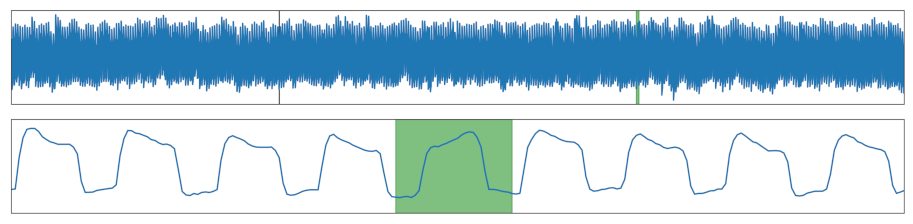 |
| Sampling Rate | The sampling rate of the signal was increased or decreased in a section. | 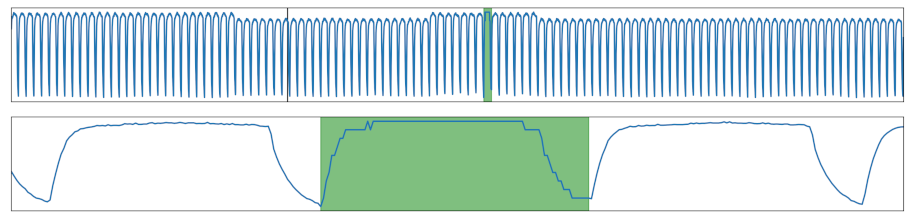 |
| Signal Shift | A section was shifted up or down. | 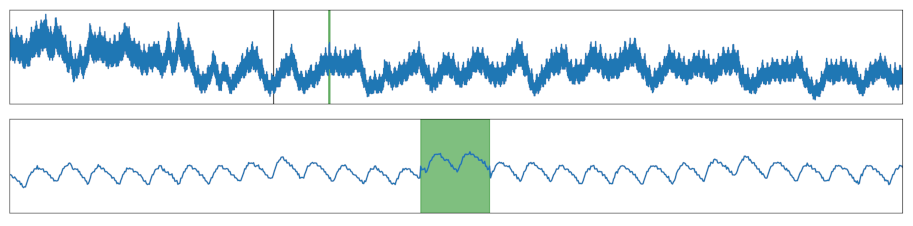 |
| Smoothed Increase | A otherwise steep increase was smoothed, increasing the number of individual values in this section. | 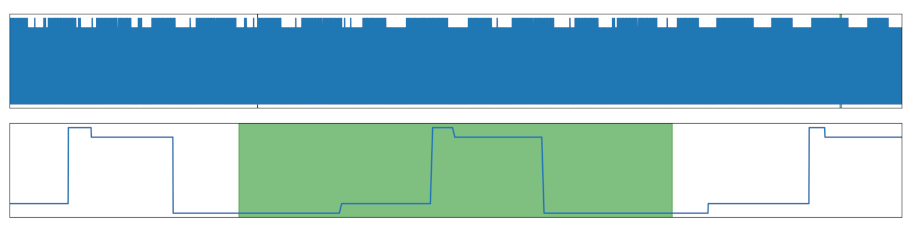 |
| Steep Increase | A otherwise smooth increase was made steep, reducing the number of individual values within this section. | 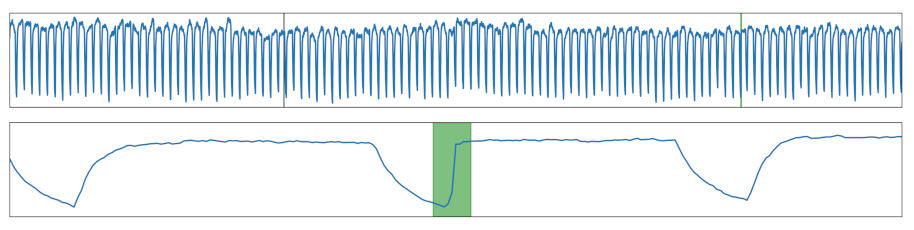 |
| Time Shift | Increasing the pause between two peaks. | 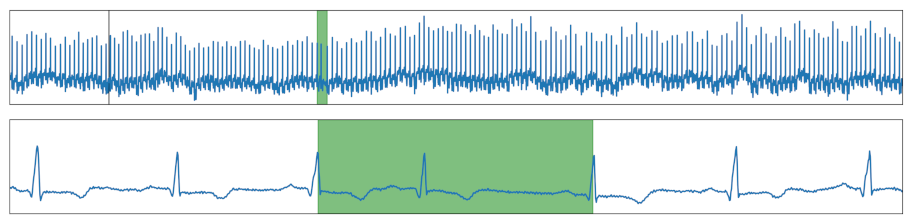 |
| Time Warping | Moving the cycle peak without changing the cycle length. |  |
| Unusual Pattern | Replacement of one or more cycle(s) with a different pattern. | 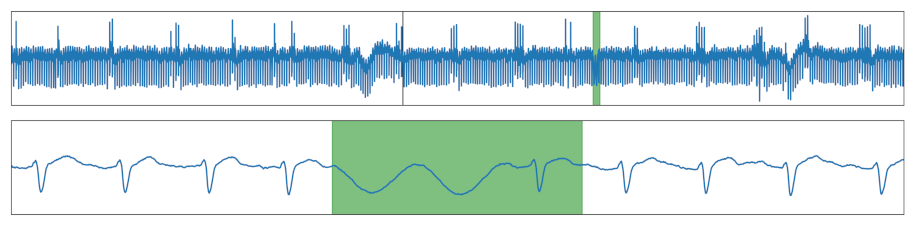 |
Appendix A.2
| Parameter | Value | Tuned? | |
|---|---|---|---|
| AE | subsequence length | 10 | no |
| stride | 10 | no | |
| epochs | 20 | no | |
| batch size | 32 | no | |
| latent space dimension | 16 | yes | |
| learning rate | 0.005 | yes | |
| weight decay | no | ||
| GANF | subsequence length | 100 | no |
| stride | 10 | no | |
| epochs | 20 + 30 | no | |
| batch size | 32 | no | |
| latent space dimension | 16 | yes | |
| learning rate | 0.003 | yes | |
| n_blocks | 4 | yes | |
| weight decay | no | ||
| h_tol | no | ||
| rho_init | 1.0 | no | |
| rho_max | no | ||
| lambda1 | 0.0 | no | |
| alpha_init | 0.0 | no | |
| MDI | 75 | no | |
| 125 | no | ||
| MERLIN | 75 | no | |
| 125 | no | ||
| RRCF | n_trees | 51 | yes |
| tree_size | 1001 | yes | |
| RRCF@sequences | subsequence length | 100 | no |
| stride | 50 | no | |
| n_trees | 68 | yes | |
| tree_size | 150 | yes | |
| TranAD | subsequence length | 10 | no |
| stride | 1 | no | |
| epochs | 1 | no | |
| batch size | 128 | no | |
| learning rate | 0.02 | yes | |
| weight decay | no | ||
| step size | 3 | yes | |
| gamma | 0.75 | yes |
Appendix A.3
References
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Müller, K.R. A Unifying Review of Deep and Shallow Anomaly Detection. Proc. IEEE 2021, 109, 756–795. [Google Scholar] [CrossRef]
- Šabić, E.; Keeley, D.; Henderson, B.; Nannemann, S. Healthcare and anomaly detection: Using machine learning to predict anomalies in heart rate data. AI Soc. 2021, 36, 149–158. [Google Scholar] [CrossRef]
- Li, D.; Chen, D.; Jin, B.; Shi, L.; Goh, J.; Ng, S.K. MAD-GAN: Multivariate Anomaly Detection for Time Series Data with Generative Adversarial Networks. In Artificial Neural Networks and Machine Learning—ICANN 2019: Text and Time Series; Tetko, I.V., Kůrková, V., Karpov, P., Theis, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 703–716. [Google Scholar]
- Buczak, A.L.; Guven, E. A Survey of Data Mining and Machine Learning Methods for Cyber Security Intrusion Detection. IEEE Commun. Surv. Tutor. 2016, 18, 1153–1176. [Google Scholar] [CrossRef]
- Sarda, K.; Acernese, A.; Nolè, V.; Manfredi, L.; Greco, L.; Glielmo, L.; Vecchio, C.D. A Multi-Step Anomaly Detection Strategy Based on Robust Distances for the Steel Industry. IEEE Access 2021, 9, 53827–53837. [Google Scholar] [CrossRef]
- Park, D.; Hoshi, Y.; Kemp, C.C. A Multimodal Anomaly Detector for Robot-Assisted Feeding Using an LSTM-Based Variational Autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar] [CrossRef]
- Freeman, C.; Merriman, J.; Beaver, I.; Mueen, A. Experimental Comparison and Survey of Twelve Time Series Anomaly Detection Algorithms. J. Artif. Intell. Res. 2022, 72, 849–899. [Google Scholar] [CrossRef]
- Laptev, N.; Amizadeh, S.; Flint, I. Generic and Scalable Framework for Automated Time-Series Anomaly Detection. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’15, Sydney, Australia, 10–13 August 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 1939–1947. [Google Scholar] [CrossRef]
- Guha, S.; Mishra, N.; Roy, G.; Schrijvers, O. Robust Random Cut Forest Based Anomaly Detection on Streams. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Balcan, M.F., Weinberger, K.Q., Eds.; PMLR: New York, NY, USA, 2016; Volume 48, pp. 2712–2721. [Google Scholar]
- Barz, B.; Rodner, E.; Garcia, Y.G.; Denzler, J. Detecting Regions of Maximal Divergence for Spatio-Temporal Anomaly Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1088–1101. [Google Scholar] [CrossRef]
- Nakamura, T.; Imamura, M.; Mercer, R.; Keogh, E. MERLIN: Parameter-Free Discovery of Arbitrary Length Anomalies in Massive Time Series Archives. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; IEEE: Sorrento, Italy, 2020; pp. 1190–1195. [Google Scholar] [CrossRef]
- Dai, E.; Chen, J. Graph-Augmented Normalizing Flows for Anomaly Detection of Multiple Time Series. In Proceedings of the 10th International Conference on Learning Representations (ICLR), Virtual, 25–29 April 2022; Available online: https://openreview.net/forum?id=45L_dgP48Vd (accessed on 18 January 2023).
- Tuli, S.; Casale, G.; Jennings, N.R. TranAD: Deep Transformer Networks for Anomaly Detection in Multivariate Time Series Data. Proc. VLDB Endow. 2022, 15, 1201–1214. [Google Scholar] [CrossRef]
- Wu, R.; Keogh, E. Current Time Series Anomaly Detection Benchmarks are Flawed and are Creating the Illusion of Progress. IEEE Trans. Knowl. Data Eng. 2021. Early Access. [Google Scholar] [CrossRef]
- Gupta, M.; Gao, J.; Aggarwal, C.C.; Han, J. Outlier detection for temporal data: A survey. IEEE Trans. Knowl. Data Eng. 2013, 26, 2250–2267. [Google Scholar] [CrossRef]
- Goldstein, M.; Uchida, S. Behavior analysis using unsupervised anomaly detection. In Proceedings of the 10th Joint Workshop on Machine Perception and Robotics (MPR 2014), Online, 16–17 October 2014. [Google Scholar]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Braei, M.; Wagner, S. Anomaly Detection in Univariate Time-series: A Survey on the State-of-the-Art. arXiv 2020, arXiv:2004.00433. [Google Scholar]
- Chalapathy, R.; Chawla, S. Deep Learning for Anomaly Detection: A Survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Pang, G.; Shen, C.; Cao, L.; van den Hengel, A. Deep Learning for Anomaly Detection: A Review. ACM Comput. Surv. 2020, 54, 1–38. [Google Scholar] [CrossRef]
- Salehi, M.; Mirzaei, H.; Hendrycks, D.; Li, Y.; Rohban, M.H.; Sabokrou, M. A Unified Survey on Anomaly, Novelty, Open-Set, and Out-of-Distribution Detection: Solutions and Future Challenges. Trans. Mach. Learn. Res. 2022. Available online: https://openreview.net/forum?id=aRtjVZvbpK (accessed on 18 January 2023).
- Bulusu, S.; Kailkhura, B.; Li, B.; Varshney, P.K.; Song, D. Anomalous Example Detection in Deep Learning: A Survey. IEEE Access 2020, 8, 132330–132347. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Yeh, C.C.M.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.A.; Zimmerman, Z.; Silva, D.F.; Mueen, A.; Keogh, E. Time series joins, motifs, discords and shapelets: A unifying view that exploits the matrix profile. Data Min. Knowl. Discov. 2018, 32, 83–123. [Google Scholar] [CrossRef]
- Xu, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; Liu, Y.; Zhao, Y.; Pei, D.; Feng, Y.; et al. Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications. In Proceedings of the 2018 World Wide Web Conference, WWW ’18, Lyon, France, 23–27 April 2018; International World Wide Web Conferences Steering Committee: Geneva, Switzerland, 2018; pp. 187–196. [Google Scholar] [CrossRef]
- Lavin, A.; Ahmad, S. Evaluating real-time anomaly detection algorithms–the Numenta anomaly benchmark. In Proceedings of the 2015 IEEE 14th international conference on machine learning and applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 38–44. [Google Scholar]
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and its associated cutoff point. Biom. J. 2005, 47, 458–472. [Google Scholar] [CrossRef]
- Graabæk, S.G.; Ancker, E.V.; Christensen, A.L.; Fugl, A.R. An Experimental Comparison of Anomaly Detection Methods for Collaborative Robot Manipulators. IEEE Access 2022. Preprint. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 3:1–3:39. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Xie, Z.; Zhao, N.; Chen, J.; Zhang, W.; Sui, K.; Pei, D. Practical and White-Box Anomaly Detection through Unsupervised and Active Learning. In Proceedings of the 2020 29th International Conference on Computer Communications and Networks (ICCCN), Honolulu, HI, USA, 3–6 August 2020; IEEE: Honolulu, HI, USA, 2020; pp. 1–9. [Google Scholar] [CrossRef]
- MacGregor, J. Statistical Process Control of Multivariate Processes. IFAC Proc. Vol. 1994, 27, 427–437. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.; Rebbapragada, U. Disk Aware Discord Discovery: Finding Unusual Time Series in Terabyte Sized Datasets. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; IEEE: Omaha, NE, USA, 2007; pp. 381–390. [Google Scholar] [CrossRef]
- De Paepe, D.; Avendano, D.N.; Van Hoecke, S. Implications of Z-Normalization in the Matrix Profile. In Proceedings of the Pattern Recognition Applications and Methods: 8th International Conference, ICPRAM 2019, Prague, Czech Republic, 19–21 February 2019; Revised Selected Papers. Springer: Berlin/Heidelberg, Germany, 2019; pp. 95–118. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L. Learning Internal Representations by Error Propagation; MIT Press: Cambridge, MA, USA, 1987; pp. 318–362. [Google Scholar]
- Baldi, P. Autoencoders, Unsupervised Learning, and Deep Architectures. In ICML Workshop on Unsupervised and Transfer Learning; Guyon, I., Dror, G., Lemaire, V., Taylor, G., Silver, D., Eds.; Proceedings of Machine Learning Research; PMLR: Bellevue, WA, USA, 2012; Volume 27, pp. 37–49. [Google Scholar]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2020, arXiv:2003.05991. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.u.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Wu, R.; Keogh, E. UCR Anomaly Archive. 2021. Available online: https://www.cs.ucr.edu/~Eeamonn/time_series_data_2018/UCR_TimeSeriesAnomalyDatasets2021.zip (accessed on 30 January 2023).
- Laptev, N.; Amizadeh, S.; Billawala, Y. S5—A Labeled Anomaly Detection Dataset, Version 1.0 (16M). 2015. Available online: https://webscope.sandbox.yahoo.com/catalog.php?datatype=s&did=70 (accessed on 18 January 2023).
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Lenis, G.; Pilia, N.; Loewe, A.; Schulze, W.H.; Dössel, O. Comparison of baseline wander removal techniques considering the preservation of ST changes in the ischemic ECG: A simulation study. Comput. Math. Methods Med. 2017, 2017, 9295029. [Google Scholar] [CrossRef]
- Wu, R.; Keogh, E. UCR_AnomalyDataSets.pptx, Supplemental Material to the UCR Anomaly Archive. 2021. Available online: https://www.cs.ucr.edu/~Eeamonn/time_series_data_2018/UCR_TimeSeriesAnomalyDatasets2021.zip (accessed on 18 January 2023).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Siffer, A.; Fouque, P.A.; Termier, A.; Largouet, C. Anomaly detection in streams with extreme value theory. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 1067–1075. [Google Scholar]
- Boniol, P.; Palpanas, T.; Meftah, M.; Remy, E. Graphan: Graph-based subsequence anomaly detection. Proc. VLDB Endow. 2020, 13, 2941–2944. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD ’19, Anchorage, AK, USA, 4–8 August 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 2828–2837. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate Time-Series Anomaly Detection via Graph Attention Network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 841–850. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, R.; Mueen, A.; Zuluaga, M.A.; Keogh, E. Matrix Profile XXIV: Scaling Time Series Anomaly Detection to Trillions of Datapoints and Ultra-fast Arriving Data Streams. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, KDD ’22, Washington, DC, USA, 14–18 August 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 1173–1182. [Google Scholar] [CrossRef]



| Mechanism | Class | Online/Offline | Training | Multivariate | Anomaly Score | |
|---|---|---|---|---|---|---|
| RRCF | Isolation Forest | Classical | Online | ✗ | ✓ | Collusive Displacement |
| MDI | Density Estimation | Classical | Offline | ✗ | ✓ | (KL/JS) Divergence |
| MERLIN | Discord Discovery | Classical | Offline | ✗ | ✗ | Discord Distance |
| AE | Reconstruction | Deep learning | Offline training Online inference | ✓ | ✓ | Reconstruction Loss |
| GANF | Density Estimation | Deep learning | Offline training Online inference | ✓ | ✓ | Density |
| TranAD | Reconstruction | Deep learning | Offline training Online inference | ✓ | ✓ | Reconstruction Loss |
| Class | Method | AUC ROC | F1 Score | UCR Score | Runtime (s) | |||
|---|---|---|---|---|---|---|---|---|
| Classical ML | MDI | 0.66 ± 0.0 | 0.58 ± 0.0006 | 0.25 ± 0.0 | 0.20 ± 0.004 | 0.47 ± 0.0 | 0.31 ± 0.0033 | 74 |
| MERLIN | 0.51 ± 0.0 | 0.27 ± 0.0 | 0.44 ± 0.0 | 291 | ||||
| RRCF | 0.56 ± 0.0019 | 0.07 ± 0.011 | 0.03 ± 0.0094 | 162 | ||||
| Deep Learning | AE | 0.58 ± 0.01 | 0.59 ± 0.002 | 0.16 ± 0.013 | 0.19 ± 0.009 | 0.28 ± 0.025 | 0.29 ± 0.007 | 149 |
| TranAD | 0.56 ± 0.003 | 0.18 ± 0.003 | 0.16 ± 0.003 | 109 | ||||
| GANF | 0.63 ± 0.009 | 0.23 ± 0.021 | 0.43 ± 0.03 | 96 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rewicki, F.; Denzler, J.; Niebling, J. Is It Worth It? Comparing Six Deep and Classical Methods for Unsupervised Anomaly Detection in Time Series. Appl. Sci. 2023, 13, 1778. https://doi.org/10.3390/app13031778
Rewicki F, Denzler J, Niebling J. Is It Worth It? Comparing Six Deep and Classical Methods for Unsupervised Anomaly Detection in Time Series. Applied Sciences. 2023; 13(3):1778. https://doi.org/10.3390/app13031778
Chicago/Turabian StyleRewicki, Ferdinand, Joachim Denzler, and Julia Niebling. 2023. "Is It Worth It? Comparing Six Deep and Classical Methods for Unsupervised Anomaly Detection in Time Series" Applied Sciences 13, no. 3: 1778. https://doi.org/10.3390/app13031778
APA StyleRewicki, F., Denzler, J., & Niebling, J. (2023). Is It Worth It? Comparing Six Deep and Classical Methods for Unsupervised Anomaly Detection in Time Series. Applied Sciences, 13(3), 1778. https://doi.org/10.3390/app13031778







