A Two-Phase Ensemble-Based Method for Predicting Learners’ Grade in MOOCs

Abstract

MOOCs are online learning environments which many students use, but the success rate of online learning is low. Machine learning can be used to predict learning success based on how people learn in MOOCs. Predicting the learning performance can promote learning through various methods, such as identifying low-performance students or by grouping students together. Recent machine learning has enabled the development of predictive models, and the ensemble method can assist in reducing the variance and bias errors associated with single-machine learning. This study uses a two-phase classification model with an ensemble technique to predict the learners’ grades. In the first phase, binary classification is used, and the non-majority class is then sent to the second phase, which is multi-class classification. The new features are computed based on the distance from the class’s center. The distance between the data and the center of an overlapping cluster is calculated using silhouette score-based feature selection. Lastly, Bayesian optimization boosts the performance by fine tuning the optimal parameter set. Using data from the HMPC- and the CNPC datasets, the experiment results demonstrate that the proposed design, the two-phase ensemble-based method, outperforms the state-of-the-art machine learning algorithms.

1. Introduction

Massive open online courses (MOOCs) provide an environment in which many learners can enhance their knowledge or skills and reach their learning goals on a global scale [1]. Even though their features are different, these and learning management systems (LMSs) are seen as innovations for learning. For example, LMSs are often used in traditional classes with a set schedule, while MOOCs can be used in many different ways. Similar to LMSs, MOOCs can be set up for learning by a program. They can accommodate enrollment and are easily used as an educational tool for short courses. One of the advantages of MOOCs over traditional classrooms is that the system can collect data on a broader range of learning aspects than that which can be achieved in traditional classrooms [2]. Typically, teachers cannot monitor their students’ behavior outside the classroom. In MOOCs, however, all of the students’ actions are collected. The system can identify courses in which learners engage in numerous actions and with videos that motivate them to watch and pay attention [3,4]. Moreover, due to a large number of learners in MOOCs, these various actions and their effects on the learners’ behaviors have become an attractive topic for researchers in the education field.

MOOCs are full of information about the learners’ behaviors, making them an attractive data source for educators. Learner behavior data are utilized in the learning process or by the system. To analyze the students’ behavior, Hogo [5] used log files from an e-learning system to investigate learners’ behaviors. Learners with similar learning patterns were clustered by applying the kernelized fuzzy C-means (KFCM) technique. The learners in the substandard performance cluster were found, and their teachers were told about it so they could plan the next steps in their education. Not only can data be used to put students into groups, but the students’ actions can also be used to figure out which course each student should take. The system can use this information to suggest courses to students with similar methods of learning [6]. The data from MOOCs are used to train simple deep learning, recommending the best course for each learner.

Some learning systems require the learners to pass assessments or submit assignments to receive grades for evaluating their performance. Nevertheless, how a learner learns will affect how well they perform at every stage of the learning process. Consequently, various studies concentrate on predicting the performance of learners. By predicting their performance, the learners can figure out their learning state and improve or change how they learn [7]. In addition, instructors or course owners might apply the prediction results to enhance their teaching or learning materials. In addition, performance information can be combined with other learning behavior characteristics in a learning analysis.

Even though many students try to gain enhanced knowledge and skills through MOOCs, the success rate is low [8]. Thus, when MOOCs discuss statistics regarding the success of their students, imbalanced data are usually one of the most prominent features. Clustering Synthetic Minority Oversampling Technique (SMOTE) oversampling is broadly applied to determine the imbalance problem for learner grade prediction [9]. However, it is important to note that resampling data will cause some biases, while undersampling will lead to information loss. In contrast, oversampling increases the risk of overfitting [10], and it cannot overcome the data distributing problem [11].

This study shows how to deal with unbalanced data using a hybrid strategy that combines a two-phase ensemble-based architecture with a centroid distance feature. Following these contributions, the proposed architecture is used to estimate the students’ grades based on two imbalanced MOOC datasets. The experiment in this research will collect data without oversampling or undersampling, which could lead to an unbalanced set of data. The new distance features will be chosen based on their silhouette score before they are added to the model. To discover the optimal set of classification parameters, Bayesian optimization is applied. These are the contributions of this research:

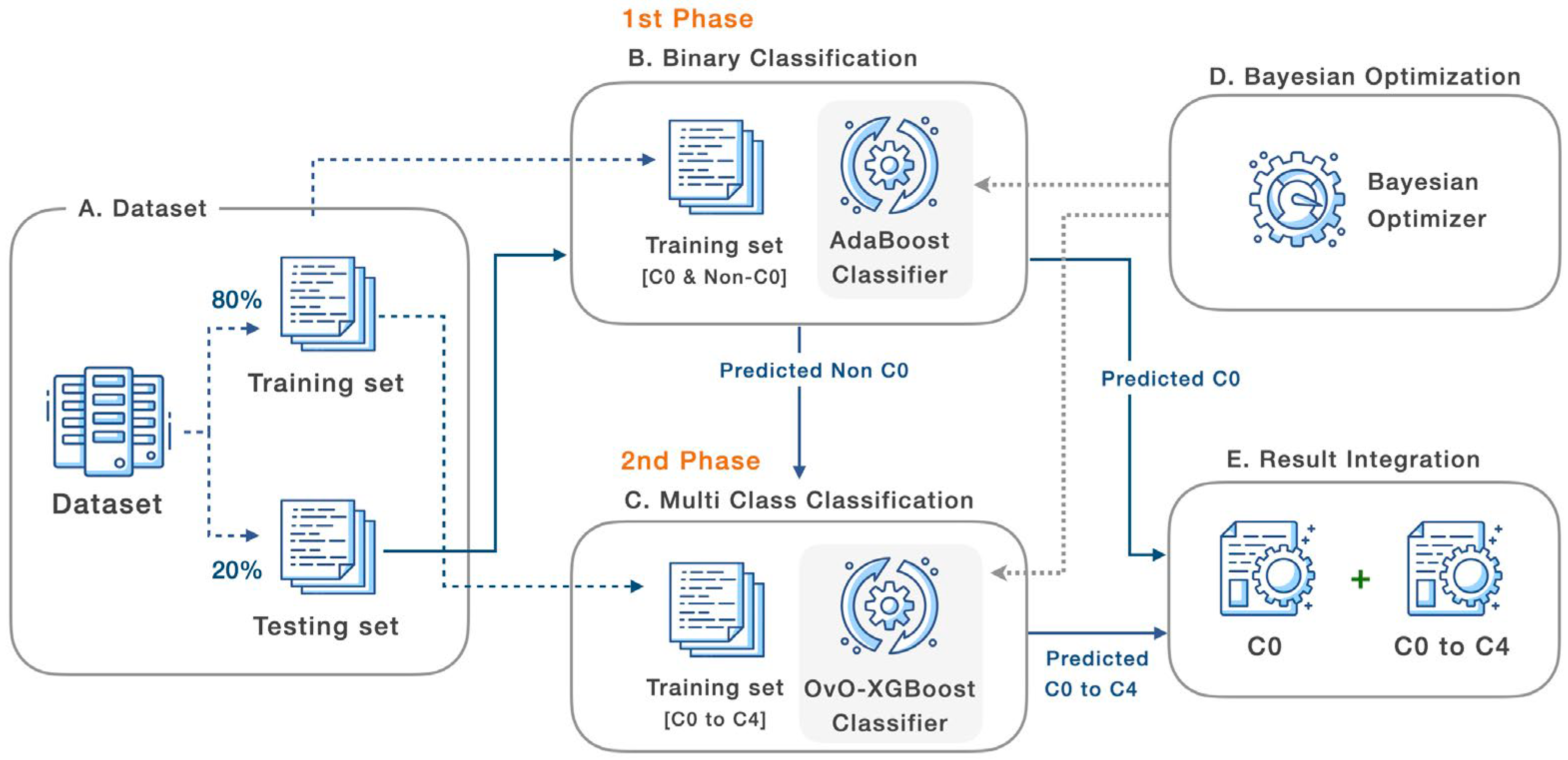
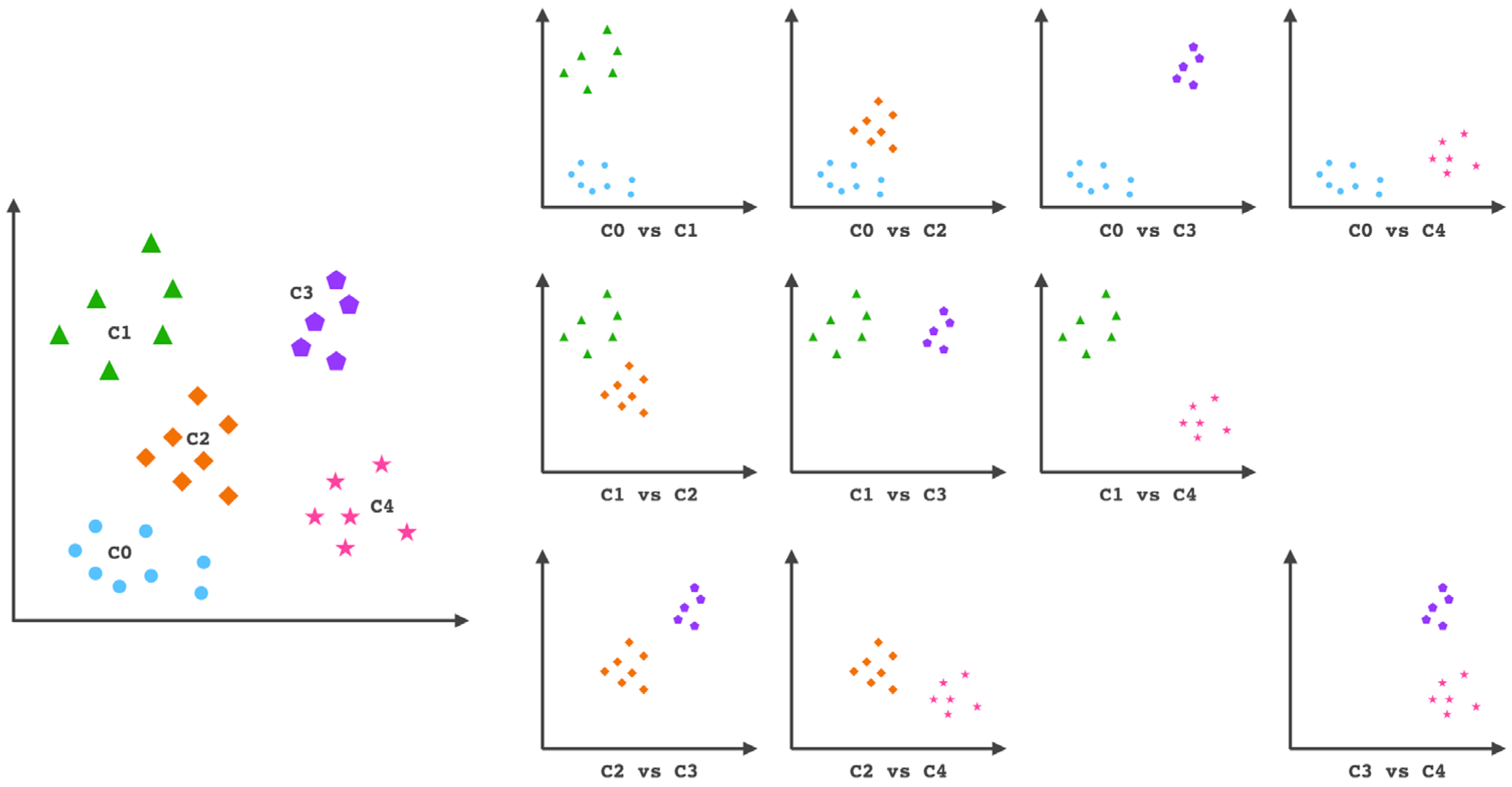
• The two-phase architecture of the grade prediction model is constructed using the ensemble approach. AdaBoost is utilized in the first phase as a binary classifier for categorizing class ‘c0’ and non-class ‘c0’. The remainder of the data will then be categorized using multi-class classification. In this phase, One-versus-One will collaborate with XGBoost to predict all of the grades. Due to the imbalanced dataset, this experiment’s data will not be over- or undersampled.
• This research presents new features that compute the distance between the data and the centroid of each grade class to determine how far the data points are from the center of each grade class.
• Adding many training features to a prediction model may diminish its performance. In this research, a silhouette coefficient-based feature selection is utilized for selecting only the data associated with the overlap of the grade clusters.
• The proposed architecture employs the Bayesian-based optimization algorithm to tune the ensemble methods’ hyperparameters.

The remainder of this paper’s content is organized as follows. Section 2 outlines the related works. Section 3 presents the research approach, which includes the data preparation procedure, the engineering of the features, and the processing steps for the two-phase architecture. Next, Section 4 describes the experimental setting, results, and discussion. Lastly, Section 5 is a conclusion.

2. Related Works

There are many proposed methods that are used for predicting grades. Mueller and Weber proposed using the RF Regressor to predict students’ grades [12]. The model was used to determine the predicted scores of the learners. From this study, one remarkable finding is that learners’ backgrounds are ineffective in forecasting their grades. In addition, Bidirectional Long Short-Term Memory (Bi-LSTM) with knowledge distillation was proposed by Kang et al. [8] as the predictor of the learner’s success rate. The model was taught to replicate the behavior of a larger model. The results were then compared to those of traditional machine learning models, including Random Forest (RF), Logical Regression (LR), and Support Vector Machine (SVM) ones, in terms of precision and F1 scores. The learners’ grade prediction model in [13] employed a de-noising auto-encoder that had been previously trained. It was utilized as the initial value for the neural network model, after which this base predictor was incorporated into an ensemble predictor whose weight was determined by the weight of each student’s year. Xing and Du [14] used deep learning to estimate the student dropout rates from the MOOC data, then they used the prediction to personalize and prioritize interventions for at-risk students. However, to apply deep learning to a prediction model, the amount of data is one of the factors that must be considered.

To handle the classification in an imbalanced dataset, many techniques for sampling training data have been proposed and applied to the predictive model, which is solving at the data level, whereas some researchers have tried to improve the classification techniques for solving the problem at an algorithm level. Using the methods at both the data and algorithm levels for classifying imbalanced data is a hybrid-level technique. However, a large portion of the studies about grade prediction using imbalanced data propose using a solving method at the data level, such as using SMOTE for oversampling the training data. The algorithm and hybrid levels are generally lacking [9]. Ashraf et al. [15] advocated for using a naïve Bayes with boosting technique and SMOTE to forecast the grades of learners. Ayienda et al. [16] attempted to identify influential features from school reports and questionnaire data, and then they used them to predict the learners’ performance with three grades (fair, good, and excellent) using a hybrid algorithm of a weighted voting classifier with logistic regression. Yang et al. presented an improved RF, one of the ensemble techniques for predicting the final grades [17]. Due to the problem of unbalanced data, the SMOTE is used to oversample the data during the training process. After the training dataset is ready, the RF model will be trained using the features that passed a threshold value in a feature selection procedure. The K-Means algorithm weights the important features in the prior task’s feature selection [18]. Deepika et al. [19] also proposed a model which applied SMOTE with RF and used Grey Wolf optimization in the feature selection process.

3. Methodology

This research classifies the learners’ predicted grades based on two well-known available datasets. In this section, we describe the details of each dataset and how they were prepared as features of the prediction model. Next, feature engineering, including how the new features are formed, are described, followed by the architecture of the proposed classification model.

3.1. Dataset

This research focuses on two open datasets that collect MOOC data. Both of the datasets include the same collection of attributes with a similar structure [20]. They have been frequently utilized in a variety of papers relating to learning analytics of MOOC data [6,8,12,17,18]. Detailed descriptions of each dataset are provided below.

3.1.1. HarvardX Person-Course Academic Year 2013 De-Identified Dataset (HMPC)

The HMPC dataset contains de-identified data from MITx and HarvardX courses offered on the edX platform during the 2013 academic year. Each record indicates a single student’s participation in a single edX course. The activity of the learners in 13 courses spanning a variety of subject areas is included in the HMPC datasets. This dataset contains 641,138 records with 16 administrative attributes that are system-provided data, three user-provided attributes, and one attribute that is a mix of system and user-provided data [21]. Figure 1 depicts an illustration of a data record.

3.1.2. Canvas Network Person-Course (1/2014–9/2015) De-Identified Dataset (CNPC)

The CNPC dataset consists of de-identified information from open Canvas Network courses held between January 2014 and September 2015. Similar to the HMPC dataset, the data set shows an individual’s participation in a single course for each record. Even the format of the attributes in the dataset is designed after HMPC’s dataset; however, the data are not associated with those of HMPC. The dataset contains 355,199 records. Seventeen administrative attributes and eight user-provided data points from two hundred and thirty-eight open courses make up CNPC’s attributes [20]. Figure 2 provides an illustration of CNPC dataset records.

3.2. Data Pre-Processing

According to Section 3.1, there are differences between the properties of the HMPC- and CNPC-collected datasets. Following each attribute in

Table 1. A comparison of the attributes of the HMPC and CNPC datasets, and the attributes after pre-processing.

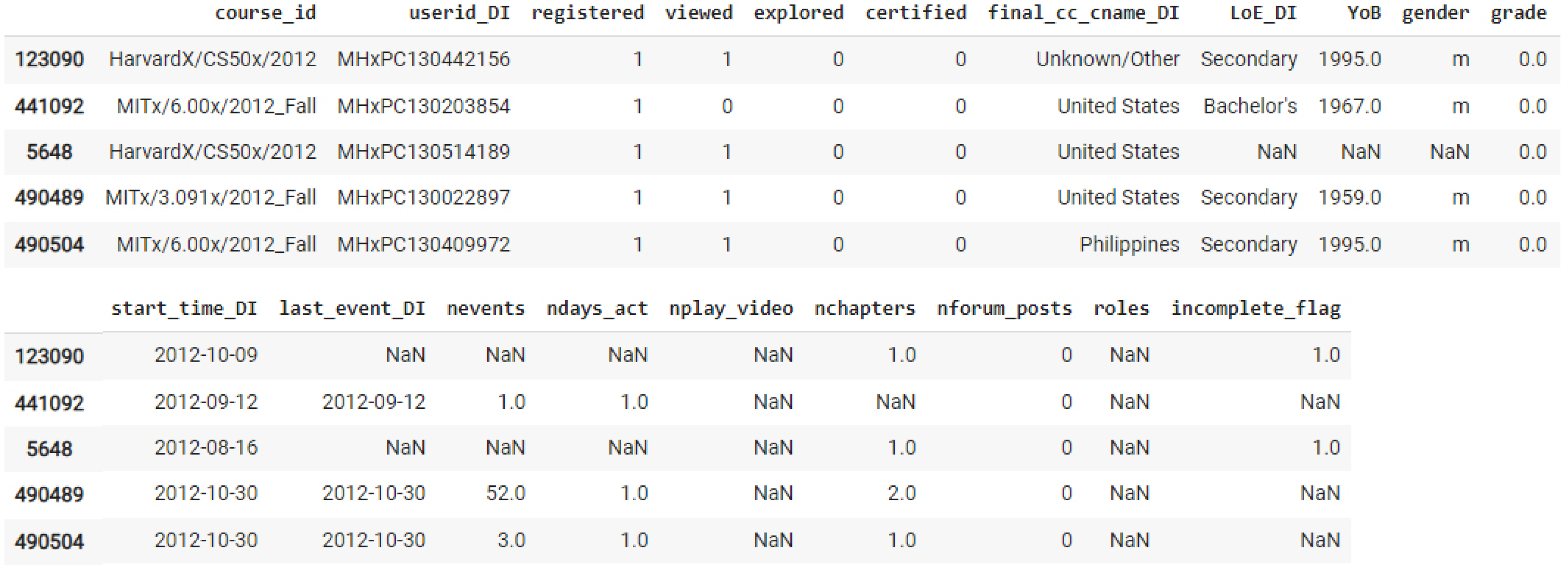
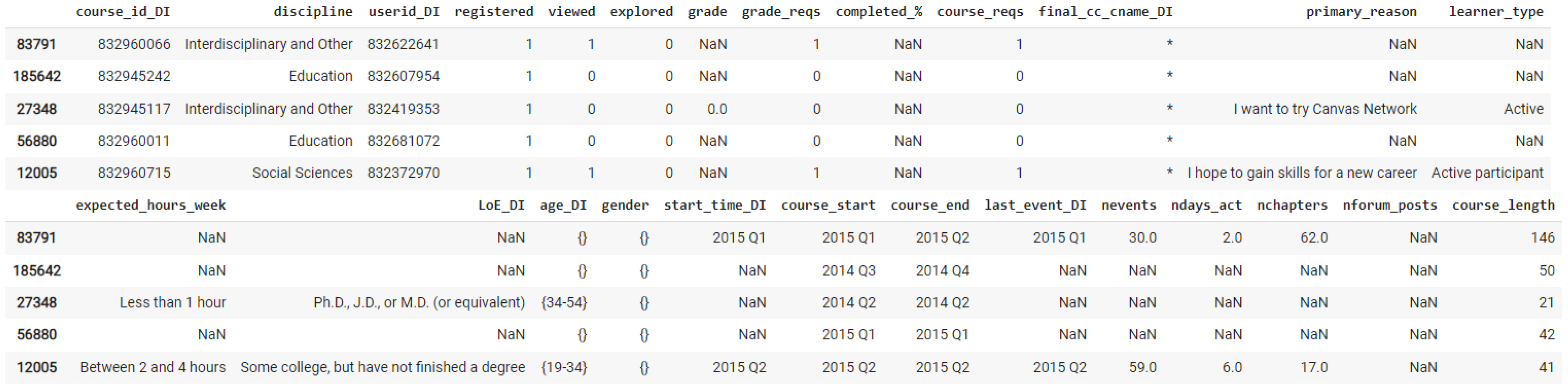
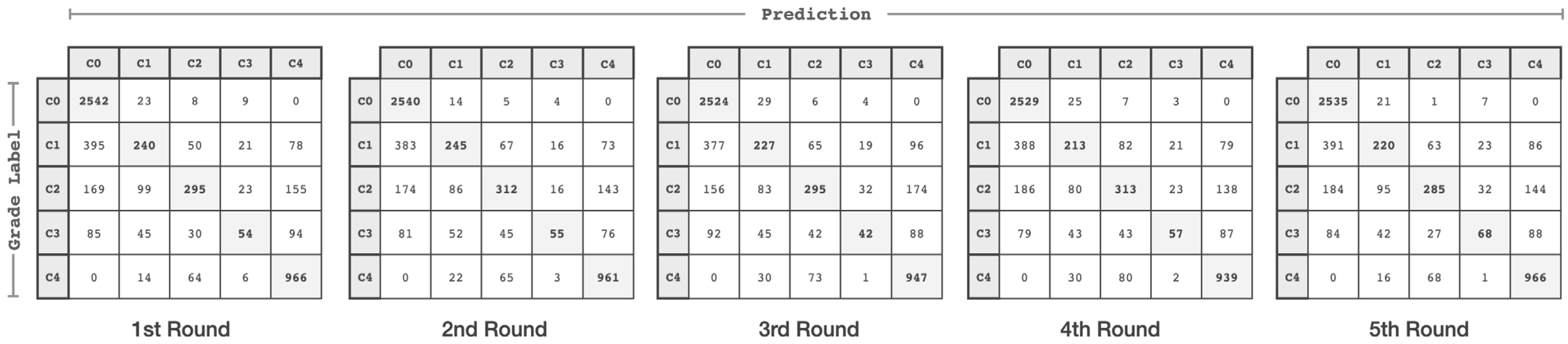
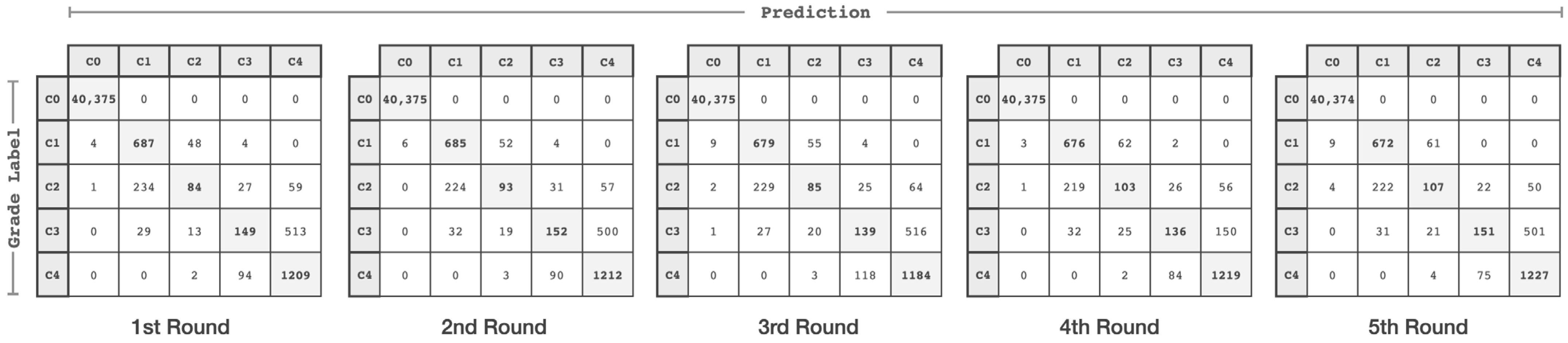
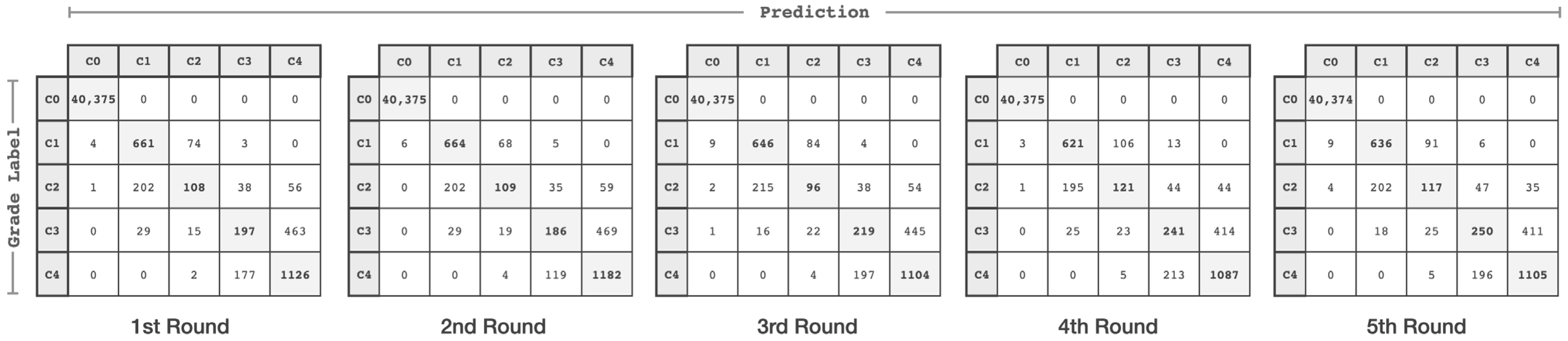
HMPC	CNPC	After Pre-Processing
Attribute	Attribute	Attribute	Example of Value
course_id	course_id_DI	-	-
userid_DI	userid_DI	-	-
registered	registered	-	-
viewed	viewed	-	-
explored	explored	explored	1
certified	completed_%	completed	1
-	course_reqs	-	-
grade	grade	grade	0.75
-	grade_reqs	-	-
-	primary_reason	-	-
final_cc_cname_DI	final_cc_cname_DI	-	-
-	primary_reason	-	-
-	learner_type	-	-
-	expected_hours_week	-	-
LoE	LoE	edu	“Bachelor’s”
YoB	age_DI	age	“{19–34}”
gender	gender	-	-
start_time_DI	start_time_DI	-	-
-	course_start	-	-
-	course_end	-	-
last_event_DI	last_event_DI	-	-
nevents	nevents	nevents	502
ndays_act	ndays_act	ndays_act	16
nchapters	nchapters	nchapters	52
nforum_posts	nforum_posts	nforum_posts	8
nplay_video	-	-	-
-	course_length	-	-
roles	-	-	-
inconsistent_flag	-	-	-

, the steps of preprocessing data are detailed in this section.

From Table 1, the attributes of two datasets are modified and translated into a similar format. In the data pre-processing step, attributes ‘user_id’ and ‘nplay_video’, etc., that only appear in one dataset and have a specific meaning are ignored. The remaining nine attributes will be categorized as eight features and one label attribute. According to Equation (1), the ‘grade’ attribute is classified into the ‘grade_code’ attribute, which includes five classes [17].

$$grade\_code=\left\{\begin{array}{c}C0, 0.0\le grade<0.2\\ C1, 0.2\le grade<0.4\\ C2, 0.4\le grade<0.6\\ C3, 0.6\le grade<0.8\\ C4, 0.8\le grade\le 1.0\end{array}\right.$$

(1)

Following Equation (1), C0 through C4 represent five grades of the learners. The records that “fail” the conditional value in Equation (1) are eliminated. However, there are still data components that need to be cleaned. Records with missing values for the user-supplied attributes of ‘age’ and ‘edu’ are discarded. The missing values for the system-provided data for ‘nevents’, ‘ndays act’, ‘nforum post’, and ‘ncharpters’, assuming there is no activity, are replaced with zero [6,22], but the missing values from ‘grade’ are rejected. Unfortunately, out of 325,199 total records in CNPC, 243,197 of them contain null values for the ‘grade’ attribute. This is a significant reason why the number of records in the CNPC dataset reduces substantially, while the missing data in the ‘grade’ attribute of HMPC comprise only 57,406 records, which is a small portion when it is compared with the total number of records. For the purpose of transforming the data into a format suitable for machine learning, all of the categorical features are encoded as numbers, and then the entire dataset’s features are normalized using Min–Max normalization. Finally, the outliers are removed from the dataset. In this step, the interquartile range (IQR) is utilized [23].

Table 2. The number of data records in each dataset.

Class	HMPC	CNPC
C0	201,874	12,818
C1	3714	3918
C2	2025	3701
C3	3517	1544
C4	6526	5254
Total	217,656	27,235

displays the number of records in each dataset after removing the outliers.

3.3. Centroid Distance Features and Selection Method

Following data preprocessing, eight features are utilized to train the model for the grade prediction. The features consist of two categorical variables, ‘edu’ and ‘age’, and six numerical features that were created by the system. Based on the number of ‘grade’ classes, five extra features are produced during the feature engineering process. The distance features are derived from the distance between each data point and the centroid point of each ‘grade’ class cluster. The distances are computed utilizing the Euclidean distance, with all of the training data being placed in the vector space, and Equation (2) is as follows:

$$d\left(p,q\right)=\sqrt{{\displaystyle \sum }_{i=1}^n{\left(q_i-p_i\right)}^2}$$

(2)

where $d\left(p,q\right)$ is the distance between the data points $p$ and $q$. $n$ is the number of dimensions of venter space. $p_i$ and $q_i$ are the value of each datum at the $i^{th}$ dimension.

Finally, each dataset contains thirteen features from eight selected original dataset and five new distance features. The example of the CNPC dataset is illustrated in Figure 3.

However, the results of the practical experiment indicate that including all of the new features as training features reduces the prediction model’s effectiveness. The method of feature selection is utilized to solve this problem. A silhouette coefficient is used to choose the appropriate features. The silhouette coefficient is derived using the average intra-class distance and the average nearest cluster distance. Typically, it is employed to assess the quality of the clustering [24,25]. The formula provided in Equation (3) is used to compute a dataset’s silhouette score of clusters.

$$silhouette coefficient=\frac{\left(b-a\right)}{\max \left(a, b\right)}$$

(3)

where $a$ is the mean cluster centroid distance. $b$ is the average nearest cluster distance for every sample.

For the purpose of understanding the silhouette score, numbers approaching zero imply overlapping clusters, but negative numbers indicate that a different cluster is more similar. The silhouette score will be closer to one the more clearly the clusters are recognized. After calculating the silhouette score based on the data from the HMPC and CNPC datasets, the results are displayed in

Table 3. The silhouette scores between each class in two datasets.

Silhouette Score between Each Class in the Dataset	HMPC	CNPC
C0 and C1	0.3299	0.1607
C0 and C2	0.4772	0.3124
C0 and C3	0.5884	0.2302
C0 and C4	0.5948	0.3527
C1 and C2	0.0676	0.0624
C1 and C3	0.3482	0.0261
C1 and C4	0.4290	0.1247
C2 and C3	0.2263	0.0324
C2 and C4	0.3281	0.0703
C3 and C4	0.0325	0.1509

.

To utilize the silhouette coefficient in the feature selection procedure, each pair of grade clusters is analyzed. Because a low silhouette score represents overlapping data between the examined clusters, the grade clusters with the lowest scores will be utilized as additional training features for the prediction model. In addition, the ‘cen_c0’ attribute will always be used to support binary classification. Consequently, the HMPC dataset’s new features are ‘cen_c0’, ‘cen_c3’, and ‘cen_c4’, whereas the CNPC dataset’s new features are ‘cen_c0’, ‘cen_c1’, and ‘cen_c3’.

3.4. Machine Learning Architecture

Ensemble learning is a machine learning technique that entails combining the predictions made by training data and multiple models to improve the performance. Ensemble algorithms ensure diversity by resampling the data or modifying the individual learners’ structure. Individual learners must perform distinct tasks to learn, and they are expected to obtain errors that differ from those of the other learners, while basic learners aim for high accuracy [26].

To predict the grades of the students based on the MOOCs data, a two-phase concatenation architecture was established as the foundation for classifying the data of the majority class, followed by the remaining classes. Consequently, the first phase will respond to specific data that should be in class ‘c0’ before pushing the remaining data to the subsequent phase. The second phase refers to the multi-class classification that the model must learn to predict data for five grade levels (from ‘c0’ to ‘c4’). Figure 4 depicts an overview of the proposed architecture: the two-phase ensemble-based grade prediction model.

A.

Dataset

To use the dataset for the building of a prediction model, it will be divided into training- and testing sets with an equal proportion of each grade class. Eighty percent of the data is used to train the model, while the remaining twenty percent is used for testing. In the first phase—binary classification—the training set’s labels will be translated into binary classes. The ‘grade code’ attribute provides five classes for usage in the second phase: multi-class classification.

The ‘grade code’ label will be binned to become a binary one in the beginning stages. The first label is ‘C0’, which corresponds to the dataset’s majority class, while ‘Non-C0’ is allocated to the other classes. The number of binary class labels is listed in

Table 4. The number of binary class labels in each dataset.

Class	HMPC	CNPC
C0	201,874	12,818
Non-C0	15,782	14,417

.

B.

Binary Classification

To specify which ensemble technique should be placed in the binary classification, one boosting method called Adaboost is used [27]. In contrast to the RF approach, which is an ensemble bagging approach that trains the model using a random subset of the data, Adaboost trains its individual models by learning from the previous model’s mistakes. Based on the preliminary test, Adaboost performed better than RF did in classifying binary grades in both of the datasets. Its basis learners are decision trees with a single split. After that, the sample weights are modified based on the predictions made by the classifier, and the samples that have been modified are the ones that will be used to train the subsequent classifier. When there is an instance of samples being misclassified, the weights that are allocated to them are increased. In contrast, the correctly identified samples are given a reduced weight. Finally, the strong classifier is constructed by employing Equation (4).

$$H\left(x\right)=sign\left({\displaystyle \sum }_{t=1}^T{\alpha }_t{h}_t\left(x\right)\right)$$

(4)

where $t$ is the number of iterations, $h\left(x\right)$ is the base classifier, and $\alpha$ is the weight of classifier $h\left(x\right)$. $sign()$ is defined by $sign\left(x\right)=1$ if $x\ge 0$ and $sign\left(x\right)=0$ otherwise. Adaboost is widely employed in the binary classification of imbalanced data, such as fraud detection, hence, this boosting method is chosen for binary classification in the starting phase.

C.

Multi-Class Classification

After the model generates the results of the binary class classification, the data labeled as ‘Non-C0’ are forwarded to the multi-class classifier. Based on the preliminary test between the One-versus-Rest (OvR) and One-versus-One (OvO) strategies, the latter one can overcome the results of the OvR. In addition, other research [28,29] shows that the combination of OvO with the other machine is better than OVR is. Hence, the OvO strategy is chosen to cooperate with the XGBoost ensemble method. In this step, the ‘Non-C0’ class will be classified as being from grade C0 to C4 in this phase.

An OvO technique can be applied to handle the imbalanced datasets [30]. It addresses the multi-class classification problem by decomposing the data from the original dataset to classify them using a binary criterion. In the second phase of the proposed architecture, the label 5 grade classes will be converted into the binary classification, as shown in Figure 5. After receiving the multiple binary classification task from OvO, the boosting ensample technique XGBoost is implemented. The XGBoost technique is a decision-tree-based ensemble that uses the gradient boosting framework, requires minimum feature engineering, and is capable of handling large datasets [27]. Each tree in XGBoost attempts to learn from the previous tree’s errors until there are no false residuals remaining. The loss function of XGBoost tries to prevent overfitting by using Equation (5).

$$L_M={\displaystyle \sum }_{i=1}^T\left[\left({\displaystyle \sum }_{i\in I_j}{g}_i\right){\omega }_j+\frac{1}{2}\left({\displaystyle \sum }_{i\in I_j}{h}_i+\lambda \right){\omega }_j^2\right]+\gamma T$$

(5)

where $g_i$ and $h_i$ represent the first and second derivatives of the loss function, respectively. The samples in leaf node $j$ are denoted by $I_j$. These will be computed for the total number of leaf nodes $T$, while $\gamma$ represents the complexity parameter, $\lambda$ is the penalty parameter, and ${\omega }_j$ is the outputs of the $j^{th}$ leaf nodes. In the preliminary experiment, the performances of XGBoost (boosting) and RF (bagging) were also evaluated to find the optimal strategy for OvO implementation. The results indicated that XGBoost performed better than RF did, which is consistent with the conclusions in [31,32] regarding using XGBoost and RF on imbalanced data. Consequently, the prediction of OvO-XGBoost will be chosen by the majority vote of the XGBoost results.

D.

Bayesian Optimization

Using a collection of appropriate parameters can aid in achieving a better performance. Due to the limitations of the boosting machine technique, they contain a large number of difficult-to-tune parameters. Bayesian optimization is utilized to find the optimal solution. The Bayesian optimization technique discovers how the values of various hyperparameters of machine learning influence the target outcomes by iteratively traversing the results based on different hyperparameter values until they converge on the highest value of the target function [33]. The following sampling point is found by optimizing the acquisition function over a Gaussian process by using Equation (6).

$$x_t=\underset{x}{\mathrm{argmax}}u(x|D_{1:t-1})$$

(6)

$$D_{1:t-1}=\left(x_1,y_1\right),\dots , \left(x_{t-1},y_{t-1}\right)$$

(7)

where $u$ is an acquisition function that directs the next sampling point ($x_t$) to targets where an improvement over the current best observation is possible. Additionally, $D_{1:t-1}$ represents the $t-1$ samples drawn from the objective function ($f\left(x_t\right)$). After calculating the possible noisy sample from the objective function ($y_t=f\left(x_t\right)+\epsilon$), where $\epsilon$ is a Gaussian noise. It is added to the previous samples as $D_{1:t}=D_{1:t-1},\left(x_t,y_t\right)$ and used to update the Gaussian process.

E.

Results Integration

After obtaining the predicted grade of the testing dataset, the records identified as ‘c0’ grade by the binary classification will be combined with the results of the multi-class classification. The metrics described in Section 4 will be used to evaluate these consolidated results.

4. Performance Evaluation

In accordance with the procedure proposed in the previous section, the experiments were configured so that we could use both the HMPC and CNPC datasets. The experiment was mainly implemented using the Python programming language and the Scikit-learn library. To avoid the problems caused by a too-small minority class in the test set, the experiments were processed using five-fold cross-validation, in which 80 percent of the total dataset was designated as the training set and the remaining 20 percent was the testing set. The training and testing process were iterated five times, and the training and testing datasets were different each time. In each iteration of the experiment, the data in each class were divided evenly depending on their respective ratios.

To evaluate the performance of a prediction model with an imbalanced dataset, the weighted-precision, weighted-recall, and weighted-average F1 scores are often considered as the standard evaluation measures [34,35]. Equations (8)–(13) explain how to compute these evaluation scores.

$$precision={\displaystyle \sum }_{i=0}^n\left(\frac{t{p}_i}{\left(t{p}_i+f{p}_i\right)}\right)$$

(8)

$$recall={\displaystyle \sum }_{i=0}^n\left(\frac{t{p}_i}{\left(t{p}_i+f{n}_i\right)}\right)$$

(9)

$$weighted precision=\frac{{{\displaystyle \sum }}_{i=0}^n\left(precisio{n}_i\times N_i\right)}{{{\displaystyle \sum }}_{i=0}^n{N}_i}$$

(10)

$$weighted recall=\frac{{{\displaystyle \sum }}_{i=0}^n\left(recal{l}_i\times N_i\right)}{{{\displaystyle \sum }}_{i=0}^n{N}_i}$$

(11)

$$F1 score=\left(2\times \frac{precision\times recall}{precision+recall}\right)$$

(12)

$$weighted average F1 score=\frac{{{\displaystyle \sum }}_{i=0}^n(F1scor{e}_i\times N_i)}{{{\displaystyle \sum }}_{i=0}^n{N}_i}$$

(13)

where $t{p}_i$ is the number of true positive instances for label $i$. $t{n}_i$ is the number of true negative instances for label $i$. $f{p}_i$ is the number of false positive instances for label $i$. $f{n}_i$ is the number of false negative instances for label $i$. $n$ is the number of class labels in the dataset. $N_i$ is the number of instances or the support value for label $i$.

The precision value typically represents the proportion of valid positive predictions, whereas the recall value indicates the proportion of positive cases that have been correctly categorized. We also calculated the F1 score, which is a harmonic mean of the precision and recall. To apply these metrics for evaluating the prediction results of an imbalanced dataset, the scores will be divided by the number of true instances of each class.

Table 5. Results of the experiments on two datasets.

Method	HMPC			CNPC
	Weighted Precision	Weighted Recall	Weighted Average F1	Weighted Precision	Weighted Recall	Weighted Average F1
RF	0.9715	0.9734	0.9720	0.6975	0.7274	0.7067
RF + Selected distance feature	0.9715	0.9734	0.9721	0.7040	0.7328	0.7127
IRF [17] (without SMOTE)	0.9720	0.9747	0.9721	0.6985	0.7272	0.7074
RF Regression [12]	0.9717	0.9747	0.9708	0.6893	0.6747	0.6779
Deep Learning [13]	0.9703	0.9705	0.9677	0.6649	0.7018	0.6712
Proposed model	0.9741	0.9764	0.9727	0.7149	0.7476	0.7110
Proposed model + Selected distance features	0.9732	0.9753	0.9734	0.7162	0.7486	0.7125
Proposed model + Selected distance features + Bayesian Optimization	0.9735	0.9756	0.9735	0.7270	0.7558	0.7236

represents the results of evaluation metrics that are average values from five-fold cross-validation.

To evaluate the performance of the proposed two-phase ensemble-based method, the state-of-the-art machine learning RF method is compared to the improved RF method [17], which is an enhanced RF that was achieved by utilizing clustering SMOTE and a hybrid indicator with a decision mechanism to select the appropriate features. However, to compare it to the proposed method, the resampling data step is left out. The comparison also includes the RF Regressor [12], which is used to predict the learners’ grades based on their exam results. Following the same conditions as in Equation (1), the outcomes of the prediction as a floating point score are binned to become a ‘grade code’. The deep learning proposed in [13], which implemented a forward-backward algorithm and minimized the cost function by the gradient descent, is also examined.

Table 5 illustrates the average weighted precision, weighted recall, and weighted average F1 scores from the five-fold cross-validation configuration of the experiment. To compare the weighted-precision and weighted-recall means, the weighted-average F1 score (weighted F1 score) is utilized. The optimization of the proposed model with the selected distance feature produced the highest weighted F1 score of the two datasets, whereas deep learning produced the lowest score. In the case of CNPC, the IRF without SMOTE was successful in overcoming the traditional RF and RF regressions, while the efficiency trend from the HMPC dataset is distinct. The outcome of the RF regression for HMPC is worse than the those for RF and IRF. However, even the proposed model is deployed without the selected distance features. For both of the datasets, its performance is better than those of RF, IRF, RF regression, and deep learning. It was compared with the tasks that have been mentioned before because all of them learn and predict the learners’ grade using the multi-class classification, which uses the imbalanced data directly. The results obtained from them cannot reach the same level as the proposed method can for all of the classes, especially for class ‘c0’, which is the majority class.

Focusing on the two-phase ensemble-based method, the proposed model’s base outperforms the previous techniques. To improve it, the centroid distance features are added, and then filtered by the lowest silhouette score between the clusters of grades in the training set. In this step, the CNPC performance improves in all of the measures, except for HMPC. In HMPC, only the weighted F1 score increases, which the confusion matrix will analyze in depth. Figure 6 shows the confusion matrix of five-fold cross-validation from the CNPC dataset experiments to support a detailed discussion. Figure 7 displays the enhancement achieved by deploying the optimization and feature selection to the proposed model’s core.

Only ‘cen_c0’, ‘cen_c1’, and ‘cen_c3’ are integrated with CNPC dataset features when feature selection is employed. The silhouette scores of all of the clusters within the dataset denote these important features. The model is then enhanced via Bayesian optimization. Adding the selected distance characteristics improves the model’s ability to predict the samples from classes ‘c1’ through to ‘c3’ compared to that of the originally proposed model. However, the number of accurate predictions from ‘c0’ to ‘c4’, which represent the majority class and the second largest in the dataset, decreases marginally.

The HMPC datasets receive ‘cen_c0’, ‘cen_c3’, and ‘cen_c4’ as additional features, and optimization is performed. However, the enhanced performance of this modified model is not very significant. Figure 8 demonstrates the confusion matrix of five-fold cross-validation for predicting the learners’ grades using the two-phase ensemble-based model that was applied to the HMPC dataset. In addition, Figure 9 displays the outcomes of applying optimization to the model and including the selected centroid distance features in the dataset.

From the confusion matrix, the first phase of the proposed model’s binary classification efficiently identifies ‘C0’ and ‘Non-C0’. This may be because class ‘c0’ of the HMPC has 13 times more data than the other classes do. The prediction of class ‘c0′ influences the quality of the grade prediction in the HMPC dataset. The accuracy values of ‘c2’ and ‘c3’ improve Figure 9’s prediction findings, whereas all of the others except for ‘c0’ decrease. This demonstrates that the specified distance features can help the model to clear the ‘c3’ feature, and they also influence ‘c2’, which has the same poor silhouette score as that of ‘c3’. This adjustment is in response to the decrease in weight precision and weighted recall and the rise in the weighted F1 scores.

To improve the classification performance, Bayesian optimization is enabled for binary and multi-class classification. The optimizer learns by iteratively traversing all of the possible sets of hyperparameters until the highest value of the given evaluation metric is obtained. In parameter spaces, only the parameters ‘n_estimators’ and ‘learning_rate’ are present for the binary classifier’s AdaBoost, while XGBoost’s parameter spaces include seven parameters: ‘n_estimators’, ‘max_depth’, ‘reg_alpha’, ‘reg_lambda’, ‘min_child_weight’, ‘num_ boost_round’, and ‘gamma’. In this step, the optimization that is represented in

Table 6. The optimal values of hyperparameters in each dataset.

Machine Learning	HMPC	CNPC
AdaBoost	n_estimators = 10 learning_rate = 0.1	n_estimators = 500 learning_rate = 1.0
OvO + XGBoost	gamma = 10 max_depth = 40 min_child_weight = 1 n_estimators = 10 num_boost_round = 100 reg_alpha = 0.1 reg_lambda = 0.0	gamma = 10 max_depth = 40 min_child_weight = 1 n_estimators = 100 num_boost_round = 1000 reg_alpha = 0.0 reg_lambda = 0.0

can improve the results from both of the datasets.

Compared to the prior discussion, the CNPC dataset is a better fit for the proposed grade prediction model than the HMPC dataset is. It is possible that the number of samples in each class in the CNPC dataset is comparable to that of the remaining classes, which differs from the HMPC dataset. According to Table 4, the ‘Non-C0’ class of CNPC receives approximately 52.94 percent of all of the records. While the ‘Non-C0’ category of HMPC accounts for only 7.25 percent of all of the records, it does represent a relatively small portion of the dataset. Changing the architecture of the prediction model from a single-phase model into a two-phase model dramatically improves the ‘c0’ class prediction accuracy, which can be further improved through the optimization procedure.

Even if the system can track and collect all of the student behaviors when it is studying or interacting with the system, the focus should be on the characteristics of the data when we are applying MOOC learner behavior data. The data from the HMPC and CNPC datasets demonstrate how imbalanced data can cause classification model difficulties. Class ‘c0’, which constitutes the majority of the dataset, influences the prediction model, whilst the remaining data are insufficient for accurately training the model. In this situation, the two-phase ensemble-based technique can combine binary and multi-class classification. Additionally, it can improve the performance by learning the applicable distance features and optimizing the associated hyperparameters.

5. Conclusions

MOOCs are a great source of data regarding the behaviors of students. Using a prediction of their performance, the learners can evaluate their learning behavior. Instructors or course administrators could utilize the forecast to improve their teaching or learning materials. In addition, the performance data may be combined with other features of learning behavior for learning analyses.

The proposed design, a two-phase ensemble-based architecture with a centroid distance feature, is utilized to estimate students’ grades based on two imbalanced MOOC datasets without using over- and undersampling methods. The centroid distance features will be chosen according to their silhouette score. In the first phase, the ensembled method selected for the binary classification is Adaboost, while the cooperation of One-versus-One and XGBoost is deployed in the second phase as the multi-class classification. Bayesian optimization is used to determine the best classification parameters for performance improvements. The experiment findings reveal that the presented two-phase ensemble-based method design outperforms the state-of-the-art machine learning algorithms in both of the HMPC and CNPC datasets.

However, making an improvement is possible by overlaying the data for each grade level in the training dataset. In the future, a new learning approach or more appropriate training elements will be required to solve the identification samples in the overlapping clusters. From the learning analysis viewpoint, it is equally interesting to analyze the behavior of the learners from each subject’s perspective. In addition, the open datasets in this work are collected at the end of the course. Using partial learning behavior data, such as the data from the sub-sections of a course, is an interesting potential topic. It can improve the prediction performance for detecting learner performance earlier, and teachers can support their students in a timely manner.