Abstract
The development of plasma accelerators for spacecraft propulsion that can capture space matter and energy shows great promise for spacecraft advancement. Such a technical approach offers a viable solution to the challenges associated with traditional rocket fuel. In the present paper, we explore the utilization of interplanetary matter as fuel for plasma thrusters on space vehicles, specifically for flights within the vicinity of Earth. Herein, solar radiation is considered a source of energy for the ionization and acceleration of particles captured from the space environment.
1. Introduction
The exploration of even near-Earth space requires creating vehicles that accelerate to high speeds. As was shown in Refs. [1,2,3,4], the maximum velocity for present-day chemical engines is only roughly m/s, with nuclear engines able to reach speeds around m/s, and end-Hall thrusters demonstrate the capability to generate exhaust speed on a scale of m/s. Notably, the potential of chemical and nuclear engines is inhibited by the energy produced during their respective reactions (as discussed in Refs. [3,4,5,6,7]). These limitations for plasma thrusters, however, may, in principle, be evaded when external power and matter sources are applied (see [8,9] and the references therein). Solar radiation could be an energy source for ionizing and propelling the operational matter collected from the interplanetary medium comprising cosmic dust and solar wind [10,11,12,13,14,15,16,17,18,19,20,21,22,23]. However, the material captured from the space between planets falls short in quantity to produce the necessary thrust for a spacecraft.
To illustrate these aspects regarding plasma thrusters, let us examine the common thrust definition T where is the rate of fuel consumption and represents the effective exhaust velocity (this is a product of the specific impulse and the standard gravitational force of Earth). As can be seen from this formula, higher flow rates require less fuel to generate the desired thrust. For plasma thrusters, the highest achievable value of exhaust velocity is only constrained by the acceleration process and the input energy. If we use the Sun as an external energy source, then we will have an almost unlimited power tank. Therefore, one may try to accelerate the plasma flow to ultrarelativistic speeds when the effect of mass increases provides an acceptable value of thrust with a relatively small number of particles that create this thrust.
A possible technical implementation for such a thruster scheme was initially described in Refs. [8,9]; a diagram of this device is displayed in Figure 1 below. Although the principle of operation for the proposed device is clear from this figure, we shall briefly describe some key points.
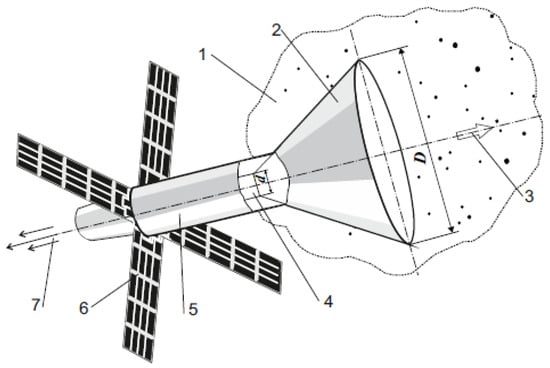
Figure 1.
Spacecraft diagram: 1—interplanetary dust; 2—particle trap; 3—the spacecraft’s movement direction; 4—discharge chamber; 5—ship; 6—solar panel; 7—plasma flow creating the ship’s thrust [9].
This scheme is a transfer of the Bussard ramjet to a plasma thruster. However, in the present scheme, even at low values of extracted from outer space, we may increase the engine thrust due to an increase in the specific impulse. Such behavior is possible only in a plasma accelerator and is a key difference from the Bussard ramjet that supposedly uses a thermonuclear spacecraft engine (see [24,25,26,27,28,29]).
In principle, such open-type technical units can provide the exchange of energy and matter of the interplanetary medium for a spacecraft’s momentum, which develops ways to create space vehicles that do not require stores of fuel. However, the real technical implementation of similar units strongly depends on the state of the interplanetary medium: the flux densities of solar energy and the interplanetary substance. In the present paper, we discuss this concept of a plasma thruster for near-Earth space.
2. Analysis of Astrophysical Data
Drawing on astrophysical research [10,11,12,13,14,15,16,17,18,19,20,21,22,23], we briefly delve into the physical properties of matter in near-Earth space that are required, analyzing the efficiency of the proposed scheme. The primary constituents of interplanetary matter we focus on are the solar wind, high-energy charged particles, interplanetary dust, and neutral gas [19,20,21,22].
Solar wind mainly comprises of hydrogen plasma, with a minute portion of helium ions, generated from the transfer processes within the Sun’s corona. Direct observations [10,11,12,13,14,16,23] suggest the formation of non-stationary, spherically asymmetric flows that vary significantly over time depending on the solar corona’s state. Plasma expulsion creates non-stationary shockwaves within the interplanetary space close to the Sun, exhibiting sudden changes in velocity, density, and temperature when faster flows overtake slower ones. As these waves move away from the Sun, they interact, resulting in a quasi-stationary plasma flow at a distance of about one Astronomical Unit () directly in near-Earth space.
This flow constantly contains a relatively slower part of the solar wind with typical speeds of and a density of [19,23], originating from the gas-dynamic expansion of the solar corona’s “quiet” portion (the so-called slow flow). The quasi-stationary flow (the so-called fast flow), with speeds of and a density of , comprises particles emanating directly from the Sun’s surface [16,19,23]. This phenomenon appears within several months and repeats every 27 days.
Another component is the relativistic flow of protons generated during solar flares, but this is typically short-lived and sparse; thus, its contribution is often disregarded [19,23]. As a result, the quasi-stationary plasma flow’s average speed is with a density range of , as observed in Earth’s orbit [10,19,23]. As was shown in [10,23], both the pressure gradient and the Sun’s gravitational force can be ignored at a distance of around This implies that for distances , the wind speed can be considered steady, and the flow’s density declines with the distance as a function, , whereas at a distance of , the density would fall within the range. Therefore, this value can be utilized for approximate calculations within a distance range of . Clearly, if , this value would increase as we move closer to the Sun.
Now, we shall move on to discussing the component composition of cosmic dust. According to [14,15,17,19], interplanetary dust comprises three main chemical elements: magnesium (Mg), silicon (Si), and iron (Fe). The present elements are included in approximately equal proportions, and silicon has the highest ionization potential, [14,19]; this value will be used in subsequent estimations. One can expect that these components create the main part of the thrust since they have the largest atom masses and the highest percentages in the compounds of interplanetary dust. To simplify the present rude calculations, instead of all dust components, we introduce a “medial” dust particle with mass , where , , and are the molecular weights of magnesium, silicon, and iron, respectively.
Proceeding from this point, we can approximate the density of dust particles by estimating the annual influx of dust from the zodiacal cloud into Earth’s atmosphere as it orbits the Sun. The observations in [17,20,22] indicate that approximately 25,000 to 45,000 tons of interplanetary dust settles on Earth each year, corresponding to a mass flow rate of . For our analysis, let us consider a characteristic value for the mass of the dust flow reaching the Earth’s surface. On the other hand, this dust flux can also be estimated as a function of the cross-sectional area of Earth’s orbit around the Sun and the density of interplanetary dust
where is the mass of a dust particle, is the dust density, is the speed of the dust flow relative to the Earth, and is an effective cross-section of the Earth through which the dust flow enters the Earth’s atmosphere. To determine the value of near Earth, we shall proceed from the point that coincides with the speed of the Earth’s rotation around the Sun, . This assumption considers the dust to be stationary, and the effective cross-section is considered to be a circle with a radius , where is the radius of the Earth and is the height of the atmosphere, above which there are no collisions with particles. Using these astrophysical data and setting , from Equation (1), we find . Note that this result coincides in its order of magnitude with the experimental values in [15,18,19] in which the density was observed in near-Earth space. Therefore, based on this information, we can estimate the dust density in the near-Earth space to be .
According to experimental data [11,19,22], the density of neutral gas in the solar system is much smaller than the density of the solar wind and dust. Therefore, as fuel for plasma thrusters, one may consider only the solar wind and interplanetary dust as a fuel medium. As can be seen from our estimations, in the near-Earth space (at a distance of about 1 ), these components of the interplanetary medium provide the maximum density, . However, in order to use this value of density, we must consider the magnitude and direction of the solar wind flow relative to the ship. To simplify our estimations, we shall consider only a stationary, immobile interplanetary medium with a low density of 10 . As a result, we shall obtain a rough assessment of the process under study, as shown below.
To determine the possibility of using solar radiation for ionizing neutral atoms and their subsequent acceleration we must take the solar radiation power distribution as a function of the distance from the Sun. As a characteristic temperature of the Sun, we take at a distance of [11,16,23]. Then, using the Stephan–Boltzmann law, we find
where is the Stefan–Boltzmann constant. This dependence is sketched in Figure 2, and for the convenience of perception, the distances from the Sun to the planets that fall inside a sphere of radius are labeled, where is the distance from the Sun to the edge of the asteroid belt since there is no dust beyond this boundary. In the present case, the value is the natural boundary of the area in which the proposed scheme can be used. The results presented in Figure 2 coincide with the experimental data [19,20]. So, it is possible to use Equation (2) in order to make rude estimates in the near-Earth region.
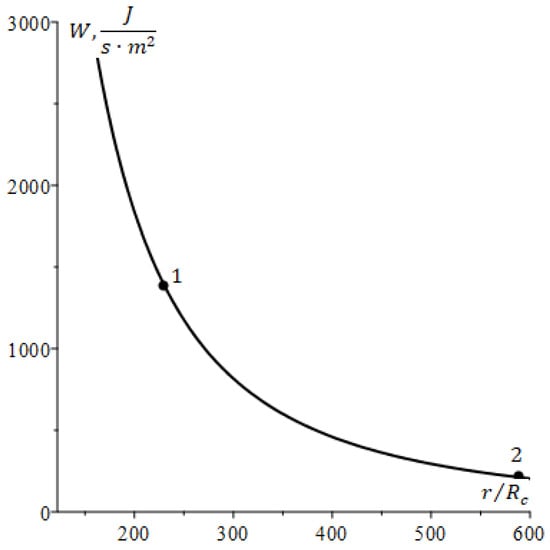
Figure 2.
Dependence of solar radiation power as a function of distance between Sun and Ceres. Here, 1 corresponds to the Earth orbit (.) and 2—the Ceres orbit () [8,9].
Again, we would like to emphasize that all values presented in this section must be considered from the point of view of the rude estimate below, which only shows the physical and technical feasibility of the present idea in principle.
3. Dynamics of Spacecraft Acceleration
We study the acceleration of a nonrelativistic object (i.e., for the spacecraft’s speed, we have ) with an allowance for the particles collected from the interplanetary medium ejected after acceleration to relativistic velocities. We focus on the case in which the effects of external factors (e.g., frictional force in the atmosphere, gravitational fields near massive objects) on the movement of the spacecraft are negligible, i.e., we shall proceed from the generalized Meshchersky equation [2,30]:
where is the mass of spacecraft, is the spacecraft’s speed in the laboratory frame of reference, and are the respective mass and speed of particles captured by the spacecraft, and and are the respective mass and speed of particles emitted into space. Note that Equation (3) is valid only if the following conditions hold:
We shall consider the simplest one-dimensional case in which the interplanetary medium is immobile, i.e., we set , and the velocity of the ejected particles is considered in a nonrelativistic way in a laboratory frame. This may be accomplished due to the nonrelativistic spacecraft speed
Herein, the exhaust plasma flow may be relativistic so far as the value of is defined by the absorption and dissipation of radiation flux, as well as the number of particles trapped per unit time:
where the cross-section of the trap, , through which interplanetary matter is captured by the spacecraft is defined by the inlet diameter of the trap, (see Figure 1). In this case, the attached mass is created only by an incoming flow of captured particles:
Assuming all ejected mass is the accelerated flow of incoming particles, we can write
Note that the exhaust velocity depends on the solar radiation power which, in turn, is a function of the distance from the Sun to the spacecraft (see Equations (13)–(15)). Such a consideration is necessary for flight over long distances (say, of the order of ) when the radiation power varies greatly (see Figure 2). With allowance for immobile interplanetary medium, substituting (5), (7) and (8) into Equation (3), in one-dimensional geometry, we derive
To use this equation, we need to define the relationship between the kinetic energy of the accelerating particles which form the outgoing plasma flux and the processes of the absorption and dissipation of radiation. Generally, the kinetic energy of an exhaust particle is determined by the expression
If we consider only elastic head-on collisions with the spacecraft’s surface and assume that the energy of the coming particles is spent on the deceleration of the spacecraft, one can write the power balance relation for absorbed radiation as
where is the area of the solar panel and is the conversion coefficient of solar radiation into power going to the production and acceleration of plasma flow. We introduced this factor to take into account some energy losses in solar batteries in the processes of ionization and acceleration, etc. The use of such an integral value makes it possible to account for all energy losses in a parametrical way without considering the physical essence of these parasitic processes. On the other hand, the choice of requires a detailed analysis of all technical elements determining the operation of the plasma thruster. However, while this question emerges from the framework of the present paper, we hope to discuss this point later. Here, we shall limit ourselves to choosing some acceptable value for .
As an example of using expression (11), we consider the analytically simplest case when , which allows us to neglect the second term on left-hand side in Equation (11). Also, we assume that , i.e., , and the ionization losses are negligibly small (in our case, this means ). In this range of spacecraft speeds, setting for simplicity, from Equation (11), we derive
Then, from (10) and (12), we arrive at
where
and the value
is the characteristic velocity scale for the problem under consideration and reflects the dynamics of the transformation from radiation energy into the kinetic energy of the accelerated plasma flux. At this stage, we would again like to emphasize that is in fact the specific impulse for the problem under consideration.
To understand the order of this value, we shall make a rough estimate for typical conditions. Assuming that the energy conversion factor is (this value is used in all further calculations), and if as a characteristic estimate of radiation flux near the Earth we take W (see Figure 2), then, using these values in Equation (15), we obtain . In our further estimations we shall use the value as a characteristic magnitude. That is, the value is very small for the dynamic scales of the problem under consideration.
The relation (13) shows how depends on the spacecraft’s velocity and the characteristics of the interplanetary medium via the parameter . As an illustration of this, Figure 3 presents a graph of for relatively small values of . As can be seen in Figure 3, for greater values a nonrelativistic case is realized in which . Such dynamics result from the growing number of particles captured with an increase in velocity when the absorbed energy per particle falls.
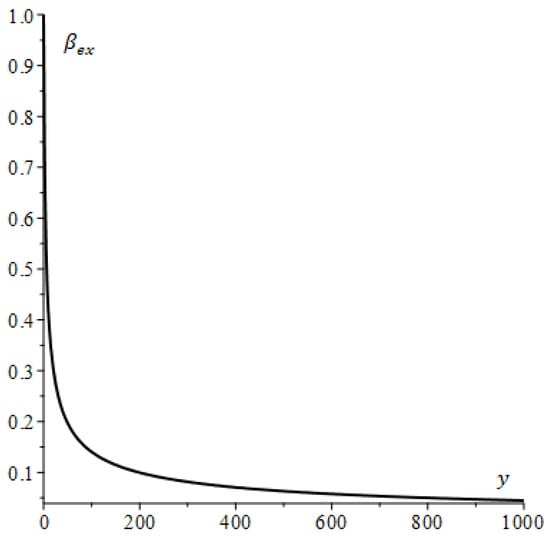
Figure 3.
Dependence of on .
We now return to the analysis of the generalized Meshchersky equation. Inserting (13) into (9), we derive
written in the dimensionless form using (13), and
where the value plays the role of a natural temporal scale for the process under study and may be considered the characteristic time of the spacecraft’s acceleration. Thus, Equation (16) completely describes the acceleration of the spacecraft with an allowance for the capture and ejection of interplanetary matter and forms the basis of the following analysis.
However, in the present study, we restrict ourselves to the analysis of the initial stage of an acceleration when the last term in Equation (16) is a negligibly small quantity. Such approximation shall be realized if
where . So, from this inequality, it follows that
In this case, Equation (16) transforms into
The solution of this equation is
This relationship describes the initial transient stage for spacecraft acceleration as long as condition (17) is satisfied. The use of Equation (19) makes it possible to estimate the characteristic time for which our spacecraft shall reach its maximum velocity . Substituting this value into (19), we obtain the following rude estimation:
which can be rewritten for clarity in a dimensional form as
As can be seen from this relation, there is a strong, linear dependence with respect to the characteristic time and a very weak power dependence on the parameter . In the discussed case, the influence of varying parameters and on the acceleration time is negligible. That is, the inaccuracy in determining these parameters shall have little effect on the value of .
We now estimate the spacecraft thrust:
With allowance for (13)–(15), Equation (21) transforms into
For , by again setting , we rewrite this relation in dimensional form as
where we denote , and the thrust is defined in Newtons. As can be seen from this relation, the thrust is increased with respect to an increase in values. This point is a fundamental otherness from chemical and nuclear thrusters for which there is no dependence of spacecraft speed. Also, this dependence shows that the proposed scheme shall be effective at high spacecraft speeds as well as increasing the effective capture area . The value of depends on both technical characteristics via the parameter and the interplanetary conditions.
It is clear that the set of these factors defines the technical implementation of the proposed conception. On the other hand, the present dependence of spacecraft thrust is brought about by the simplifying assumptions with respect to Equations (11) and (16). For a more accurate estimate, we should analyze the exact version of Equation (16) with an allowance for friction power. However, even the present rude estimate allows us to draw a tentative conclusion about the implementation of the proposed scheme.
4. Implementation of Spacecraft Using Interplanetary Medium
Proceeding from the provided data regarding the distribution of the interplanetary medium in the near-Earth region, it becomes apparent that the direct utilization of the interplanetary medium as fuel for future plasma engines is impossible. So, we ought to apply some technical means of providing the required characteristics of a spacecraft thruster. For example, we should provide the required density of neutral gas in the discharge chamber (say, ; this value will be used in the subsequent estimations).
To enhance the efficiency of capturing the interplanetary medium for the designed plasma engine out, a conical trap can be utilized. This trap is placed on a moving spacecraft in the direction of its motion (see Figure 1), allowing for an increased density of neutral particles in the narrow section of the trap compared to the area of the inlet trap. For example, assuming the inlet diameter of the conical trap is and the effective inlet diameter of the discharge chamber is , we can then achieve a density increase of times solely through the geometric properties of the trap.
In this case, we assume that the entire process of capturing the interplanetary medium occurs in a free molecular mode as long as the medium remains collisionless even in the narrow region of the trap. In other words, the mean free path, calculated from the density in the outlet chamber area, should be at least comparable to the characteristic size of the device (e.g., the diameter d). An estimation for the mean free path can be obtained using the following formula:
Considering the gas kinetic cross-section, σg = 10−16 cm2, we find that for the chosen value of , the mean free path is approximately equal to the chosen characteristic dimension of the discharge chamber, d. Hence, the collisionless regime may be maintained with the chosen geometric parameters of the discharge chamber.
Furthermore, the effective operation of this method requires a relatively high spacecraft velocity. This is because the accumulation time of particles in the discharge chamber is proportional to its volume, , and inversely proportional to the spacecraft’s speed. To illustrate these points, let us consider a specific example of a real discharge chamber that could be utilized in the given context.
Similar to the concept of a space scavenger [9,31], we can take a cylindrical discharge chamber with a volume of , operating at low pressure. Typically, radio frequency fields can produce such discharges in different gas media at pressures of around [32,33,34]. This corresponds to particle densities inside the discharge chamber of . Then, based on the continuity condition of the flow, we conclude that the flow of particles incident on the concentrator shall fill the selected volume in time up to a number of particles :
where is the length of the discharge chamber and . At this stage, we want to emphasize once again that the speed of particles entering the trap relative to the ship coincides with the instantaneous speed of the spacecraft since only immobile interplanetary dust was chosen as fuel. Figure 4 shows the characteristic particle accumulation times for these values as a function of the spacecraft’s speed for different values of the geometric parameter , which provides an indication of the time scale of the process.
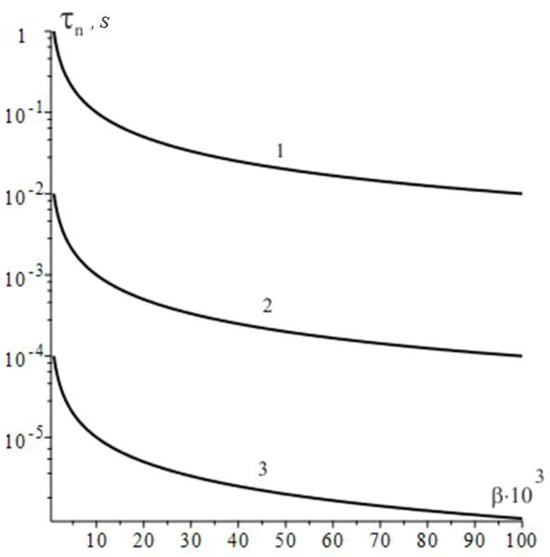
Figure 4.
The characteristic accumulation time as a function of for different values of . Curve 1 corresponds ; curve 2 corresponds and curve 3 corresponds .
As seen from Figure 4, with allowance for the time scale of plasma production and thrust, one may pay no regard to the time of capturing matter from space for and . In the first approximation, the process of plasma capture and acceleration can be considered a continuous process for when the space medium might serve as a matter tank for the plasma thruster. In this regard, two questions immediately arise: Is there enough radiation energy to create thrust? For how long shall the spacecraft accelerate?
As already mentioned, the energy required for the acceleration and ionization of trapped particles is obtained from a solar battery situated on the surface of the device (as depicted in Figure 1). The final plasma flow velocity is determined by the radiation flux and the method adopted for plasma acceleration. For example, one can use the collective acceleration method based on the momentum transfer of the external electromagnetic field to the particles of the flow [35,36,37,38] or some type of Hall thruster (see [3,4,5,6,7,39,40,41,42]). However, as our scheme necessitates various particle types of different masses, it is imperative to take into account the effects of mass and charge separation in crossed electric and magnetic fields (see [43,44,45]).
In the present work, we do not focus on these points in detail, limiting ourselves to considering only the energy and material aspects of the discussed scheme (we hope to touch on these questions in future works). Nevertheless, as an illustration, we now consider one of possible technical approaches to the acceleration of the captured matter sketched in Figure 5 [35,36,37,38]. As is seen from Figure 5a, the flow of collected particles is injected into the acceleration section from the discharge chamber (if the captured matter is neutral particles). Figure 5b explains the physical idea of this plasma accelerator for a flow containing electrons, single-positive-charged ions, and heavy multiply charged negative particles. In this configuration, an alternating axial magnetic field, , generates an azimuthal component of the electric field which, in turn, rotates the electron current, , the dust particle current, , and the ion current, , in different directions.
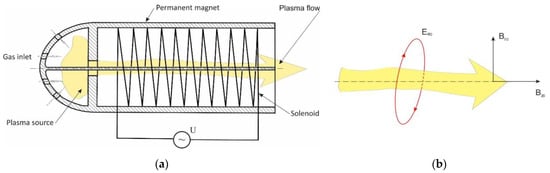
Figure 5.
Schematic of acceleration section: (a) accelerator design and (b) acceleration zone with plasma containing electrons, dust particles, and ions.
Herein, the acceleration effect depends on the ratio between and , but it does not depend on the magnitude of itself. So, there is no need to create a large current in the solenoid, and one can expect to achieve significant acceleration of the plasma flow. Unfortunately, the described method of creating the required configuration of magnetic fields does not seem optimal since the ideal field distribution presented in Figure 5b can hardly be fully realized in the scheme shown in Figure 5a.
However, one can say that this is a solvable issue from the technical and physical point of view, and we hope to discuss this question later. In this regard, we consider the energy losses associated with these factors via the parameter , changes in which have a relatively weak effect on the value . For example, by varying the value in Equation (20), we can estimate the characteristic time with respect to the conceivable characteristics of a spacecraft actually used for near-Earth flight.
We shall proceed using information about Apollo 11, the first spacecraft that made such a flight. As is known [2], the mass of Apollo 11 was 15 tons, of which 10 tons were fuel. In our estimations, we take the characteristic spacecraft mass from the range . Recall that for and W , we have which yields . For the above-specified spacecraft geometry, we take . At the indicated values of and , Equation (20) is reduced to
where the mass of the ship is defined in kilograms, and the trap diameter is defined in meters. This dependence is presented in Figure 6.
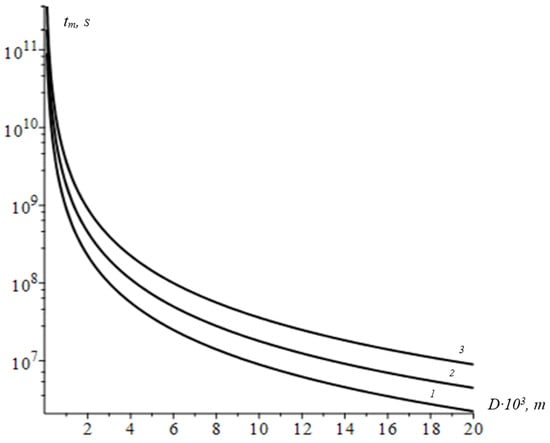
Figure 6.
The dependence of on for different conceivable values of spacecraft mass. Curve 1 corresponds ; curve 2 corresponds to and curve 3 corresponds to .
The value is approximately equal to 100 days. These graphs shows that one may obtain the acceptable acceleration time () only for a spacecraft of relatively light weight ( ) with a trap diameter . Such parameters are difficult to achieve at the current technical level. However, we used obviously underestimated values for , , and especially the area of the solar panel which, for simplicity, was equal to the area of the trap. In reality, the area of the solar panel may differ from that of the trap by an order of magnitude. Therefore, the present results are preliminary, rough estimates indicating the direction of further work.
To display the potential possibilities of the discussed scheme using relation (22), we calculate the thrust generated by the attached mass. Figure 7 shows the dependence of on for different values of . As can be seen from these graphs, we observe the increasing thrust with respect to the spacecraft’s velocity. However, there is a stronger dependence on since , , and this feature again returns us to the problem of the spacecraft’s size. This aspect of the problem shall be discussed in our forthcoming works.
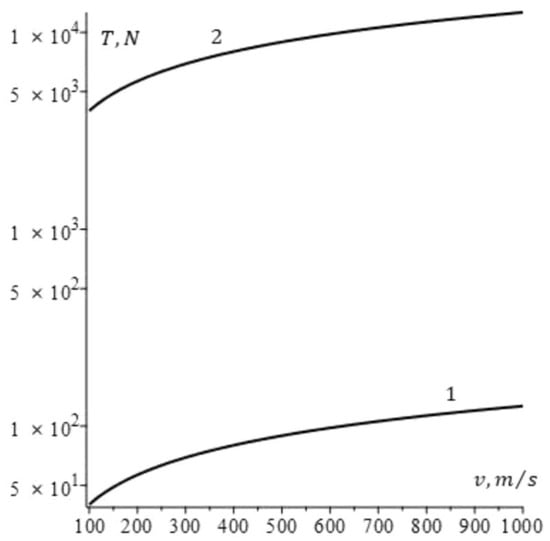
Figure 7.
Thrust as a function of spacecraft velocity for different values of . Curve 1 corresponds to , and curve 2 corresponds to .
5. Conclusions
The present study explored a possible scheme of a plasma thruster, utilizing high-speed plasma flows comprising electrons, ions, and heavy multiply charged dust particles. These high-speed particle flows are generated from captured matter by utilizing solar radiation as the spacecraft follows a specific trajectory.
Certainly, it would be interesting to analyze this conception from the point of view of long-range flights in the solar system. However, at present, the region of near-Earth space is the most well-studied region. Therefore, using information about the interplanetary medium near Earth, we considered the proposed scheme of a plasma engine for flights only in near-Earth space. It should be noted that we greatly simplified our calculations; we disregarded the contribution of solar wind and focused solely on stationary interplanetary dust in a vicinity of approximately 1 As a result, the findings presented in this study should be regarded as a lower rough estimate that highlights the potential for the technical realization of the proposed scheme. Also, we would like to point out that there are many technical applications and developments for the proposed idea (see [31,45,46]).
From graphs depicted in Figure 5, it follows that the use of the proposed scheme for small velocities is impractical, as one requires a huge trap ( ). However, bearing in mind the dependence (23), one can expect that the proposed approach shall be effective at high spacecraft speeds. It is also worth noting that in the present estimations, we used a very low-density value of captured matter, 10 , whereas from the estimates of Section 2, it follows that the real density value can be increased by at least four times, which means the size of may be reduced by a corresponding number of times.
Note that the coupling of the trap and plasma accelerator chamber can be carried out in various ways; this point strictly depends on the interplanetary medium composition, as well as the method for plasma generation and the acceleration of plasma flow. A sample of such coupling is presented in Figure 5a, where the neutral dust flow accumulated in the trap is directly introduced into the discharge chamber through a set of inlet holes. If only solar wind particles are used as fuel for a plasma thruster, one can abandon the conical trap and replace it with a magnetic trap (see [24,29] and the references therein). The charged particles can be collected in the proposed magnetic field (so-called magnetic mirrors [47]) and guided into an inlet of the plasma accelerator. In this case, we escape the problems with the size and weight of the conical trap, and there is no need for a discharge chamber; the magnetic trap shall act as a brake.
In this regard, we would again like to emphasize that in the discussed case, there is no need for a large number of trapped particles to create acceptable thrust since the exacted thrust value can be obtained owing the relativistic increase in the momentum of the rejected particle flow.
Moreover, it is crucial to account for the energy losses associated with the implementation of low-pressure discharge and the method of plasma acceleration, along with the transformation of solar energy within the solar cells. To abstract away from the considerations of such points, we introduced an energy conversion factor which accounts for the impacts of these processes and for any unknown factors. In this context, we set . One should expect that the value of can be enhanced; hence, the current estimates should only be viewed as preliminary. They principally exhibit the feasibility of implementing the discussed scheme, and we intend to discuss these questions in our forthcoming works.
Author Contributions
Conceptualization, A.R.K. and P.A.M.; methodology, A.R.K. and P.A.M.; validation, A.R.K. and V.A.Y.; investigation, A.R.K., V.A.Y. and D.S.B.; writing review and editing, A.R.K. and V.A.Y.; supervision, A.R.K.; funding acquisition, A.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (State Assignment No. 075-01129-23-00).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
Paul A. Murad, one of the authors of this paper, has passed away, so we would like to dedicate our present research to the memory of Associate Fellow of the AIAA P.A. Murad. The authors would like to express their profound gratitude to the referees and A. N. Dolgov for their valuable remarks and suggestions for lines of further research. Also, we wish to thank Andre P. Murad for her help in the preparation of this manuscript.
Conflicts of Interest
Author Paul A. Murad was employed by the Kepler Aerospace Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sutton, G.P.; Biblarz, O. Rocket Propulsion Elements, 7th ed.; Wiley& Sons: New York, NY, USA, 2001. [Google Scholar]
- Ulrich, W. Astronautics: The Physics of Space Flight, 2nd ed.; Wiley& Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Bathgate, S.N.; Bilek, M.M.M.; Mckenzie, D.R. Electrodeless plasma thruster for spacecraft: A review. Plasma Sci. Technol. 2017, 19, 083001. [Google Scholar] [CrossRef]
- Morozov, A.I.; Savelyev, V.V. Fundamentals of stationary plasma thruster theory. In Reviews of Plasma Physics; Kadomtsev, B.B., Shafranov, V.D., Eds.; Springer: Boston, MA, USA, 2000; Volume 21, pp. 203–291. [Google Scholar]
- Brown, N.P.; Walker, M.L.R. Review of Plasma-Induced Hall Thruster Erosion. Appl. Sci. 2020, 10, 3775. [Google Scholar] [CrossRef]
- Smirnov, A.; Raitses, Y.; Fisch, N.J. Experimental and theoretical studies of cylindrical Hall thrusters. Phys. Plasmas 2007, 14, 057106. [Google Scholar] [CrossRef]
- Karimov, A.R.; Yakovlev, O.V.; Murad, P.A. The use of interplanetary medium as fuel for plasma thrusters. J. Phys. Conf. Ser. 2019, 1238, 012063. [Google Scholar] [CrossRef]
- Karimov, A.R.; Murad, P.A.; Terekhov, S.A.; Yamschikov, V.A. Electrophysical Means in Space Research and Applications for the Near-Earth Space. In Proceedings of the AIAA Propulsion and Energy Forum, Virtual Event, USA, 9–11 August 2021. [Google Scholar]
- Brady, P.; Ditmire, T.; Horton, W.; Mays, M.L.; Zakharov, Y. Laboratory experiments simulating solar wind driven magnetospheres. Phys. Plasmas 2009, 16, 043112. [Google Scholar] [CrossRef]
- Podgorniy, I.M.; Sagdeev, R.Z. Physics of interplanetary plasma and laboratory experiments. Adv. Phys. Sci. 1969, 98, 410. [Google Scholar] [CrossRef]
- Simpson, J.A.; Connell, J.J.; Lopate, C.; McKibben, R.B.; Zhang, M.; Anglin, J.D.; Ferrando, P.; Rastoin, C.; Raviart, A.; Heber, B.; et al. Cosmic ray and solar particle investigations over the south polar regions of the Sun. Science 1995, 268, 1019. [Google Scholar] [CrossRef]
- Pikel’Ner, S.B. Structure and dynamics of the interstellar medium. Annu. Rev. Astron. Astrophys. 1968, 6, 165. [Google Scholar] [CrossRef]
- Zook, H.A. Spacecraft Measurements of the Cosmic Dust Flux. In Accretion of Extraterrestrial Matter Throughout Earth’s History; Peucker-Ehrenbrink, B., Schmitz, B., Eds.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2001; pp. 75–92. [Google Scholar]
- Meyer-Vernet, N.; Mann, I.; Le Chat, G.; Schippers, P.; Belheouane, S.; Issautier, K.; Lecacheux, A.; Maksimovic, M.; Pantellini, F.; Zaslavsky, A. The physics and detection of nanodust in the solar system. Plasma Phys. Control. Fusion 2015, 57, 014015. [Google Scholar] [CrossRef]
- Allen, C.W. Astrophysical Quantities, 3rd ed.; Athlone Press: London, UK, 1973. [Google Scholar]
- Mironova, E.N. Dust in the Solar System, Preprint No.10; Lebedev Physical Institute of RAS: Moscow, Russia, 2015. (In Russian) [Google Scholar]
- Mann, I.; Czechowski, A.; Meyer-Vernet, N.; Zaslavsky, A.; Lamy, H. Dust in interplanetary medium. Plasma Phys. Control. Fusion 2010, 52, 124012. [Google Scholar] [CrossRef]
- Kivelson, M.; Russell, C. Introduction to Space Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gosling, J.T. The Solar Wind. In Encyclopedia of the Solar System, 2nd ed.; McFadden, L.-A., Johnson, T., Weissman, P., Eds.; Academic Press: San Diego, CA, USA, 2007; pp. 99–116. [Google Scholar]
- Makarova, E.A.; Kharitonov, A.V.; Kazachevskaya, T.V. Solar Radiation Flow; Nauka: Moscow, Russia, 1991. (In Russian) [Google Scholar]
- Beirman, L. Solar corona and interplanetary space. Adv. Phys. Sci. 1966, 90, 163. [Google Scholar]
- Pudovkin, M.I. Energy transfer in the solar-terrestrial system. Rep. Prog. Phys. 1995, 58, 929–976. [Google Scholar] [CrossRef]
- Bussard, R.W. Galactic matter and interstellar flight. Acta Astronaut. 1960, 6, 179. [Google Scholar]
- Cassenti, B.N. Conceptual designs for antiproton space propulsion systems. J. Propuls. Power 1991, 7, 368. [Google Scholar] [CrossRef]
- Singh, L.A.; Walker, M.L.R. A review of research in low earth orbit propellant collection. Prog. Aerosp. Sci. 2015, 75, 15. [Google Scholar] [CrossRef]
- Whitmire, D.P. Relativistic spaceflight and the catalytic nuclear ramjet. Acta Astronaut. 1975, 2, 497. [Google Scholar] [CrossRef]
- Blatter, H.; Greber, T. Tau Zero: In the cockpit of a Bussard ramjet. Am. J. Phys. 2017, 85, 915. [Google Scholar] [CrossRef]
- Schattschneider, P.; Jackson, A.A. The Fishback ramjet revisited. Acta Astronaut. 2022, 191, 227. [Google Scholar] [CrossRef]
- Kosmodemyansky, A.A. Theoretical Mechanics Course, Part II; Prosveshchenie: Moscow, Russia, 1965. (In Russian) [Google Scholar]
- Karimov, A.R.; Terekhov, S.A.; Shikanov, A.E.; Yamschikov, V.A. Use of plasma flows to clean the near-Earth space. Plasma Phys. Rep. 2021, 47, 1038. [Google Scholar] [CrossRef]
- Raizer, Y.P. Gas Discharge Physics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Chapurin, O.; Smolyakov, A.I.; Hagelaar, G.; Raitses, Y. On the mechanism of ionization oscillations in Hall thrusters. J. Appl. Phys. 2021, 129, 233307. [Google Scholar] [CrossRef]
- Tirila, V.-G.; Demaire, A.; Ryan, C.N. Review of alternative propellants in Hall thrusters. Acta Astronaut. 2023, 212, 284. [Google Scholar] [CrossRef]
- Karimov, A.R.; Murad, P.A. Acceleration of rotating plasma flows in crossed magnetic fields. IEEE Trans. Plasma Sci. 2017, 45, 1710. [Google Scholar] [CrossRef]
- Karimov, A.R.; Murad, P.A. Plasma thruster using momentum exchange in crossed magnetic fields. IEEE Trans. Plasma Sci. 2018, 46, 882. [Google Scholar] [CrossRef]
- Karimov, A.R.; Terekhov, S.A.; Shikanov, A.E.; Murad, P.A. Acceleration of macroscopic clusters in crossed magnetic fields. IEEE Trans. Plasma Sci. 2019, 47, 1520. [Google Scholar] [CrossRef]
- Karimov, A.R.; Terekhov, S.A.; Yamschikov, V. Pulsed plasma accelerator. Plasma 2023, 6, 3. [Google Scholar] [CrossRef]
- Hall, S.J.; Jorns, B.A.; Cusson, S.E.; Gallimore, A.D.; Kamhawi, H.; Peterson, P.Y.; Haag, T.W.; Mackey, J.A.; Baird, M.J.; Gilland, J.H. Performance and high-speed characterization of a 100-kW nested Hall thruster. J. Propuls. Power 2022, 38, 40. [Google Scholar] [CrossRef]
- Mazouffre, S. Electric propulsion for satellites and spacecraft: Established technologies and novel approaches. Plasma Sources Sci. Technol. 2016, 25, 033002. [Google Scholar] [CrossRef]
- Bathgate, S.N.; Bilek, M.M.M.; Cairns, I.H.; Mckenzie, D.R. A thruster using magnetic reconnection to create a high-speed plasma jet. EPJ Appl. Phys. 2018, 84, 20801. [Google Scholar] [CrossRef]
- Lev, D.R.; Mikellides, I.G.; Pedrini, D.; Goebel, D.M.; Jorns, B.A.; McDonald, M.S. Recent progress in research and development of hollow cathodes for electric propulsion. Rev. Mod. Plasma Phys. 2019, 3, 1. [Google Scholar] [CrossRef]
- Borisevich, V.; Potanin, E.; Whichello, J.V. Plasma centrifuge with crossed E × B fields and thermally driven countercurrent flow. IEEE Trans. Plasma Sci. 2020, 48, 3472. [Google Scholar] [CrossRef]
- Gueroult, R.; Zweben, S.J.; Fisch, N.J.; Rax, J.-M. E × B configurations for high-throughput plasma mass separation: An outlook on possibilities and challenges. Phys. Plasmas 2019, 26, 043511. [Google Scholar] [CrossRef]
- M’Guire, T.J.; Sedwick, R.J. Aero-assisted orbital transfer vehicles utilizing atmosphere ingestion. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Hampton, VA, USA, 8–11 January 2001; p. 102856. [Google Scholar]
- Popel, S.I.; Kopnin, S.I.; Yu, M.Y.; Ma, J.X.; Huang, F. The effect of microscopic charged particulates in space weather. J. Phys. D Appl. Phys. 2011, 44, 174036. [Google Scholar] [CrossRef]
- Chen, F. Introduction to Plasma Physics and Controlled Fusion; Plenum: New York, NY, USA, 1984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).