Robust Control of An Inverted Pendulum System Based on Policy Iteration in Reinforcement Learning
Abstract
:1. Introduction
2. Model Formulation
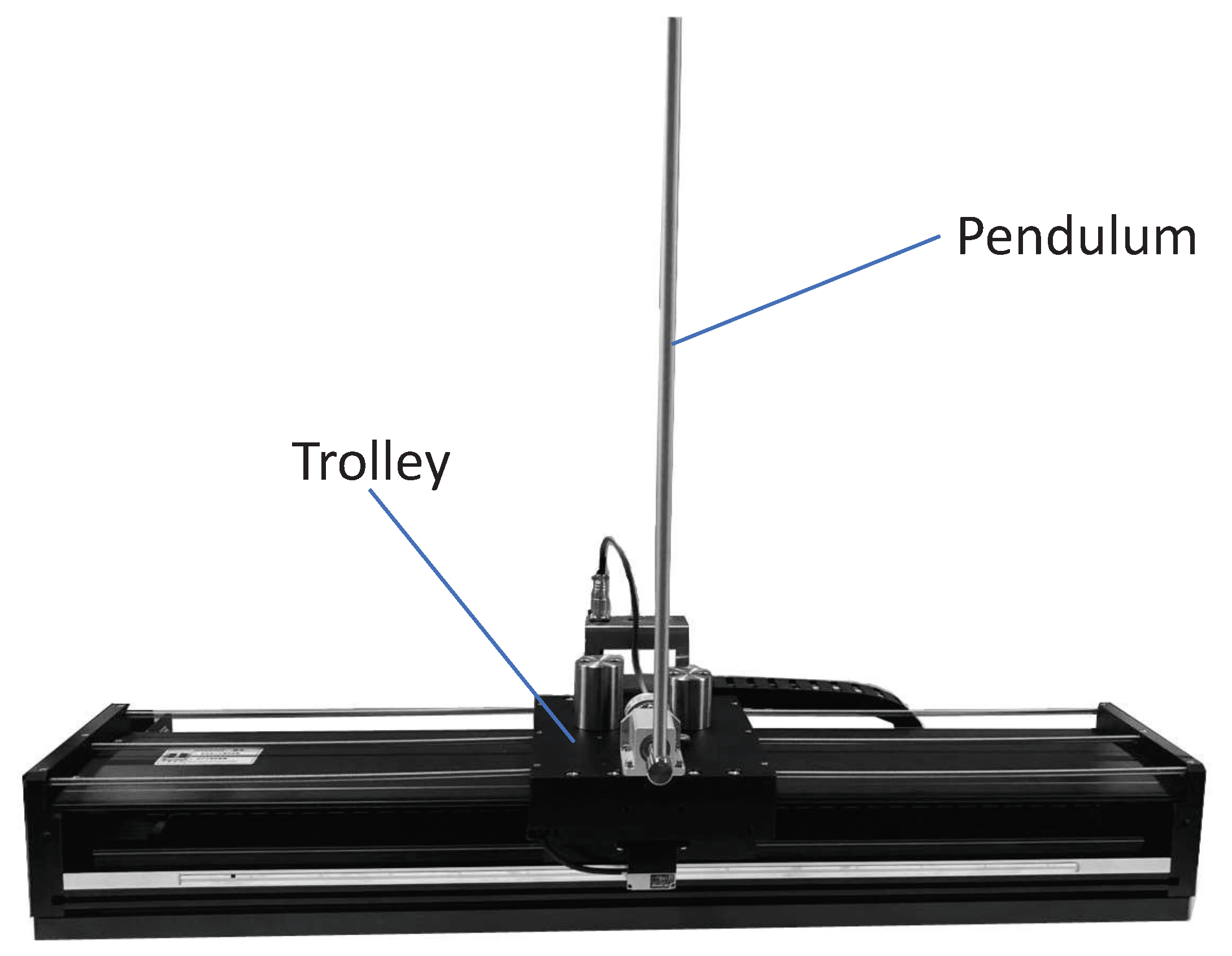
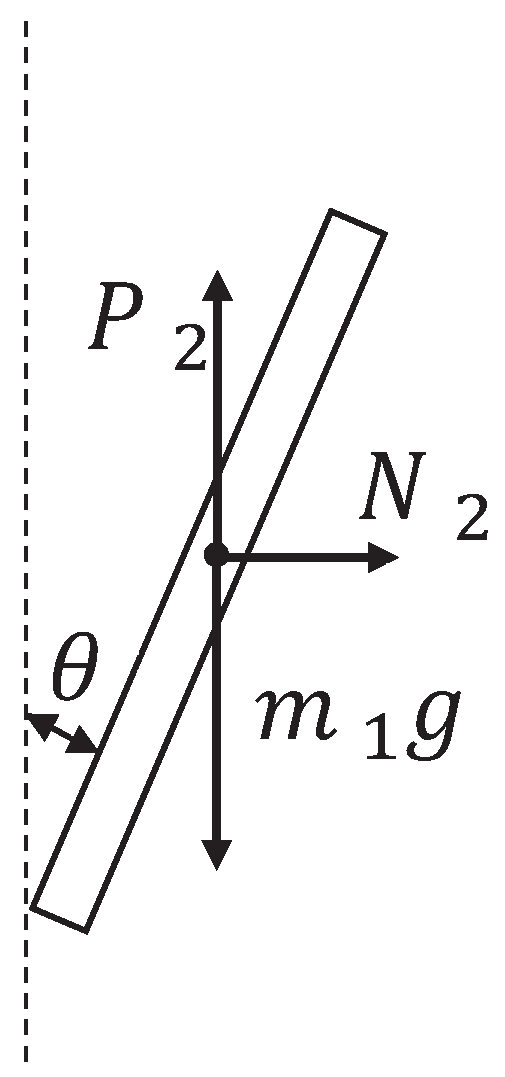
2.1. Modeling of Inverted Pendulum System
2.2. State-Space Model with Uncertainty
3. Robust Control of Uncertain Linear System
4. RL Algorithm for Robust Optimal Control
| Algorithm 1 RL Algorithm for Uncertain Linear IPS |
|
5. Robust Control of Nonlinear IPS
5.1. Nonlinear State-Space Representation of IPS
5.2. Robust Control of Nonlinear IPS
5.3. RL Algorithm for Nonlinear IPS
| Algorithm 2 RL Algorithm of Uncertain Nonlinear IPS |
|
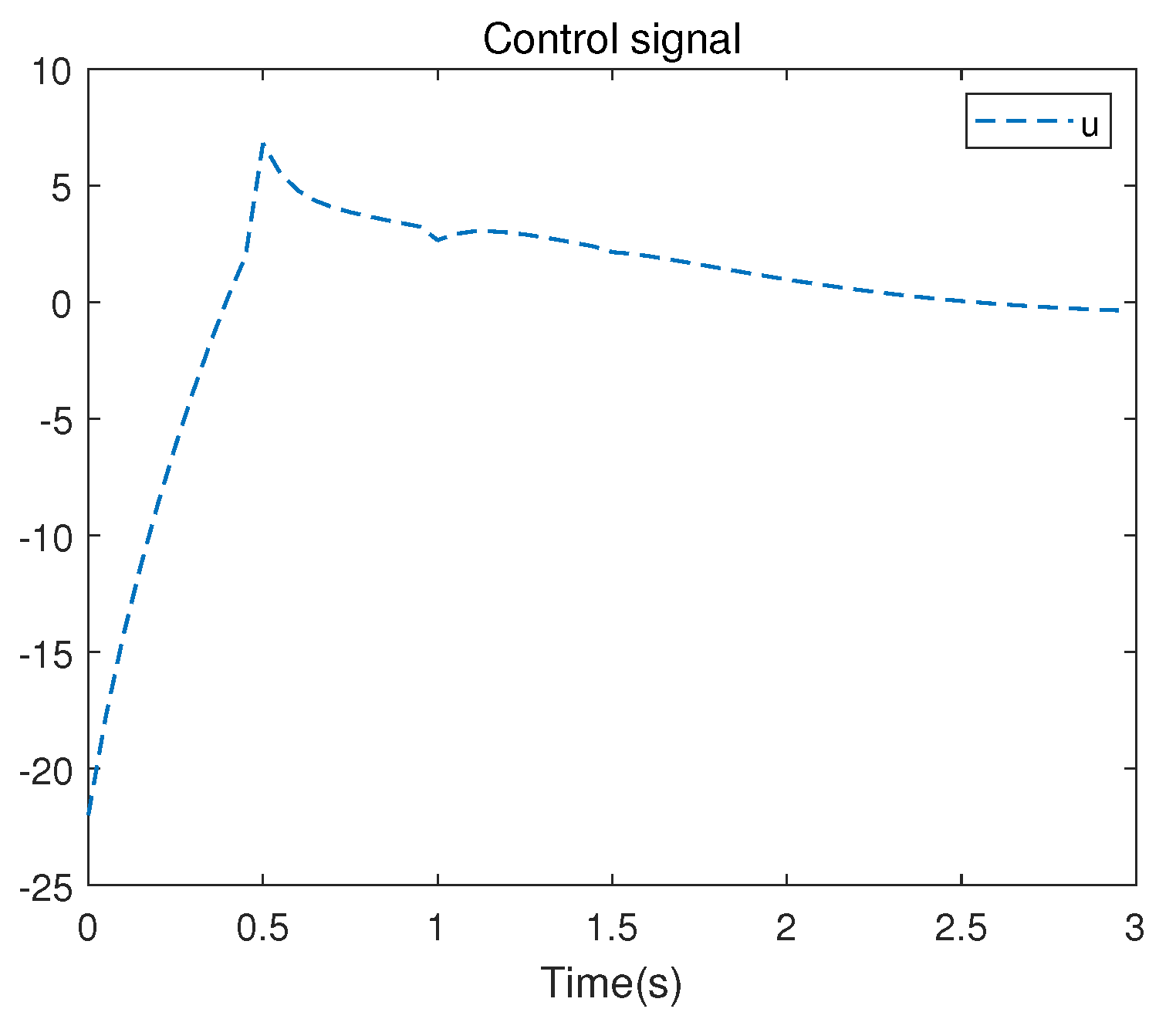
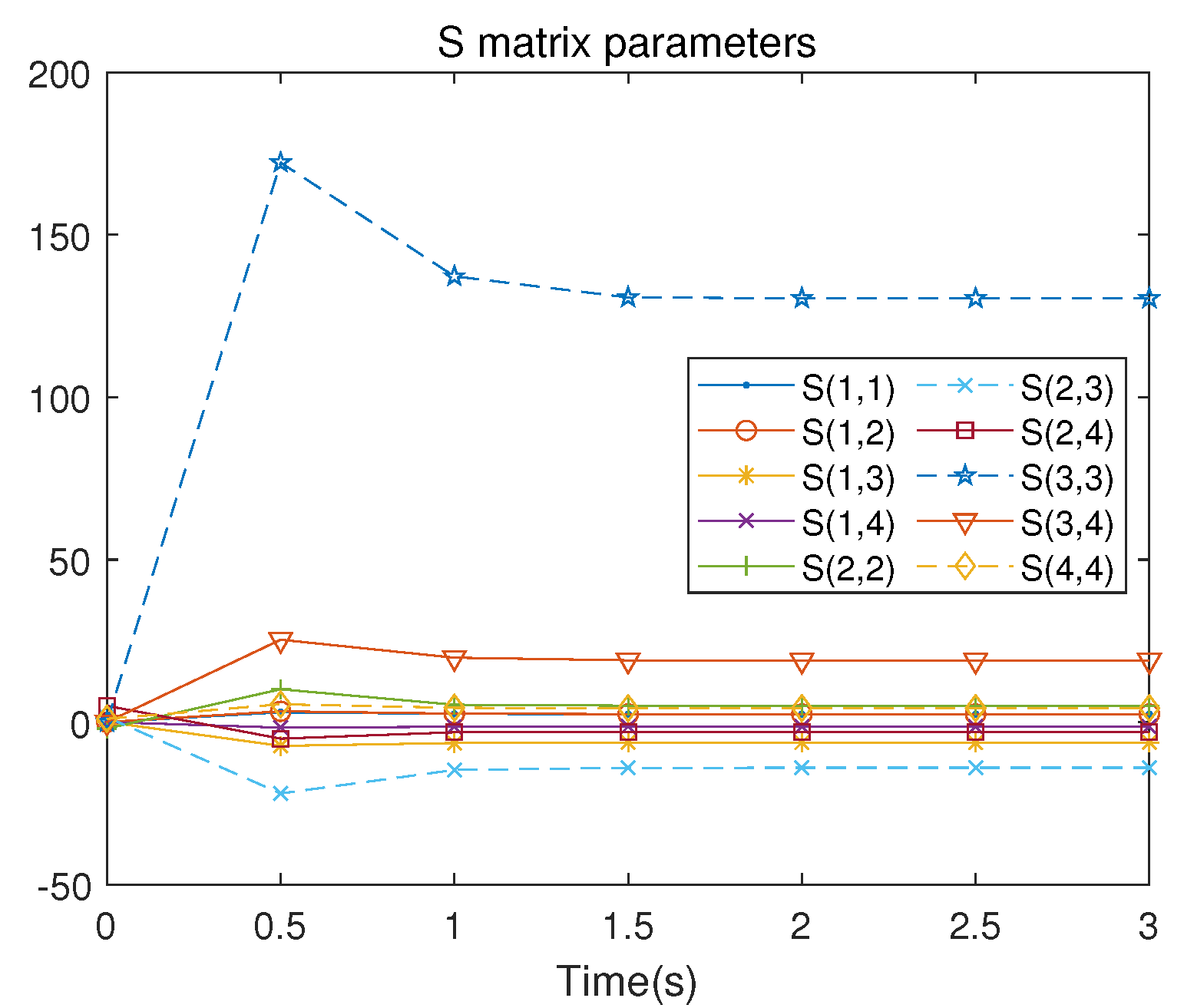
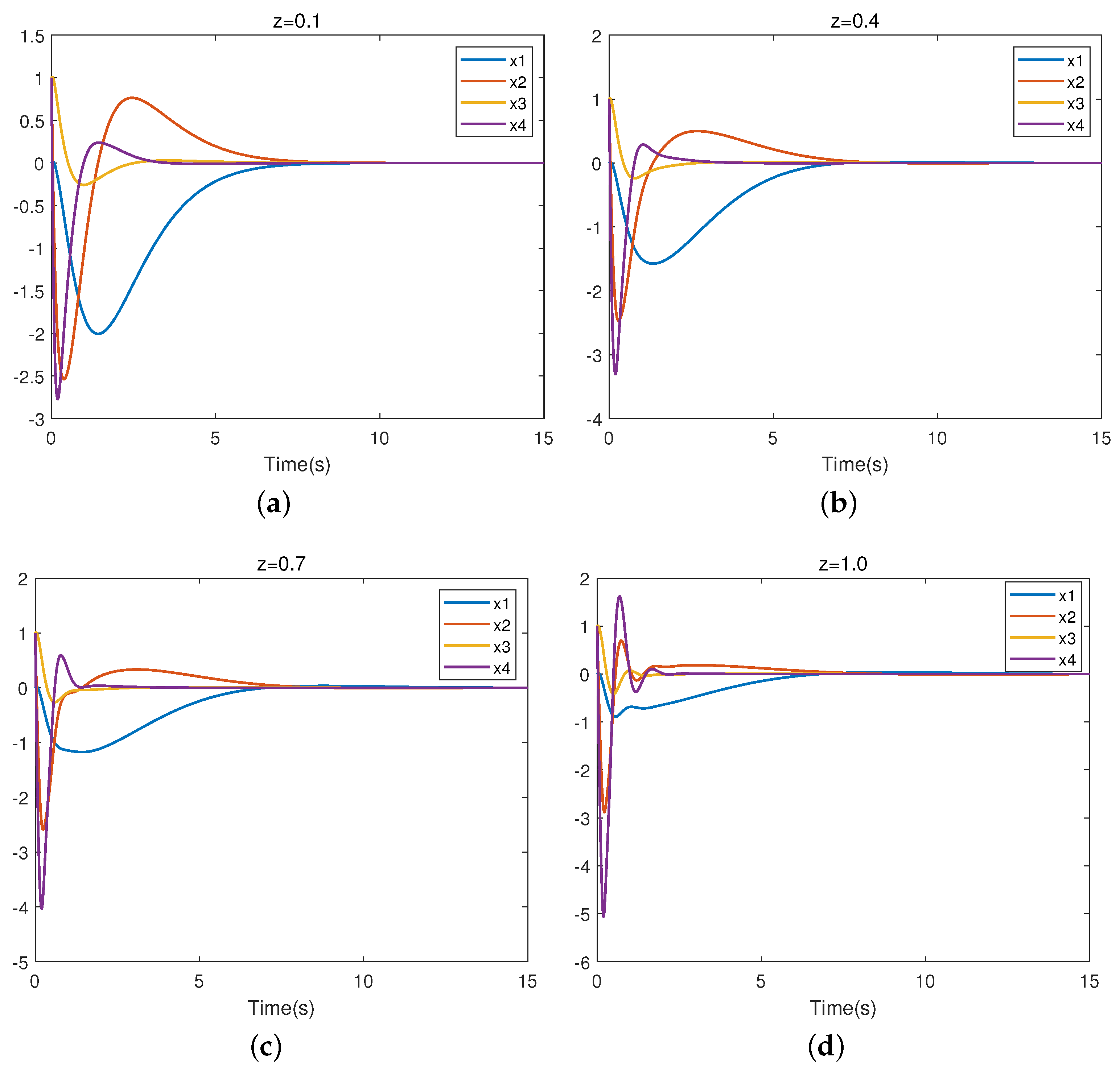
6. Numerical Simulation Results
6.1. Example 1
6.2. Example 2
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marrison, C.I.; Stengel, R.F. Design of Robust Control Systems for a Hypersonic Aircraft. J. Guid. Control Dyn. 1998, 21, 58–63. [Google Scholar] [CrossRef]
- Yao, B.; Al-Majed, M.; Tomizuka, M. High-Performance Robust Motion Control of Machine Tools: An Adaptive Robust Control Approach and Comparative Experiments. IEEE/ASME Trans. Mechatron. 1997, 2, 63–76. [Google Scholar]
- Stephenson, A. A New Type of Dynamical Stability; Manchester Philosophical Society: Manchester, UK, 1908; Volume 52, pp. 1–10. [Google Scholar]
- Housner, G.W. The behavior of inverted pendulum structures during earthquakes. Bull. Seismol. Soc. Am. 1963, 53, 403–417. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation studies of inverted pendulum based on PID controllers. Simul. Model. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
- Li, D.; Chen, H.; Fan, J.; Shen, C. A novel qualitative control method to inverted pendulum systems. IFAC Proc. Vol. 1999, 32, 1495–1500. [Google Scholar] [CrossRef]
- Nasir, A.N.K.; Razak, A.A.A. Opposition-based spiral dynamic algorithm with an application to optimize type-2 fuzzy control for an inverted pendulum system. Expert Syst. Appl. 2022, 195, 116661. [Google Scholar] [CrossRef]
- Tsay, S.C.; Fong, I.K.; Kuo, T.S. Robust linear quadratic optimal control for systems with linear uncertainties. Int. J. Control 1991, 53, 81–96. [Google Scholar] [CrossRef]
- Lin, F.; Brandt, R.D. An optimal control approach to robust control of robot manipulators. IEEE Trans. Robot. Autom. 1998, 14, 69–77. [Google Scholar]
- Lin, F. An optimal control approach to robust control design. Int. J. Control 2000, 73, 177–186. [Google Scholar] [CrossRef]
- Zhang, X.; Kamgarpour, M.; Georghiou, A.; Goulart, P.; Lygeros, J. Robust optimal control with adjustable uncertainty sets. Automatica 2017, 75, 249–259. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.; Zhang, Q.; Zhao, D. Data-based adaptive critic designs for nonlinear robust optimal control with uncertain dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 1544–1555. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Neustadt, L.W.; Pontrjagin, L.S.; Trirogoff, K. The Mathematical Theory of Optimal Processes; Interscience: London, UK, 1962. [Google Scholar]
- Powell, W.B. Approximate Dynamic Programming: Solving the Curses of Dimensionality; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 703. [Google Scholar]
- Li, H.; Liu, D. Optimal control for discrete-time affine non-linear systems using general value iteration. IET Control Theory Appl. 2012, 6, 2725–2736. [Google Scholar] [CrossRef]
- Wei, Q.; Liu, D.; Lin, H. Value iteration adaptive dynamic programming for optimal control of discrete-time nonlinear systems. IEEE Trans. Cybern. 2015, 46, 840–853. [Google Scholar] [CrossRef] [PubMed]
- Tesauro, G. TD-Gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 1994, 6, 215–219. [Google Scholar] [CrossRef]
- Singh, S.; Bertsekas, D. Reinforcement learning for dynamic channel allocation in cellular telephone systems. Adv. Neural Inf. Process. Syst. 1996, 9, 974–980. [Google Scholar]
- Maja, J.M. Reward Functions for Accelerated Learning. In Machine Learning Proceedings 1994, 1st ed.; Cohen, W.W., Hirsh, H., Eds.; Morgan Kaufmann: Burlington, MA, USA, 1994; pp. 181–189. [Google Scholar]
- Doya, K. Reinforcement learning in continuous time and space. Neural Comput. 2000, 12, 219–245. [Google Scholar] [CrossRef]
- Krstic, M.; Kokotovic, P.V.; Kanellakopoulos, I. Nonlinear and Adaptive Control Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Ioannou, P.; Fidan, B. Adaptive Control Tutorial, Vol. 11 of Advances in Design and Control; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Åström, K.J.; Wittenmark, B. Adaptive Control; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Vrabie, D.; Pastravanu, O.; Abu-Khalaf, M.; Lewis, F.L. Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 2009, 45, 477–484. [Google Scholar] [CrossRef]
- Xu, D.; Wang, Q.; Li, Y. Adaptive optimal control approach to robust tracking of uncertain linear systems based on policy iteration. Meas. Control 2021, 54, 668–680. [Google Scholar] [CrossRef]
- Xu, D.; Wang, Q.; Li, Y. Optimal guaranteed cost tracking of uncertain nonlinear systems using adaptive dynamic programming with concurrent learning. Int. J. Control Autom. Syst. 2020, 18, 1116–1127. [Google Scholar] [CrossRef]
- Bates, D. A hybrid approach for reinforcement learning using virtual policy gradient for balancing an inverted pendulum. arXiv 2021, arXiv:2102.08362. [Google Scholar]
- Israilov, S.; Fu, L.; Sánchez-Rodríguez, J.; Fusco, F.; Allibert, G.; Raufaste, C.; Argentina, M. Reinforcement learning approach to control an inverted pendulum: A general framework for educational purposes. PLoS ONE 2023, 18, e0280071. [Google Scholar] [CrossRef]
- Lin, B.; Zhang, Q.; Fan, F.; Shen, S. A damped bipedal inverted pendulum for human–structure interaction analysis. Appl. Math. Model. 2020, 87, 606–624. [Google Scholar] [CrossRef]
- Puriel-Gil, G.; Yu, W.; Sossa, H. Reinforcement learning compensation based PD control for inverted pendulum. In Proceedings of the 2018 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), Mexico City, Mexico, 5–7 September 2018; pp. 1–6. [Google Scholar]
- Surriani, A.; Wahyunggoro, O.; Cahyadi, A.I. Reinforcement learning for cart pole inverted pendulum system. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 22–23 November 2021; pp. 297–301. [Google Scholar]
- Landry, M.; Campbell, S.A.; Morris, K.; Aguilar, C.O. Dynamics of an inverted pendulum with delayed feedback control. SIAM J. Appl. Dyn. Syst. 2005, 4, 333–351. [Google Scholar] [CrossRef]
- Muskinja, N.; Tovornik, B. Swinging up and stabilization of a real inverted pendulum. IEEE Trans. Ind. Electron. 2006, 53, 631–639. [Google Scholar] [CrossRef]
- Bhatia, N.P.; Szegö, G.P. Stability Theory of Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Kleinman, D. On an iterative technique for Riccati equation computations. IEEE Trans. Autom. Control 1968, 13, 114–115. [Google Scholar] [CrossRef]
- Abu-Khalaf, M.; Lewis, F.L. Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica 2005, 41, 779–791. [Google Scholar] [CrossRef]



| Parameter | Unit | Significance |
|---|---|---|
| kg | Mass of the trolley | |
| kg | Mass of the pendulum | |
| L | m | Half the length of the pendulum |
| z | N/m/s | Friction coefficient between the trolley and guide rail |
| x | m | Displacement of the trolley |
| rad | Angle from the upright position | |
| I | kg·m2 | Moment of inertia of pendulum |
| z | ||||
|---|---|---|---|---|
| 0.1 | −6.60 | −4.23 | −0.85 + 0.32i | −0.85 − 0.32i |
| 0.2 | −6.73 | −4.33 | −0.78 + 0.43i | −0.78 − 0.43i |
| 0.3 | −6.86 | −4.41 | −0.71 + 0.50i | −0.71 − 0.50i |
| 0.4 | −7.00 | −4.48 | −0.65 + 0.55i | −0.65 − 0.55i |
| 0.5 | −7.14 | −4.54 | −0.60 + 0.59i | −0.60 − 0.59i |
| 0.6 | −7.28 | −4.59 | −0.55 + 0.62i | −0.55 − 0.62i |
| 0.7 | −7.42 | −4.63 | −0.50 + 0.65i | −0.50 − 0.65i |
| 0.8 | −7.56 | −4.67 | −0.46 + 0.67i | −0.46 − 0.67i |
| 0.9 | −7.70 | −4.70 | −0.42 + 0.68i | −0.42 − 0.68i |
| 1.0 | −7.84 | −4.73 | −0.38 + 0.69i | −0.38 − 0.69i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Xu, D.; Huang, J.; Li, Y. Robust Control of An Inverted Pendulum System Based on Policy Iteration in Reinforcement Learning. Appl. Sci. 2023, 13, 13181. https://doi.org/10.3390/app132413181
Ma Y, Xu D, Huang J, Li Y. Robust Control of An Inverted Pendulum System Based on Policy Iteration in Reinforcement Learning. Applied Sciences. 2023; 13(24):13181. https://doi.org/10.3390/app132413181
Chicago/Turabian StyleMa, Yan, Dengguo Xu, Jiashun Huang, and Yahui Li. 2023. "Robust Control of An Inverted Pendulum System Based on Policy Iteration in Reinforcement Learning" Applied Sciences 13, no. 24: 13181. https://doi.org/10.3390/app132413181
APA StyleMa, Y., Xu, D., Huang, J., & Li, Y. (2023). Robust Control of An Inverted Pendulum System Based on Policy Iteration in Reinforcement Learning. Applied Sciences, 13(24), 13181. https://doi.org/10.3390/app132413181






